E-mail Alert
RSS
-
摘要:
携带角动量的矢量光场在微粒操控、光通信与显示、光学信息加密、高维量子信息处理等领域具有广阔应用。然而，传统的方法实现矢量光场调控通常需要使用多个级联的光学元件，如螺旋相位板、偏振片、四分之一波片、涡旋波片、空间光调制器等，导致器件体积庞大，不符合未来光子器件集成化的需求。超构表面的快速发展为集成化矢量光场调控器件的实现提供变革性解决方案。本文概述了国内外基于超构表面的矢量光场调控和检测的相关研究进展。在此基础上，系统总结了现阶段超构表面矢量光场在微粒操控、边缘增强成像、全息显示以及机器视觉等领域的应用。最后，我们对全文进行了总结和讨论，并提出超构表面矢量光场所面临的挑战和未来发展方向。
Abstract:The vector light field carrying angular momentum finds wide applications in various fields, such as particle manipulation, optical communication and display, optical information encryption, and high-dimensional quantum information processing. However, the conventional approach to vector light field regulation typically involves a series of cascaded optical elements, such as spiral phase plates, polarizers, quarter wave plates, vortex wave plates, spatial light modulators, etc., resulting in a bulky device that does not meet the requirements for future photonic device integration. The rapid development of metasurfaces offers a transformative solution for realizing integrated meta-devices for vector light field control. In this paper, we summarize the research progress on metasurface-based control and detection of vector light fields. Then, we systematically summarize the current applications of metasurface-based vector light fields in particle manipulation, edge enhancement imaging, holographic display, machine vision, and so on. Finally, we have summarized and discussed the full text as well as the challenges and provided an outlook on this emerging field.
-
Key words:
- metasurface /
- vector field /
- polarization /
- regulation
-
Overview: The vector light field carrying angular momentum finds wide applications in various fields such as particle manipulation, optical communication and display, optical information encryption, and high-dimensional quantum information processing. However, the conventional approach to vector light field regulation and detection typically involves a series of cascaded optical elements, such as spiral phase plates, polarizers, quarter wave plates, vortex wave plates, spatial light modulators, etc., resulting in a bulky device that does not meet the requirements for future photonic device integration. Metasurfaces, which are subwavelength spatially arrayed nanostructures at an interface, possess the ability to accurately control the abundant physical dimensions of light, including phase, amplitude, wavelength, polarization, and angular momentum. Owning to the unprecedented wavefront manipulation capacities, metasurfaces have enabled a series of highly compact and efficient meta-devices. The rapid development of metasurfaces also offers a transformative solution for realizing integrated meta-devices for vector light field control. In this paper, we summarize the research progress on metasurface-based control and detection of vector light fields. The basic principle and typical design strategy for vector light field modulation and detection are introduced in detail. For vector light field modulation, we review the principles and methods of generating vortex light field (donut distribution of light field energy) and vector holography (various patterns of light field energy), respectively. For vector light field detection based on metasurfaces, we introduce the development process from angular momentum detection to total Stokes parameters detection. Then, we systematically summarize the current applications of metasurface-based vector light fields in particle manipulation, edge enhancement imaging, holographic display, machine vision, and so on. Finally, we have summarized and discussed the full text as well as the challenges and provided an outlook on this emerging field.
-
1. 引 言
作为电磁波的基本特性之一，偏振表征了电磁波电场振荡的矢量性质，决定着电磁波与物质的相互作用，在通讯、遥感、成像及显微等诸多领域具有重要应用[1-2]。根据偏振的空间分布，可以将光束分为标量光束(偏振均匀分布)和矢量光束，其中矢量光束是指偏振非均匀分布的光束，譬如柱矢量光束[3]。矢量光场在突破衍射极限聚焦、微粒操控、多通道全息技术、自由空间和光纤通信、非线性光转换、手性传感和量子信息处理等领域展现出独特的应用[4-9]。然而，传统的方法实现矢量光场调控通常需要使用多个级联的光学元件，譬如螺旋相位板、偏振片、四分之一波片、Q-plate、空间光调制器(spatial light modulator，SLM)和数字微镜器件(digital mirror device，DMD)等，导致器件体积庞大，难以满足未来光子器件集成化的需求。
超构表面是一种人工制造的二维电磁材料，其物理特性可以突破自然材料的极限，在实现对光几乎无限制操控方面提供了一个理想平台[10-12]。与传统材料完全不同，超构表面实现相位调制的机理源于亚波长尺寸单元的相位突变，而非传统材料在传播路径上的相位积累。通过调制亚波长单元的拓扑形状、尺寸和空间排布，超构表面可以在亚波长尺度内实现对光子多个物理维度(波长、相位、振幅、偏振等)的任意调控[13]。因此，它的出现为光子器件的多功能化、小型化和集成化提供了变革性解决方案[2,14-15]。基于超构表面优越的波前调控特性，近年来科研工作者在理论和实验上取得了一系列重要成果，譬如异常反射与折射[10,16]、光学全息[17-22]、光学霍尔效应[23-24]、光学超构透镜[25-29]，以及偏振调控[2,30-33]等。超构表面研究的快速发展也为集成化矢量光场调控、检测以及应用器件的实现提供重大契机。一方面，超构表面亚波长的单元结构尺寸可以有效减小器件的尺寸(将SLM和DMD的微米级像素单元减小为纳米级)，有利于器件的小型化和集成化。另一方面，超构表面独特的相位调控机制可以实现像素化的偏振调控，与矢量光场偏振特性分布具有天然的契合度，同时也可以提升器件的空间调制精度。迄今为止，国内外学者基于超构表面对矢量光场开展了深入研究，并取得了一系列有意义的成果[3,34-38]。
本综述中，我们首先介绍矢量光束的基本定义及表征方法。然后系统总结基于超构表面矢量光场调控、检测以及应用方面的相关研究进展，并详细介绍了其基本原理和典型的设计策略。对于超构表面矢量光场调控，分别综述了涡旋光场(光场能量呈现甜甜圈分布)和矢量全息(光场能量呈现各种各样的图案)的产生原理与方法。针对超构表面矢量光场的检测，介绍了从角动量检测到全斯托克斯参数检测的发展历程。在此基础上，我们系统总结了现阶段超构表面矢量光场在微粒操控、边缘增强成像、全息显示以及机器视觉等领域的应用。最后，对全文进行了总结和讨论，并提出了超构表面矢量光场所面临的挑战与未来发展方向。
2. 矢量光束的定义及表征
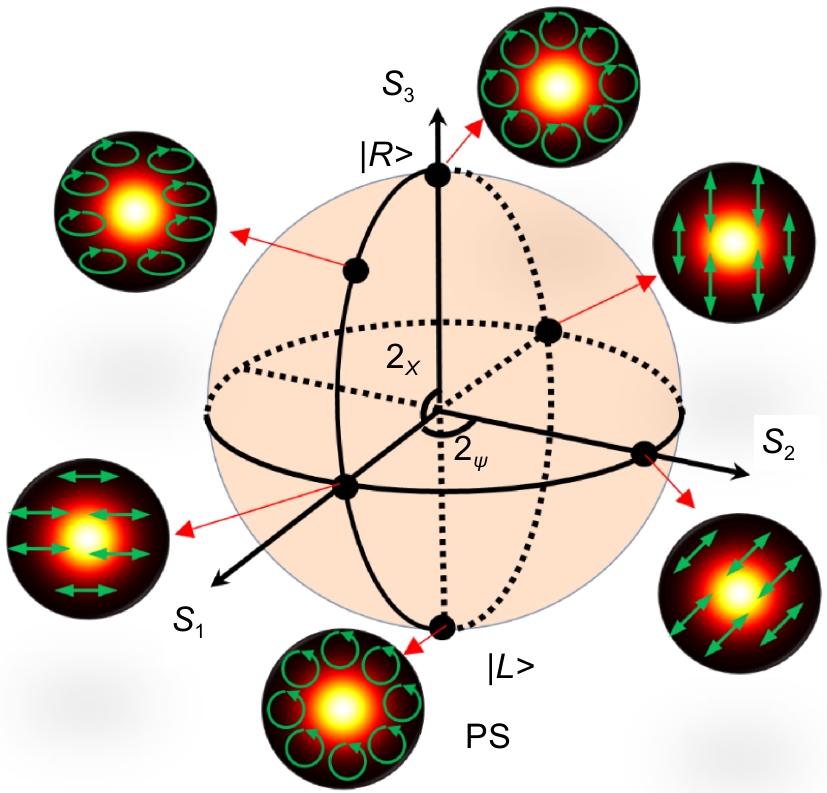
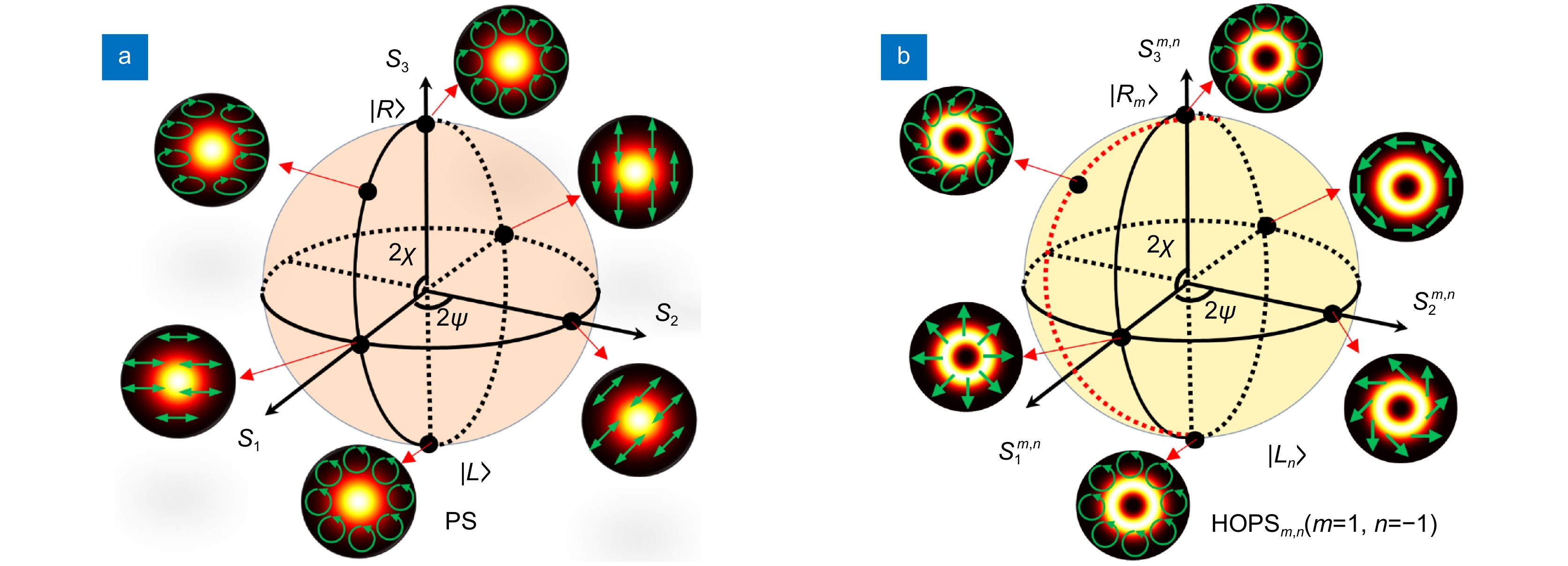
为了在数学上准确地描述电磁波的偏振态，Poincaré在1892年提出了一种几何表示方法，称为庞加莱球(Poincaré sphere, PS)[39]。该方法利用斯托克斯(Stokes)参数(S0, S1, S2, S3)将偏振态映射到PS的球面上，从而统一了所有呈现空间均匀分布的偏振态(圆偏振、线偏振和椭圆偏振)，如图1(a)。PS上光束的偏振态空间各处都一样，因而也通常被称为标量光束。然而，PS局限于描述具有空间均匀偏振分布的光束。为了表示具有空间非均匀偏振分布的矢量光束(譬如矢量涡旋光束)，研究人员提出了一种扩展的广义几何表示方法，称为高阶庞加莱球(higher-order Poincaré sphere, HOPS)[40-42]。与PS相比，HOPS的南北两极分别表示螺旋性相反的右旋涡旋和左旋涡旋圆偏振态，球面上任意一点对应的偏振态表示为两者的线性叠加，如图1(b)。值得注意的是，携带轨道角动量的涡旋光束也通常被认为是矢量光束(因为其能量零点处的偏振态也为零，偏振呈现空间非均匀分布)。对于HOPS上的任意光束，其琼斯矢量可以表示成两个圆偏振涡旋态的叠加[40-41]：
图 1. (a)标准庞加莱球及其典型标量光束表示；(b)高阶庞加莱球及其典型矢量光束表示，此处展示1阶庞加莱球Figure 1. (a) Representation of typical scalar beams on the standard PS; (b) Representation of typical vector beams on the HOPS. Here we choose the 1-order HOPS as an example|ψm,n⟩=AmR|Rm⟩+AnL|Ln⟩, (1) 式中:
\left| {{R_m}} \right\rangle = \exp ({\mathrm{i}}m\varphi )( {\boldsymbol{x}}-{\rm{i}}\sigma {\boldsymbol{y}})/\sqrt 2 \;, (2) \left| {{L_n}} \right\rangle = \exp ({\mathrm{i}}n\varphi )( {\boldsymbol{x}}{\text{ + }}{\rm{i}}\sigma {\boldsymbol{y}})/\sqrt 2 \;, (3) 式中：\left| {{R_m}} \right\rangle 和\left| {{L_n}} \right\rangle 表示两个圆偏振涡旋光，它们的拓扑电荷数分别为m和n。x和y表示沿x和y轴方向的单位矢量，σ为光子自旋，φ=arctan(y/x)表示方位角。因此，通过选取一套合适的系数 A_{\rm{R}}^m 和 A_{\rm{L}}^n , HOPS上的任意光束都可以表示为两个圆偏振涡旋光的线性叠加。对于HOPS上的任意光束，相应的斯托克斯(Stokes)参数在球坐标系下可以表示为[40]
S_0^{m,n} = {\left| {A_{\rm{R}}^m} \right|^2} + {\left| {A_{\rm{L}}^n} \right|^2} \;, (4) S_1^{m,n} = 2\left| {A_{\rm{R}}^m} \right|\left| {A_{\rm{L}}^n} \right|\cos (\phi )\;, (5) S_2^{m,n} = 2\left| {A_{\rm{R}}^m} \right|\left| {A_{\rm{L}}^n} \right|\sin (\phi ) \;, (6) S_3^{m,n} = {\left| {A_{\rm{R}}^m} \right|^2}-{\left| {A_{\rm{L}}^n} \right|^2} \;, (7) 式中： {\left| {A_{\rm{R}}^m} \right|^2} 和 {\left| {A_{\rm{L}}^n} \right|^2} 分别对应\left| {{R_m}} \right\rangle 和\left| {{L_n}} \right\rangle 的能量强度， \phi = \arg (A_{\rm{R}}^m) - \arg (A_{\rm{L}}^n) 表示两个圆偏振涡旋光之间的相位差。
3. 超构表面矢量光场调控
3.1 超构表面矢量光束研究现状
超构表面可以在亚波长尺度操控光子的多个自由度，为集成化矢量光场调控提供全新平台。值得注意的是，携带轨道角动量的涡旋光束也通常被视为矢量光束。本节中，我们主要关注能量呈现甜甜圈分布的矢量光束。近年来，国内外科研工作者基于超构表面开展了一系列矢量光束产生的研究工作，在微粒操控、光通信、显示和信息加密等领域具有潜在应用[3,34,43-45]。
2011年，Capasso教授团队首次提出超构表面概念，利用V形金属纳米结构实现了相位突变，并以此构建特定相位梯度验证了广义的折反射定律[10]。并在此基础上，沿着角向构建分区的相位梯度，成功实现了0到2π的相位覆盖。在入射平面高斯光下，实现了拓扑电荷数为l=1的涡旋光束，如图2(a)所示。拓扑电荷数可以通过其与斜入射的平面高斯光束或者共轴传播的高斯球面光束干涉来识别。为了解决等离子体器件效率相对较低的问题，Yang等人提出了一种杂化的介质金属结构，在宽波段(1500~1600 nm)范围内实现了高效率的交叉极化涡旋光束[46]。除了表面等离子体的吸收损耗外，离散结构的非连续相位调控也是导致效率受限和OAM纯度受限的一个主要原因。为了克服这些局限，连续型微纳结构应运而生，在宽带高效光束调控和OAM产生方面发挥了重要作用[47-50]。Pu等人基于连续型悬链线结构的连续相位调控，在宽带范围内实现了消色差的完美OAM光束产生[47]。基于自旋-轨道相互作用可以产生不同拓扑荷数的涡旋光束，但是普遍存在一个限制：左右旋圆偏振光只能产生拓扑荷数相反的涡旋光束(类似于传统的Q-plate)。为了克服这一局限，国内外科研工作者通过结合结构的几何相位和传输相位，实现了自旋解耦合的相位调控，为任意拓扑电荷数的OAM产生提供前提条件[45,51-52]。Capasso教授团队提出了一个全新的超构表面OAM生成工具—J-plate，它可以将任意正交偏振对转化为具有独立拓扑电荷值的两束涡旋光，如图2(b)所示[45]。另一方面，完美涡旋光束的环形强度分布独立于拓扑电荷，在粒子操纵和光纤通信方面具有潜在应用前景。Bao等人基于多原子组合超构表面并结合优化算法实现了独立的振幅、相位和偏振调控，并基于此展示了不同拓扑荷的完美矢量涡旋光束，如图2(c)所示[53]。Liu等人基于自旋复用的超构表面，协同调控传输相位与几何相位，在宽带范围内实现了完美庞加莱球矢量光束的产生，如图2(d)所示[54]。在此基础上，Ahmed等人基于超构表面与旋转的波片，展示了杂交嫁接完美矢量涡旋光的动态调控，该矢量光场具有空间变化的偏振变化率，如图2(e)所示[55]。前面讨论的涡旋光束均基于超构表面像素化的相位调制，实现2lπ的相位覆盖范围通常需要大量的单元结构，从而导致器件的尺寸较大。Chen等人基于四元体超构表面全新的相位调控机制，有效克服这一难题，并实现了高效率的涡旋光束，如图2(f)所示[56]。其相位来源于耦合纳米柱中不同传播模式的杂交在间隙内产生的相位梯度，从而可以在亚波长的四元体内实现2lπ的相位变化。
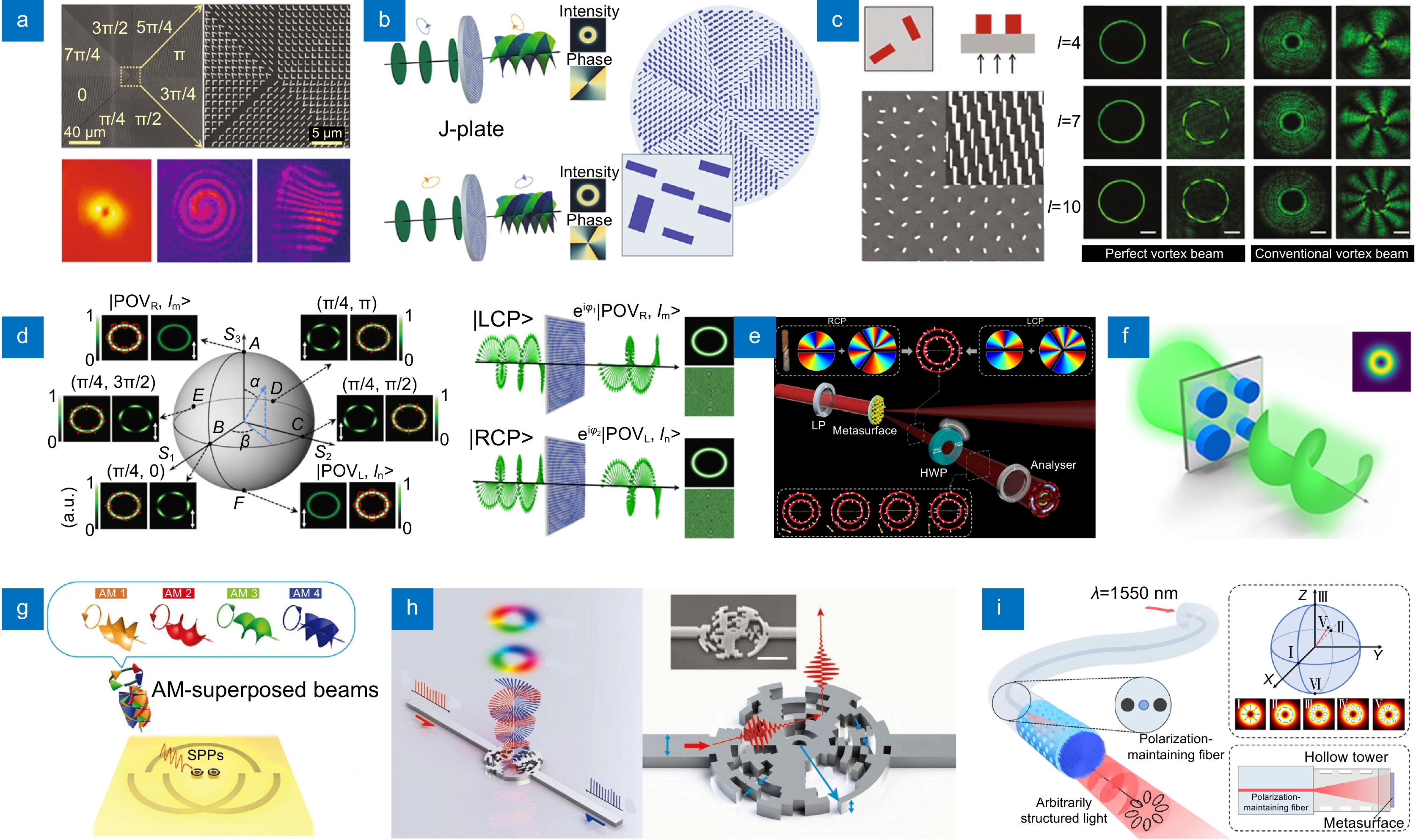Figure 2. Current researches on metasurface vector beam regulation. (a) SEM image of the plasmonic vortex beam generator and the measured far-field intensity profiles[10]; (b) Schematic and operating concept of the J-plate that converts an arbitrary pair of orthogonal polarization states into two beams with independent values of topological charges[45]; (c) Generation of perfect vector vortex beams with various topological charges via a composite element metasurface[53]; (d) Schematic of generating broadband perfect Poincaré sphere vector beams[54]; (e) Dynamic generation of hybrid grafted perfect vector vortex beams[55]; (f) Schematic of the meta-quadrumer for vortex generation[56]; (g) Schematic of the nano-ring aperture unit for on-chip noninterference AM multiplexing[59]; (h) Schematic of a silicon-based OAM emitter[60]; (i) Schematic of generating arbitrarily structured light on meta-fibers[3]与此同时，受实际应用需求驱动，近年来国内外科研工作者基于超构表面开发了一系列片上矢量光束产生器件[57-62]。Ren等人基于纳米环形孔径单元实现了片上无干扰角动量复用器，该器件可以产生多个轨道角动量(orbital angular momentum, OAM)叠加的涡旋光束，如图2(g)所示[59]。通过金属薄膜上纳米环形切口选择性地耦合出不同的OAM模式，该器件可以在超过150 nm的带宽范围内实现片上并行OAM复用。尽管该器件可以在宽带范围内实现OAM的复用，金属本征的欧姆损耗会影响器件的最终性能。为了克服效率局限，Xie等人基于逆向设计的优化方法提出了超宽带的片上OAM发射器，如图2(h)所示[60]。该发射器的半径仅有几十微米，并且能够在1450到1650 nm的带宽范围内发射同轴OAM光束。这些结果在片上和超快光子信息处理领域具有潜在应用。此外，Li等人利用3D打印技术，在光纤端面上直接制备超构表面结构。这些超构表面可以在光纤端输出不同的结构光场，包括圆柱矢量光束，圆偏振涡旋光束和任意矢量光场，如图2(i)所示[3]。该工作为光纤科学技术的发展提供了一个范例，在光纤通信、光纤激光器和传感器、内窥镜成像、光纤光刻技术等领域具有重要的应用。上述OAM光束产生都在沿传输轴特定的平面上，这也会在某种程度上限制其应用。为此，科研工作者基于特定的超构表面结构，实现了沿轴上变化的OAM光场[63-66]，为矢量光场的应用拓展提供新的可能。
3.2 超构表面矢量全息研究现状
此外，另一种具有空间非均匀偏振分布的矢量光场—矢量全息，也受到了科研工作者广泛关注[67-71]。本节中，我们主要回顾能量呈现特定图案分布的超构表面矢量全息。Mueller等人基于琼斯矩阵原理，结合传输相位与几何相位实现了任意正交偏振(线偏、圆偏或椭偏)下的独立相位调制[72]。该功能通过控制超构表面原子的面内尺寸以及面内旋转角度实现，并基于该原理展示了圆偏振可切换的矢量全息切换，可以实现“卡通猫”和“卡通狗”的切换，如图3(a)所示。正交偏振调制方法被普遍认为是理所当然的，这在某些情况下会限制器件的功能，譬如该先验性会降低了全息信息编码的安全性。为了解决这一问题，Deng等人采用组合单元结构将这一限制解锁为任意非正交偏振通道[73]。作为概念验证，他们展示了一种能够在任意非正交偏振通道编码两种灰度图像的超构表面。为了进一步拓展矢量全息偏振通道数，Hu等人通过巧妙地求解琼斯矩阵，可以在三个线偏振通道上实现独立的相位调控[74]。此外，通过组合三偏振通道与三原色，展示了一只鹦鹉的全彩色矢量全息图像，如图3(b)所示。
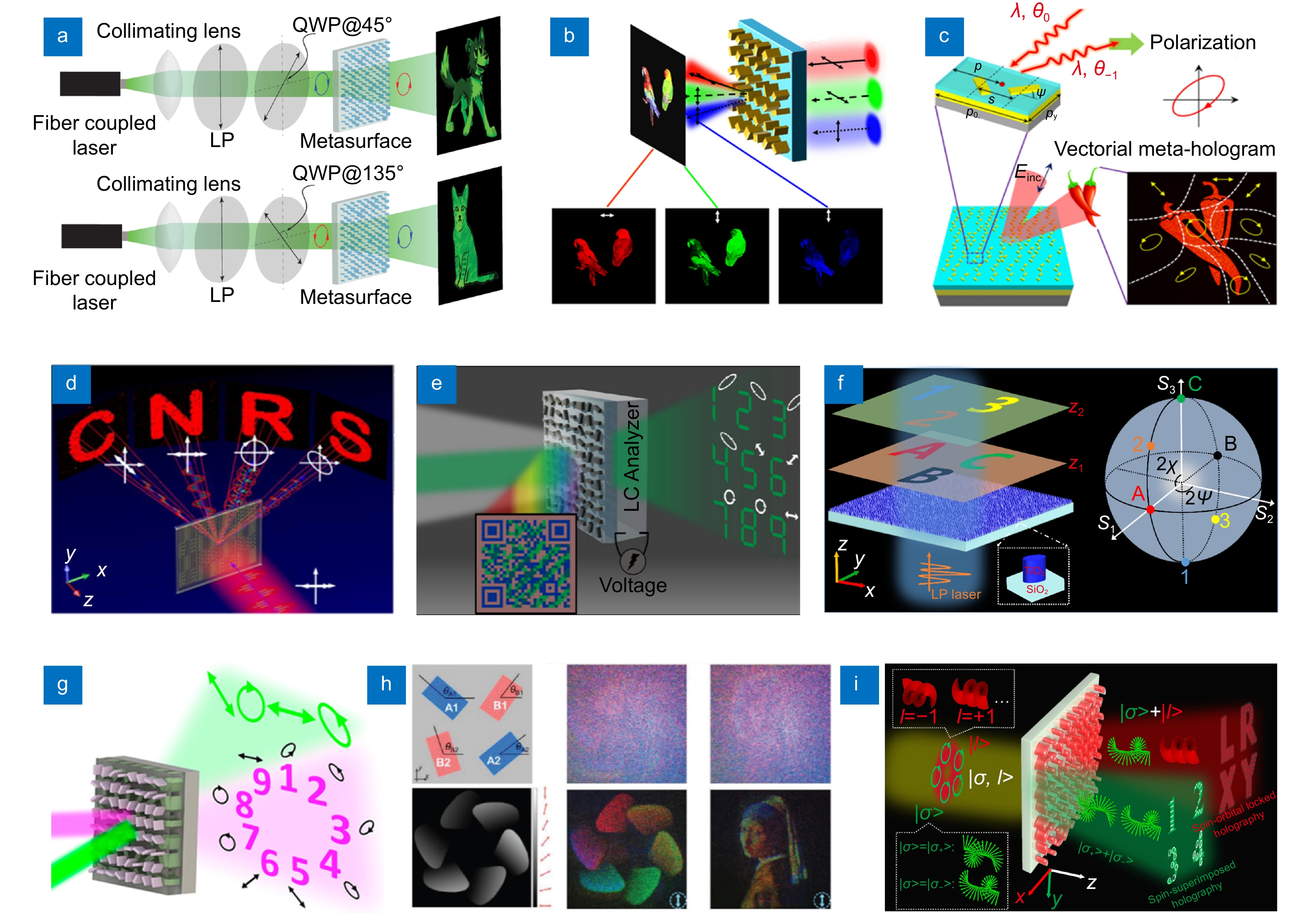Figure 3. Current researches on metasurface vectorial holography. (a) Schematic of the orthogonal circularly polarization switchable metasurface hologram[72]; (b) Demonstration of three LP channel multiplexing for vectorial full color holographic display[74]; (c) Full-polarization vector holography based on diatomic metasurfaces[75]; (d) Broadband full-polarization vector holography based on geometric phase metasurfaces[76]; (e) Liquid crystal integrated color printing and vector holographic dual-function meat-devices[77]; (f) Schematic of the 3D full-polarization vectorial holography based on noninterleaved metasurfaces[78]; (g) Illustration of the dual-wavelength vectorial meta-hologram[79]; (h) Schematic of the color full-polarization vectorial hologram[80]; (i) Schematic of the angular momentum holography via a minimalist metasurface[81]尽管矢量全息取得了一系列可观的进展，但是上述报道的矢量全息无法实现全偏振通道。为了克服这一限制，Deng等人利用相互垂直的双原子单元超构表面，在斜入射条件下实现了全偏振通道的矢量全息，并展示了矢量全息在信息防伪领域的应用，如图3(c)所示[75]。该器件中，两个超构表面原子的相对位置和取向角可以精心设计以实现相位和偏振的调控，从而产生具有任意偏振分布的全息图图像。为了克服该器件中金属的本征损耗并拓展其工作波长，Song等人利用组合的介质几何相位单元实现了宽带的全偏振矢量全息，并基于叠层成像技术测定了全息图像的空间偏振分布[76]，如图3(d)所示。该课题组制备了超构表面器件并在空间不同的衍射角度实现了高效率的四幅矢量全息图像。在此基础上，Kim等人进一步拓展其功能，实现了具有彩色打印和全偏振矢量全息的双功能器件，并结合液晶展示了一个双重动态加密平台，如图3(e)所示[77]。所有这些报道中提到的全偏振矢量全息都基于组合的单元结构，这会引入不可避免的串扰，此外，这些矢量全息的能量分布全部局限于二维平面。为了突破这些限制，Yang等人基于非交错的超构表面实现了三维全偏振通道的矢量全息，其功能展示如图3(f)所示[78]。该实现策略基于对两个自旋本征态的独立相位调控，然后通过在工作通道上任意叠加不同功能的自旋本征态，从而实现全偏振矢量全息。此外，光子的其他维度譬如波长和角动量也得到开发，以进一步拓展矢量全息的复用通道数。Kim等人通过独立设计双层超构表面结构，实现了能够同时工作于可见和紫外波长的矢量全息，其功能示意图如图3(g)所示[79]。超构表面全息图在紫外线光(波长为325 nm)下呈现出九个矢量全息图像，在绿光(波长为532 nm)下展现独立全息图像，并基于此展示了一个双层加密和解密的平台。Guo等人进一步拓展波长自由度，利用四个原子组合的超构表面相位结构实现了全彩色的全偏振通道矢量全息，并展示了信息加密应用，如图3(h)所示[80]。Yang等人将角动量自由度引入矢量全息，基于极简的超构表面展示了角动量全息，其功能如图3(i)所示[81]。该角动量全息源于对自旋和轨道角动量的任意协同调控，自旋与轨道角动量的叠加可以实现自旋-轨道锁定的全息，自旋-自旋的叠加可以获得全偏振矢量全息，并基于这两套独立的全息展示了一个高容量和高安全性的嵌套加密平台。
4. 超构表面矢量光场检测
正如前文所述，矢量光场在诸多领域具有潜在应用，因此快速而有效地实现矢量光束偏振态的测定具有非常重要的现实意义。根据第二部分的内容可知，任意矢量光束偏振态的测定可以转化为光学奇点(自旋和轨道角动量)以及Stokes参数的精确测定。传统方法通常利用组合光学元件 (比如光学波片、分束器和探测器、Q片、叉形光栅等)测量不同正交偏振态下的能量强度和光学奇点，并通过反演计算实现Stokes参数的精确测定。然而，传统的偏振态测定方法引入了一系列的光学元件，这也会导致庞大的测试系统和复杂的测量过程，不符合光子器件小型化和集成化趋势。超构表面的迅速发展促进了集成化矢量光束检测器件的发展，可以部分或完全实现矢量光束偏振态的精确测定[2,82-86]。这些矢量光束检测器件不仅简化了传统的测定过程，而且其亚波长尺寸能更好地符合光子器件集成化趋势。
首先，我们回顾了近年来基于超构表面的光学奇点检测器件。Mei等人基于半环形等离子体纳米狭缝结构，实现了片上OAM模式探测，如图4(a)所示[83]。当拓扑电荷为l的圆偏振涡旋光束入射时，相当于对半环形等离子体纳米狭缝沿角向赋予了2lπ的相位，可以视为一个半圆形光源。因此，该纳米狭缝能够将不同OAM模式光束在空间上分为模式间隔约为120 nm的不同焦点。尽管可以实现OAM的检测，但是该器件需要严格的对准，这会限制其实际应用。为此，Chen等人设计了一个由等离子体纳米光栅结构组成的OAM检测器，可以将入射的OAM光束耦合成两个具有不同劈裂角度的表面等离子波，通过分析劈裂角度实现OAM的检测，该器件的示意图如图4(b)所示[87]。为了实现自旋角动量(spin angular momentum, SAM)和OAM的同时检测，Feng等人提出了一个基于自旋-霍尔超光栅结构的奇点检测器件，如图4(c)所示[86]。该器件对入射矢量光束的自旋敏感，可以同时实现入射光束相位和偏振奇点的检测(即SAM和OAM的同步测定)。除片上矢量光束检测器件外，科研工作者同样在自由空间也进行了一系列的探索[84-85,88]。Li等人利用自旋解耦合的超构表面结构，设计自旋复用的角透镜，实现了SAM和OAM的同时检测，如图4(d)所示。在此基础上，他们进一步拓展了器件的检测范围，可以检测的OAM模式数高达250[89]。
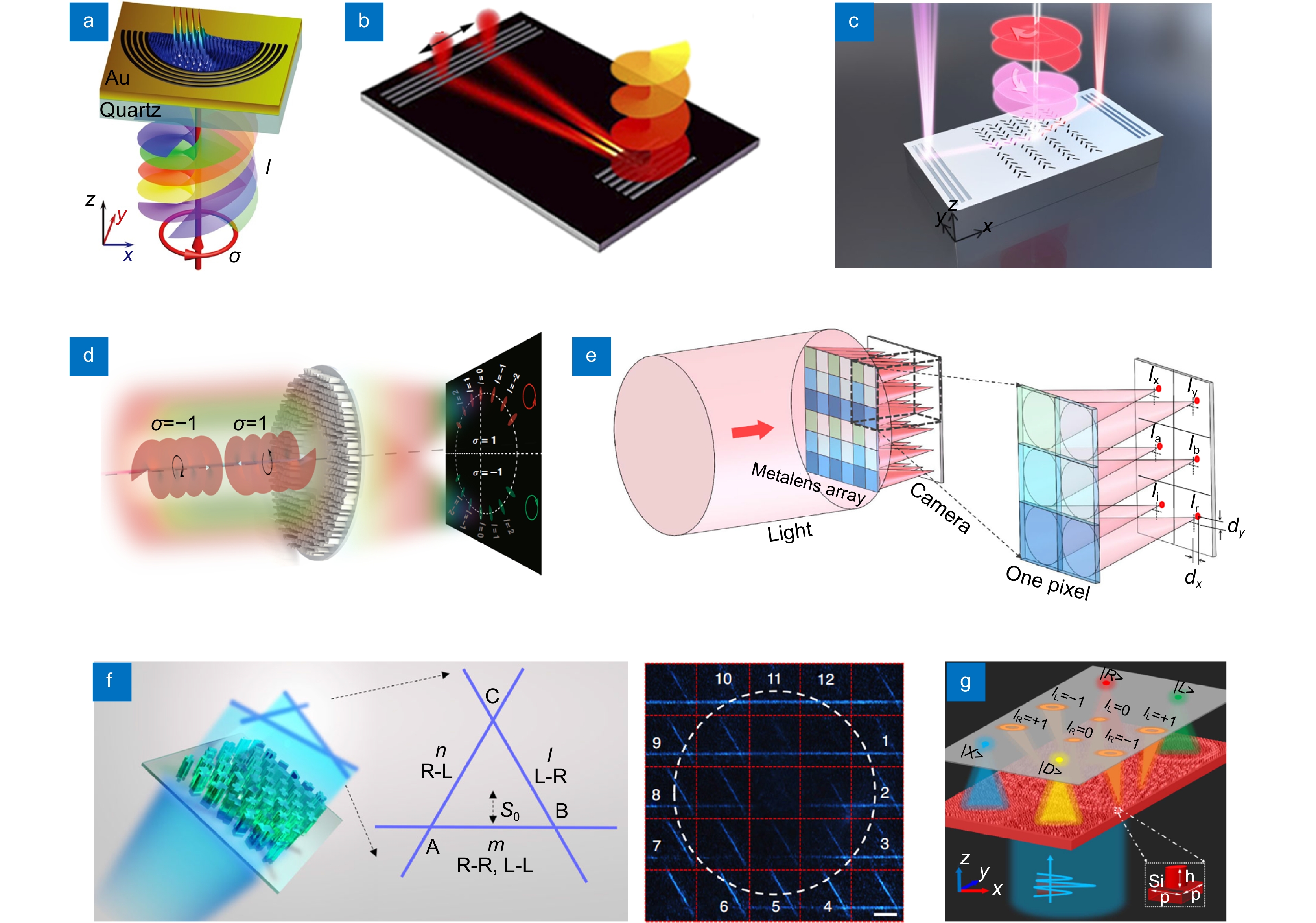Figure 4. Current researches on metasurface vectorial beam detection devices. (a) Schematic of an on-chip OAM mode detector[83];(b) Schematic of the OAM detector based on a plamonic grating[87]; (c) Schematic of the singularity detector based on a spin-Hall meta-grating[86]; (d) Schematic of the singularity detector based on a spin-decoupled metasurface[89]; (e) Schematic of the general Hartmann-Shack sensor based on metalenses[82]; (f) Schematic of the vector beam detector based on non-interleaved chiral metasurfaces[90]; (g) Schematic of the vector beam detector based on all-silicon metasurfaces[91]尽管在矢量光束SAM和OAM检测方面取得了显著成就，由于不能完全确定高阶斯托克斯参数，这些器件不能完全测定矢量光束的偏振态。接下来，我们详细讨论基于超构表面的矢量光束偏振态完全测定器件。Yang等人提出了一种基于六个偏振依赖介质超构透镜组合的广义Hartmann-Shack传感器，该传感器不仅可以根据透镜焦点的偏心距离实现波前的测定，同时还可以根据不同偏振依赖透镜的效率反演斯托克斯参数，实现偏振态的测定，如图4(e)所示[82]。同时，将该器件阵列排布，可以测定多个像素点上偏振，然后对比标准化矢量光束的偏振分布，从而实现矢量光束偏振态的检测。但是，该器件的单个功能单元由六个偏振依赖介质超构透镜组成，这会直接降低器件的空间分辨率。为了解决这一问题，Chen等人利用非交错的手性超构表面，结合神经网络实现了一个高分辨的矢量光束测定器件，如图4(f)所示[90]。该器件实现矢量光束偏振态测定的过程与广义Hartmann-Shack传感器类似，也需要与标准的矢量光束比对，无法直观地测定光学奇点。为了克服这一局限，Yang等人基于单层的全硅超构表面结构在理论上展示了矢量光束光学奇点和斯托克斯参数的单次直观测定，如图4(g)所示[91]。该器件由一个自旋解耦的聚焦涡旋产生器和四个偏振敏感的超构透镜组成，分别用于测定矢量光束的光学奇点和斯托克斯参数。因此，我们坚信随着超构表面的进一步发展，未来必将出现矢量光束快速、直观、精确测定的小型化器件。
5. 超构表面矢量光场应用
众所周知，矢量光场可广泛应用于光学捕获和操纵、光学加工、焦场工程、量子信息处理、超分辨率显微成像、光通信等领域。基于超构表面的矢量光场能够实现相关系统的轻量化和集成化，从而进一步推动其在相关领域的应用。在本小节中，我们回顾了矢量光场的几个典型应用，如微粒子捕获、边缘检测图像处理、光通信、全息成像以及机器视觉[92-95]。
在过去的几十年里，超构表面矢量光束已经广泛应用于微粒捕获和操作，相比于标量光束提供了前所未有的精度。Chantakit等人提出了一种基于超构表面涡旋超构透镜的二维高效光镊装置，如图5(a)所示[92]。该多功能光学镊子装置允许偏振敏感的粒子操作，而无需使用额外的传统光学元件。Huo等人设计了一种自旋复用的超构表面器件，在不同圆偏振入射下可以实现聚焦与涡旋[96]。将该器件放置在一个传统的4F光学成像系统之中，高斯光斑和涡旋光场相当于对频谱进行低通和高通滤波操作，最终可以实现明场成像和边缘增强成像的切换，如图5(b)所示。近年来，矢量光场也被应用于高容量信息通信领域，因其具备本征无限的正交模式。图5(c)展示了一种基于超构表面的多通道角动量复用与解复器件，呈现了10个独立信息通道，且每个通道的效率高达8%且通道间的串扰最大值为−12.8 dB[97]。为了设计该器件，利用了自旋轨道霍尔效应以及离轴复用技术。此外，在多通道复用方面柱矢量光束也作为携带信息载体得到应用。Fang等人在通讯波段演示了少模光纤和自由空间系统中的柱矢量光束多路复用通信，并展现了可以增强现今通讯系统容量一到两个数量级的潜力，如图5(d)所示[93]。Ren等人首次将OAM作为信息载体基于超构表面实现了OAM复用的全息技术，只有在特定的OAM模式下才出现目标全息图像，如图5(e)所示[98]。实现OAM复用全息的关键是构建OAM依赖的空间采样，从而在全息计算中保存OAM的信息。为了进一步提升OAM复用全息的信息通道数，该团队采用复振幅调制的超构表面，将OAM复用全息的通道数拓展到200[99]。基于超构表面的OAM复用全息在三维显示以及高容量信息传输及加密领域具体潜在应用。此外，OAM模式也可以作为载体用于构建深度衍射神经网络，实现高精度模式特征编码以及多个目标物体的精确分类，如图5(f)所示[100]。
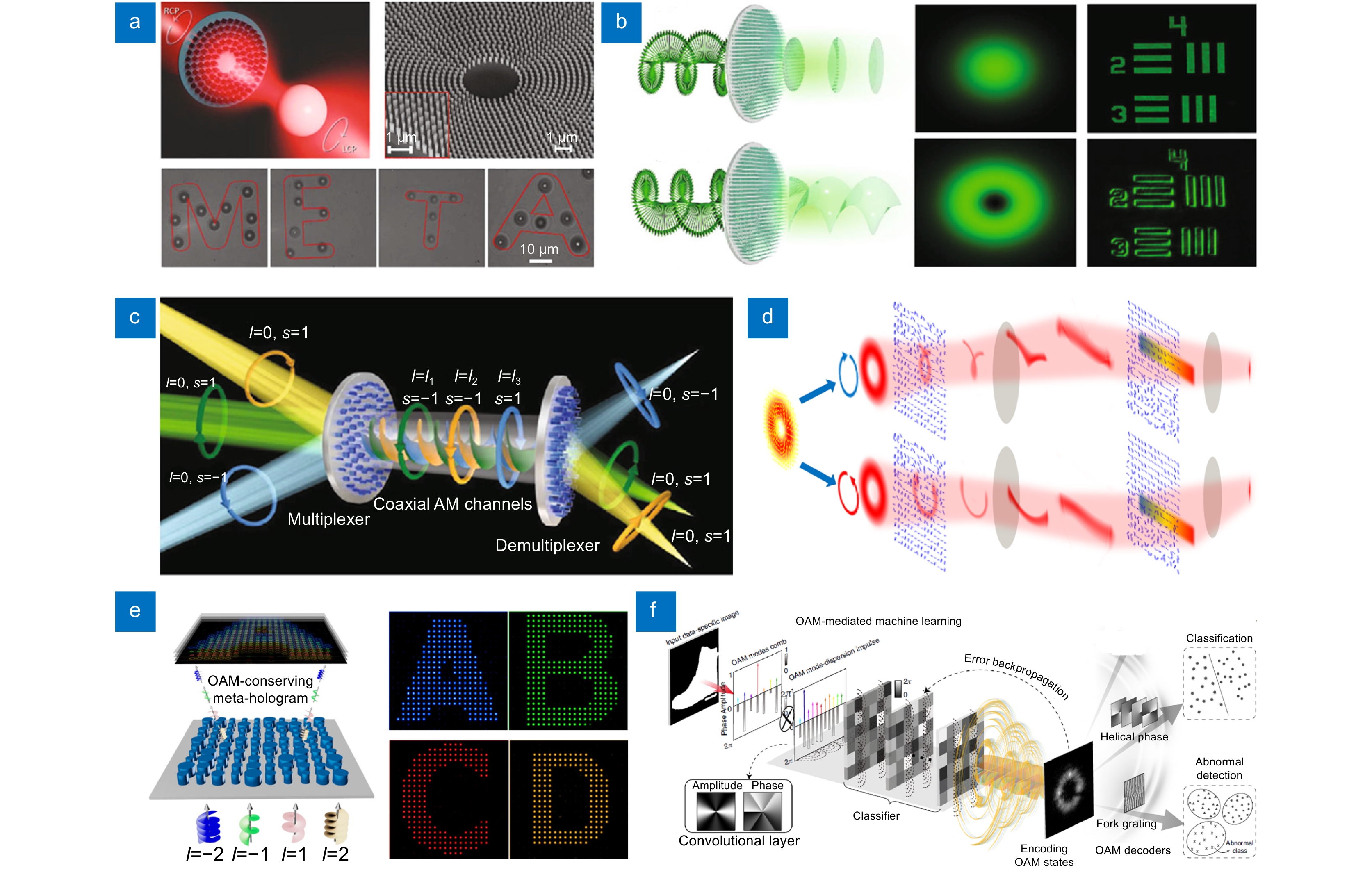Figure 5. Current researches on metasurface vectorial beam applications. (a) Schematic of optical tweezers based on metasurface focusing vortex field[92]; (b) Schematic of the spin-multiplexed metasurface for bright-field imaging and edge-enhanced contrast imaging[96]; (c) Schematic of the multi-channel AM multiplexer/demultiplexer[97]; (d) Schematic of the cylindrical vectorial beam multiplexing communication system[93]; (e) Schematic of the metasurface OAM-multiplexed holography[98]; (f) Schematic of OAM-mediated machine learning for high-accuracy mode-feature encoding[100]6. 结论与展望
综上所述，超构表面展现出空前的优越性，能在亚波长范围内实现电磁波的精准操控，为高效调控矢量光场提供了一个极具前景的平台。本综述系统总结了基于超构表面的矢量光场调控、检测以及应用的最新研究进展。对于超构表面矢量光场调控，我们分别综述了涡旋光场和矢量全息的国内外最近进展。对于超构表面矢量光场的检测，我们分析了从角动量检测到全斯托克斯参数检测的发展历程。在此过程中，我们详细介绍了基本原理和典型的设计策略。此外，我们系统总结了现阶段超构表面矢量光场在微粒操控、边缘增强成像、全息显示以及机器视觉等领域的应用。
尽管超表面矢量光场调控技术取得了显著的进展，但现阶段仍然面临一些挑战。首先，现阶段实现的超构表面矢量光场调控器件大多为静态器件，一旦制备完成，其功能即固定不变，静态器件在某种程度上会限制其特定场景的应用。近年来，基于不同调制机制，譬如光调控、热调控、电调控和机械调控等已经实现了一系列动态调控器件[101-105]。相应地，一系列可调的功能材料包括石墨烯[106-109]、相变材料[110-114]以及液晶[115-117]等被用于实现这些调控机制。这些动态调控机制以及功能材料也可用于实现动态矢量光场调控，为集成化动态可调矢量光场调控开辟新的途径。目前，基于相变材料覆盖的铝纳米条天线结构在中红外波段实现了像素化的振幅和相位的调制，但是其相位调制范围有限[118]。尽管如此，在此基础上构建双层结构或者引入几何相位可以拓展其相位覆盖范围，为像素化的动态矢量光场调控提供可能。此外，现有的编码超构表面调控机制与相变材料结合也可以为实现像素化的动态矢量光场调控提供有效途径[119]。其次，除了基于先验性的正向设计方法，另一种基于人工智能的逆向设计方法也逐渐用于设计超构表面器件，譬如拓扑优化、机器学习等[120-123]。这些算法依赖对器件目标性能函数的不断迭代优化，可以获得一些正向算法无法实现的复杂、独特或者违反直觉的功能。因而，逆向设计方法也为超构表面矢量光场调控提供新的思路。最后，现今报道的超构表面矢量光场调控器件都处于实验室阶段，他们通常都只有很小的幅面(微米到毫米量级)且制造成本昂贵(源于常用的电子束曝光以及聚焦离子束刻蚀工艺)[124-126]。我们相信随着智能材料、纳米制备技术和各种巧妙设计策略的出现，新兴的基于超构表面的矢量光场调控器件将在不久的将来得以商业化，真正进入消费市场。
利益冲突：所有作者声明无利益冲突
-
图 1 (a)标准庞加莱球及其典型标量光束表示；(b)高阶庞加莱球及其典型矢量光束表示，此处展示1阶庞加莱球
Figure 1. (a) Representation of typical scalar beams on the standard PS; (b) Representation of typical vector beams on the HOPS. Here we choose the 1-order HOPS as an example
图 2 超构表面矢量光束调控国内外研究现状。(a)等离子体超构表面涡旋产生器的SEM图像及测试的远场能量图像[10]；(b) J-片的原理工作图，它可以将任意正交偏振对转化为具有独立拓扑电荷值的两束涡旋光[45]；(c)基于多原子组合超构表面的完美矢量涡旋光束[53]；(d)宽带完美庞加莱球矢量光束的产生[54]；(e)动态调控的杂交嫁接完美矢量涡旋光[55]；(f)基于四元体超构表面的涡旋光束产生[56]；(g)基于纳米环形孔径单元的片上无干扰角动量复用器原理图[59]；(h) 硅基OAM片上发射器的原理图[60]；(i)光纤端面产生任意结构光束的示意图[3]
Figure 2. Current researches on metasurface vector beam regulation. (a) SEM image of the plasmonic vortex beam generator and the measured far-field intensity profiles[10]; (b) Schematic and operating concept of the J-plate that converts an arbitrary pair of orthogonal polarization states into two beams with independent values of topological charges[45]; (c) Generation of perfect vector vortex beams with various topological charges via a composite element metasurface[53]; (d) Schematic of generating broadband perfect Poincaré sphere vector beams[54]; (e) Dynamic generation of hybrid grafted perfect vector vortex beams[55]; (f) Schematic of the meta-quadrumer for vortex generation[56]; (g) Schematic of the nano-ring aperture unit for on-chip noninterference AM multiplexing[59]; (h) Schematic of a silicon-based OAM emitter[60]; (i) Schematic of generating arbitrarily structured light on meta-fibers[3]
图 3 超构表面矢量全息国内外研究现状。(a)正交圆偏振切换的超构表面全息[72]；(b)三线偏振通道组合的彩色矢量全息展示[74]；(c)基于双原子单元超构表面的全偏振矢量全息[75]；(d)基于组合几何相位单元的宽带全偏振矢量全息[76]；(e)液晶集成的彩色打印和矢量全息双功能器件[77]；(f)基于非交错超构表面的三维全偏振矢量全息示意图[78]；(g)双波长矢量全息示意图[79]；(h) 彩色全偏振矢量全息示意图[80]；(i)基于极简超构表面的角动量全息示意图[81]
Figure 3. Current researches on metasurface vectorial holography. (a) Schematic of the orthogonal circularly polarization switchable metasurface hologram[72]; (b) Demonstration of three LP channel multiplexing for vectorial full color holographic display[74]; (c) Full-polarization vector holography based on diatomic metasurfaces[75]; (d) Broadband full-polarization vector holography based on geometric phase metasurfaces[76]; (e) Liquid crystal integrated color printing and vector holographic dual-function meat-devices[77]; (f) Schematic of the 3D full-polarization vectorial holography based on noninterleaved metasurfaces[78]; (g) Illustration of the dual-wavelength vectorial meta-hologram[79]; (h) Schematic of the color full-polarization vectorial hologram[80]; (i) Schematic of the angular momentum holography via a minimalist metasurface[81]
图 4 超构表面矢量光束检测器件研究现状。(a)片上轨道角动量模式检测器的示意图[83]；(b)基于等离子体纳米光栅结构的OAM检测器[87]；(c)基于自旋-霍尔超光栅结构的奇点检测器[86]；(d)自旋解耦合的超构表面实现光学奇点的检测[89]；(e)基于超构透镜组合的广义Hartmann-Shack传感器[82]；(f) 非交错的手性超构表面矢量光束测定器件示意图[90]；(g)全硅超构表面矢量光束测定器件示意图[91]
Figure 4. Current researches on metasurface vectorial beam detection devices. (a) Schematic of an on-chip OAM mode detector[83];(b) Schematic of the OAM detector based on a plamonic grating[87]; (c) Schematic of the singularity detector based on a spin-Hall meta-grating[86]; (d) Schematic of the singularity detector based on a spin-decoupled metasurface[89]; (e) Schematic of the general Hartmann-Shack sensor based on metalenses[82]; (f) Schematic of the vector beam detector based on non-interleaved chiral metasurfaces[90]; (g) Schematic of the vector beam detector based on all-silicon metasurfaces[91]
图 5 超构表面矢量光束应用研究现状。(a)超构表面聚焦涡旋光场光镊示意图[92]；(b)基于自旋复用的超构表面明场与边缘成像示意图[96]；(c)多通道角动量复用与解复器件示意图[97]；(d) 柱矢量光束复用通信系统示意图[93]；(e)超构表面OAM复用全息示意图[98]；(f)高精度模式特征编码的OAM机器学习原理图[100]
Figure 5. Current researches on metasurface vectorial beam applications. (a) Schematic of optical tweezers based on metasurface focusing vortex field[92]; (b) Schematic of the spin-multiplexed metasurface for bright-field imaging and edge-enhanced contrast imaging[96]; (c) Schematic of the multi-channel AM multiplexer/demultiplexer[97]; (d) Schematic of the cylindrical vectorial beam multiplexing communication system[93]; (e) Schematic of the metasurface OAM-multiplexed holography[98]; (f) Schematic of OAM-mediated machine learning for high-accuracy mode-feature encoding[100]
-
[1] Hao J M, Yuan Y, Ran L X, et al. Manipulating electromagnetic wave polarizations by anisotropic metamaterials[J]. Phys Rev Lett, 2007, 99(6): 063908. doi: 10.1103/PhysRevLett.99.063908
[2] Cao G T, Xu H X, Zhou L M, et al. Infrared metasurface-enabled compact polarization nanodevices[J]. Mater Today, 2021, 50: 499−515. doi: 10.1016/j.mattod.2021.06.014
[3] Li C H, Wieduwilt T, Wendisch F J, et al. Metafiber transforming arbitrarily structured light[J]. Nat Commun, 2023, 14(1): 7222. doi: 10.1038/s41467-023-43068-7
[4] Li X P, Venugopalan P, Ren H R, et al. Super-resolved pure-transverse focal fields with an enhanced energy density through focus of an azimuthally polarized first-order vortex beam[J]. Opt Lett, 2014, 39(20): 5961−5964. doi: 10.1364/OL.39.005961
[5] Choi Y, Yoon C, Kim M, et al. Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber[J]. Phys Rev Lett, 2012, 109(20): 203901. doi: 10.1103/PhysRevLett.109.203901
[6] Mair A, Vaziri A, Weihs G, et al. Entanglement of the orbital angular momentum states of photons[J]. Nature, 2001, 412(6844): 313−316. doi: 10.1038/35085529
[7] Wang J, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nat Photonics, 2012, 6(7): 488−496. doi: 10.1038/nphoton.2012.138
[8] Erhard M, Fickler R, Krenn M, et al. Twisted photons: new quantum perspectives in high dimensions[J]. Light Sci Appl, 2018, 7: 17146. doi: 10.1038/lsa.2017.146
[9] Bégin J L, Jain A, Parks A, et al. Nonlinear helical dichroism in chiral and achiral molecules[J]. Nat Photonics, 2023, 17(1): 82−88. doi: 10.1038/s41566-022-01100-0
[10] Yu N F, Genevet P, Kats M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333−337. doi: 10.1126/science.1210713
[11] Dorrah A H, Capasso F. Tunable structured light with flat optics[J]. Science, 2022, 376(6591): eabi6860. doi: 10.1126/science.abi6860
[12] Xiong B, Liu Y, Xu Y H, et al. Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise[J]. Science, 2023, 379(6629): 294−299. doi: 10.1126/science.ade5140
[13] Yang H, Ou K, Wan HY, et al. Metasurface-empowered optical cryptography[J]. Mater Today, 2023, 67: 424−445. doi: 10.1016/j.mattod.2023.06.003
[14] Yang Y, Seong J, Choi M, et al. Integrated metasurfaces for re-envisioning a near-future disruptive optical platform[J]. Light Sci Appl, 2023, 12(1): 152. doi: 10.1038/s41377-023-01169-4
[15] 许可, 王星儿, 范旭浩, 等. 超表面全息术: 从概念到实现[J]. 光电工程, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
Xu K, Wang X E, Fan X H, et al. Meta-holography: from concept to realization[J]. Opto-Electron Eng, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
[16] Sun S L, Yang K Y, Wang C M, et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces[J]. Nano Lett, 2012, 12(12): 6223−6229. doi: 10.1021/nl3032668
[17] Hu Y Q, Luo X H, Chen Y Q, et al. 3D-Integrated metasurfaces for full-colour holography[J]. Light Sci Appl, 2019, 8: 86. doi: 10.1038/s41377-019-0198-y
[18] Zheng G X, Mühlenbernd H, Kenney M, et al. Metasurface holograms reaching 80% efficiency[J]. Nat Nanotechnol, 2015, 10(4): 308−312. doi: 10.1038/nnano.2015.2
[19] Zheng P X, Dai Q, Li Z L, et al. Metasurface-based key for computational imaging encryption[J]. Sci Adv, 2021, 7(21): eabg0363. doi: 10.1126/sciadv.abg0363
[20] Defienne H, Ndagano B, Lyons A, et al. Polarization entanglement-enabled quantum holography[J]. Nat Phys, 2021, 17(5): 591−597. doi: 10.1038/s41567-020-01156-1
[21] Qu G Y, Yang W H, Song Q H, et al. Reprogrammable meta-hologram for optical encryption[J]. Nat Commun, 2020, 11(1): 5484. doi: 10.1038/s41467-020-19312-9
[22] Zhao R Z, Huang L L, Wang Y T. Recent advances in multi-dimensional metasurfaces holographic technologies[J]. PhotoniX, 2020, 1(1): 20. doi: 10.1186/s43074-020-00020-y
[23] Yin X B, Ye Z L, Rho J, et al. Photonic spin Hall effect at metasurfaces[J]. Science, 2013, 339(6126): 1405−1407. doi: 10.1126/science.1231758
[24] Xiao S Y, Zhong F, Liu H, et al. Flexible coherent control of plasmonic spin-Hall effect[J]. Nat Commun, 2015, 6: 8360. doi: 10.1038/ncomms9360
[25] Ou K, Yu F L, Li G H, et al. Mid-infrared polarization-controlled broadband achromatic metadevice[J]. Sci Adv, 2020, 6(37): eabc0711. doi: 10.1126/sciadv.abc0711
[26] Hu Y Q, Jiang Y T, Zhang Y, et al. Asymptotic dispersion engineering for ultra-broadband meta-optics[J]. Nat Commun, 2023, 14(1): 6649. doi: 10.1038/s41467-023-42268-5
[27] Rubin N A, D’Aversa G, Chevalier P, et al. Matrix Fourier optics enables a compact full-Stokes polarization camera[J]. Science, 2019, 365(6448): eaax1839. doi: 10.1126/science.aax1839
[28] Wang Y J, Chen Q M, Yang W H, et al. High-efficiency broadband achromatic metalens for near-IR biological imaging window[J]. Nat Commun, 2021, 12(1): 5560. doi: 10.1038/s41467-021-25797-9
[29] Xie L Y, Wan H Y, Ou K, et al. High‐efficiency broadband achromatic metadevice for spin‐to‐orbital angular momentum conversion of light in the near-infrared[J]. Small Sci, 2024, 4(5): 2300273. doi: 10.1002/smsc.202300273
[30] Arbabi A, Horie Y, Bagheri M, et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission[J]. Nat Nanotechnol, 2015, 10(11): 937−943. doi: 10.1038/nnano.2015.186
[31] Yang H, Xie Z W, Zhou Z Y, et al. Full-space polarization-regulated lightwave steering via single-layer metasurfaces[J]. J Phys D Appl Phys, 2020, 54(1): 015102. doi: 10.1088/1361-6463/abb7b8
[32] Yu N F, Aieta F, Genevet P, et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces[J]. Nano Lett, 2012, 12(12): 6328−6333. doi: 10.1021/nl303445u
[33] Hu Y Q, Wang X D, Luo X H, et al. All-dielectric metasurfaces for polarization manipulation: principles and emerging applications[J]. Nanophotonics, 2020, 9(12): 3755−3780. doi: 10.1515/nanoph-2020-0220
[34] Wen D D, Pan K, Meng J J, et al. Broadband multichannel cylindrical vector beam generation by a single metasurface[J]. Laser Photon Rev, 2022, 16(10): 2200206. doi: 10.1002/lpor.202200206
[35] Shen Y J, Wang X J, Xie Z W, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities[J]. Light Sci Appl, 2019, 8: 90. doi: 10.1038/s41377-019-0194-2
[36] Wang H T, Wang H, Ruan Q F, et al. Coloured vortex beams with incoherent white light illumination[J]. Nat Nanotechnol, 2023, 18(3): 264−272. doi: 10.1038/s41565-023-01319-0
[37] Yang H, Xie Z W, He H R, et al. A perspective on twisted light from on-chip devices[J]. APL Photonics, 2021, 6(11): 110901. doi: 10.1063/5.0060736
[38] 张雪妍, 郁步昭, 王吉明, 等. 基于几何相位超表面的Ince-Gaussian矢量涡旋光场聚焦[J]. 激光技术, 2022, 46(1): 85−93. doi: 10.7510/jgjs.issn.1001-3806.2022.01.008
Zhang X Y, Yu B Z, Wang J M, et al. Focusing of Ince-Gaussian vector vortex optical field based on geometric phase metasurface[J]. Laser Technol, 2022, 46(1): 85−93. doi: 10.7510/jgjs.issn.1001-3806.2022.01.008
[39] Azzam R M A, Bashara N M. Ellipsometry and Polarized Light[M]. Amsterdam: North-Holland Pub. Co. , 1977.
[40] Milione G, Sztul H I, Nolan D A, et al. Higher-order poincaré sphere, stokes parameters, and the angular momentum of light[J]. Phys Rev Lett, 2011, 107(5): 053601. doi: 10.1103/PhysRevLett.107.053601
[41] Naidoo D, Roux F S, Dudley A, et al. Controlled generation of higher-order Poincaré sphere beams from a laser[J]. Nat Photonics, 2016, 10(5): 327−332. doi: 10.1038/nphoton.2016.37
[42] Xu R, Chen P, Tang J, et al. Perfect higher-order poincaré sphere beams from digitalized geometric phases[J]. Phys Rev Appl, 2018, 10(3): 034061. doi: 10.1103/PhysRevApplied.10.034061
[43] Huang L L, Song X, Reineke B, et al. Volumetric generation of optical vortices with metasurfaces[J]. ACS Photonics, 2017, 4(2): 338−346. doi: 10.1021/acsphotonics.6b00808
[44] Wang X W, Nie Z Q, Liang Y, et al. Recent advances on optical vortex generation[J]. Nanophotonics, 2018, 7(9): 1533−1556. doi: 10.1515/nanoph-2018-0072
[45] Devlin R C, Ambrosio A, Rubin N A, et al. Arbitrary spin-to–orbital angular momentum conversion of light[J]. Science, 2017, 358(6365): 896−901. doi: 10.1126/science.aao5392
[46] Yang Y M, Wang W Y, Moitra P, et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation[J]. Nano Lett, 2014, 14(3): 1394−1399. doi: 10.1021/nl4044482
[47] Pu M B, Li X, Ma X L, et al. Catenary optics for achromatic generation of perfect optical angular momentum[J]. Sci Adv, 2015, 1(9): e1500396. doi: 10.1126/sciadv.1500396
[48] Luo X G, Pu M B, Li X, et al. Broadband spin Hall effect of light in single nanoapertures[J]. Light Sci Appl, 2017, 6(6): e16276. doi: 10.1038/lsa.2016.276
[49] Zhang F, Pu M B, Li X, et al. Extreme‐angle silicon infrared optics enabled by streamlined surfaces[J]. Adv Mater, 2021, 33(11): 2008157. doi: 10.1002/adma.202008157
[50] Zhang X H, Chen Q M, Tang D L, et al. Broadband high-efficiency dielectric metalenses based on quasi-continuous nanostrips[J]. Opto-Electron Adv, 2024, 7(5): 230126. doi: 10.29026/oea.2024.230126
[51] Guo Y H, Pu M B, Zhao Z Y, et al. Merging geometric phase and plasmon retardation phase in continuously shaped metasurfaces for arbitrary orbital angular momentum generation[J]. ACS Photonics, 2016, 3(11): 2022−2029. doi: 10.1021/acsphotonics.6b00564
[52] Zhang F, Pu M B, Luo J, et al. Symmetry breaking of photonic spin-orbit interactions in metasurfaces[J]. Opto-Electron Eng, 2017, 44(3): 319−325. doi: 10.3969/j.issn.1003-501X.2017.03.006
[53] Bao Y J, Ni J C, Qiu C W. A minimalist single-layer metasurface for arbitrary and full control of vector vortex beams[J]. Adv Mater, 2020, 32(6): 1905659. doi: 10.1002/adma.201905659
[54] Liu M Z, Huo P C, Zhu W Q, et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface[J]. Nat Commun, 2021, 12(1): 2230. doi: 10.1038/s41467-021-22462-z
[55] Ahmed H, Ansari M A, Li Y, et al. Dynamic control of hybrid grafted perfect vector vortex beams[J]. Nat Commun, 2023, 14(1): 3915. doi: 10.1038/s41467-023-39599-8
[56] Chen Q M, Qu G Y, Yin J, et al. Highly efficient vortex generation at the nanoscale[J]. Nat Nanotechnol, 2024, 19(7): 1000−1006. doi: 10.1038/s41565-024-01636-y
[57] Chen C F, Ku C T, Tai Y H, et al. Creating optical near-field orbital angular momentum in a gold metasurface[J]. Nano Lett, 2015, 15(4): 2746−2750. doi: 10.1021/acs.nanolett.5b00601
[58] Liu A P, Zou C L, Ren X F, et al. On-chip generation and control of the vortex beam[J]. Appl Phys Lett, 2016, 108(18): 181103. doi: 10.1063/1.4948519
[59] Ren H R, Li X P, Zhang Q M, et al. On-chip noninterference angular momentum multiplexing of broadband light[J]. Science, 2016, 352(6287): 805−809. doi: 10.1126/science.aaf1112
[60] Xie Z W, Lei T, Li F, et al. Ultra-broadband on-chip twisted light emitter for optical communications[J]. Light Sci Appl, 2018, 7: 18001. doi: 10.1038/lsa.2018.1
[61] Zhou N, Zheng S, Cao X P, et al. Ultra-compact broadband polarization diversity orbital angular momentum generator with 3.6× 3.6 μm2 footprint[J]. Sci Adv, 2019, 5(5): eaau9593. doi: 10.1126/sciadv.aau9593
[62] Ji J T, Wang Z Z, Sun J C, et al. Metasurface-enabled on-chip manipulation of higher-order poincaré sphere beams[J]. Nano Lett, 2023, 23(7): 2750−2757. doi: 10.1021/acs.nanolett.3c00021
[63] Dorrah A H, Rubin N A, Tamagnone M, et al. Structuring total angular momentum of light along the propagation direction with polarization-controlled meta-optics[J]. Nat Commun, 2021, 12: 6249. doi: 10.1038/s41467-021-26253-4
[64] Buono W T, Forbes A. Nonlinear optics with structured light[J]. Opto-Electron Adv, 2022, 5(6): 210174. doi: 10.29026/oea.2022.210174
[65] Luo X G, Pu M B, Zhang F, et al. Vector optical field manipulation via structural functional materials: tutorial[J]. J Appl Phys, 2022, 131(18): 181101. doi: 10.1063/5.0089859
[66] Nan T, Zhao H, Guo J Y, et al. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces[J]. Opto-Electron Sci, 2024, 3(5): 230052 doi: 10.29026/oes.2024.230052
[67] Song Q H, Liu X S, Qiu C W, et al. Vectorial metasurface holography[J]. Appl Phys Rev, 2022, 9(1): 011311. doi: 10.1063/5.0078610
[68] Zhao R Z, Sain B, Wei Q S, et al. Multichannel vectorial holographic display and encryption[J]. Light Sci Appl, 2018, 7: 95. doi: 10.1038/s41377-018-0091-0
[69] Rubin N A, Zaidi A, Dorrah A H, et al. Jones matrix holography with metasurfaces[J]. Sci Adv, 2021, 7(33): eabg7488. doi: 10.1126/sciadv.abg7488
[70] Ding F, Chang B D, Wei Q S, et al. Versatile polarization generation and manipulation using dielectric metasurfaces[J]. Laser Photon Rev, 2020, 14(11): 2000116. doi: 10.1002/lpor.202000116
[71] Bao Y J, Wen L, Chen Q, et al. Toward the capacity limit of 2D planar Jones matrix with a single-layer metasurface[J]. Sci Adv, 2021, 7(25): eabh0365. doi: 10.1126/sciadv.abh0365
[72] Mueller J P B, Rubin N A, Devlin R C, et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization[J]. Phys Rev Lett, 2017, 118(11): 113901. doi: 10.1103/PhysRevLett.118.113901
[73] Deng Z L, Tu Q A, Wang Y J, et al. Vectorial compound metapixels for arbitrary nonorthogonal polarization steganography[J]. Adv Mater, 2021, 33(43): 2103472. doi: 10.1002/adma.202103472
[74] Hu Y Q, Li L, Wang Y J, et al. Trichromatic and tripolarization-channel holography with noninterleaved dielectric metasurface[J]. Nano Lett, 2020, 20(2): 994−1002. doi: 10.1021/acs.nanolett.9b04107
[75] Deng Z L, Deng J H, Zhuang X, et al. Diatomic metasurface for vectorial holography[J]. Nano Lett, 2018, 18(5): 2885−2892. doi: 10.1021/acs.nanolett.8b00047
[76] Song Q H, Baroni A, Sawant R, et al. Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces[J]. Nat Commun, 2020, 11(1): 2651. doi: 10.1038/s41467-020-16437-9
[77] Kim I, Jang J, Kim G, et al. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform[J]. Nat Commun, 2021, 12(1): 3614. doi: 10.1038/s41467-021-23814-5
[78] Yang H, Jiang Y T, Hu Y Q, et al. Noninterleaved metasurface for full‐polarization three‐dimensional vectorial holography[J]. Laser Photon Rev, 2022, 16(11): 2200351. doi: 10.1002/lpor.202200351
[79] Kim J, Jeon D, Seong J, et al. Photonic encryption platform via dual-band vectorial metaholograms in the ultraviolet and visible[J]. ACS Nano, 2022, 16(3): 3546−3553. doi: 10.1021/acsnano.1c10100
[80] Guo X Y, Zhong J Z, Li B J, et al. Full‐color holographic display and encryption with full‐polarization degree of freedom[J]. Adv Mater, 2022, 34(3): 2103192. doi: 10.1002/adma.202103192
[81] Yang H, He P, Ou K, et al. Angular momentum holography via a minimalist metasurface for optical nested encryption[J]. Light Sci Appl, 2023, 12(1): 79. doi: 10.1038/s41377-023-01125-2
[82] Yang Z Y, Wang Z K, Wang Y X, et al. Generalized Hartmann-Shack array of dielectric metalens sub-arrays for polarimetric beam profiling[J]. Nat Commun, 2018, 9(1): 4607. doi: 10.1038/s41467-018-07056-6
[83] Mei S T, Huang K, Liu H, et al. On-chip discrimination of orbital angular momentum of light with plasmonic nanoslits[J]. Nanoscale, 2016, 8(4): 2227−2233. doi: 10.1039/C5NR07374J
[84] Ou K, Li G H, Li T X, et al. High efficiency focusing vortex generation and detection with polarization-insensitive dielectric metasurfaces[J]. Nanoscale, 2018, 10(40): 19154−19161. doi: 10.1039/C8NR07480A
[85] Zhang S, Huo P C, Zhu W Q, et al. Broadband detection of multiple spin and orbital angular momenta via dielectric metasurface[J]. Laser Photon Rev, 2020, 14(9): 2000062. doi: 10.1002/lpor.202000062
[86] Feng F, Si G Y, Min C J, et al. On-chip plasmonic spin-Hall nanograting for simultaneously detecting phase and polarization singularities[J]. Light Sci Appl, 2020, 9: 95. doi: 10.1038/s41377-020-0330-z
[87] Chen J, Chen X, Li T, et al. On‐chip detection of orbital angular momentum beam by plasmonic nanogratings[J]. Laser Photon Rev, 2018, 12(8): 1700331. doi: 10.1002/lpor.201700331
[88] Guo Y H, Zhang S C, Pu M B, et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation[J]. Light Sci Appl, 2021, 10(1): 63. doi: 10.1038/s41377-021-00497-7
[89] Li X Y, Chen C, Guo Y H, et al. Monolithic spiral metalens for ultrahigh‐capacity and single‐shot sorting of full angular momentum state[J]. Adv Funct Mater, 2024, 34(7): 2311286. doi: 10.1002/adfm.202311286
[90] Chen C, Xiao X J, Ye X, et al. Neural network assisted high-spatial-resolution polarimetry with non-interleaved chiral metasurfaces[J]. Light Sci Appl, 2023, 12(1): 288. doi: 10.1038/s41377-023-01337-6
[91] Yang H, Xie Z W, Li G H, et al. All-dielectric metasurface for fully resolving arbitrary beams on a higher-order Poincaré sphere[J]. Photonics Res, 2021, 9(3): 331−343. doi: 10.1364/PRJ.411503
[92] Chantakit T, Schlickriede C, Sain B, et al. All-dielectric silicon metalens for two-dimensional particle manipulation in optical tweezers[J]. Photonics Res, 2020, 8(9): 1435−1440. doi: 10.1364/PRJ.389200
[93] Fang J C, Xie Z W, Lei T, et al. Spin-dependent optical geometric transformation for cylindrical vector beam multiplexing communication[J]. ACS Photonics, 2018, 5(9): 3478−3484. doi: 10.1021/acsphotonics.8b00680
[94] Kim Y, Lee G Y, Sung J, et al. Spiral metalens for phase contrast imaging[J]. Adv Funct Mater, 2022, 32(5): 2106050. doi: 10.1002/adfm.202106050
[95] Zhao H, Quan B G, Wang X K, et al. Demonstration of orbital angular momentum multiplexing and demultiplexing based on a metasurface in the terahertz band[J]. ACS Photonics, 2018, 5(5): 1726−1732. doi: 10.1021/acsphotonics.7b01149
[96] Huo P C, Zhang C, Zhu W Q, et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging[J]. Nano Lett, 2020, 20(4): 2791−2798. doi: 10.1021/acs.nanolett.0c00471
[97] Li Y, Li X, Chen L W, et al. Orbital angular momentum multiplexing and demultiplexing by a single metasurface[J]. Adv Opt Mater, 2017, 5(2): 1600502. doi: 10.1002/adom.201600502
[98] Ren H R, Briere G, Fang X Y, et al. Metasurface orbital angular momentum holography[J]. Nat Commun, 2019, 10(1): 2986. doi: 10.1038/s41467-019-11030-1
[99] Ren H R, Fang X Y, Jang J, et al. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space[J]. Nat Nanotechnol, 2020, 15(11): 948−955. doi: 10.1038/s41565-020-0768-4
[100] Fang X Y, Hu X N, Li B L, et al. Orbital angular momentum-mediated machine learning for high-accuracy mode-feature encoding[J]. Light Sci Appl, 2024, 13(1): 49. doi: 10.1038/s41377-024-01386-5
[101] Han Z L, Frydendahl C, Mazurski N, et al. MEMS cantilever–controlled plasmonic colors for sustainable optical displays[J]. Sci Adv, 2022, 8(16): eabn0889. doi: 10.1126/sciadv.abn0889
[102] Ahmed R, Butt H. Strain‐multiplex metalens array for tunable focusing and imaging[J]. Adv Sci, 2021, 8(4): 2003394. doi: 10.1002/advs.202003394
[103] Shaltout A M, Shalaev V M, Brongersma M L. Spatiotemporal light control with active metasurfaces[J]. Science, 2019, 364(6441): eaat3100. doi: 10.1126/science.aat3100
[104] Yu P, Li J X, Liu N. Electrically tunable optical metasurfaces for dynamic polarization conversion[J]. Nano Lett, 2021, 21(15): 6690−6695. doi: 10.1021/acs.nanolett.1c02318
[105] Jung C, Kim G, Jeong M, et al. Metasurface-driven optically variable devices[J]. Chem Rev, 2021, 121(21): 13013−13050. doi: 10.1021/acs.chemrev.1c00294
[106] Shang X J, Xu L, Yang H, et al. Graphene-enabled reconfigurable terahertz wavefront modulator based on complete Fermi level modulated phase[J]. New J Phys, 2020, 22: 063054. doi: 10.1088/1367-2630/ab9428
[107] Fei Z, Rodin A S, Andreev G O, et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging[J]. Nature, 2012, 487(7405): 82−85. doi: 10.1038/nature11253
[108] Rajabalipanah H, Rouhi K, Abdolali A, et al. Real-time terahertz meta-cryptography using polarization-multiplexed graphene-based computer-generated holograms[J]. Nanophotonics, 2020, 9(9): 2861−2877. doi: 10.1515/nanoph-2020-0110
[109] Han S J, Kim S, Kim S, et al. Complete complex amplitude modulation with electronically tunable graphene plasmonic metamolecules[J]. ACS Nano, 2020, 14(1): 1166−1175. doi: 10.1021/acsnano.9b09277
[110] de Galarreta C R, Alexeev A M, Au Y Y, et al. Nonvolatile reconfigurable phase‐change metadevices for beam steering in the near infrared[J]. Adv Funct Mater, 2018, 28(10): 1704993. doi: 10.1002/adfm.201704993
[111] Liu H L, Dong W L, Wang H, et al. Rewritable color nanoprints in antimony trisulfide films[J]. Sci adv, 2020, 6(51): eabb7171. doi: 10.1126/sciadv.abb7171
[112] Zhang F, Xie X, Pu M B, et al. Multistate switching of photonic angular momentum coupling in phase‐change metadevices[J]. Adv Mater, 2020, 32(39): 1908194. doi: 10.1002/adma.201908194
[113] Xu Z Q, Luo H, Zhu H Z, et al. Nonvolatile optically reconfigurable radiative metasurface with visible tunability for anticounterfeiting[J]. Nano Lett, 2021, 21(12): 5269−5276. doi: 10.1021/acs.nanolett.1c01396
[114] Yang H, Xie Z W, He H R, et al. Switchable imaging between edge-enhanced and bright-field based on a phase-change metasurface[J]. Opt Lett, 2021, 46(15): 3741−3744. doi: 10.1364/OL.428870
[115] Hu Y Q, Ou X N, Zeng T B, et al. Electrically tunable multifunctional polarization-dependent metasurfaces integrated with liquid crystals in the visible region[J]. Nano Lett, 2021, 21(11): 4554−4562. doi: 10.1021/acs.nanolett.1c00104
[116] Li J X, Yu P, Zhang S, et al. Electrically-controlled digital metasurface device for light projection displays[J]. Nat Commun, 2020, 11(1): 3574. doi: 10.1038/s41467-020-17390-3
[117] Li S Q, Xu X W, Veetil R M, et al. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface[J]. Science, 2019, 364(6445): 1087−1090. doi: 10.1126/science.aaw6747
[118] Michel A K U, Heßler A, Meyer S, et al. Advanced optical programming of individual meta‐atoms beyond the effective medium approach[J]. Adv Mater, 2019, 31(29): 1901033. doi: 10.1002/adma.201901033
[119] Li L L, Jun Cui T, Ji W, et al. Electromagnetic reprogrammable coding-metasurface holograms[J]. Nat Commun, 2017, 8(1): 197. doi: 10.1038/s41467-017-00164-9
[120] Ma W, Liu Z C, Kudyshev Z A, et al. Deep learning for the design of photonic structures[J]. Nat Photonics, 2021, 15(2): 77−90. doi: 10.1038/s41566-020-0685-y
[121] Molesky S, Lin Z, Piggott A Y, et al. Inverse design in nanophotonics[J]. Nat Photonics, 2018, 12(11): 659−670. doi: 10.1038/s41566-018-0246-9
[122] Xu M F, He Q, Pu M B, et al. Emerging long‐range order from a freeform disordered metasurface[J]. Adv Mater, 2022, 34(12): 2108709. doi: 10.1002/adma.202108709
[123] Luo X H, Hu Y Q, Ou X N, et al. Metasurface-enabled on-chip multiplexed diffractive neural networks in the visible[J]. Light Sci Appl, 2022, 11(1): 158. doi: 10.1038/s41377-022-00844-2
[124] Zheng H Y, Zhou Y, Ugwu C F, et al. Large-scale metasurfaces based on grayscale nanosphere lithography[J]. ACS Photonics, 2021, 8(6): 1824−1831. doi: 10.1021/acsphotonics.1c00424
[125] Chen Y Q, Shu Z W, Zhang S, et al. Sub-10 nm fabrication: methods and applications[J]. Int J Extrem Manuf, 2021, 3(3): 032002. doi: 10.1088/2631-7990/ac087c
[126] Lu X L, Wang X J, Wang S S, et al. Polarization-directed growth of spiral nanostructures by laser direct writing with vector beams[J]. Nat Commun, 2023, 14(1): 1422. doi: 10.1038/s41467-023-37048-0
-
下载:
点击扫一扫
图(6)
计量
- 文章访问数: 1981
- PDF下载数: 515
