-
摘要:
对光场各自由度的单一或协同调控获得的结构光场由于具有新颖的物理性质,展现了重要的研究意义和应用价值。例如,轨道角动量作为一种全新的调控自由度直接影响光场相位与空间分布,常通过单独作用或共同作用构造高维空间,调控生成的涡旋光场及矢量光场已广泛应用于超大容量光通信、遥感探测、量子通信等领域。在此基础上,针对日益发展的前沿应用需求,引入新的光场调控自由度与传统自由度结合,进一步拓展高维和多维的结构光场研究成为了亟待解决的问题。本文首先从双自由度调控技术出发,以矢量涡旋光场为重点介绍了两种典型内癝自由度的耦合以及作用方式;在此基础上,结合本课题组的相关工作,系统综述了超越传统自由度并打破双自由度数目限制的复杂结构光场调控技术。
Abstract:Structured beams manipulated by single or multiple degrees of freedom (DoFs) present novel physical properties, showing important research significance and practical value. Among them, orbital angular momentum (OAM), as a novel DoF, directly decides the phase and spatial distribution of laser beams. The independent manipulation of OAM or the coupled manipulation with spin angular momentum enables the construction of high-dimensional Hilbert space, which has already found broad applications in domains like ultra-large capacity optical communication, remote sensing detection and quantum communication. On this basis, considering the rapidly evolving application requirements, there is still a significant challenge to integrate the novel degrees of freedom with the traditional degrees of freedom, limiting the extension and expansion of high-dimensional and multi-dimensional structured beams. In this paper, from the perspective of two-degree-of-freedom manipulation methods, a series of structured beams coupled by two intrinsic DoFs is reviewed with emphasis on the vectorial vortex beams. Furthermore, we systematically review the manipulation of complex structured beams with multiple degrees of freedom that overcome the limitations of conventional two-degree-of-freedom. Also, the related work of our team is discussed here.
-
Overview: By tailoring single or multiple degrees of freedom, structured beams with novel physical properties have gained numerous interests. With the development of modern optics, the increasing advanced applications require more DoFs of laser field to be coupled and flexibly manipulated. Among the various DoFs, SAM, as an intrinsic DoF, has been applied to modulate vector beams. While OAM, as an emerging DoF, decides the vortex beams with helical phase. The coupling of above two enabling the construction of high-dimensional Hilbert space, forms the vector vortex beams with phase and polarization singularities, which has already found broad applications in domains like ultra-large capacity optical communication, remote sensing detection and quantum communication. Besides the vector vortex beams, most structured beams are manipulated by only one or two coupled DoFs, like ray-wave structured light and spatiotemporal light. The ability to simultaneously tailor more DoFs and generate a family of complex structured beams is crucial in the cutting-edge realm. The non-separable states, optical skyrmions and photonic hopfions can be seen as the typical instance. However, there is still a significant challenge to integrate the novel degrees of freedom with the traditional degrees of freedom, limiting the extension and expansion of high-dimensional and multi-dimensional structured beams. In this paper, from the perspective of extent of the multi-DoFs coupling, we systematically review the manipulation methods and a series of corresponding structured beams. Begin with the SAM-OAM coupled vectorial vortex beams, the principle and representation is briefly presented. Classified by the generation mechanism, the extra-cavity and intra-cavity manipulation methods are also summarized. The extra-cavity generation is mainly achieved by combining orthogonally polarized beams with different OAMs, while the intra-cavity manipulation is achieved by inserting SAM-OAM coupling devices like Q-Plate and metasurface. Further, the "super-degree-of-freedom" complex structured light field, denoting the three and more DoFs combined beams, are introduced here: A bunch of SU(2) beams have the unique properties as ray-wave duality, capable of unveiling more flexibly controlled DoFs; complex vortex arrays, manipulated with the path DoF, can be simply achieved by the diffractive optical elements; spatiotemporal vortex beams has extending the OAM to time domain. Such structured beams have already exploited more than five DoFs. Of course, due to the abundant degrees of freedom of the light field and the various ways of combination, this paper does not cover all the complex structured light fields, but selects the most representative and common structured light fields with great practical value, and it is not difficult to find the possibility of further expansion of the degree of freedom in the further study.
-

-
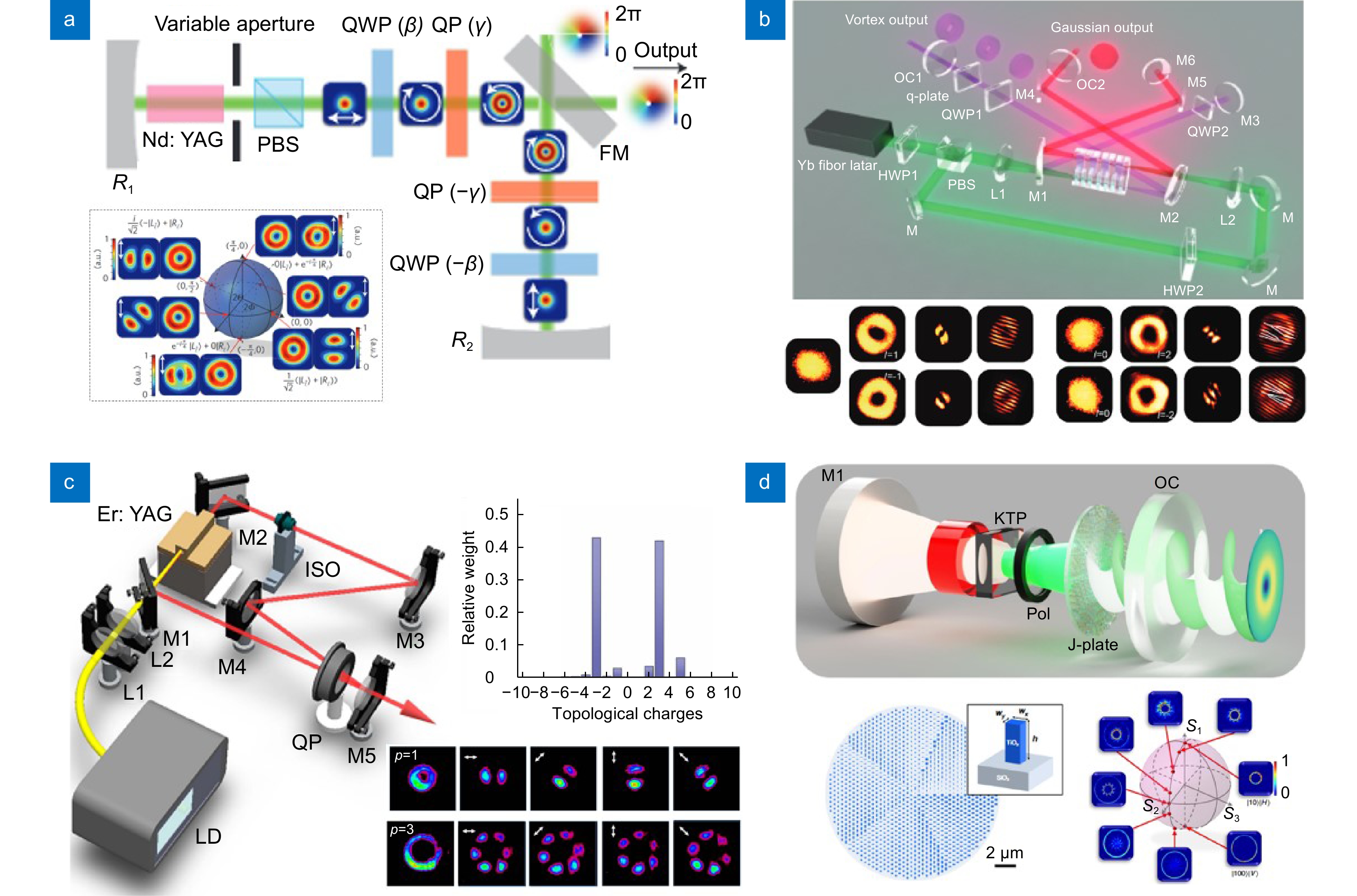
图 2 矢量涡旋光场的腔内调控方法。(a) 基于Q波片与QWP耦合作用的高阶庞加莱球光束腔内调控过程[75];(b) 基于Q波片与QWP耦合作用对特定矢量涡旋光场的非线性腔内调控结构[76];(c) 基于Q波片与环腔作用的单频柱矢量涡旋光束的调控结构[78];(d) 基于J板对杂合庞加莱球上光束的腔内调控结构[79]
Figure 2. The intra-cavity manipulation of VVBs. (a) The generation of high-order Poincare sphere beams from a laser using Q-plate [75]; (b) The non-linear generation of wave-tunable CVBs in OPO cavity[76]; (c) The scheme of single-frequency CVBs laser[78]; (d) The generation of hybrid Poincare sphere beams using meta-surface[79]
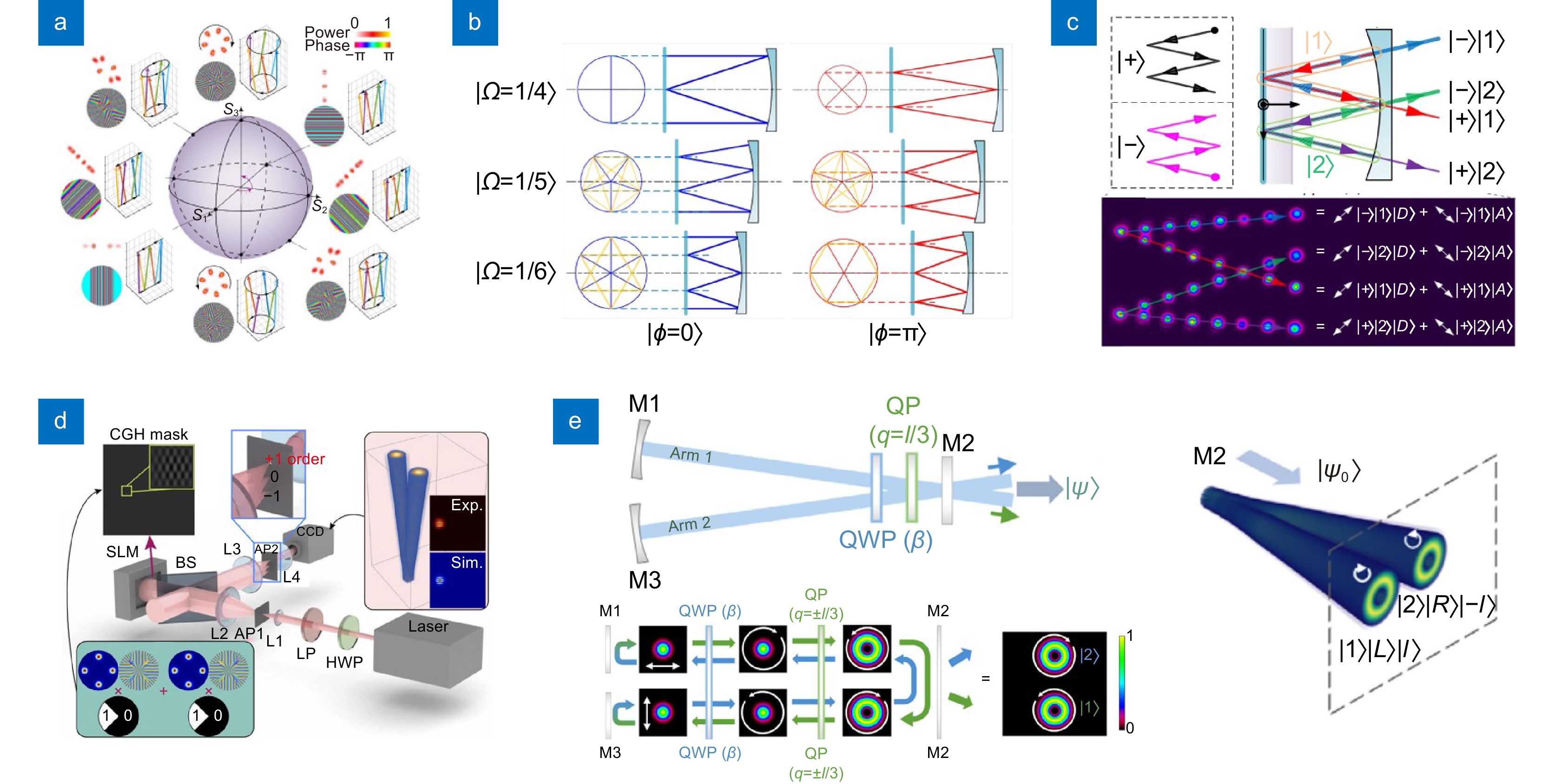
图 3 SU(2)相干态光场的表征与调控方式。(a) SU(2)庞加莱球[80];(b) SU(2)基本相干态中频率简并度与相对相位自由度对射线簇的影响[86];(c) 基于偏振、射线振动方向、周期振荡位置三自由度八维光场的基本调控原理[88];(d) 基于SLM对标量光场调控模拟(c)中不可分离态的装置[90];(e) 基于OAM、SAM与路径三自由度最大不可分离态的调控[93]
Figure 3. The representation and manipulation of SU (2) coherent states. (a) SU (2) Poincare sphere beams[80]; (b) The SU(2) coherent states decided by the frequency degeneracy and the coherent phase[83]; (c) The manipulation principle of 3-DoFs 8-dimensional nonseparable states[85]; (d) The digital modulation of SU(2) coherent states[87]; (e) The intra-cavity manipulation of 3-DoF nonseparable states[90]
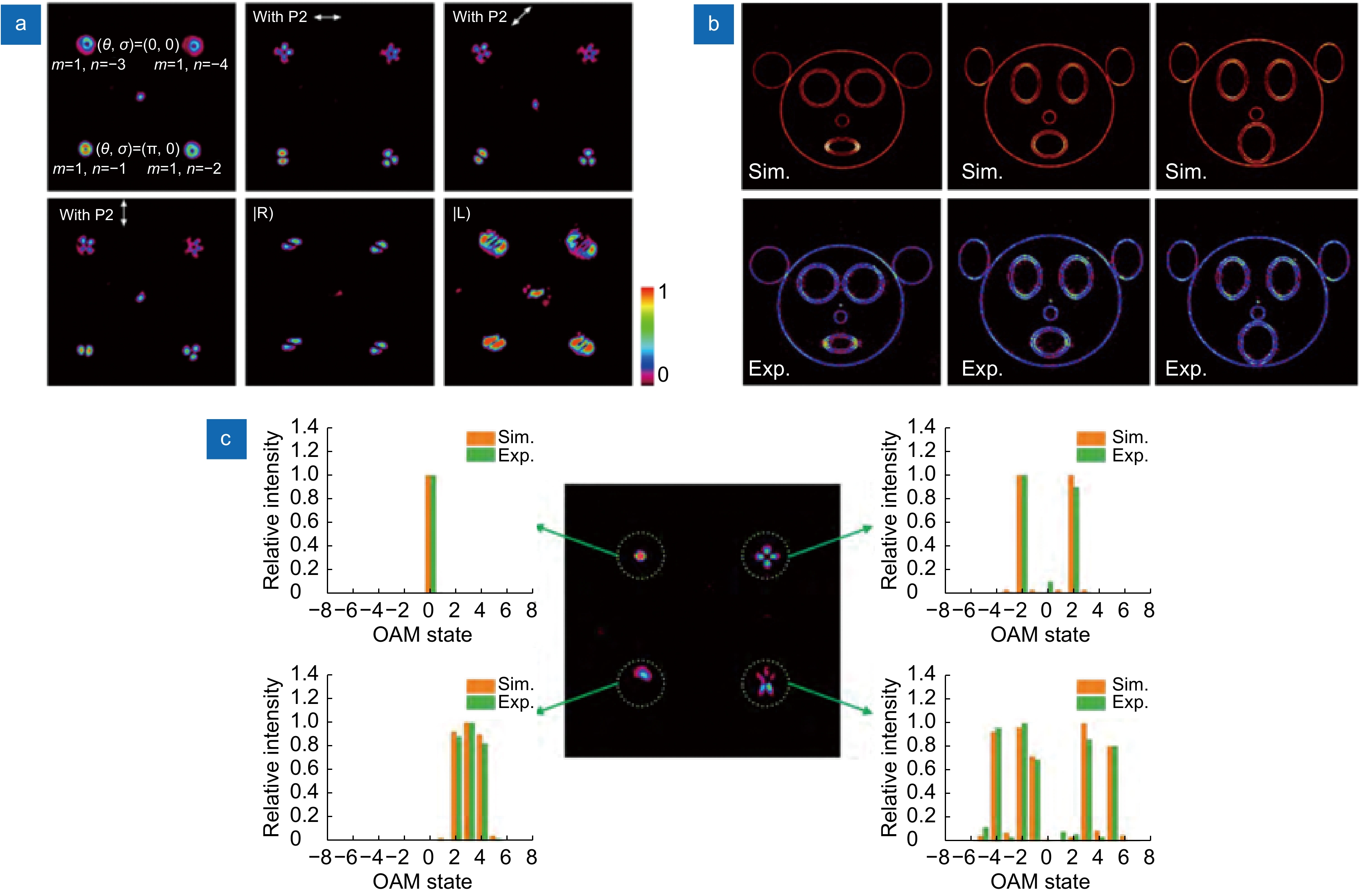
图 4 多自由度耦合的复杂涡旋阵列光场。(a) 二维光栅调控SAM-OAM产生的矢量涡旋阵列[99];(b) 由纯相位光栅调控的五自由度矢量涡旋阵列[98];(c) 三自由度调控下的高维涡旋阵列[100]
Figure 4. The complex vortex array coupled by multi-DoFs. (a) The vector vortices array manipulated by 2D grating[99]; (b) The five DoFs manipulation on vector vortices array using phase-only grating[98]; (c) The higher dimensional vector vortices array manipulated by 3-DoFs[100]
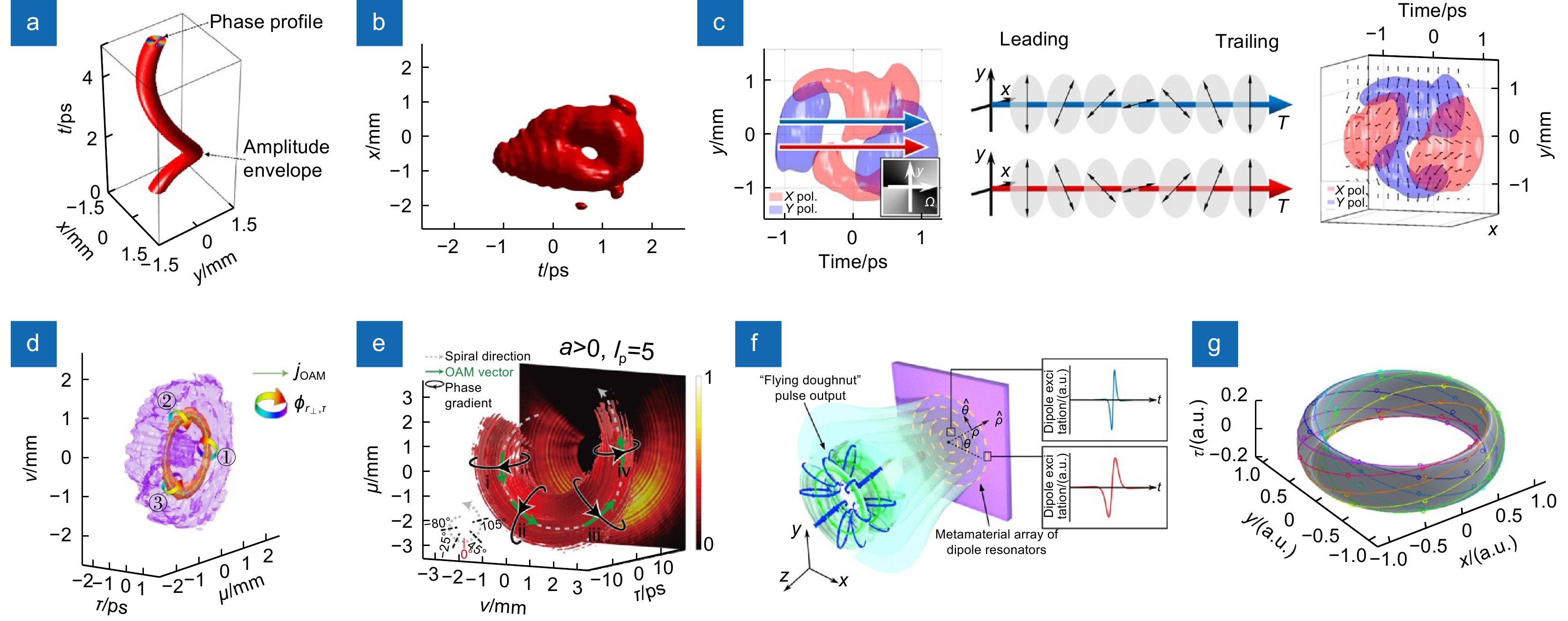
图 5 时空域多自由度协同调控光场。(a) 双OAM可调时空光场[106];(b) 标量时空涡旋光场[107];(c)矢量时空涡旋光场[109];(d) “光学涡环”[110];(e) “光学海螺”[111];(f) 超表面调控环形脉冲[112];(g)超越二维拓扑结构的光学霍普夫子[113]
Figure 5. The novel structured beams manipulated by multi-DoFs in the space-time domain. (a) Spatiotemporal beams with two OAMs[106]; (b) The schematic diagram of scalar spatiotemporal vortices[107]; (c) The experimental scheme and the mode conversion of vector spatiotemporal vortices[109]; (d) Vortex rings of light[110]; (e) “Photonic conchs” [111]; (f) Flying electromagnetic doughnuts manipulated by metasurface[112]; (g) The photonic hopfions with 3D topological structure[113]
-
[1] Forbes A, de Oliveira M, Dennis M R. Structured light[J]. Nat Photonics, 2021, 15(4): 253−262. doi: 10.1038/s41566-021-00780-4
[2] Forbes A. Structured light from lasers[J]. Laser Photonics Rev, 2019, 13(11): 1900140. doi: 10.1002/lpor.201900140
[3] Li W, Yu J W, Yan A M. Research progress of vortex beam array generation technology[J]. Laser Optoelectron Prog, 2020, 57(9): 090002. doi: 10.3788/LOP57.090002
[4] Fermann M E, Hartl I. Ultrafast fibre lasers[J]. Nat Photonics, 2013, 7(11): 868−874. doi: 10.1038/nphoton.2013.280
[5] Fortier T, Baumann E. 20 years of developments in optical frequency comb technology and applications[J]. Commun Phys, 2019, 2(1): 153. doi: 10.1038/s42005-019-0249-y
[6] Chang L, Liu S T, Bowers J E. Integrated optical frequency comb technologies[J]. Nat Photonics, 2022, 16(2): 95−108. doi: 10.1038/s41566-021-00945-1
[7] Zuo J X, Lin X C. High-power laser systems[J]. Laser Photonics Rev, 2022, 16(5): 2100741. doi: 10.1002/lpor.202100741
[8] Rosales-Guzmán C, Ndagano B, Forbes A. A review of complex vector light fields and their applications[J]. J Opt, 2018, 20(12): 123001. doi: 10.1088/2040-8986/aaeb7d
[9] 郑淑君, 林枭, 黄志云, 等. 基于偏光全息的光场调控研究进展[J]. 光电工程, 2022, 49(11): 220114. doi: 10.12086/oee.2022.220114
Zheng S J, Lin X, Huang Z Y, et al. Light field regulation based on polarization holography[J]. Opto-Electron Eng, 2022, 49(11): 220114. doi: 10.12086/oee.2022.220114
[10] Allen L, Beijersbergen M W, Spreeuw R J C, et al. Orbital angular momentum of light and the transformation of laguerre-gaussian laser modes[J]. Phys Rev A, 1992, 45(11): 8185−8189. doi: 10.1103/PhysRevA.45.8185
[11] Zhang Z C, Hai L, Fu S Y, et al. Advances on solid-state vortex laser[J]. Photonics, 2022, 9(4): 215. doi: 10.3390/photonics9040215
[12] Yao A M, Padgett M J. Orbital angular momentum: origins, behavior and applications[J]. Adv Opt Photonics, 2011, 3(2): 161−204. doi: 10.1364/AOP.3.000161
[13] Zeng R Y, Zhao Q, Shen Y J, et al. Structural stability of open vortex beams[J]. Appl Phys Lett, 2021, 119(17): 171105. doi: 10.1063/5.0062967
[14] Bai Y H, Lv H R, Fu X, et al. Vortex beam: generation and detection of orbital angular momentum [Invited][J]. Chin Opt Lett, 2022, 20(1): 012601. doi: 10.3788/COL202220.012601
[15] Wang J, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nat Photonics, 2012, 6(7): 488−496. doi: 10.1038/nphoton.2012.138
[16] Bozinovic N, Yue Y, Ren Y X, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers[J]. Science, 2013, 340(6140): 1545−1548. doi: 10.1126/science.1237861
[17] Willner A E, Huang H, Yan Y, et al. Optical communications using orbital angular momentum beams[J]. Adv Opt Photonics, 2015, 7(1): 66−106. doi: 10.1364/AOP.7.000066
[18] Yu S Y. Potentials and challenges of using orbital angular momentum communications in optical interconnects[J]. Opt Express, 2015, 23(3): 3075−3087. doi: 10.1364/OE.23.003075
[19] Wang J. Advances in communications using optical vortices[J]. Photonics Res, 2016, 4(5): B14−B28. doi: 10.1364/PRJ.4.000B14
[20] Fu S Y, Zhai Y W, Zhou H, et al. Demonstration of high-dimensional free-space data coding/decoding through multi-ring optical vortices[J]. Chin Opt Lett, 2019, 17(8): 080602. doi: 10.3788/COL201917.080602
[21] Fu S Y, Zhai Y W, Zhou H, et al. Experimental demonstration of free-space multi-state orbital angular momentum shift keying[J]. Opt Express, 2019, 27(23): 33111−33119. doi: 10.1364/OE.27.033111
[22] Fu S Y, Zhai Y W, Zhou H, et al. Demonstration of free-space one-to-many multicasting link from orbital angular momentum encoding[J]. Opt Lett, 2019, 44(19): 4753−4756. doi: 10.1364/OL.44.004753
[23] Lavery M P J, Speirits F C, Barnett S M, et al. Detection of a spinning object using light's orbital angular momentum[J]. Science, 2013, 341(6145): 537−540. doi: 10.1126/science.1239936
[24] Lavery M P J, Barnett S M, Speirits F C, et al. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body[J]. Optica, 2014, 1(1): 1−4. doi: 10.1364/OPTICA.1.000001
[25] Fang L, Padgett M J, Wang J. Sharing a common origin between the rotational and linear doppler effects (Laser Photonics Rev. 11(6)/2017)[J]. Laser Photonics Rev, 2017, 11(6): 1770064. doi: 10.1002/lpor.201770064
[26] Fu S Y, Wang T L, Zhang Z Y, et al. Non-diffractive Bessel-Gauss beams for the detection of rotating object free of obstructions[J]. Opt Express, 2017, 25(17): 20098−20108. doi: 10.1364/OE.25.020098
[27] Zhang W H, Gao J S, Zhang D K, et al. Free-space remote sensing of rotation at the photon-counting level[J]. Phys Rev Appl, 2018, 10(4): 044014. doi: 10.1103/PhysRevApplied.10.044014
[28] Qiu S, Liu T, Ren Y, et al. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect[J]. Opt Express, 2019, 27(17): 24781−24792. doi: 10.1364/OE.27.024781
[29] Zhai Y W, Fu S Y, Yin C, et al. Detection of angular acceleration based on optical rotational Doppler effect[J]. Opt Express, 2019, 27(11): 15518−15527. doi: 10.1364/OE.27.015518
[30] Zhai Y W, Fu S Y, Zhang J Q, et al. Remote detection of a rotator based on rotational Doppler effect[J]. Appl Phys Express, 2020, 13(2): 022012. doi: 10.35848/1882-0786/ab6e0c
[31] Padgett M, Bowman R. Tweezers with a twist[J]. Nat Photonics, 2011, 5(6): 343−348. doi: 10.1038/nphoton.2011.81
[32] Chen M Z, Mazilu M, Arita Y, et al. Dynamics of microparticles trapped in a perfect vortex beam[J]. Opt Lett, 2013, 38(22): 4919−4922. doi: 10.1364/OL.38.004919
[33] Gecevičius M, Drevinskas R, Beresna M, et al. Single beam optical vortex tweezers with tunable orbital angular momentum[J]. Appl Phys Lett, 2014, 104(23): 231110. doi: 10.1063/1.4882418
[34] Liang Y S, Yao B L, Ma B H, et al. Holographic optical trapping and manipulation based on phase-only liquid-crystal spatial light modulator[J]. Acta Opt Sin, 2016, 36(3): 309001. doi: 10.3788/aos201636.0309001
[35] Yang Y J, Ren Y X, Chen M Z, et al. Optical trapping with structured light: a review[J]. Adv Photonics, 2021, 3(3): 034001. doi: 10.1117/1.AP.3.3.034001
[36] Fickler R, Lapkiewicz R, Huber M, et al. Interface between path and orbital angular momentum entanglement for high-dimensional photonic quantum information[J]. Nat Commun, 2014, 5(1): 4502. doi: 10.1038/ncomms5502
[37] Cao H, Gao S C, Zhang C, et al. Distribution of high-dimensional orbital angular momentum entanglement over a 1 km few-mode fiber[J]. Optica, 2020, 7(3): 232−237. doi: 10.1364/OPTICA.381403
[38] Li Z X, Zhu D, Lin P C, et al. High-dimensional entanglement generation based on a Pancharatnam-Berry phase metasurface[J]. Photonics Res, 2022, 10(12): 2702−2707. doi: 10.1364/PRJ.470663
[39] Shen Y J, Rosales-Guzmán C. Nonseparable states of light: from quantum to classical[J]. Laser Photonics Rev, 2022, 16(7): 2100533. doi: 10.1002/lpor.202100533
[40] Wan Z S, Wang H, Liu Q, et al. Ultra-degree-of-freedom structured light for ultracapacity information carriers[J]. ACS Photonics, 2023, 10(7): 2149−2164. doi: 10.1021/acsphotonics.2c01640
[41] 刘永雷, 董震, 陈亚红, 等. 新型相干结构光场调控及应用研究进展[J]. 光电工程, 2022, 49(11): 220178. doi: 10.12086/oee.2022.220178
Liu Y L, Dong Z, Chen Y H, et al. Research advances of partially coherent beams with novel coherence structures: engineering and applications[J]. Opto-Electron Eng, 2022, 49(11): 220178. doi: 10.12086/oee.2022.220178
[42] Zhang D K, Feng X, Cui K Y, et al. Identifying orbital angular momentum of vectorial vortices with pancharatnam phase and stokes parameters[J]. Sci Rep, 2015, 5(1): 11982. doi: 10.1038/srep11982
[43] Niziev V G, Nesterov A V. Influence of beam polarization on laser cutting efficiency[J]. J Phys D: Appl Phys, 1999, 32(13): 1455−1461. doi: 10.1088/0022-3727/32/13/304
[44] Meier M, Romano V, Feurer T. Material processing with pulsed radially and azimuthally polarized laser radiation[J]. Appl Phys A Mater Sci Process, 2007, 86(3): 329−334. doi: 10.1007/s00339-006-3784-9
[45] Zhao W Q, Tang F, Qiu L R, et al. Research status and application on the focusing properties of cylindrical vector beams[J]. Acta Phys Sin, 2013, 62(5): 054201. doi: 10.7498/aps.62.054201
[46] Zhou Z H, Tan Q F, Jin G F. Surface plasmon interference formed by tightly focused higher polarization order axially symmetric polarized beams[J]. Chin Opt Lett, 2010, 8(12): 1178−1181.
[47] Töppel F, Aiello A, Marquardt C, et al. Classical entanglement in polarization metrology[J]. New J Phys, 2014, 16: 073019. doi: 10.1088/1367-2630/16/7/073019
[48] Shen Y J, Zhang Q, Shi P, et al. Optical skyrmions and other topological quasiparticles of light[J]. Nat Photonics, 2024, 18(1): 15−25. doi: 10.1038/s41566-023-01325-7
[49] Lazarev G, Chen P J, Strauss J, et al. Beyond the display: phase-only liquid crystal on Silicon devices and their applications in photonics [Invited][J]. Opt Express, 2019, 27(11): 16206−16249. doi: 10.1364/OE.27.016206
[50] Mirhosseini M, Magaña-Loaiza O S, Chen C C, et al. Rapid generation of light beams carrying orbital angular momentum[J]. Opt Express, 2013, 21(25): 30196−30203. doi: 10.1364/OE.21.030196
[51] Ren Y X, Li M, Huang K, et al. Experimental generation of Laguerre-Gaussian beam using digital micromirror device[J]. Appl Opt, 2010, 49(10): 1838−1844. doi: 10.1364/AO.49.001838
[52] Chen Y, Fang Z X, Ren Y X, et al. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device[J]. Appl Opt, 2015, 54(27): 8030−8035. doi: 10.1364/AO.54.008030
[53] Ji W, Lee C H, Chen P, et al. Meta-q-plate for complex beam shaping[J]. Sci Rep, 2016, 6: 25528. doi: 10.1038/srep25528
[54] Zhou H, Yang J Q, Gao C Q, et al. High-efficiency, broadband all-dielectric transmission metasurface for optical vortex generation[J]. Opt Mater Express, 2019, 9(6): 2699−2707. doi: 10.1364/OME.9.002699
[55] Shaltout A M, Lagoudakis K G, Van De Groep J, et al. Spatiotemporal light control with frequency-gradient metasurfaces[J]. Science, 2019, 365(6451): 374−377. doi: 10.1126/science.aax2357
[56] Shaltout A M, Shalaev V M, Brongersma M L. Spatiotemporal light control with active metasurfaces[J]. Science, 2019, 364(6441): eaat3100. doi: 10.1126/science.aat3100
[57] Jones P H, Rashid M, Makita M, et al. Sagnac interferometer method for synthesis of fractional polarization vortices[J]. Opt Lett, 2009, 34(17): 2560−2562. doi: 10.1364/OL.34.002560
[58] Liu S, Li P, Peng T, et al. Generation of arbitrary spatially variant polarization beams with a trapezoid Sagnac interferometer[J]. Opt Express, 2012, 20(19): 21715−21721. doi: 10.1364/OE.20.021715
[59] Li P, Zhang Y, Liu S, et al. Generation of perfect vectorial vortex beams[J]. Opt Lett, 2016, 41(10): 2205−2208. doi: 10.1364/OL.41.002205
[60] Liu S, Qi S X, Zhang Y, et al. Highly efficient generation of arbitrary vector beams with tunable polarization, phase, and amplitude[J]. Photonics Res, 2018, 6(4): 228−233. doi: 10.1364/PRJ.6.000228
[61] Maurer C, Jesacher A, Fürhapter S, et al. Tailoring of arbitrary optical vector beams[J]. New J Phys, 2007, 9: 78. doi: 10.1088/1367-2630/9/3/078
[62] Wang X L, Ding J P, Ni W J, et al. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement[J]. Opt Lett, 2007, 32(24): 3549−3551. doi: 10.1364/OL.32.003549
[63] Xie Y Y, Cheng Z J, Liu X, et al. Simple method for generation of vector beams using a small-angle birefringent beam splitter[J]. Opt Lett, 2015, 40(21): 5109−5112. doi: 10.1364/OL.40.005109
[64] Shen Y J, Martínez E C, Rosales-Guzmán C. Generation of optical skyrmions with tunable topological textures[J]. ACS Photonics, 2022, 9(1): 296−303. doi: 10.1021/acsphotonics.1c01703
[65] Moreno I, Davis J A, Cottrell D M, et al. Encoding high-order cylindrically polarized light beams[J]. Appl Opt, 2014, 53(24): 5493−5501. doi: 10.1364/AO.53.005493
[66] Fu S Y, Gao C Q, Shi Y, et al. Generating polarization vortices by using helical beams and a Twyman Green interferometer[J]. Opt Lett, 2015, 40(8): 1775−1778. doi: 10.1364/OL.40.001775
[67] Fu S Y, Wang T L, Gao C Q. Generating perfect polarization vortices through encoding liquid-crystal display devices[J]. Appl Opt, 2016, 55(23): 6501−6505. doi: 10.1364/AO.55.006501
[68] Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]. Phys Rev Lett, 2006, 96(16): 163905. doi: 10.1103/PhysRevLett.96.163905
[69] Yi X N, Ling X H, Zhang Z Y, et al. Generation of cylindrical vector vortex beams by two cascaded metasurfaces[J]. Opt Express, 2014, 22(14): 17207−17215. doi: 10.1364/OE.22.017207
[70] Fu S Y, Gao C Q, Wang T L, et al. Simultaneous generation of multiple perfect polarization vortices with selective spatial states in various diffraction orders[J]. Opt Lett, 2016, 41(23): 5454−5457. doi: 10.1364/OL.41.005454
[71] Yue F Y, Wen D D, Zhang C M, et al. Multichannel polarization-controllable superpositions of orbital angular momentum states[J]. Adv Mater, 2017, 29(15): 1603838. doi: 10.1002/adma.201603838
[72] Zhang X, Huang L L, Zhao R Z, et al. Multiplexed generation of generalized vortex beams with on-demand intensity profiles based on metasurfaces[J]. Laser Photonics Rev, 2022, 16(3): 2100451. doi: 10.1002/lpor.202100451
[73] Wu H S, Zeng Q J, Wang X R, et al. Polarization-dependent phase-modulation metasurface for vortex beam (de)multiplexing[J]. Nanophotonics, 2023, 12(6): 1129−1135. doi: 10.1515/nanoph-2022-0710
[74] 柯岚, 章思梦, 李晨霞, 等. 超表面实现复杂矢量涡旋光束的研究进展[J]. 光电工程, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
Ke L, Zhang S M, Li C X, et al. Research progress on hybrid vector beam implementation by metasurfaces[J]. Opto-Electron Eng, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
[75] Naidoo D, Roux F S, Dudley A, et al. Controlled generation of higher-order Poincaré sphere beams from a laser[J]. Nat Photonics, 2016, 10(5): 327−332. doi: 10.1038/nphoton.2016.37
[76] Fan J T, Zhao J, Shi L P, et al. Two-channel, dual-beam-mode, wavelength-tunable femtosecond optical parametric oscillator[J]. Adv Photonics, 2020, 2(4): 045001. doi: 10.1117/1.AP.2.4.045001
[77] Song R, Gao C Q, Zhou H, et al. Resonantly pumped Er: YAG vector laser with selective polarization states at 1.6 µm[J]. Opt Lett, 2020, 45(16): 4626−4629. doi: 10.1364/OL.400835
[78] Song R, Liu X T, Fu S Y, et al. Simultaneous tailoring of longitudinal and transverse mode inside an Er: YAG laser[J]. Chin Opt Lett, 2021, 19(11): 111404.
[79] Sroor H, Huang Y W, Sephton B, et al. High-purity orbital angular momentum states from a visible metasurface laser[J]. Nat Photonics, 2020, 14(8): 498−503. doi: 10.1038/s41566-020-0623-z
[80] Shen Y J, Wang Z Y, Fu X, et al. SU(2) Poincare sphere: A generalized representation for multidimensional structured light[J]. Phys Rev A, 2020, 102(3): 031501. doi: 10.1103/PhysRevA.102.031501
[81] Shen Y J. Rays, waves, SU(2) symmetry and geometry: toolkits for structured light[J]. J Opt, 2021, 23(12): 124004. doi: 10.1088/2040-8986/ac3676
[82] Chen Y F, Jiang C H, Lan Y P, et al. Wave representation of geometrical laser beam trajectories in a hemiconfocal cavity[J]. Phys Rev A, 2004, 69(5): 053807. doi: 10.1103/PhysRevA.69.053807
[83] Dingjan J, van Exter M P, Woerdman J P. Geometric modes in a single-frequency Nd: YVO4 laser[J]. Opt Commun, 2001, 188(5-6): 345−351. doi: 10.1016/S0030-4018(00)01157-3
[84] Shen Y J, Yang X L, Fu X, et al. Periodic-trajectory-controlled, coherent-state-phase-switched, and wavelength-tunable SU(2) geometric modes in a frequency-degenerate resonator[J]. Appl Opt, 2018, 57(32): 9543−9549. doi: 10.1364/AO.57.009543
[85] Tung J C, Liang H C, Lu T H, et al. Exploring vortex structures in orbital-angular-momentum beams generated from planar geometric modes with a mode converter[J]. Opt Express, 2016, 24(20): 22796−22805. doi: 10.1364/OE.24.022796
[86] Shen Y J, Yang X L, Naidoo D, et al. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser: erratum[J]. Optica, 2020, 7(12): 1705. doi: 10.1364/OPTICA.414397
[87] Wan Z S, Wang Z Y, Yang X L, et al. Digitally tailoring arbitrary structured light of generalized ray-wave duality[J]. Opt Express, 2020, 28(21): 31043−31056. doi: 10.1364/OE.400587
[88] Shen Y J, Nape I, Yang X L, et al. Creation and control of high-dimensional multi-partite classically entangled light[J]. Light Sci Appl, 2021, 10(1): 50. doi: 10.1038/s41377-021-00493-x
[89] Wang Z Y, Shen Y J, Naidoo D, et al. Astigmatic hybrid SU(2) vector vortex beams: towards versatile structures in longitudinally variant polarized optics[J]. Opt Express, 2021, 29(1): 315−329. doi: 10.1364/OE.414674
[90] Wan Z S, Shen Y J, Liu Q, et al. Multipartite classically entangled scalar beams[J]. Opt Lett, 2022, 47(8): 2052−2055. doi: 10.1364/OL.451046
[91] Pan J, Wang Z Y, Zhan Z Y, et al. Multiaxial super-geometric mode laser[J]. Opt Lett, 2023, 48(7): 1630−1633. doi: 10.1364/OL.485163
[92] Wan Z S, Shen Y J, Wang Z Y, et al. Divergence-degenerate spatial multiplexing towards future ultrahigh capacity, low error-rate optical communications[J]. Light Sci Appl, 2022, 11(1): 144. doi: 10.1038/s41377-022-00834-4.
[93] Hai L, Zhang Z C, Liu S L, et al. Intra-cavity laser manipulation of high-dimensional non-separable states[J]. Laser Photonics Rev, 2024, 18(4): 2300593. doi: 10.1002/lpor.202300593
[94] Grier D G. A revolution in optical manipulation[J]. Nature, 2003, 424(6950): 810−816. doi: 10.1038/nature01935
[95] Fu S Y, Wang T L, Gao C Q. Perfect optical vortex array with controllable diffraction order and topological charge[J]. J Opt Soc America A, 2016, 33(9): 1836−1842. doi: 10.1364/JOSAA.33.001836
[96] Fu S Y, Zhang S K, Wang T L, et al. Rectilinear lattices of polarization vortices with various spatial polarization distributions[J]. Opt Express, 2016, 24(16): 18486−18491. doi: 10.1364/OE.24.018486
[97] Fu S Y, Gao C Q, Wang T L, et al. Detection of topological charges for coaxial multiplexed perfect vortices[C]//Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 2017: 1–2. https://doi.org/10.1109/OECC.2017.8114895.
[98] Wang H, Fu S Y, Gao C Q. Tailoring a complex perfect optical vortex array with multiple selective degrees of freedom[J]. Opt Express, 2021, 29(7): 10811−10824. doi: 10.1364/OE.422301
[99] Fu S Y, Wang T L, Zhang Z Y, et al. Selective acquisition of multiple states on hybrid Poincare sphere[J]. Appl Phys Lett, 2017, 110(19): 191102. doi: 10.1063/1.4983284
[100] Shang Z J, Fu S Y, Hai L, et al. Multiplexed vortex state array toward high-dimensional data multicasting[J]. Opt Express, 2022, 30(19): 34053−34063. doi: 10.1364/OE.466353
[101] Piccardo M, de Oliveira M, Toma A, et al. Vortex laser arrays with topological charge control and self-healing of defects[J]. Nat Photonics, 2022, 16(5): 359−365. doi: 10.1038/s41566-022-00986-0
[102] Yessenov M, Hall L A, Schepler K L, et al. Space-time wave packets[J]. Adv Opt Photonics, 2022, 14(3): 455−570. doi: 10.1364/AOP.450016
[103] Cao Q, Zhan Q W. Spatiotemporal sculpturing of light and recent development in spatiotemporal optical vortices wavepackets (Invited)[J]. Acta Photonica Sin, 2022, 51(1): 0151102. doi: 10.3788/gzxb20225101.0151102
[104] Ni J C, Wang C W, Zhang C C, et al. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material[J]. Light Sci Appl, 2017, 6(7): e17011. doi: 10.1038/lsa.2017.11
[105] Ruffato G. Non-destructive OAM measurement via light-matter interaction[J]. Light Sci Appl, 2022, 11(1): 55. doi: 10.1038/s41377-022-00749-0
[106] Zhao Z, Song H, Zhang R Z, et al. Dynamic spatiotemporal beams that combine two independent and controllable orbital-angular-momenta using multiple optical-frequency-comb lines[J]. Nat Commun, 2020, 11(1): 4099. doi: 10.1038/s41467-020-17805-1
[107] Chong A, Wan C H, Chen J, et al. Generation of spatiotemporal optical vortices with controllable transverse orbital angular momentum[J]. Nat Photonics, 2020, 14(6): 350−354. doi: 10.1038/s41566-020-0587-z
[108] Wan C H, Chen J, Chong A, et al. Photonic orbital angular momentum with controllable orientation[J]. Natl Sci Rev, 2022, 9(7): nwab149. doi: 10.1093/nsr/nwab149
[109] Cao Q, Zheng P K, Zhan Q W. Vectorial sculpturing of spatiotemporal wavepackets[J]. APL Photonics, 2022, 7(9): 096102. doi: 10.1063/5.0107411
[110] Wan C H, Cao Q, Chen J, et al. Toroidal vortices of light[J]. Nat Photonics, 2022, 16(7): 519−522. doi: 10.1038/s41566-022-01013-y
[111] Chen W, Liu Y, Yu A Z, et al. Observation of chiral symmetry breaking in toroidal vortices of light[J]. Phys Rev Lett, 2024, 132(15): 153801. doi: 10.1103/PhysRevLett.132.153801
[112] Papasimakis N, Raybould T, Fedotov V A, et al. Pulse generation scheme for flying electromagnetic doughnuts[J]. Phys Rev B, 2018, 97(20): 201409. doi: 10.1103/PhysRevB.97.201409
[113] Shen Y J, Yu B S, Wu H J, et al. Topological transformation and free-space transport of photonic hopfions[J]. Adv Photonics, 2023, 5(1): 015001. doi: 10.1117/1.AP.5.1.015001
[114] Zdagkas A, McDonnell C, Deng J H, et al. Observation of toroidal pulses of light[J]. Nat Photonics, 2022, 16(7): 523−528. doi: 10.1038/s41566-022-01028-5
[115] Guo C, Xiao M, Orenstein M, et al. Structured 3D linear space-time light bullets by nonlocal nanophotonics[J]. Light Sci Appl, 2021, 10(1): 160. doi: 10.1038/s41377-021-00595-6
-


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: