Metasurface beamsplitter with large field of view and equal diffraction angle interval
-
摘要
激光雷达目前主要使用达曼光栅实现激光分束。然而,达曼光栅作为周期性衍射光学器件需要满足光栅方程,其各衍射角的正弦值成等差数列,无法实现均匀的角度分束,同时理论衍射效率受到限制。本文将角谱法和随机搜索算法结合,设计了一种非周期性红外超构表面激光分束器。该分束器可实现70°的分束全角等角度间隔的41分束。其理论衍射效率达84%,高于二元相位器件的理论极限。在实验测试中,超构表面分束器具有较好的分束均匀性,可促进激光雷达的发展。
Abstract
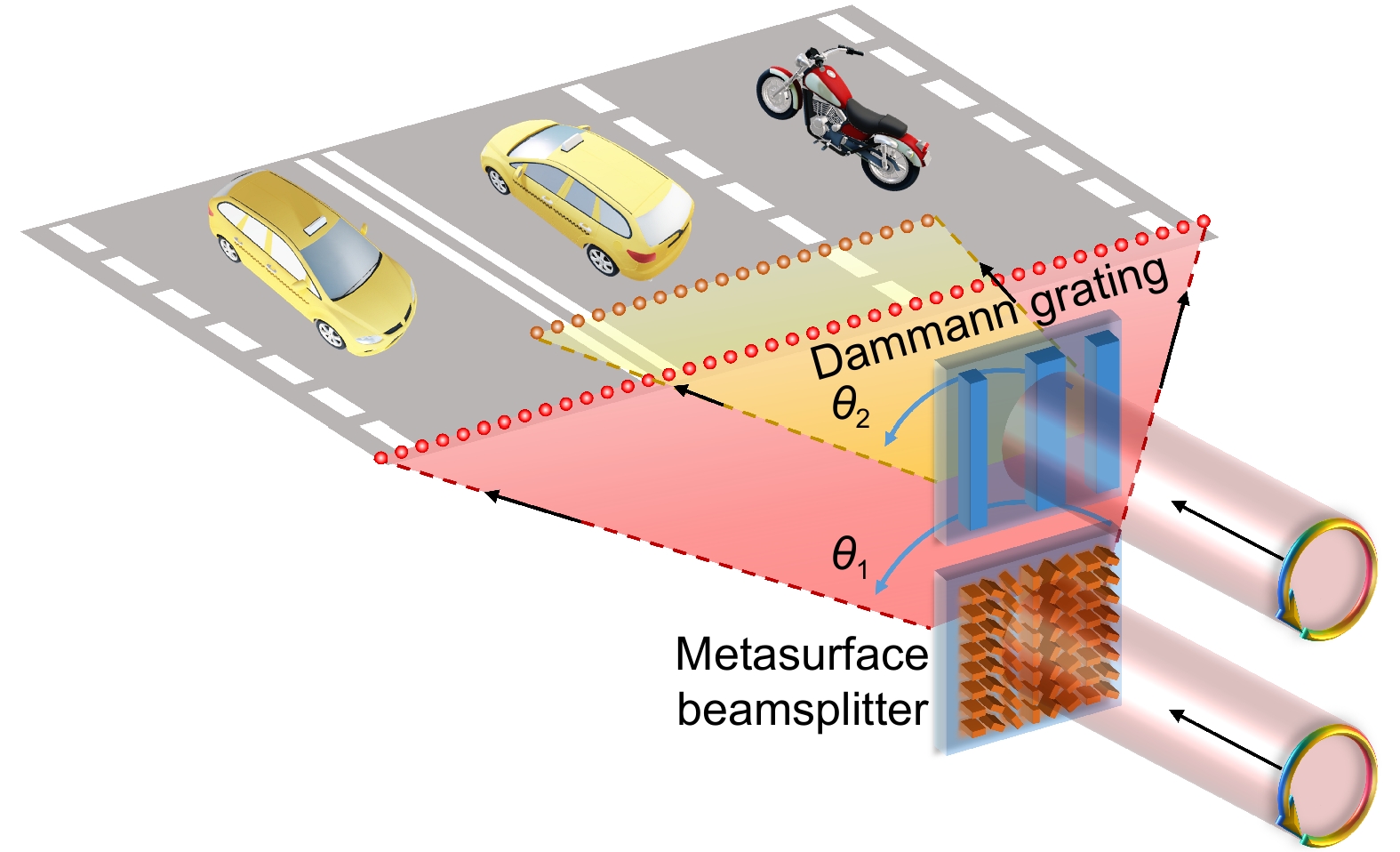
LiDAR currently mainly uses a Dammann grating as the laser beamsplitter. However, as a periodic diffraction optical device, the Dammann grating satisfies the grating equation requiring each diffraction angle's sine value to form an arithmetic progression, which cannot achieve uniform angular beam-splitting. The theoretical diffraction efficiency is also limited. This paper uses the angular spectrum and random search optimization algorithm to design a more flexible non-periodic beamsplitter. Simulations show that the metasurface beamsplitter can achieve a 70-degree field angle of 41 beams with an equal diffraction angle interval. The simulated diffraction efficiency reaches 84% which is higher than the diffraction limit of a binary phase device. In experiments, the metasurface beamsplitter has good beam-splitting uniformity and can promote the development of LiDAR.
-
Key words:
- metasurface /
- beamsplitter /
- Dammann grating /
- DOE
-
Overview
Overview: Autonomous driving has made significant progress in the past few years. LiDAR which can precisely measure the distance to reflecting surfaces is an important sensor for autonomous driving. Multi-line LiDAR is required to improve the accuracy and frame of LiDAR. Dammann gratings are commonly used as laser beamsplitters in multi-line LiDAR. As binary phase diffraction optical devices, they are relatively easy to process. Numerical solutions for Dammann gratings with common numbers of beam-splitting have been studied. However, as a periodic diffraction optical device, Dammann grating satisfies the grating equation requiring each diffraction angle's sine value to form an arithmetic progression.
In this paper, we use the angular spectrum and random search optimization algorithm to design a more flexible non-periodic beamsplitter. The angular spectrum, a discrete Fourier transform of the incident complex amplitude array, can calculate the angular response in the far field. We propose to expand the diffraction calculation window to reduce the frequency interval of the Fourier transform. Using the finer frequency grid, we build the far-field angular target function with equal angle interval beam-splitting. We set the evaluation function as a linear combination of root mean square error and efficiency. This evaluation function setting can take into account both error control and device diffraction efficiency. The random search optimization algorithm only adopts the optimization with a decreasing evaluation function according to the evaluation function. Simulations show that the metasurface beamsplitter can generate 41 beams with a 70° field angle. The normalized standard deviation of the simulated light intensity of each spot is 0.011. The simulated diffraction efficiency reaches 84% which is higher than the diffraction limit of the binary phase device.
To realize such phase modulation, we use full-wave simulation to design an efficient amorphous silicon nanopillar with geometric phase modulation at the 1550-nm wavelength. We use electron beam lithography to process a 1-mm diameter metasurface beamsplitter. Experimental measurements confirm the beam-splitting function of the metasurface. The experimentally measured standard deviation of beam power is 0.179, and the average half-maximum full width of the beam-splitting direction is 0.143°.
-

-
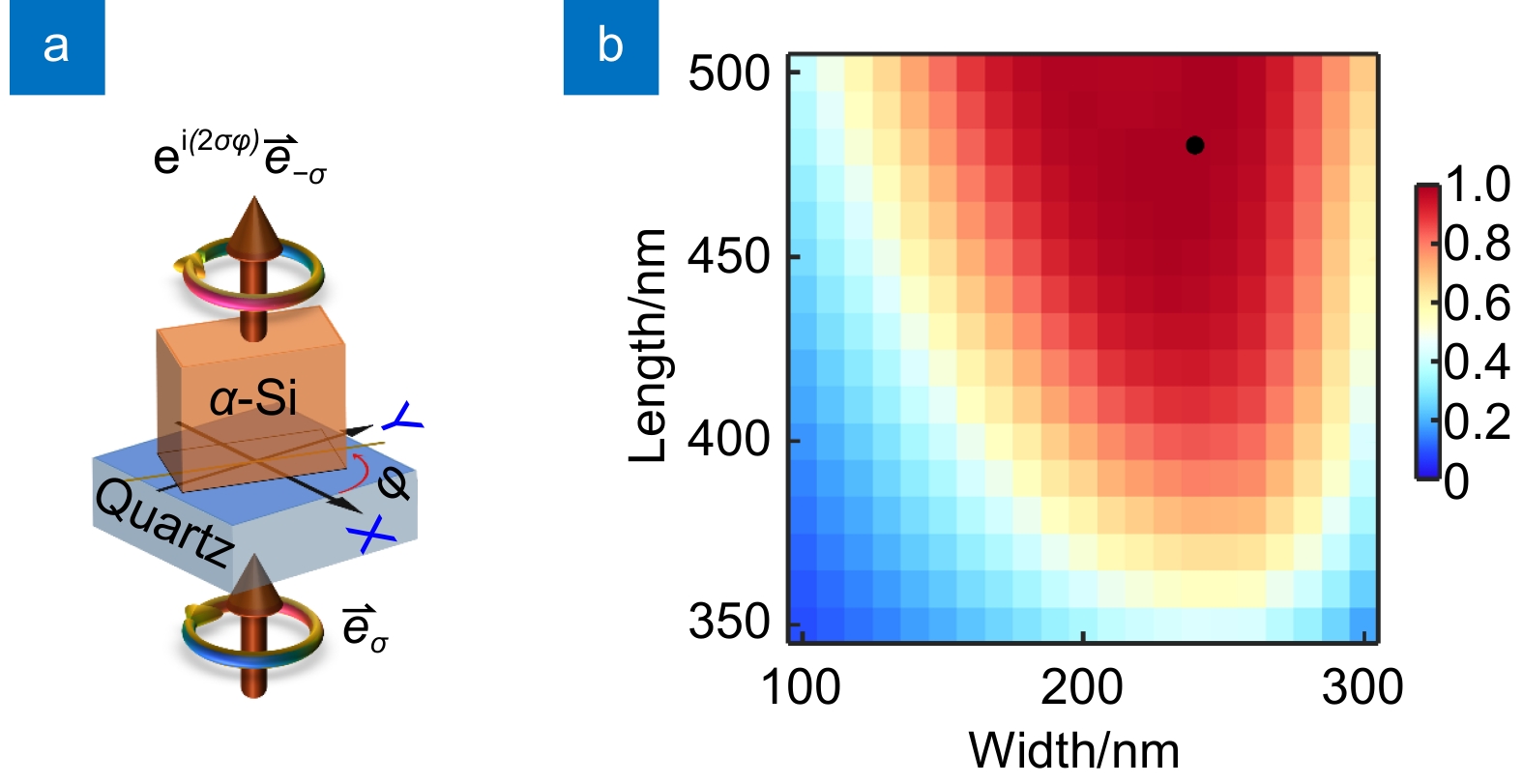
图 2 (a) 超构表面单元示意图,基底为500 μm的石英,硅膜厚度为760 nm,超构表面结构单元周期为650 nm;(b) 周期650 nm时相反手性圆偏振光的效率,图中黑点标注选取的超构表面结构单元,其长为480 nm,宽为240 nm,转化效率为99.2%
Figure 2. (a) Schematic diagram of the metasurface cell, with a length of 480 nm, a width of 240 nm, a height of 760 nm, and a period of 650 nm. The substrate is 500-μm thick; (b) Efficiency of cross circularly polarized light at 650 nm period. The black dot in (b) is the selected metasurface cell; the length and width of the nanopillar are 480 nm and 240 nm, respectively; the conversion efficiency is 99.2%
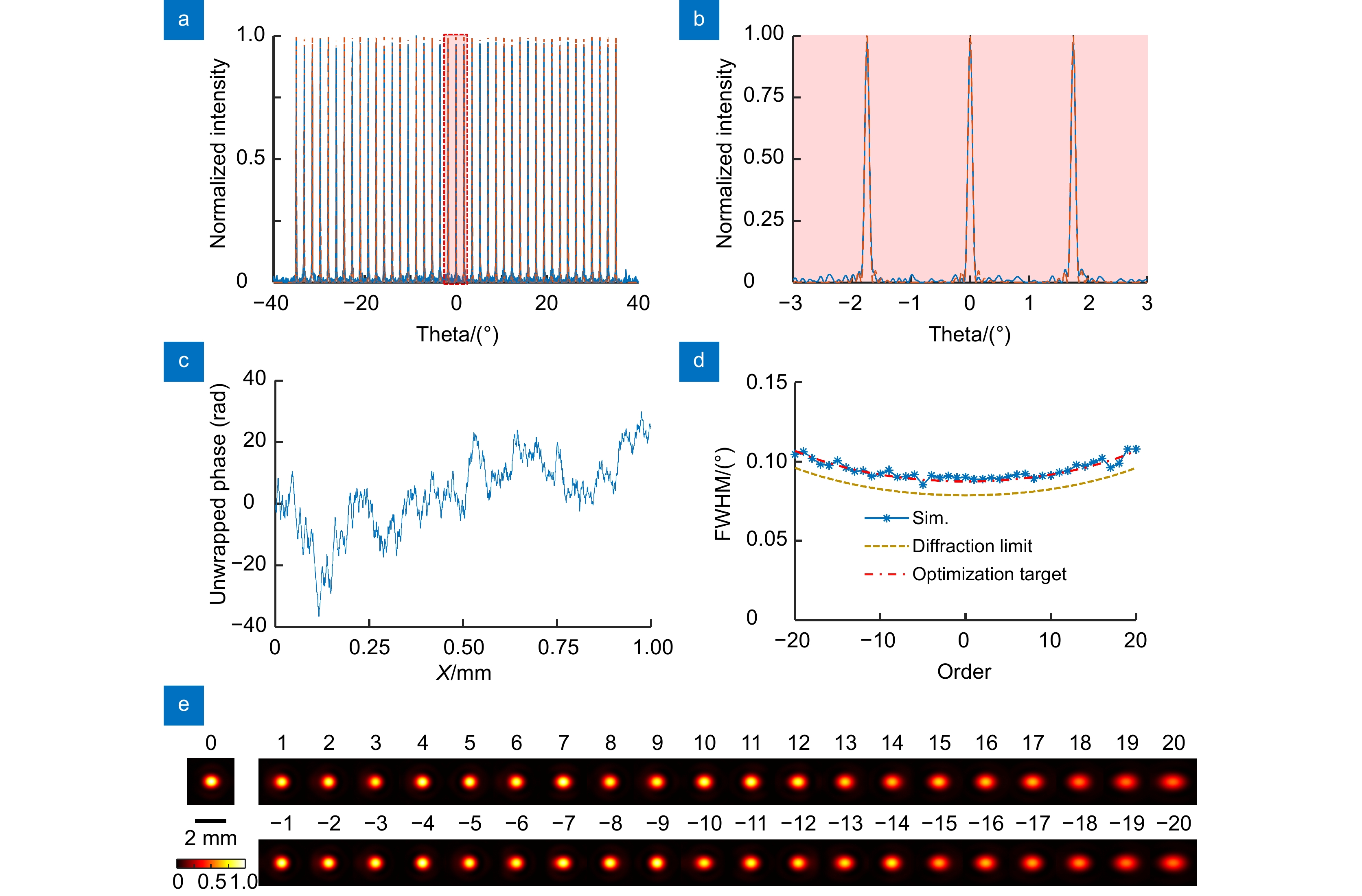
图 3 (a, b) 一维仿真的分束器远场强度的角度分布,蓝色实线为仿真结果,橙色虚线为强度优化目标,(b)为(a)中橘色区域的放大展示;(c) 解包裹后的分束器相位;(d) 为(a)中各衍射级次光斑的半高全宽,蓝色星标实线为仿真结果,红色点划线为优化目标,黄色虚线为衍射极限;(e) 利用瑞利-索莫非衍射积分数值计算得到的距离器件40 cm处平面上的41束光斑。每个光斑裁切为3 mm大小的方块后拼接在一起
Figure 3. (a, b) One-dimensional simulation of the beamsplitter intensity angle distribution. The blue line is the simulation result, and the orange dashed line is the optimization target; (c) The unwrapped phase of the beamsplitter; (d) The full width at half maximums (FWHMs) of spots in (a). The blue line is the simulation result, the yellow dashed line is the diffraction limit, and the red dotted line is the optimization target; (e) 41 rays on the 40 cm distancing plane obtained by the numerical Rayleigh-Somerphy diffraction integral. Each light spot is cut into 3 mm squares and spliced together
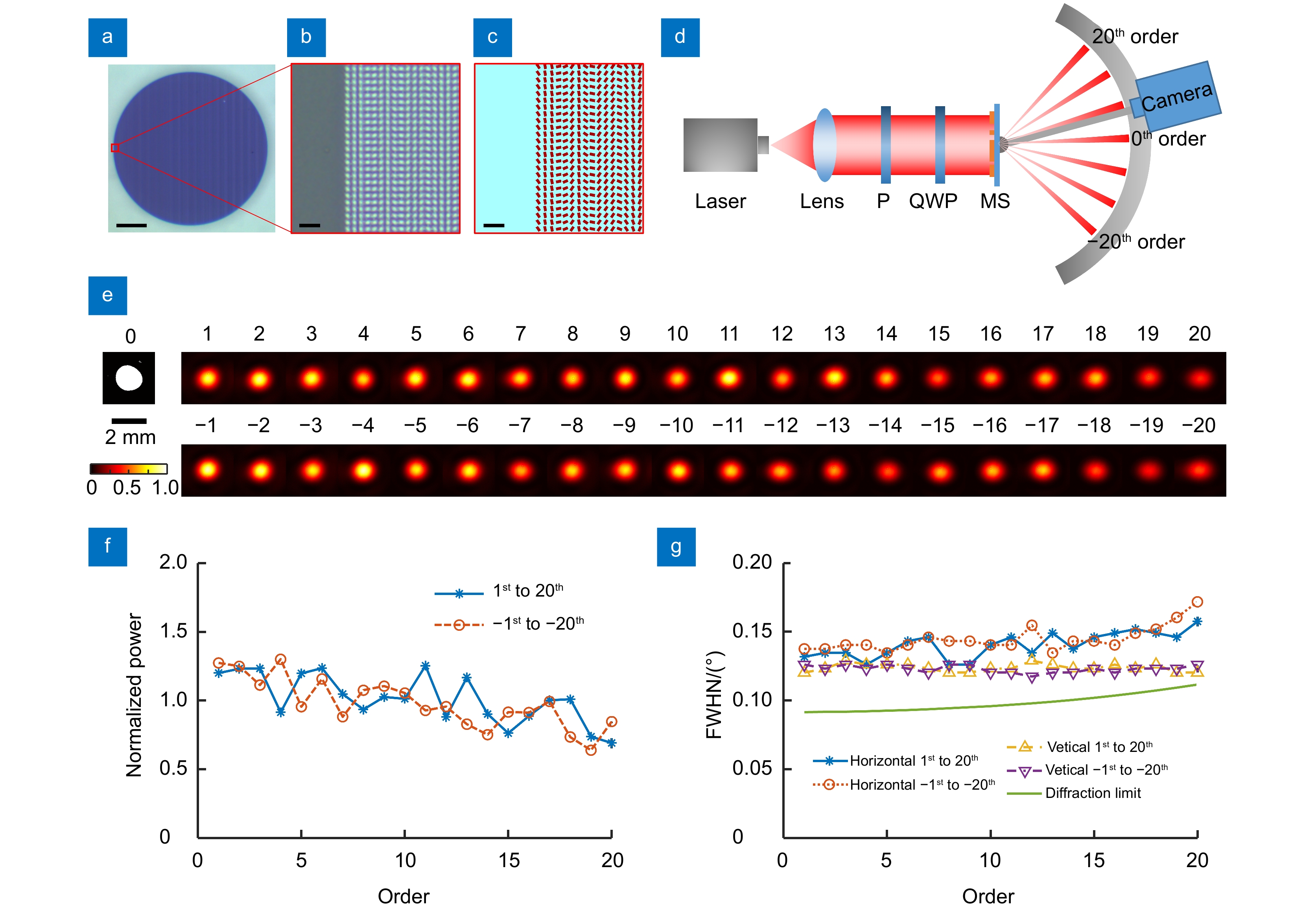
图 4 (a, b)加工的超构表面的光学显微镜图像。(a) 5倍物镜,比例尺为200 μm;(b)100倍物镜,比例尺为2 μm;(c) (b)超构表面相同区域的设计图纸,比例尺为2 μm;(d) 实验光路示意图,P、QWP、MS分别表示偏振片,四分之一波片和超构表面;(e) 相机采集的不同衍射级次的41束光斑。每个光斑裁切为3 mm大小的方块后拼接在一起;(f) 实验测得的光斑功率。蓝色星标为1至20级光斑,橙色圆标为−1至−20级光斑;(g) 实验测得的光斑半高全宽。蓝色星标实和橙色圆标点线分别为1至20级和−1至−20级的水平方向半高全宽。黄色正三角形虚线和紫色倒三角形点划线分别为1至20级和−1至−20级的竖直方向半高全宽。绿色实线为光斑横向的衍射极限
Figure 4. (a, b) Metasurface morphology imaged by 5x and 100x objective microscopes. Scalebars: 200 μm and 2 μm; (c) Design drawing of the same area in Fig. 4(b), with a scale of 2 μm; (d) Schematic diagram of the experimental optical path. P: polarizer; QWP: quarter-wave plate; MS: metasurface; (e) Captured 41 rays. Each beam is cut into 3 mm squares and spliced together; (f) Experimentally measured power of beams. The blue line represents the beams from the 1st to 20th orders and the orange dotted line is from the −1st to −20th orders; (g)Experimentally measured FWHMs. The solid blue line with asterisks and the orange dotted line with circles are the horizontal FWHMs from the 1st to the 20th orders and from the −1st to the −20th orders, respectively. The dashed yellow line with regular triangles and the dashed-dotted purple line with inverted triangles are the vertical FWHMs from the 1st to the 20th orders and from the −1st to the −20th orders, respectively. The solid green line is the horizontal diffraction limit.
-
参考文献
[1] Li Y, Ibanez-Guzman J. Lidar for autonomous driving: the principles, challenges, and trends for automotive lidar and perception systems[J]. IEEE Signal Process Mag, 2020, 37(4): 50−61. doi: 10.1109/MSP.2020.2973615
[2] Leonard J, How J, Teller S, et al. A perception‐driven autonomous urban vehicle[J]. J Field Robot, 2008, 25(10): 727−774. doi: 10.1002/rob.20262
[3] Dammann H, Görtler K. High-efficiency in-line multiple imaging by means of multiple phase holograms[J]. Opt Commun, 1971, 3(5): 312−315. doi: 10.1016/0030-4018(71)90095-2
[4] Zhou C H, Liu L R. Numerical study of Dammann array illuminators[J]. Appl Opt, 1995, 34(26): 5961−5969. doi: 10.1364/AO.34.005961
[5] Zhao S, Chung P S. Design of a circular Dammann grating[J]. Opt Lett, 2006, 31(16): 2387−2389. doi: 10.1364/OL.31.002387
[6] Wen F J, Chung P S. Use of the circular Dammann grating in angle measurement[J]. Appl Opt, 2008, 47(28): 5197−5200. doi: 10.1364/AO.47.005197
[7] Yu J J, Zhou C H, Jia W, et al. Three-dimensional Dammann array[J]. Appl Opt, 2012, 51(10): 1619−1630. doi: 10.1364/AO.51.001619
[8] Yu J J, Zhou C H, Jia W, et al. Three-dimensional Dammann vortex array with tunable topological charge[J]. Appl Opt, 2012, 51(13): 2485−2490. doi: 10.1364/AO.51.002485
[9] Fu W W, Zhao D, Li Z Q, et al. Ultracompact meta-imagers for arbitrary all-optical convolution[J]. Light Sci Appl, 2022, 11(1): 62. doi: 10.1038/s41377-022-00752-5
[10] Zhao D, Dong Z G, Huang K. High-efficiency holographic metacoder for optical masquerade[J]. Opt Lett, 2021, 46(6): 1462−1465. doi: 10.1364/OL.419542
[11] 李瑞琛, 邹毅军, 陈天航, 等. 宽频消色散超表面全息成像[J]. 光电工程, 2023, 50(8): 230118. doi: 10.12086/oee.2023.230118
Li R C, Zou Y J, Chen T H, et al. Broadband achromatic metasurface holography[J]. Opto-Electron Eng, 2023, 50(8): 230118. doi: 10.12086/oee.2023.230118
[12] 杨睿, 于千茜, 潘一苇, 等. 基于片上超表面的多路方向复用全息术[J]. 光电工程, 2022, 49(10): 220177. doi: 10.12086/oee.2022.220177
Yang R, Yu Q Q, Pan Y W, et al. Directional-multiplexing holography by on-chip metasurface[J]. Opto-Electron Eng, 2022, 49(10): 220177. doi: 10.12086/oee.2022.220177
[13] Li G X, Zhang S, Zentgraf T. Nonlinear photonic metasurfaces[J]. Nat Rev Mater, 2017, 2(5): 17010. doi: 10.1038/natrevmats.2017.10
[14] 冯睿, 田耀恺, 刘亚龙, 等. 拓扑优化超表面的偏振复用光学微分运算[J]. 光电工程, 2023, 50(9): 230172. doi: 10.12086/oee.2023.230172
Feng R, Tian Y K, Liu Y L, et al. Polarization-multiplexed optical differentiation using topological metasurfaces[J]. Opto-Electron Eng, 2023, 50(9): 230172. doi: 10.12086/oee.2023.230172
[15] Zhao H, Wang X K, Liu S T, et al. Highly efficient vectorial field manipulation using a transmitted tri-layer metasurface in the terahertz band[J]. Opto-Electron Adv, 2023, 6(2): 220012. doi: 10.29026/oea.2023.220012
[16] Song X, Huang L L, Tang C C, et al. Selective diffraction with complex amplitude modulation by dielectric metasurfaces[J]. Adv Opt Mater, 2018, 6(4): 1701181. doi: 10.1002/adom.201701181
[17] Ni Y B, Chen S, Wang Y J, et al. Metasurface for structured light projection over 120° field of view[J]. Nano Lett, 2020, 20(9): 6719−6724. doi: 10.1021/acs.nanolett.0c02586
[18] Xie X, Pu M B, Jin J J, et al. Generalized pancharatnam-berry phase in rotationally symmetric meta-atoms[J]. Phys Rev Lett, 2021, 126(18): 183902. doi: 10.1103/PhysRevLett.126.183902
[19] Lin D M, Fan P Y, Hasman E, et al. Dielectric gradient metasurface optical elements[J]. Science, 2014, 345(6194): 298−302. doi: 10.1126/science.1253213
[20] Johnson S G, Frigo M. A modified split-radix FFT with fewer arithmetic operations[J]. IEEE Trans Signal Process, 2007, 55(1): 111−119. doi: 10.1109/TSP.2006.882087
[21] Shen F B, Wang A B. Fast-Fourier-transform based numerical integration method for the Rayleigh-Sommerfeld diffraction formula[J]. Appl Opt, 2006, 45(6): 1102−1110. doi: 10.1364/AO.45.001102
[22] Kim S, Kim J, Kim K, et al. Anti-aliased metasurfaces beyond the Nyquist limit[Z]. arXiv: 2406.11261, 2024. https://doi.org/10.48550/arXiv.2406.11261.
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: