E-mail Alert
RSS
Torsion pendulum design for metasurface-based diffraction light sail optical force measurement
-
摘要:
基于超构表面技术的衍射光帆在矢量光场的作用下，其最大加速度、自稳定推进力和姿态可控性可以得到提高。在真空环境中，精确测量衍射光帆在矢量光场作用下产生的光力对建立完整的空间动力学模型至关重要。基于扭秤弱力测量技术，本文分别设计了面向形状规则与不规则的衍射光帆的光力测量扭秤。对于形状规则的光帆，可通过严格控制扭秤的尺寸及各部件相对位置误差等方法提高测量精度，该扭秤理论测量误差为0.55‰。形状不规则光帆样品的转动惯量及误差难以精确计算，通过在扭秤上增加可随时取放的标准球，标准球的转动惯量可以通过其几何尺寸及位置严格计算，测量扭秤在有无标准球的状态下的周期即可以给出其受到的光力大小。本研究提升了光力测量实验的效率和灵活性，为光帆推进、空间碎片轨道操控等应用提供数据支撑。
Abstract:When a vector optical field acts on the metasurface-based diffractive light sail, the maximum acceleration, self-stabilizing thrust, and attitude controllability of the diffractive light sail can be enhanced. In a vacuum environment, it is important to measure the optical force acting on the diffraction light sail to establish a comprehensive space dynamics model under the influence of vector optical fields. Based on the weak force measurement technique, we have designed an optical force measurement torsion pendulum for both regular and irregular shaped diffraction light sails. The measurement accuracy of regular-shaped light sails can be enhanced by ensuring that the size of the torsion pendulum and relative position errors of each component are strictly controlled. The force measurement has a relative error of 0.55‰. We have also designed a torsion pendulum to measure the optical force of the irregular-shaped light sails, which can hardly calculate the moment of inertia. There are two standard spheres on the torsion pendulum that can be placed or removed at any time. The magnitude of the optical force acting on the complex object can be measured by calculating the moment of inertia of the spheres. This research enhances the efficiency and flexibility of optical force measurement experiments, providing data support for applications such as laser-driven light sail and space debris remediation.
-
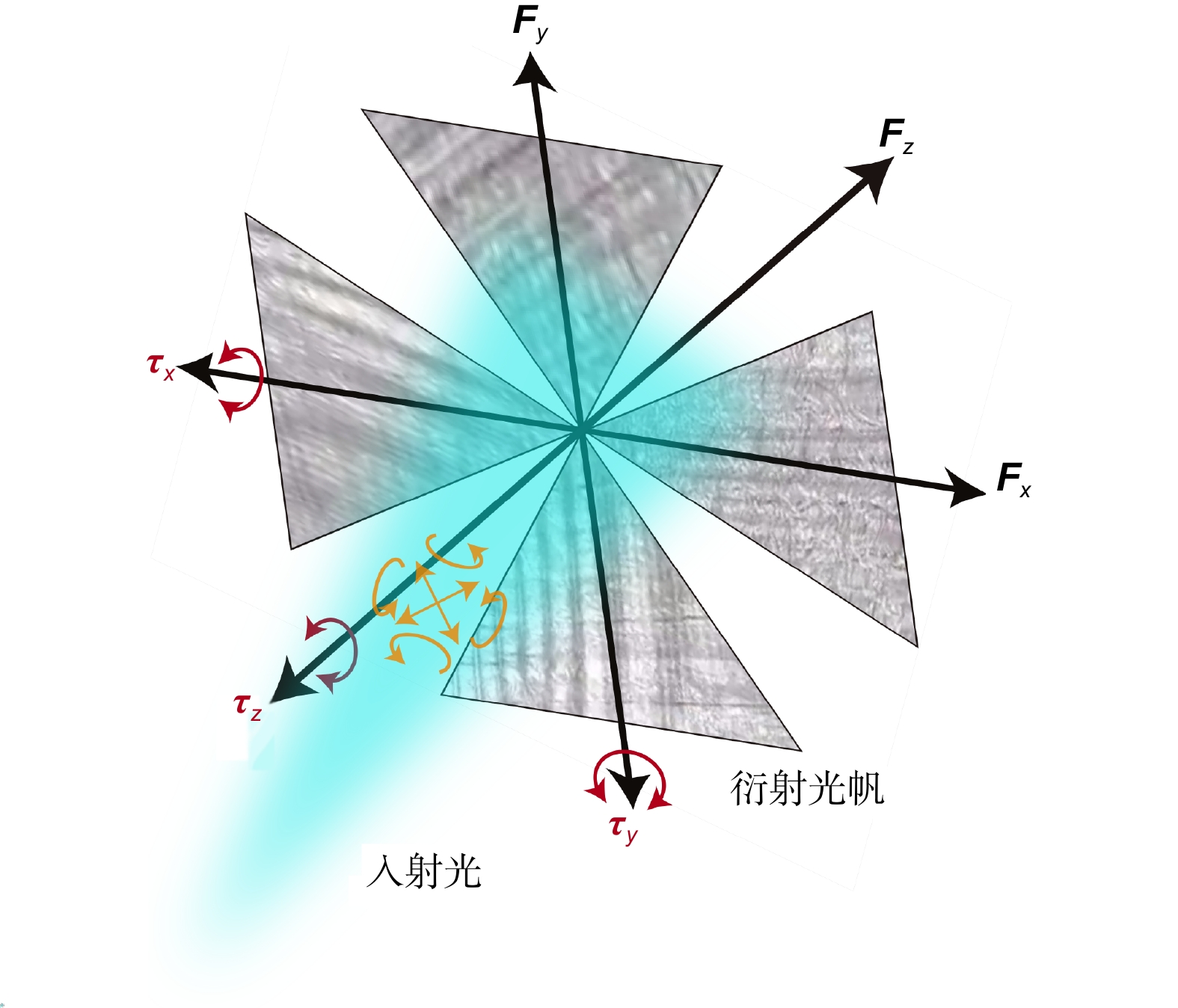
Key words:
- optical force /
- light sail /
- torsion pendulum /
- weak force measurement /
- metasurface
-
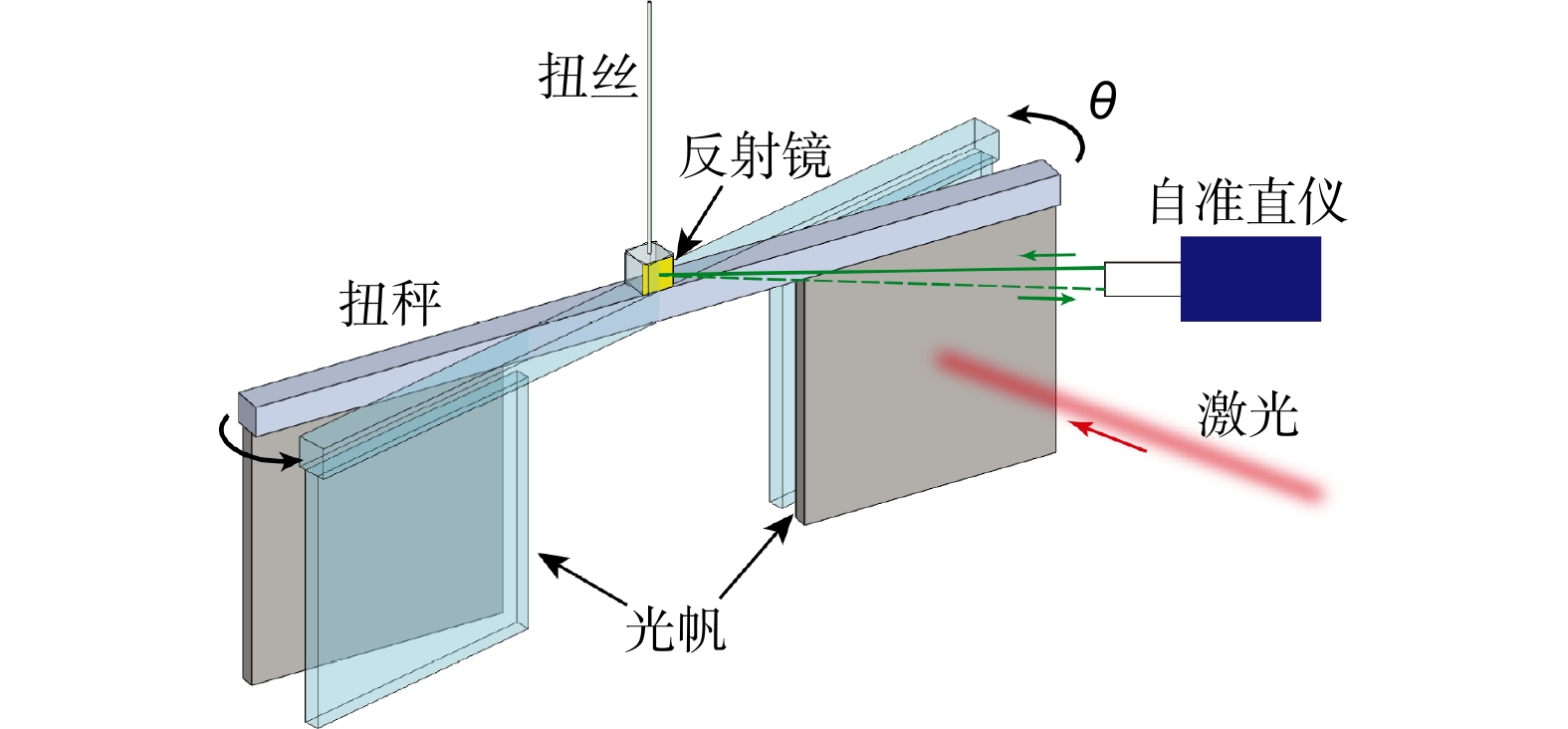
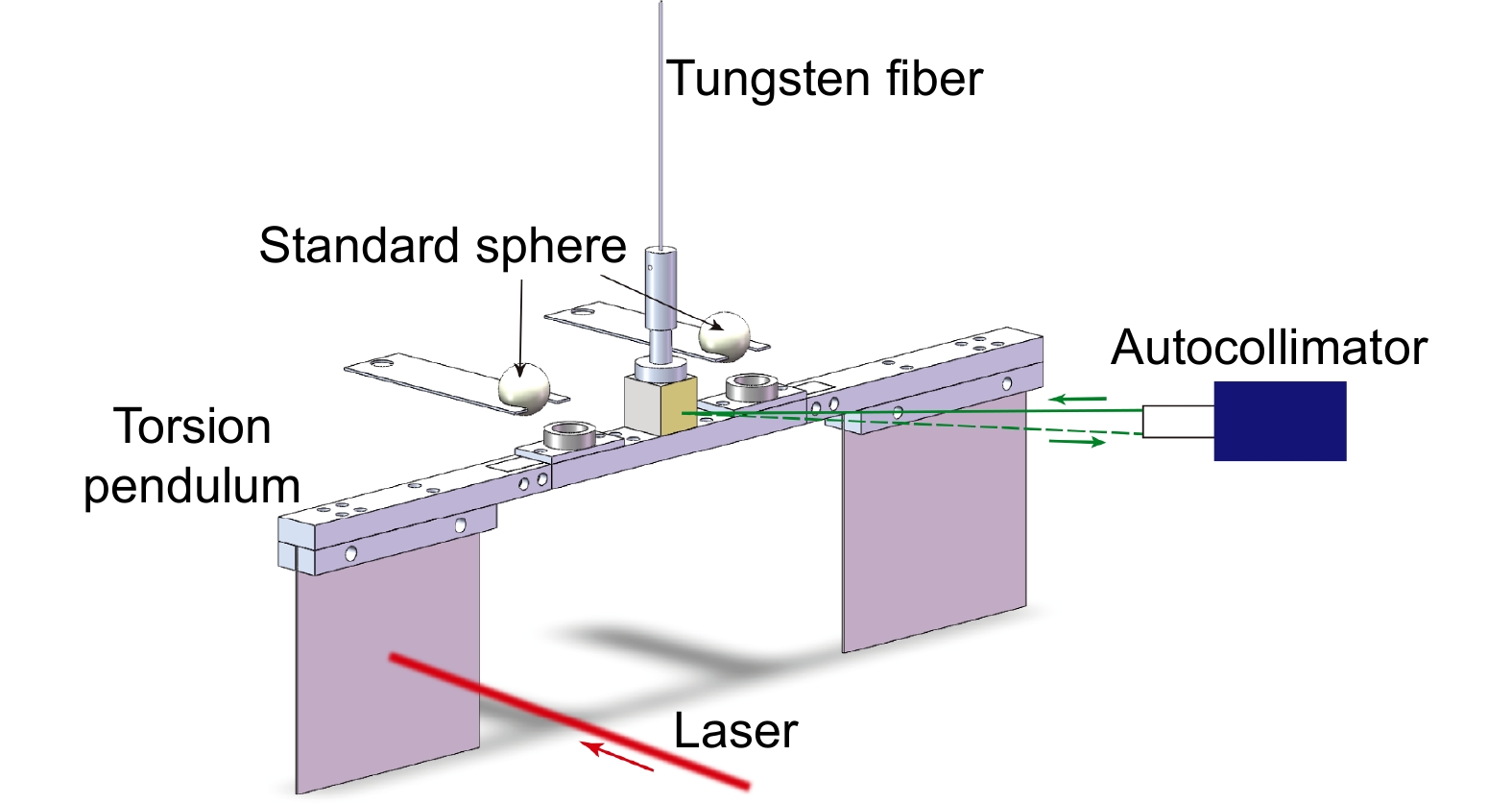
Overview: The exchange of momentum between photons and objects is what optical force is all about. The research of optical forces can be traced back to the astronomer Kepler's observations of comet tails. The understanding of the optical force has been enhanced by the Maxwell's classical electromagnetic field theory and Einstein's light quantum model. The continuous development of lasers has led to a new stage in optical technology, such as optical tweezers, laser cooling, and solar sails. Light sails are considered one of the ways to achieve interstellar travel, with the advantages of not needing to carry propellant and carrying a high payload. In recent years, the continuous development of metasurface technology has enabled researchers to apply diffraction optical force technology based on sub-wavelength structures to light sails to solve the problems of traditional solar sails, such as difficult attitude control and limited acceleration, thereby improving the feasibility of light sail driving technology. Spatial positions have an impact on the polarization state of the vector optical. When combined with spatially multiplexed metamaterial surfaces, the degrees of freedom for attitude manipulation of the diffractive light sail can be increased, leading to greater maximum acceleration, self-stabilizing thrust, and attitude controllability. In space, even subtle mechanical effects can cause the flight trajectory of the diffraction light sail to deviate from the preset orbit. Experimentally verification is necessary for the mechanical effects between the diffraction light sail and the vector optical field. Therefore, accurately measuring the multi-axis optical force generated by the diffraction light sail under vector light fields is crucial. There are few experiments that directly measure optical force in the world, and the measurement accuracy is generally not high. These experiments usually use torsion pendulums, piezoelectric crystals, flat capacitors, and other measurement tools. Based on the weak force measurement technology of torsion pendulums, this paper proposes the design of optical force torsion pendulums for regular-shaped and irregular-shaped diffraction light sails, and performs error analysis on the two torsion pendulums. For regular-shaped light sails, measurement accuracy can be improved by strictly controlling the size of the torsion pendulum and the relative position errors of each component. The force measurement has a relative error of 0.55‰. In order to meet the optical force measurement of irregular-shaped light sails and reduce the requirements for the processing accuracy and assembly accuracy of each component of the torsion pendulum, this article proposes a design scheme for an optical torsion pendulum suitable for complex objects. The fundamental element is the mid torsion pendulum horizontal rod and two standard balls. Measurement of the torsion pendulum’s motion with and without the ball allows for accurate k-value estimation of the system. Different fixtures designed to match the main body of the torsion pendulum cam be used to measure the light force on different samples. Complex shapes can be accommodated by this design. The optical power measurement needs to be tested on the sample. The optical torsion pendulum for irregular-shaped light sails is theoretically capable of achieving a relative error of 0.38% through theoretical error analysis. The design of this article enhances the accuracy of optical force measurement and the efficiency and flexibility of experiments, paving the way for applications like laser-driven light sail propulsion and space debris remediation.
-
-
图 1 圆偏光作用下的反射型几何相位超构表面
Figure 1. Reflective-type geometric-phase metasurface under the illumination of circularly polarized light
图 2 矢量光场作用下衍射光帆的多轴运动
Figure 2. Multi-axis movement of the diffractive light sail under the illumination of vector optical fields
图 4 面向形状规则光帆样品的光力扭秤
Figure 4. Optical force torsion pendulum for the regular-shaped light sail
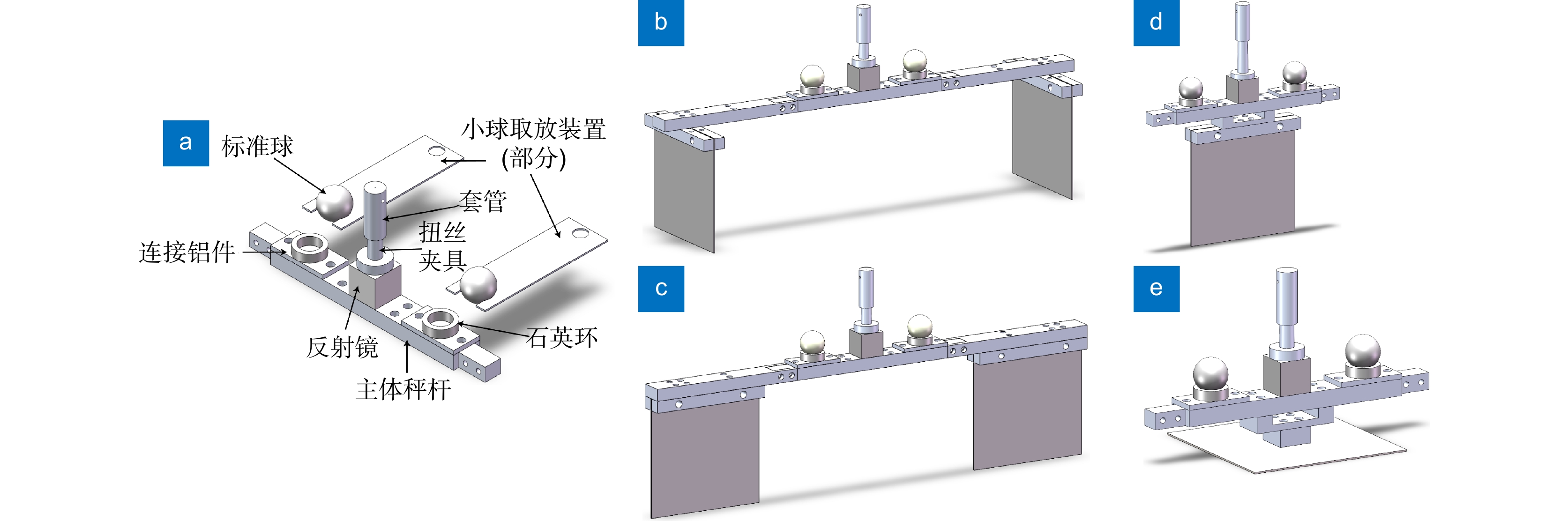
图 5 面向形状复杂光帆样品的光力扭秤。(a)扭秤核心部分；(b-e)六轴光力扭秤：(b) x,y方向光力扭秤；(c) z方向光力扭秤；(d) x,y方向光转矩扭秤；(e) z方向光转矩扭秤
Figure 5. Optical force torsion pendulum for the irregular-shaped light sail. (a) Core part of the torsion pendulum; (b-e) Six-axis optical force torsion pendulum: (b) Optical force torsion pendulum in the x and y directions; (c) Optical force torsion pendulum in the z direction; (d) Optical torque torsion pendulum in the x and y directions; (e) Optical torque torsion pendulum in the z direction
表 1 面向形状规则光帆样品的光力扭秤测光力理论误差
Table 1. Theoretical error in optical force measurement for the optical force torsion pendulum for the regular-shaped light sail
参数名称 中心值 理论误差 对待测力的影响/N 光力F ±2.0×10−9 力臂R 75 mm 0.03 mm 8.0×10−13 转动惯量I 2.73×10−4 kg·m2 6.0×10−8 kg·m2 4.4×10−13 扭秤振幅$\Delta \theta $ ±7.4 mrad 1.2 μrad 3.2×10−13 扭秤周期T 730.1 s 0.1 s 5.5×10−13 总误差 1.1×10−12 
下载: 导出CSV
表 2 z方向光力扭秤测光力理论误差
Table 2. Theoretical error in optical force measurement for the optical force torsion pendulum in the z direction
参数名称 中心值 理论误差 对待测力的影响/N 光力F ±2.0×10−9 — — 力臂R 75 mm 0.03 mm 8.0×10−13 扭秤振幅$\Delta \theta $ ±7.44 mrad 1.2 μrad 3.2×10−13 标准球转动惯量IB 2.457×10−5 kg∙m2 1.79×10−8 kg∙m2 1.5×10−12 扭秤周期T1(有球) 649.3 s 0.1 s 5.4×10−12 扭秤周期T2(无球) 611.2 s 0.1 s 5.1×10−12 总误差 7.6×10−12
下载: 导出CSV
-
[1] Nichols E F, Hull G F. The pressure due to radiation. (second paper. )[J]. Phys Rev (Series I), 1903, 17(1): 26−50. doi: 10.1103/PhysRevSeriesI.17.26
[2] Maxwell J C. A treatise on electricity and magnetism[J]. Nature, 1873, 7(182): 478−480. doi: 10.1038/007478a0
[3] Einstein A. Concerning an heuristic point of view toward the emission and transformation of light[J]. Am J Phys, 1965, 33(5): 367
[4] Ashkin A, Dziedzic J M, Bjorkholm J E, et al. Observation of a single-beam gradient force optical trap for dielectric particles[J]. Opt Lett, 1986, 11(5): 288−290. doi: 10.1364/OL.11.000288
[5] Long L, Deng Q R, Huang R T, et al. 3D printing of plasmonic nanofocusing tip enabling high resolution, high throughput and high contrast optical near-field imaging[J]. Light Sci Appl, 2023, 12(1): 219. doi: 10.1038/s41377-023-01272-6
[6] Chan J, Alegre T P M, Safavi-Naeini A H, et al. Laser cooling of a nanomechanical oscillator into its quantum ground state[J]. Nature, 2011, 478(7367): 89−92. doi: 10.1038/nature10461
[7] Peterson R W, Purdy T P, Kampel N S, et al. Laser cooling of a micromechanical membrane to the quantum backaction limit[J]. Phys Rev Lett, 2016, 116(6): 063601. doi: 10.1103/PhysRevLett.116.063601
[8] Tsuda Y, Mori O, Funase R, et al. Flight status of IKAROS deep space solar sail demonstrator[J]. Acta Astronaut, 2011, 69(9-10): 833−840. doi: 10.1016/j.actaastro.2011.06.005
[9] Johnson L, Whorton M, Heaton A, et al. NanoSail-D: a solar sail demonstration mission[J]. Acta Astronaut, 2011, 68(5-6): 571−575. doi: 10.1016/j.actaastro.2010.02.008
[10] Atwater H A, Davoyan A R, Ilic O, et al. Materials challenges for the Starshot lightsail[J]. Nat Mater, 2018, 17(10): 861−867. doi: 10.1038/s41563-018-0075-8
[11] Achouri K, Céspedes O V, Caloz C. Solar “meta-sails” for agile optical force control[J]. IEEE Trans Antennas Propag, 2019, 67(11): 6924−6934. doi: 10.1109/TAP.2019.2925279
[12] Ilic O, Atwater H A. Self-stabilizing photonic levitation and propulsion of nanostructured macroscopic objects[J]. Nat Photonics, 2019, 13(4): 289−295. doi: 10.1038/s41566-019-0373-y
[13] Swartzlander G A. Theory of radiation pressure on a diffractive solar sail[J]. J Opt Sci Am B, 2022, 39(9): 2556−2563. doi: 10.1364/JOSAB.468588
[14] 许可, 王星儿, 范旭浩, 等. 超表面全息术: 从概念到实现[J]. 光电工程, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
Xu K, Wang X E, Fan X H, et al. Meta-holography: from concept to realization[J]. Opto-Electron Eng, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
[15] Pu M B, Luo X G. Advancing nonlinear nanophotonics: harnessing membrane metasurfaces for third-harmonic generation and imaging[J]. Opto-Electron Adv, 2023, 6(8): 230153. doi: 10.29026/oea.2023.230153
[16] Zhang F, Pu M B, Li X, et al. Extreme-angle silicon infrared optics enabled by streamlined surfaces[J]. Adv Mater, 2021, 33(11): 2008157. doi: 10.1002/adma.202008157
[17] Zhang Y X, Pu M B, Jin J J, et al. Crosstalk-free achromatic full Stokes imaging polarimetry metasurface enabled by polarization-dependent phase optimization[J]. Opto-Electron Adv, 2022, 5(11): 220058. doi: 10.29026/oea.2022.220058
[18] 杨港, 郭迎辉, 蒲明博, 等. 基于相关性选择的微型计算光谱探测技术[J]. 光电工程, 2022, 49(10): 220130. doi: 10.12086/oee.2022.220130
Yang G, Guo Y H, Pu M B, et al. Miniature computational spectral detection technology based on correlation value selection[J]. Opto-Electron Eng, 2022, 49(10): 220130. doi: 10.12086/oee.2022.220130
[19] 刘博, 谢鑫, 甘雪涛, 等. 全金属超表面在电磁波相位调控中的应用及进展[J]. 光电工程, 2023, 50(9): 230119. doi: 10.12086/oee.2023.230119
Liu B, Xie X, Gan X T, et al. Applications and progress of all-metal metasurfaces in phase manipulation of electromagnetic waves[J]. Opto-Electron Eng, 2023, 50(9): 230119. doi: 10.12086/oee.2023.230119
[20] Jiang M N, Chen Y, Zhang F, et al. Alignment-free angular momentum detection via spin-independent astigmatic transformation[J]. Adv Opt Mater, 2024, 12(2): 2301314. doi: 10.1002/adom.202301314
[21] Xie T, Zhang F, Pu M B, et al. Ultrathin, wide-angle, and high-resolution meta-imaging system via rear-position wavevector filter[J]. Laser Photonics Rev, 2023, 17(9): 2300119. doi: 10.1002/lpor.202300119
[22] Zhang F, Guo Y H, Pu M B, et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption[J]. Nat Commun, 2023, 14(1): 1946. doi: 10.1038/s41467-023-37510-z
[23] 蓝翔, 邓钦荣, 张汶婷, 等. 基于扭转悬链线结构的高效手性吸波器[J]. 光电工程, 2022, 49(10): 220157. doi: 10.12086/oee.2022.220157
Lan X, Deng Q R, Zhang W T, et al. Efficient chiral absorber based on twisted catenary structure[J]. Opto-Electron Eng, 2022, 49(10): 220157. doi: 10.12086/oee.2022.220157
[24] 柯岚, 章思梦, 李晨霞, 等. 超表面实现复杂矢量涡旋光束的研究进展[J]. 光电工程, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
Ke L, Zhang S M, Li C X, et al. Research progress on hybrid vector beam implementation by metasurfaces[J]. Opto-Electron Eng, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
[25] 陈宜臻, 潘威康, 金相宇, 等. 片上光学近场的远场辐射调控[J]. 光电工程, 2023, 50(8): 230173. doi: 10.12086/oee.2023.230173
Chen Y Z, Pan W K, Jin X Y, et al. Far-field radiation manipulations of on-chip optical near-fields[J]. Opto-Electron Eng, 2023, 50(8): 230173. doi: 10.12086/oee.2023.230173
[26] Shi Y Z, Xu X H, Nieto-Vesperinas M, et al. Advances in light transverse momenta and optical lateral forces[J]. Adv Opt Photonics, 2023, 15(3): 835−906. doi: 10.1364/AOP.489300
[27] Shen K H, Duan Y, Ju P, et al. On-chip optical levitation with a metalens in vacuum[J]. Optica, 2021, 8(11): 1359−1362. doi: 10.1364/OPTICA.438410
[28] Xu F, Liu Y, Zhang C, et al. Optically levitated conveyor belt based on polarization-dependent metasurface lens arrays[J]. Opt Lett, 2022, 47(9): 2194−2197. doi: 10.1364/OL.457314
[29] Li X Y, Zhou Y, Ge S Y, et al. Experimental demonstration of optical trapping and manipulation with multifunctional metasurface[J]. Opt Lett, 2022, 47(4): 977−980. doi: 10.1364/OL.450490
[30] Andrén D, Baranov D G, Jones S, et al. Microscopic metavehicles powered and steered by embedded optical metasurfaces[J]. Nat Nanotechnol, 2021, 16(9): 970−974. doi: 10.1038/s41565-021-00941-0
[31] Li H, Cao Y Y, Shi B J, et al. Momentum-topology-induced optical pulling force[J]. Phys Rev Lett, 2020, 124(14): 143901. doi: 10.1103/PhysRevLett.124.143901
[32] Jin R C, Xu Y H, Dong Z G, et al. Optical pulling forces enabled by hyperbolic metamaterials[J]. Nano Lett, 2021, 21(24): 10431−10437. doi: 10.1021/acs.nanolett.1c03772
[33] Joly-Jehenne T, Davoyan A R. Anomalous reflection under ambient sunlight: accessing in-plane radiation pressure for solar sailing[Z]. arXiv: 2307.09750, 2023. https://doi.org/10.48550/arXiv.2307.09750.
[34] Dorrah A H, Rubin N A, Zaidi A, et al. Metasurface optics for on-demand polarization transformations along the optical path[J]. Nat Photonics, 2021, 15(4): 287−296. doi: 10.1038/s41566-020-00750-2
[35] Liu W W, Li Z C, Ansari M A, et al. Design strategies and applications of dimensional optical field manipulation based on metasurfaces[J]. Adv Mater, 2023, 35(30): 2208884. doi: 10.1002/adma.202208884
[36] Luo X G. Multiscale optical field manipulation via planar digital optics[J]. ACS Photonics, 2023, 10(7): 2116−2127. doi: 10.1021/acsphotonics.2c01752
[37] Ziebart M, Adhya S, Sibthorpe A, et al. Combined radiation pressure and thermal modelling of complex satellites: algorithms and on-orbit tests[J]. Adv Space Res, 2005, 36(3): 424−430. doi: 10.1016/j.asr.2005.01.014
[38] 崔金松, 李成仁, 刘玉凤. 光压观测仪的研制[J]. 物理实验, 1999, 19(1): 29−30. doi: 10.3969/j.issn.1005-4642.1999.1.006
Cui J S, Li C R, Liu Y F. Development of a light pressure observatory[J]. Phys Exp, 1999, 19(1): 29−30. doi: 10.3969/j.issn.1005-4642.1999.1.006
[39] 龙腾, 赵改清, 杜炳清, 等. 应用压电陶瓷测量光压[J]. 物理实验, 2016, 36(11): 20−22. doi: 10.3969/j.issn.1005-4642.2016.11.006
Long T, Zhao G Q, Du B Q, et al. Measuring light pressure using piezoelectric ceramic[J]. Phys Exp, 2016, 36(11): 20−22. doi: 10.3969/j.issn.1005-4642.2016.11.006
[40] Nesterov V. Facility and methods for the measurement of micro and nano forces in the range below 10−5 N with a resolution of 10−12 N (development concept)[J]. Meas Sci Technol, 2007, 18(2): 360−366. doi: 10.1088/0957-0233/18/2/S06
[41] Nesterov V. A nanonewton force facility and a novel method for measurements of the air and vacuum permittivity at zero frequencies[J]. Meas Sci Technol, 2009, 20(8): 084012. doi: 10.1088/0957-0233/20/8/084012
[42] Nesterov V, Mueller M, Frumin L L, et al. A new facility to realize a nanonewton force standard based on electrostatic methods[J]. Metrologia, 2009, 46(3): 277−282. doi: 10.1088/0026-1394/46/3/016
[43] Williams P A, Artusio-Glimpse A B, Hadler J A, et al. Radiation-pressure-enabled traceable laser sources at CW powers up to 50 kW[J]. IEEE Trans Instrum Meas, 2019, 68(6): 1833−1839. doi: 10.1109/TIM.2018.2886108
[44] Williams P, Hadler J, Maring F, et al. Portable, high-accuracy, non-absorbing laser power measurement at kilowatt levels by means of radiation pressure[J]. Opt Express, 2017, 25(4): 4382−4392. doi: 10.1364/OE.25.004382
[45] 赵利强, 孙振山, 于东钰, 等. 光压型高功率激光测量装置的测量重复性研究[J]. 中国光学(中英文), 2023, 16(2): 382−389. doi: 10.37188/CO.2022-0092
Zhao L Q, Sun Z S, Yu D Y, et al. Measurement repeatability of high power laser measuring device based on light pressure[J]. Chin Opt, 2023, 16(2): 382−389. doi: 10.37188/CO.2022-0092
[46] Masalov A V. First experiments on measuring light pressure I (pyotr nikolaevich lebedev)[M]//Boyd R W, Lukishova S G, Zadkov V N. Quantum Photonics: Pioneering Advances and Emerging Applications. Cham: Springer, 2019: 425–453.https://doi.org/10.1007/978-3-319-98402-5_12.
[47] Chu Y J L, Jansson E M, Swartzlander Jr G A. Measurements of radiation pressure owing to the grating momentum[J]. Phys Rev Lett, 2018, 121(6): 063903. doi: 10.1103/PhysRevLett.121.063903
[48] Chu Y J L, Tabiryan N V, Swartzlander Jr G A. Experimental verification of a bigrating beam rider[J]. Phys Rev Lett, 2019, 123(24): 244302. doi: 10.1103/PhysRevLett.123.244302
[49] 刘泽刚, 黄耿石, 李振柱, 等. 基于谐振的光压测量[J]. 物理实验, 2017, 37(1): 1−6,12. doi: 10.3969/j.issn.1005-4642.2017.01.001
Liu Z G, Huang G S, Li Z Z, et al. Measuring light pressure based on mechanical resonance[J]. Phys Exp, 2017, 37(1): 1−6,12. doi: 10.3969/j.issn.1005-4642.2017.01.001
[50] 郭硕鸿. 电动力学[M]. 3版. 北京: 高等教育出版社, 2008: 180–185.
Guo S H. Electricity and Magnetism[M]. 3rd ed. Beijing: Higher Education Press, 2008: 180–185.
[51] Ye Q, Lin H Z. On deriving the Maxwell stress tensor method for calculating the optical force and torque on an object in harmonic electromagnetic fields[J]. Eur J Phys, 2017, 38(4): 045202. doi: 10.1088/1361-6404/aa6e1d
[52] 赵泽宇, 蒲明博, 王彦钦, 等. 广义折反射定律[J]. 光电工程, 2017, 44(2): 129−139. doi: 10.3969/j.issn.1003-501X.2017.02.001
Zhao Z Y, Pu M B, Wang Y Q, et al. The generalized laws of refraction and reflection[J]. Opto-Electron Eng, 2017, 44(2): 129−139. doi: 10.3969/j.issn.1003-501X.2017.02.001
-
点击扫一扫
图(6)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
