-
摘要:
矢量光场由于其独特的光场分布特性,在许多领域都得到了广泛且深入的研究与应用。传统光场调控手段受限于材料的光学特性及物理尺寸,难以实现灵活高效的动态操控功能。超表面凭借其亚波长结构设计所带来的额外自由度,突破了上述局限,使得对矢量光场的振幅、相位、偏振态乃至传播方向等的独立调控成为可能。本文结合国内外矢量光场领域的基础理论及最新进展,系统地阐述了矢量光场的基本原理及其数学模型,重点介绍了目前超表面生成矢量光场的方法,以及这种矢量光场在聚焦、轨道角动量检测、高精度定位等方面应用的具体案例与创新成果。
Abstract:Due to their unique field distribution properties, vectorial optical fields have been extensively researched and applied across various domains. However, traditional methods for controlling optical fields are limited by material properties and physical dimensions, which restrict flexible and efficient dynamic manipulation capabilities. In contrast, metasurfaces overcome these constraints with subwavelength structural designs that provide additional degrees of freedom for independent control over attributes such as amplitude, phase, polarization, and propagation direction of vectorial optical fields. This paper systematically combines foundational theories with recent advancements in domestic and international research on vectorial optical fields to elucidate the fundamental principles and mathematical models underlying them. It particularly focuses on current methodologies using metasurfaces to generate vectorial optical fields, along with specific case studies and innovative outcomes in applications including focusing, orbital angular momentum detection, and high-precision positioning.
-
Key words:
- vectorial optical field /
- metasurfaces /
- light field control
-

-
图 1 几种常规模式和柱对称矢量模式瞬时电场的空间分布[37]。(a) x偏振高斯基模;(b) x偏振HG10模式;(c) x偏振HG01模式;(d) y偏振HG01模式;(e) y极化HG01模式;(f) x偏振LG01模式;(g)径向极化模式;(h)角向偏振模式;(i)广义圆柱矢量光束
Figure 1. Spatial distribution of instantaneous electric vector field for several conventional modes and CV modes[37]. (a) x-polarized fundamental Gaussian mode; (b) x-polarized HG10 mode; (c) x-polarized HG01 mode; (d) y-polarized HG01 mode; (e) y-polarized HG01 mode; (f) x-polarized LG01 mode; (g) Radially polarized mode; (h) Azimuthally polarized mode; (i) Generalized CV beams
图 5 时空涡流管到涡流环的保角映射仿真[76]。时空涡旋管相位Ф1(x, y)在自由空间传播并转换,成为涡流环后,第二相位掩模Ф2(u, v)可以被应用于准直,颜色坐标表示展开相位的大小
Figure 5. Conformal mapping simulation of a spatiotemporal vortex tube transforming into a vortex ring[76]. The spatial-temporal vortex tube phase Ф1(x, y) propagates and evolves in free space to become a vortex ring, after which a second phase mask Ф2(u, v) can be applied for collimation, with color coding representing the magnitude of the expanded phase
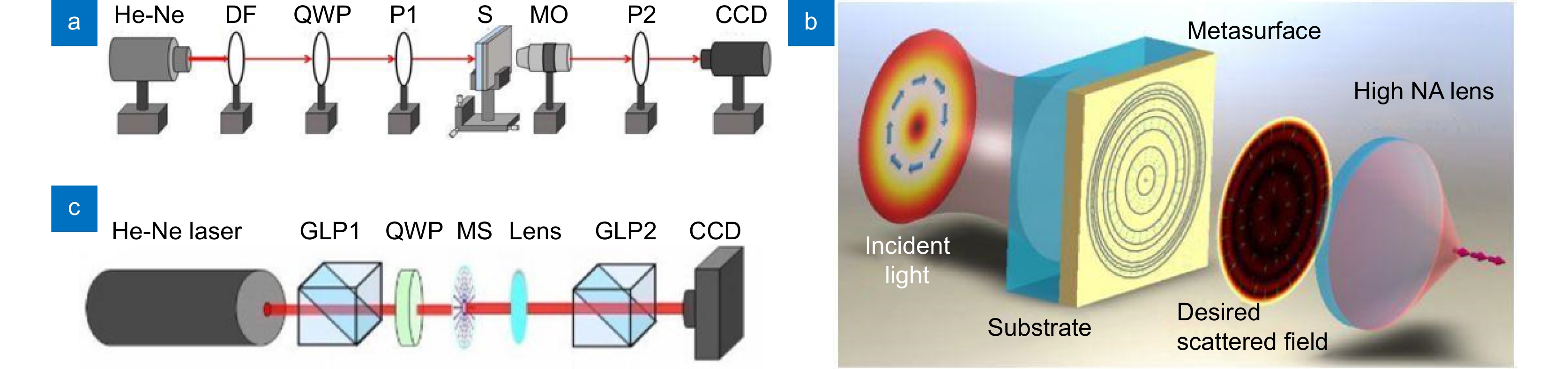
图 6 基于狭缝结构的超表面矢量光束生成系统。He-Ne,He-Ne laser:氦氖激光器;DF:强度滤波器;QWP:四分之一波片;P1,P2:偏振片;S:样品;MO:显微镜物镜;CCD:电荷耦合器件;GLP1,GLP2:Glan激光偏振器;MS:超表面;Lens:透镜。(a)不同阶次的柱状矢量场生成装置[78];(b) 基于超表面的光学针场生成系统配置示意图(光学针场用紫色箭头表示)[79];(c)利用超表面的矢量涡旋光束生成装置[80]
Figure 6. System configuration for vector beam generation based on a slit-structured metasurface. He-Ne, He-Ne laser: Helium-neon laser; DF: Intensity filter; QWP: Quarter-wave plate; P1, P2: Polarizers; S: Sample; MO: Microscope objective lens; CCD: Charge-coupled device; GLP1, GLP2: Glan laser polarizers; MS: Metasurface; Lens: Lenses. (a) Apparatus for the generation of different orders of cylindrical vector fields[78]; (b) Schematic diagram of the optical needle field generation system configuration using a metasurface (the optical needle field is represented by purple arrows)[79]; (c) Setup for generating vector vortex beams utilizing a metasurface[80]
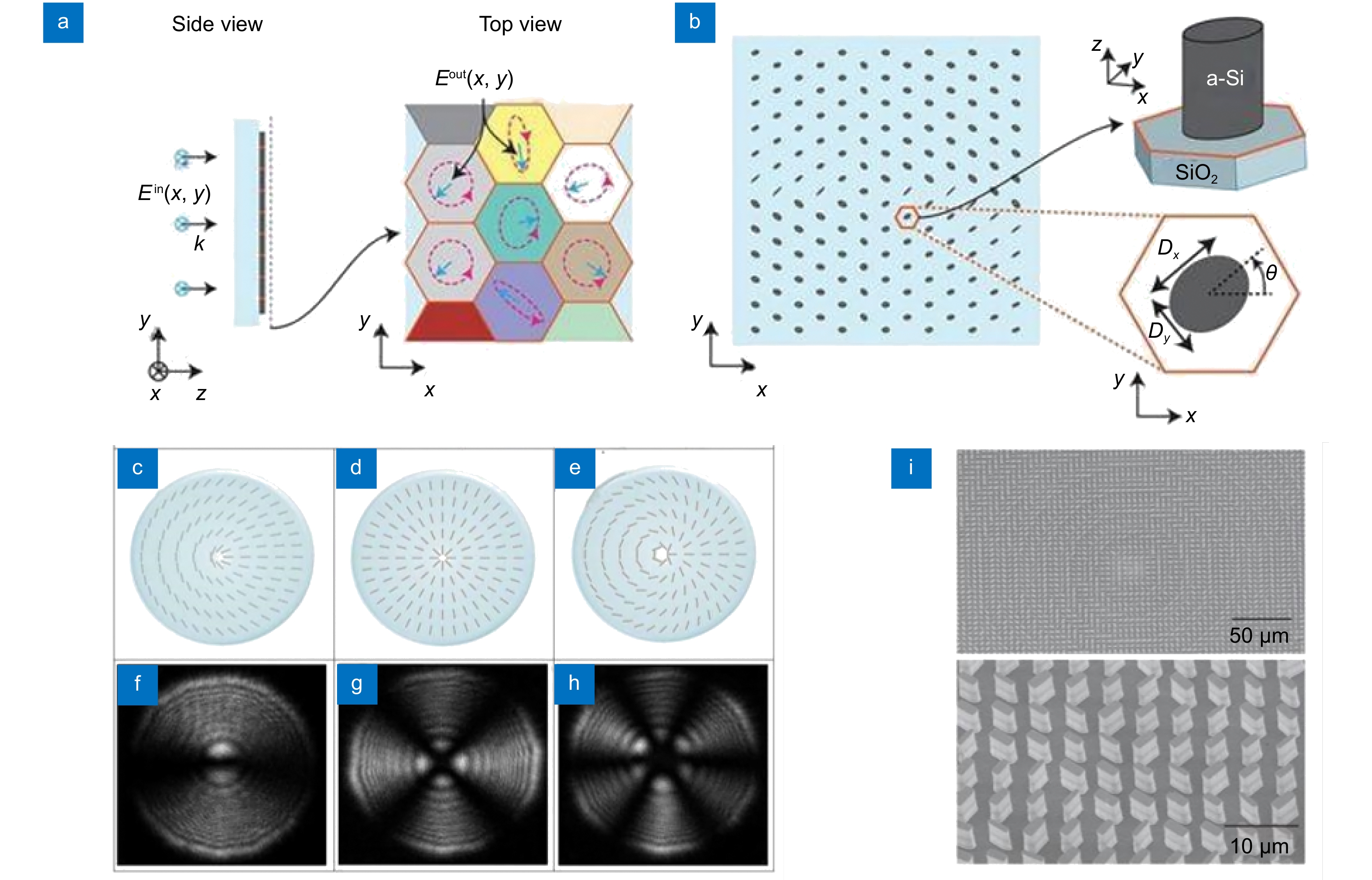
图 7 用于矢量光场生成的柱状纳米结构的超表面和级联超表面。(a)由六边形单元组成的超表面的侧视图(左)和俯视图(右)[81];(b)六边形单元中的椭圆形非晶硅柱结构[81];(c-e)是q = 0.5、1.0和1.5的级联超表面近光轴分布示意图[83];(f-h) q = 0.5, 1.0和1.5的超表面的交叉偏振显微图像,这里q是由超表面单元结构的位置变化和慢轴取向决定的一个常数[83];(i)生成三维柱状矢量光场的超表面纳米结构和SEM图像[87]
Figure 7. Cylindrical nanostuctured metasurfaces and cascaded metasurfaces for vector optical field generation. (a) Side view (left) and top view (right) of a metasurface composed of hexagonal units[81]; (b) Elliptical amorphous silicon pillar structure within the hexagonal unit cell[81]; (c-e) Schematic illustrations of near-axis distributions for cascaded metasurfaces with topological charges q = 0.5, 1.0, and 1.5, respectively[83]; (f-h) Cross-polarized microscopy images of metasurfaces with q values of 0.5, 1.0, and 1.5, where q is a constant determined by the positional variation and slow axis orientation of the metasurface unit structures[83]; (i) Nanoscale structure of the metasurface for generating three-dimensional cylindrical vector optical fields accompanied by SEM images[87]
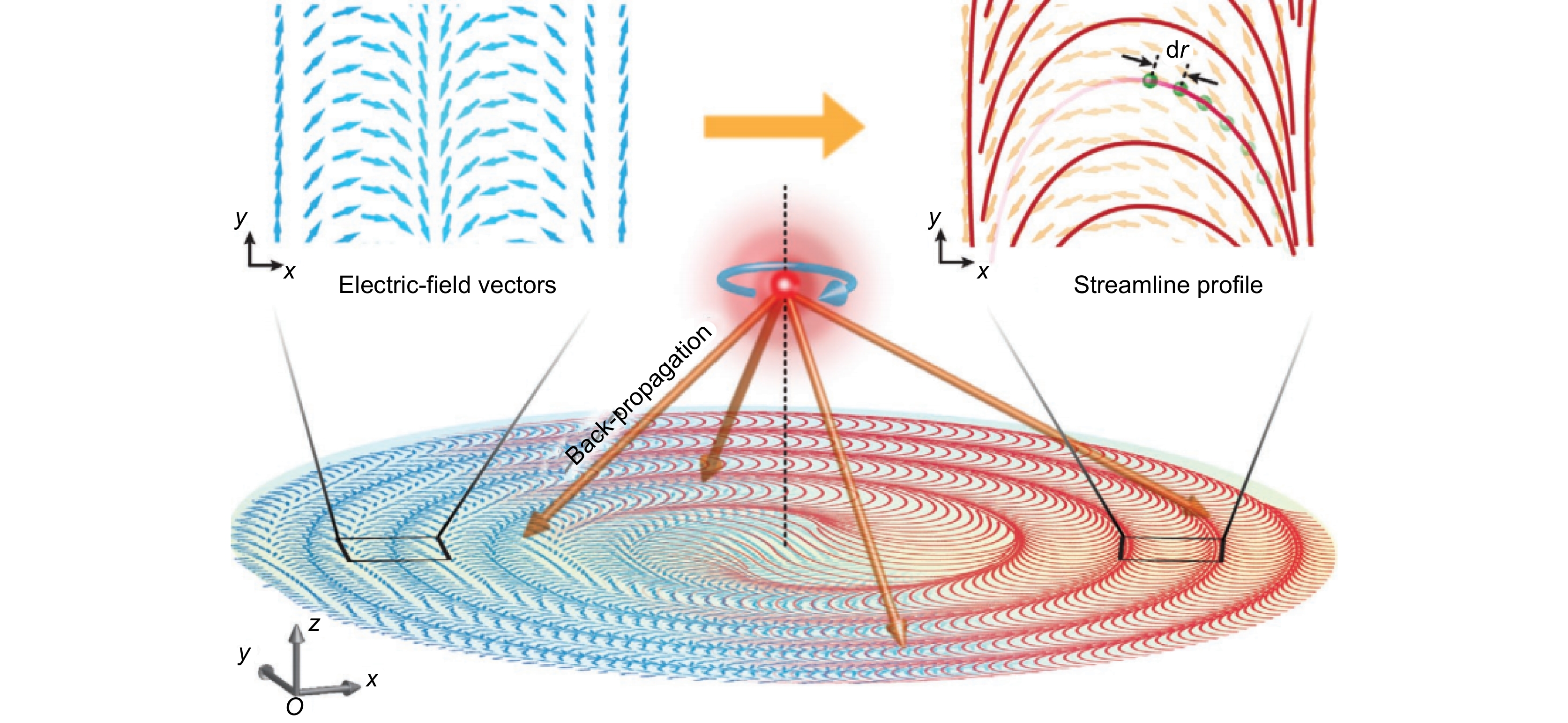
图 8 流线型金属透镜的概念图[89]。通过圆偏振点光源辐射获得时间反转电场(蓝色箭头)源,并且可以由具有空间变化的各向异性轴的半波片产生。红色流线是由上述空间变化的各向异性轴形成的矢量场的轨迹(橙色箭头)获得的
Figure 8. Concept illustration of the streamlined metalens[89]. The time-reversed electric fields (blue arrows) are obtained by the radiation of a circularly polarized point source and could be generated by a half-wave plate with spatially variant anisotropic axes. The red streamline is obtained by the trajectory of the vectorial field (orange arrows) formed by spatially variant anisotropic axes mentioned above
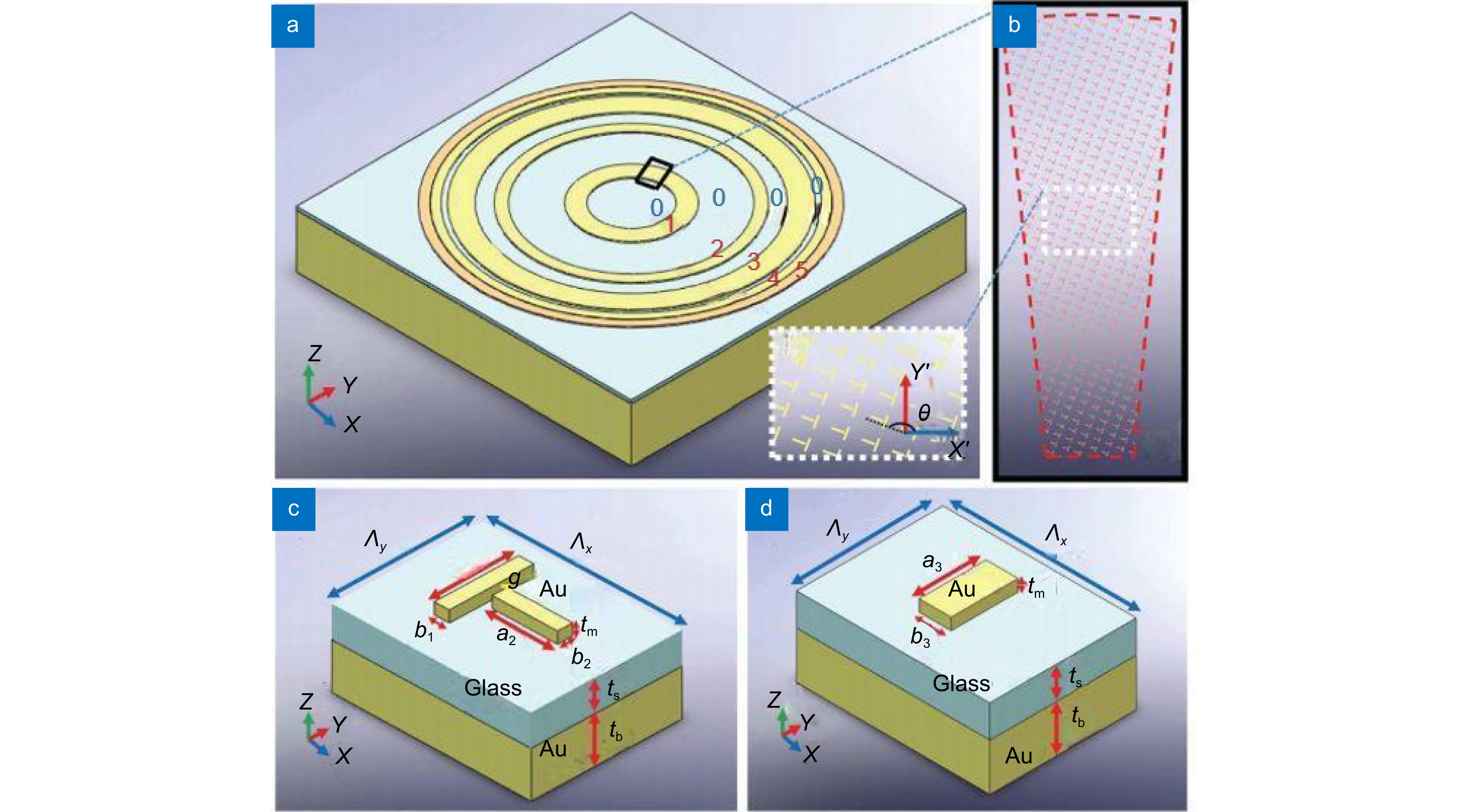
图 10 MIM超表面结构[102]。(a) 超表面的结构,其中黄色环为双纳米棒结构,浅棕色环为单纳米棒结构。插图:结构放大图;(b) 第一个环中的一个扇区;(c) 双纳米棒结构;(d) 单纳米棒结构
Figure 10. MIM metasurface structure[102]. (a) The metasurface configuration, where yellow rings denote double-nanorod structures and light brown rings represent single-nanorod structures. Inset: Magnified view of the structure; (b) A sector within the first ring; (c) Detailed illustration of the double-nanorod structure; (d) Single-nanorod structure depicted explicitly
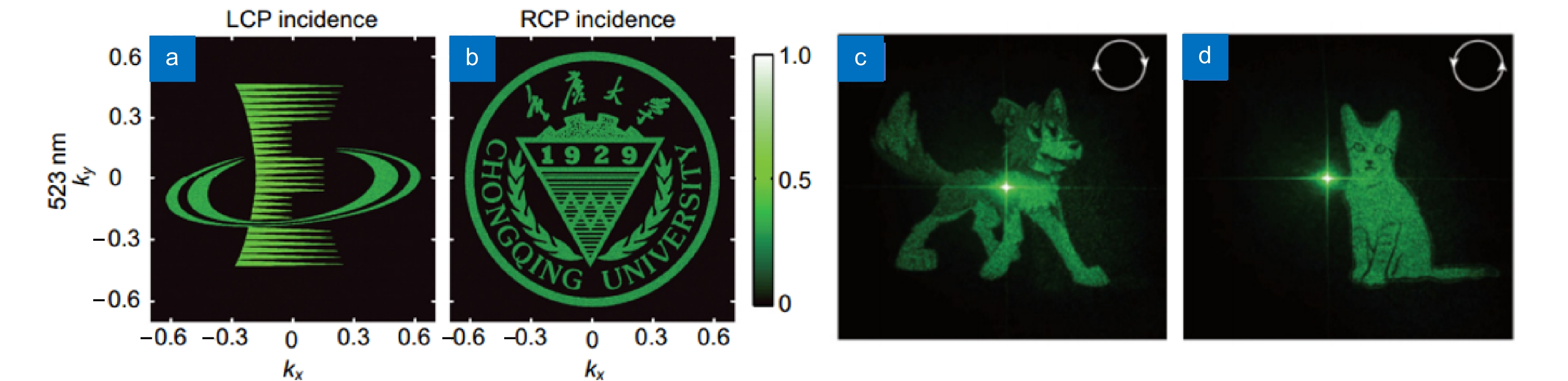
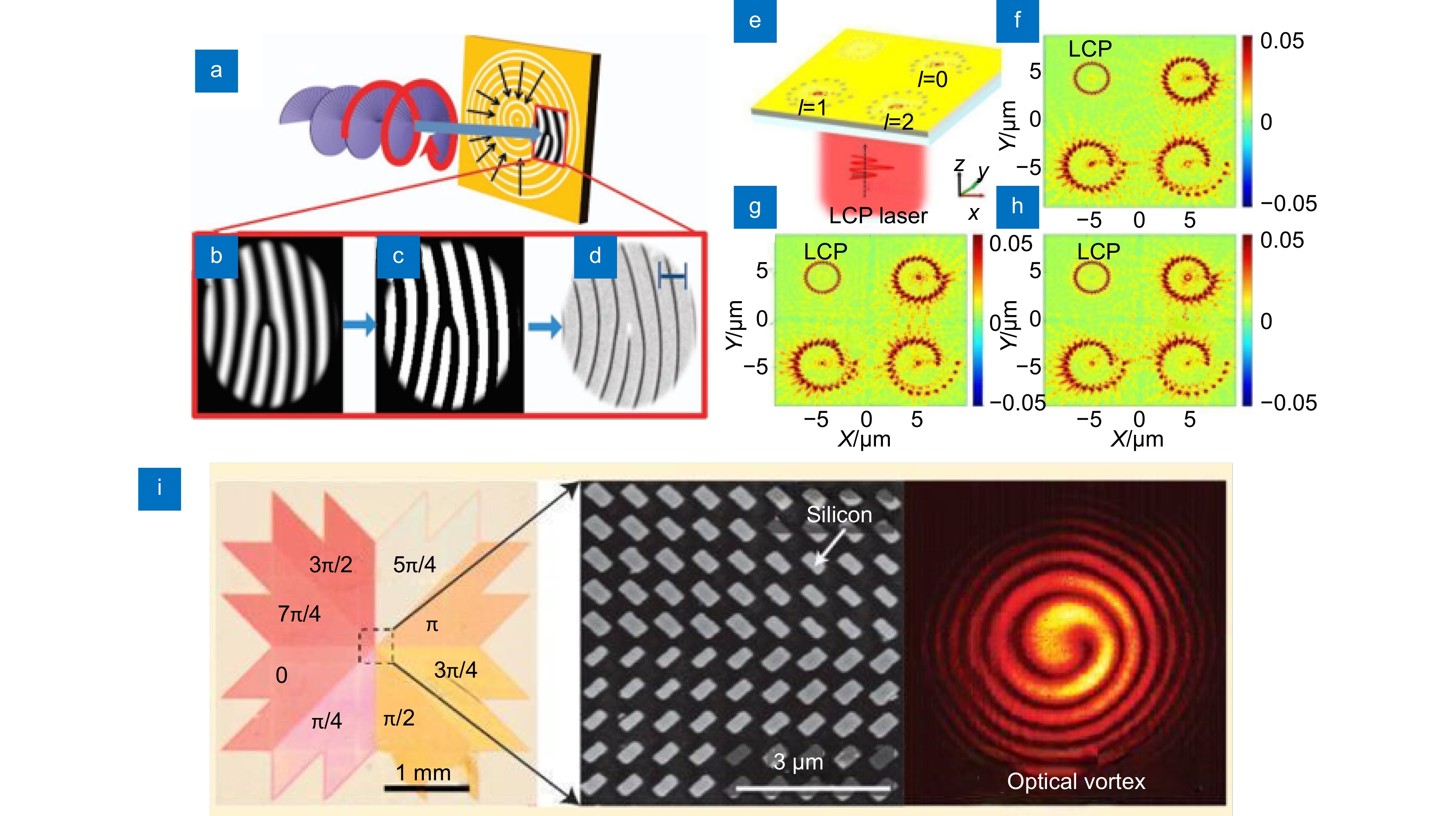
图 11 超表面的轨道角动量检测。(a)全息表面的结构[105];(b)仿真生成的干涉图[105];(c)仿真结果的二值化图像[105];(d)全息表面的扫描电子显微镜照片,凹槽在等相位置[105];(e) LCP入射时的OAM探测器[106];(f-h) 携带不同拓扑荷的涡旋光束((f) l= 0,(g) l=−1,(h) l=−2) 入射时OAM探测器的模拟强度分布图[106];(i) 左图为具有π/4相位步进的八段Si截止线螺旋相位板的光学显微图像,右图为该结构的SEM图像及相应的涡旋光束强度分布图[106]
Figure 11. Orbital angular momentum detection with a metasurface. (a) Structure of the holographic metasurface[105]; (b) Simulated interference pattern generated[105]; (c) Binary representation of the simulated results[105]; (d) Scanning electron microscope (SEM) image of the holographic surface, showing grooves at phase-matched positions[105]; (e) The OAM detector upon left-handed circularly polarized (LCP) incidence[106]; (f-h) Simulated intensity distributions of the OAM detector when illuminated by vortex beams carrying different topological charges: (f) l = 0, (g) l = −1, and (h) l = −2[106]; (i) Optical micrograph of an eight-segment silicon cutoff-line spiral phase plate with π/4 phase steps on the left, and on the right, the SEM image of this structure alongside its corresponding vortex beam intensity distribution map[106]
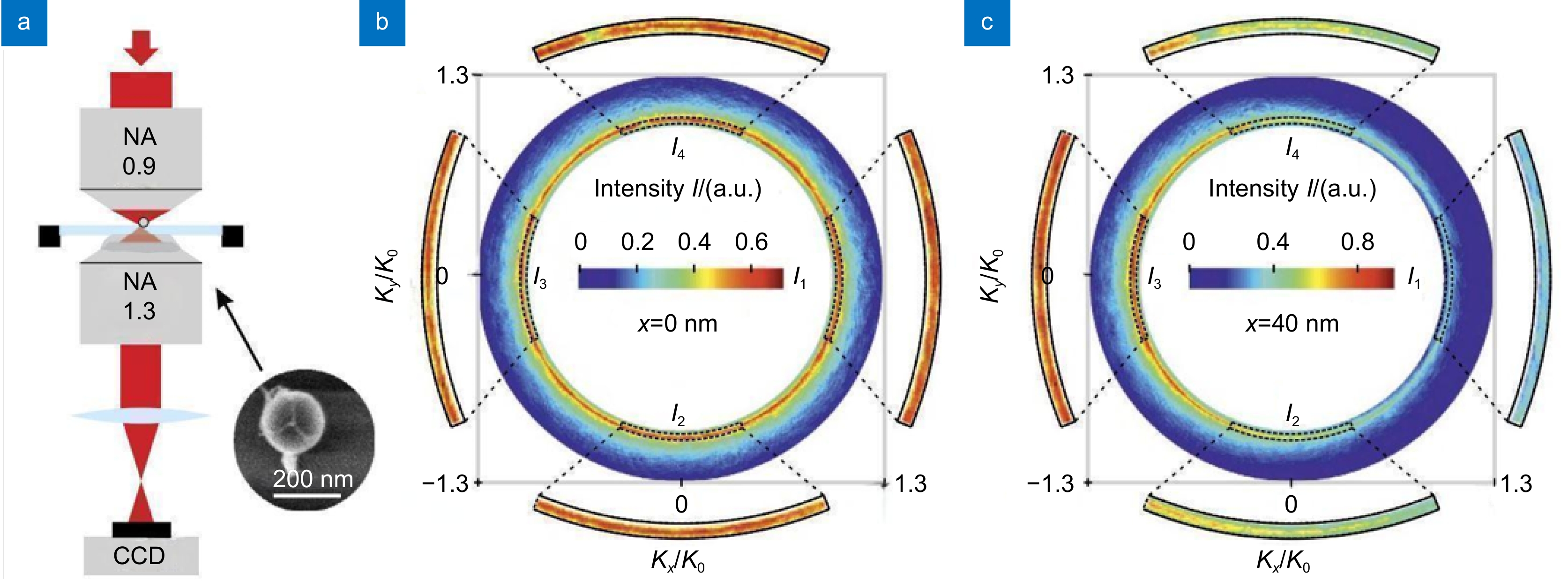
图 12 纳米颗粒定位[112]。(a) 显微镜物镜将径向偏振光束紧密聚焦在玻璃基板上的硅天线上,浸油物镜将NA在(0.95,1.3)之间的光收集并聚焦,CCD在后焦面上;(b) 光轴上的天线的远场强度分布图;(c) 横向位移为40 nm的远场强度分布图
Figure 12. Nanoparticle localization[112]. (a) A microscope objective tightly focuses a radially polarized light beam onto silicon antennas on a glass substrate, where an oil-immersion objective collects and focuses light with numerical aperture (NA) ranging between 0.95 to 1.3, and a CCD is positioned at the rear focal plane; (b) Far-field intensity distribution diagram of the antenna along the optical axis; (c) Far-field intensity distribution diagram for a lateral displacement of 40 nm
-
[1] Zang X F, Dong F L, Yue F Y, et al. Polarization encoded color image embedded in a dielectric metasurface[J]. Adv Mater, 2018, 30(21): 1707499. doi: 10.1002/adma.201707499
[2] Sasagawa K, Wakama N, Noda T, et al. On-chip polarizer on image sensor using advanced CMOS technology[J]. Proc SPIE, 2014, 8974: 89740I. doi: 10.1117/12.2040012
[3] Pattanayak D N, Agrawal G P. Representation of vector electromagnetic beams[J]. Phys Rev A, 1980, 22(3): 1159−1164. doi: 10.1103/PhysRevA.22.1159
[4] Snitzer E. Cylindrical dielectric waveguide modes[J]. J Opt Soc Am, 1961, 51(5): 491−498. doi: 10.1364/JOSA.51.000491
[5] Mushiake Y, Matsumura K, Nakajima N. Generation of radially polarized optical beam mode by laser oscillation[J]. Proc IEEE, 1972, 60(9): 1107−1109. doi: 10.1109/PROC.1972.8865
[6] Pohl D. Operation of a ruby laser in the purely transverse electric mode TE01[J]. Appl Phys Lett, 1972, 20(7): 266−267. doi: 10.1063/1.1654142
[7] Youngworth K S, Brown T G. Focusing of high numerical aperture cylindrical-vector beams[J]. Opt Express, 2000, 7(2): 77−87. doi: 10.1364/OE.7.000077
[8] Richards B, Wolf E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system[J]. Proc Roy Soc A Math Phys Eng Sci, 1959, 253(1274): 358−379. doi: 10.1098/rspa.1959.0200
[9] Beckley A M, Brown T G, Alonso M A. Full Poincaré beams II: partial polarization[J]. Opt Express, 2012, 20(9): 9357−9362. doi: 10.1364/OE.20.009357
[10] Beckley A M, Brown T G, Alonso M A. Full Poincaré beams[J]. Opt Express, 2010, 18(10): 10777−10785. doi: 10.1364/OE.18.010777
[11] Lou K, Qian S X, Ren Z C, et al. Femtosecond laser processing by using patterned vector optical fields[J]. Sci Rep, 2013, 3: 2281. doi: 10.1038/srep02281
[12] Cai M Q, Tu C H, Zhang H H, et al. Subwavelength multiple focal spots produced by tight focusing the patterned vector optical fields[J]. Opt Express, 2013, 21(25): 31469−31482. doi: 10.1364/OE.21.031469
[13] 夏小兰, 曾宪智, 宋世超, 等. 基于柱矢量光调控的纵向超分辨率准球形多焦点阵列[J]. 光电工程, 2022, 49(11): 220109. doi: 10.12086/oee.2022.220109
Xia X L, Zeng X Z, Song S C, et al. Longitudinal super-resolution spherical multi-focus array based on column vector light modulation[J]. Opto-Electron Eng, 2022, 49(11): 220109. doi: 10.12086/oee.2022.220109
[14] Zhang Y J, Bai J P. Improving the recording ability of a near-field optical storage system by higher-order radially polarized beams[J]. Opt Express, 2009, 17(5): 3698−3706. doi: 10.1364/OE.17.003698
[15] Hao X, Kuang C F, Wang T T, et al. Phase encoding for sharper focus of the azimuthally polarized beam[J]. Opt Lett, 2010, 35(23): 3928−3930. doi: 10.1364/OL.35.003928
[16] Pan Y, Li Y N, Li S M, et al. Vector optical fields with bipolar symmetry of linear polarization[J]. Opt Lett, 2013, 38(18): 3700−3703. doi: 10.1364/OL.38.003700
[17] Pan Y, Li Y N, Ren Z C, et al. Parabolic-symmetry vector optical fields and their tightly focusing properties[J]. Phys Rev A, 2014, 89(3): 035801. doi: 10.1103/PhysRevA.89.035801
[18] Milione G, Nguyen T A, Leach J, et al. Using the nonseparability of vector beams to encode information for optical communication[J]. Opt Lett, 2015, 40(21): 4887−4890. doi: 10.1364/OL.40.004887
[19] Zhao Y F, Wang J. High-base vector beam encoding/decoding for visible-light communications[J]. Opt Lett, 2015, 40(21): 4843−4846. doi: 10.1364/OL.40.004843
[20] Klug A, Peters C, Forbes A. Robust structured light in atmospheric turbulence[J]. Adv Photonics, 2023, 5(1): 016006. doi: 10.1117/1.AP.5.1.016006
[21] Cao Q, Chen Z, Zhang C, et al. Propagation of transverse photonic orbital angular momentum through few-mode fiber[J]. Adv Photonics, 2023, 5(3): 036002. doi: 10.1117/1.AP.5.3.036002
[22] Holloway C L, Kuester E F, Gordon J A, et al. An overview of the theory and applications of metasurfaces: the two-dimensional equivalents of metamaterials[J]. IEEE Antennas Propag Mag, 2012, 54(2): 10−35. doi: 10.1109/MAP.2012.6230714
[23] 朱潜, 田翰闱, 蒋卫祥. 电磁超表面对辐射波的调控与应用[J]. 光电工程, 2023, 50(9): 230115. doi: 10.12086/oee.2023.230115
Zhu Q, Tian H W, Jiang W X. Manipulations and applications of radiating waves using electromagnetic metasurfaces[J]. Opto-Electron Eng, 2023, 50(9): 230115. doi: 10.12086/oee.2023.230115
[24] 许可, 王星儿, 范旭浩, 等. 超表面全息术: 从概念到实现[J]. 光电工程, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
Xu K, Wang X E, Fan X H, et al. Meta-holography: from concept to realization[J]. Opto-Electron Eng, 2022, 49(10): 220183. doi: 10.12086/oee.2022.220183
[25] 刘博, 谢鑫, 甘雪涛, 等. 全金属超表面在电磁波相位调控中的应用及进展[J]. 光电工程, 2023, 50(9): 230119. doi: 10.12086/oee.2023.230119
Liu B, Xie X, Gan X T, et al. Applications and progress of all-metal metasurfaces in phase manipulation of electromagnetic waves[J]. Opto-Electron Eng, 2023, 50(9): 230119. doi: 10.12086/oee.2023.230119
[26] Dorrah A H, Capasso F. Tunable structured light with flat optics[J]. Science, 2022, 376(6591): eabi6860. doi: 10.1126/science.abi6860
[27] He C, Shen Y J, Forbes A. Towards higher-dimensional structured light[J]. Light Sci Appl, 2022, 11(1): 205. doi: 10.1038/s41377-022-00897-3
[28] Otte E, Alpmann C, Denz C. Polarization singularity explosions in tailored light fields[J]. Laser Photonics Rev, 2018, 12(6): 1700200. doi: 10.1002/lpor.201700200
[29] Wang X W, Nie Z Q, Liang Y, et al. Recent advances on optical vortex generation[J]. Nanophotonics, 2018, 7(9): 1533−1556. doi: 10.1515/nanoph-2018-0072
[30] Forbes A. Structured light from lasers[J]. Laser Photonics Rev, 2019, 13(11): 1900140. doi: 10.1002/lpor.201900140
[31] Oughstun K E. Electromagnetic theory of gratings[J]. Proc IEEE, 1982, 70(6): 687. doi: 10.1109/PROC.1982.12371
[32] Herzig H P. Micro-Optics: Elements, Systems and Applications[M]. London: CRC Press, 1997.https://doi.org/10.1201/9781482272802.
[33] Wang D Y, Liu T, Zhou Y J, et al. High-efficiency metadevices for bifunctional generations of vectorial optical fields[J]. Nanophotonics, 2020, 10(1): 685−695. doi: 10.1515/nanoph-2020-0465
[34] Luo X G, Pu M B, Zhang F, et al. Vector optical field manipulation via structural functional materials: tutorial[J]. J Appl Phys, 2022, 131(18): 181101. doi: 10.1063/5.0089859
[35] Hall D G. Vector-beam solutions of Maxwell’s wave equation[J]. Opt Lett, 1996, 21(1): 9−11. doi: 10.1364/OL.21.000009
[36] Galvez E J, Khadka S, Schubert W H, et al. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre–Gauss and polarization modes of light[J]. Appl Opt, 2012, 51(15): 2925−2934. doi: 10.1364/AO.51.002925
[37] Zhan Q W. Cylindrical vector beams: from mathematical concepts to applications[J]. Adv Opt Photonics, 2009, 1(1): 1−57. doi: 10.1364/AOP.1.000001
[38] Wang X L, Ding J P, Ni W J, et al. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement[J]. Opt Lett, 2007, 32(24): 3549−3551. doi: 10.1364/OL.32.003549
[39] Rosales-Guzmán C, Ndagano B, Forbes A. A review of complex vector light fields and their applications[J]. J Opt, 2018, 20(12): 123001. doi: 10.1088/2040-8986/aaeb7d
[40] Padgett M J, Courtial J. Poincaré-sphere equivalent for light beams containing orbital angular momentum[J]. Opt Lett, 1999, 24(7): 430−432. doi: 10.1364/OL.24.000430
[41] Han W, Cheng W, Zhan Q W. Flattop focusing with full Poincaré beams under low numerical aperture illumination[J]. Opt Lett, 2011, 36(9): 1605−1607. doi: 10.1364/OL.36.001605
[42] Cheng W, Han W, Zhan Q W. Compact flattop laser beam shaper using vectorial vortex[J]. Appl Opt, 2013, 52(19): 4608−4612. doi: 10.1364/AO.52.004608
[43] Xue Y X, Wang Y S, Zhou S C, et al. Focus shaping and optical manipulation using highly focused second-order full Poincaré beam[J]. J Opt Soc Am A, 2018, 35(6): 953−958. doi: 10.1364/JOSAA.35.000953
[44] Wang L G. Optical forces on submicron particles induced by full Poincaré beams[J]. Opt Express, 2012, 20(19): 20814−20826. doi: 10.1364/OE.20.020814
[45] Ferrer-Garcia M F, Lopez-Mago D. Newtonian orbits of nanoparticles interacting with structured light beams[J]. J Opt, 2019, 21(12): 125403. doi: 10.1088/2040-8986/ab4f9a
[46] Donato M G, Vasi S, Sayed R, et al. Optical trapping of nanotubes with cylindrical vector beams[J]. Opt Lett, 2012, 37(16): 3381−3383. doi: 10.1364/OL.37.003381
[47] Gu Y L, Gbur G. Reduction of turbulence-induced scintillation by nonuniformly polarized beam arrays[J]. Opt Lett, 2012, 37(9): 1553−1555. doi: 10.1364/OL.37.001553
[48] Wei C, Wu D, Liang C H, et al. Experimental verification of significant reduction of turbulence-induced scintillation in a full Poincaré beam[J]. Opt Express, 2015, 23(19): 24331−24341. doi: 10.1364/OE.23.024331
[49] Milione G, Sztul H I, Alfano R R. Stokes polarimetry of a hybrid vector beam from a spun elliptical core optical fiber[J]. Proc SPIE, 2010, 7613: 761305. doi: 10.1117/12.841920
[50] Milione G, Sztul H I, Nolan D A, et al. Higher-order Poincaré sphere, stokes parameters, and the angular momentum of light[J]. Phys Rev Lett, 2011, 107(5): 053601. doi: 10.1103/PhysRevLett.107.053601
[51] Holleczek A, Aiello A, Gabriel C, et al. Classical and quantum properties of cylindrically polarized states of light[J]. Opt Express, 2011, 19(10): 9714−9736. doi: 10.1364/OE.19.009714
[52] Chen S Z, Zhou X X, Liu Y C, et al. Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere[J]. Opt Lett, 2014, 39(18): 5274−5276. doi: 10.1364/OL.39.005274
[53] Liu Y C, Ling X H, Yi X N, et al. Realization of polarization evolution on higher-order Poincaré sphere with metasurface[J]. Appl Phys Lett, 2014, 104(19): 191110. doi: 10.1063/1.4878409
[54] He Y L, Liu Z X, Liu Y C, et al. Higher-order laser mode converters with dielectric metasurfaces[J]. Opt Lett, 2015, 40(23): 5506−5509. doi: 10.1364/OL.40.005506
[55] Fernandes G M, Muga N J, Pinto A N. Space-demultiplexing based on higher-order Poincaré spheres[J]. Opt Express, 2017, 25(4): 3899−3915. doi: 10.1364/OE.25.003899
[56] Yang H, Xie Z W, Li G H, et al. All-dielectric metasurface for fully resolving arbitrary beams on a higher-order Poincaré sphere[J]. Photonics Res, 2021, 9(3): 331−343. doi: 10.1364/PRJ.411503
[57] Yi X N, Liu Y C, Ling X H, et al. Hybrid-order Poincaré sphere[J]. Phys Rev A, 2015, 91(2): 023801. doi: 10.1103/PhysRevA.91.023801
[58] Liu Z X, Liu Y Y, Ke Y G, et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere[J]. Photonics Res, 2017, 5(1): 15−21. doi: 10.1364/PRJ.5.000015
[59] Lou S Z, Zhou Y Q, Yuan Y D, et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere based on liquid crystal device[J]. Opt Express, 2019, 27(6): 8596−8604. doi: 10.1364/OE.27.008596
[60] Wang R S, He S S, Chen S Z, et al. Electrically driven generation of arbitrary vector vortex beams on the hybrid-order Poincaré sphere[J]. Opt Lett, 2018, 43(15): 3570−3573. doi: 10.1364/OL.43.003570
[61] Dai X B, Li Y Q, Liu L H. Tight focusing properties of hybrid-order Poincaré sphere beams[J]. Opt Commun, 2018, 426: 46−53. doi: 10.1016/j.optcom.2018.05.017
[62] Ren Z C, Kong L J, Li S M, et al. Generalized Poincaré sphere[J]. Opt Express, 2015, 23(20): 26586−26595. doi: 10.1364/OE.23.026586
[63] Man Z S, Bai Z D, Li J J, et al. Focus shaping by tailoring arbitrary hybrid polarization states that have a combination of orthogonal linear polarization bases[J]. Appl Opt, 2018, 57(12): 3047−3055. doi: 10.1364/AO.57.003047
[64] Pan Y, Gao X Z, Ren Z C, et al. Arbitrarily tunable orbital angular momentum of photons[J]. Sci Rep, 2016, 6: 29212. doi: 10.1038/srep29212
[65] Ishihara J, Mori T, Suzuki T, et al. Imprinting spatial helicity structure of vector vortex beam on spin texture in semiconductors[J]. Phys Rev Lett, 2023, 130(12): 126701. doi: 10.1103/PhysRevLett.130.126701
[66] D’Ambrosio V, Carvacho G, Agresti I, et al. Tunable two-photon quantum interference of structured light[J]. Phys Rev Lett, 2019, 122(1): 013601. doi: 10.1103/PhysRevLett.122.013601
[67] Meier M, Romano V, Feurer T. Material processing with pulsed radially and azimuthally polarized laser radiation[J]. Appl Phys A, 2007, 86(3): 329−334. doi: 10.1007/s00339-006-3784-9
[68] Tamburini F, Thidé B, Molina-Terriza G, et al. Twisting of light around rotating black holes[J]. Nat Phys, 2011, 7(3): 195−197. doi: 10.1038/nphys1907
[69] Nicolas A, Veissier L, Giner L, et al. A quantum memory for orbital angular momentum photonic qubits[J]. Nat Photonics, 2014, 8(3): 234−238. doi: 10.1038/nphoton.2013.355
[70] Xie J Y, Qian J, Wang T J, et al. Integrated terahertz vortex beam emitter for rotating target detection[J]. Adv Photonics, 2023, 5(6): 066002. doi: 10.1117/1.AP.5.6.066002
[71] Lin Z Z, Hu J Q, Chen Y J, et al. Single-shot Kramers–Kronig complex orbital angular momentum spectrum retrieval[J]. Adv Photonics, 2023, 5(3): 036006. doi: 10.1117/1.AP.5.3.036006
[72] Li L, Guo Y C, Zhang Z C, et al. Photon total angular momentum manipulation[J]. Adv Photonics, 2023, 5(5): 056002. doi: 10.1117/1.AP.5.5.056002
[73] Jia W H, Gao C X, Zhao Y M, et al. Intracavity spatiotemporal metasurfaces[J]. Adv Photonics, 2023, 5(2): 026002. doi: 10.1117/1.AP.5.2.026002
[74] 方桂娟, 孙顺红, 蒲继雄. 分数阶双涡旋光束的实验研究[J]. 物理学报, 2012, 61(6): 064210. doi: 10.7498/aps.61.064210
Fang G J, Sun S H, Pu J X. Experimental study on fractional double-vortex beams[J]. Acta Phys Sin, 2012, 61(6): 064210. doi: 10.7498/aps.61.064210
[75] Chong A, Wan C H, Chen J, et al. Generation of spatiotemporal optical vortices with controllable transverse orbital angular momentum[J]. Nat Photonics, 2020, 14(6): 350−354. doi: 10.1038/s41566-020-0587-z
[76] Wan C H, Cao Q, Chen J, et al. Toroidal vortices of light[J]. Nat Photonics, 2022, 16(7): 519−522. doi: 10.1038/s41566-022-01013-y
[77] Xu Q, Su X Q, Zhang X Q, et al. Mechanically reprogrammable Pancharatnam–Berry metasurface for microwaves[J]. Adv Photonics, 2022, 4(1): 016002. doi: 10.1117/1.AP.4.1.016002
[78] Lv H R, Lu X Q, Han Y S, et al. Metasurface cylindrical vector light generators based on nanometer holes[J]. New J Phys, 2019, 21(12): 123047. doi: 10.1088/1367-2630/ab5f44
[79] Wang S Y, Abeysinghe D C, Zhan Q W. Generation of vectorial optical fields with slot-antenna-based metasurface[J]. Opt Lett, 2015, 40(20): 4711−4714. doi: 10.1364/OL.40.004711
[80] Yi X N, Ling X H, He W G, et al. Generation and representation of vector vortex beams based on metasurfaces[J]. Proc SPIE, 2016, 10022: 1002225. doi: 10.1117/12.2246393
[81] Arbabi A, Horie Y, Bagheri M, et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission[J]. Nat Nanotechnol, 2015, 10(11): 937−943. doi: 10.1038/nnano.2015.186
[82] Li T, Hu X B, Chen H M, et al. High-efficiency broadband vector beams using polarization rotation metasurfaces[J]. IEEE Photonics Technol Lett, 2017, 29(17): 1463−1466. doi: 10.1109/LPT.2017.2728811
[83] Yi X N, Huang P L, Huang X Z, et al. Operation of polarization order of vector beams with cascaded metasurfaces[J]. Appl Phys B, 2017, 123(9): 243. doi: 10.1007/s00340-017-6816-6
[84] 柯岚, 章思梦, 李晨霞, 等. 超表面实现复杂矢量涡旋光束的研究进展[J]. 光电工程, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
Ke L, Zhang S M, Li C X, et al. Research progress on hybrid vector beam implementation by metasurfaces[J]. Opto-Electron Eng, 2023, 50(8): 230117. doi: 10.12086/oee.2023.230117
[85] Shen Z, Li R, Xue Y Z, et al. Generation of optical vortices with polarization-insensitive metasurfaces[J]. IEEE Photonics J, 2020, 12(4): 4601010. doi: 10.1109/JPHOT.2020.3014918
[86] Ding F, Chen Y T, Yang Y Q, et al. Gap-surface Plasmon metasurfaces for structured beams generation[C]//2019 Photonics & Electromagnetics Research Symposium, 2019: 1276–1280.https://doi.org/10.1109/PIERS-Spring46901.2019.9017466.
[87] Zhang F, Pu M B, Guo Y H, et al. Synthetic vector optical fields with spatial and temporal tunability[J]. Sci China Phys Mech Astron, 2022, 65(5): 254211. doi: 10.1007/s11433-021-1851-0
[88] Pu M B, Li X, Ma X L, et al. Catenary optics for achromatic generation of perfect optical angular momentum[J]. Sci Adv, 2015, 1(9): e1500396. doi: 10.1126/sciadv.1500396
[89] Zhang F, Pu M B, Li X, et al. Extreme-angle silicon infrared optics enabled by streamlined surfaces[J]. Adv Mater, 2021, 33(11): 2008157. doi: 10.1002/adma.202008157
[90] Shi Z J, Zhu A Y, Li Z Y, et al. Continuous angle-tunable birefringence with freeform metasurfaces for arbitrary polarization conversion[J]. Sci Adv, 2020, 6(23): eaba3367. doi: 10.1126/sciadv.aba3367
[91] Luo X G, Li X, Pu M B, et al. Symmetric and asymmetric photonic spin-orbit interaction in metasurfaces[J]. Prog Quantum Electron, 2021, 79: 100344. doi: 10.1016/j.pquantelec.2021.100344
[92] 张飞, 郭迎辉, 蒲明博, 等. 基于非对称光子自旋—轨道相互作用的超构表面[J]. 光电工程, 2020, 47(10): 200366. doi: 10.12086/oee.2020.200366
Zhang F, Guo Y H, Pu M B, et al. Metasurfaces enabled by asymmetric photonic spin-orbit interactions[J]. Opto-Electron Eng, 2020, 47(10): 200366. doi: 10.12086/oee.2020.200366
[93] Zhang F, Pu M B, Luo J, et al. Symmetry breaking of photonic spin-orbit interactions in metasurfaces[J]. Opto-Electron Eng, 2017, 44(3): 319−325. doi: 10.3969/j.issn.1003-501X.2017.03.006
[94] Balthasar Mueller J P, Rubin N A, Devlin R C, et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization[J]. Phys Rev Lett, 2017, 118(11): 113901. doi: 10.1103/PhysRevLett.118.113901
[95] Zhang F, Xie X, Pu M B, et al. Multistate switching of photonic angular momentum coupling in phase-change metadevices[J]. Adv Mater, 2020, 32(39): 1908194. doi: 10.1002/adma.201908194
[96] Zhan Q W. Evanescent bessel beam generation via surface Plasmon resonance excitation by a radially polarized beam[J]. Opt Lett, 2006, 31(11): 1726−1728. doi: 10.1364/OL.31.001726
[97] Martínez-Herrero R, Mejías P M, Juvells I, et al. Transverse and longitudinal components of the propagating and evanescent waves associated to radially polarized nonparaxial fields[J]. Appl Phys B, 2012, 106(1): 151−159. doi: 10.1007/s00340-011-4720-z
[98] Chen W B, Zhan Q W. Realization of an evanescent Bessel beam via surface Plasmon interference excited by a radially polarized beam[J]. Opt Lett, 2009, 34(6): 722−724. doi: 10.1364/OL.34.000722
[99] Chen W B, Abeysinghe D C, Nelson R L, et al. Plasmonic lens made of multiple concentric metallic rings under radially polarized illumination[J]. Nano Lett, 2009, 9(12): 4320−4325. doi: 10.1021/nl903145p
[100] Diao J S, Yuan W Z, Yu Y T, et al. Controllable design of super-oscillatory planar lenses for sub-diffraction-limit optical needles[J]. Opt Express, 2016, 24(3): 1924−1933. doi: 10.1364/OE.24.001924
[101] Khorasaninejad M, Chen W T, Devlin R C, et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging[J]. Science, 2016, 352(6290): 1190−1194. doi: 10.1126/science.aaf6644
[102] Wang S Y, Zhan Q W. Reflection type metasurface designed for high efficiency vectorial field generation[J]. Sci Rep, 2016, 6: 29626. doi: 10.1038/srep29626
[103] Berkhout G C G, Lavery M P J, Courtial J, et al. Efficient sorting of orbital angular momentum states of light[J]. Phys Rev Lett, 2010, 105(15): 153601. doi: 10.1103/PhysRevLett.105.153601
[104] Bryngdahl O. Geometrical transformations in optics[J]. J Opt Soc Am, 1974, 64(8): 1092−1099. doi: 10.1364/JOSA.64.001092
[105] Genevet P, Lin J, Kats M A, et al. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes[J]. Nat Commun, 2012, 3: 1278. doi: 10.1038/ncomms2293
[106] Yang H, Chen Z Q, Liu Q, et al. Near-field orbital angular momentum generation and detection based on spin-orbit interaction in gold metasurfaces[J]. Adv Theory Simul, 2019, 2(10): 1900133. doi: 10.1002/adts.201900133
[107] Yang Y M, Wang W Y, Moitra P, et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation[J]. Nano Lett, 2014, 14(3): 1394−1399. doi: 10.1021/nl4044482
[108] Ou K, Li G H, Li T X, et al. High efficiency focusing vortex generation and detection with polarization-insensitive dielectric metasurfaces[J]. Nanoscale, 2018, 10(40): 19154−19161. doi: 10.1039/C8NR07480A
[109] Li G, Shi P. Weak measurement of the optical polarization, chirality and orbital angular momentum via metasurface with polarization filtering[J]. J Phys Commun, 2020, 4(9): 095003. doi: 10.1088/2399-6528/abab3e
[110] Guo Y H, Zhang S C, Pu M B, et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation[J]. Light Sci Appl, 2021, 10(1): 63. doi: 10.1038/s41377-021-00497-7
[111] Roy S, Ushakova K, van den Berg Q, et al. Radially polarized light for detection and nanolocalization of dielectric particles on a planar substrate[J]. Phys Rev Lett, 2015, 114(10): 103903. doi: 10.1103/PhysRevLett.114.103903
[112] Neugebauer M, Woźniak P, Bag A, et al. Polarization-controlled directional scattering for nanoscopic position sensing[J]. Nat Commun, 2016, 7: 11286. doi: 10.1038/ncomms11286
[113] Bag A, Neugebauer M, Woźniak P, et al. Transverse kerker scattering for angstrom localization of nanoparticles[J]. Phys Rev Lett, 2018, 121(19): 193902. doi: 10.1103/PhysRevLett.121.193902
[114] Shang W Y, Xiao F J, Zhu W R, et al. Unidirectional scattering exploited transverse displacement sensor with tunable measuring range[J]. Opt Express, 2019, 27(4): 4944−4955. doi: 10.1364/OE.27.004944
[115] Liu H C, Yang B, Guo Q H, et al. Single-pixel computational ghost imaging with helicity-dependent metasurface hologram[J]. Sci Adv, 2017, 3(9): e1701477. doi: 10.1126/sciadv.1701477
[116] Li X, Zhao R Z, Wei Q S, et al. Code division multiplexing inspired dynamic metasurface holography[J]. Adv Funct Mater, 2021, 31(35): 2103326. doi: 10.1002/adfm.202103326
[117] Georgi P, Wei Q S, Sain B, et al. Optical secret sharing with cascaded metasurface holography[J]. Sci Adv, 2021, 7(16): eabf9718. doi: 10.1126/sciadv.abf9718
[118] Zhang J X, Li P X, Cheung R C C, et al. Generation of time-varying orbital angular momentum beams with space-time-coding digital metasurface[J]. Adv Photonics, 2023, 5(3): 036001. doi: 10.1117/1.AP.5.3.036001
[119] Shaltout A M, Shalaev V M, Brongersma M L. Spatiotemporal light control with active metasurfaces[J]. Science, 2019, 364(6441): eaat3100. doi: 10.1126/science.aat3100
[120] Liu M Z, Huo P C, Zhu W Q, et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface[J]. Nat Commun, 2021, 12(1): 2230. doi: 10.1038/s41467-021-22462-z
[121] Wang S, Deng Z L, Wang Y J, et al. Arbitrary polarization conversion dichroism metasurfaces for all-in-one full Poincaré sphere polarizers[J]. Light Sci Appl, 2021, 10(1): 24. doi: 10.1038/s41377-021-00468-y
[122] Zhou Q W, Liu M Z, Zhu W Q, et al. Generation of perfect vortex beams by dielectric geometric metasurface for visible light[J]. Laser Photonics Rev, 2021, 15(12): 2100390. doi: 10.1002/lpor.202100390
[123] Fang X Y, Ren H R, Gu M. Orbital angular momentum holography for high-security encryption[J]. Nat Photonics, 2020, 14(2): 102−108. doi: 10.1038/s41566-019-0560-x
[124] Zhang F, Guo Y H, Pu M B, et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption[J]. Nat Commun, 2023, 14(1): 1946. doi: 10.1038/s41467-023-37510-z
[125] Guo X Y, Li P, Zhong J Z, et al. Stokes meta-hologram toward optical cryptography[J]. Nat Commun, 2022, 13(1): 6687. doi: 10.1038/s41467-022-34542-9
[126] Lochab P, Senthilkumaran P, Khare K. Designer vector beams maintaining a robust intensity profile on propagation through turbulence[J]. Phys Rev A, 2018, 98(2): 023831. doi: 10.1103/PhysRevA.98.023831
[127] Wang D Y, Liu F F, Liu T, et al. Efficient generation of complex vectorial optical fields with metasurfaces[J]. Light Sci Appl, 2021, 10(1): 67. doi: 10.1038/s41377-021-00504-x
-


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: