-
摘要
全息技术能够记录和重建物光波的全部信息,自问世发展至今已经取得了显著的进步。近年来,矢量全息的出现为这一领域带来新的发展。矢量全息技术不仅继承了传统标量全息技术记录振幅和相位的能力,还额外引入了对偏振维度的调控,因此能够显著提高记录信息的密度,并在多个领域得以广泛应用。本文旨在从偏振调控的角度深入探讨矢量全息技术。首先介绍了标量全息技术和矢量全息技术的概念,并比较了二者的优缺点,重点阐述了矢量全息技术的优势;然后详细地介绍了矢量全息技术的两种偏振态调控方式,包括对入射光和出射光偏振态的调控;同时阐述了矢量全息技术在三维显示和加密领域的应用;最后总结了矢量全息技术目前面临的挑战,并展望了其未来的发展趋势。
Abstract
Holography, which can record and reconstruct all the information of object light waves, has made remarkable progress since its invention. In recent years, the emergence of vectorial holography has brought new developments to this field. Vectorial holography not only inherits the ability to record the amplitude and phase of traditional scalar holography but also introduces the additional control of the polarization dimension, which can significantly improve the density of the recorded information and has been widely used in many fields. This paper discusses vectorial holography in depth from the perspective of polarization modulation. Firstly, the concepts of scalar holography and vectorial holography are introduced, and their advantages and disadvantages are compared. Then, the two polarization modulation methods of vectorial holography are introduced in detail, including the polarization modulation of incident light and output light. Meanwhile, the applications of vectorial holography in the field of 3D display and encryption are described. Finally, the challenges faced by vectorial holography are summarized, and the future development of vectorial holography is expected.
-
Key words:
- holography /
- vectorial holography /
- polarization modulation
-
Overview
Overview: Holography can record and reconstruct the full information of object light waves based on the principle of interference and diffraction. Due to its outstanding ability, holography is widely used in the fields of display, imaging, communication, encryption, etc. However, scalar holography only records the amplitude and phase information and has certain limitations in polarization information. The emergence of vectorial holography provides the possibility of modulating polarization information. Different from scalar holography, vectorial holography technology can record not only amplitude and phase information but also polarization information, which improves the freedom of modulation and the density of the recorded. Hence, vectorial holography holds promising applications in high-definition display, high-quality imaging, high-security encryption and high-speed communication. According to the development history of holography technology, this paper introduces the principles of scalar holography, and vectorial holography and highlights the advantages of vectorial holography in the aspect of polarization modulation. At the same time, the principles and designs of two different polarization control methods of vectorial holography are described, including the polarization control of incident light and output light, which provide important guidance and theoretical support for researchers. For the polarization control of reconstructed light waves, a 2×2 Jones matrix is widely used to express the relationship between the polarization state of the incident light wave and the outgoing light wave. In practice, the parameters of the hologram are deliberately designed to match the unique relationships between the polarization state of the incident light wave and the outgoing light wave for different reconstructed images. In this way, different reconstructed images can be switched by selecting the desired polarization with negligible polarization crosstalk. For the polarization control of output light, the incident light wave is decomposed into a couple of orthogonal polarized light, such as left circular polarization and right circular polarization, x-polarized light and y-polarized light, etc. By intentionally controlling the phase and amplitude of the two orthogonal polarized lights, an arbitrary state of polarization that covers the entire Poincare sphere can be generated. In addition, the advantages of vectorial holography in the field of display and encryption are demonstrated. Compared with scalar holography, vectorial holography has the advantages of being able to improve the quality of holographic images, better flexibility, and applicability, and solves some of the problems that scalar holography is currently facing. Finally, the problems and possible solutions in the development of vectorial holography technology and the future development trend are also discussed.
-

-
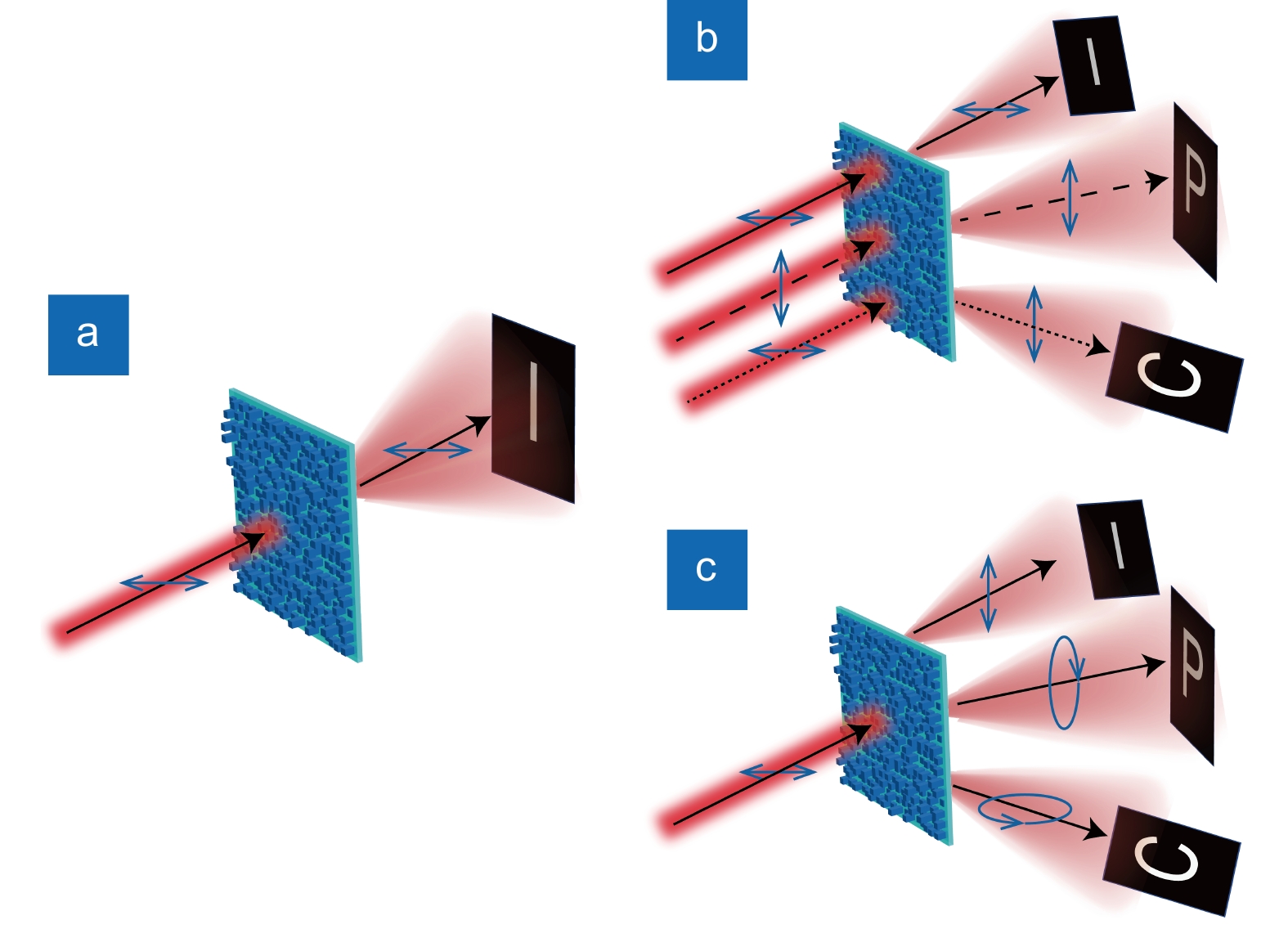
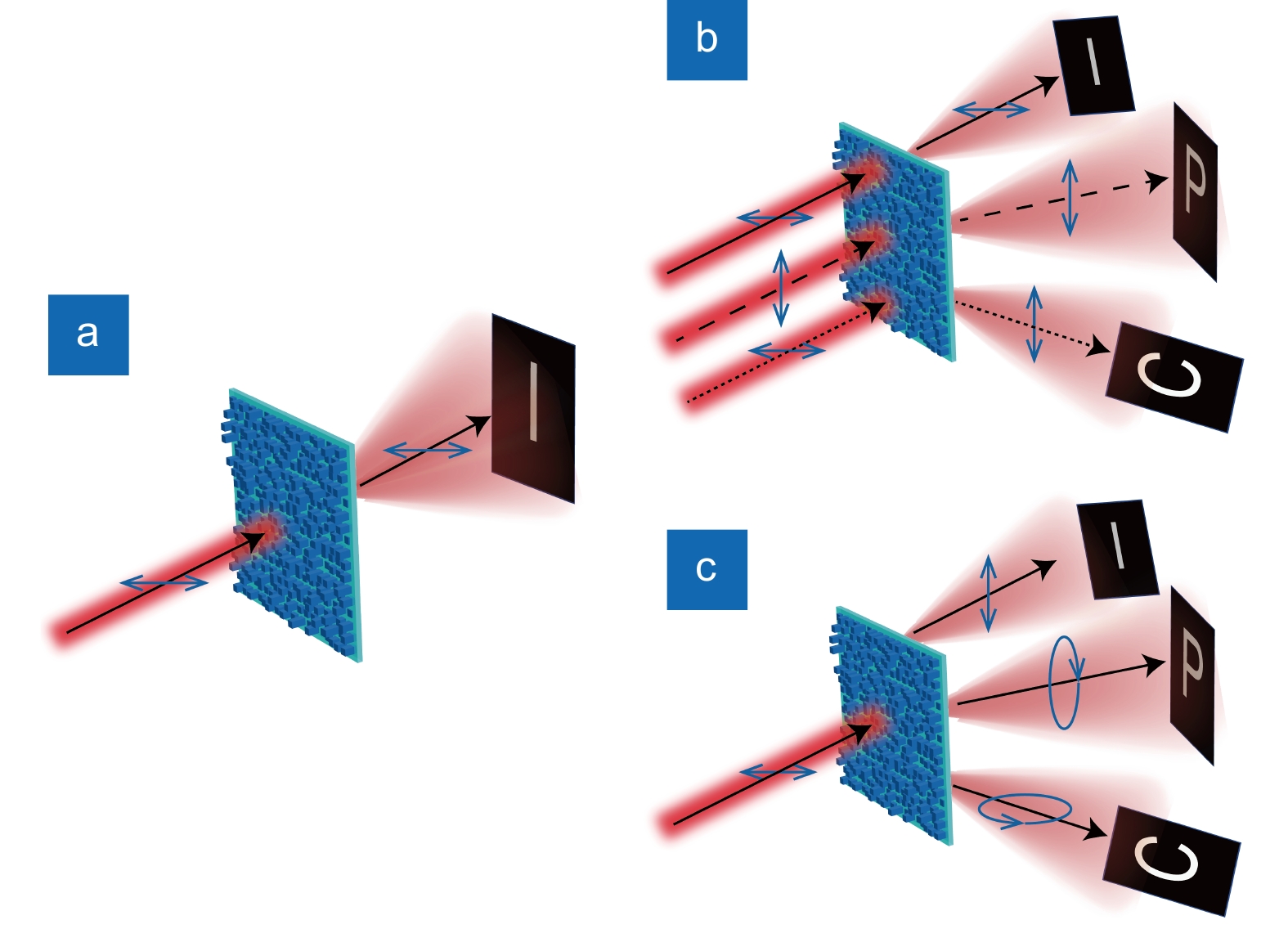
图 3 标量全息技术与矢量全息技术。(a)标量全息技术;(b)矢量全息技术—对入射光的偏振态进行调控;(c)矢量全息技术—对出射光的偏振态进行调控
Figure 3. Scalar holography and vectorial holography. (a) Scalar holography; (b) Vectorial holography - modulation of the polarization state of the incident light; (c) Vectorial holography - modulation of the polarization state of the output light
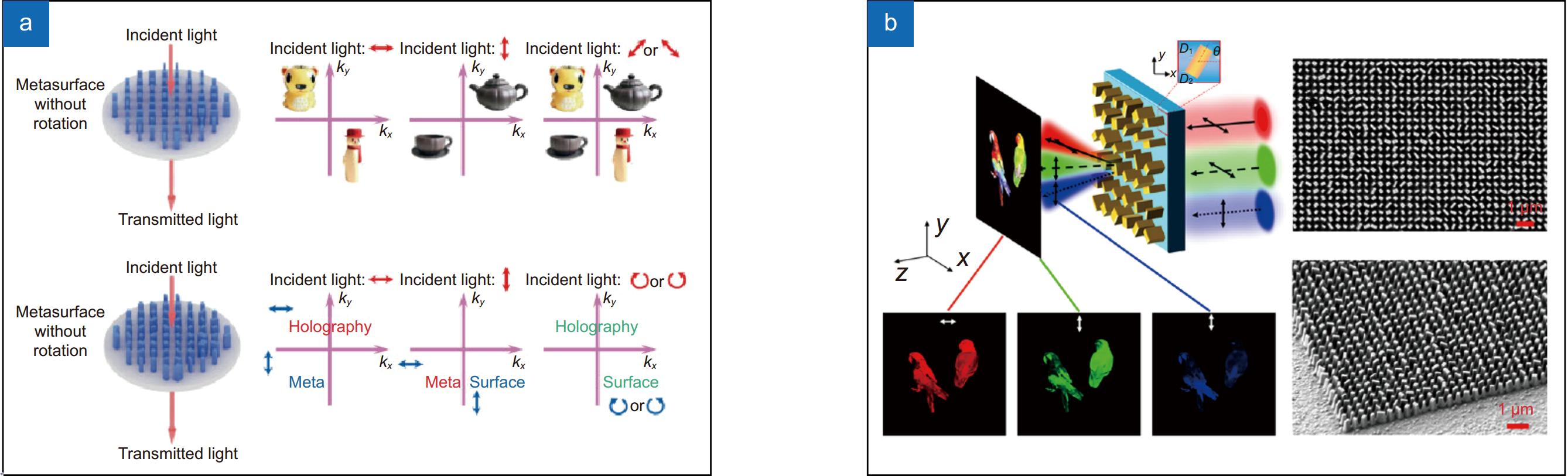
图 4 对入射光偏振态调控的矢量全息技术。(a)基于双折射全介质超表面的多通道矢量全息技术[79];(b)基于非交错的TiO2超表面的全彩矢量全息技术[81]
Figure 4. Vectorial holography for modulation of the polarization state of incident light. (a) Multi-channel vectorial holography based on birefringent fully dielectric hypersurfaces[79]; (b) Full-color vectorial holography based on non-interlaced TiO2 hypersurfaces[81]
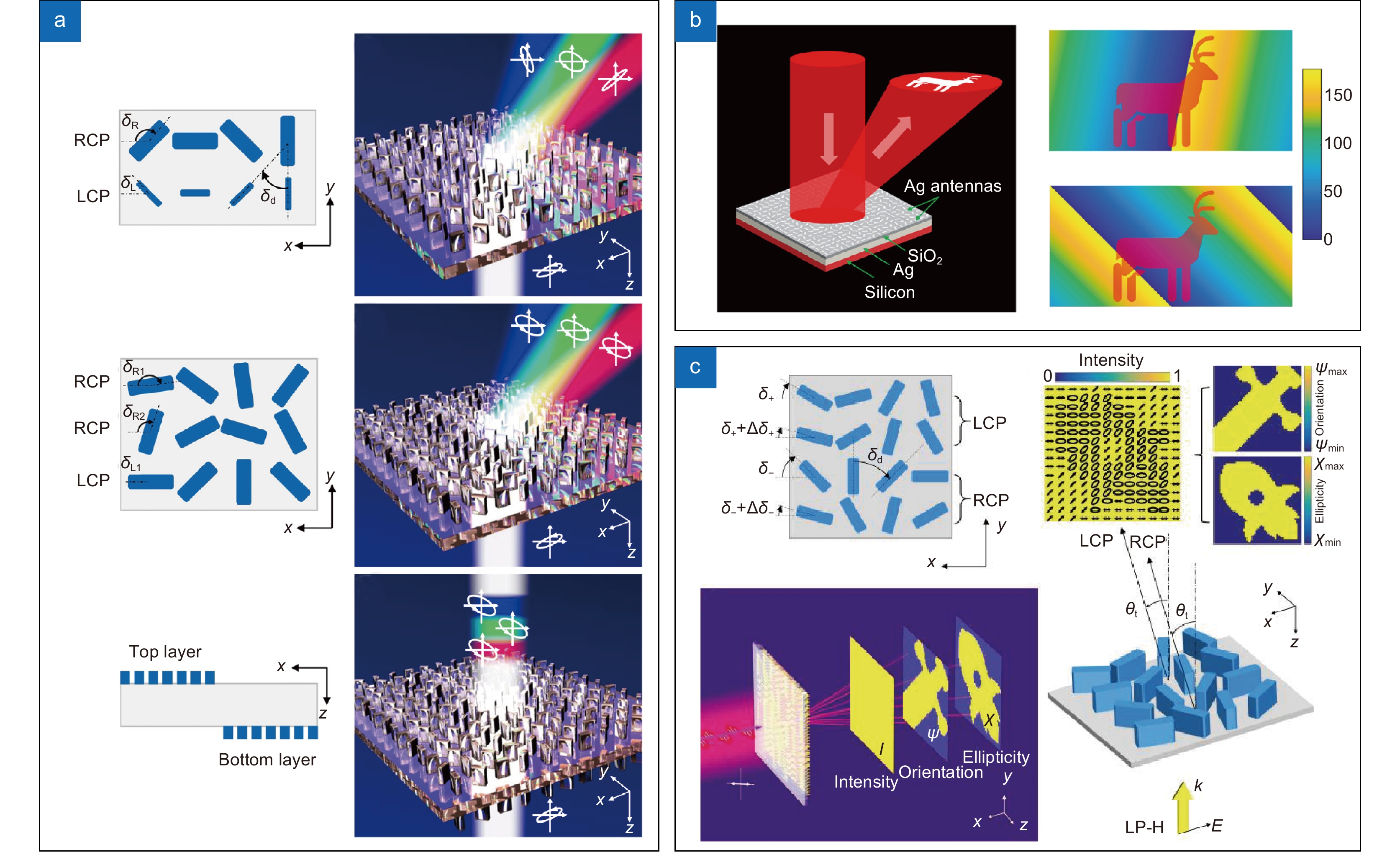
图 5 对入射光偏振态调控的矢量全息技术。(a)基于6个自由度琼斯矩阵超表面矢量全息技术[82];(b)基于动态相位和几何相位介电超表面的矢量全息技术[83];(c)结合梯度下降算法的双层超表面结构的矢量全息技术[84]
Figure 5. Vectorial holography for polarization state modulation of incident light. (a) Vectorial holography based on a 6-degree-of-freedom Jones matrix hypersurface[82]; (b) Vectorial holography based on a dynamically phased and geometrically phased dielectric hypersurface[83]; (c) Vectorial holography of a bilayer superstructure surface structure combined with a gradient descent algorithm[84]
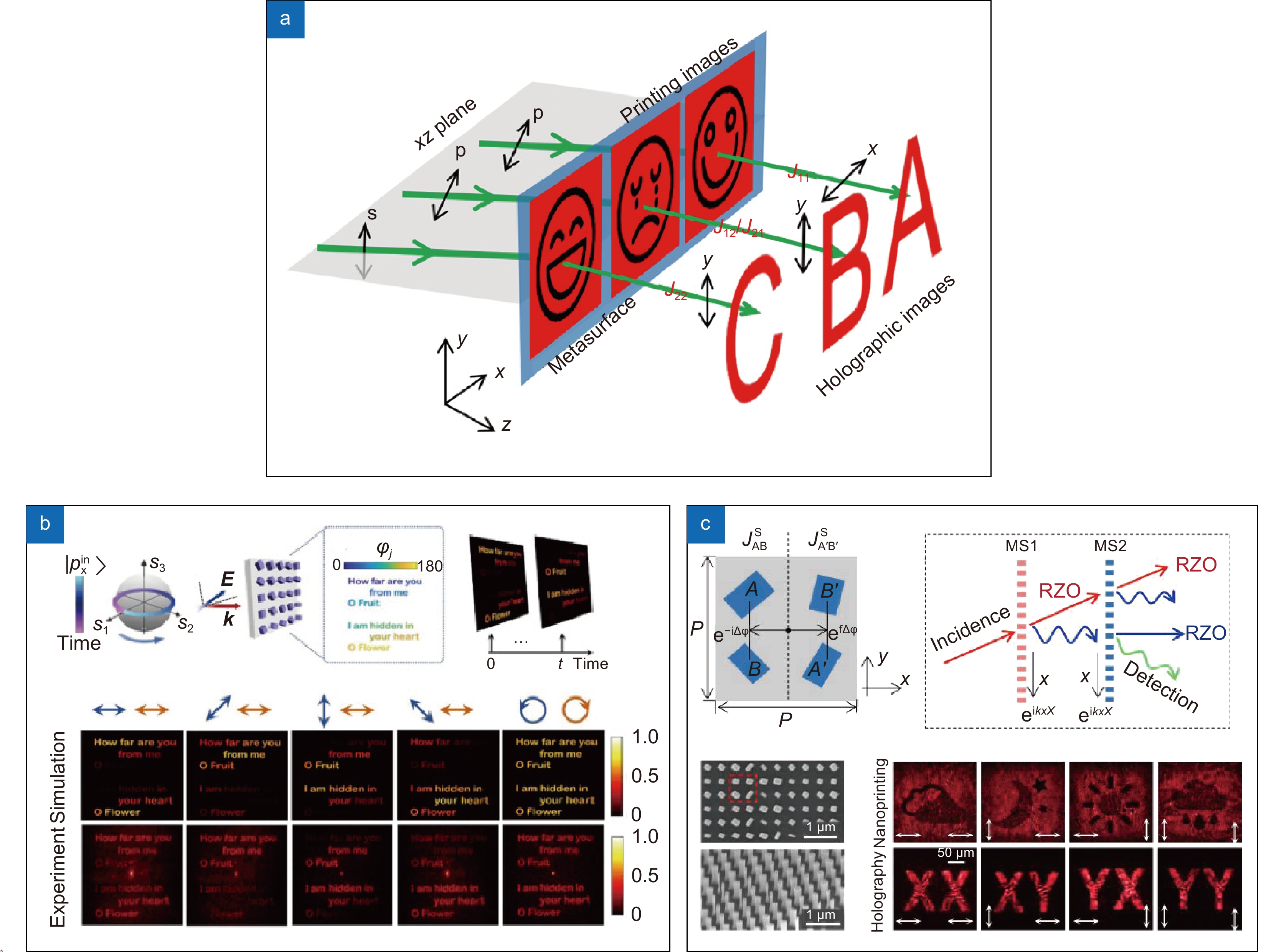
图 6 对出射光偏振态调控的矢量全息技术。(a)基于双原子等离子体结构单元的矢量全息技术[86];(b)基于介电超表面偏振发生器的矢量全息技术[87];(c)基于控制偏振传递函数的矢量全息技术[88];(d)基于氮化镓纳米柱像素化超表面的矢量全息技术[89]
Figure 6. Vectorial holography for the modulation of the polarization state of an output light. (a) Vectorial holography based on a diatomic plasma structural unit[86]; (b) Vectorial holography based on a dielectric-super surface polarization generator[87]; (c) Vectorial holography based on control of polarization transfer function[88]; (d) Vectorial holography based on a pixelated hypersurface with GaN nanopillars[89]
图 7 对出射光偏振态调控的矢量全息技术。(a)基于正交圆偏振叠加的矢量全息技术[90];(b)基于反射型等离子体超表面的矢量全息技术[91];(c)基于矢量傅里叶超表面的矢量全息技术[92]
Figure 7. Vectorial holography for polarization state modulation of output light. (a) Vectorial holography based on orthogonal circular polarization superposition[90]; (b) Vectorial holography based on a reflective plasma hypersurface[91]; (c) Vectorial holography based on a vector Fourier hypersurface[92]
图 9 彩色矢量全息技术。(a)基于新型的自旋波长编码的矢量全息技术[95];(b)基于改进Gerchberg-Saxton算法的矢量全息技术[96];(c)基于双原子等离子体单元结构的全彩色复振幅矢量全息技术[44]
Figure 9. Color vectorial holography. (a) Vectorial holography based on novel spin-wavelength encoding hypersurface[95]; (b) Vectorial holography based on the improved Gerchberg-Saxton algorithm[96]; (c) Full-color complex amplitude vectorial holography based on diatomic plasma cell structures[44]
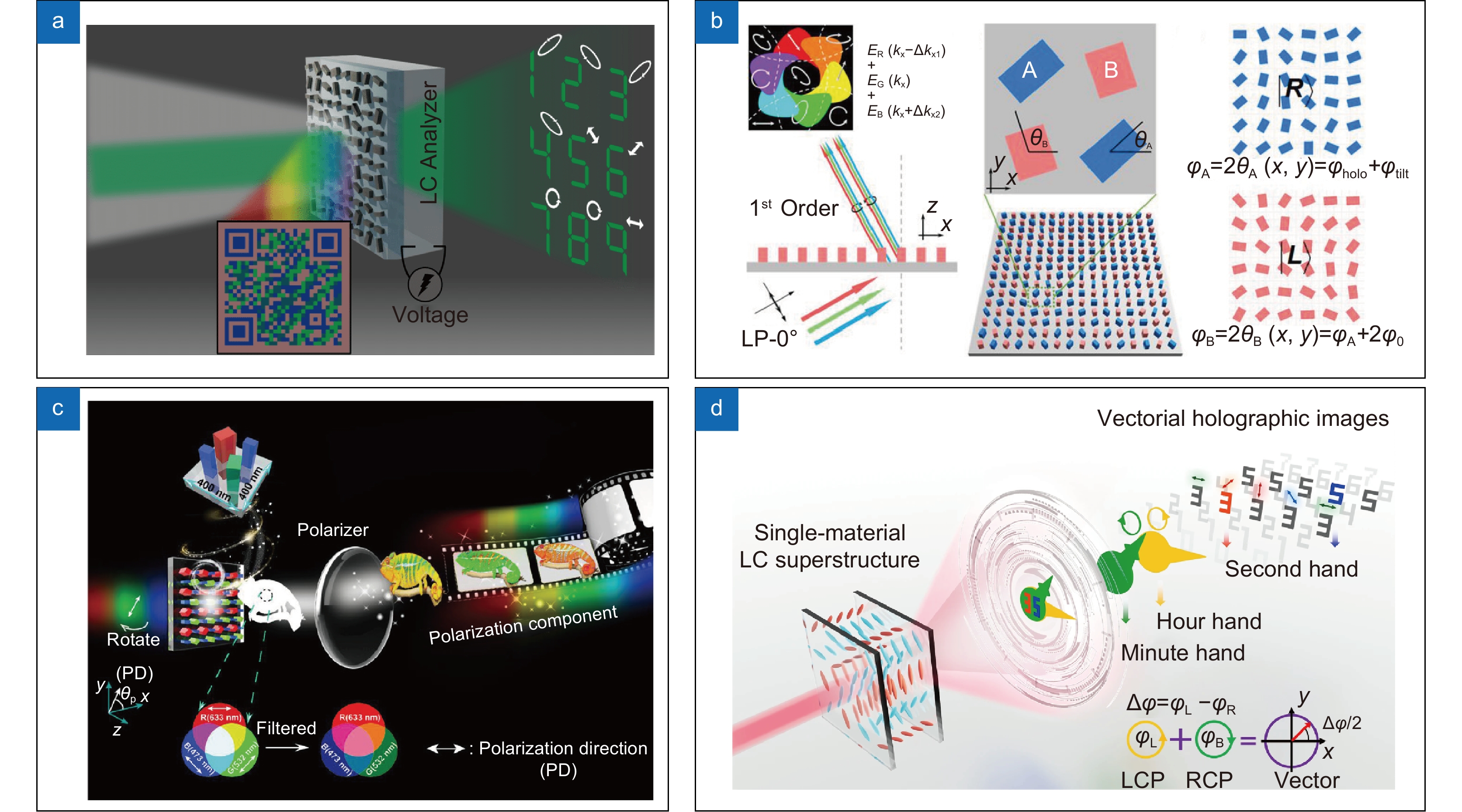
图 10 对出射光偏振态调控的矢量全息技术。(a)基于双功能超表面的彩色矢量全息技术[97];(b)全偏振通道的的全彩色矢量全息技术[98]; (c)基于正交圆偏振光的矢量全息技术[99]; (d) 基于像素化液晶超结构的矢量全息技术[100]
Figure 10. Vectorial holography for polarization state modulation of output light. (a) Vectorial holography based on a novel spin-wavelength-encoded multi-tasking hypersurface[97]; (b) Full-color vectorial holography with fully polarized channels[98]; (c) Vectorial holography based on orthogonal circularly polarized light[99]; (d) Vectorial holography based on pixelated liquid crystal superstructures[100]
表 1 光学全息技术与计算全息技术对比
Table 1. Comparison between optical holography and computational holography
是否可以记录虚拟物体 全息图类型 环境影响 图像质量是否受限 成本 信息传输 光学全息技术 否 静态 较大 是 高 复杂 计算全息技术 是 静态/动态 较小 是 低 灵活 表 2 常见的偏振光的归一化Stokes参量
Table 2. Normalized Stokes coefficients for common polarized light
偏振光 归一化Stokes参量 x方向线偏振光 [1,1,0,0]T y方向线偏振光 [1,-1,0,0]T 45°线偏振光 [1,0,1,0]T −45°线偏振光 [1,0,-1,0]T 左旋圆偏振光 [1,0,0,-1]T 右旋圆偏振光 [1,0,0,1]T 表 3 常见偏振光的归一化琼斯矢量
Table 3. Normalised Jones vectors for commonly polarised light
偏振光 归一化琼斯矢量 x方向线偏振光 $ \left[ {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right] $ y方向线偏振光 $ \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right] $ 45°线偏振光 $ \dfrac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right] $ −45°线偏振光 $ \dfrac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1 \\ { - 1} \end{array}} \right] $ 左旋圆偏振光 $ \dfrac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1 \\ {\text{i}} \end{array}} \right] $ 右旋圆偏振光 $ \dfrac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1 \\ { - {\text{i}}} \end{array}} \right] $ -
参考文献
[1] Fang X Y, Ren H R, Gu M. Orbital angular momentum holography for high-security encryption[J]. Nat Photonics, 2020, 14(2): 102−108. doi: 10.1038/s41566-019-0560-x
[2] Shi L, Li B C, Kim C, et al. Towards real-time photorealistic 3D holography with deep neural networks[J]. Nature, 2021, 591(7849): 234−239. doi: 10.1038/s41586-020-03152-0
[3] Chang C L, Bang K, Wetzstein G, et al. Toward the next-generation VR/AR optics: a review of holographic near-eye displays from a human-centric perspective[J]. Optica, 2020, 7(11): 1563−1578. doi: 10.1364/OPTICA.406004
[4] Blanche P A. Holography, and the future of 3D display[J]. Light Adv Manuf, 2021, 2(4): 446−459. doi: 10.37188/lam.2021.028
[5] Pi D P, Liu J, Wang Y T. Review of computer-generated hologram algorithms for color dynamic holographic three-dimensional display[J]. Light Sci Appl, 2022, 11(1): 231. doi: 10.1038/s41377-022-00916-3
[6] Gabor D. A new microscopic principle[J]. Nature, 1948, 161(4098): 777−778. doi: 10.1038/161777a0
[7] Leith E N, Upatnieks J. Reconstructed wavefronts and communication theory[J]. J Opt Soc Am, 1962, 52(10): 1123−1130. doi: 10.1364/JOSA.52.001123
[8] Leith EN, Upatnieks J. Wavefront reconstruction with continuous-tone objects[J]. J Opt Soc Am, 1963, 53(12): 1377−1381. doi: 10.1364/JOSA.53.001377
[9] Leith E N, Upatnieks J. Wavefront reconstruction with diffused illumination and three-dimensional objects[J]. J Opt Soc Am, 1964, 54(11): 1295−1301. doi: 10.1364/JOSA.54.00129
[10] Lohmann A W, Paris D P. Binary fraunhofer holograms, generated by computer[J]. Appl Opt, 1967, 6(10): 1739−1748. doi: 10.1364/AO.6.001739
[11] Lesem L B, Hirsch P M, Jordan J A. The kinoform: a new wavefront reconstruction device[J]. IBM J Res Dev, 1969, 13(2): 150−155. doi: 10.1147/rd.132.0150
[12] Lee W H. Binary computer-generated holograms[J]. Appl Opt, 1979, 18(21): 3661−3669. doi: 10.1364/AO.18.003661
[13] Pi D P, Liu J, Kang R F, et al. Reducing the memory usage of computer-generated hologram calculation using accurate high-compressed look-up-table method in color 3D holographic display[J]. Opt Express, 2019, 27(20): 28410−28422. doi: 10.1364/OE.27.028410
[14] Wang Z, Lv G Q, Feng Q B, et al. Resolution priority holographic stereogram based on integral imaging with enhanced depth range[J]. Opt Express, 2019, 27(3): 2689−2702. doi: 10.1364/OE.27.002689
[15] Wang Z, Zhu L M, Zhang X, et al. Computer-generated photorealistic hologram using ray-wavefront conversion based on the additive compressive light field approach[J]. Opt Lett, 2020, 45(3): 615−618. doi: 10.1364/OL.383508
[16] Chang C L, Cui W, Gao L. Holographic multiplane near-eye display based on amplitude-only wavefront modulation[J]. Opt Express, 2019, 27(21): 30960−30970. doi: 10.1364/OE.27.030960
[17] Sui X M, He Z H, Jin G F, et al. Band-limited double-phase method for enhancing image sharpness in complex modulated computer -generated holograms[J]. Opt Express, 2021, 29(2): 2597−2612. doi: 10.1364/OE.414299
[18] Slinger C, Cameron C, Stanley M. Computer-generated holography as a generic display technology[J]. Computer, 2005, 38(8): 46−53. doi: 10.1109/MC.2005.260
[19] Kelly D P, Monaghan D S, Pandey N, et al. Digital holographic capture and optoelectronic reconstruction for 3D displays[J]. Int J Digit Multimed Broadcast, 2010, 2010: 759323. doi: 10.1155/2010/75932
[20] Geng J. Three-dimensional display technologies[J]. Adv Opt Photonics, 2013, 5(4): 456−535. doi: 10.1364/AOP.5.000456
[21] Chen L Z, Zhu R Z, Zhang H. Speckle-free compact holographic near-eye display using camera-in-the-loop optimization with phase constraint[J]. Opt Express, 2022, 30(26): 46649−46665. doi: 10.1364/OE.475066
[22] Liu K X, Wu J C, He Z H, et al. 4K-DMDNet: diffraction model-driven network for 4K computer-generated holography[J]. Opto-Electron Adv, 2023, 6(5): 220135. doi: 10.29026/oea.2023.220135
[23] 隋晓萌, 何泽浩, 曹良才, 等. 基于液晶空间光调制器的计算全息波前编码方法[J]. 液晶与显示, 2022, 37(5): 613−624. doi: 10.37188/CJLCD.2022-0047
Sui X M, He Z H, Cao L C, et al. Wave-front encoding method of computer-generated holography based on liquid-crystal spatial light modulator[J]. Chin J Liq Cryst Dis, 2022, 37(5): 613−624. doi: 10.37188/CJLCD.2022-0047
[24] 刘娟, 皮大普, 王涌天. 实时全息三维显示技术研究进展[J]. 光学学报, 2023, 43(15): 1509001. doi: 10.3788/AOS230744
Liu J, Pi D P, Wang Y T. Research progress of real-time holographic 3D display technology[J]. Acta Opt Sin, 2023, 43(15): 1509001. doi: 10.3788/AOS230744
[25] Pi D P, Wang J, Liu J, et al. Color dynamic holographic display based on complex amplitude modulation with bandwidth constraint strategy[J]. Opt Lett, 2022, 47(17): 4379−4382. doi: 10.1364/OL.469463
[26] Sun K, Tan D Z, Fang X Y, et al. Three-dimensional direct lithography of stable perovskite nanocrystals in glass[J]. Science, 2022, 375(6578): 307−310. doi: 10.1126/science.abj2691
[27] Pi D P, Liu J, Wang J, et al. Optimized computer-generated hologram for enhancing depth cue based on complex amplitude modulation[J]. Opt Lett, 2022, 47(24): 6377−6380. doi: 10.1364/OL.476443
[28] Pi D P, Liu J, Han Y, et al. Acceleration of computer-generated hologram using wavefront-recording plane and look-up table in three-dimensional holographic display[J]. Opt Express, 2020, 28(7): 9833−9841. doi: 10.1364/OE.385388
[29] Peng Y, Nagase T, Kanamoto T, et al. A virtual optical holographic encryption system using expanded diffie-hellman algorithm[J]. IEEE Access, 2021, 9: 22071−22077. doi: 10.1109/ACCESS.2021.3055866
[30] Li J Y, Chen L, Cai W Y, et al. Holographic encryption algorithm based on bit-plane decomposition and hyperchaotic Lorenz system[J]. Opt Laser Technol, 2022, 152: 108127. doi: 10.1016/j.optlastec.2022.108127
[31] Hamadi I A, Jamal R K, Mousa S K. Image encryption based on computer generated hologram and rossler chaotic system[J]. Opt Quant Electron, 2022, 54(1): 33. doi: 10.1007/s11082-021-03406-9
[32] Dong Y B, Luan H T, Lin D J, et al. Laser-induced graphene hologram reconfiguration for countersurveillance multisecret sharing[J]. Laser Photonics Rev, 2023, 17(8): 2200805. doi: 10.1002/lpor.202200805
[33] Li K Y, Wang Y M, Pi D P, et al. Multi-dimensional multiplexing optical secret sharing framework with cascaded liquid crystal holograms[J]. Opto-Electron Adv, 2024, 7(1): 230121. doi: 10.29026/oea.2024.230121
[34] Song M H, Wang H J, Wu J B, et al. A robust watermarking hybrid algorithm for color image[J]. MATEC Web Conf, 2021, 336: 07012. doi: 10.1051/matecconf/202133607012
[35] Cheremkhin P A, Evtikhiev N N, Krasnov V V, et al. Iterative synthesis of binary inline fresnel holograms for high-quality reconstruction in divergent beams with DMD[J]. Opt Lasers Eng, 2022, 150: 106859. doi: 10.1016/j.optlaseng.2021.106859
[36] Huang L L, Chen X Z, Mühlenbernd H, et al. Three-dimensional optical holography using a plasmonic metasurface[J]. Nat Commun, 2013, 4(1): 2808. doi: 10.1038/ncomms3808
[37] Wen D D, Cadusch J J, Meng J J, et al. Light field on a chip: metasurface-based multicolor holograms[J]. Adv Photonics, 2021, 3(2): 024001. doi: 10.1117/1.AP.3.2.024001
[38] Kim J, Seong J, Yang Y, et al. Tunable metasurfaces towards versatile metalenses and metaholograms: a review[J]. Adv Photonics, 2022, 4(2): 024001. doi: 10.1117/1.AP.4.2.024001
[39] Zheng G X, Mühlenbernd H, Kenney M, et al. Metasurface holograms reaching 80% efficiency[J]. Nat Nanotechnol, 2015, 10(4): 308−312. doi: 10.1038/nnano.2015.2
[40] Ding X M, Wang Z C, Hu G W, et al. Metasurface holographic image projection based on mathematical properties of fourier transform[J]. PhotoniX, 2020, 1(1): 16. doi: 10.1186/s43074-020-00016-8
[41] Yu N F, Genevet P, Kats M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333−337. doi: 10.1126/science.1210713
[42] Li G X, Zhang S, Zentgraf T. Nonlinear photonic metasurfaces[J]. Nat Rev Mater, 2017, 2(5): 17010. doi: 10.1038/natrevmats.2017.10
[43] Chen S Q, Liu W W, Li Z C, et al. Metasurface‐empowered optical multiplexing and multifunction[J]. Ad Mater, 2020, 32(3): 1805912. doi: 10.1002/adma.201805912
[44] Deng Z L, Jin M K, Ye X, et al. Full-color complex-amplitude vectorial holograms based on multi-freedom metasurfaces[J]. Adv Funct Mater, 2020, 30(21): 1910610. doi: 10.1002/adfm.201910610
[45] Nemati A, Wang Q, Hong M H, et al. Tunable and reconfigurable metasurfaces and metadevices[J]. Opto-Electron Adv, 2018, 1(5): 180009. doi: 10.29026/oea.2018.180009
[46] Yu N F, Capasso F. Flat optics with designer metasurfaces[J]. Nat Mater, 2014, 13(2): 139−150. doi: 10.1038/nmat3839
[47] Aieta F, Genevet P, Kats M A, et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces[J]. Nano Lett, 2012, 12(9): 4932−4936. doi: 10.1021/nl302516v
[48] Kildishev A V, Boltasseva A, Shalaev V M. Planar photonics with metasurfaces[J]. Science, 2013, 339(6125): 1232009. doi: 10.1126/science.1232009
[49] Lin D M, Fan P Y, Hasman E, et al. Dielectric gradient metasurface optical elements[J]. Science, 2014, 345(6194): 298−302. doi: 10.1126/science.1253213
[50] Holloway C L, Kuester E F, Gordon J A, et al. An overview of the theory and applications of metasurfaces: the two-dimensional equivalents of metamaterials[J]. IEEE Antennas Propag Mag, 2012, 54(2): 10−35. doi: 10.1109/MAP.2012.6230714
[51] Ni X J, Kildishev A V, Shalaev V M. Metasurface holograms for visible light[J]. Nat Commun, 2013, 4(1): 2807. doi: 10.1038/ncomms3807
[52] Arbabi A, Horie Y, Bagheri M, et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission[J]. Nat Nanotechnol, 2015, 10(11): 937−943. doi: 10.1038/nnano.2015.186
[53] Khorasaninejad M, Chen W T, Devlin R C, et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging[J]. Science, 2016, 352(6290): 1190−1194. doi: 10.1126/science.aaf6644
[54] Pors A, Nielsen M G, Eriksen R L, et al. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces[J]. Nano Lett, 2013, 13(2): 829−834. doi: 10.1021/nl304761m
[55] Wu P C, Tsai W Y, Chen W T, et al. Versatile polarization generation with an aluminum plasmonic metasurface[J]. Nano Lett, 2017, 17(1): 445−452. doi: 10.1021/acs.nanolett.6b04446
[56] Wang S, Deng Z L, Wang Y J, et al. Arbitrary polarization conversion dichroism metasurfaces for all-in-one full Poincaré sphere polarizers[J]. Light Sci Appl, 2021, 10(1): 24. doi: 10.1038/s41377-021-00468-y
[57] Fan Q B, Liu M Z, Zhang C, et al. Independent amplitude control of arbitrary orthogonal states of polarization via dielectric metasurfaces[J]. Phys Rev Lett, 2020, 125(26): 267402. doi: 10.1103/PhysRevLett.125.267402
[58] Cao L C, He Z H, Liu K X, et al. Progress and challenges in dynamic holographic 3D display for the metaverse (Invited)[J]. Infrared Laser Eng, 2022, 51(1): 20210935. doi: 10.3788/IRLA20210935
[59] 郑淑君, 林枭, 黄志云, 等. 基于偏光全息的光场调控研究进展[J]. 光电工程, 2022, 49(11): 220114. doi: 10.12086/oee.2022.220114
Zheng S J, Lin X, Huang Z Y, et al. Light field regulation based on polarization holography[J]. Opto-Electron Eng, 2022, 49(11): 220114. doi: 10.12086/oee.2022.220114
[60] 胡孟霞, 王志强, 李向平, 等. 超表面偏振信息编码[J]. 中国激光, 2023, 50(18): 1813010. doi: 10.3788/CJL230724
Hu M X, Wang Z Q, Li X P, et al. Metasurface polarization information encoding[J]. Chin J Lasers, 2023, 50(18): 1813010. doi: 10.3788/CJL230724
[61] Born M, Wolf E, Hecht E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light[J]. Phys Today, 2000, 53(10): 77−78. doi: 10.1063/1.1325200
[62] Dorrah A H, Rubin N A, Zaidi A, et al. Metasurface optics for on-demand polarization transformations along the optical path[J]. Nat Photonics, 2021, 15(4): 287−296. doi: 10.1038/s41566-020-00750-2
[63] Zhao R Z, Xiao X F, Geng G Z, et al. Polarization and holography recording in real- and k-space based on dielectric metasurface[J]. Adv Funct Mater, 2021, 31(27): 2100406. doi: 10.1002/adfm.202100406
[64] Grady N K, Heyes J E, Chowdhury D R, et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction[J]. Science, 2013, 340(6138): 1304−1307. doi: 10.1126/science.1235399
[65] Gao Y J, Xiong X, Wang Z H, et al. Simultaneous generation of arbitrary assembly of polarization states with geometrical-scaling-induced phase modulation[J]. Phys Rev X, 2020, 10(3): 031035. doi: 10.1103/PhysRevX.10.031035
[66] Arbabi E, Kamali S M, Arbabi A, et al. Full-stokes imaging polarimetry using dielectric metasurfaces[J]. ACS Photonics, 2018, 5(8): 3132−3140. doi: 10.1021/acsphotonics.8b00362
[67] Balthasar Mueller J P, Rubin N A, Devlin RC, et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization[J]. Phys Rev Lett, 2017, 118(11): 113901. doi: 10.1103/PhysRevLett.118.113901
[68] Wen D D, Yue F Y, Li G X, et al. Helicity multiplexed broadband metasurface holograms[J]. Nat Commun, 2015, 6(1): 8241. doi: 10.1038/ncomms9241
[69] Goldstein D H. Polarized Light[M]. 3rd ed. Boca Raton: CRC Press, 2017.https://doi.org/10.1201/b10436.
[70] Kumar A, Ghatak A. Polarization of Light with Applications in Optical Fibers[M]. Bellingham: SPIE Press, 2011.
[71] Chipman R A, Lam W S T, Young G. Polarized Light and Optical Systems[M]. Boca Raton: CRC Press, 2018.https://doi.org/10.1201/9781351129121.
[72] Azzam R M A, Bashara N M, Ballard S S. Ellipsometry and polarized light[J]. Phys Today, 1978, 31(11): 72−72. doi: 10.1063/1.2994821
[73] Ozaki M, Kato J I, Kawata S. Surface-plasmon holography with white-light illumination[J]. Science, 2011, 332(6026): 218−220. doi: 10.1126/science.1201045
[74] Montelongo Y, Tenorio-Pearl J O, Williams C, et al. Plasmonic nanoparticle scattering for color holograms[J]. Proc Natl Acad Sci USA, 2014, 111(35): 12679−12683. doi: 10.1073/pnas.1405262111
[75] Walther B, Helgert C, Rockstuhl C, et al. Spatial and spectral light shaping with metamaterials[J]. Adv Mater, 2012, 24(47): 6300−6304. doi: 10.1002/adma.201202540
[76] Huang Y W, Chen W T, Tsai W Y, et al. Aluminum plasmonic multicolor meta-hologram[J]. Nano Lett, 2015, 15(5): 3122−3127. doi: 10.1021/acs.nanolett.5b00184
[77] Wan W W, Gao J, Yang X D. Full-color plasmonic metasurface holograms[J]. ACS Nano, 2016, 10(12): 10671−10680. doi: 10.1021/acsnano.6b05453
[78] Masters B R. Fundamentals of photonics, second edition[J]. J Biomed Opt, 2008, 13(4): 049901. doi: 10.1117/1.2976006
[79] Zhao R Z, Sain B, Wei Q S, et al. Multichannel vectorial holographic display and encryption[J]. Light Sci Appl, 2018, 7: 95. doi: 10.1038/s41377-018-0091-0
[80] Gerchberg R W, Saxton W O. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik, 1972, 35 (2): 237–246.
[81] Hu Y Q, Li L, Wang Y J, et al. Trichromatic and tripolarization-channel holography with noninterleaved dielectric metasurface[J]. Nano Lett, 2020, 20(2): 994−1002. doi: 10.1021/acs.nanolett.9b04107
[82] Bao Y J, Wen L, Chen Q, et al. Toward the capacity limit of 2D planar Jones matrix with a single-layer metasurface[J]. Sci Adv, 2021, 7(25): eabh0365. doi: 10.1126/sciadv.abh0365
[83] Zhang S F, Huang L L, Geng G Z, et al. Full-stokes polarization transformations and time sequence metasurface holographic display[J]. Photonics Res, 2022, 10(4): 1031−1038. doi: 10.1364/PRJ.450354
[84] Bao Y J, Nan F, Yan J H, et al. Observation of full-parameter Jones matrix in bilayer metasurface[J]. Nat Commun, 2022, 13(1): 7550. doi: 10.1038/s41467-022-35313-2
[85] Zhang F, Pu M B, Luo J, et al. Symmetry breaking of photonic spin-orbit interactions in metasurfaces[J]. Opto-Electron Eng, 2017, 44(3): 319−325. doi: 10.3969/j.issn.1003-501X.2017.03.006
[86] Deng Z L, Deng J H, Zhuang X, et al. Diatomic metasurface for vectorial holography[J]. Nano Lett, 2018, 18(5): 2885−2892. doi: 10.1021/acs.nanolett.8b00047
[87] Ding F, Chang B D, Wei Q S, et al. Versatile polarization generation and manipulation using dielectric metasurfaces[J]. Laser Photonics Rev, 2020, 14(11): 2000116. doi: 10.1002/lpor.202000116
[88] Rubin N A, Zaidi A, Dorrah A H, et al. Jones matrix holography with metasurfaces[J]. Sci Adv, 2021, 7(33): eabg7488. doi: 10.1126/sciadv.abg7488
[89] Song Q H, Baroni A, Sawant R, et al. Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces[J]. Nat Commun, 2020, 11(1): 2651. doi: 10.1038/s41467-020-16437-9
[90] Song Q, Khadir S, Vézian S, et al. Bandwidth-unlimited polarization-maintaining metasurfaces[J]. Sci Adv, 2021, 7(5): eabe1112. doi: 10.1126/sciadv.abe1112
[91] Wen D D, Cadusch J J, Meng J J, et al. Vectorial holograms with spatially continuous polarization distributions[J]. Nano Lett, 2021, 21(4): 1735−1741. doi: 10.1021/acs.nanolett.0c04555
[92] Song Q H, Baroni A, Wu P C, et al. Broadband decoupling of intensity and polarization with vectorial Fourier metasurfaces[J]. Nat Commun, 2021, 12(1): 3631. doi: 10.1038/s41467-021-23908-0
[93] Wan W P, Yang W H, Feng H, et al. Multiplexing vectorial holographic images with arbitrary metaholograms[J]. Adv Opt Mater, 2021, 9(20): 2100626. doi: 10.1002/adom.202100626
[94] Mao N B, Zhang G Q, Tang Y T, et al. Nonlinear vectorial holography with quad-atom metasurfaces[J]. Proc Natl Acad Sci USA, 2022, 119(22): e2204418119. doi: 10.1073/pnas.2204418119
[95] Jin L, Dong Z G, Mei S T, et al. Noninterleaved metasurface for (26–1) spin- and wavelength-encoded holograms[J]. Nano Lett, 2018, 18(12): 8016−8024. doi: 10.1021/acs.nanolett.8b04246
[96] Arbabi E, Kamali S M, Arbabi A, et al. Vectorial holograms with a dielectric metasurface: ultimate polarization pattern generation[J]. ACS Photonics, 2019, 6(11): 2712−2718. doi: 10.1021/acsphotonics.9b00678
[97] Kim I, Jang J, Kim G, et al. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform[J]. Nat Commun, 2021, 12(1): 3614. doi: 10.1038/s41467-021-23814-5
[98] Guo X Y, Zhong J Z, Li B J, et al. Full-color holographic display and encryption with full-polarization degree of freedom[J]. Adv Mater, 2022, 34(3): 2103192. doi: 10.1002/adma.202103192
[99] Wan W P, Yang W H, Ye S, et al. Tunable full-color vectorial meta-holography[J]. Adv Opt Mater, 2022, 10(22): 2201478. doi: 10.1002/adom.202201478
[100] Wang Z Y, Zhou Z, Zhang H, et al. Vectorial liquid-crystal holography[J]. eLight, 2024, 4(1): 5. doi: 10.1186/s43593-024-00061-x
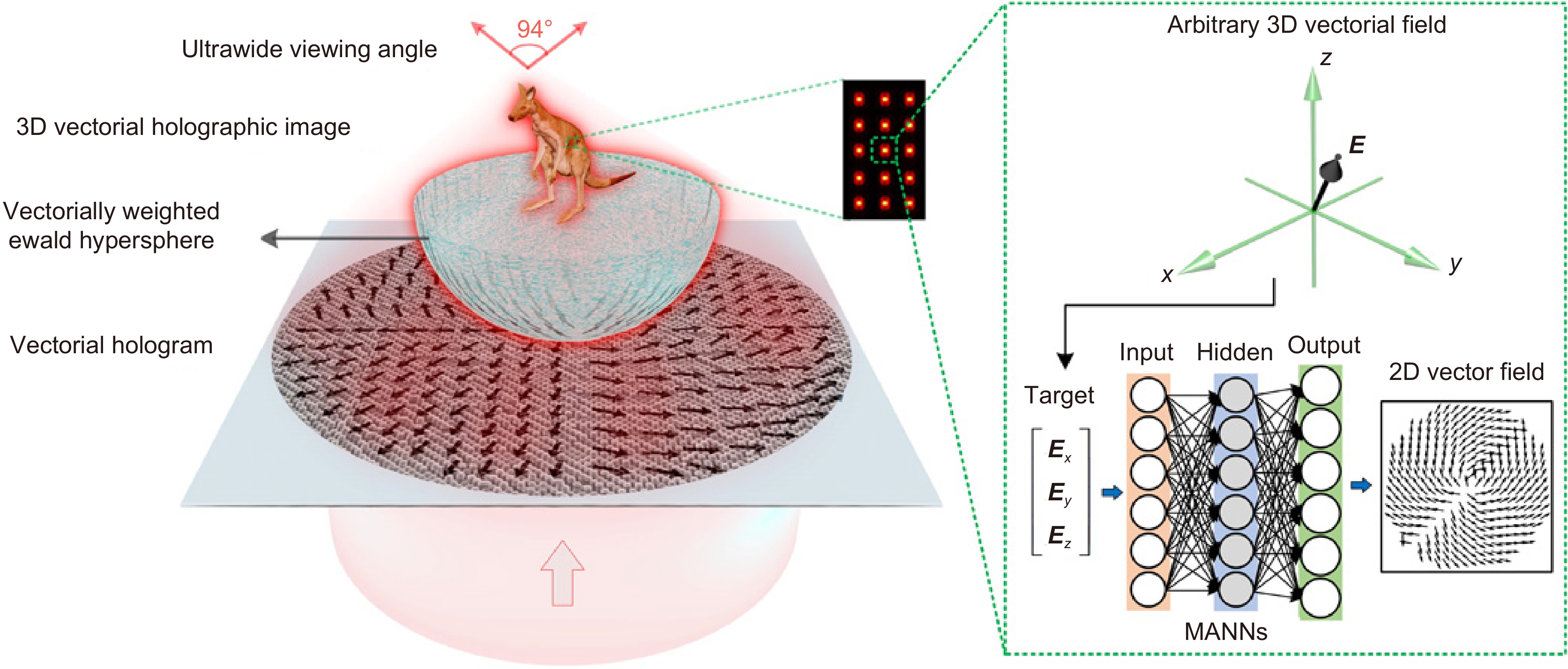
[101] Ren H R, Shao W, Li Y, et al. Three-dimensional vectorial holography based on machine learning inverse design[J]. Sci Adv, 2020, 6(16): eaaz4261. doi: 10.1126/sciadv.aaz4261
[102] Fang X Y, Hu X N, Li B L, et al. Orbital angular momentum-mediated machine learning for high-accuracy mode-feature encoding[J]. Light Sci Appl, 2024, 13(1): 49. doi: 10.1038/s41377-024-01386-5
[103] Ni J C, Huang C, Zhou L M, et al. Multidimensional phase singularities in nanophotonics[J]. Science, 2021, 374(6566): eabj0039. doi: 10.1126/science.abj0039
[104] Ahmed S, Jiang X T, Wang C, et al. An insightful picture of nonlinear photonics in 2D materials and their applications: recent advances and future prospects[J]. Adv Opt Mater, 2021, 9(11): 2001671. doi: 10.1002/adom.202001671
[105] Fang X Y, Ren H R, Li K Y, et al. Nanophotonic manipulation of optical angular momentum for high-dimensional information optics[J]. Adv Opt Photonics, 2021, 13(4): 772−833. doi: 10.1364/AOP.414320
[106] Ren H R, Fang X Y, Jang J, et al. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space[J]. Nat Nanotechnol, 2020, 15(11): 948−955. doi: 10.1038/s41565-020-0768-4
[107] Meng W J, Hua Y H, Cheng K, et al. 100 Hertz frame-rate switching three-dimensional orbital angular momentum multiplexing holography via cross convolution[J]. Opto-Electron Sci, 2022, 1(9): 220004. doi: 10.29026/oes.2022.220004
[108] Guo Y H, Pu M B, Zhao Z Y, et al. Merging geometric phase and plasmon retardation phase in continuously shaped metasurfaces for arbitrary orbital angular momentum generation[J]. ACS Photonics, 2016, 3(11): 2022−2029. doi: 10.1021/acsphotonics.6b00564
[109] Xiong B, Liu Y, Xu Y H, et al. Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise[J]. Science, 2023, 379(6629): 294−299. doi: 10.1126/science.ade5140
[110] Liu Y C, Xu K, Fan X H, et al. Dynamic interactive bitwise meta-holography with ultra-high computational and display frame rates[J]. Opto-Electron Adv, 2024, 7(1): 230108. doi: 10.29026/oea.2024.230108
[111] Zhang F, Pu M B, Li X, et al. All-dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions[J]. Adv Funct Mater, 2017, 27(47): 1704295. doi: 10.1002/adfm.201704295
[112] Li X P, Ren H R, Chen X, et al. Athermally photoreduced graphene oxides for three-dimensional holographic images[J]. Nat Commun, 2015, 6(1): 6984. doi: 10.1038/ncomms7984
[113] Li X, Chen L W, Li Y, et al. Multicolor 3D meta-holography by broadband plasmonic modulation[J]. Sci Adv, 2016, 2(11): e1601102. doi: 10.1126/sciadv.1601102
[114] Lim K T P, Liu H L, Liu Y J, et al. Holographic colour prints for enhanced optical security by combined phase and amplitude control[J]. Nat Commun, 2019, 10(1): 25. doi: 10.1038/s41467-018-07808-4
[115] Feldmann J, Youngblood N, Wright C D, et al. All-optical spiking neurosynaptic networks with self-learning capabilities[J]. Nature, 2019, 569(7755): 208−214. doi: 10.1038/s41586-019-1157-8
[116] Li X, Chen Q M, Zhang X, et al. Time-sequential color code division multiplexing holographic display with metasurface[J]. Opto-Electron Adv, 2023, 6(8): 220060. doi: 10.29026/oea.2023.220060
[117] Zhu S K, Zheng Z H, Meng W J, et al. Harnessing disordered photonics via multi-task learning towards intelligent four-dimensional light field sensors[J]. PhotoniX, 2023, 4(1): 26. doi: 10.1186/s43074-023-00102-7
[118] Wang J Y, Tan X D, Qi P L, et al. Linear polarization holography[J]. Opto-Electron Sci, 2022, 1(2): 210009. doi: 10.29026/oes.2022.210009
[119] Lalanne P, Astilean S, Chavel P, et al. Design and fabrication of blazed binary diffractive elements with sampling periods smaller than the structural cutoff[J]. J Opt Soc Am A, 1999, 16(5): 1143−1156. doi: 10.1364/JOSAA.16.001143
[120] Genevet P, Capasso F, Aieta F, et al. Recent advances in planar optics: from plasmonic to dielectric metasurfaces[J]. Optica, 2017, 4(1): 139−152. doi: 10.1364/OPTICA.4.000139
[121] Lalanne P, Chavel P. Metalenses at visible wavelengths: past, present, perspectives[J]. Laser Photonics Rev, 2017, 11(3): 1600295. doi: 10.1002/lpor.201600295
[122] Chen H T, Taylor A J, Yu N F. A review of metasurfaces: physics and applications[J]. Rep Prog Phys, 2016, 79(7): 076401. doi: 10.1088/0034-4885/79/7/076401
[123] Wang S M, Wu P C, Su V C, et al. A broadband achromatic metalens in the visible[J]. Nat Nanotechnol, 2018, 13(3): 227−232. doi: 10.1038/s41565-017-0052-4
[124] Bomzon Z, Biener G, Kleiner V, et al. Space-variant Pancharatnam–berry phase optical elements with computer-generated subwavelength gratings[J]. Opt Lett, 2002, 27(13): 1141−1143. doi: 10.1364/OL.27.001141
[125] Yan L B, Zhu W M, Karim M F, et al. 0.2 λ0 Thick adaptive retroreflector made of spin‐locked metasurface[J]. Adv Mater, 2018, 30(39): 1802721. doi: 10.1002/adma.201802721
[126] Song Q H, Wu P C, Zhu W M, et al. Split archimedean spiral metasurface for controllable GHz asymmetric transmission[J]. Appl Phys Lett, 2019, 114(15): 151105. doi: 10.1063/1.5084329
[127] Lassaline N, Brechbühler R, Vonk S J W, et al. Optical fourier surfaces[J]. Nature, 2020, 582(7813): 506−510. doi: 10.1038/s41586-020-2390-x
[128] Ren H R, Briere G, Fang X Y, et al. Metasurface orbital angular momentum holography[J]. Nat Commun, 2019, 10(1): 2986. doi: 10.1038/s41467-019-11030-1
[129] Yin X B, Ye Z L, Rho J, et al. Photonic spin hall effect at metasurfaces[J]. Science, 2013, 339(6126): 1405−1407. doi: 10.1126/science.1231758
[130] Devlin R C, Ambrosio A, Rubin N A, et al. Arbitrary spin-to–orbital angular momentum conversion of light[J]. Science, 2017, 358(6365): 896−901. doi: 10.1126/science.aao5392
[131] Zhao H, Wang X K, Liu S T, et al. Highly efficient vectorial field manipulation using a transmitted tri-layer metasurface in the terahertz band[J]. Opto-Electron Adv, 2023, 6(2): 220012. doi: 10.29026/oea.2023.220012
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: