-
摘要
Zernike多项式因其正交性和旋转不变性,被广泛应用于光学表面的表征和优化中。它能够有效地减少拟合误差,并通过少量的系数实现对复杂曲面的高精度描述,有助于提升光学系统的成像质量和简化性能分析。本文首先对自由曲面描述方法进行了概括,包括全局描述与局部描述两种方式;随后讨论了国内外关于Zernike多项式在曲面表征中的研究进展,探讨了Zernike多项式在曲面表征中的实际应用;最后展望了Zernike多项式在曲面表征领域的发展前景。
-
关键词:
- Zernike多项式 /
- 自由曲面 /
- 曲面表征 /
- 光学设计
Abstract
Zernike polynomials, due to their orthogonality and rotational invariance, are widely used in the characterization and optimization of optical surfaces. They can effectively reduce fitting errors and provide high-precision descriptions of complex surfaces with only a few coefficients, contributing to improved imaging quality and simplified performance analysis in optical systems. This paper provides an overview of freeform surface description methods, including both global and local approaches. It discusses the research progress on Zernike polynomials in surface characterization, both domestically and internationally, explores their practical applications in this field, and finally anticipates the future prospects of Zernike polynomials in surface characterization.
-
Key words:
- Zernike polynomials /
- freeform surface /
- surface characterization /
- optical design
-
Overview
Overview: This manuscript offers a detailed review of the advancements in the application of Zernike polynomials for surface characterization in optics. Zernike polynomials, known for their orthogonality and rotational invariance, have been extensively utilized in the characterization and optimization of optical surfaces. This paper first provides an overview of freeform surface description methods and discusses significant progress in the research of Zernike polynomials both domestically and internationally, exploring their practical applications in surface characterization. Finally, it anticipates the future prospects of Zernike polynomials in the field of surface characterization. Freeform surfaces, due to their non-rotational symmetric properties, present significant challenges for traditional optical design. Zernike polynomials offer a precise method to describe these complex surfaces, significantly improving the imaging quality and overall performance of optical systems. The paper highlights the application of Zernike polynomials in optical wavefront analysis and wavefront distortion, emphasizing their ability to decompose complex surfaces into independent components, reducing redundancy, and simplifying error analysis and characterization processes. International research has expanded the application range of Zernike polynomials beyond circular apertures, addressing limitations in traditional methods. These studies have explored applications, such as wavefront reconstruction and optical surface characterization. By developing orthogonal polynomials for elliptical, rectangular, and square apertures, researchers have significantly broadened the applicability of Zernike polynomials. Domestically, Chinese researchers have made significant contributions by generating orthogonal polynomials for non-circular apertures and studying the impact of sampling points on fitting accuracy. This research has enhanced the precision of Zernike polynomials in surface characterization, with applications including wavefront reconstruction and wavefront analysis, demonstrating the versatility and accuracy of Zernike polynomials in various optical design tasks. Compared with other characterization methods such as Q-type polynomials and XY polynomials, Zernike polynomials stand out for their high precision and flexibility, though combining these methods can further enhance the accuracy and efficiency of surface characterization. The manuscript suggests future research should focus on continued theoretical advancements, improved computational efficiency, and integration with other polynomial methods. These improvements will expand the application range and precision of Zernike polynomials in optical system design and optimization, driving progress in optical technology. Continued research and innovation in this field will further enhance the accuracy and efficiency of surface characterization, making Zernike polynomials an increasingly important tool in the advancement of optical systems.
-
1. 引 言
自由曲面 (Freeform surface)是指形状不受传统旋转对称限制的复杂曲面。与球面或非球面不同,自由曲面的几何形状可以在多个维度上任意变化,从而实现更加灵活和精确的光学设计[1]。然而,自由曲面的复杂形状给传统光学设计带来了巨大挑战,如何准确、高效地描述这类型曲面成为光学研究中的一个关键问题[2]。Zernike多项式可以精确分解和描述曲面,利用Zernike多项式系数的动态调整,能够实现对波前像差形态的精确匹配,特别适用于光学系统中的自由曲面表征[3]。
波前分析在光学系统设计中具有举足轻重的意义。它作为评估光学系统性能的重要手段,通过Zernike多项式能够深入剖析并精确描述复杂曲面的波前形态。这一过程不仅能准确识别并量化波前畸变,如像差等不利因素,还为实现波前畸变的有效校正提供了依据[4]。
Q-type多项式、XY多项式以及高斯径向基等表征函数在光学表面表征中分别具有各自优势与不足[5]。通过不同多项式方法的相互转换与结合应用[6],可以为光学表面表征提供更为丰富和高效的工具集。
文中对自由曲面描述方式进行了整体概括,阐述了Zernike多项式及其曲面表征中的发展现状,讨论了Zernike多项式及其扩展,介绍了在光学应用领域的具体实践,包括光学系统中的波前分析和波前畸变。最后,对该领域发展方向做出了展望。
2. 自由曲面的描述
自由曲面的面型数学描述方法繁多,均遵循灵活多变的原则,旨在精准刻画多种复杂面型,同时展现出强大的像差校正能力,以及高效的光线追踪与优化收敛速度。这些方法依据面型控制方式,可归结为全局控制与局部控制两类[1]。
对于自由曲面,通常可以在基底球面或基底二次曲面上附加非旋转对称元素来表达。若以二次曲面为基底,则描述为[7]
z(x,y)=c(x2+y2)1+√1−(1+k)c2(x2+y2)+NRST. (1) 若以球面为基底,则表示为
z(x,y)=c(x2+y2)1+√1−c2(x2+y2)+NRST, (2) 其中:NRST表示非旋转对称(non-rotationally symmetric term)元素,z(x,y)表示曲面上任意点(x,y)的高度 (或称为“矢高”);c表示基础曲面的曲率;k是二次曲面系数。
2.1 全局描述曲面
在全局控制方法下,单一参数的调整即能影响曲面整体形状,矢高与斜率随之全局变动,常见的有Zernike多项式、Q型多项式以及XY多项式等描述方法。
2.1.1 Zernike多项式
Zernike多项式是一组定义在单位圆盘上的完备正交多项式,可以有效地分解和描述波前误差。此处以归一化的Zernike多项式进行描述,如下表示[3]
Zj(ρ,θ)=Zmn(ρ,θ)={√2(n+1)Rmn(ρ)cos(mθ),ifm≠0andjis even√2(n+1)Rmn(ρ)sin(mθ),ifm≠0andjis odd√n+1Rmn(ρ),ifm=0, (3) 其中:
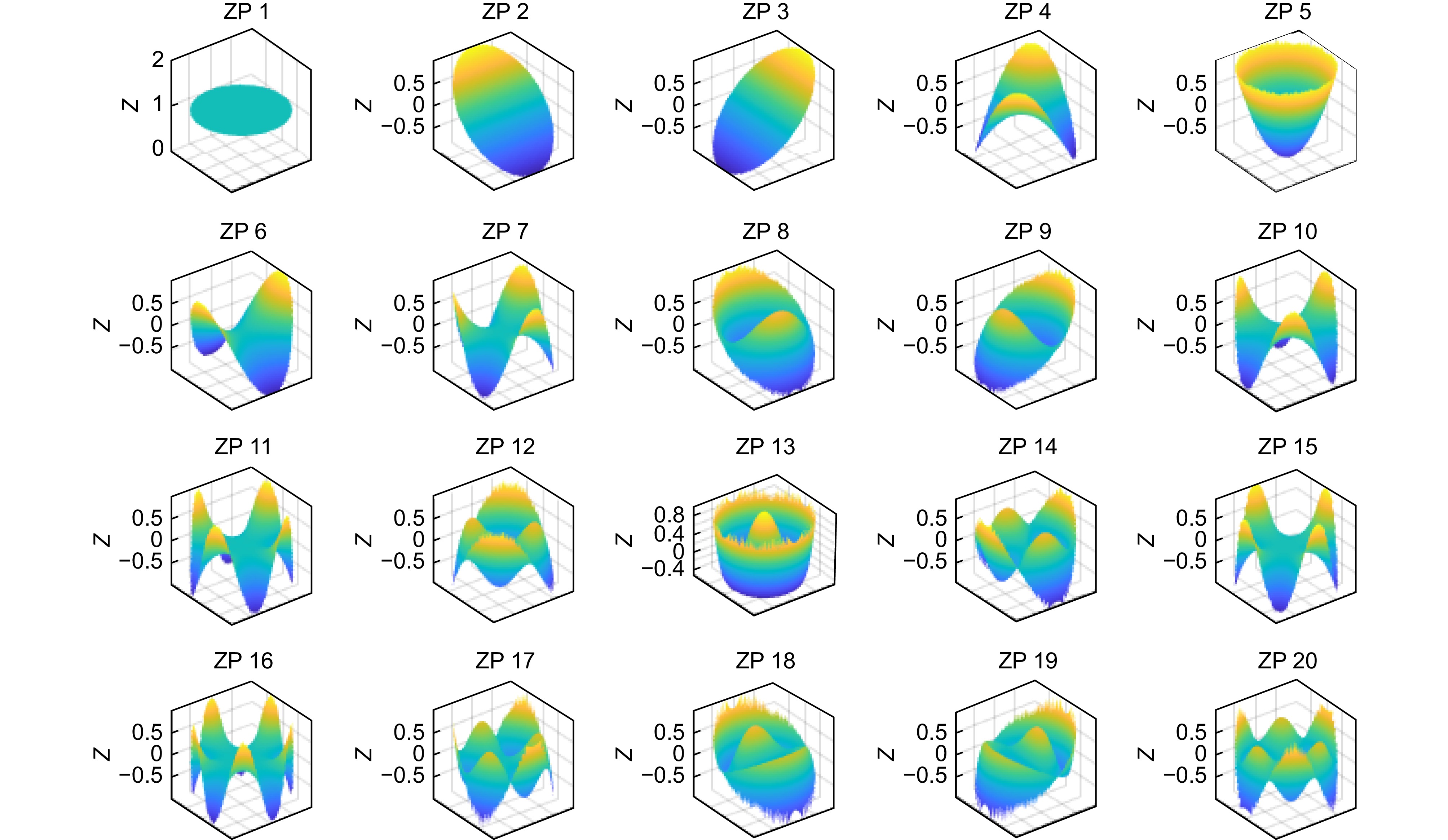
Rmn(ρ)=∑(n−m)/2s=0(−1)s(n−s)!s!(n+m2−s)!(n−m2−s)!ρn−2s, (4) Rmn(ρ)通过对不同的s取值进行求和,生成了一个与ρ的n次方相关多项式。ρ是径向坐标;θ表示极坐标中的角度分量;指数n是径向多项式Rmn(ρ)的次数;m是描述角函数重复的方位角频率;其中n和m是非负整数,满足n-m=0和n-m=偶数;j是从1开始的模序数。图1是使用Matlab生成前20项Zernike多项式的3D图像,这些图像按照Zernike Polynomials (ZP)阶数增加顺序排列。每个子图展示了一个Zernike多项式的表面形状及其对应的项号。通过这些图像,可以直观地看到不同Zernike多项式的特征和差异。
2.1.2 Q型正交多项式
偶次非球面多项式系数间干扰大且量级小,影响光学系统优化效率,同时缺乏加工与检测控制手段,给非球面零件制造与检验带来不便[8]。为此美国QED公司Forbes教授提出Qconm(u2)与Qbfsm(u2)正交多项式,分别适用于大偏差与非球面梯度变化小的非球面表征。并随后提出可用于表征自由曲面的Qmn(u2)的正交多项式。在Qbfsm(u2)多项式的基础上,Forbes教授增加了非回转对称项[9]。首先定义u=ρ/ρmax,其中ρmax是紧密封闭的圆柱体的半径。则曲面可以表示为
z=f(ρ,θ)=cρ21+√1−c2ρ2+1√1−c2ρ2{u2(1−u2)⋅∑Nn=0a0nQ0n(u2)+∑Mm=1um∑Nn=0[amncos(mθ)+bmnsin(mθ)]Qmn(u2)}, (5) 其中:Qmn(v)是v的n阶多项式;c是“最佳拟合球体”的曲率;√1−c2ρ2是z轴与该球体法线之间的夹角的余弦值;θ是极坐标中的角度;ρ是极坐标中的径向距离;amn和bmn同时为多项式的系数;f(ρmax,θ)中的θ的平均值恰好是ρ=ρmax最佳拟合球面的矢高,并且大括号内的分量平均为零[8]。
Q型多项式在表征自由曲面时展现出正交性的显著优势,能够独立地表征曲面的各个成分,有助于提升表征的精确度和效率。然而,其高阶计算相对复杂,且尚未广泛集成到通用的光学设计软件中,这是其在实际应用中的一些局限性。
2.1.3 XY多项式
XY多项式自由曲面基于二次曲面基底,通过精细叠加泰勒级数展开项,实现了对复杂曲面形状的高精度描述。使用XY多项式可以灵活地表征复杂的光学曲面,并且这种方法在光学系统的初步设计和优化中有着广泛的应用,表达式为[1]
z=c(x2+y2)1+√1−(k+1)c2(x2+y2)+∑pi=0∑pj=0Ai,jxiyj,1⩽ (6) 其中:c是曲率;k为二次曲面系数; {A}_{i,j} 是 各xy单项式的系数;曲面的最高阶次为 p,意味着 i+j 的值大于等于 1 且不超过 p。在 CODEV 软件中,通常将 p 限制在10 以内。
XY多项式以其灵活的系数配置能力,在精确调控光学曲面对称性方面展现出显著优势。在光学设计领域, XY多项式通过精细调整其各阶项的系数,能够直接而有效地实现所需的对称特性。XY多项式不属于正交函数。XY多项式无直接相差对应,不直接用于波前解析,但面型表征力与正交多项式相当,且与Zernike多项式可转换,具有较强像差校正能力[10]。XY多项式易于与加工设备进行数据交换,并获得了较为广泛的应用。
2.2 局部描述曲面
局部控制方法则精细地限制参数作用范围,允许通过调整特定参数来优化曲面局部特征,此类方法包括NURBS (非均匀有理B样条)曲面和高斯径向基函数组合曲面等。
2.2.1 径向基函数
径向基函数在构建自由曲面时,是采用一系列以不同点为旋转对称中心、且这些中心不重合的二维径向基函数为基本单元,基于Conic曲面进行叠加。若以二次曲面为基底,则表示为
{\textit{z}}(x,y)=\frac{c\left({x}^{2}+{y}^{2}\right)}{1+\sqrt{1-({k}+1){c}^{2}\left({x}^{2}+{y}^{2}\right)}}+\sum _{n=1}^{N} {w}_{n}{{\varPhi }}_{n}, (7) \varPhi_{n}\left(p\right)=\phi \left({\|p-{p}_{n}\|}_{2}\right)\;, (8) 其中:c为曲率;k为二次曲面系数; {w}_{n} 表示每个基底的权重; \varPhi_{n} 表示径向基函数;ϕ是 构 成 径 向 基 函 数 的 径 向 函 数 ; {\|p-{p}_{n}\|}_{2} 是支撑域内任意一点p到中心点 {p}_{n} 之间的欧几里得距离。
径向基函数凭借其卓越的局部形变调控能力,其特性允许设计者在维持整体曲面轮廓的同时,精确调整局部区域的形状变化。最常用的是高斯径向基函数,表达式为
\varphi \left(r\right)={\mathrm{e}}^{-{r}^{2}/{\mathrm{\sigma }}^{2}}\;, (9) 其中:r表示径向距离, \mathrm{\sigma } 为标准差。
高斯径向基函数表达形式极为简洁,其次具备优异的对称性,允许通过调整形状因子实现精确控制。再者,高斯径向函数任意阶可导的特性,确保了所描述的自由曲面拥有卓越的光滑特性。最后,其独特的构造形式赋予了高斯径向函数强大的局部表征能力,使得该函数在细节处理上更为精准。
2.2.2 NURBS函数
非均匀有理B样条曲面 (Non-uniform rational B-spline surface,简称NURBS)通过控制点、权重和基函数的结合,能够灵活且精确地表示复杂的几何形状,数学表达式如下:
{\textit{z}}(u,v)=\dfrac{\displaystyle{\sum} _{i-0}^{n}\displaystyle{\sum} _{j-0}^{m}{B}_{i,p}\left(u\right){B}_{j,q}\left(v\right){P}_{ij}{w}_{ij}}{\displaystyle{\sum} _{i-0}^{n}\displaystyle{\sum} _{j-0}^{m}{B}_{i,p}\left(u\right){B}_{j,q}\left(v\right){w}_{ij}}\;, (10) 其中:控制点 {P}_{ij} 及其权重因子 {w}_{ij} 共同定义了曲面的形状, {B}_{i,p}(u )和 {B}_{j,q}\left(v\right) 分别代表u方向上p阶B样条基函数以及v方向的q阶B样条基函数。 {B}_{i,p}(u )表达示为
\left\{ {\begin{array}{*{20}{l}} {p = 0,\;{B_{i,0}}(u) = \left\{ {\begin{array}{*{20}{l}} 1,\;&{{\rm{if}}\;{u_i} \leqslant u \lt {u_{i + 1}}\;{\rm{ and }}\;{u_i} \lt {u_{i + 1}}}\\ 0,\;&{{\rm{otherwise}}} \end{array}} \right.}\\ \begin{split} p \geqslant 1,\;{B_{i,p}}(u) =& \frac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{B_{i,p - 1}}(u) \\ &+\frac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{B_{i + 1,p - 1}}(u) \end{split} \end{array}} \right.\;. (11) 非均匀有理B样条 (NURBS)曲面以其对局部形状变化的高度控制能力著称。该框架的普适性和高度灵活性,使得通过调整控制顶点与相应的权重参数,能够灵活地塑造自由曲面的几何形态。然而,这种灵活性的背后是更为复杂的构造过程,难以同时兼顾构造曲面的精度和速度[10]。
表1对几种表征函数优劣性进行了总结比较。
表 1. 常见表征函数优劣性比较Table 1. Comparison of common characterization functions: advantages and disadvantages曲面表征函数与方法 优势 缺点 Zernike多项式 正交,与经典相差一一对应,解析波前等 对局部凸起难以精确表征,高阶项计算复杂 Q型正交多项式 正交,加工可控性强,适合表征全局特性等 高阶计算复杂,尚未广泛集成到计算机软件当中 XY多项式 设计自由度高,适合表征全局特性等 非正交,不可解析波前 径向基函数 局部表征能力强 非正交 NURBS函数 局部表征能力强,构造灵活 非正交,构造复杂 3. 国内外研究进展
曲面表征是指对物体表面的几何形状进行数学描述。Zernike多项式在曲面表征中具有独特的优势。近年来,国内外学者在Zernike多项式及其曲面表征方面进行了广泛研究,取得了许多重要成果。
3.1 国外研究进展
Zernike多项式的全局和局部的高表征精度,使其能够简化误差分析和表征过程,提高光学系统的整体性能。在Zernike多项式表征曲面的发展历程中,研究发现Zernike圆多项式在表征曲面时存在一些局限性。2010年,Mahajan等人[11]比较了用于环形波前分析的环形多项式和Zernike多项式,发现在使用非圆形干涉图时,Zernike圆多项式的系数不能正确表征波前。2011年,Kaya等人[12]用Zernike多项式表征光学表面上的小凸起,发现有效参数数量无法扩展到数千个光学设计环境。2015年,Svechnikov等人[13]用Zernike圆域多项式表征复杂曲面,探讨了Zernike多项式项数与其表征复杂曲面精度之间的实际关系。研究表明,Zernike多项式对于局部特征凸出或极不规则的面形进行表征时往往需要进行大规模的展开才能满足精度需求[12]。
由于Zernike多项式对于椭圆形,方形等非圆形孔径不满足正交要求。随着现代光学设计制造发展,多种因素将导致在光学系统设计与制造过程中,Zernike圆域多项式并不能很好的表征面形以满足需求。研究人员对Zernike多项式扩展开展了相关研究。1994年,Mahajan等人[14]提出了具有环状瞳孔系统的Zernike环多项式。2006年,Virendra等人[15] 采用Gram-Schmidt正交法对Zernike圆多项式进行了系统性的正交化处理,生成并提供了六边形光瞳的正交闭合多项式。2007年,Mahajan等人[16]基于Zernike圆多项式的正交性,推导了在椭圆、矩形和方形孔径上正交的多项式。2008年,Dai等人[17]探讨了Zernike多项式在非圆孔径上的局限性,并在非圆孔径上使用正交归一化多项式。2016年,Ferreira等人[18]研究了一种普遍且严谨的理论框架,由此可以得到在圆域内正交的基函数,对比了通过该法获得的基函数与Zernike多项式表征曲面的差别。2017年,Broemel等人[19]运用了格林姆-施密特正交化技术,以条纹Zernike多项式为构建基,设计并提出了一种在方形区域内具备梯度正交特性的多项式曲面模型。2017年, Area等人[20] 提出了一种新颖的算法,巧妙融合了微分算子的运算优势与连接矩阵的结构特性,为不同形状的孔径提供了统一的表示框架。这些研究扩展了Zernike多项式的应用范围,为复杂孔径波前分析和像差矫正等应用提供了重要理论基础。
Zernike多项式的扩展主要包括环域Zernike多项式和条纹Zernike多项式等变体。环域Zernike多项式用于描述和分析具有环形孔径的光学系统波前,优化处理中心遮挡的环形区域,提升表征精度。条纹Zernike多项式则专为光学干涉测量中的波前分析和像差表征设计,提供了更高的适应性和精度。格林姆-施密特正交法通过迭代方式将线性无关向量转化为正交向量,在曲面表征中常用于处理基函数,特别是在多项式曲面拟合中,有助于提升Zernike多项式表征的准确性和效率。
为了能够更全面和精确地描述复杂系统的特征,Zernike与其他表征多项式的对比混合研究被大量展开。2006年,Ares等人[21]使用三次B样条曲面和Zernike多项式曲面分别拟合波前,结果表明二者对于简单波前皆可有效表征。对于复杂波前,B样条曲面为最佳选择。2012年,Kaya等人[22]通过比较梯度Q型正交多项式和Zernike多项式,量化了两者在描述旋转非对称自由曲面方面的等效性,说明这两种多项式在处理复杂表面特征时均能有效表征。2013年,Rahbar等人[23]使用Zernike多项式和伪Zernike (方形域的扩展Zernike形式)多项式结合来建模波前,增强了波前分布估计过程的鲁棒性。2013年,Trevino等人[24] 在深入分析人眼复杂角膜地形图的领域中,将第一类贝塞尔圆形域函数与Zernike多项式相结合。研究表明,贝塞尔圆形域函数在表征复杂角膜曲面形态时展现出了更为优越的性能。2021年,Badar等人[25]对样条模型和Zernike模型进行了波前相位构建的比较分析,结果表明两种模型都有效地表征了不规则域形状下的简单波前。当表征不规则域形状的复杂波前时,样条模型的性能比Zernike模型好得多。
Zernike多项式曲面表征特性被广泛应用于光学各领域。2011年,Raasch等人[26]使用Zernike多项式对渐进多焦镜片 (progressive addition lens,PAL)表面进行全面表征,为PAL表面的定义和设计提供了新的思路。2021年,Ivanova等人[27]在光学系统整体输入孔径的非圆对称部分上,使用Zernike多项式表征变形的误差。2022年,Omidi等人[28]使用不同阶的Zernike多项式来表征角膜表面,研究了正常角膜和病理性角膜所需合理数量的Zernike系数。2024年,Puentes等人[29]利用Zernike多项式对宏观流体透镜的光学像差进行了光谱表征,发现不同光谱条件下的像差可以通过Zernike多项式的系数进行准确描述和分类,为进一步优化流体透镜的设计和应用提供了重要的数学工具和理论基础。以上研究使得Zernike多项式的曲面表征促进了各个领域的进一步发展。
3.2 国内研究进展
国内研究人员对Zernike多项式进行了深入研究,在曲面表征方面取得了重要进展。
2002年,李新阳等人[30]讨论了在非圆形孔径中使用Zernike多项式进行波前描述的问题,在非圆孔径中使用Gram-Schmidt正交化过程生成了一系列基于Zernike多项式的正交多项式。2012年,王庆丰等人[31] 探索了单位圆域与单位方域环境下双变量正交多项式曲面的数学模型构建,剖析了这些模型在自由曲面形态精确表征方面的拟合精度特性与潜在优势。2014年,李萌阳等人[32] 在方形域内归一化Zernike正交基生成的理论研究上取得了进展,他们成功构建了一组创新性的正交多项式。该多项式不仅具备直接表征波前的能力,而且通过精妙的线性反变换机制,能够转化为标准Zernike模式的线性组合形式。2017年,赵齐等人[33]对Zernike多项式使用施密特正交法,获得不同遮光比环形光阑下的正交基底,以此基底对矩形光阑下的波面进行了波前重构。这些研究使Zernike多项式适用于更多实际应用场景,从而提升其在复杂曲面表征中的广泛性和精确性。
曲面拟合通过奇异值分解法、最小二乘法等其他优化算法来拟合实验数据可求得Zernike多项式系数[34],可以提高曲面表征的精度和质量,从而精确描述自由曲面的形状。1991年,莫卫东[35]验证了最小二乘法与施密特正交法在Zernike多项式拟合干涉面中的等效性。2002年,莫卫东[36]分析Zernike多项式拟合干涉波面过程,发现采用低于被测光瞳中干涉条纹总数的Zernike多项式阶数作为拟合基,可有效预防拟合过程中的“病态”现象。2005年,张伟等人[37] 通过Zernike多项式,分别针对具有差异性空间频率特征的径向误差以及基于不同口径尺度的局部误差实施了细致的拟合处理,得到了不同条件下Zernike阶数选择规律。2008年,孙学真等人[38]研究了抽样点数对曲面拟合精度的影响,表明对于含有误差的抽样点,可以通过增加抽样点数来增加曲面拟合精度。2010年,谢苏隆等人[39] 研究了采样点数量对拟合曲面精确程度的影响机制,并在确保拟合质量优越的前提下,进一步探究了Zernike多项式项数与所需采样点数量之间的具体量化关联。2011年,冯婕[40] 探讨了Zernike多项式阶数以及采样点配置对拟合精度的具体影响。结果显示,当Zernike多项式的阶数被设定得过高时,可能引发拟合结果的不稳定,表现为显著的“病态”现象。2018年,郭良贤等人[41]对常见的三种镜面展开了Zernike多项式项数与拟合精度关系的研究,表明过多的多项式项数不仅未能有效提升拟合精度,反而可能导致精度的降低,并可能引发矩阵的“病态”现象。2019年,韩路等人[42]提出了一种基于Zernike多项式的条纹反射三维面形重建算法,研究了Zernike多项式的项数和采样点对重建结果的影响。此类研究通过优化采样点数以及Zernike多项式项数,提高了曲面拟合的精度和效率,为精确描述复杂曲面的几何形状并提升整体表征质量做出了重要贡献。
关于拟合研究表明利用Zernike多项式拟合曲面时,需合理匹配曲面复杂度选择Zernike多项式阶数。阶数定后,增多采样点可提升拟合精度。采样点非唯一要素,合理阶数选择同样保障拟合效果。
关于Zernike多项式的曲面表征在光学领域的应用方面,国内学者也展开了广泛的研究。
在理想情况下,一个无畸变的波前应当是平面的。然而,受环境因素如大气湍流的影响,波前会变得无规则。Zernike多项式特别适用于描述由湍流等随机因素引起的不规则波前。波前分析的目的是通过测量波前数据重建完整的波前曲面。1994年,魏学业等人[43]提出了使用Zernike多项式进行波前重构的方法,并进行了验证。1998年,张强等人[44]使用Zernike模式法重构湍流波前,证明模式阶数的取值会影响重构的精度。2006年,罗智锋等人[45]使用Zernike多项式对激光束小尺度畸变波前进行重构,并探讨了波前幅度大小等因素对重构精度的影响。2014年,叶井飞等人[6]提出了利用Zernike多项式以及径向基函数进行自由曲面重构的方法,研究表明自由曲面重构精度优于纳米量级,该方法在现代光学系统制造中表现出一定的应用前景。2018年,张航等人[46]提出了一种利用Zernike多项式进行曲面表征优化的方法,通过曲面插值方式完成了曲面重构,确保了光斑的形状和照度分布均匀,为均匀方斑的设计提供了一种新的思路。2023年,杨德荃等人[47]基于Zernike多项式表征特性,提出高效仿真大气湍流波前畸变方法。实验证明,该法显著提升仿真速度,并为湍流图像校正提供坚实技术支持。
Zernike多项式可以精准的描述光学表面,被广泛地应用于光学系统的设计。2003年,莫卫东[48]使用Zernike多项式表征光学玻璃表面,探讨了Zernike多项式拟合系数的大小与表面误差类型的关联。2010年,杨佳文等人[49]通过Zernik多项式表征变形镜面,分离了刚体位移和表面变形,为大口径轻量反射镜的设计提供了保障。2016年,庞志海等人[50]通过研究利用条纹Zernike多项式表征自由曲面光学元件,研究了光学系统中不同位置自由曲面的校正效应,这些校正显著优化了非对称光学系统的像差表现。2017年,关姝等人[51]在其研究中提出并开发了采用自由曲面设计的离轴两镜反射望远镜,并利用Zernike多项式对次镜进行表征,增加了曲面设计自由度,增强了系统平衡像差的能力。2019年,Xiang等人[52]通过Zernike多项式来表征天线失真,研究了反射天线表面畸变的分布特性对其电磁性能的影响。2020年,施胤成等人[53]通过使用Zernike多项式表征镜面的变形,计算了Zernike系数相对于拓扑优化设计变量的敏感度,为如何调整设计以获得最佳的光学性能作出了指导。2021年,周颋等人[54]提出了一种基于Zernike多项式表征的可变形镜面形优化设计方法,实现了对自由曲面部分补偿干涉测量的高效优化。2022年,闫钧华等人[55]利用zernike多项式自由曲面表征特性,设计并优化了紧凑型离轴三反无焦光学系统,显著降低了系统的波像差,满足了结构紧凑和小型化的设计要求。2023年,解博夫等人[56]采用18项条纹Zernike多项式表征的自由曲面相位板,有效地补偿了飞秒激光成丝系统中的像差,显著提高了聚焦光斑的质量和光丝强度。2023年,韩继周等人[57]通过在Offner成像光谱仪中引入自由曲面,并采用条纹Zernike多项式来表征光学表面,实现了大视场和宽波段成像系统的设计。这些研究为Zernike多项式在自由曲面表征中的应用提供了理论依据和实践参考。
4. Zernike多项式曲面表征
4.1 波前分析
在波前分析中,Zernike多项式将测量到的波前数据展开成基函数的线性组合,精确描述波前形状。由于光学系统的孔径通常是圆形的,这里我们在一个圆形孔径内进行分析。假设我们有一个波前误差函数 W(\rho ,\theta ) ,可以用泽尼克多项式展开:
W(\rho ,\theta )\approx \sum _{n,m} {a}_{nm}{Z}_{n}^{m}(\rho ,\theta )\;, (12) 其中: {a}_{nm} 是泽尼克多项式的系数。
通过Shack-Hartmann传感器直接测量的波前斜率数据来构建线性方程组,求解泽尼克多项式的系数。Shack-Hartmann传感器测量波前斜率 \dfrac{\partial \varphi (x,y)}{\partial x} 和 \dfrac{\partial \varphi (x,y)}{\partial y} ,公式如下[58]:
\begin{split} {{\boldsymbol{G}}}_{ jx}=&\frac{1}{{{S}}_{ j}}{\iint }_{{S}_{ j}}\left[\frac{\partial \varphi (x,y)}{\partial x}\right]\mathrm{d}x\mathrm{d}y=\sum _{k=1}^{l}\left(\frac{{a}_{k}}{{{S}}_{ j}}\right)\\ & \cdot {\iint }_{{S}_{ j}}\left[\frac{\partial {{\boldsymbol{F}}}_{ kj}(x,y)}{\partial x}\right]\mathrm{d}x\mathrm{d}y=\sum _{k=1}^{l}{a}_{k}{{\boldsymbol{F}}}_{ jkx} \end{split}\;, (13) \begin{split} {{\boldsymbol{G}}}_{ jy}=&\frac{1}{{{S}}_{ j}}{\iint }_{{S}_{ j}}\left[\frac{\partial \varphi (x,y)}{\partial y}\right]\mathrm{d}x\mathrm{d}y=\sum _{k=1}^{l}\left(\frac{{a}_{k}}{{{S}}_{ j}}\right)\\ &\cdot {\iint }_{{S}_{ j}}\left[\frac{\partial {{\boldsymbol{F}}}_{ kj}(x,y)}{\partial y}\right]\mathrm{d}x\mathrm{d}y=\sum _{k=1}^{l}{a}_{k}{{\boldsymbol{F}}}_{ jky} \end{split}\;, (14) 其中: {{\boldsymbol{G}}}_{ jx} 和 {{\boldsymbol{G}}}_{ jy} 分别是第j个子孔径内的波前斜率在x和y方向的平均值; {S}_{ j} 是第j个子孔径的面积; \partial \varphi (x,y) 是波前相位函数; {a}_{k} 是Zernike多项式的系数; {{\boldsymbol{F}}}_{ kj}(x,y) 是Zernike多项式的分量,具体到这里是波前斜率的部分; {{\boldsymbol{F}}}_{ jkx} 是波前重构矩阵中的元素,表示第j个子孔径内第k项Zernike多项式的波前斜率。
利用Shack-Hartmann传感器测量到的波前斜率数据 {G}_{jx} 和 {G}_{jy} ,可以建立一个线性方程组:
\boldsymbol{G}=\boldsymbol{F}\cdot \boldsymbol{A}\;, (15) 其中:G为波前斜率向量,F为波前重构矩阵,A为Zernike多项式系数向量。通过求解这个线性方程组,可以得到Zernike多项式的系数 {a}_{k} 实现波前拟合。
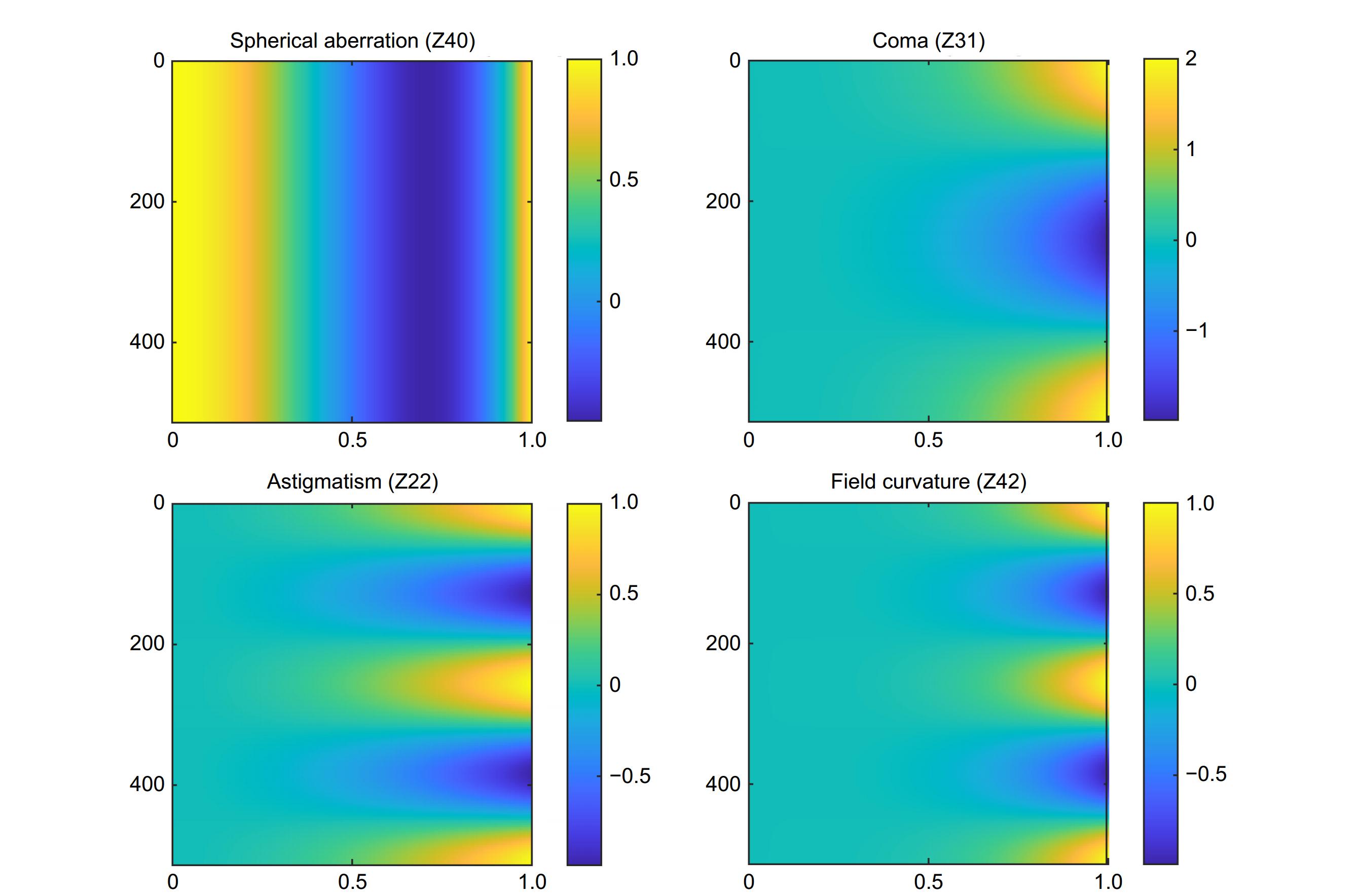
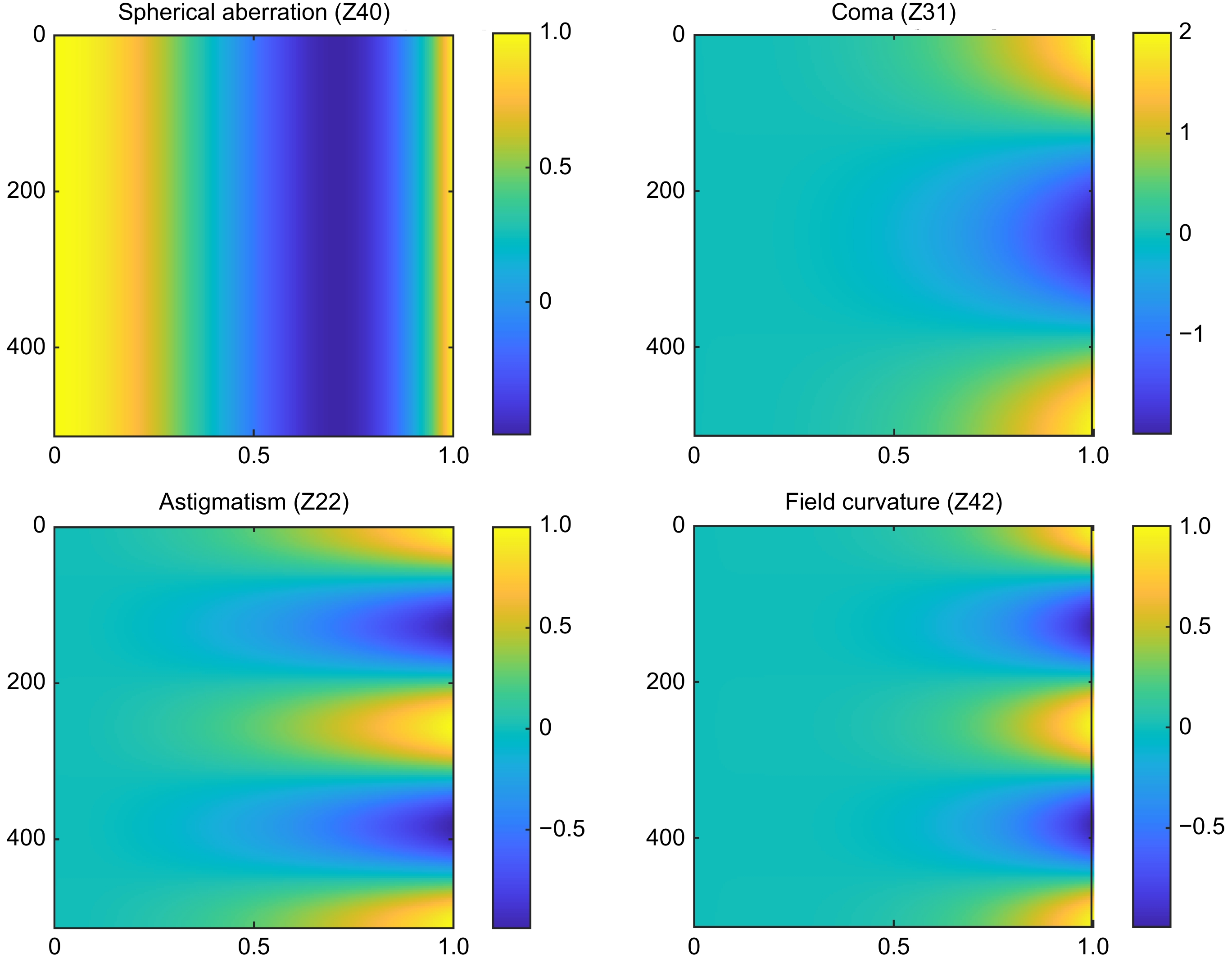
由于Zernike多项式与经典赛德尔像差具有如表2中的一一对应关系。确定了最佳拟合的Zernike多项式系数 {a}_{nm} 后,我们可以进一步使用像差分析技术,量化和分类光学系统中的各类像差。
表 2. Zernike多项式前9项与像差对应关系[5]Table 2. Correspondence between the first 9 Zernike polynomials and optical aberrations[5]项数 Zernike多项式 像差 Z1 1 平移 Z2 \rho \mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right) X轴倾斜 Z3 \rho \mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right) Y轴倾斜 Z4 {\rho }^{2}\mathrm{c}\mathrm{o}\mathrm{s}2\theta 初级像散 ( 0\text{° }\text{或 90}\text{°}\text{轴)} Z5 2{\rho }^{2}-1 离焦 Z6 {\rho }^{2}\mathrm{s}\mathrm{i}\mathrm{n}2\theta 初级像散 ( \pm {45}^{\circ } 轴) Z7 {\rho }^{3}\mathrm{c}\mathrm{o}\mathrm{s}3\theta 初级三叶草 (X-轴) Z8 \left(3{\rho }^{3}-2\rho \right)\mathrm{c}\mathrm{o}\mathrm{s}\theta 初级慧差 (X-轴) Z9 \left(3{\rho }^{3}-2\rho \right)\mathrm{s}\mathrm{i}\mathrm{n}\theta 初级慧差 (Y-轴) 为了可以更全面地理解光学系统中的各种像差,如图2所示,通过仿真可以将这些波前像差以图形化的方式呈现出来。
4.2 波前畸变
在光通信中一般选用多相位屏来模拟光经湍流传输后的畸变波前。Zernike多项式在构建模拟大气湍流相位屏的模型中具有显著应用[59]。大气湍流引起的波前畸变φ(r)可通过正交化手段,在圆形区域内以Zernike多项式序列进行有效分解与表达:
\varphi \left(r\right)=\sum _{j=1}^{\mathrm{\infty }} {a}_{j}\cdot { {\textit{z}}}_{j}\left(r\right)\;, (16) 其中: { {\textit{z}}}_{j}\left(r\right) 表示Zernike多项式。 {a}_{j} 表示第j项的Zernike系数,可以通过示Zernike模式间具有的统计相关性以及Karhunen-Loeve函数 (K-L函数)展开求出[60]。具体求解系数步骤如下[61]:
假设湍流波前Zernike多项式系数向量为
\boldsymbol{A}=\left[{a}_{1},{a}_{2},\right.\left.\cdots ,{a}_{i}\right]. (17) 系数向量A的协方差矩阵为
\boldsymbol{C}={\boldsymbol{E}}\left[\boldsymbol{A}\cdot {\boldsymbol{A}}'\right]. (18) 1)首先选择Zernike多项式的阶数,并计算矩阵C。
2)对协方差矩阵实施奇异值分解处理,即
\boldsymbol{C}=\boldsymbol{U}\boldsymbol{S}{\boldsymbol{U}}^{\rm{T}}, (19) 其中:U矩阵由协方差矩阵Z的特征向量构成,形成了一个酉矩阵,而S则是一个对角矩阵,其元素对应于Z的奇异值。
3)产生零均值且协方差矩阵为S的随机向量B,计算
\boldsymbol{A}=\boldsymbol{UB}. (20) 依此步骤可以求得Zernike多项式系数。在光通信领域,采用Zernike多项式作为波前畸变的数学描述,我们能够构建一个精确的模型来模拟湍流如何干扰和改变光束的传播路径及其特性,从而进行预先补偿和校正。这种方法可以在实际通信和成像过程中,通过自适应光学技术实时调整波前畸变,提高传输效率和图像质量。
5. 结 论
5.1 总 结
Zernike多项式广泛应用于光学系统的曲面表征。近年来,Zernike多项式的衍生形式得到了进一步发展,它们扩展了Zernike多项式的应用范围。这些扩展形式在复杂光学系统和自由曲面设计中表现出了更高的实用性。在国内外,研究人员不断改进算法,将Zernike多项式应用于更广泛的领域,如波前分析,曲面重构等。Zernike多项式凭借独特的数学性质和像差对应关系,在曲面表征中与其他表征函数相比,提供了更高的精度和灵活性。将这些多项式方法结合起来使用,可以进一步提升对复杂光学系统的表征精度和误差分析能力,发挥各自优势。随着光学技术的不断发展,Zernike多项式在自由曲面表征中的应用将进一步深化和扩展,推动光学系统的不断进步。
5.2 展 望
Zernike多项式在光学系统设计与优化中已经取得了显著成果,未来发展趋势可以围绕以下几点展开。
1) Zernike多项式已经有较为完善的理论基础,未来的研究可以继续发展新的理论和模型,以更好地理解和应用Zernike多项式。进一步研究和开发适用于各种特殊光学系统的扩展Zernike多项式,如针对非圆形孔径的多项式和更复杂自由曲面的多项式[10]。
2) Zernike多项式拟合曲面中的研究中,可以通过优化拟合算法、提升计算效率和提高拟合精度,全方位提升Zernike多项式的应用水平,以应对越来越多样化和复杂化的实际需求。
3)虽然Zernike多项式在许多应用中表现出色,但在某些特定应用中,其他多项式 (如Q型正交多项式和径向基函数等)可能更适合。未来的研究可以探讨将Zernike多项式与其他多项式结合使用,以发挥各自的优势,从而实现更加精确和高效的表征。
利益冲突:所有作者声明无利益冲突
-
表 1 常见表征函数优劣性比较
Table 1. Comparison of common characterization functions: advantages and disadvantages
曲面表征函数与方法 优势 缺点 Zernike多项式 正交,与经典相差一一对应,解析波前等 对局部凸起难以精确表征,高阶项计算复杂 Q型正交多项式 正交,加工可控性强,适合表征全局特性等 高阶计算复杂,尚未广泛集成到计算机软件当中 XY多项式 设计自由度高,适合表征全局特性等 非正交,不可解析波前 径向基函数 局部表征能力强 非正交 NURBS函数 局部表征能力强,构造灵活 非正交,构造复杂 表 2 Zernike多项式前9项与像差对应关系[5]
Table 2. Correspondence between the first 9 Zernike polynomials and optical aberrations[5]
项数 Zernike多项式 像差 Z1 1 平移 Z2 \rho \mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right) X轴倾斜 Z3 \rho \mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right) Y轴倾斜 Z4 {\rho }^{2}\mathrm{c}\mathrm{o}\mathrm{s}2\theta 初级像散 ( 0\text{° }\text{或 90}\text{°}\text{轴)} Z5 2{\rho }^{2}-1 离焦 Z6 {\rho }^{2}\mathrm{s}\mathrm{i}\mathrm{n}2\theta 初级像散 ( \pm {45}^{\circ } 轴) Z7 {\rho }^{3}\mathrm{c}\mathrm{o}\mathrm{s}3\theta 初级三叶草 (X-轴) Z8 \left(3{\rho }^{3}-2\rho \right)\mathrm{c}\mathrm{o}\mathrm{s}\theta 初级慧差 (X-轴) Z9 \left(3{\rho }^{3}-2\rho \right)\mathrm{s}\mathrm{i}\mathrm{n}\theta 初级慧差 (Y-轴) -
参考文献
[1] 杨通, 段璎哲, 程德文, 等. 自由曲面成像光学系统设计: 理论、发展与应用[J]. 光学学报, 2021, 41(1): 0108001. doi: 10.3788/AOS202141.0108001
Yang T, Duan Y Z, Cheng D W, et al. Freeform imaging optical system design: theories, development, and applications[J]. Acta Opt Sin, 2021, 41(1): 0108001. doi: 10.3788/AOS202141.0108001
[2] 程德文, 陈海龙, 王涌天, 等. 复杂光学曲面数理描述和设计方法研究[J]. 光学学报, 2023, 43(8): 0822008. doi: 10.3788/AOS221980
Cheng D W, Chen H L, Wang Y T, et al. Mathematical description and design methods of complex optical surfaces[J]. Acta Opt Sin, 2023, 43(8): 0822008. doi: 10.3788/AOS221980
[3] Niu K, Tian C. Zernike polynomials and their applications[J]. J Opt, 2022, 24(12): 123001. doi: 10.1088/2040-8986/ac9e08
[4] 杨华峰, 姜宗福. 对Zernike模式法重构19单元哈特曼测量波前的研究[J]. 激光技术, 2005, 29 (5): 484–487.
Yang H F, Jiang Z F. Research of Zernike modal wavefront reconstruction of 19-element Hartmann-Shack wavefront sensor[J]. Laser Technol 2005, 29 (5): 484–487.
[5] 王超. 自由曲面表征函数及其应用研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014.
Wang C. Research on characterization function and application of free-form surface[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2014.
[6] 叶井飞, 高志山, 刘晓莉, 等. 基于Zernike多项式和径向基函数的自由曲面重构方法[J]. 光学学报, 2014, 34(8): 0822003. doi: 10.3788/AOS201434.0822003
Ye J F, Gao Z S, Liu X L, et al. Freeform surfaces reconstruction based on Zernike polynomials and radial basis function[J]. Acta Opt Sin, 2014, 34(8): 0822003. doi: 10.3788/AOS201434.0822003
[7] 杨通, 王永东, 吕鑫, 等. 融合自由曲面光学与全息光学元件的成像与显示系统设计[J]. 光学学报, 2024, 44(9): 0900001. doi: 10.3788/AOS231830
Yang T, Wang Y D, Lü X, et al. Design of Imaging and display systems combining freeform optics and holographic optical elements[J]. Acta Opt Sin, 2024, 44(9): 0900001. doi: 10.3788/AOS231830
[8] 郎常富. Q-Type自由曲面优化设计与制造的约束条件研究[D]. 长春: 长春理工大学, 2022.
Lang C F. Studies on constraints of optimal design and manufacturing of Q-Type freeform surface[D]. Changchun: Changchun University of Science and Technology, 2022.
[9] Forbes G W. Robust and fast computation for the polynomials of optics[J]. Opt Express, 2010, 18(13): 13851−13862. doi: 10.1364/OE.18.013851
[10] 叶井飞. 光学自由曲面的表征方法与技术研究[D]. 南京: 南京理工大学, 2016.
Ye J F. Research on the method and technique for characterizing freeform optical surface[D]. Nanjing: Nanjing University of Science & Technology, 2016.
[11] Mahajan V N, Aftab M. Systematic comparison of the use of annular and Zernike circle polynomials for annular wavefronts[J]. Appl Opt, 2010, 49(33): 6489−6501. doi: 10.1364/AO.49.006489
[12] Kaya I, Thompson K P, Rolland J P. Edge clustered fitting grids for φ-polynomial characterization of freeform optical surfaces[J]. Opt Express, 2011, 19(27): 26962−26974. doi: 10.1364/OE.19.026962
[13] Svechnikov M V, Chkhalo N I, Toropov M N, et al. Resolving capacity of the circular Zernike polynomials[J]. Opt Express, 2015, 23(11): 14677−14694. doi: 10.1364/OE.23.014677
[14] Mahajan V N. Zernike annular polynomials and optical aberrations of systems with annular pupils[J]. Appl Opt, 1994, 33(34): 8125−8127. doi: 10.1364/AO.33.008125
[15] Mahajan V N, Dai G M. Orthonormal polynomials for hexagonal pupils[J]. Opt Lett, 2006, 31(16): 2462−2464. doi: 10.1364/OL.31.002462
[16] Mahajan V N, Dai G M. Orthonormal polynomials in wavefront analysis: analytical solution[J]. J Opt Soc Am A, 2007, 24(9): 2994−3016. doi: 10.1364/JOSAA.24.002994
[17] Dai G M, Mahajan V N. Orthonormal polynomials in wavefront analysis: error analysis[J]. Appl Opt, 2008, 47(19): 3433−3445. doi: 10.1364/AO.47.003433
[18] Ferreira C, López J L, Navarro R, et al. Orthogonal basis with a conicoid first mode for shape specification of optical surfaces[J]. Opt Express, 2016, 24(5): 5448−5462. doi: 10.1364/OE.24.005448
[19] Broemel A, Lippmann U, Gross H. Freeform surface descriptions. Part I: mathematical representations[I]. Adv Opt Technol, 2017, 6 (5): 327–336. https://doi.org/10.1515/aot-2017-0030.
[20] Area I, Dimitrov D K, Godoy E. Recursive computation of generalised Zernike polynomials[J]. J Comput Appl Math, 2017, 312: 58−64. doi: 10.1016/j.cam.2015.11.017
[21] Ares M, Royo S. Comparison of cubic B-spline and Zernike-fitting techniques in complex wavefront reconstruction[J]. Appl Opt, 2006, 45(27): 6954−6964. doi: 10.1364/AO.45.006954
[22] Kaya I, Thompson K P, Rolland J P. Comparative assessment of freeform polynomials as optical surface descriptions[J]. Opt Express, 2012, 20(20): 22683−22691. doi: 10.1364/OE.20.022683
[23] Rahbar K, Faez K, Kakhki E A. Phase wavefront aberration modeling using Zernike and pseudo-Zernike polynomials[J]. J Opt Soc Am A, 2013, 30(10): 1988−1993. doi: 10.1364/JOSAA.30.001988
[24] Trevino J P, Gómez‐Correa J E, Iskander D R, et al. Zernike vs. Bessel circular functions in visual optics[J]. Ophthalmic Physiol Opt, 2013, 33(4): 394−402. doi: 10.1111/opo.12065
[25] Badar I, Hellmann C, Wyrowski F. Wavefront phase representation by Zernike and spline models: a comparison[J]. J Opt Soc Am A, 2021, 38(8): 1178−1186. doi: 10.1364/JOSAA.427519
[26] Raasch T W, Su L J, Yi A. Whole-surface characterization of progressive addition lenses[J]. Optom Vis Sci, 2011, 88(2): E217−E226. doi: 10.1097/OPX.0b013e3182084807
[27] Ivanova T V, Zavgorodniĭ D S. Zernike-polynomial description of the deformation of a known surface profile with a noncircularly symmetric shape[J]. J Opt Technol, 2021, 88(1): 8−13. doi: 10.1364/JOT.88.000008
[28] Omidi P, Cayless A, Langenbucher A. Evaluation of optimal Zernike radial degree for representing corneal surfaces[J]. PLoS One, 2022, 17(5): e0269119. doi: 10.1371/journal.pone.0269119
[29] Puentes G, Minotti F. Spectral characterization of optical aberrations in fluidic lenses[J]. Front Phys, 2024, 11: 1299393. doi: 10.3389/FPHY.2023.1299393
[30] Li X Y, Jiang W H. Modal description of wavefront aberration in non-circle apertures[J]. Chin J Lasers, 2002, B11(4): 259−266.
[31] 王庆丰, 程德文, 王涌天. 双变量正交多项式描述光学自由曲面[J]. 光学学报, 2012, 32(9): 0922002. doi: 10.3788/AOS201232.0922002
Wang Q F, Cheng D W, Wang Y T. Description of free-form optical curved surface using two-variable orthogonal polynomials[J]. Acta Opt Sin, 2012, 32(9): 0922002. doi: 10.3788/AOS201232.0922002
[32] 李萌阳, 李大海, 王琼华, 等. 用方形区域内的标准正交多项式重构波前[J]. 中国激光, 2012, 39(11): 1108011. doi: 10.3788/CJL201239.1108011
Li M Y, Li D H, Wang Q H, et al. Wavefront reconstruction with orthonormal polynomials in a Square Area[J]. Chin J Lasers, 2012, 39(11): 1108011. doi: 10.3788/CJL201239.1108011
[33] 赵齐, 王允, 王平, 等. 波面重构中非圆域Zernike正交基底构造方法[J]. 光学技术, 2017, 43(3): 228−233. doi: 10.13741/j.cnki.11-1879/o4.2017.03.008
Zhao Q, Wang Y, Wang P, et al. Construction method of non-circular pupil Zernike orthogonal basis in wavefront reconstruction[J]. Opt Tech, 2017, 43(3): 228−233. doi: 10.13741/j.cnki.11-1879/o4.2017.03.008
[34] 鄢静舟, 雷凡, 周必方, 等. 用Zernike多项式进行波面拟合的几种算法[J]. 光学 精密工程, 1999, 7(5): 119−128. doi: 10.3321/j.issn:1004-924X.1999.05.020
Yan J Z, Lei F, Zhou B F, et al. Algorithms for wavefront fitting using Zernike polynomial[J]. Opt Precis Eng, 1999, 7(5): 119−128. doi: 10.3321/j.issn:1004-924X.1999.05.020
[35] 莫卫东. Zernike多项式拟合干涉面方法研究[J]. 高速摄影与光子学, 1991, 20(4): 389−396.
Mo W D. The reseach into the method to fit interferogram with Zernike polynomials[J]. High Speed Photog Photonics, 1991, 20(4): 389−396.
[36] 莫卫东. Zernike多项式拟合干涉波面的基本原则[J]. 空军工程大学学报(自然科学版), 2002, 3(3): 35−38. doi: 10.3969/j.issn.1009-3516.2002.03.010
Mo W D. The principle of fitting Interferogram with Zernike polynomials[J]. J Air Force Eng Univ (Nat Sci Ed), 2002, 3(3): 35−38. doi: 10.3969/j.issn.1009-3516.2002.03.010
[37] 张伟, 刘剑峰, 龙夫年, 等. 基于Zernike多项式进行波面拟合研究[J]. 光学技术, 2005, 31(5): 675−678. doi: 10.3321/j.issn:1002-1582.2005.05.006
Zhang W, Liu J F, Long F N, et al. Study on wavefront fitting using Zernike polynomials[J]. Opt Tech, 2005, 31(5): 675−678. doi: 10.3321/j.issn:1002-1582.2005.05.006
[38] 孙学真, 苏显渝, 荆海龙. 抽样点对基于Zernike多项式曲面拟合精度的影响[J]. 光学仪器, 2008, 30(4): 6−10. doi: 10.3969/j.issn.1005-5630.2008.04.002
Sun X Z, Su X Y, Jing H L. The influence of sampling points on the precision of curved surface fitting based on Zernike polynomials[J]. Opt Instrum, 2008, 30(4): 6−10. doi: 10.3969/j.issn.1005-5630.2008.04.002
[39] 谢苏隆. Zernike多项式拟合曲面中拟合精度与采样点数目研究[J]. 应用光学, 2010, 31(6): 943−949. doi: 10.3969/j.issn.1002-2082.2010.06.015
Xie S L. Sampling point number in curved surface fitting with Zernike polynomials[J]. J Appl Opt, 2010, 31(6): 943−949. doi: 10.3969/j.issn.1002-2082.2010.06.015
[40] 冯婕, 白瑜, 邢廷文. Zernike多项式波面拟合精度研究[J]. 光电技术应用, 2011, 26(2): 31−34. doi: 10.3969/j.issn.1673-1255.2011.02.009
Feng J, Bai Y, Xing T W. Fitting accuracy of wavefront using Zernike polynomials[J]. Electro-Opt Technol Appl, 2011, 26(2): 31−34. doi: 10.3969/j.issn.1673-1255.2011.02.009
[41] 郭良贤, 卫俊杰, 唐培. Zernike圆域多项式镜面拟合仿真与精度研究[J]. 光学与光电技术, 2018, 16(6): 56−62. doi: 10.19519/j.cnki.1672-3392.2018.06.010
Guo L X, Wei J J, Tang P. Fitting simulation and precision of mirror surface with Zernike circular polynomial[J]. Opt Optoelectron Technol, 2018, 16(6): 56−62. doi: 10.19519/j.cnki.1672-3392.2018.06.010
[42] 韩路, 田爱玲, 聂凤明, 等. Zernike多项式的条纹反射三维面形重建算法研究[J]. 西安工业大学学报, 2019, 39(2): 137−144. doi: 10.16185/j.jxatu.edu.cn.2019.02.003
Han L, Tian A L, Nie F M, et al. Algorithm for three-dimensional surface reconstruction of fringe reflection using Zernike polynomial[J]. J Xi'an Technol Univ, 2019, 39(2): 137−144. doi: 10.16185/j.jxatu.edu.cn.2019.02.003
[43] 魏学业, 俞信. 一种基于Zernike多项式的波前探测和重构方法[J]. 光学学报, 1994, 14(7): 718−723. doi: 10.3321/j.issn:0253-2239.1994.07.011
Wei X Y, Yu X. An optical wavefront seuing and reconstruction method based on Zernike polynomials[J]. Acta Opt Sin, 1994, 14(7): 718−723. doi: 10.3321/j.issn:0253-2239.1994.07.011
[44] 张强, 姜文汉, 许冰. 利用Zernike多项式对湍流波前进行波前重构[J]. 光电工程, 1998, 25(6): 15−19.
Zhang Q, Jiang W H, Xu B. Reconstruction of turbulent optical wavefront realized by Zernike polynomial[J]. Opto-Electron Eng, 1998, 25(6): 15−19.
[45] 罗智锋, 陈怀新, 丁磊. 利用Zernike法进行激光小尺度畸变波前的重构[J]. 激光杂志, 2006, 27(3): 35−36. doi: 10.3969/j.issn.0253-2743.2006.03.015
Luo Z F, Chen H X, Ding L. Wavefront measurement and reconstruction of small phase-distortion on laser beam[J]. Laser J, 2006, 27(3): 35−36. doi: 10.3969/j.issn.0253-2743.2006.03.015
[46] 张航, 陆建东, 刘锐, 等. 基于Zernike多项式光滑优化的均匀方斑透镜设计[J]. 激光与光电子学进展, 2018, 55(10): 102202. doi: 10.3788/LOP55.102202
Zhang H, Lu J D, Liu R, et al. Design of uniform square spot Lens based on smooth optimization of Zernike polynomials[J]. Laser Optoelectron Prog, 2018, 55(10): 102202. doi: 10.3788/LOP55.102202
[47] 杨德荃, 陶彦辉, 赵刚练, 等. 基于神经网络的大气湍流退化图像的快速仿真[J]. 航天返回与遥感, 2023, 44(6): 57−67. doi: 10.3969/j.issn.1009-8518.2023.06.006
Yang D Q, Tao Y H, Zhao G L, et al. Rapid simulation of atmospheric turbulence degradation images based on neural networks[J]. Spacecr Recovery Remote Sens, 2023, 44(6): 57−67. doi: 10.3969/j.issn.1009-8518.2023.06.006
[48] 莫卫东. 数字平面检测系统误差和精度评价方法的研究[J]. 光学学报, 2003, 23(7): 879−883. doi: 10.3321/j.issn:0253-2239.2003.07.023
Mo W D. Error and precision evaluation of a system for Inspecting surface of optical plane[J]. Acta Opt Sin, 2003, 23(7): 879−883. doi: 10.3321/j.issn:0253-2239.2003.07.023
[49] 杨佳文, 黄巧林, 韩友民. Zernike多项式在拟合光学表面面形中的应用及仿真[J]. 航天返回与遥感, 2010, 31(5): 49−55. doi: 10.3969/j.issn.1009-8518.2010.05.009
Yang J W, Huang Q L, Han Y M. Application and simulation in fitting optical surface with Zernike polynomial[J]. Spacecr Recovery Remote Sens, 2010, 31(5): 49−55. doi: 10.3969/j.issn.1009-8518.2010.05.009
[50] 庞志海, 樊学武, 马臻, 等. 自由曲面校正光学系统像差的研究[J]. 光学学报, 2016, 36(5): 0522001. doi: 10.3788/AOS201636.0522001
Pang Z H, Fan X W, Ma Z, et al. Free-form optical elements corrected aberrations of optical system[J]. Acta Opt Sin, 2016, 36(5): 0522001. doi: 10.3788/AOS201636.0522001
[51] 关姝, 王超, 佟首峰, 等. 空间激光通信离轴两镜反射望远镜自由曲面光学天线设计[J]. 红外与激光工程, 2017, 46(12): 1205002. doi: 10.3788/IRLA201746.1222003
Guan S, Wang C, Tong S F, et al. Optical antenna design of off-axis two-mirror reflective telescope with freeform surface for space laser communication[J]. Infrared Laser Eng, 2017, 46(12): 1205002. doi: 10.3788/IRLA201746.1222003
[52] Xiang B B, Wang C S, Lian P Y. Effect of surface error distribution and aberration on electromagnetic performance of a reflector antenna[J]. Int J Antennas Propagation, 2019, 2019: 5062545. doi: 10.1155/2019/5062545
[53] 施胤成, 闫怀德, 宫鹏, 等. 基于Zernike系数优化模型的光学反射镜支撑结构拓扑优化设计方法[J]. 光子学报, 2020, 49(6): 0622001. doi: 10.3788/gzxb20204906.0622001
Shi Y C, Yan H D, Gong P, et al. Topology optimization design method for supporting structures of optical reflective mirrors based on Zernike coefficient optimization model[J]. Acta Photonica Sin, 2020, 49(6): 0622001. doi: 10.3788/gzxb20204906.0622001
[54] 周颋, 郝群, 胡摇, 等. 用于自由曲面部分补偿干涉测量的可变形镜面形设计的优化方法[J]. 光学技术, 2021, 47(3): 257−264. doi: 10.13741/j.cnki.11-1879/o4.2021.03.001
Zhou T, Hao Q, Hu Y, et al. An optimization method of deformable mirror shape design for freeform surface partial compensation interferometry[J]. Opt Tech, 2021, 47(3): 257−264. doi: 10.13741/j.cnki.11-1879/o4.2021.03.001
[55] 闫钧华, 胡子佳, 朱德燕, 等. 基于自由曲面的紧凑型离轴三反无焦系统设计[J]. 光子学报, 2022, 51(5): 0511002. doi: 10.3788/gzxb20225105.0511002
Yan J H, Hu Z J, Zhu D Y, et al. Design of compact off-axis three-mirror afocal system based on freeform surface[J]. Acta Photonica Sin, 2022, 51(5): 0511002. doi: 10.3788/gzxb20225105.0511002
[56] 解博夫, 赵星, 陶诗诗, 等. 自由曲面补偿飞秒激光成丝系统像差的应用[J]. 光学学报, 2023, 43(8): 0822020. doi: 10.3788/AOS221720
Xie B F, Zhao X, Tao S S, et al. Application of freeform surface in aberration compensation of femtosecond laser filamentation system[J]. Acta Opt Sin, 2023, 43(8): 0822020. doi: 10.3788/AOS221720
[57] 韩继周, 赵世家, 冯安伟, 等. 基于自由曲面的紧凑型宽波段成像光谱仪设计[J]. 光学学报, 2023, 43(14): 1422002. doi: 10.3788/AOS230474
Han J Z, Zhao S J, Feng A W, et al. Design of compact and broadband imaging spectrometer based on free-form surface[J]. Acta Opt Sin, 2023, 43(14): 1422002. doi: 10.3788/AOS230474
[58] 张强, 吕百达, 姜文汉. 环形区域上Zernike模式法波前重构[J]. 强激光与粒子束, 2000, 12(3): 306−310.
Zhang Q, Lü B D, Jiang W H. Zernike model wavefront reconstruction for annular field[J]. High Power Laser Part Beams, 2000, 12(3): 306−310.
[59] 王奇涛, 佟首峰, 徐友会. 采用Zernike多项式对大气湍流相位屏的仿真和验证[J]. 红外与激光工程, 2013, 42(7): 1907−1911. doi: 10.3969/j.issn.1007-2276.2013.07.046
Wang Q T, Tong S F, Xu Y H. On simulation and verification of the atmospheric turbulent phase screen with Zernike polynomials[J]. Infrared Laser Eng, 2013, 42(7): 1907−1911. doi: 10.3969/j.issn.1007-2276.2013.07.046
[60] 吴加丽, 柯熙政. 无波前传感器的自适应光学校正[J]. 激光与光电子学进展, 2018, 55(3): 030103. doi: 10.3788/LOP55.030103
Wu J L, Ke X Z. Adaptive optics correction of wavefront sensorless[J]. Laser Optoelectron Prog, 2018, 55(3): 030103. doi: 10.3788/LOP55.030103
[61] 张慧敏, 李新阳. 大气湍流畸变相位屏的数值模拟方法研究[J]. 光电工程, 2006, 33(1): 14−19. doi: 10.3969/j.issn.1003-501X.2006.01.004
Zhang H M, Li X Y. Numerical simulation of wavefront phase screen distorted by atmospheric turbulence[J]. Opto-Electron Eng, 2006, 33(1): 14−19. doi: 10.3969/j.issn.1003-501X.2006.01.004
-
访问统计



 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: