Multi-exposure image fusion based on tensor decomposition and convolution sparse representation
-
摘要
针对多曝光图像融合中存在细节丢失和颜色失真等问题,本文提出了一种基于张量分解和卷积稀疏表示的多曝光图像融合方法。张量分解作为一种对高维数据低秩逼近的方式,在多曝光图像特征提取方面有较大的潜力,而卷积稀疏表示是对整幅图像进行稀疏优化,能最大程度地保留图像的细节信息。同时,为了避免融合图像出现颜色失真,本文采取亮度与色度分别融合的方式。首先通过张量分解得到源图像的核心张量;然后在包含信息最多的第一子带上提取边缘特征;接着对边缘特征图进行卷积稀疏分解,继而利用分解系数的L1范数来得到每个像素的活跃水平;最后用"赢者取全"策略生成权重图,从而加权得到融合后的亮度分量。与亮度融合不同的是,色度分量则采用简单的高斯加权方式进行融合,在一定程度上解决了融合图像的颜色失真问题。实验结果表明,所提出的方法具有良好的细节保留能力。
Abstract
In view of the problem about the loss of detail and color distortion in multi-exposure image fusion, this paper proposed a multi-exposure image fusion method based on tensor decomposition and convolution sparse representation. Tensor decomposition, as an approach of low-rank approximation for high-dimensional data, has great potential in feature extraction of multi-exposure images. Convolution sparse representation is a sparse optimization method for the whole image, which can preserve the detail information of the image to the greatest extent. At the same time, in order to avoid color distortion in the fused image, this paper adopted the method of separately fusing luminance and chrominance. Firstly, the core tensor of the source image was obtained by tensor decomposition. Besides, edge features were extracted on the first sub-band which contains the most information. Then the edge feature map was sparsely decomposed to obtain the activity level of each pixel by using L1 norm of the decomposition coefficient. Finally, take "winner-take-all" strategy to generate weight map so as to obtain the fused luminance components. Unlike the process of luminance fusion, chrominance components were fused by simple Gaussian weighting method, which solves the color distortion problem for the fused image to a certain extent. The experimental results show that the proposed method has great detail preservation ability.
-
Overview

Overview: The real scene usually has a luminance range from 10-5 cd/m2 to 108 cd/m2, but the existing image video devices can capture a limited luminance dynamic range. Thus, it cannot retain all the details of the real scene. In recent years, multi-exposure fusion (MEF), as an effective quality enhancement technology, has gradually become a hot research topic in digital media field. This technique combines multiple low dynamic range (LDR) images with different exposures taken by ordinary cameras to generate an image with rich details and saturated color. At present, many MEF algorithms have been proposed by relevant researchers and they can achieve great results when processing image sequences with simple background. However, when multi-exposure image sequences contain many objects with complex textures, the performance of these algorithms is not satisfactory and the terrible phenomena such as detail loss and color distortion often appear in the fused images. To solve the above problem, this paper proposesd a multi-exposure image fusion method based on tensor decomposition (TD) and convolution sparse representation (CSR). Among them, TD, as a method of low rank approximation for high-dimensional data, has great potential in multi-exposure image feature extraction, while CSR performs sparse optimization on the whole image, which can retain the detail information to the greatest extent. At the same time, in order to avoid color distortion in the fused image, luminance and chrominance were fused separately. Firstly, the core tensor of the source image was obtained through tensor decomposition and the edge feature extraction was carried out on the first sub-band which contains the most information. Secondly, the edge feature map was sparsely decomposed to obtain the activity level of each pixel by using L1 norm of the decomposition coefficient. Finally, take the "winner-take-all" strategy to generate the weight map so as to obtain the fused luminance component. Different from the luminance fusion process, chrominance components were fused by Gaussian weighting method simply according to the color space characteristics. The experiment used two sets of image sequences with complex background. Compared with other five advanced MEF algorithms, the fusion image by the proposed algorithm not only had rich details, but also did not appear the large-scale color distortion. In addition, in order to evaluate the detail preserving ability of the proposed algorithm more comprehensively, seven groups of multi-exposure image sequences were selected for objective measurement. Experimental results show that the proposed method has strong edge information preserving ability.
-
1. 引言
现实世界的场景通常具有10-5 cd/m2~108 cd/m2的亮度范围,而现有的图像视频设备能够捕捉的亮度动态范围十分有限,无法保留真实场景中的所有细节信息[1]。目前,随着高动态范围成像技术(high dynamic range imaging, HDRI)的快速发展,这个问题正在得到解决。HDRI是用普通相机拍摄多幅不同曝光的低动态范围(low dynamic range, LDR)图像并将其融合成一幅动态范围宽的图像,但是合成的高动态范围(high dynamic range, HDR)图像质量极其依赖于相机响应曲线(camera response function, CRF)的精度[2]。由于现有的终端显示设备大多为LDR类型,近年来,多曝光图像融合(multi-exposure image fusion, MEF)技术正成为成像领域的研究热点。它通过合并多张LDR图像间的互补信息来直接获得一幅视觉效果类似于HDR图像的LDR图像,而无需进行CRF估计和色调映射(Tone mapping, TM)等处理,且能够在普通的LDR显示设备上直接观看[3]。从图像变换的角度,图像融合方法可分为4类[4]:基于多尺度分解(multi-scale decomposition, MSD)的方法[5],基于稀疏表示(sparse representation, SR)的方法[6],基于空间域[7]和基于混合变换的方法[8]。这些融合方法的思想可以近一步延伸到多曝光融合领域中,Mertens等[9]在多尺度图像分解下,利用对比度、饱和度及曝光量三个特征来构造融合权重值,但该方法在场景灰暗或明亮处会丢失较多细节。Kang等[10]提出一种基于引导滤波的多曝光融合方法,它充分利用空间一致性原则来消除融合图像中的边缘伪影现象,但该算法在场景较复杂时仍会丢失一些细节。Liu等[11]提出了一种基于稠密尺度不变特征变换(dense scale invariant feature transformation, DSIFT)的多曝光融合方法,该方法能较好地保留源图像的边缘信息,但容易出现颜色退化等现象。Ma等[12]将图像块信号分解成强度、结构和平均强度三部分,并分别对各部分进行融合,能较好地保留源图像的结构信息,但在复杂的场景下容易出现块伪影。Ma等[13]在文献[12]基础上又提出一种基于结构相似度指标来优化融合图像的方法,但该算法很大程度上依赖于原始融合图像的质量。虽然现有的多曝光融合算法能较好地融合简单背景下的图像序列,但是当场景中出现较多纹理复杂的物体时,这些算法均不能很好地保留源图像的细节和纹理信息。
本文提出一种结合张量分解(tensor decomposition, TD)和卷积稀疏表示(convolution sparse representation, CSR)的多曝光融合算法,主要从三方面提高了融合图像的性能:首先通过张量分解将源图像的三个通道的信息高度汇聚到三个子带图中,而第一子带所包含的信息量和特征最多,方便进行特征提取,这既避免了算法同时处理三通道的复杂性,也提高了特征提取的完整性;其次对第一子带图提取的边缘特征进行卷积稀疏表示,相较于传统的稀疏表示方法具有更出色的细节保留能力;最后分别采用不同的融合策略来处理源图像的亮度信息和色度信息,一定程度上避免了融合图像中出现颜色失真现象。
2. 基于张量分解和卷积稀疏表示的多曝光图像融合
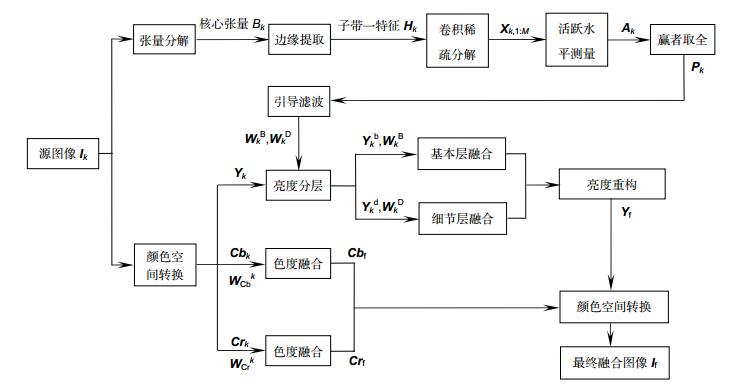
现有的多曝光图像融合算法在处理复杂背景下的图像序列时,容易出现细节丢失、颜色失真和光晕等视觉现象。本文先对源图像{\mathit{\boldsymbol{I}}_k}进行颜色空间转换,继而利用不同的融合策略来处理图像的亮度信息{\mathit{\boldsymbol{Y}}_k}和色度信息{\mathit{\boldsymbol{Cb}}_k}、{\mathit{\boldsymbol{Cr}}_k},以减少融合图像的颜色失真;考虑到多曝光源图像的亮度信息对最终融合图像的细节、纹理等特征的保留有较大影响,故提出一种结合张量分解和卷积稀疏表示的多曝光图像亮度融合方法,具体流程如图 1所示。其中,张量分解作为一种对高维数据低秩逼近的方法,利于特征提取,而卷积稀疏表示是对整幅图像进行稀疏优化,避免了融合图像中细节特征的大量丢失。
假设有K幅预先配准好的源图像{\mathit{\boldsymbol{I}}_k}, k \in \{ 1, ..., K\} 和一组已经训练完的字典滤波器{\mathit{\boldsymbol{d}}_m}, m \in \{ 1, ..., M\} 。首先对第k幅源图像{\mathit{\boldsymbol{I}}_k}进行张量分解得到核心张量{\mathcal{B}_k},由于核心张量中的子带一\mathit{\boldsymbol{C}}_1^k中包含的信息和能量最多,所以为了降低算法的复杂度,只在子带一上进行特征提取;又由于人类视觉系统对边缘信息十分敏感,因此采用拉普拉斯算子对子带一进行边缘提取,得到边缘特征图{\mathit{\boldsymbol{H}}_k};再根据训练好的字典滤波器,对边缘特征图进行卷积稀疏分解得到稀疏系数图{\mathit{\boldsymbol{X}}_{k, 1:M}};接着用稀疏系数的L1范数分别求取每个像素点的活跃水平{\mathit{\boldsymbol{A}}_k},并利用"赢者取全"策略生成初始权重图;最后根据空间一致性原则精细化权重图。同时,为了更好地保留{\mathit{\boldsymbol{Y}}_k}中的细节信息,采用基本层和细节层分别融合的方式得到融合亮度分量{\mathit{\boldsymbol{Y}}_{\text{f}}}。在此基础上,结合由不同融合策略得到的两个色度分量{\mathit{\boldsymbol{Cb}}_{\text{f}}}、{\mathit{\boldsymbol{Cr}}_{\text{f}}},并进行颜色空间转换,从而得到最终的融合图像{\mathit{\boldsymbol{I}}_{\text{f}}}。
2.1 张量分解和特征提取
由于现实数据的多维性,使用向量描述显然不能很好反映它们复杂的结构和本质,因此Leopold Kronecker提出了张量的概念。一个N阶张量\mathcal{A}可以如下表述:
\mathcal{A} \in {\mathfrak{R} ^{{l_1} \times {l_2} \times ... \times {l_N}}}, (1) 其中:{l_1}, {l_2}, ..., {l_N}表示每个维度上的元素个数。张量分解作为一种处理高维数据的有效手段,已经在数据分类、图像水印和图像恢复等众多计算机视觉领域上取得了显著效果。张量分解有两种基本形式:CP分解和Tucker分解[14]。本文将Tucker分解应用到多曝光图像融合领域。Tucker分解是将一个N阶张量\mathcal{A} \in {\mathfrak{R} ^{{l_1} \times {l_2} \times ... \times {l_N}}}分解成一个核心张量\mathcal{B} \in {\mathfrak{R} ^{{l_1} \times {l_2} \times ... \times {l_N}}}与N个矩阵{{\mathit{\boldsymbol{U}}}^{(n)}} \in {{\mathit{\boldsymbol{R}}}^{{l_n} \times {R_n}}}, (n = 1, 2, ..., N)的n模式乘积形式,即:
\mathcal{A} \approx [\mathcal{B};{{\mathit{\boldsymbol{U}}}^{(1)}}, {{\mathit{\boldsymbol{U}}}^{(2)}}, \cdots , {{\mathit{\boldsymbol{U}}}^{(N)}}]\\ = \mathcal{B}{ \times _1}{{\mathit{\boldsymbol{U}}}^{(1)}}{ \times _2} \cdots { \times _N}{{\mathit{\boldsymbol{U}}}^{(N)}}, (2) 其中:{ \times _n}(n = 1, ..., N)表示张量与矩阵的n模式乘积,即张量\mathcal{B}沿着第n维展开成对应矩阵形式后与{{\mathit{\boldsymbol{U}}}^{(n)}}的乘积。当{{\mathit{\boldsymbol{U}}}^{(n)}}为正交矩阵时,N阶张量\mathcal{A}与核心张量\mathcal{B}存在如下的转换关系:
\mathcal{A} \approx \mathcal{B}{ \times _1}{{\mathit{\boldsymbol{U}}}^{(1)}}{ \times _2}{{\mathit{\boldsymbol{U}}}^{(2)}} \cdots { \times _N}{{\mathit{\boldsymbol{U}}}^{(N)}}\\ \Leftrightarrow \mathcal{B} \approx \mathcal{A}{ \times _1}{({{\mathit{\boldsymbol{U}}}^{(1)}})^{\text{T}}}{ \times _2}{({{\mathit{\boldsymbol{U}}}^{(2)}})^{\text{T}}} \cdots { \times _N}{({{\mathit{\boldsymbol{U}}}^{(N)}})^{\text{T}}}。 (3) 多曝光图像融合的难点在于融合图像的边缘和纹理等细节特征难以保留,而Tucker分解后的核心张量较大程度地保留了源图像中的所有信息和特征,因此更利于进行特征提取。
首先每幅RGB源图像{\mathit{\boldsymbol{I}}_k}(k = 1, ..., K)可以表示为三阶张量\chi \in {\mathfrak{R} ^{{l_1} \times {l_2} \times 3}},{l_1}和{l_2}分别为图像的宽和高。然后将该三阶张量分别进行模式1、模式2和模式3展开,得到对应的矩阵形式
\{ {{\mathit{\boldsymbol{X}}}^{(1)}} \in {{\mathit{\boldsymbol{R}}}^{{l_1} \times (3{l_2})}}, {{\mathit{\boldsymbol{X}}}^{(2)}} \in {{\mathit{\boldsymbol{R}}}^{{l_2} \times (3{l_1})}}, {{\mathit{\boldsymbol{X}}}^{(3)}} \in {{\mathit{\boldsymbol{R}}}^{3 \times ({l_1}{l_2})}}\}, 再对上述矩阵进行SVD分解,得到正交矩阵{{\mathit{\boldsymbol{U}}}^{(1)}}, {{\mathit{\boldsymbol{U}}}^{(2)}}, {{\mathit{\boldsymbol{U}}}^{(3)}},大小分别为{l_1} \times {l_1},{l_2} \times {l_2}和3 \times 3。
[{{\mathit{\boldsymbol{U}}}^{(i)}}, {{\mathit{\boldsymbol{S}}}^{(i)}}, {{\mathit{\boldsymbol{V}}}^{(i)}}] = {\text{SVD}}({{\mathit{\boldsymbol{X}}}^{(i)}})(i = 1, 2, 3), (4) 其中:{\text{SVD}}( \cdot )表示矩阵的奇异值分解。最后根据式(2)得到对应的核心张量C \in {\mathfrak{R} ^{{l_1} \times {l_2} \times 3}},用于进行特征提取。又由于核心张量\mathcal{B}的子张量满足有序性[15],即对任意1 \leqslant n \leqslant N,有{\mathcal{B}_{{i_n} = 1}} \geqslant {\mathcal{B}_{{i_n} = 2}} \geqslant ... \geqslant {\mathcal{B}_{{i_n} = {l_N}}} \geqslant 0。所以对于每幅RGB图像的核心张量C \in {\mathfrak{R} ^{{l_1} \times {l_2} \times 3}},满足:
{{\mathit{\boldsymbol{C}}}_1} \geqslant {{\mathit{\boldsymbol{C}}}_2} \geqslant {{\mathit{\boldsymbol{C}}}_3} \geqslant 0。 (5) 在这里,定义{\mathit{\boldsymbol{C}}_1}为子带一,{\mathit{\boldsymbol{C}}_2}为子带二,{\mathit{\boldsymbol{C}}_3}为子带三。根据核心张量的有序性,{\mathit{\boldsymbol{C}}_1}携带的信息和能量最多,故在第一子带图上提取特征。又由于人类视觉系统对边缘特征比较敏感,因此采用拉普拉斯算子在第一子带图上提取边缘信息,从而得到{\mathit{\boldsymbol{C}}_1}的高频分量\mathit{\boldsymbol{H}}:
{\mathit{\boldsymbol{H}}_k} = \mathit{\boldsymbol{C}}_1^k \times L, (6) 其中:\mathit{\boldsymbol{L}} = \left[ {0, 1, 0;1, - 4, 1;0, 1, 0} \right],该算子相比于一阶微分算子具有更好的细节保留能力,\mathit{\boldsymbol{C}}_1^k表示第k幅源图像的第一子带图,{\mathit{\boldsymbol{H}}_k}表示第k幅第一子带图上提取的边缘特征。图 2为House序列的多曝光图像组[9],图 3为图 2中图像经Tucker分解得到的核心张量图,图 4为在图 3所示的第一子带图上提取的边缘特征。
2.2 卷积稀疏表示和字典学习
当给定一个原始信号{\mathit{\boldsymbol{S}}} \in {{\mathit{\boldsymbol{R}}}^n}和一个过完备字典矩阵{\mathit{\boldsymbol{D}}} \in {{\mathit{\boldsymbol{R}}}^{n \times m}}(n < m),SR的目标是为了估计一个只有几个非零项的稀疏向量{\mathit{\boldsymbol{x}}} \in {{\mathit{\boldsymbol{R}}}^m},例如{\mathit{\boldsymbol{S}}} \approx {\mathit{\boldsymbol{Dx}}}。因此大多数稀疏编码问题可以表述为以下优化问题[6]:
\mathop {\arg {\text{ min}}}\limits_{\mathit{\boldsymbol{x}}} {\text{ }}\frac{1}{2}||{\mathit{\boldsymbol{Dx}}} - {\mathit{\boldsymbol{S}}}||_2^2 + \lambda ||{\mathit{\boldsymbol{x}}}|{|_1}, (7) 其中:|| \cdot |{|_1}表示L1范数,用来计算矩阵中非零项的数目。{\mathit{\boldsymbol{D}}}表示训练好的字典矩阵,{\mathit{\boldsymbol{x}}}表示稀疏系数,{\mathit{\boldsymbol{S}}}表示原始图像,\lambda 表示正则化参数。
传统的SR方法是通过对一组重叠块进行稀疏表示,其结果往往是多值的且没有对整幅图像进行优化。所以Zeiler[16]提出用带卷积操作的稀疏编码来代替传统的稀疏表示,即利用字典滤波器与相应特征响应的卷积形式来替代字典矩阵与稀疏编码系数的乘积形式,该表示是单值的且对整幅图像进行了联合优化。类似于式(7)中的基追踪去噪[17](basis pursuit denoising, BPDN)问题,相应的卷积基追踪去噪(convolutional basis pursuit denoising, CBPDN)问题定义如下:
\mathop {\arg {\text{ min}}}\limits_{\{ {{\mathit{\boldsymbol{x}}}_m}\} } {\text{ }}\frac{1}{2}||\sum\limits_m {{{\mathit{\boldsymbol{d}}}_m} \otimes {{\mathit{\boldsymbol{x}}}_m} - {\mathit{\boldsymbol{s}}}} ||_2^2 + \lambda {\sum\limits_m {||{{\mathit{\boldsymbol{x}}}_m}||} _{^{^1}}}, (8) 其中:\{ {{\mathit{\boldsymbol{d}}}_m}\} 是由M个滤波器组成的卷积字典, \otimes 表示卷积操作,\{ {{\mathit{\boldsymbol{x}}}_m}\} 是M维稀疏系数图。
目前,已经提出了很多算法来解决式(8)中的卷积稀疏分解问题。本文是用改进的交替方向乘法器算法(alternating direction method of multipliers, ADMM) [18]来解决该优化问题,该算法能较大地提高计算效率。除此之外,相应的卷积字典学习问题同样具有挑战性。大多数卷积字典学习是在稀疏编码步骤和字典更新步骤之间交替进行工作,当训练数据很大时,通常会使计算成本急剧增大。另外,传统的基于批量处理的字典学习算法是直接对所有训练数据进行处理,这还会造成大量的内存消耗,因此本文采用在线卷积字典学习[19]算法来解决这两个限制。
CSR作为一种有效的图像表示模型,在多曝光图像融合领域主要有两个优点:1) CSR是对整幅图像进行稀疏表示,而不是基于块的多值表示,图像细节保留问题可以得到有效的解决;2) CSR是一个移位不变的图像表示模型,当融合误配准的区域时,融合质量也可以得到显著提高。
基于上述分析,本文采用在线字典学习方法,用50张尺寸为256×256的高清自然图像训练字典滤波器。为了在算法复杂度和融合质量之间取得平衡,本文设置每个字典滤波器的空间大小为8 \times 8,字典滤波器的数量为32。图 5是训练得到的卷积字典{\mathit{\boldsymbol{D}}}。
2.3 亮度权重图生成
通过训练得到的卷积字典{\mathit{\boldsymbol{D}}},对核心张量中第一子带的边缘特征图{\mathit{\boldsymbol{H}}_k}进行卷积稀疏分解,它的稀疏系数图{\mathit{\boldsymbol{X}}_{k, m}}, m \in \{ 1, ..., M\} 通过求解式(8)中的CSR模型得到。
\mathop {\arg {\text{ min}}}\limits_{\{ {X_{k, m}}\} } {\text{ }}\frac{1}{2}||\sum\limits_{m{\text{ = }}1}^M {{D_m} \times {X_{k, m}} - {H_k}} ||_2^2 + \lambda \sum\limits_{m{\text{ = }}1}^M {||{X_{k, m}}|{|_1}} , (9) 其中:{\mathit{\boldsymbol{X}}_{k, 1:M}}(x, y)表示第k幅源图像在像素(x, y)位置处的稀疏系数,M是稀疏系数图的数量,{\mathit{\boldsymbol{D}}_m}是通过在线学习方法得到的卷积字典,\lambda 为0.01。由于源图像中各像素点的活跃水平是衡量权重的依据,它反映了源图像的特征信息,因此活跃水平{\mathit{\boldsymbol{A}}_k}(x, y)可用稀疏系数{\mathit{\boldsymbol{X}}_{k, 1:M}}(x, y)的L1范数来获取。
{\mathit{\boldsymbol{A}}_k}(x, y) = ||{\mathit{\boldsymbol{X}}_{k, 1:M}}(x, y)|{|_1}。 (10) 同时,为了减少噪声的影响,对{\mathit{\boldsymbol{A}}_k}(x, y)执行基于窗口的平均策略来获得最终的活跃水平图{\mathit{\boldsymbol{A}}_k}(x, y):
{ \mathit{\boldsymbol{\overline{A}}} _k}(x, y) = \frac{{\sum\limits_{p{\text{ = }} - r}^r {\sum\limits_{q{\text{ = }} - r}^r {{\mathit{\boldsymbol{A}}_k}(x + p, y + p)} } }}{{{{(2r + 1)}^2}}}。 (11) 其中r是窗口大小。若r很大时,这种方法会对噪声更加鲁棒,但是可能会丢失一些细节。在多曝光图像融合中,源图像的边缘和纹理这些特征信息会对最终的融合结果有很大影响,故在本文中,窗口大小r设定为3。最后采用"赢者取全"策略得到初始权重图\mathit{\boldsymbol{P}}_k^i,图 6是House序列的初始权重图。
\mathit{\boldsymbol{P}}_k^i = \left\{ \begin{array}{l} 1,~~{\rm{ if }}~~\mathit{\boldsymbol{\overline A}} _k^i = \max (\mathit{\boldsymbol{\overline A}} _1^i, \mathit{\boldsymbol{\overline A}} _2^i, ..., \mathit{\boldsymbol{\overline A}} _K^i)\\ 0,~~{\rm{ otherwise}} \end{array} \right.。 (12) 然而,如图 7所示,初始权重图中存在大量噪声和边缘匹配不准的情况,这可能会在融合图像中产生边缘伪影。例如图 7(a)中的红色框部分的场景十分暗,该处的像素点处于欠曝光区域,理论上不应分配权重,但图 7(b)的红色框部分却表明分配了权重,说明该初始权重图需要进一步精细化。而使用空间一致性是解决这个问题的有效途径,这里的空间一致性是指如果两个相邻像素点具有相似的亮度,它们将具有相似的权重。而引导滤波器作为一种边缘保留滤波器,可以促使滤波后的图像保留引导图像的边缘信息,因此Kang等[10]将初始权重图和多曝光序列分别作为滤波输入图像和引导图像,使得滤波输出图像与引导图像的边缘进行对准,从而解决了空间一致性的问题。本文在此基础上,利用引导滤波器对初始权重图进行精细化,即将初始权重图{\mathit{\boldsymbol{P}}_k}作为滤波输入图像,相应的多曝光图像的亮度分量{\mathit{\boldsymbol{Y}}_k}作为引导图像。同时,为了更好地保留{\mathit{\boldsymbol{Y}}_k}中的细节信息,采用基本层和细节层分别融合的方式,而基本层图像表示亮度分量的低频信息,其看起来在空间上平滑,那么对应的权重图也应平滑,否则会出现边缘伪影现象。因此,对于基本层来说,优先选择较大的滤波半径和正则化参数,而对于细节层而言,优先选择较小的滤波半径和正则化参数。
\left\{ \begin{gathered} \mathit{\boldsymbol{W}}_k^{\text{B}} = {{\text{G}}_{{r_1}, {\varepsilon _1}}}({\mathit{\boldsymbol{P}}_k}, {\mathit{\boldsymbol{Y}}_k}) \hfill \\ \mathit{\boldsymbol{W}}_k^{\text{D}} = {{\text{G}}_{{r_2}, {\varepsilon _2}}}({\mathit{\boldsymbol{P}}_k}, {\mathit{\boldsymbol{Y}}_k}) \hfill \\ \end{gathered} \right. , (13) 其中:{{\text{G}}_{r, \varepsilon }}( \cdot )代表引导滤波器,{r_1},{r_2}和{\varepsilon _1},{\varepsilon _2}分别是引导滤波器的窗口半径和正则化参数,文中设置为45,7,0.3,10-6。\mathit{\boldsymbol{W}}_k^{\text{B}}和\mathit{\boldsymbol{W}}_k^{\text{D}}分别是滤波后的基本层和细节层的权重图。最后,将K个精细化的权重图归一化,使得它们在每个像素点上的权重和为1,图 8是精细化后的权重图。
\left\{ \begin{array}{l} \mathit{\boldsymbol{\bar W}}_k^{\rm{B}} = \mathit{\boldsymbol{W}}_k^{\rm{B}}/\sum\limits_{k{\rm{ = }}1}^K {\mathit{\boldsymbol{W}}_k^{\rm{B}}} \\ \mathit{\boldsymbol{\bar W}}_k^{\rm{D}} = \mathit{\boldsymbol{W}}_k^{\rm{D}}/\sum\limits_{k{\rm{ = }}1}^K {\mathit{\boldsymbol{W}}_k^{\rm{D}}} \end{array} \right.。 (14) 2.4 亮度融合
每幅源图像的亮度分量{\mathit{\boldsymbol{Y}}_k}首先被分解成基本层\mathit{\boldsymbol{Y}}_k^{\text{b}}和细节层\mathit{\boldsymbol{Y}}_k^{\text{d}},而获取基本层和细节层的方法有很多,例如双边滤波、引导滤波等。本文通过解决以下优化问题[20]来获得基本层:
\begin{array}{l} \mathop {\arg {\rm{ min}}}\limits_{\mathit{\boldsymbol{Y}}_k^{\rm{b}}} ||{\mathit{\boldsymbol{Y}}_k} - \mathit{\boldsymbol{Y}}_k^{\rm{b}}||_{\rm{F}}^2\\ + \eta (||{\mathit{\boldsymbol{g}}_x} \times \mathit{\boldsymbol{Y}}_k^{\rm{b}}||_{\rm{F}}^2 + ||{\mathit{\boldsymbol{g}}_y} \times \mathit{\boldsymbol{Y}}_k^{\rm{b}}||_{\rm{F}}^2)。 \end{array} (15) 该问题等同于利用\eta 作为正则化参数,离散梯度作为算子的Tikhonov正则化问题,可以通过快速傅里叶变换解决。其中{{\mathit{\boldsymbol{g}}}_x} = [ - 1\;\;1]和{{\mathit{\boldsymbol{g}}}_y} = {[ - 1\;\;1]^{\text{T}}}分别是水平和垂直梯度算子,\eta 是正则化参数,在本文中设置为5。通过式(15)得到基本层\mathit{\boldsymbol{Y}}_k^{\text{b}}后,细节层\mathit{\boldsymbol{Y}}_k^{\text{d}}可以通过下式得到:
\mathit{\boldsymbol{Y}}_k^{\text{d}} = {\mathit{\boldsymbol{Y}}_k} - \mathit{\boldsymbol{Y}}_k^{\text{b}}。 (16) 最后根据式(14)和式(16)重构得到融合亮度{\mathit{\boldsymbol{Y}}_{\text{f}}}。
{\mathit{\boldsymbol{Y}}_{\rm{f}}} = \sum\limits_{k{\rm{ = }}1}^K {\mathit{\boldsymbol{Y}}_k^{\rm{b}}\mathit{\boldsymbol{\bar W}}_k^{\rm{B}} + } \sum\limits_{k{\rm{ = }}1}^K {\mathit{\boldsymbol{Y}}_k^{\rm{d}}} \mathit{\boldsymbol{\bar W}}_k^{\rm{D}}。 (17) 2.5 色度融合
与亮度融合过程不同的是,色度融合过程直接决定了最终融合图像的颜色特征,所以本文采取不同的融合策略来处理色度分量。首先将每幅RGB源图像{\mathit{\boldsymbol{I}}_k}转换颜色空间,得到两个色度分量{\mathit{\boldsymbol{Cb}}_k}和{\mathit{\boldsymbol{Cr}}_k},过程如下:
\left[ \begin{gathered} \mathit{\boldsymbol{Y}} \hfill \\ \mathit{\boldsymbol{Cb}} \hfill \\ \mathit{\boldsymbol{Cr}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {\text{ }}0.299{\text{ 0}}{\text{.587 0}}{\text{.114}} \hfill \\ - 0.169{\text{ }} - {\text{0}}{\text{.331 0}}{\text{.500}} \hfill \\ {\text{ }}0.500{\text{ }} - 0.419{\text{ }} - 0.081 \hfill \\ \end{gathered} \right]\left[ \begin{gathered} \mathit{\boldsymbol{R}} \hfill \\ \mathit{\boldsymbol{G}} \hfill \\ \mathit{\boldsymbol{B}} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} {\text{ 0}} \hfill \\ 128 \hfill \\ 128 \hfill \\ \end{gathered} \right]。 (18) 而式(18)的逆过程可以如下表示:
\left\{ \begin{array}{l} \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{Y}} + 1.402(\mathit{\boldsymbol{Cr}} - 128)\\ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{Y}} - 0.344(\mathit{\boldsymbol{Cb}} - 128) - 0.714(\mathit{\boldsymbol{Cr}} - 128)\\ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{Y}} + 1.772(\mathit{\boldsymbol{Cb}} - 128) \end{array} \right.。 (19) 根据式(19),当\mathit{\boldsymbol{Cb}}、\mathit{\boldsymbol{Cr}}值越接近128时,图像的视觉效果越接近灰度图像,因此携带了较少的色度信息,而当Cb、\mathit{\boldsymbol{Cr}}值越远离128时,图像的颜色会越丰富。基于上述特性,Paul等[21]利用Cb、\mathit{\boldsymbol{Cr}}值与128之间的L1范数来构造线性色度融合权重,即当色度分量越接近128时,则分配较少的权重,从而保证融合图像具有丰富的色彩信息。本文在此基础上,对该权重进行了简单的改进,即采用非线性高斯曲线进行加权。首先令{\mathit{\boldsymbol{Cb}}_k}和{\mathit{\boldsymbol{Cr}}_k}(k = 1, 2, ..., K)表示归一化后的源图像{\mathit{\boldsymbol{I}}_k}的色度分量,则融合后的色度分量{\mathit{\boldsymbol{Cb}}_{\text{f}}}和{\mathit{\boldsymbol{Cr}}_{\text{f}}}可根据下式得到。
\left\{ \begin{gathered} {\mathit{\boldsymbol{Cb}}_{\text{f}}} = \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{Cb}}_k}\mathit{\boldsymbol{W}}_{{\text{Cb}}}^k} /\sum\limits_{k = 1}^K {\mathit{\boldsymbol{W}}_{{\text{Cb}}}^k} {\text{ }} \hfill \\ {\mathit{\boldsymbol{Cr}}_{\text{f}}} = \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{Cr}}_k}\mathit{\boldsymbol{W}}_{{\text{Cr}}}^k} /\sum\limits_{k = 1}^K {\mathit{\boldsymbol{W}}_{{\text{Cr}}}^k} {\text{ }} \hfill \\ \end{gathered} \right.{\text{ }}, (20) 其中:
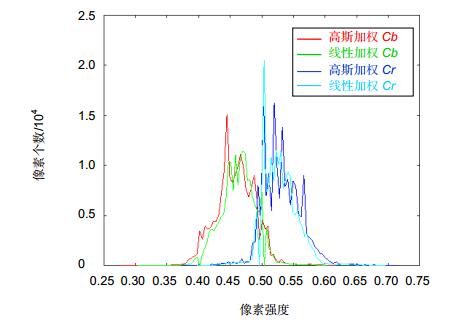
\mathit{\boldsymbol{W}}_{{\text{Cb}}}^k = 1 - \exp [ - \frac{{{{({\mathit{\boldsymbol{Cb}}_k} - \mu )}^2}}}{{2{\sigma ^2}}}], \mathit{\boldsymbol{W}}_{{\text{Cr}}}^k = 1 - \exp [ - \frac{{{{({\mathit{\boldsymbol{Cr}}_k} - \mu )}^2}}}{{2{\sigma ^2}}}], \mu 是衡量色度信息的标准值,在本文中设置为0.5,即当源图像中某个像素的色度值等于0.5时,对应的权重值为0。\sigma 控制高斯曲线的平坦程度,在本文中设置为0.5。图 9为线性加权与高斯加权方式得到的色度分量间的直方图对比结果,可以看出,用高斯加权方式得到的色度分量值在0.5附近的像素个数明显少于用线性加权方式得到的结果,而图 10(a)和10(b)分别为Paul等[21]和本文所提出色度融合方法得到的最终融合图像。可以看出,图 10(b)在窗外的树木、室内的窗帘和墙壁上具有更加丰富的颜色,而图 10(a)在红色框内的墙壁区域有明显的颜色退化现象,因此本文所提出的高斯色度加权方法能更好地处理多曝光源图像序列的色度信息。
2.6 融合图像生成
最后,根据上述求取的融合亮度和融合色度分量,通过颜色空间转换得到最终的融合图像{I_{\text{f}}}。
3. 实验结果与分析
为了评估所提出算法的性能,选取两组含有复杂背景的多曝光图像序列—Lamp序列[22]和Studio序列[23]进行实验,并将实验结果与Mertens等[9]、Kang等[10]、Liu等[11]、Ma等[12]、Ma等[13]这五种多曝光图像融合算法进行主观比较。同时,为了更加全面地衡量这六种算法之间的细节保留能力,选取7组多曝光图像序列并采用图像融合中最常用的客观指标QAB/F[24]进行度量,该指标反映了源图像序列与融合图像之间的边缘细节保留情况,如果QAB/F大,则融合图像的细节信息越丰富。
图 11展示了Lamp序列多曝光图像组,图 12是六种算法关于Lamp序列融合的对比结果。由于Lamp序列的多曝光图像之间的曝光值跨度较大,所以在最终的融合图像中极容易丢失某些细节信息,如台灯内部纹理和花瓶上的纹理。除此之外,在融合图像中还容易产生颜色失真和光晕等不好的视觉现象。因此除了对这六种算法的结果图进行全局比较外,再分别对台灯周围及花瓶纹理部分进行放大比较,如图 13所示。图 12中,Liu等[11]和Ma等[13]的方法均出现了颜色失真现象,Liu等的台灯后方墙壁部分的颜色出现退化及分布不均匀的现象,Ma等[13]的整体画面颜色过于饱和。而通过放大比较发现Mertens等和Ma等[12]的结果中台灯内部纹理结构均不清晰,且有严重的光晕现象;Liu等和Ma等[13]的结果中虽然能看清台灯内部纹理,但在花瓶上均出现颜色失真现象,Ma等[13]的台灯颜色过于饱和。而Kang等和本文算法无论在台灯内部结构还是花瓶纹理部分均能较好地保留细节信息,但本文算法在台灯灯泡部分比Kang等有更高的颜色饱和度,因此具有更好的视觉效果。
图 14和图 15分别为Studio序列多曝光图像组及六种算法之间的对比图。由于该多曝光图像序列由室内室外两个场景组成,而室外又由天空、马路以及纹理复杂的树木组成,因此对融合算法的精度要求很高。图 16和图 17为图 15中窗外场景和室内台灯的局部放大。由图 15可见Ma等[12]的方法在窗外出现了大块的伪影,造成了极其不好的视觉效果,其他算法总体上没有出现类似的伪影现象。而通过放大比较发现Mertens等和Ma等[12]的方法在室内台灯部分丢失了灯泡等细节信息,Kang等和Liu等的方法则在台灯内壁部分出现了大范围的颜色退化现象。另外,Ma等[12]和Ma等[13]的方法在窗外的树木和窗户边缘上出现了严重的光晕现象,Liu等的方法总体画面对比度欠佳。而本文所提出的算法在这些区域上均能保持较好的效果。
通过上述对六种算法的主观比较可知,所提出算法在处理含有复杂背景的图像序列时仍然具有出色的细节保留能力。另外,从客观角度,选取7组多曝光图像序列并对六种算法产生的融合图像进行QAB/F的测量,测量结果如表 1所示。通过比较表 1中的数据可知,在大多数图像序列中,所提出算法下的QAB/F指标均高于其它五种算法,且总体平均指标也略高于其余算法。因此,无论从主观评价还是客观评价来看,所提出算法对细节保留具有良好的鲁棒性。
表 1. 不同算法的QAB/F指标比较Table 1. Comparison of QAB/F in different algorithmsSequences Mertens[9] Kang[10] Liu[11] Ma[12] Ma[13] The proposed Room 0.6629 0.6653 0.6573 0.6263 0.6598 0.6721 House 0.6878 0.6962 0.6910 0.5894 0.6780 0.6997 Forth4 0.6462 0.6477 0.6418 0.6258 0.6331 0.6539 Garage 0.6860 0.6864 0.6837 0.6686 0.6785 0.6956 Cafe 0.6755 0.6842 0.6865 0.6721 0.6665 0.6866 Tower 0.7598 0.7699 0.7793 0.7707 0.7689 0.7695 SwissSunset 0.6331 0.6132 0.6028 0.5971 0.6077 0.6279 Average 0.6788 0.6804 0.6775 0.6500 0.6704 0.6865 4. 总结
现有的多曝光融合算法在处理含有复杂背景的图像序列时无法很好地保留细节信息,因此本文提出了一种结合张量分解和卷积稀疏表示的多曝光图像融合方法。同时,为了避免融合图像中出现大范围的颜色失真,本文采用亮度与色度分量分别融合的方式。首先利用张量分解后的核心张量来提取边缘细节特征;然后对特征图进行卷积稀疏表示,从而利用分解系数的L1范数来得到每个像素的活跃水平;最后用"赢者取全"策略生成权重图,继而得到融合图像的亮度信息。与复杂的亮度融合过程不同,融合后的色度分量则简单利用高斯曲线加权得到。研究结果表明,相比于其它五种先进的算法,所提出算法在处理复杂背景下的图像序列时仍然具有出色的细节保存能力,且不会出现大范围的颜色失真现象。在后续的研究中,将近一步考虑如何降低算法的复杂度以及使用更好的融合策略,从而提高融合图像的视觉效果。
-
表 1 不同算法的QAB/F指标比较
Table 1. Comparison of QAB/F in different algorithms
Sequences Mertens[9] Kang[10] Liu[11] Ma[12] Ma[13] The proposed Room 0.6629 0.6653 0.6573 0.6263 0.6598 0.6721 House 0.6878 0.6962 0.6910 0.5894 0.6780 0.6997 Forth4 0.6462 0.6477 0.6418 0.6258 0.6331 0.6539 Garage 0.6860 0.6864 0.6837 0.6686 0.6785 0.6956 Cafe 0.6755 0.6842 0.6865 0.6721 0.6665 0.6866 Tower 0.7598 0.7699 0.7793 0.7707 0.7689 0.7695 SwissSunset 0.6331 0.6132 0.6028 0.5971 0.6077 0.6279 Average 0.6788 0.6804 0.6775 0.6500 0.6704 0.6865 -
参考文献
[1] Artusi A, Richter T, Ebrahimi T, et al. High dynamic range imaging technology[J]. IEEE Signal Processing Magazine, 2017, 34(5): 165-172. doi: 10.1109/MSP.2017.2716957
[2] Chiang J C, Kao P H, Chen Y S, et al. High-dynamic-range image generation and coding for multi-exposure multi-view images[J]. Circuits, Systems, and Signal Processing, 2017, 36(7): 2786-2814. doi: 10.1007/s00034-016-0437-x
[3] 都琳, 孙华燕, 王帅, 等.针对动态目标的高动态范围图像融合算法研究[J].光学学报, 2017, 37(4): 101-109. 10.3788/aos201737.0410001
Du L, Sun H Y, Wang S, et al. High dynamic range image fusion algorithm for moving targets[J]. Acta Optica Sinica, 2017, 37(4): 101-109. 10.3788/aos201737.0410001
[4] Li S T, Kang X D, Fang L Y, et al. Pixel-level image fusion: a survey of the state of the art[J]. Information Fusion, 2017, 33: 100-112. doi: 10.1016/j.inffus.2016.05.004
[5] Zhao C H, Guo Y T, Wang Y L. A fast fusion scheme for infrared and visible light images in NSCT domain[J]. Infrared Physics & Technology, 2015, 72: 266-275. 10.1016/j.infrared.2015.07.026
[6] Chen C, Li Y Q, Liu W, et al. Image fusion with local spectral consistency and dynamic gradient sparsity[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 2014: 2760-2765.
[7] Sun J, Zhu H Y, Xu Z B, et al. Poisson image fusion based on Markov random field fusion model[J]. Information Fusion, 2013, 14(3): 241-254. doi: 10.1016/j.inffus.2012.07.003
[8] Liu Y, Liu S P, Wang Z F. A general framework for image fusion based on multi-scale transform and sparse representation[J]. Information Fusion, 2015, 24: 147-164. doi: 10.1016/j.inffus.2014.09.004
[9] Mertens T, Kautz J, van Reeth F. Exposure fusion: a simple and practical alternative to high dynamic range photography[J]. Computer Graphics Forum, 2009, 28(1): 161-171. doi: 10.1111/cgf.2009.28.issue-1
[10] Li S T, Kang X D, Hu J W. Image fusion with guided filtering[J]. IEEE Transactions on Image Processing, 2013, 22(7): 2864-2875. doi: 10.1109/TIP.2013.2244222
[11] Liu Y, Wang Z F. Dense SIFT for ghost-free multi-exposure fusion[J]. Journal of Visual Communication and Image Representation, 2015, 31: 208-224. doi: 10.1016/j.jvcir.2015.06.021
[12] Ma K D, Li H, Yong H W, et al. Robust multi-exposure image fusion: a structural patch decomposition approach[J]. IEEE Transactions on Image Processing, 2017, 26(5): 2519-2532. doi: 10.1109/TIP.2017.2671921
[13] Ma K D, Duanmu Z F, Yeganeh H, et al. Multi-exposure image fusion by optimizing a structural similarity index[J]. IEEE Transactions on Computational Imaging, 2018, 4(1): 60-72. doi: 10.1109/TCI.2017.2786138
[14] Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455-500. doi: 10.1137/07070111X
[15] Wang H Z, Ahuja N. A tensor approximation approach to dimensionality reduction[J]. International Journal of Computer Vision, 2008, 76(3): 217-229. 10.1007/s11263-007-0053-0
[16] Zeiler M D, Krishnan D, Taylor G W, et al. Deconvolutional networks[C]//Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 2010: 2528-2535.
[17] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. doi: 10.1137/S1064827596304010
[18] Wohlberg B. Efficient algorithms for convolutional sparse representations[J]. IEEE Transactions on Image Processing, 2016, 25(1): 301-315. doi: 10.1109/TIP.2015.2495260
[19] Liu J L, Garcia-Cardona C, Wohlberg B, et al. Online convolutional dictionary learning[C]//Proceedings of 2017 IEEE International Conference on Image Processing, Beijing, China, 2017.
[20] Liu Y, Chen X, Ward R K, et al. Image fusion with convolutional sparse representation[J]. IEEE Signal Processing Letters, 2016, 23(12): 1882-1886. doi: 10.1109/LSP.2016.2618776
[21] Paul S, Sevcenco I S, Agathoklis P. Multi-exposure and multi-focus image fusion in gradient domain[J]. Journal of Circuits, Systems, and Computers, 2016, 25(10): 1650123. doi: 10.1142/S0218126616501231
[22] Banterle F, Artusi A, Debattista K, et al. Advanced High Dynamic Range Imaging: Theory and Practice[M]. Natick, MA: A K Peters, 2011.
[23] Ma K D. Multi-Exposure Image Fusion by Optimizing A Structural Similarity Index[DB/OL]. https://ece.uwaterloo.ca/~k29ma/dataset/MEFOpt_Database, 2018.
[24] Xydeas C S, Petrovic V. Objective image fusion performance measure[J]. Electronics Letters, 2000, 36(4): 308-309. doi: 10.1049/el:20000267
施引文献
期刊类型引用(6)
1. 史艳琼,王昌文,卢荣胜,查昭,朱广. 基于低秩稀疏矩阵分解和离散余弦变换实现多聚焦图像融合的算法. 激光与光电子学进展. 2024(10): 416-423 .  百度学术
百度学术
2. 徐胜超,熊茂华. 基于子模式的人脸局部遮挡智能识别方法. 信息技术. 2023(03): 35-39 .  百度学术
百度学术
3. 蒙友波,廖艳梅,覃锋,王晓红. 遥感影像融合下自然资源地类特征提取仿真. 计算机仿真. 2023(09): 162-166 .  百度学术
百度学术
4. 王树泽,张志华,邓砚学. 基于机载高光谱遥感图像的城市绿地覆盖研究. 激光杂志. 2022(02): 77-81 .  百度学术
百度学术
5. 杨涛,闫杰. 乡村建筑群形态结构的演变过程三维仿真. 计算机仿真. 2022(07): 238-242 .  百度学术
百度学术
6. 王娟,柯聪,刘敏,熊炜,袁旭亮,丁畅. 神经网络框架下的红外与可见光图像融合算法综述. 激光杂志. 2020(07): 7-12 .  百度学术
百度学术
其他类型引用(9)
-
访问统计



 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: