1.   引言

近年来，由于光纤中的布里渊散射信号对温度和应变均敏感，基于布里渊散射的分布式光纤传感技术越来越受到重视，广泛应用在电力、石油、矿探、结构安全监测等领域^[1]。目前，基于布里渊散射的分布式传感系统主要有两大类系统架构^[2]：基于光时域反射技术的布里渊光时域反射仪(Brillouin optical time-domain reflectometer, BOTDR)和基于光时域分析技术的布里渊光时域分析仪(Brillouin optical time-domain analyzer, BOTDA)。其中，BOTDR系统由于采用了反射仪的结构，只需要在传感光纤的同一端发射和接收光信号，更易于在实际应用中使用，并且在光纤断裂的情况下具有更强的生存性，因此其应用领域更加广泛^[3]。

在BOTDR系统中，需要对光纤沿线的布里渊散射谱的中心频率，即布里渊频移进行测量，以反演出光纤沿线的温度或者应变的分布情况。因此，需要对光纤布里渊散射信号进行频谱分析，以获得布里渊散射谱峰值处所对应的频率，即布里渊频移。传统上，可以通过频率扫描^[4]的方式来获得这一信息，即将布里渊散射信号通过一个中心频率可调谐的窄带带通滤波器，测量滤波器输出的信号功率随滤波器中心频率的变化来获得布里渊散射谱，进而确定散射谱峰的频率。这种方案的优点在于结构简单，窄带接收也使得后续的信号处理更加容易。但是这种方案由于扫描的不连续性，间隔太大得到的频谱精细度不好，导致提取的中心频率信息误差大，而间隔太小的话又会增加信号处理的时间，从而降低系统的实时性。另外一种方案则是采用宽带接收的方案，即全频带的将光纤沿线各处散射回来的布里渊散射信号接收下来，然后通过时频分析的方法来分析光纤沿线各处的布里渊散射谱。这种方案对接收带宽和信号处理要求比较高，但是由于避免了逐点扫描，其测量速度比较快，具有很好的应用前景。

在宽带接收的方案中，不可避免地会遇到空间分辨率与测量精度之间相互制约的问题^[5]。当要求空间分辨率高时，则意味着只能用很短的数据长度来分析布里渊散射谱，而数据长度短则意味着频谱的分辨率低，导致测量精度变差。比如，时频分析领域常用的短时傅里叶变换方法就存在频谱泄露和栅栏效应的问题^[6]，频率估计结果方差性能较差，在短数据长度、低信噪比的情况下更加明显。

为了改善宽带接收方案的BOTDR系统中空间分辨率与测量精度之间相互制约的问题，并提高测量速度，本文研究了基于旋转不变技术的信号参数估计技术(estimation of signal parameters via rotational invariance technique, ESPRIT)的布里渊频移估计方法，能够在保证较高空间分辨率和测量性能的情况下，以较短的数据长度获得较好的频率估计性能，从而可以提高测量速度。

2.   基本原理

ESPRIT是一种现代谱估计算法，其含义就是利用旋转不变子空间估计信号参数。它具有计算量小、对噪声不敏感、无需对整个时域进行谱峰搜索等特点，在信号处理领域得到广泛使用^[7]。通常基于周期图或者短时傅里叶变换(short-time Fourier transform, STFT)的频谱分析方法，其频率分辨能力受到数据长度的制约，在数据长度较短时其频谱分辨能力变差。而理论上，ESPRIT算法则不受该问题的制约，能对短数据量的频谱进行高分辨率的分析。因此，ESPRIT算法非常适合BOTDR分布式光纤传感系统中布里渊散射谱中心频率在高空间分辨率情况下的快速估计。

用ESPRIT算法估计信号参数时，要求阵列的几何结构存在不变性。而这个不变性可以通过两种手段获得：一种是阵列本身存在两个或两个以上的相同子阵；二是通过某些变换获得两个或两个以上的相同子阵。而存在两个完全相同的子阵是ESPRIT算法最基本的假设。假设一个信号含有p个频率分量，且存在两个结构完全相同的子阵，子阵间距为Δ、阵元数为m。则对于同一信号而言，由观测数据序列构成的两个子阵的输出只有一个相位差ϕ_i，i∈[1, p]。下面假设第一个子阵的接收数据为X₁；第二个子阵的接收数据为X₂，N是均值为零、方差为σ²的高斯白噪声。根据阵列模型知识^[8]可得：

式中：子阵列(1)的范德蒙德矩阵A₁=A；子阵列(2)的范德蒙德矩阵A₂=Aϕ；S是一对角矩阵，且有$\boldsymbol{\phi} = {\rm{diag}}\left[{{{\rm{e}}^{{\rm{j}}{w_1}}}, {{\rm{e}}^{{\rm{j}}{w_2}}}, ..., {{\rm{e}}^{{\rm{j}}{w_p}}}} \right]$，其中ϕ为一酉矩阵，它将两个子阵列联系在一起；w_p为第p个信号的角频率。由以上推导可知，信号的频率信息包含在矩阵ϕ中。因此只要得到两个子阵间的旋转不变关系ϕ，就可以方便地得到关于信号的频率信息。若要得到两子阵列间的关系，需先将其模型进行合并，即：

在理想条件下，可对上式的协方差矩阵R进行特征分解，可得：

显然，上式中得到的特征值，有如下关系：${\lambda _1} \ge ... \ge {\lambda _N} \ge {\lambda _{N + 1}} = ... = {\lambda _{2m}}$。且U_s为大特征值对应的特征矢量张成的信号子空间，U_n为小特征值对应的特征矢量张成的噪声子空间。由阵列模型知识，存在一个唯一的非奇异矩阵T使下式成立：

由子阵列流型间的旋转不变性，进一步可推导出两个子阵的信号子空间的关系是

其说明了两个子阵的阵列接收数据的信号子空间的旋转不变性^[9-10]。若阵列流型A是满秩矩阵，则ψ的特征值组成的对角阵一定等于ϕ。而矩阵T的各列就是矩阵ψ的特征矢量，所以一旦得到上述的旋转不变关系矩阵ψ，就可以得到信号的频率信息。总而言之，ESPRIT算法的基本原理就是基于式(6)的旋转不变性。

在对布里渊散射信号进行分析时，设布里渊散射信号x(n)由一系列幅值按指数规律变化的正弦信号与白噪声的组合，在采样时刻n，其表达式如下：

式中：s_i(n)和ω_i∈(-π，π)分别是第i个正弦信号的归一化幅值和频率，ω(n)是加性高斯白噪声。则由观测数据序列x(0), x(1), …, x(k-1)可构造相应数据矩阵X：

式中：L>p，M>p，L+M-1=k。因此可以按照式(4)~式(6)构造协方差矩阵和特征分解从而计算出布里渊谱信号的中心频率。由于ESPRIT算法对在有噪声时性能会劣化，因此本文在得到布里渊谱信号的协方差矩阵前进行了噪声白化处理。具体而言，是将带有布里渊信号的接收数据的功率谱除以不带布里渊信号的噪声功率谱，将其结果经傅里叶逆变换后得到自相关函数，进而求得协方差矩阵后采用ESPRIT算法估计布里渊谱中心频率。

3.   实验结果与分析

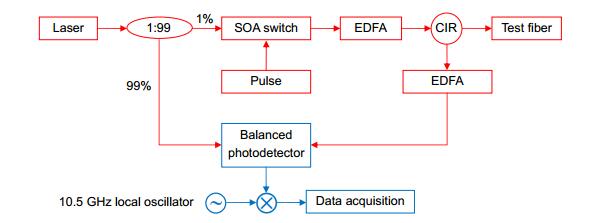
装置示意图如图 1所示。实验中激光器工作波长为1550.12 nm，线宽小于100 kHz，其输出经耦合器后分为两路。其中一路经过开关型半导体光放大器进行脉冲调制后变成脉冲光并经过光脉冲放大器放大再进入传感光纤；另一路作为参考光进入平衡探测器用于接收布里渊散射信号。第一路光在传感光纤中传输时，会产生后向自发布里渊散射光，经环形器和掺铒光纤放大器后再在平衡探测器中与参考光进行相干检测并转换为10.8 GHz附近的微波信号。在与10.5 GHz本振信号混频后，接收到的10.8 GHz布里渊散射信号被变频到500 MHz以内。数据的采集速率为1 Gsps，传感光纤长度为2 km，其中有一段约400 m长度光纤被置于水浴锅中加热。注入传感光纤的光脉冲宽度为250 ns。所采集到的数据中属于被加热段光纤的数据用于做频谱分析。

图 1.  BOTDR实验装置示意图。SOA：半导体光放大器；EDFA：掺铒光纤放大器；CIR：光环形器

Figure 1.  The schematic diagram of experiment device. SOA: semiconductor optical amplifier; EDFA: erbium-doped fiber amplifier; CIR: circulator

下载: 全尺寸图片 幻灯片

基于STFT算法和基于ESPRIT算法的布里渊频率估计进行对比分析。由于STFT算法的频谱分辨率与FFT(fast Fourier transformation)的分析点数有关，因此我们分别考虑了分析点数等于原始数据长度的算法和将分析点数通过对原始数据补零到1024点后进行FFT分析的算法，分别简称为FFT和补零FFT算法。另外，对于基于STFT的两种算法，在经过FFT分析后，还对频谱进行了洛伦兹拟合以进一步提高算法的性能。

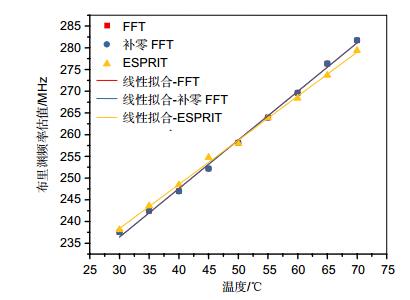
首先比较了在数据长度足够时各算法的性能。图 2显示当数据长度为1024个采样点时，FFT、补零FFT和ESPRIT算法在不同温度下所估计出的布里渊频率值。算法使用1024个连续的采样数据进行分析，且对于每个温度下的频率估计。图 2所示的结果都是对2500组脉冲的分析结果的叠加平均。如图 2所示，在数据长度为1024时，FFT、补零FFT和ESPRIT算法所估计出的布里渊频率和温度都具有良好的线性度。三种算法得到的斜率非常接近，其中FFT和补零FFT算法为1.1178 MHz/℃，ESPRIT算法为1.0148 MHz/℃，表明ESPRIT算法可以有效地估计布里渊频率。

图 2.  当数据长度为1024采样点时，不同温度下不同算法估计所得的布里渊频率

Figure 2.  Brillouin frequency estimated by different algorithms at different temperatures using 1024 samples

下载: 全尺寸图片 幻灯片

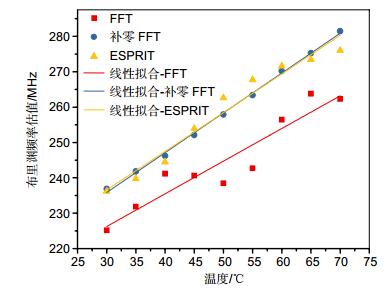
当需要提高分布式传感的空间分辨率时，随着空间上分析长度的缩短，用来进行频谱分析的数据长度也会缩短，进而导致算法的性能下降。如图 3所示是数据长度为32个采样数据时，FFT、补零FFT和ESPRIT三种算法在不同温度下所得到的布里渊频率估计值。可以看到，补零FFT和ESPRIT算法所得到的结果和1024点数据长度时的结果很接近，但FFT算法所得结果则与1024点数据长度时的结果有较大偏差，算法的准确性变差。并且，FFT算法所得结果的斜率为0.9235 MHz/℃，相比数据长度为1024时的斜率减小了17.4%。与之对比，补零FFT和ESPRIT算法所得结果的斜率分别为1.1256 MHz/℃和1.0935 MHz/℃，相比数据长度为1024时的斜率分别增加了0.7%和5%，表现出更好的稳定性。

图 3.  当数据长度为32采样点时，不同温度下不同算法估计所得的布里渊频率

Figure 3.  Brillouin frequency estimated by different algorithms at different temperatures using 32 samples

下载: 全尺寸图片 幻灯片

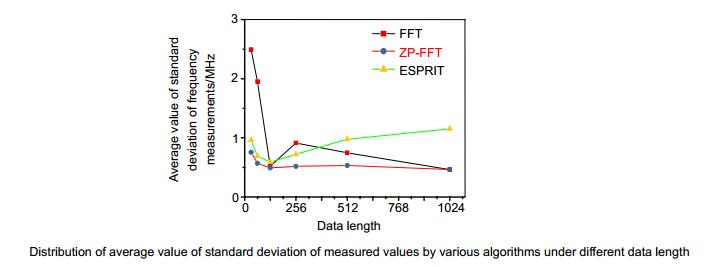
为了衡量算法的稳定性，对各算法所得测量结果的标准差进行了分析。同时，标准差也是衡量算法的测量精度的重要指标。图 4显示了不同数据长度下，FFT、补零FFT和ESPRIT算法对同一批采样数据的布里渊频率进行估计所得结果的标准差的平均值。为了计算标准差，将2500个脉冲的采样数据均分成10组，每组250个脉冲。针对每一个待测温度，由每组的采样数据估计出一个布里渊频率，再由10组采样数据所得的10个布里渊频率估计值计算出该温度下布里渊频率估计值的标准差，进而将几个待测温度下的标准差求平均值，让其代表该数据长度下的标准差。从图 4可以看出，当数据长度大于128时，补零FFT算法的标准差最小，约为0.5 MHz。FFT和ESPRIT算法的标准差也不太大，分别为约0.66 MHz和约0.86 MHz。当数据长度为128甚至更小时，ESPRIT算法的标准差接近于补零FFT算法，虽然二者均会有小幅增加，但是即使在数据长度为32时，标准差也不超过1 MHz。而FFT算法的标准差随着数据长度的减小急剧增大，在数据长度为32时增大到2.5 MHz。

图 4.  不同数据长度下各算法多次测量时测量值的标准差平均值

Figure 4.  Average value of standard deviation of measured values by various algorithms under different data length

下载: 全尺寸图片 幻灯片

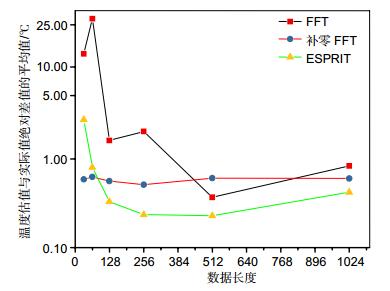
图 5通过计算不同数据长度下三种算法所得的布里渊频率估计结果换算所得的温度测量值与实际温度的绝对差值的均值来比较各算法对布里渊频率估计的准确性。由图 5可以看出，FFT和ESPRIT算法测量温度与实际温度的差值总体随着数据长度的减小而增大，补零FFT算法始终保持在0.58 ℃左右。这是因为FFT算法随着数据长度减小，频率分辨率相应变大，随之误差增大；补零FFT算法由于数据长度始终保持1024，所以频率分辨率不变，误差也比较稳定；而ESPRIT算法随着数据长度减小，接收数据的协方差矩阵估计出的参数不可靠，造成误差增大。此外，由图还可以看出当数据长度大于或等于128时，ESPRIT算法测量温度与实际温度差值的平均值比FFT和补零FFT算法都要小。其中ESPRIT算法为0.31 ℃左右；补零FFT算法为0.57 ℃左右；FFT算法为1.21 ℃左右，比ESPRIT大了约0.9 ℃。但是在数据长度小于128时，ESPRIT算法测量温度与实际温度的差值虽然稍高于补零FFT算法，但显著优于FFT算法。

图 5.  不同数据长度下各算法测量温度与实际温度绝对差值的平均值

Figure 5.  Distribution of the mean value of the absolute difference between measured temperatures and actual temperatures for different data lengths

下载: 全尺寸图片 幻灯片

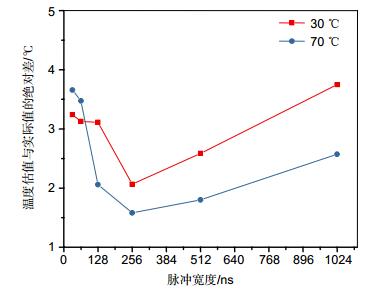
虽然采用ESPRIT算法可以利用较小的数据长度实现较高的测量精度。但由于BOTDR系统中空间分辨率还受脉冲宽度的制约，例如在1 Gsps采样率下，当脉冲宽度为250 ns时，即使数据长度小于250个点也并不会提高系统的空间分辨率。对于在保证较高分辨率的情况下，脉冲宽度和数据长度如何较好选取这一问题，我们分别在30 ℃和70 ℃两个温度时计算了不同脉冲宽度下ESPRIT算法测量温度与实际温度的绝对差值来进一步分析，如图 6所示。图中温度差值的绝对值为不同脉冲宽度下，数据长度取相应脉冲宽度值时计算得到，即ESPRIT算法在理论上能达到最高空间分辨率的情况。从图中可以看出ESPRIT算法在各个脉冲宽度上均有效，意味着最终的空间分辨率仍然是决定于脉冲宽度，而非算法所使用的数据长度。空间分辨率随着脉冲宽度的增加而逐渐降低，但是当脉冲宽度接近或者小于声子寿命(约为10 ns，对应单模光纤空间长度1 m)时，由于后向布里渊散射谱急剧展宽，使得无法准确获得叠加后的散射谱中心频率，造成测量精度的降低。在本次实验中，当脉冲宽度取256 ns，数据长度取256时，ESPRIT算法的测量精度达到了最优。更低的脉冲宽度和数据长度提高了空间分辨率，但是也带来了测量精度的牺牲。

图 6.  不同脉冲宽度下ESPRIT算法测量温度与实际温度的绝对差值

Figure 6.  The absolute difference between measured temperatures and actual temperatures by ESPRIT algorithm under different pulse width

下载: 全尺寸图片 幻灯片

总体而言，补零FFT算法表现出了最优的性能，ESPRIT算法次之但优于FFT算法。但是，为了保证频谱的分析精度，补零FFT算法需要将短数据长度补零到很长的分析长度，其运算量随着频谱分析精度的提高而显著增加，并不随着数据长度的减小而降低运算量。在分布式传感要求的空间分辨率较高时，补零FFT算法在数据存储空间和运算速度方面，都有较大的挑战。补零FFT因为拟合和寻峰操作，需要存储线路上各处的傅里叶变换后的谱。当补零FFT的点数比较大时，需要很大的存储空间，内存与计算单元之间的数据吞吐是个很大的瓶颈，严重制约运算速度。以1024点补零FFT算法和128点ESPRIT算法比较，前者需要的存储空间是后者的8倍，因此前者的运算速度受到内存读写的影响会更严重。而ESPRIT算法在数据长度减小时性能劣化较小，但运算量则显著下降，数据吞吐量也没有显著增加，因此在高空间分辨率的快速分布式传感方面具有一定的优势。

4.   结论

采用ESPRIT算法对BOTDR系统中布里渊散射谱中心频率进行估计，具有与补零FFT算法配合上洛伦兹频谱拟合所得结果相近的性能。在较短数据长度下，ESPRIT算法比FFT算法拥有更好的多次测量稳定性和单次测量准确性，能够使空间分辨率和测量性能达到一个良好的平衡。并且ESPRIT算法本身具有计算量小、对噪声不敏感、无需对整个频域进行谱峰搜索等特点，因此非常适合在保证较高空间分辨率和测量性能的情况下，快速地估计BOTDR系统中的布里渊散射谱中心频率。