E-mail Alert
RSS
Overlapping group sparsity on hyper-Laplacian prior of sparse angle CT reconstruction
-
摘要
对于稀疏角度下的投影数据，计算机断层扫描在图像重建中容易出现伪影和噪声较多的问题，难以满足工业及医学诊断要求。本文提出一种基于重叠组稀疏和超拉普拉斯先验的稀疏角度CT迭代图像重建算法。其中重叠组稀疏反映图像梯度稀疏性，从图像梯度的角度考虑相邻元素之间互相重叠交叉的关系。而超拉普拉斯先验能够精确地近似图像梯度的重尾分布，能够使得重建图像整体的质量提升。本文提出的算法模型采用交替方向乘子法，主分量最小化法和梯度下降法求解目标函数。实验结果表明，在稀疏角度CT重建的条件下，本文提出的算法在保留结构细节、抑制图像重建过程中产生的噪声和阶梯伪影方面有着一定的改善。
Abstract
For the sparse angle projection data, the problem of artifact and noise is easy to appear in the image reconstruction of computed tomography, which is difficult to meet the requirements of industrial and medical diagnosis. In this paper, a sparse angle CT iterative reconstruction algorithm based on overlapping group sparsity and hyper-Laplacian prior is proposed. The overlapping group sparsity reflects the sparsity of image gradient, and the overlapping cross relation between the adjacent elements is considered from the perspective of the image gradient. The hyper-Laplacian prior can accurately approximate the heavy-tailed distribution of the image gradient and improve the overall quality of the reconstructed image. The algorithm model proposed in this paper uses alternating direction multiplier method, principal component minimization method and gradient descent method to solve the objective function. The experimental results show that under the condition of the sparse angle CT reconstruction, the proposed algorithm has certain improvement in preserving structural details and suppressing noise and staircase artifacts generated in the process of image reconstruction.
-
Key words:
- CT reconstruction /
- sparse angle /
- image gradient /
- overlapping group sparsity /
- hyper-Laplacian prior
-
Overview
Overview: X-ray computed tomography (CT) is an imaging technique to obtain the across section information of an object through X-ray projection measurement at different angles, which has been widely used in industry, clinical diagnosis and other fields. However, additional X-ray radiation during clinical examination can lead to cancer and other genetic changes. In order to reduce the dose of X-ray radiation, sparse angle projection is used to add the scanning interval and reduce the number of projection times, and a small amount of projection data is used to achieve image reconstruction. However, this method will reduce the quality of the reconstructed image, there will be more artifacts and noise, and it is difficult to meet the requirements of industrial and medical diagnosis. In order to improve the quality of reconstructed images under sparse sampling, a sparse angle CT reconstruction algorithm based on overlapping group sparsity and hyper-Laplacian prior is proposed in this paper. The sparse regular term of the overlapping group improves the sparsity of the image gradient. The structure information of the image gradient is used as the measurement standard of the image gradient sparsity, which fully considers the gradient information of the pixel neighborhood, and regroups the gradient information by two norms to increase the difference between the smooth region and the image edge region. Since the gradient of the image basically follows the heavy-tailed distribution, the hyper-Laplacian prior can accurately approximate the heavy tail distribute-on of the image gradient, this regular term can suppress the noise generated in the reconstruction process. Combining the advantages of the two regular terms, the algorithm can effectively overcome the staircase artifacts while recovering the edge of the image, and remove the noise generated in the reconstruction. In this paper, alternate direction multiplier method, principal component minimization method and gradient descent method are used to solve the objective function. The experimental data of the simulated mouse model and the clinical mouse model were used in this study. The peak signal-to-noise ratio (PSNR), normalized root-mean-square error (NRMSE) and structural similarity index (SSIM) were used as indicators to evaluate different algorithms, and regions of interest were added to compare the reconstructed images, so that the differences of different algorithms could be more clearly seen from the structural details of the mouse model. The experimental results show that the proposed algorithm has some improvements in preserving the details of image structure and suppressing noise and staircase artifacts in the process of image reconstruction.
-
1. 引 言
X射线计算机断层扫描(computed tomography, CT)成像技术可以获取人体和物体的内部结构信息，已广泛应用于工业无损检测、医学临床诊断等领域[1]。然而，在临床检查时额外的X射线辐射可能导致癌症和其他遗传病变[2]。因此，降低辐射剂量和重建高质量图像是目前的研究重点。降低X射线辐射量的方法主要分两方面：第一种方法是减少每个投影中的X射线曝光，第二种方法是减少投影采样数，即稀疏投影[3]。第一种方法会产生含有噪声的投影，重建图像含有大量的噪声和伪影[4]。第二种方法是应用稀疏角度CT，但由于投影数据的采样不足，重建图像会产生严重的伪影[5]。
一些传统的CT图像重建算法比如滤波反投影(filtered back projection, FBP)算法和联合代数重建(simultaneous algebraic reconstruction technique, SART)算法，这两个基础算法无法对不完整的投影数据重建出高质量的图像。压缩感知(Compressed sensing, CS)理论的出现使得图像处理中的不适定问题可以有效地解决[6]。基于CS的图像重建算法主要利用图像的先验知识，特别是图像的稀疏性，如全变分[7]、字典学习[8]、小波变换等[9]。近年来，全变分(total variational, TV)算法被广泛应用于不同场景下的CT重建，该算法可以很好地平滑图像以达到去噪的目的[10]。Sidky等将TV最小化引入到不完全投影数据重建中，提出了一种基于投影到凸集(projections onto convex sets, POCS)的高效迭代重建算法TV-POCS[11]。虽然TV正则项能够很好地恢复图像的边缘信息，但是过渡的平滑图像会导致图像产生阶梯伪影。为了克服这一现象，Zhang等将非零像素稀疏性和图像连续性假设两个正则项来代替TV正则项，提出了一种基于大规模线性规划的稀疏角度层析重建算法[12]。连祥媛等提出一种多通道联合的广义全变分 (Total Generalized Variational, TGV)的能谱CT迭代重建算法，利用通道之间的相关性来消除重建过程中产生的噪声和阶梯伪影[13]。Peng等将组稀疏(group sparse representation, GSR)正则化引入稀疏角度CT重建，利用图像中相似补丁构成的图像组来表示GSR的基本单元，并且成功将其应用于稀疏角度CT重建中[14]。Jon等将重叠组稀疏(overlapping group sparsity, OGS)和超拉普拉斯先验(hyper-Laplacian, HL)相结合，提出了一种基于重叠组稀疏超拉普拉斯先验(overlapping group sparsity on hyper-Laplacian, OGS-HL)的图像去噪算法[15]。
本文将OGS正则项和HL正则项应用于稀疏角度CT图像重建。相比于传统的TV正则项，OGS正则项改进图像梯度的稀疏性，由于重叠组采用图像梯度的结构信息作为图像梯度稀疏性的度量标准，因此该算法能够在恢复图像边缘的同时消除阶梯伪影，基于HL先验可以很好地近似图像梯度的重尾分布，对于重建图像细节的保留有着更好的效果。
2. 理论推导
2.1 基于TV的稀疏角度CT重建算法
稀疏角度CT图像重建与传统CT图像重建的过程基本相同，设稀疏角度CT重建中需要重建的图像为f，从探测器上获得的投影数据为p，数据采集的投影矩阵用A表示，稀疏角度CT重建问题可表示为
min12‖Af−p‖22. (1) 在稀疏角度CT重建的情况下，由于投影采样不足会使重建图像产生噪声和伪影。为了重建高质量图像，使用CS理论将图像进行稀疏变换，例如对重建图像进行离散梯度变换(discrete gradient transform, DGT)，则任意图像f=(∇fi,j)n×n的DGT定义为
(∇f)i,j=√((∇xf)i,j)2+((∇yf)i,j)2, (2) 则对于任意图像f，其TV表达式为
TV(f)=∑i,j√((∇xf)i,j)2+((∇yf)i,j)2, (3) 其中∇x，∇y分别表示水平方向和竖直方向上的梯度算子，其表达式分别为
(∇xf)i,j={fi+1,j−fi,jifi<nf1,j−fn,jifi=n, (4) (∇yf)i,j={fi,j+1−fi,jifj<nfi,1−fi,nifj=n. (5) 故基于TV正则项的稀疏角度CT重建模型为
minfμ2‖Af−p‖22+λφTV(f), (6) 其中：第一项为数据保真项，A为投影矩阵，p为投影数据，μ为保真项系数。第二项为TV正则项，λ为正则项系数。
2.2 基于OGS-TV的稀疏角度CT重建算法
TV正则项已被广泛应用，其虽然能够保留图像的锐利边缘，但是过渡的平滑图像会导致图像产生阶梯伪影。为了进一步提升图像的质量，消除重建中产生的阶梯伪影，Liu等将一维信号的OGS推广到二维图像中并成功应用于图像去噪[16]。
为了描述图像梯度的结构稀疏性，首先定义一个二维图像的像素组˜d(i,j),K，形式如
˜d(i,j),K=[di−m1,j−m1di−m1,j−m1+1⋯di−m1,j+m2di−m1+1,j−m1di−m1+1,j−m1+1⋯di−m1+1,j+m2⋮⋮⋱⋮di+m2,j−m1di+m2,j−m1+1⋯di+m2,j+m2]∈RK×K, (7) 其中：m1=⌊(K−1)/(K−1)22⌋，m2=⌊K/K22⌋，⌊⋅⌋表示的是取整函数，保证图像中每个重叠组的大小都是K×K，则二维图像的OGS正则项可表示为
ϕOT(d)=n∑i,j=1‖d(i,j),K‖2, (8) 其中：d(i,j),K是矩阵˜d(i,j),K中所有元素组成的列向量，即：d(i,j),K=˜d(i,j),K(:)。根据式(8)可知当K = 1时，该正则项就转变为传统的TV正则项，则OGS-TV正则项可定义为
φOT(f)=ϕOT(∇xf)+ϕOT(∇yf). (9) 由于OGS正则项考虑了每个像素点梯度的K×K方形领域内的信息，是一个非局部的稀疏先验，因此OGS-TV正则项不仅拥有和TV正则项一样的图像边缘保留能力，还能克服TV重建中图像边缘产生的阶梯伪影。故基于OGS-TV的稀疏角度CT重建算法为
minfμ2‖Af−p‖22+λφOT(f), (10) 其中：第一项为数据保真项，第二项为OGS-TV正则项，λ为正则项系数。
2.3 基于OGS-HL的稀疏角度CT重建算法
OGS-TV虽然可以克服图像的阶梯伪影，但它难以恢复图像中较为复杂的纹理和细节。为进一步扩展OGS-TV，Kong等强调图像的梯度服从重尾分布[17]，并且超拉普拉斯算子先验将会使得重尾分布获得更好的近似，提出的HL先验的模型为
p(f)∝n∏i,j=1e−‖(∇f)i,j‖qq, (11) 其中：‖ ⋅ ‖q表示拟范数lq，0<q<1。q为超拉普拉斯参数，通常参数q的范围为0.5⩽。根据式(11)， \left\| {{{(\nabla f)}_{i,j}}} \right\|_q^q = {\left| {{{({\nabla _x}f)}_{i,j}}} \right|^q} + {\left| {{{({\nabla _y}f)}_{i,j}}} \right|^q} ，将HL先验代入OGS正则项得
{\phi _{\rm{OH}}}({\boldsymbol{d}}) = \sum\limits_{i,j = 1}^n {{{\left\| {{{\left| {{{\boldsymbol{d}}_{(i,j),K}}} \right|}^q}} \right\|}_2}} \;. (12) 根据式(12)，当超拉普拉斯参数 q = 1 时，该正则项就转变为OGS-TV正则项。OGS-HL的正则项可表示为
{\varphi _{{\rm{OH}}}}({\boldsymbol{f}}) = {\phi _{{\rm{OH}}}}({\nabla _x}{\boldsymbol{f}}) + {\phi _{{\rm{OH}}}}({\nabla _y}{\boldsymbol{f}}) \;, (13) 故基于OGS-HL的稀疏角度CT重建算法，算法模型为
\mathop {\min }\limits_{\boldsymbol{f}} \frac{\mu }{2}\left\| {{\boldsymbol{Af}} -{\boldsymbol{ p}}} \right\|_2^2 + \lambda {\varphi _{{\rm{OH}}}}({\boldsymbol{f}}) \;, (14) 其中：第一项为数据保真项，第二项为OGS-HL正则项， \lambda 为正则项系数。
3. 模型求解
OGS-HL算法的模型是一个综合算法模型，TV，OGS-TV，OGS-HL算法可以通过对模型设置不同的参数值来分别表示，如表1所示。
表 1. 不同算法的参数设置Table 1. Parameter settings for different algorithms算法 K q TV 1 1 OGS-TV 2n+1(n=1, 2, …, n) 1 OGS-HL 2n+1(n=1, 2, …, n) {\text{0}}{\text{.5}} \leqslant q < {\text{1}} | Show Table
DownLoad:
CSV
由于算法模型包含的矩阵数据量大并且复杂，因此本文采用交替方向乘子 (alternating direction method of multipliers, ADMM)算法[18]，将模型转化为多个子问题来求解，式(14)引入变量u，将模型转化为
\mathop {\min }\limits_{{\boldsymbol{f,u}}} \frac{\mu }{2}\left\| {{\boldsymbol{Af}} -{\boldsymbol{ p}}} \right\|_2^2 + \lambda {\varphi _{\rm{OH}}}({\boldsymbol{u}}){\text{ s}}{\text{.t}}{\text{.}}{\boldsymbol{f}}{\text{ = }}{\boldsymbol{u}} \;. (15) 通过引入惩罚项 \dfrac{1}{2}\left\| {{\boldsymbol{f}} -{\boldsymbol{ }}{\boldsymbol{u}}} \right\|_2^2 ，得到一个无约束的优化函数：
\mathop {\min }\limits_{{\boldsymbol{f,u}}} \frac{\mu }{2}\left\| {{\boldsymbol{Af}} - {\boldsymbol{p}}} \right\|_2^2 + \lambda {\varphi _{\rm{OH}}}({\boldsymbol{u}}) + \frac{1}{2}\left\| {{\boldsymbol{f}} - {\boldsymbol{u}}} \right\|_2^2 \;. (16) 上述优化函数可分解为2个子问题来分别更新f和u：
\mathop {\min }\limits_{\boldsymbol{f}} \frac{\mu }{2}\left\| {{\boldsymbol{Af}} - {\boldsymbol{p}}} \right\|_2^2 + \frac{1}{2}\left\| {{\boldsymbol{f }}- {{\boldsymbol{u}}^{\left( k \right)}}} \right\|_2^2 \;, (17) \mathop {\min }\limits_{\boldsymbol{u}} \lambda {\varphi _{{\rm{OH}}}}({\boldsymbol{u}}) + \frac{1}{2}\left\| {{{\boldsymbol{f}}^{\left( {k + 1} \right)}} - {\boldsymbol{u}}} \right\|_2^2 \;, (18) 其中：式(17)采用梯度下降法来更新f：
{{\boldsymbol{f}}^{(k + 1)}} = {{\boldsymbol{f}}^{(k)}} - \left[ {\mu {{\boldsymbol{A}}^{\rm{T}}}\left( {{\boldsymbol{A}}{{\boldsymbol{f}}^{(k)}} - {\boldsymbol{p}}} \right) + \left( {{{\boldsymbol{f}}^{\left( k \right)}} - {{\boldsymbol{u}}^{\left( k \right)}}} \right)} \right] \;. (19) 式(18)进一步采用ADMM算法来求解，引入辅助变量 {{\boldsymbol{x}}_1} 和 {{\boldsymbol{x}}_2} ，引入拉格朗日乘子 {{\boldsymbol{w}}_1} ， {{\boldsymbol{w}}_2} 和惩罚参数 \delta ，转化为以下包含多个变量的增广拉格朗日函数来更新：
\begin{split} L\left( {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},{\boldsymbol{u}},{\boldsymbol{w}}} \right) =& \frac{1}{2}\left\| {{{\boldsymbol{f}}^{\left( {k + 1} \right)}} - {\boldsymbol{u}}} \right\|_2^2 + \lambda \left\{ {\phi ({{\boldsymbol{x}}_1}) + \phi ({{\boldsymbol{x}}_2})} \right\} \\& + {\boldsymbol{w}}_1^{\rm{T}}({\nabla _x}{\boldsymbol{u}} - {{\boldsymbol{x}}_1}) + {\boldsymbol{w}}_2^{\rm{T}}({\nabla _y}{\boldsymbol{u}} - {{\boldsymbol{x}}_2}) \\& + \frac{\delta }{2}\left\{ {\left\| {{\nabla _x}{\boldsymbol{u}} - {{\boldsymbol{x}}_1}} \right\|_2^2 + \left\| {{\nabla _y}{\boldsymbol{u}} - {{\boldsymbol{x}}_2}} \right\|_2^2} \right\} \;, \\ & {\rm{ s.t.}} {\text{ }}{{\boldsymbol{x}}_1} = {\nabla _x}{\boldsymbol{u}},{{\boldsymbol{x}}_2} = {\nabla _y}{\boldsymbol{u}} \;. \end{split} (20) Step1：更新 {{\boldsymbol{x}}_1} 和 {{\boldsymbol{x}}_2} ，根据式(20)， {{\boldsymbol{x}}_1} 和 {{\boldsymbol{x}}_2} 的子问题可以由式(21)和式(22)来更新：
{\boldsymbol{x}}_1^{\left( {k + 1} \right)} = \mathop {\arg \min }\limits_{{{\boldsymbol{x}}_1}} \lambda {\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_1}} \right) + \frac{\delta }{2}\left\| {{\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} - {{\boldsymbol{x}}_1} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right\|_2^2 \;, (21) {\boldsymbol{x}}_2^{\left( {k + 1} \right)} = \mathop {\arg \min }\limits_{{{\boldsymbol{x}}_2}} \lambda {\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_2}} \right) + \frac{\delta }{2}\left\| {{\nabla _y}{{\boldsymbol{u}}^{\left( k \right)}} - {{\boldsymbol{x}}_2} + \frac{{{\boldsymbol{w}}_2^{\left( k \right)}}}{\delta }} \right\|_2^2 \;. (22) 该子问题的结构比较复杂，故采用主分量最小化法(majorization minimization, MM)来求解上述最小化问题[19]。由于2个子问题是相同的结构，下面只阐述式(21)的更新步骤。
为了方便后续计算，式(21)可简化为
\ {\boldsymbol{x}}_1^{\left( {k + 1} \right)} = \mathop {\arg \min }\limits_{{{\boldsymbol{x}}_1}} \left\{ {R\left( {{{\boldsymbol{x}}_1}} \right) : = \frac{\delta }{2} \left\| {{{\boldsymbol{x}}_1} - \left( { {\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right)} \right\|_2^2 + \lambda {\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_1}} \right)} \right\} . (23) 首先，需找到{\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_1}} \right)的优化目标函数，根据均值不等式，可以得到：
\begin{split} & \frac{1}{2\left\|\left|\boldsymbol{a}_{(i, j), K}\right|^q\right\|_2}\left(q\left\|\left|\boldsymbol{a}_{(i, j), K}\right|^{q-1} \odot\left|\boldsymbol{x}_{1(i, j), K}\right|\right\|_2^2\right. \\& \left.+(2-q)\left\| |\boldsymbol{a}_{(i, j), K}|^q\right\|_2^2\right)\geqslant \left\| |\boldsymbol{x}_{1(i, j), K} |^q\right\|_2^2 \text {, } \end{split} (24) 其中： {{\boldsymbol{a}}_{\left( {i,j} \right),K}} 是{\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_1}} \right)中的任意一项，对于任意的{{\boldsymbol{a}}}_{\left(i,j\right),K}，{{\boldsymbol{x}}}_{1(i,j),K}\ne 0，并且{{\boldsymbol{a}}_{\left( {i,j} \right),K}} = {{\boldsymbol{x}}_{1(i,j),K}}时，对每一个稀疏组，代入式(24)可以得到{\phi _{{\rm{OH}}}}\left( {{{\boldsymbol{x}}_1}} \right)的优化目标函数：
\begin{split} \psi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{a}}} \right) =& \frac{1}{2}\sum\limits_{i,j = 1}^n \frac{1}{{{{\left\| {{{ | {{{\boldsymbol{a}}_{\left( {i,j} \right),K}}} |}^q}} \right\|}_2}}}\left( {q\left\| {{{\left| {{{\boldsymbol{a}}_{\left( {i,j} \right),K}}} \right|}^{q - 1}} \odot \left| {{{\boldsymbol{x}}_{1(i,j),K}}} \right|} \right\|_2^2 } \right. \\ &\left. {+ \left( {2 - q} \right)\left\| {{{ | {{{\boldsymbol{a}}_{\left( {i,j} \right),K}}} |}^q}} \right\|_2^2} \right) \;. \\[-10pt] \end{split} (25) 根据式 (24)能够证明 \psi \left({{\boldsymbol{x}}}_{1},{\boldsymbol{a}}\right)\geqslant \phi \left({{\boldsymbol{x}}}_{1}\right) ，并且 \psi \left( {{\boldsymbol{a}},{\boldsymbol{a}}} \right) = \phi \left( {\boldsymbol{a}} \right) 。通过简单的计算， \psi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{a}}} \right) 可以写为
\psi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{a}}} \right) = \frac{q}{2}\left\| {{\boldsymbol{\varLambda}} \left( {\boldsymbol{a}} \right)\left( {{{\left| {\boldsymbol{a}} \right|}^{q - 1}} \odot \left| {{{\boldsymbol{x}}_1}} \right|} \right)} \right\|_2^2 + {\rm{C}} \;, (26) 其中：C是一个常数， {\boldsymbol{\varLambda }} \left({\boldsymbol{ a}} \right) 是对角矩阵，其对角的元素为
{\left[ {{\boldsymbol{\varLambda}} \left( {\boldsymbol{a }}\right)} \right]_{l,l}} = \sqrt {\sum\limits_{i,j = - {m_1}}^{m_2} {{{\left( {\sum\limits_{{k_1},{k_2} = - {m_1}}^{m_2} {{{\left| {{{\boldsymbol{a}}_{r - i + {k_1},t - j + {k_2}}}} \right|}^{2q}}} } \right)}^{ - {1}/{2}}}} } \;, (27) 其中： r,t = 1,2,...,n,{\text{ }}l = 1,2,...,{n^2} ， {\boldsymbol{\varLambda}} \left( {\boldsymbol{a}} \right) 是通过二维卷积运算来求解，则式(23)中 R\left( {{{\boldsymbol{x}}_1}} \right) 的优化目标函数如：
\begin{split} \xi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{a}}} \right) =& \frac{\delta }{2}\left\| {{{\boldsymbol{x}}_1} - \left( {{\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right)} \right\|_2^2 + \lambda \psi \left( {{{\boldsymbol{x}}_1},a} \right) \\ =& \frac{\delta }{2}\left\| {{{\boldsymbol{x}}_1} - \left( {{\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right)} \right\|_2^2 \\ & + \frac{{\lambda q}}{2}\left\| {{\boldsymbol{\varLambda}} \left({\boldsymbol{ a}} \right)\left( {{{\left| {\boldsymbol{a}} \right|}^{q - 1}} \odot \left| {{{\boldsymbol{x}}_1}} \right|} \right)} \right\|_2^2 + \lambda {\rm{C}} \;. \end{split} (28) 式(28)可以得出 \xi \left({{\boldsymbol{x}}}_{1},{\boldsymbol{a}}\right)\geqslant R\left({{\boldsymbol{x}}}_{1}\right) ， \xi \left( {{\boldsymbol{a}},{\boldsymbol{a}}} \right) = R\left( \boldsymbol{a} \right) 。故 \xi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{a}}} \right) 也满足MM算法的前提条件，为了极小化 R\left( {{{\boldsymbol{x}}_1}} \right) ，使用MM算法迭代，初始化 {\boldsymbol{x}}_1^{\left( 0 \right)} ，反复极小化替代函数 \xi \left( {{{\boldsymbol{x}}_1},{\boldsymbol{x}}_1^{\left( k \right)}} \right) ，得到
\begin{split} {\boldsymbol{x}}_1^{\left( {k + 1} \right)} = & \mathop {\arg \min }\limits_{{{\boldsymbol{x}}_1}} \xi \left( {{{\boldsymbol{x}}_1},\boldsymbol{x}_1^{\left( k \right)}} \right) \\ =& \mathop {\arg \min }\limits_{{{\boldsymbol{x}}_1}} \frac{\delta }{2}\left\| {{{\boldsymbol{x}}_1} - \left( {{\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right)} \right\|_2^2 \\ & +\frac{{\lambda q}}{2}\left\| {{\boldsymbol{\varLambda}} \left( {{\boldsymbol{x}}_1^{\left( k \right)}} \right)\left( {{{\left| {{\boldsymbol{x}}_1^{\left( k \right)}} \right|}^{q - 1}} \odot \left| {{{\boldsymbol{x}}_1}} \right|} \right)} \right\|_2^2 \;. \end{split} (29) 根据欧拉—拉格朗日方程，式(29)可写为
\begin{split} {\boldsymbol{x}}_1^{\left( {k + 1} \right)} = &{\left[ {\delta {\boldsymbol{E}} + \lambda q{\boldsymbol{\varLambda}} {{\left( {{\boldsymbol{x}}_1^{\left( k \right)}} \right)}^{\rm{T}}}{\boldsymbol{\varLambda}} \left( {{\boldsymbol{x}}_1^{\left( k \right)}} \right)S\left( {{\boldsymbol{x}}_1^{\left( k \right)}} \right)} \right]^{ - 1}}\\ &\cdot\left( {{\nabla _x}{{\boldsymbol{u}}^{\left( k \right)}} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right) \;, \end{split} (30) 其中：E是一个全1的单位矩阵， S\left( {{\boldsymbol{x}_1}} \right) = diag \left( {{{\left| {{\boldsymbol{x}_1}} \right|}^{2q - 2}}} \right) 。
Step2：更新 {\boldsymbol{w}_1} 和 {\boldsymbol{w}_2} ，拉格朗日乘子 {\boldsymbol{w}_1} 和 {\boldsymbol{w}_2} 的更新公式为
{\boldsymbol{w}}_1^{\left( {k + 1} \right)} ={\boldsymbol{ w}}_1^{\left( k \right)} + \delta \left( {{\nabla _x}{{\boldsymbol{u}}^{\left( {k + 1} \right)}} - {\boldsymbol{x}}_1^{\left( {k + 1} \right)}} \right) \;, (31) {\boldsymbol{w}}_2^{\left( {k + 1} \right)} = {\boldsymbol{w}}_2^{\left( k \right)} + \delta \left( {{\nabla _y}{{\boldsymbol{u}}^{\left( {k + 1} \right)}} - {\boldsymbol{x}}_2^{\left( {k + 1} \right)}} \right) \;. (32) Step3：更新u，u的子问题的更新公式为
\begin{split} {{\boldsymbol{u}}^{\left( {k + 1} \right)}} = & \mathop {\arg \min }\limits_{\boldsymbol{u}} \frac{1}{2}\left\| {{{\boldsymbol{f}}^{\left( {k + 1} \right)}} - \boldsymbol{u}} \right\|_2^2 + \frac{\delta }{2}\left\{ {\left\| {{\nabla _x}\boldsymbol{u} - {\boldsymbol{x}}_1^{\left( {k + 1} \right)} + \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right\|_2^2 } \right. \\& \left. { + \left\| {{\nabla _y}{\boldsymbol{u}} - {\boldsymbol{x}}_2^{\left( {k + 1} \right)} + \frac{{{\boldsymbol{w}}_2^{\left( k \right)}}}{\delta }} \right\|_2^2} \right\} \;.\\[-10pt] \end{split} (33) 上述u子问题的优化目标是二次泛函，故可以求解下述等效正态方程：
\begin{split} \left[ {{\boldsymbol{E}} + \delta \left( {\nabla _x^{\rm{T}}{\nabla _x} + \nabla _y^{\rm{T}}{\nabla _y}} \right)} \right]{\boldsymbol{u}} = &{f^{\left( {k + 1} \right)}} + \delta \left[ {\nabla _x^{\rm{T}}\left( {{\boldsymbol{x}}_1^{\left( {k + 1} \right)} - \frac{{{\boldsymbol{w}}_1^{\left( k \right)}}}{\delta }} \right) } \right. \\& + \left. { \nabla _y^{\rm{T}}\left( {{\boldsymbol{x}}_2^{\left( {k + 1} \right)} - \frac{{{\boldsymbol{w}}_2^{\left( k \right)}}}{\delta }} \right)} \right] \;. \\[-10pt] \end{split} (34) 显然，式(34)含有二维卷积运算，因此不能直接求出u子问题的最优解，空域中的卷积运算在频域中会转化为普通的乘法运算，故采用二维快速傅里叶变换与逆变换来求解：
\begin{split} & {\boldsymbol{u}^{\left( {k + 1} \right)}} = \\& {F^{ - 1}} \left\{ {\frac{{F\left( {{\boldsymbol{f}^{\left( {k + 1} \right)}}} \right) + \delta F\left[ {\nabla _x^{\rm{T}}\left( {\boldsymbol{x}_1^{\left( {k + 1} \right)} - {{\boldsymbol{w}_1^{\left( k \right)}} \mathord{\left/ {\vphantom {{w_1^{\left( k \right)}} \delta }} \right. } \delta }} \right) + \nabla _y^{\rm{T}}\left( {\boldsymbol{x}_2^{\left( {k + 1} \right)} - {{\boldsymbol{w}_2^{\left( k \right)}} \mathord{\left/ {\vphantom {{w_2^{\left( k \right)}} \delta }} \right. } \delta }} \right)} \right]}}{{{\boldsymbol{E}} + \delta F\left( {\nabla _x^{\rm{T}}{\nabla _x} + \nabla _y^{\rm{T}}{\nabla _y}} \right)}}} \right\} , \end{split} (35) 其中：F和F−1分别是快速傅里叶变换和快速傅里叶逆变换。
基于OGS-HL的稀疏角度CT重建算法步骤：
初始化变量：{{\boldsymbol{f}}^{(0)}} = {{\boldsymbol{u}}^{(0)}} = 0，{\boldsymbol{w}}_1^{(0)} = {\boldsymbol{w}}_2^{(0)} = 0，{\boldsymbol{x}}_1^{(0)} = {\boldsymbol{x}}_2^{(0)} = 0， {k} = 0 ，{\rm{maxloop}} = 30； 选择参数：\mu ,\lambda ,\delta ,q,K; 主程序迭代： {k} < {\rm{maxloop}} ； 利用式(16)来更新 {\boldsymbol{f}^{(k + 1)}} ； 利用式(18)、式(19)使用MM算法来更新{\boldsymbol{x}}_1^{(k + 1)}，{\boldsymbol{ x}}_2^{(k + 1)}； 利用式(28)、式(29)来更新拉格朗日乘子{\boldsymbol{w}}_2^{(k + 1)}，{\boldsymbol{ w}}_2^{(k + 1)}； 利用式(30)来更新{{\boldsymbol{u}}^{(k + 1)}}；
k = k + 1 ；结束迭代：k=maxloop，输出u； 4. 实验结果
4.1 实验设置
为验证OGS-HL算法在稀疏角度CT重建下的效果，本文选取其他经典的算法与OGS-HL算法作对比。实验采用仿真模型和真实模型来验证算法。实验配置为：11th Gen Intel (R) Core (TM) i5-11260H @ 2.60 GHz的CPU，Nvidia RTX3050ti (4 GB)的GPU，16 GB的内存，实验软件为MATLAB R2019b。本文算法与选取的对比算法均在MATLAB和使用MEX函数编译的C++的混合模式中实现，接口在MATLAB中实现。
4.2 仿真小鼠实验
仿真实验采用MOBY软件生成的小鼠胸腔截面作为测试模型，在血液中注入1.2%的碘造影剂，胸腔模型尺寸为20 mm×20 mm，分辨率为512×512，如图1所示。
图 1. 仿真小鼠胸腔模型和碘造影剂Figure 1. The simulated mouse thorax phantom and the iodine contrast agent投影数据由等距扇形束几何采集，X射线源到旋转中心的距离为100 mm，物体半径为10 mm，每个探测器长度为20 mm，探测器有320个单元，每个单元的长度为0.0625 mm。每条X射线发射的光子数为5×104，计算沿每条X射线路径的预期光子数，为了模拟数据噪声，根据泊松分布生成随机数，其中方差为上述期望的光子数，然后进行对数运算，得到无噪声和有噪声的投影数据。使用分裂布雷格曼(Split-Bregman, SB)算法的重建的无噪声图像作为参考图像[20]。在360°范围内进行等间隔采样，设置的采样间隔角度分别为6°、4°、3°和2°，得到的稀疏投影角度个数为60、90、120和180。本节实验采用归一化均方根误差(NRMSE)、峰值信噪比(PSNR)和结构相似度指数(SSIM)来评价噪声投影数据中重建图像的质量。
在OGS-TV算法中，经过多次实验，参数为 \mu = 50 ， \lambda = 2 \times {10^{ - 4}} ， \delta = 1 ， q = 1 ， K = 3 。在OGS-HL算法中，参数为 \mu = 50 ， \lambda = 2 \times {10^{ - 4}} ， \delta = 1 ， q = 0.8 ， K = 3 。
图2展示了6种不同算法下不同角度的仿真小鼠重建图像，图3展现了仿真小鼠骨的部分ROI区域。从图2可以看出，FBP和SART两种算法在四个不同的角度下重建的图像中含有大量的伪影和噪声。从图3的ROI区域中仿真小鼠的骨切面可以看出TV算法重建的图像出现阶梯伪影，使得骨切面的边缘变得不清晰。TGV算法虽然能够克服TV算法出现的问题，但对60、90和120角度下骨切面周围产生的条纹伪影去除效果较差。OGS-TV算法在稀疏角度下重建的图像都有较大的改进，但对噪声的抑制效果一般。OGS-HL算法不仅能够消除稀疏角度下产生的伪影，并且能够很好地抑制噪声，对小鼠骨切面周围的噪声消除以及骨切面的边缘保护有着良好的效果。
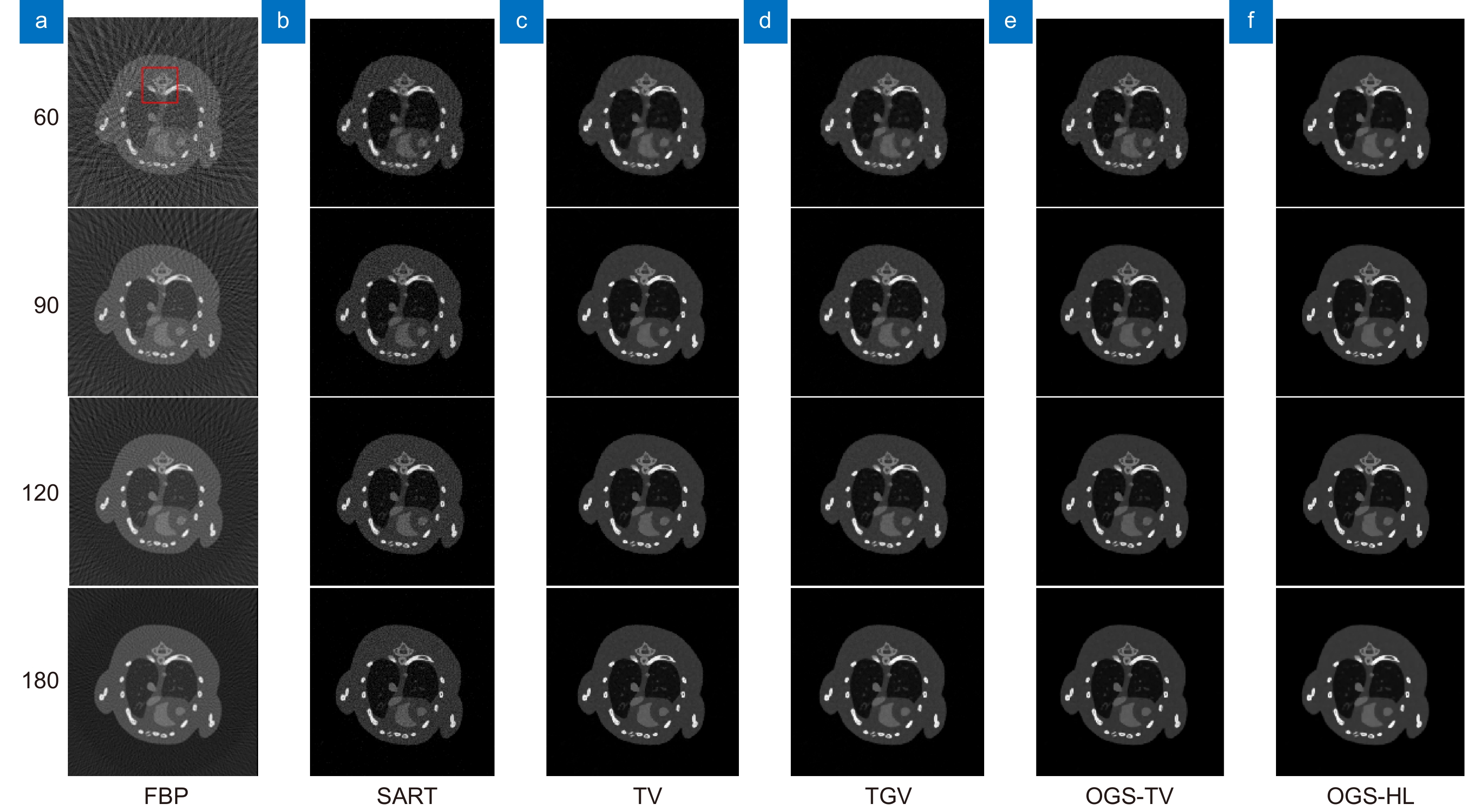图 2. 仿真小鼠重建结果: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的重建图像Figure 2. The reconstruction results of the simulated mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the reconstructed images are from 60, 90, 120 and 180
图 3. 仿真小鼠重建图像ROI区域: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的ROI区域Figure 3. The reconstruction results of the simulated mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the ROI regions are 60, 90, 120 and 180图4绘制了五种算法在重建图像过程中在四个不同角度下NRMSE、PSNR和SSIM评价指标的收敛曲线图。从图4可以看出，OGS-HL算法对于图像重建的效果对比其他算法有所提升，其在180角度下的提升较小，在120角度下重建的效果提升，在60和90角度下的重建效果提升较为明显。仿真试验结果表明，OGS-HL算法在稀疏角度重建的条件下会保持良好的优势，能够提升重建图像的质量。
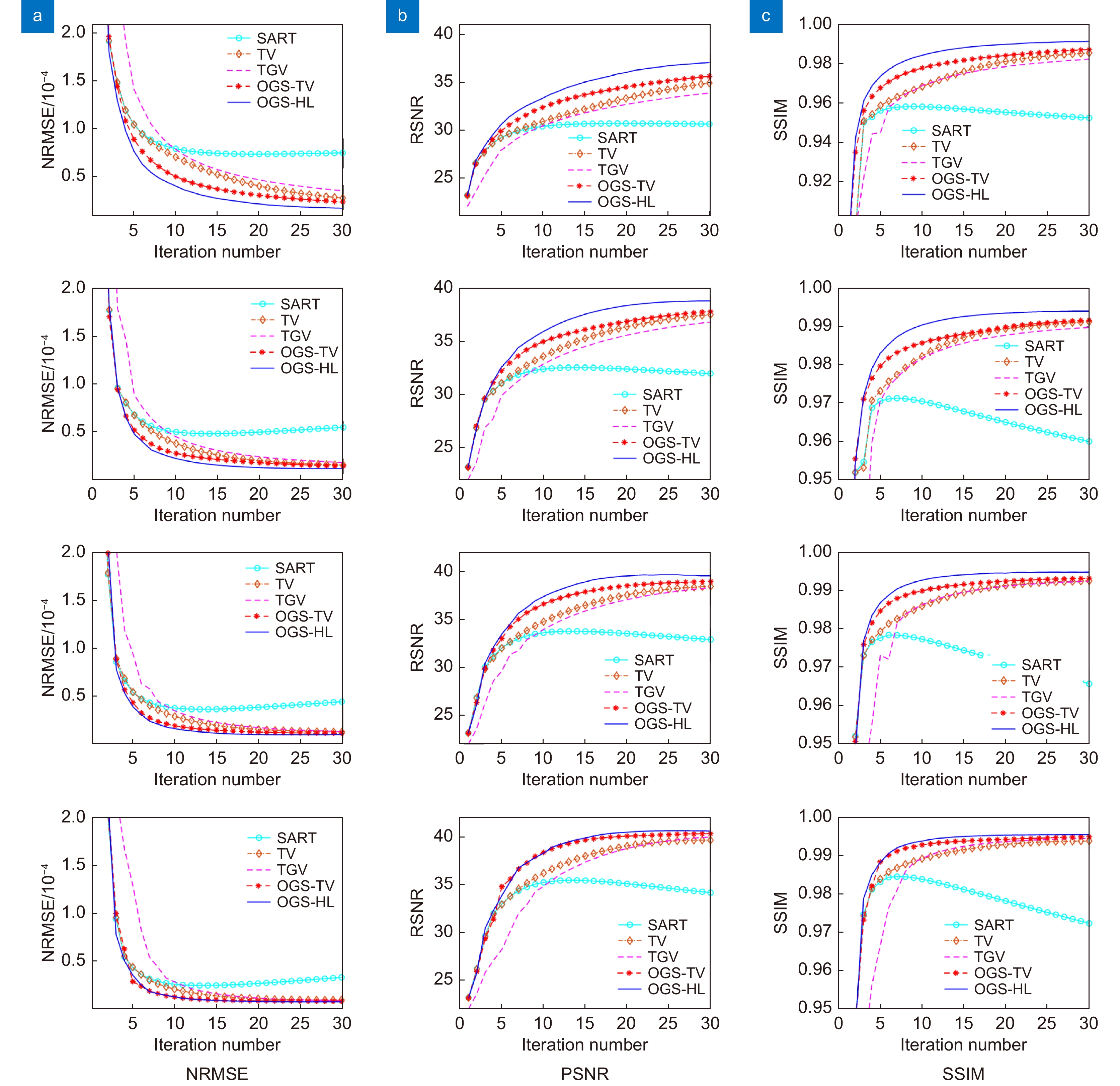图 4. 仿真小鼠模型重建效果的三种评价指标：(a) NRMSE; (b) PSNR; (c) SSIM。从上到下依次为投影幅数为60、90、120和180的重建图像的数量性评价指标Figure 4. Three quantitative evaluation indexes of the reconstruction effect of the simulated mouse model: (a) NRMSE; (b) PSNR; (c) SSIM. From top to bottom, the quantitative evaluation indexes of the reconstructed images from 60, 90, 120 and 1804.3 临床小鼠实验
为了进一步说明OGS-HL算法的有效性，本节实验使用MARS (Medipix All Resolution System)微型CT上采集的来自真实临床前小鼠的投影数据。重建的CT图像覆盖面积为18.41 mm×18.41 mm，分辨率为512×512。投影数据采用等距扇形束几何采集，X射线源到旋转中心的距离为158 mm，到探测器的距离为255 mm。在360°范围内进行等间隔采样，设置的采样间隔角度分别为6°、4°、3°和2°，得到的稀疏投影角度个数为60、90、120和180。
在OGS-TV算法中，经过多次实验，参数为 \mu = 50 ， \lambda = 2 \times {10^{ - 4}} ， \delta = 0.1 ， q = 1 ， K = 3 。在OGS-HL算法中，参数为 \mu = 50 ， \lambda = 2 \times {10^{ - 4}} ， \delta = 0.1 ， q = 0.8 ， K = 3 。
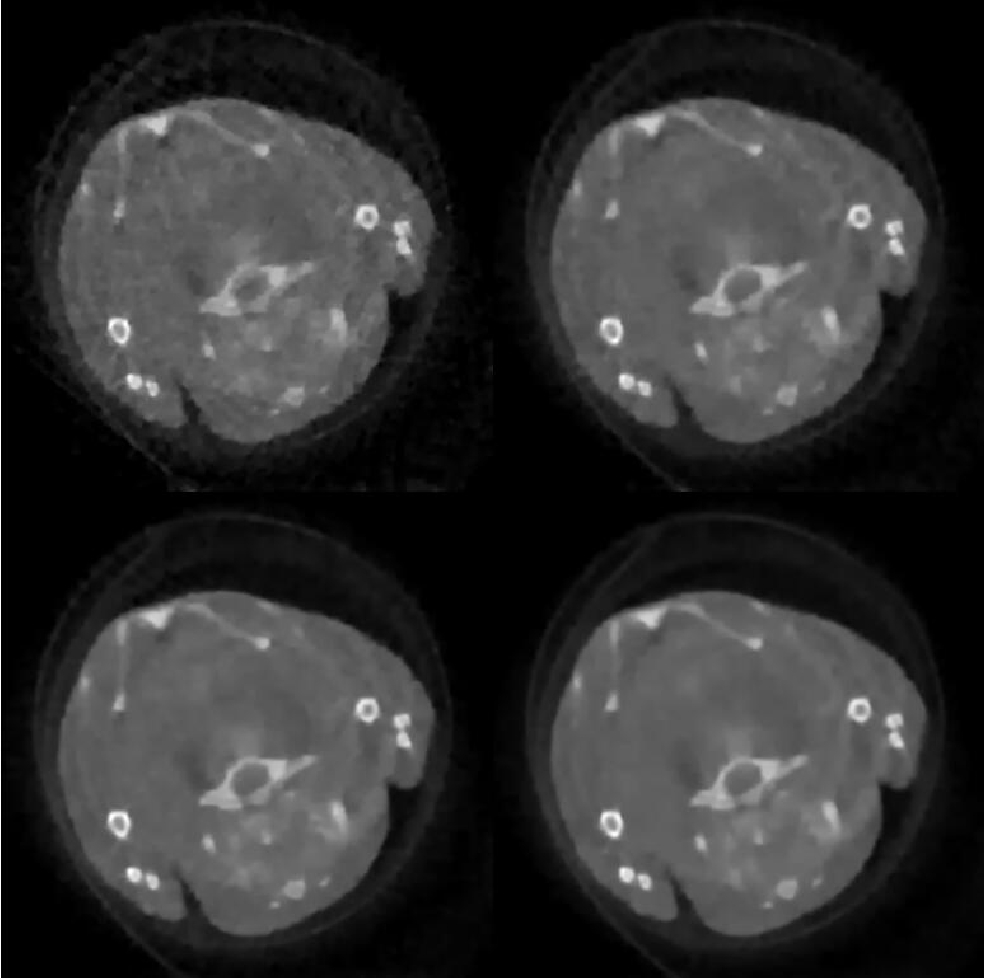
图5展示了6种不同算法下不同角度的临床真实小鼠重建图像，图6展现了临床真实小鼠骨的部分ROI区域。从图5可以看出，每个算法重建的效果与以上仿真小鼠重建实验的效果基本相同，在四个不同的角度下FBP算法和SART算法重建过程产生了大量的伪影和噪声。从图6的ROI区域看出，TV算法下小鼠骨切面的边缘出现伪影，且含有少量的噪声，TGV算法在60、90角度和120角度下的噪声去除并不明显，OGS-TV算法也含有少量的噪声，OGS-HL对于骨切面周围噪声的消除和边缘的保护有良好的效果。从实验结果和ROI区域可以看出，OGS-HL算法在稀疏角度条件下的重建效果优于其他算法。
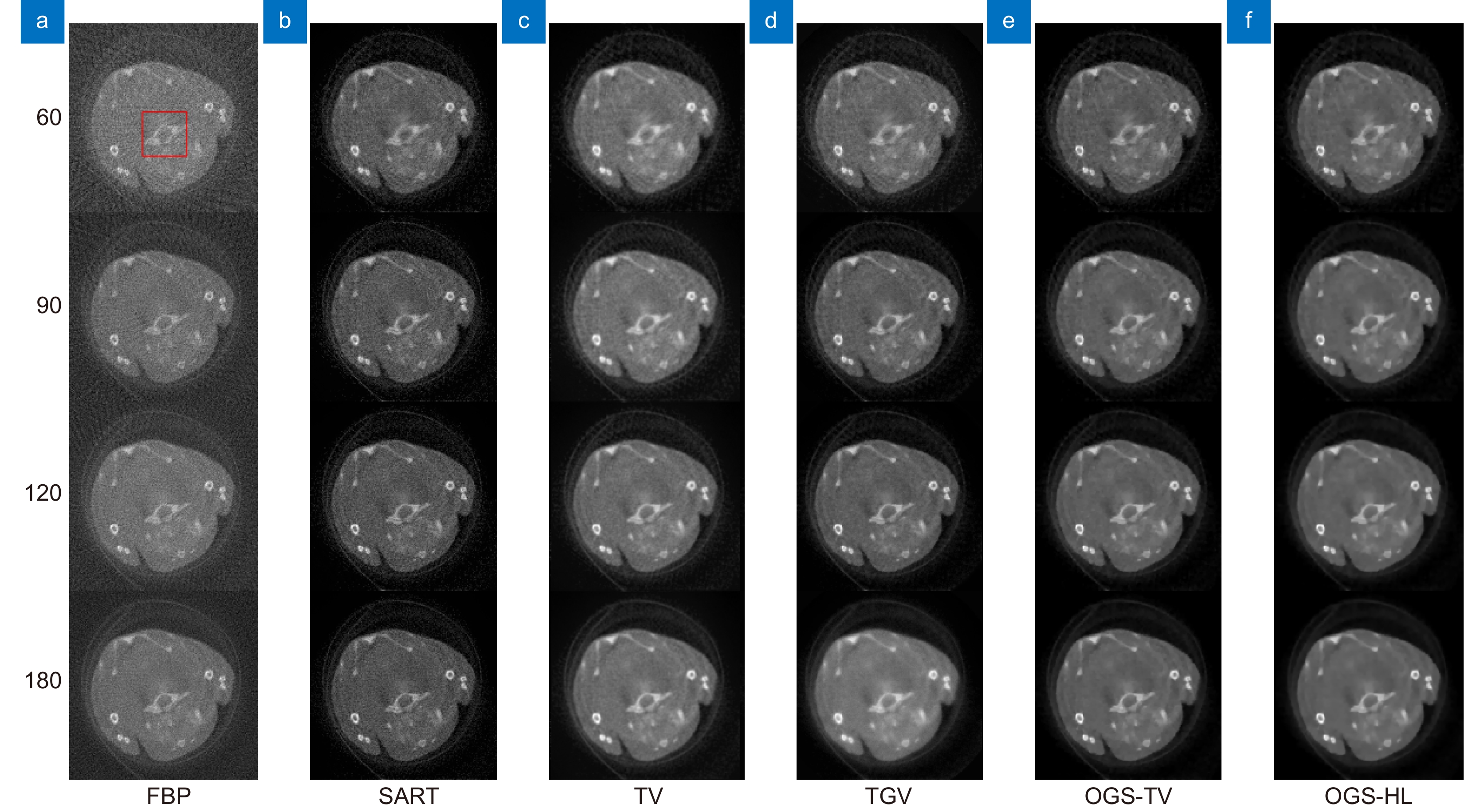图 5. 临床小鼠模型重建结果: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为 投影幅数为60、90、120和180的重建图像Figure 5. The reconstruction results of the clinical mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the reconstructed images are from 60, 90, 120 and 180
图 6. 临床小鼠模型重建图像ROI区域: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的ROI区域Figure 6. The reconstruction results of the clinical mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the ROI regions are 60, 90, 120, and 1805. 结 论
为了进一步提升稀疏角度CT图像的重建质量，本文将OGS和HL应用于稀疏角度CT图重建，得到OGS-HL稀疏角度CT迭代重建算法。相比于传统的TV正则项，OGS正则项考虑每个像素点梯度重叠组的信息，度量图像梯度稀疏性，克服了图像重建过程中产生的阶梯伪影，取得了不错的重建效果。图像的梯度服从重尾分布，HL先验可以很好地近似图像梯度的重尾分布，达到抑制噪声的效果。通过以上仿真小鼠和临床小鼠两个实验结果表明，OGS-HL算法对于稀疏角度CT图像重建的图像质量提升明显，具有较好的鲁棒性。本文是基于模型的稀疏CT重建方法，侧重于物理模型和数学算法，而基于深度学习的稀疏CT重建方法则注重于数据驱动和自主学习能力，更侧重于大量的CT数据作为训练样本，通过学习数据中的信息来实现重建。由于本文进行的实验没有大量的训练数据集，故采用基于模型的算法来实现重建。在参数选择上，正则项参数 \lambda 和惩罚参数 \delta 的选择对重建图像的效果极为重要，但是，本文这两个参数的选取为经验选取，导致进行实验时耗费的时间较长，之后的研究会进一步改进模型，使算法模型更加灵活简便。
利益冲突：所有作者声明无利益冲突
-
图 1 仿真小鼠胸腔模型和碘造影剂
Figure 1. The simulated mouse thorax phantom and the iodine contrast agent
图 2 仿真小鼠重建结果: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的重建图像
Figure 2. The reconstruction results of the simulated mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the reconstructed images are from 60, 90, 120 and 180
图 3 仿真小鼠重建图像ROI区域: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的ROI区域
Figure 3. The reconstruction results of the simulated mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the ROI regions are 60, 90, 120 and 180
图 4 仿真小鼠模型重建效果的三种评价指标：(a) NRMSE; (b) PSNR; (c) SSIM。从上到下依次为投影幅数为60、90、120和180的重建图像的数量性评价指标
Figure 4. Three quantitative evaluation indexes of the reconstruction effect of the simulated mouse model: (a) NRMSE; (b) PSNR; (c) SSIM. From top to bottom, the quantitative evaluation indexes of the reconstructed images from 60, 90, 120 and 180
图 5 临床小鼠模型重建结果: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为 投影幅数为60、90、120和180的重建图像
Figure 5. The reconstruction results of the clinical mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the reconstructed images are from 60, 90, 120 and 180
图 6 临床小鼠模型重建图像ROI区域: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL。从上到下依次为投影幅数为60、90、120和180的ROI区域
Figure 6. The reconstruction results of the clinical mouse model: (a) FBP; (b) SART; (c) TV; (d) TGV; (e) OGS-TV; (f) OGS-HL. From top to bottom, the ROI regions are 60, 90, 120, and 180
表 1 不同算法的参数设置
Table 1. Parameter settings for different algorithms
算法 K q TV 1 1 OGS-TV 2n+1(n=1, 2, …, n) 1 OGS-HL 2n+1(n=1, 2, …, n) {\text{0}}{\text{.5}} \leqslant q < {\text{1}}
下载: 导出CSV
初始化变量：{{\boldsymbol{f}}^{(0)}} = {{\boldsymbol{u}}^{(0)}} = 0，{\boldsymbol{w}}_1^{(0)} = {\boldsymbol{w}}_2^{(0)} = 0，{\boldsymbol{x}}_1^{(0)} = {\boldsymbol{x}}_2^{(0)} = 0， {k} = 0 ，{\rm{maxloop}} = 30； 选择参数：\mu ,\lambda ,\delta ,q,K; 主程序迭代： {k} < {\rm{maxloop}} ； 利用式(16)来更新 {\boldsymbol{f}^{(k + 1)}} ； 利用式(18)、式(19)使用MM算法来更新{\boldsymbol{x}}_1^{(k + 1)}，{\boldsymbol{ x}}_2^{(k + 1)}； 利用式(28)、式(29)来更新拉格朗日乘子{\boldsymbol{w}}_2^{(k + 1)}，{\boldsymbol{ w}}_2^{(k + 1)}； 利用式(30)来更新{{\boldsymbol{u}}^{(k + 1)}}；
k = k + 1 ；结束迭代：k=maxloop，输出u；
下载: 导出CSV
-
参考文献
[1] Jouini M S, Keskes N. Numerical estimation of rock properties and textural facies classification of core samples using X-ray computed tomography images[J]. Appl Math Modell, 2017, 41: 562−581. doi: 10.1016/j.apm.2016.09.021
[2] Brenner D J, Hall E J. Computed tomography-an increasing source of radiation exposure[J]. N Engl J Med, 2007, 357(22): 2277−2284. doi: 10.1056/NEJMra072149
[3] Wang G, Yu H Y, Ye Y B. A scheme for multisource interior tomography[J]. Med Phys, 2009, 36(8): 3575−3581. doi: 10.1118/1.3157103
[4] Xu Q, Yu H Y, Mou X Q, et al. Low-dose X-ray CT reconstruction via dictionary learning[J]. IEEE Trans Med Imaging, 2012, 31(9): 1682−1697. doi: 10.1109/TMI.2012.2195669
[5] Yu W, Wang C X, Nie X Y, et al. Image reconstruction for few-view computed tomography based on ℓ0 sparse regularization[J]. Procedia Comput Sci, 2017, 107: 808−813. doi: 10.1016/j.procs.2017.03.178
[6] Donoho D L. Compressed sensing[J]. IEEE Trans Inform Theory, 2006, 52(4): 1289−1306. doi: 10.1109/TIT.2006.871582
[7] Zhang W K, Zhang H M, Wang L Y, et al. Limited angle CT reconstruction by simultaneous spatial and radon domain regularization based on TV and data-driven tight frame[J]. Nucl Instrum Methods Phys Res Sect A:Accel, Spectrom, Detect Assoc Equip, 2018, 880: 107−117. doi: 10.1016/j.nima.2017.10.056
[8] Miao J Y, Cao H L, Jin X B, et al. Joint sparse regularization for dictionary learning[J]. Cogn Comput, 2019, 11(5): 697−710. doi: 10.1007/s12559-019-09650-2
[9] Li M, Fan Z T, Ji H, et al. Wavelet frame based algorithm for 3D reconstruction in electron microscopy[J]. SIAM J Sci Comput, 2014, 36(1): B45−B69. doi: 10.1137/130914474
[10] Wang Y L, Yang J F, Yin W T, et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM J Imaging Sci, 2008, 1(3): 248−272. doi: 10.1137/080724265
[11] Sidky E Y, Kao C M, Pan X C. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J]. J X-Ray Sci Technol, 2006, 14(2): 119−139.
[12] Zhang X F, Liu H B. Linear programming-based reconstruction algorithm for limited angular sparse-view tomography[J]. Opt Lasers Eng, 2021, 140: 106524. doi: 10.1016/j.optlaseng.2020.106524
[13] 连祥媛, 孔慧华, 潘晋孝, 等. 多通道联合的广义总变分能谱CT重建[J]. 光电工程, 2021, 48(9): 210211. doi: 10.12086/oee.2021.210211
Lian X Y, Kong H H, Pan J X, et al. Joint multi-channel total generalized variational algorithm for spectral CT reconstruction[J]. Opto-Electron Eng, 2021, 48(9): 210211. doi: 10.12086/oee.2021.210211
[14] Bao P, Zhou J L, Zhang Y. Few-view CT reconstruction with group-sparsity regularization[J]. Int J Numer Methods Biomed Eng, 2018, 34(9): e3101. doi: 10.1002/cnm.3101
[15] Jon K, Sun Y, Li Q X, et al. Image restoration using overlapping group sparsity on hyper-Laplacian prior of image gradient[J]. Neurocomputing, 2021, 420: 57−69. doi: 10.1016/j.neucom.2020.08.053
[16] Liu J, Huang T Z, Selesnick I W, et al. Image restoration using total variation with overlapping group sparsity[J]. Inform Sci, 2015, 295: 232−246. doi: 10.1016/j.ins.2014.10.041
[17] Kong J, Lu K S, Jiang M. A new blind deblurring method via Hyper-Laplacian prior[J]. Procedia Comput Sci, 2017, 107: 789−795. doi: 10.1016/j.procs.2017.03.170
[18] Boyd S P, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Found Trends Mach Learn, 2011, 3(1): 1−122.
[19] Hunter D R, Lange K. A tutorial on MM algorithms[J]. Am Stat, 2004, 58(1): 30−37. doi: 10.1198/0003130042836
[20] Kong H H, Liu R, Yu H Y. Ordered-subset split-Bregman algorithm for interior tomography[J]. J X-Ray Sci Technol, 2016, 24(2): 221−240. doi: 10.3233/XST-160547
施引文献
期刊类型引用(1)
1. 宋一娇，孔慧华，李剑，齐子文，张然. 基于超拉普拉斯正则化的冲击波超压层析重建. 电子测量技术. 2024(10): 160-167 . 
百度学术
其他类型引用(1)
-
访问统计
点击扫一扫
图(7)
表(2)
计量
- 文章访问数: 2025
- PDF下载数: 796
- 施引文献: 2
