基于深度学习的真实尺度运动恢复结构方法

陈朋; 任金金; 王海霞; 汤粤生; 梁荣华

doi:10.12086/oee.2019.190006

基于深度学习的真实尺度运动恢复结构方法

- 浙江工业大学信息工程学院，浙江杭州 310023
基金项目:
国家自然科学基金资助项目(61527808, 61602414)；杭州市重大科技创新专项项目(20172011A027)

详细信息

作者简介:
陈朋(1981-)，男，博士，副教授，硕士生导师，主要从事嵌入式系统设计、图像处理和模式识别的研究。E-mail：chenpeng@zjut.edu.cn

**^*通讯作者:** 陈朋, E-mail: chenpeng@zjut.edu.cn

中图分类号: TP391

收稿日期: 2019-01-08

修回日期: 2019-02-18

刊出日期: 2019-12-01

Equal-scale structure from motion method based on deep learning

- College of Information Engineering, Zhejiang University of Technology, Hangzhou, Zhejiang 310023, China
Fund Project: Supported by National Natural Science Foundation of China (61527808, 61602414) and Hangzhou Major Science and Technology Innovation Project (20172011A027)

More Information

**^*Corresponding author:** Chen Peng, E-mail: chenpeng@zjut.edu.cn

Received Date 08 January 2019

Revised Date 18 February 2019

Published Date 01 December 2019

摘要

摘要:
传统的多视图几何方法获取场景结构存在两个问题：一是因图片模糊和低纹理带来的特征点误匹配，从而导致重建精度降低；二是单目相机缺少尺度信息，重建结果只能确定未知的比例因子，无法获取准确的场景结构。针对这些问题本文提出一种基于深度学习的真实尺度运动恢复结构方法。首先使用卷积神经网络获取图片的深度信息；接着为了恢复单目相机的尺度信息，引入惯性传感单元(IMU)，将IMU获取的加速度和角速度与ORB-SLAM2获取的相机位姿进行时域和频域上的协同，在频域中获取单目相机的尺度信息；最后将图片的深度图和具有尺度因子的相机位姿进行融合，重建出场景的三维结构。实验表明，使用Depth CNN网络获取的单目图像深度图解决了多层卷积池化操作输出图像分辨率低和缺少重要特征信息的问题，绝对值误差达到了0.192，准确率高达0.959；采用多传感器融合的方法，在频域上获取单目相机的尺度能够达到0.24 m的尺度误差，相比于VIORB方法获取的相机尺度精度更高；重建的三维模型与真实大小具有0.2 m左右的误差，验证了本文方法的有效性。
- 三维重建 /
- 深度学习 /
- 单目相机 /
- 尺度因子 /
- IMU
Abstract:
Two problems exist in traditional multi-view geometry method to obtain the three-dimensional structure of the scene. First, the mismatching of the feature points caused by the blurred image and low texture, which reduces the accuracy of reconstruction; second, as the information obtained by monocular camera is lack of scale, the reconstruction results can only determine the unknown scale factor, and cannot get accurate scene structure. This paper proposes a method of equal-scale motion restoration structure based on deep learning. First, the convolutional neural network is used to obtain the depth information of the image; then, to restore the scale information of the monocular camera, an inertial measurement unit (IMU) is introduced, and the acceleration and angular velocity acquired by the IMU and the camera position acquired by the ORB-SLAM2 are demonstrated. The pose is coordinated in both time domain and frequency domain, and the scale information from the monocular camera is acquired in the frequency domain; finally, the depth information of the image and the camera pose with the scale factor are merged to reconstruct the three-dimensional structure of the scene. Experiments show that the monocular image depth map obtained by the Depth CNN network solves the problem that the output image of the multi-level convolution pooling operation has low resolution and lacks important feature information, and the absolute value error reaches 0.192, and the accuracy rate is up to 0.959. The multi-sensor fusion method can achieve a scale error of 0.24 m in the frequency domain, which is more accurate than that of the VIORB method in the frequency domain. The error between the reconstructed 3D model and the real size is about 0.2 m, which verifies the effectiveness of the proposed method.
- 3D reconstruction /
- deep learning /
- monocular camera /
- scale factor /
- IMU

Overview

Overview: With the continuous development of technologies such as computer vision, virtual reality, and multimedia communication, it is necessary to realize the targets of real-time obstacle avoidance, robot autonomous navigation, and unmanned driving, so that the equipment can more accurately recognize and understand the surrounding environment. Obtaining a real-sized 3D model is a tendency in the future. The traditional three-dimensional structure restoration methods rely too much on geometric calculations in obtaining image information and camera attitude information from two-dimensional images, which is difficult to play a good role in the absence of little texture, complicated geometric conditions, and monotonous structure. With the development of computer vision, the use of deep learning network to learn pictures and extract hierarchical features has been successfully applied to depth estimation, camera pose estimation, and three-dimensional structure recovery. Meanwhile, acquiring 3D models of real scale of objects is a problem that has always been explored in the field of computer vision.

Two problems exist in the traditional multi-view geometry method to obtain the three-dimensional structure of the scene. First, the mismatching of the feature points caused by the blurred image and low texture, which reduces the accuracy of reconstruction; second, as the information obtained by monocular camera is lack of scale, the reconstruction results can only determine the unknown scale factor, and cannot get accurate scene structure. This paper proposes a method of equal-scale motion restoration structure based on deep learning. First, the convolutional neural network is used to obtain the depth information of the image; then, to restore the scale information of the monocular camera, an inertial measurement unit (IMU) is introduced, and the acceleration and angular velocity acquired by the IMU and the camera position acquired by the ORB-SLAM2 are demonstrated. The pose is coordinated in the both time domain and frequency domain, and the scale information from the monocular camera is acquired in the frequency domain; finally, the depth information of the image and the camera pose with the scale factor are merged to reconstruct the three-dimensional structure of the scene. Experiments show that the monocular image depth map obtained by the Depth CNN network solves the problem that the output image of the multi-level convolution pooling operation has low resolution and lacks important feature information, and the absolute value error reaches 0.192, and the accuracy rate is up to 0.959. The multi-sensor fusion method can achieve a scale error of 0.24 m in the frequency domain, which is more accurate than that of the VIORB method in the frequency domain. The error between the reconstructed 3D model and the real size is about 0.2 m, which verifies the effectiveness of the proposed method.

HTML全文

1. 引言

随着计算机视觉、虚拟现实、多媒体通信等技术的不断发展，要真正实现无人机实时避障、机器人自主导航、无人驾驶等目标，让设备能够更加准确地认知、理解周围的环境至关重要，获取真实大小的三维模型是未来发展的一大趋势^[1-2]。基于运动恢复结构(structure from motion，SFM)的多幅图像重建是三维重建技术的重要方法，该方法通过分析相机运动信息来获取目标的三维结构。在自动驾驶、教学实验等众多领域方面有着广泛的应用。

基于相机的三维重建^[3]是从二维图像或视频中恢复出三维空间结构，实现自身定位等功能，进而在二维图像中获取深度以及相机的姿态信息。Pollefeys等^[4]采用自标定方法得到相机的内外参数，依据分层重建原理计算像素点在空间坐标系下的三维坐标，但是由于算法复杂、消耗时间较长，因此实时性不高。戴嘉境等人^[5]提出了自动式纹理贴图方法和局部不变特征的二阶段点云配准算法，适用于多幅图像的三维重建。张涛等^[6]提出利用射影重建和欧式原理重建出真实场景的空间稀疏点云，但只在Matlab下进行了仿真验证。传统的三维结构恢复方法过于依赖几何计算^[7-8]，在低纹理、结构单调等情况下效果不佳。

近年来，利用深度学习网络对图片进行学习提取结构化特征^[9]，预测场景图片的深度信息，得到了快速发展。He等^[10]的ResNet网络在估计单幅图像深度中添加了残差模块训练网络，克服了传统CNN存在的信息丢失、梯度消失问题。Newell等^[11]采用对称网络结构，通过卷积层和上采样层模块解决了多层卷积池化操作带来的图像特征信息丢失、分辨率低等问题。Zhou等^[12]采用了无监督的方法对视频数据进行训练，预测单张图片的深度和车辆运动的轨迹，推动了卷积神经网络在自动驾驶领域中的应用。

获取物体真实尺度的三维模型是计算机视觉领域不断研究、探索的问题。文献[13]中使用Kinect for Windows传感器来获取场景的深度图像，通过移动传感器绕着待重建物体或场景移动可以扫描出物体的三维模型，但是该方法缺少尺度信息，无法获取真实尺度的三维结构。文献[14-16]将视觉与惯性传感单元(inertial measurement unit，IMU)进行融合实现了实时定位与建图，但这些方法需要使用定制的相机IMU硬件装备。VIORB^[17]是在ORB-SLAM2^[18]的基础上将单目相机和IMU进行紧耦合的SLAM(simultaneous localization and mapping)算法，融合IMU的观测不仅能够解决单目的绝对尺度问题，还可以提高系统的精度和鲁棒性。Ham等^[19]借助已有的视觉跟踪软件获取相机的当前位姿，并将其和IMU进行融合，进而得到单目相机的绝对尺度。Mustaniemi等^[20]通过视觉与IMU的加速度在频域上的协同，并成功估计出手机上单目相机的绝对尺度。

本文提出一种基于视觉和惯性传感器的运动恢复结构方法，解决传统三维重建方法受图片质量影响大和单目相机缺乏尺度的问题。主要工作为

1) 在基于视觉的三维重建方法中引入IMU的观测数据，在时域和频率上对相机位姿进行协调，在频率中获取单目相机的尺度因子，解决了单目相机用于三维重建缺少尺度的问题，提升了重建模型的真实性；

2) 将单幅图像深度估计的卷积神经网络应用到运动恢复结构中，通过卷积-反卷积的对称型网络预测单幅图像的深度图，解决了卷积神经网络输出图像分辨率低，缺失重要特征信息的问题，提高了单幅图像深度预测的精度。

2. 基于Depth CNN网络的真实尺度运动恢复结构方法介绍

本文提出的基于Depth CNN网络的真实尺度运动恢复结构方法流程如图 1所示，首先使用Depth CNN网络结构学习图像的深度信息，由于单目相机缺乏尺度信息，Depth CNN网络学习到的深度图存在尺度不确定性；接着为了恢复出真实尺度的相机运动结构，本文在单目相机基础上，引入了惯性传感器。采用相机位姿(旋转矩阵与平移向量)和IMU获取的加速度计以及陀螺仪参数进行时域和频域上的对齐。在时域阶段实现时间同步；在频域中根据同一时刻基于视觉获取的加速度以及角速度，理论上与惯性传感器获取的加速度和角速度相等的原理，求解出单目相机的尺度因子，其中相机的位姿通过ORB-SLAM2获取。最后，将深度图像和带有尺度信息的相机运动位姿进行了点云的拼接，获取稠密点云，实现真实尺度的三维场景重建。

图 1. 基于深度学习真实尺度运动恢复结构流程图

Figure 1. Equal scale structure from motion based on deep learning

下载: 全尺寸图片幻灯片

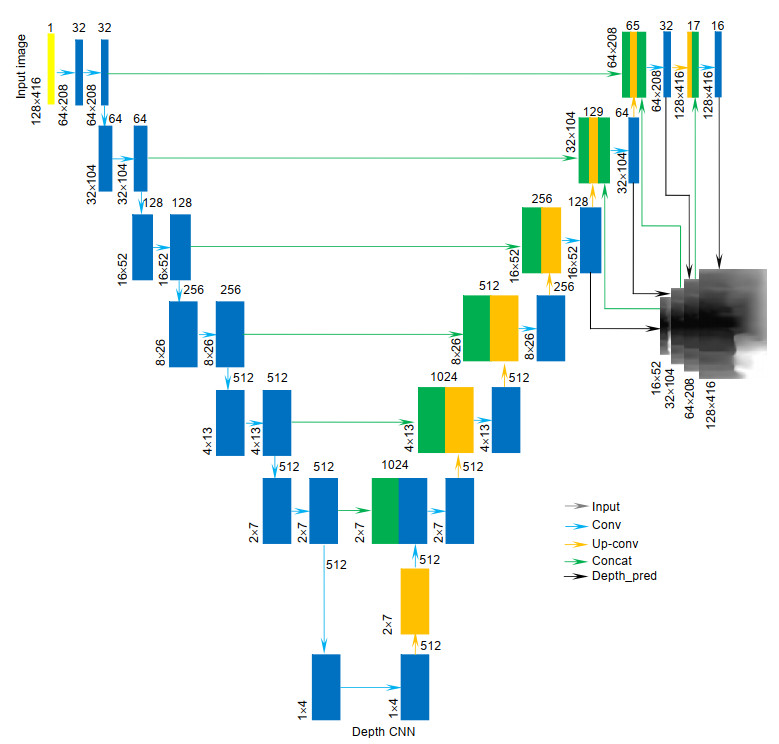
Depth CNN网络采用无监督学习方法，将文献[12]中端到端的卷积神经网络应用于运动恢复结构，对单张图像深度进行估计。整体思路主要分为两个部分：1)收缩部分，主要由卷积层组成，用于提取图像的特征；2)放大部分，主要由反卷积层组成，将结果由粗到细，恢复到高像素。网络结构是在DispNet网络基础上进行了改正，如图 2所示，其中，网络架构主要由收缩和扩展两个部分组成。收缩部分是典型的卷积网络架构，是一种重复结构，每次重复中都有两个卷积层。除了卷积层(cnv1、cnv1b)中卷积核大小是7×7和卷积层(cnv2、cnv2b)中卷积核大小是5×5，其他10个卷积层的卷积核大小都是3×3。扩展部分中每一步都是先使用反卷积(up-convolution)；接着将反卷积结果与收缩部分中对应步骤的特征图拼接起来，收缩部分中特征值稍大，将其进行修剪之后进行拼接；将拼接后的map进行3×3的卷积；从第四层反卷积中开始添加一个输出层disp和一个双线性插值disp_up，最终输出128×416的深度图。除了预测输出层外，所有的卷积层的激活函数都是ReLu。由于深度学习不能够获取真实大小的三维物体结构信息，本文引入IMU传感器获取尺度因子。

图 2. 深度图网络结构

Figure 2. Network architecture for depth

下载: 全尺寸图片幻灯片

3. 基于IMU和ORB-SLAM2的频域单目相机尺度获取

为了克服现有的单目相机重建三维结构缺少尺度信息，本方法使用高清单目摄像头和惯性传感单元，添加的IMU不仅能够有助于单目相机确定尺度，也能在摄像机被遮挡时提供相机的位姿估计。具体方法是将ORB-SLAM2获取的相机位姿(位置 $\mathit{\boldsymbol{P}}_{\rm{W}}^{\rm{V}}$ 和旋转矩阵 $\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}$ )与IMU获取的加速度计和陀螺仪参数进行时域和频域上的对准。为方便阅读，在此规定上下标含义：下标W、B、C分别表示世界坐标系、IMU坐标系、相机坐标系；上标V、I表示通过视觉和IMU计算得到的值。本文中将所有坐标系都统一变换到相机坐标系下进行计算，将重力加速度转换到相机坐标系下表达式：

${g_C}(t) = \mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}{g_W}(t),$

(1)

其中： $\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}$ 表示世界坐标系到相机坐标系的旋转矩阵； ${g_{\rm{W}}}$ 表示世界坐标系下的重力加速度； ${g_{\rm{C}}}$ 表示相机坐标系下的重力加速度。

同理可将IMU坐标系下的加速度和角速度同样旋转到相机坐标系下，表达式：

$\left\{\begin{array}{l}{\boldsymbol{\alpha}_{\mathrm{C}}^{\mathrm{I}}(t)=\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}} \boldsymbol{\alpha}_{\mathrm{B}}^{\mathrm{I}}(t)} \\ {\boldsymbol{\omega}_{\mathrm{C}}^{\mathrm{I}}(t)=\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}} \boldsymbol{\omega}_{\mathrm{B}}^{\mathrm{I}}(t)}\end{array}\right.$

(2)

其中： $\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}}$ 表示IMU坐标系到相机坐标系的旋转矩阵； $\boldsymbol{\alpha}_{\mathrm{B}}^{\mathrm{I}}$ 、 $\boldsymbol{\omega}_{\mathrm{B}}^{\mathrm{I}}$ 分别表示IMU中加速度计测量的加速度和陀螺仪测量的角速度； $\boldsymbol{\alpha}_{\mathrm{C}}^{\mathrm{I}}$ 、 $\boldsymbol{\omega}_{\mathrm{C}}^{\mathrm{I}}$ 分别表示在相机坐标系下IMU获取的加速度和角速度。

3.1 视觉和IMU参数时域上的同步

由于相机和IMU是两种不同的传感器，其获取的图片时间戳和IMU可能不在同一个时钟，即使同时采集图片和IMU信息也会存在未知的时间偏移量。因此需要对相机和IMU的时间戳进行同步处理。本文时间同步方法是比较陀螺仪的时间戳和由ORB-SLAM2获取的角速度时间戳，将最小平方差的偏移值设置为最优的时间偏移量t_o，通过把较小的时间戳加上最优的时间偏移量，从而实现视觉和IMU在时间上的同步。由视觉获取的角速度是根据相机位姿中的旋转矩阵 $\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}$ 变换而来。变换关系式：

${\left[ {{\bf{ \pmb{\mathit{ ω}} }}_{\rm{C}}^{\rm{V}}} \right]_{\rm X}} = \frac{{{\rm{d}}\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}}}{{{\rm{d}}x}}{(\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}})^{\rm{T}}},$

(3)

${\left[ {{\bf{ \pmb{\mathit{ ω}} }}_{\rm{C}}^{\rm{V}}} \right]_{\rm X}} = \left[ {\begin{array}{*{20}{c}} {\;0}&{ - {{\bf{ \pmb{\mathit{ ω}} }}_z}}&{\;\;{{\bf{ \pmb{\mathit{ ω}} }}_y}} \\ {\;\;{{\bf{ \pmb{\mathit{ ω}} }}_z}}&0&{ - {{\bf{ \pmb{\mathit{ ω}} }}_x}} \\ { - {{\bf{ \pmb{\mathit{ ω}} }}_y}}&{\;{{\bf{ \pmb{\mathit{ ω}} }}_x}}&0 \end{array}} \right],$

(4)

其中： $\mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}$ 表示世界坐标系到相机坐标系的旋转矩阵； ${\bf{ \pmb{\mathit{ ω}} }}_{\rm{C}}^{\rm{V}}$ 表示在相机标系下的视觉角速度； ${{\bf{ \pmb{\mathit{ ω}} }}_x}$ 、 ${{\bf{ \pmb{\mathit{ ω}} }}_y}$ 、 ${{\bf{ \pmb{\mathit{ ω}} }}_z}$ 分别表示相机坐标系下x、y、z轴上的角速度。

3.2 视觉和IMU参数频域上的同步

由式(4)获取的基于视觉的角速度与从陀螺仪读出的角速度分别在两个坐标系下，即相机坐标系和IMU坐标系。为了同步基于视觉和IMU的参数，需要相机坐标系和IMU坐标系的旋转矩阵，其表达式：

$\left\{\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}}, \boldsymbol{b}_{\mathrm{C}}^{\mathrm{\omega}}, t_{\mathrm{o}}\right\}=\arg \min \sum\limits_{t}\left\|\boldsymbol{\omega}_{\mathrm{C}}^{\mathrm{V}}(t)-\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}} \boldsymbol{\omega}_{\mathrm{B}}^{\mathrm{I}}\left(t+t_{\mathrm{o}}\right)+\boldsymbol{b}_{\mathrm{C}}^{\omega}\right\|^{2},$

(5)

其中： $\mathit{\boldsymbol{R}}_{\rm{B}}^{\rm{C}}$ 表示IMU坐标系到相机坐标系的旋转矩阵， $\mathit{\boldsymbol{b}}_{\rm{C}}^{\rm{ \mathit{ ω} }}$ 为在相机坐标系下的陀螺仪零偏，t_o为最优的时间戳偏移量。

3.3 相机坐标系下重力加速度的估计

单目相机尺度因子估计的目的是求解出一个相对精确的尺度来修正重建目标的大小。本文采用比较基于视觉和基于IMU获取的加速度值进行尺度估计的方法。由于世界坐标系下的重力加速度 ${g_{\rm{W}}}$ 不能通过相机直接观测到，所以基于视觉和基于IMU的加速度值不能直接进行比较，需要估计相机坐标系下的重力加速度，其式：

$\begin{array}{*{20}{c}} {\left\{\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}}, \boldsymbol{b}_{\mathrm{C}}^{\mathrm{a}}, g_{\mathrm{W}}\right\}=\arg \min \sum\limits_{t}\left\|s \boldsymbol{\alpha}_{\mathrm{C}}^{\mathrm{V}}(t)-\boldsymbol{\alpha}_{\mathrm{C}}^{\mathrm{I}}(t)+\boldsymbol{b}_{\mathrm{C}}^{\mathrm{a}}+\boldsymbol{R}_{\mathrm{W}}^{\mathrm{V}} g_{\mathrm{w}}\right\|^{2}}, \\ {\boldsymbol{\alpha}_{\mathrm{C}}^{\mathrm{I}}(t)=\boldsymbol{R}_{\mathrm{B}}^{\mathrm{C}} \boldsymbol{\alpha}_{\mathrm{B}}^{\mathrm{I}}}, \end{array}$

(6)

其中： ${\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{V}}$ 表示由相机坐标系下的加速度，可由视觉获取的位置坐标二次积分获取； ${\bf{ \pmb{\mathit{ α}} }}_{\rm{B}}^{\rm{I}}$ 表示IMU坐标系下加速度计的读数； ${\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{I}}$ 表示经过旋转变换后的在相机坐标系下的加速度； $s$ 表示单目相机的初始尺度因子； ${\bf{ \pmb{\mathit{ b}} }}_{\rm{C}}^{\rm{ \mathit{ α} }}$ 表示加速度计的零偏。他们的计算式：

$s = \arg \min {\sum\limits_t {\left\| {s{\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{V}}(t) - {\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{I}}(t)} \right\|} ^2},$

(7)

$\left\{ {s, {\bf{ \pmb{\mathit{ b}} }}_{\rm{C}}^{\rm{ \mathit{ α} }}} \right\}{\rm{ = arg}}\;{\rm{min}}{\sum\limits_t {\left\| {s{\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{V}}(t) - {\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{I}}(t){\rm{ + }}{\bf{ \pmb{\mathit{ b}} }}_{\rm{C}}^{\rm{ \mathit{ α} }}} \right\|} ^2}。$

(8)

3.4 单目相机绝对尺度的估计

上一步估计的单目尺度是在时域上获取，但是相机和IMU观测的时间戳偏移量可能会随着时间的变化而略有变化，在时域中估计的单目相机尺度具有不准确性。接下来将在频域中估计单目相机的尺度，通过傅里叶变换将时域中的相机坐标系下的视觉和IMU的加速度变换到频域中，如下所示：

${A^{\rm{V}}}(f) = \mathcal{F}\left\{ {\left. {s{\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{V}}(t)} \right\}} \right.,$

(9)

${A^{\rm{I}}}(f) = \mathcal{F}\left\{ {\left. {s{\bf{ \pmb{\mathit{ α}} }}_{\rm{C}}^{\rm{I}}(t) - {\bf{ \pmb{\mathit{ b}} }}_{\rm{C}}^{\rm{ \mathit{ α} }} - \mathit{\boldsymbol{R}}_{\rm{W}}^{\rm{V}}(t){g_{\rm{W}}}} \right\}} \right.,$

(10)

其中： ${\left\| {{g_{\rm{W}}}} \right\|^2}{\rm{ = }}9.8$ ； $\mathcal{F}\left\{ \cdot \right\}$ 表示傅里叶变化； ${A^{\rm{V}}}(f)$ 为相机坐标系下的基于视觉的加速度在频域上的表示； ${A^{\rm{I}}}(f)$ 为相机坐标系下的基于IMU的加速度在频域上的表示。通过最小化视觉和IMU加速度的幅值，在频域中估算的单目相机尺度为

$\left\{ {s, {\bf{ \pmb{\mathit{ b}} }}_{\rm{C}}^{\rm{ \mathit{ α} }}, {g_{\rm{W}}}} \right\}{\rm{ = }}\arg \;\min \sum\limits_f^{{f_{\max }}} {{{\left\| {{\rm{ }}\left| {{A^{\rm{V}}}(f)} \right| - \left| {{A^{\rm{I}}}(f)} \right|{\rm{ }}} \right\|}^2}} ,$

(11)

其中 ${f_{\max }}$ 设置为默认值1.2。

4. 基于截断符号距离场算法的点云融合

本文在进行点云融合时使用了截断符号距离场(truncated signed distance function，TSDF)算法，该方法只存储距离真实表面较近的数层体素，而不是所有体素，因此能够大幅降低计算机的内存消耗，减少模型冗余点。

对于某个度量空间中一个集合Ω的TSDF，它决定了度量空间中任意一点x到集合Ω边界的距离，如果x在Ω的内部，则TSDF为正；如果x在Ω的外部，则TSDF值为负，并且x距离Ω的边界越近，TSDF的值越接近0。在Ω的边界处，TSDF的值为0。

点云融合需要在全局坐标系中进行，因此结合TSDF的理论，用一个立方体来表示全局坐标系所在的三维空间，可以称其为每一个体素存放的是该体素到重建后模型表面的距离D和权重W。令(X，d)表示一个度量空间，则TSDF的大小用如下表达式：

$f(x) = \left\{ \begin{gathered} d(x, {\Omega ^c})\;, \;x \in \Omega \\ - d(x, \Omega )\;, \;x \in {\Omega ^c} \\ \end{gathered} \right.\;\;,\\ d(x, \Omega ) = \mathop {\inf d(x, y)\;\;}\limits_{y \in \Omega },$

(12)

其中：inf(d(x, y))是最大下界，指小于等于d(x, y)的所有其他元素的最大元素。

正负表示在表面内部和外部，体素中距离为负值表示当前这个体素在模型内部，距离为正表示当前这个体素在模型外部，距离为0表示当前这个体素在模型的表面。

要进行点云融合首先要建立全局数据立方体。为了通过GPU提高运算速度，全局数据立方体存储在显存中。将立方体的边长设定为3 m，每个坐标轴的体素数量N设定为512，则每个体素的边长为6 mm，距离D和权重W都用short类型保存，因此需要512 M显存，增加N的大小可以提高重建模型的精度，但是也会提高所需显存的大小。初始化时，立方体中的所有体素初始值为D=1，W=0，立方体中心的坐标为(1.5，1.5，1.5)，相机的初始位置为(−1.5，−1.5，−0.5)(在此位置相机的视野较好，可以拍摄到大部分位置)，在获取第i帧点云后，对于立方体中的每一个体素，需要进行以下步骤：

(a) 首先获得体素在全局坐标系下的坐标 ${V^{\rm{g}}}(x, y, z)$ ，然后根据ORB-SLAM2获取的变换矩阵将其从全局坐标系转换到相机坐标系，得到 $V(x, y, z)$ ；

(b) 根据相机的内参矩阵转换到图像坐标系，得到一个图像坐标 $(u, v)$ ；

(c) 如果第i帧深度图像 $D(u, v)$ 处的深度值不为0，则比较 $D(u, v)$ 与体素相机坐标 $V(x, y, z)$ 中z的大小，如果 $D(u, v) > z$ ，说明此体素离相机更近，在重建表面的外部；如果 $D(u, v) < z$ ，说明此体素离相机更远，在重建表面的内部；

(d) 最后根据(c)中的结果更新此体素中距离值D和权重W。更新式为

${W_i}(x, y, z) = \min ({W_{\max }}, {W_{i{\rm{ - 1}}}}(x, y, z) + 1),$

${D_i}(x, y, z) = \frac{{{W_{i - {\rm{1}}}}(x, y, z){D_{i - 1}}(x, y, z) + {W_i}(x, y, z){d_i}(x, y, z)}}{{{W_{i{\rm{ - 1}}}}(x, y, z) + {W_i}(x, y, z)}}$ $sd{f_i} = {D_i}(u, v) - V.z$ ,

$d_{i}(x, y, z)=\left\{\begin{array}{l}{\min \left(1, s \mathrm{d} f_{i} / T_{\max }\right) \quad \operatorname{sd} f_{i} \gt 0} \\ {\max \left(-1, s \mathrm{d} f_{i} / T_{\max }\right) \quad \operatorname{sd} f_{i} \lt 0}\end{array}\right.,$

(13)

其中： ${W_i}(x, y, z)$ 为当前帧全局数据立方体中体素的权重， ${W_{i - {\rm{1}}}}(x, y, z)$ 为上一帧全局数据立方体中体素的权重，W_max为最大权重，本文中设定为1， ${D_i}(x, y, z)$ 为当前帧全局数据立方体中体素到物体表面的距离， ${D_{i - 1}}(x, y, z)$ 为上一帧全局数据立方体体素到物体表面的距离， ${d_i}(x, y, z)$ 为根据当前帧深度数据计算得到的全局数据立方体中体素到物体表面的距离， $V.z$ 表示体素在相机坐标系下的z轴坐标， ${D_i}(u, v)$ 表示当帧图像深度 $(u, v)$ 处的深度值，T_max为截断范围，范围的大小会影响重建结果的精细程度。

在全局数据立方体的二维示意图中，网格中的值代表对应体素到重建表面的距离，其中在交界处的位置即是模型表面所在的位置。因此，在全局数据立方体中就隐含了重建出的模型表面信息，只需要遍历所有体素就可以提取出模型点云数据。使用TSDF全局数据立方体来进行点云融合，由于全局数据立方体是由体素组成，且体素的数目是固定的，可以避免造成点云的冗余，且计算过程在GPU中进行，计算速度快，从而加速点云的融合。

5. 实验分析与结果

本文运动恢复结构方法的深度图预测采用Depth CNN模型，在此基础上调整训练的学习率和平滑权重参数，最终在自己采集的数据上进行训练。而单目相机的尺度恢复借助于IMU传感单元，同一时刻通过视觉获取的加速度、角速度和IMU采集到的加速度、角速度相同。将ORB-SLAM2获取的基于视觉的旋转矩阵和IMU获取的数据进行融合，即可获取单目相机的尺度。再根据已有的深度图、运动轨迹的旋转矩阵，采用TSDF融合算法恢复出场景的三维结构。

5.1 实验配置

为了验证本文方法的可靠性与准确性，搭建的实验平台如图 3所示，平台主要包括ZED双目立体相机、IMU、USB单目摄像头。其中ZED双目立体相机是一款商业化的双目相机，数据采集系统精度在1%以内，可以采集左右图像、深度图、相机运动轨迹以及图像点云；IMU采用的LP-RESEARCH公司的LPMS-USBAL惯性传感器，采用USB通信接口，是一款小型高精度金属外壳型的姿态传感器，集成了陀螺仪、加速度计、磁力计；USB单目相机采用全局快门灰度相机，结构简单，价格低廉，可以快速捕捉运动物体，在实验中用来采集分辨率为416×128的灰度图片，用于Depth CNN的测试数据和单目相机尺度的恢复。实验中主要用到的硬件为主频3.4 GHz的Intel Xeon E5处理器和双核24 GB显存的Nvidia Tesla K80显卡。

图 3. 实验平台

Figure 3. The experiment platform

下载: 全尺寸图片幻灯片

5.2 数据采集

数据采集主要分为训练数据和测试数据。训练数据包括ZED相机的左侧图像序列和对应的深度图，针对校园一角的雕塑进行采集，共7组数据，14837张单幅RGB图像以及相应的14837张深度图，图像分辨率为1920×1080，采样率为30 f/s。测试数据主要包括灰度图像和IMU数据，单幅灰度图像由USB全局快门单目相机采集，分辨率为752×480，采集率为30 f/s；IMU数据包括时间戳、加速度以及角速度，采样率为200 f/s。

5.3 实验结果

为验证本文提出方法的性能，基于KITTI数据集训练得到网络模型，使用采集的数据进一步进行优化训练，训练数据集包含14837张分辨率为1920×1080的图片，这些图片经过下采样生成分辨率为416×128的图片作为网络的输出。训练的学习率(Learning_rate)设置为0.0002，平滑权重(Smooth_weight)为0.5，整个模型训练耗时约为50 h，共迭代了20000步。将本文采用的Depth CNN网络和Godard等^[21]提出的左右一致性检测的神经网络进行对比，使用一张左图生成左图视差值，再根据左图视差值获取右图视差值，由于左右视差一致性，可将该网络估计出的左视差图和右视差图进行匹配，利用匹配后RGB图像的强度偏差来构建损失函数，是一种无监督的学习方式。单幅图像深度预测如图 4所示，图 4(a)是在校园拍摄的博弈雕塑原图；图 4(b)是本文使用Depth CNN预测的深度图；图 4(c)是相应的真实深度图，真实深度图是通过ZED双目立体相机采集得到；图 4(d)是Godard等^[21]提出的网络预测结果。与Godard等^[21]相对比，本文网络在收缩部分融合了卷积层的特征信息，使得该网络对卷积特征的局部信息利用得更加充分，从而对输出的深度图的局部细节处理更好，从图中可知本文方法预测的深度图更加接近于真实深度图。

图 4. 博弈雕塑的Depth CNN预测效果图。(a)原图；(b) Depth CNN预测深度图；(c)真实图；(d) Godard等^[21]预测深度图

Figure 4. Predictions on sculpture. (a) Origin image; (b) Depth CNN; (c) Ground truth; (d) Godard et al^[21]

下载: 全尺寸图片幻灯片

深度估计误差如表 1所示，前四列数据为深度估计的误差值，该值越小表示预测的单幅图像的深度图越精确；后三列数据是深度估计的准确率，其值越接近于1，表示预测效果越接近于真实深度图。第一行是Depth CNN在KITTI数据集上的实验结果，第二行是Godard等^[21]在KITTI数据集上的预测结果，可以看出Godard等^[21]方法在精确度和准确率略优于本文使用的方法，但是从第三、四行在自己采集的数据集上的实验效果，可以得到Depth CNN网络更优于文献[21]的方法，误差明显小于文献[21]的实验结果。这是由于文献[21]网络预测的单幅图像实质上是基于双目相机的左右图实现的，该网络在训练和测试步骤都需要双目相机之间的基线；而在本文实验中训练采用的是双目相机，基线是双目相机的左右相机的距离，但是在测试阶段使用的是单目全局快门采集测试的图像序列，因此本文的方法优于文献[21]。

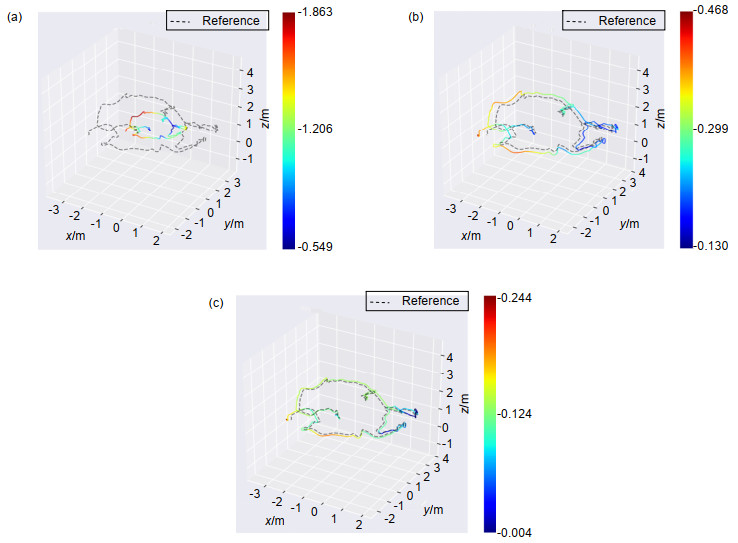
表 1. 深度估计误差表

Table 1. Errors of depth prediction

Method	Dataset	Abs_rel	Sq_rel	RMS	Log_RMS	a₁ < 1.25	a₂ < 1.25²	a₃ < 1.25³
Depth CNN	Kitti	0.208	1.768	6.856	0.283	0.678	0.885	0.975
Godard等^[21]	Kitti	0.148	1.344	5.927	0.247	0.803	0.922	0.964
Depth CNN	Ours	0.192	1.576	6.857	0.2737	0.737	0.903	0.959
Godard等^[21]	Ours	0.213	3.819	8.519	0.322	0.758	0.889	0.943

| Show Table

DownLoad: CSV

为了恢复场景中物体的真实大小，本文提出融合视觉和IMU数据获取单目相机的尺度因子。使用ORB-SLAM2算法可以获取到相机的轨迹与真实轨迹的对比如图 5所示，其中实线表示ORB-SLAM2的获取的运动轨迹，虚线表示运动轨迹的真实值。其中运动轨迹的真实值是由ZED双目立体相机采集获取。从图中清楚地看到，通过ORB-SLAM2获取的运动轨迹与真实值存在一个尺度差异，通过本文提出的单目相机尺度恢复方法，将获取的图像和IMU参数进行融合，获取单目相机的真实运动轨迹。为验证本文单目尺度恢复方法的准确性，将本文方法与VIORB方法进行对比，VIORB算法是在ORB-SLAM2基础上，加入了IMU的观测，恢复出具有尺度信息的三维场景结构。图 5(a)表示ORB-SLAM2方法的轨迹与真实轨迹的对比图，图 5(b)为VIORB方法的轨迹估计与真实轨迹的对比图，图 5(c)为本文使用的恢复尺度的方法。表 2是三种方法的运动轨迹误差，可以清晰地看出，ORB-SLAM2方法的相机运动轨迹与真实轨迹缺少一个尺度因子的关系，最大误差为1.863 m，平均误差为1.676 m；加入IMU的VIORB方法的最大误差在0.468 m，平均误差为0.259 m。由此可以看出，相比于基于视觉的轨迹估计，视觉-IMU的轨迹估计具有较好精确性；本文基于IMU和ORB-SLAM2的频域恢复单目尺度方法，最大误差为0.244 m，平均误差为0.111 m。由此可见，本文方法估计的单目相机尺度具有更高的准确性。

图 5. 运动轨迹对比图。(a) ORB-SLAM2；(b) VIORB；(c)本文方法

Figure 5. Comparison of trajectory. (a) ORB-SLAM2; (b) VIORB; (c) Ours method

下载: 全尺寸图片幻灯片

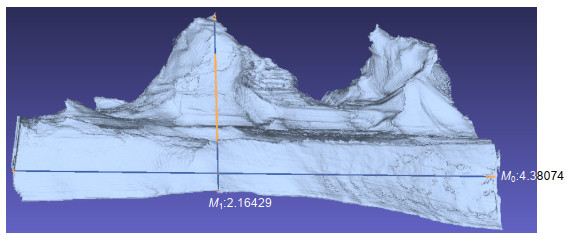
表 2. 运动轨迹误差表

Table 2. Errors of trajectory

	RMSE	Maximum	Minimum	Median	Mean
ORB-SLAM2^[12]	1.207	1.8631	0.5493	1.1391	1.6763
VIORB^[17]	0.2672	0.4675	0.1295	0.2538	0.2594
本文方法	0.1174	0.2435	0.00422	0.1188	0.1112

| Show Table

DownLoad: CSV

在已获取深度图片和具有真实尺度的运动轨迹基础上，最后采用TSDF体素融合的方法，快速恢复出场景的三维点云。选择相机的初始坐标为(−1.5，−1.5，0.5)，立方体的边长设定为3 m，每个坐标轴的体素数量为500，则每个体素的边长为6 mm，最终恢复出真实尺度模型如图 6所示。重建博弈雕塑模型的对比如表 3所示，表中真实值是使用卷尺实际测量获取。博弈雕塑的真实长度为4.5 m，高位1.9 m，重建的模型长度为4.38 m，高为2.16 m。通过本文方法恢复的三维结构与物体的真实尺寸相差0.2 m，证明了本文真实尺度恢复三维结构的可行性与准确性。

图 6. 博弈雕塑真实尺度模型

Figure 6. Equal scale model of sculpture

下载: 全尺寸图片幻灯片

表 3. 真实尺度模型的对比表

Table 3. Comparison of real size reconstruction

	Height/m	Width/m
Reconstruction size	2.16	4.38
Real size	1.9	4.5

| Show Table

DownLoad: CSV

6. 结论

本文提出了一种基于深度学习真实尺度恢复三维结构的方法。在基于视觉的三维重建方法中引入IMU的观测数据，在时域和频域上对相机位姿进行协调，在频域中获取单目相机的尺度因子，解决了单目相机用于三维重建缺少尺度的问题，提升了重建模型的真实性；将单幅图像深度估计的卷积神经网络应用到运动恢复结构中，通过卷积-反卷积的对称型网络预测单幅图像的深度图，解决了卷积神经网络输出图像分辨率低，缺少重要特征信息的问题，提高了单幅图像深度预测的精度。通过实验得到，Depth CNN网络获取的单目图像绝对值误差达到了0.192，准确率高达0.959；相比于VIORB，本文恢复单目相机尺度的方法获取的相机运动轨迹的最大误差由0.48 m减少到0.24 m；最终重建的三维模型与真实大小之间有0.2 m左右的误差，验证了本文方法的有效性与准确性。

图 1 基于深度学习真实尺度运动恢复结构流程图

Figure 1. Equal scale structure from motion based on deep learning

下载: 全尺寸图片幻灯片

图 2 深度图网络结构

Figure 2. Network architecture for depth

下载: 全尺寸图片幻灯片

图 3 实验平台

Figure 3. The experiment platform

下载: 全尺寸图片幻灯片

图 4 博弈雕塑的Depth CNN预测效果图。(a)原图；(b) Depth CNN预测深度图；(c)真实图；(d) Godard等^[21]预测深度图

Figure 4. Predictions on sculpture. (a) Origin image; (b) Depth CNN; (c) Ground truth; (d) Godard et al^[21]

下载: 全尺寸图片幻灯片

图 5 运动轨迹对比图。(a) ORB-SLAM2；(b) VIORB；(c)本文方法

Figure 5. Comparison of trajectory. (a) ORB-SLAM2; (b) VIORB; (c) Ours method

下载: 全尺寸图片幻灯片

图 6 博弈雕塑真实尺度模型

Figure 6. Equal scale model of sculpture

下载: 全尺寸图片幻灯片

表 1 深度估计误差表

Table 1. Errors of depth prediction

Method	Dataset	Abs_rel	Sq_rel	RMS	Log_RMS	a₁ < 1.25	a₂ < 1.25²	a₃ < 1.25³
Depth CNN	Kitti	0.208	1.768	6.856	0.283	0.678	0.885	0.975
Godard等^[21]	Kitti	0.148	1.344	5.927	0.247	0.803	0.922	0.964
Depth CNN	Ours	0.192	1.576	6.857	0.2737	0.737	0.903	0.959
Godard等^[21]	Ours	0.213	3.819	8.519	0.322	0.758	0.889	0.943

下载: 导出CSV

表 2 运动轨迹误差表

Table 2. Errors of trajectory

	RMSE	Maximum	Minimum	Median	Mean
ORB-SLAM2^[12]	1.207	1.8631	0.5493	1.1391	1.6763
VIORB^[17]	0.2672	0.4675	0.1295	0.2538	0.2594
本文方法	0.1174	0.2435	0.00422	0.1188	0.1112

下载: 导出CSV

表 3 真实尺度模型的对比表

Table 3. Comparison of real size reconstruction

	Height/m	Width/m
Reconstruction size	2.16	4.38
Real size	1.9	4.5

下载: 导出CSV

参考文献(21)

[1]	刘钢, 彭群生, 鲍虎军.基于多幅图像的场景交互建模系统[J].计算机辅助设计与图形学学报, 2004, 16(10): 1419-1424, 1429. doi: 10.3321/j.issn:1003-9775.2004.10.017 Liu G, Peng Q S, Bao H J. An interactive modeling system from multiple images[J]. Journal of Computer-Aided Design & Computer Graphics, 2004, 16(10): 1419-1424, 1429. doi: 10.3321/j.issn:1003-9775.2004.10.017
[2]	曹天扬, 蔡浩原, 方东明, 等.基于视觉内容匹配的机器人自主定位系统[J].光电工程, 2017, 44(5): 523-533. doi: 10.3969/j.issn.1003-501X.2017.05.008 http://www.oejournal.org/J/OEE/Article/Details/A170830000017/CN Cao T Y, Cai H Y, Fang D M, et al. Robot vision localization system based on image content matching[J]. Opto-Electronic Engineering, 2017, 44(5): 523-533. doi: 10.3969/j.issn.1003-501X.2017.05.008 http://www.oejournal.org/J/OEE/Article/Details/A170830000017/CN
[3]	Tomasi C, Kanade T. Shape and motion from image streams under orthography: a factorization method[J]. International Journal of Computer Vision, 1992, 9(2): 137-154. http://d.old.wanfangdata.com.cn/NSTLQK/10.1007-BF00129684/
[4]	Pollefeys M, Koch R, van Gool L. Self-calibration and metric reconstruction inspite of varying and unknown intrinsic camera parameters[J]. International Journal of Computer Vision, 1999, 32(1): 7-25. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7849273aab77dec70570d15320209554
[5]	戴嘉境.基于多幅图像的三维重建理论及算法研究[D].上海: 上海交通大学, 2012. Dai J J. Research on the theory and algorithms of 3D reconstruction from multiple images[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[6]	张涛.基于单目视觉的三维重建[D].西安: 西安电子科技大学, 2014. Zhang T. 3D reconstruction based on monocular vision[D]. Xi'an: Xidian University, 2014.
[7]	许允喜, 陈方.基于多帧序列运动估计的实时立体视觉定位[J].光电工程, 2016, 43(2): 89-94. doi: 10.3969/j.issn.1003-501X.2016.02.015 http://www.cnki.com.cn/Article/CJFDTotal-GDGC201602016.htm Xu Y X, Chen F. Real-time stereo visual localization based on multi-frame sequence motion estimation[J]. Opto-Electronic Engineering, 2016, 43(2): 89-94. doi: 10.3969/j.issn.1003-501X.2016.02.015 http://www.cnki.com.cn/Article/CJFDTotal-GDGC201602016.htm
[8]	黄文有, 徐向民, 吴凤岐, 等.核环境水下双目视觉立体定位技术研究[J].光电工程, 2016, 43(12): 28-33. doi: 10.3969/j.issn.1003-501X.2016.12.005 http://www.oejournal.org/J/OEE/Article/Details/A180808000013/CN Huang W Y, Xu X M, Wu F Q, et al. Research of underwater binocular vision stereo positioning technology in nuclear condition[J]. Opto-Electronic Engineering, 2016, 43(12): 28-33. doi: 10.3969/j.issn.1003-501X.2016.12.005 http://www.oejournal.org/J/OEE/Article/Details/A180808000013/CN
[9]	Yi K M, Trulls E, Lepetit V, et al. LIFT: learned invariant feature transform[C]//Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 467-483.
[10]	He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 770-778.
[11]	Newell A, Yang K Y, Deng J. Stacked hourglass networks for human pose estimation[C]//Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 483-499.
[12]	Zhou T H, Brown M, Snavely N, et al. Unsupervised learning of depth and ego-motion from video[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 6612-6619.
[13]	Newcombe R A, Izadi S, Hilliges O, et al. Kinect Fusion: real-time dense surface mapping and tracking[C]//Proceedings of the 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 2011: 127-136.
[14]	Usenko V, Engel J, Stückler J, et al. Direct visual-inertial odometry with stereo cameras[C]//Proceedings of 2016 IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 2016: 1885-1892.
[15]	Concha A, Loianno G, Kumar V, et al. Visual-inertial direct SLAM[C]//Proceedings of 2016 IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 2016: 1331-1338.
[16]	Ham C, Lucey S, Singh S. Hand waving away scale[C]//Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 279-293.
[17]	Mur-Artal R, Tardós J D. Visual-inertial monocular SLAM with map reuse[J]. IEEE Robotics and Automation Letters, 2017, 2(2): 796-803. doi: 10.1109/LRA.2017.2653359
[18]	Mur-Artal R, Tardós J D. ORB-SLAM2: an open-source slam system for monocular, stereo, and RGB-D cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1255-1262. doi: 10.1109/TRO.2017.2705103
[19]	Ham C, Lucey S, Singh S. Absolute scale estimation of 3d monocular vision on smart devices[M]//Hua G, Hua X S. Mobile Cloud Visual Media Computing: From Interaction to Service. New York: Springer International Publishing, 2015: 329-344.
[20]	Mustaniemi J, Kannala J, S rkk S, et al. Inertial-based scale estimation for structure from motion on mobile devices[C]//Proceedings of 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 2017: 4394-4401.
[21]	Godard C, Mac Aodha O, Brostow G J. Unsupervised monocular depth estimation with left-right consistency[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 2017: 6602-6610.

施引文献

期刊类型引用(4)

1.	俞盛旗，胡栋，刘威. 基于视觉的光学三维重建技术及其在农作物信息感知中的应用. 激光与光电子学进展. 2024(04): 49-57 . 百度学术
2.	张波涛，李正强，华超豪，谢佳龙，吕强. 基于多视角融合的手眼协同超视野目标测量与3D重建. 光电工程. 2024(10): 113-127 . 本站查看
3.	李俊学，张国良，陈钰婕. 移动机器人VSLAM和VISLAM技术综述. 四川轻化工大学学报(自然科学版). 2021(03): 77-86 . 百度学术
4.	汪侃，龚俊，魏敬和，朱策，刘凯. 邻图配对式运动恢复结构的欧式三维重建. 红外与激光工程. 2020(06): 138-145 . 百度学术

其他类型引用(3)

资源附件(0)

访问统计

点击扫一扫

图(6)

表(3)

计量

文章访问数: 10734
PDF下载数: 3250
施引文献: 7

1. 引言
2. 基于Depth CNN网络的真实尺度运动恢复结构方法介绍
3. 基于IMU和ORB-SLAM2的频域单目相机尺度获取
3.1 视觉和IMU参数时域上的同步
3.2 视觉和IMU参数频域上的同步
3.3 相机坐标系下重力加速度的估计
3.4 单目相机绝对尺度的估计
4. 基于截断符号距离场算法的点云融合
5. 实验分析与结果
5.1 实验配置
5.2 数据采集
5.3 实验结果
6. 结论

基于深度学习的真实尺度运动恢复结构方法

作者简介:
陈朋(1981-)，男，博士，副教授，硕士生导师，主要从事嵌入式系统设计、图像处理和模式识别的研究。E-mail：chenpeng@zjut.edu.cn

**^*通讯作者:** 陈朋, E-mail: chenpeng@zjut.edu.cn