E-mail Alert
RSS
Reconstruction of the spatial temperature field based on geometric constraints under a thermal imager
-
摘要:
针对二维热图缺乏空间深度信息，而现有建立目标物体空间温度场模型的多传感器方案存在标定复杂、设备成本高和使用条件受限等问题，本研究提出了一种基于几何约束的单一热像仪下的空间温度场重建方案。首先利用热像仪采集得到温度矩阵，通过自动阈值法将其重新映射到灰度颜色空间，得到目标物清晰的边缘信息从而滤除无关背景，再通过热像仪成像过程中存在的几何约束关系和相机成像原理，直接计算目标物在热像仪坐标系中的位姿关系，然后将目标物体的三维模型投影到二维热图平面，得到三维模型的纹理映射参数，随着热像仪对目标物体多视角的数据采集，完成目标物体表面的空间温度场重建。实验结果表明，与多传感器的空间温度场重建方案相比，本文的单一热像仪方案平均误差仅4.3%，可准确稳定地完成目标物的空间温度场重建。
Abstract:In view of the lack of spatial depth information in two-dimensional heat maps and the problems of complex calibration, high equipment cost, and limited use conditions in the existing multi-sensor schemes to establish the spatial temperature field model of the target object, this study proposes a spatial temperature field reconstruction scheme under a single thermal camera based on geometric constraints. Firstly, the temperature matrix collected by the thermal imager is remapped to the gray color space through the automatic threshold method, and the clear edge information of the target is obtained to filter out the irrelevant background. Then, the pose relationship of the target in the coordinate system of the thermal imager is directly calculated by the geometric constraints existing in the imaging process of the thermal imager and the imaging principle of the camera. Then, the 3D model of the target object is projected to the 2D heat map plane, and the texture mapping parameters of the 3D model are obtained. With the multi-view data acquisition of the target object by the thermal camera, the spatial temperature field reconstruction of the target object surface is completed. The experimental results show that, compared with the multi-sensor spatial temperature field reconstruction scheme, the average error of the single thermal imager scheme in this paper is only 4.3%, which can accurately and stably complete the spatial temperature field reconstruction of the target.
-
Key words:
- temperature model /
- thermal imagery /
- visual geometry /
- 3D reconstruction /
- texture mapping /
- temperature field
-
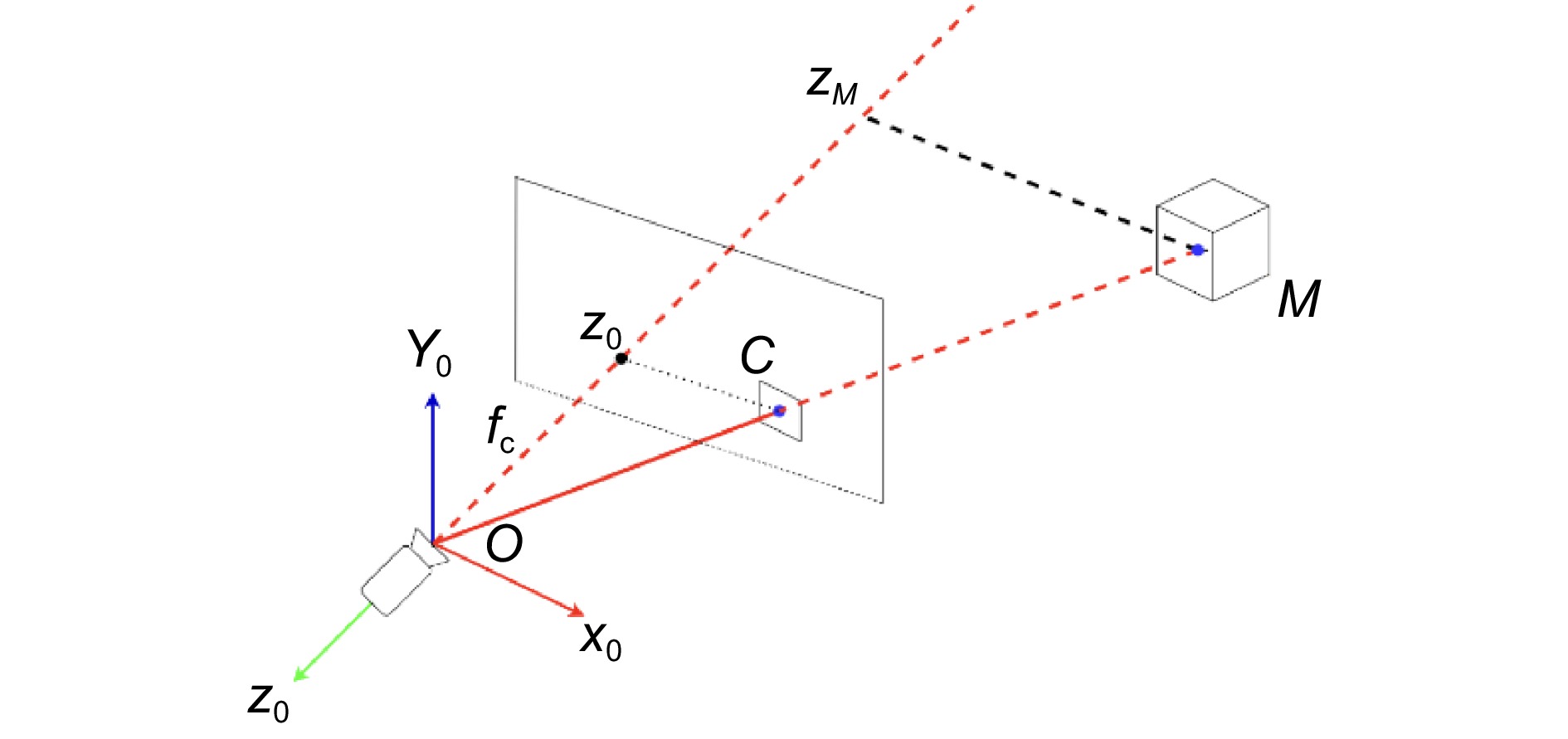
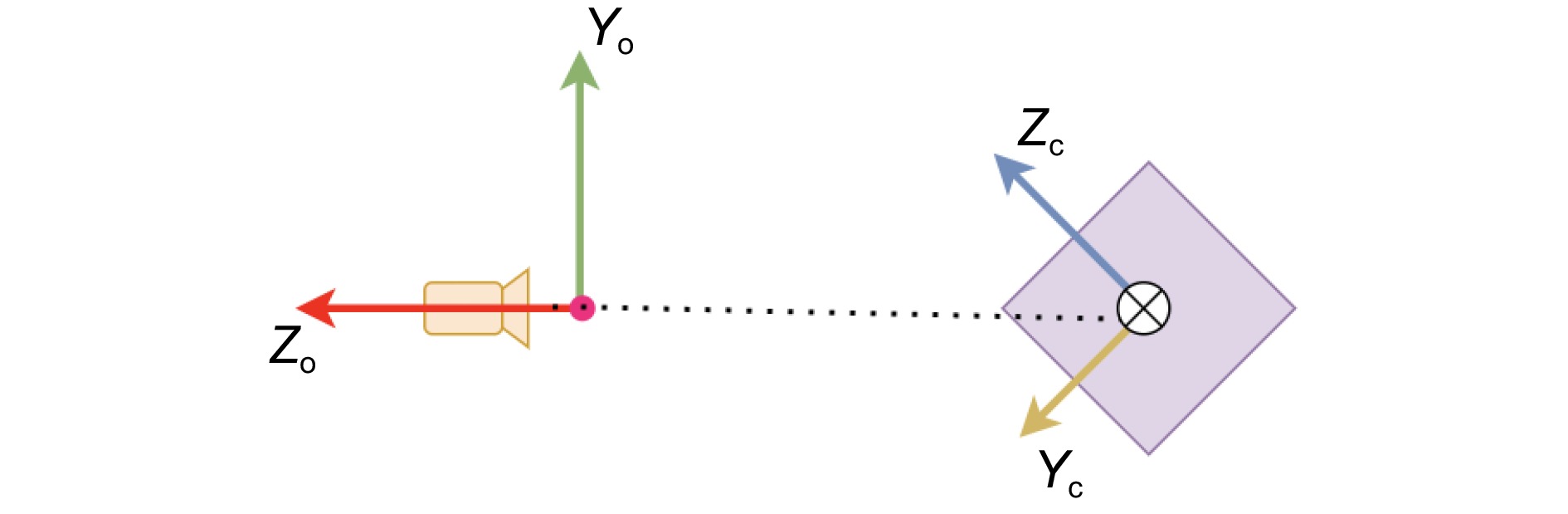
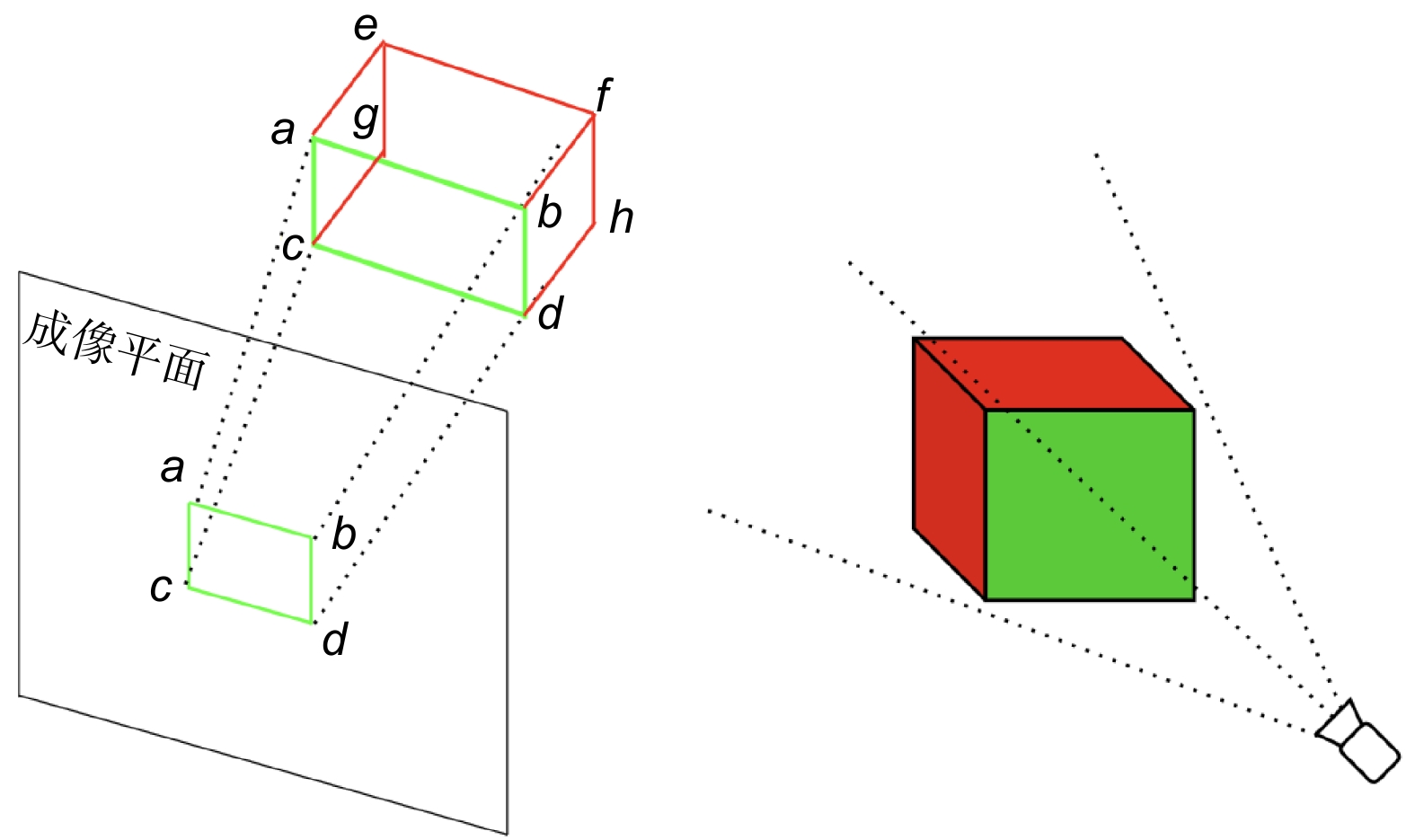
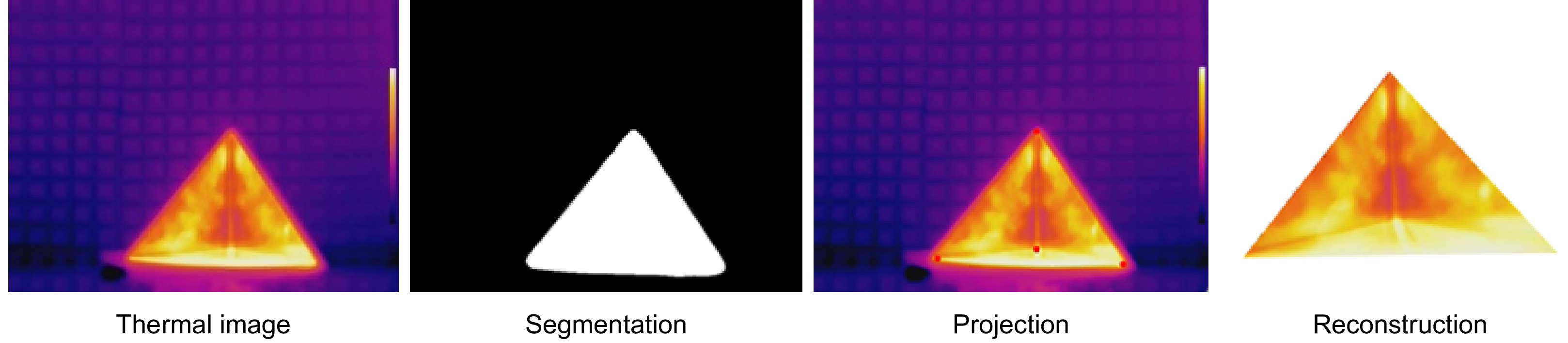
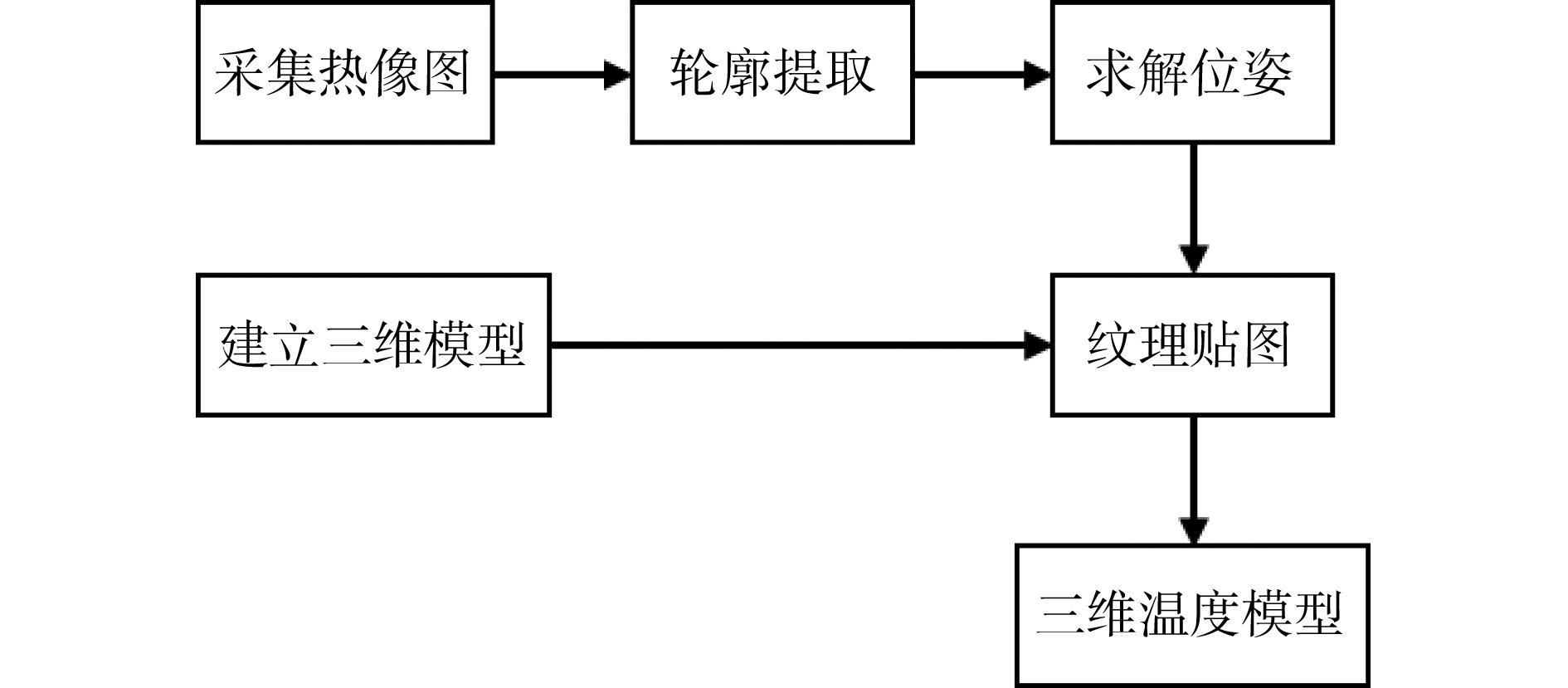
Overview: Thermal imagers can detect the heat distribution on the surface of an object through the reflection of thermal radiation, but two-dimensional heat maps lack spatial information. Establishing the space temperature field model of the target object can significantly increase the information dimension of non-contact temperature measurement and improve the temperature measurement quality. At present, most spatial temperature field reconstruction schemes are based on multi-sensor data fusion to make up for the defects of low texture and low resolution of thermal imaging. However, the existence of multiple sensors will increase the cost of the device, the difficulty of calibration, the complexity of the algorithm, and the constraints of the device. To solve the above problems, a reconstruction scheme of the space temperature field based on geometric constraints under a thermal imager is proposed. The temperature matrix is obtained by analyzing the data collected by the thermal imager and mapped to the gray space by the automatic threshold method. The interference factors are filtered out and the clear edge information of the object is calculated to complete the segmentation process. Then, according to the imaging principle of the thermal imager and the geometric constraints existing in the imaging process, the pose of the target in the thermal imager coordinate system is calculated directly, and the 3D model is projected into the 2D thermal map to get the mapping relationship between 3D and 2D. With the completion of multi-view data acquisition of the target object, the spatial temperature field reconstruction of the target object surface is finally completed, and its spatial temperature field model is obtained. The experimental results show that the proposed scheme can accurately and stably reconstruct the space temperature field of the target object with a small error. Finally, in the comparative experiment part, the proposed method is compared with the spatial temperature field reconstruction schemes under multi-sensor and single sensor respectively. Through the error analysis of the experimental data, it can be concluded that the proposed scheme has excellent performance in accuracy, stability and anti-interference. The proposed scheme also provides a new idea and a feasible scheme for the establishment and measurement of space temperature field under a single sensor.
-
-
图 2 标定板。(a)标定板正视图；(b)标定板侧边视角；(c)标定板热像图；(d)热像图二值化和反色处理
Figure 2. Calibration plates. (a) Positive view of the calibration plate; (b) Side view of the calibration plate; (c) Thermal imge of the calibration plate; (d) Binarization and inversion of the thermal image
图 6 不同目标物、不同背景、不同距离下的轮廓提取结果
Figure 6. Extracted contours of different targets, backgrounds, and distances
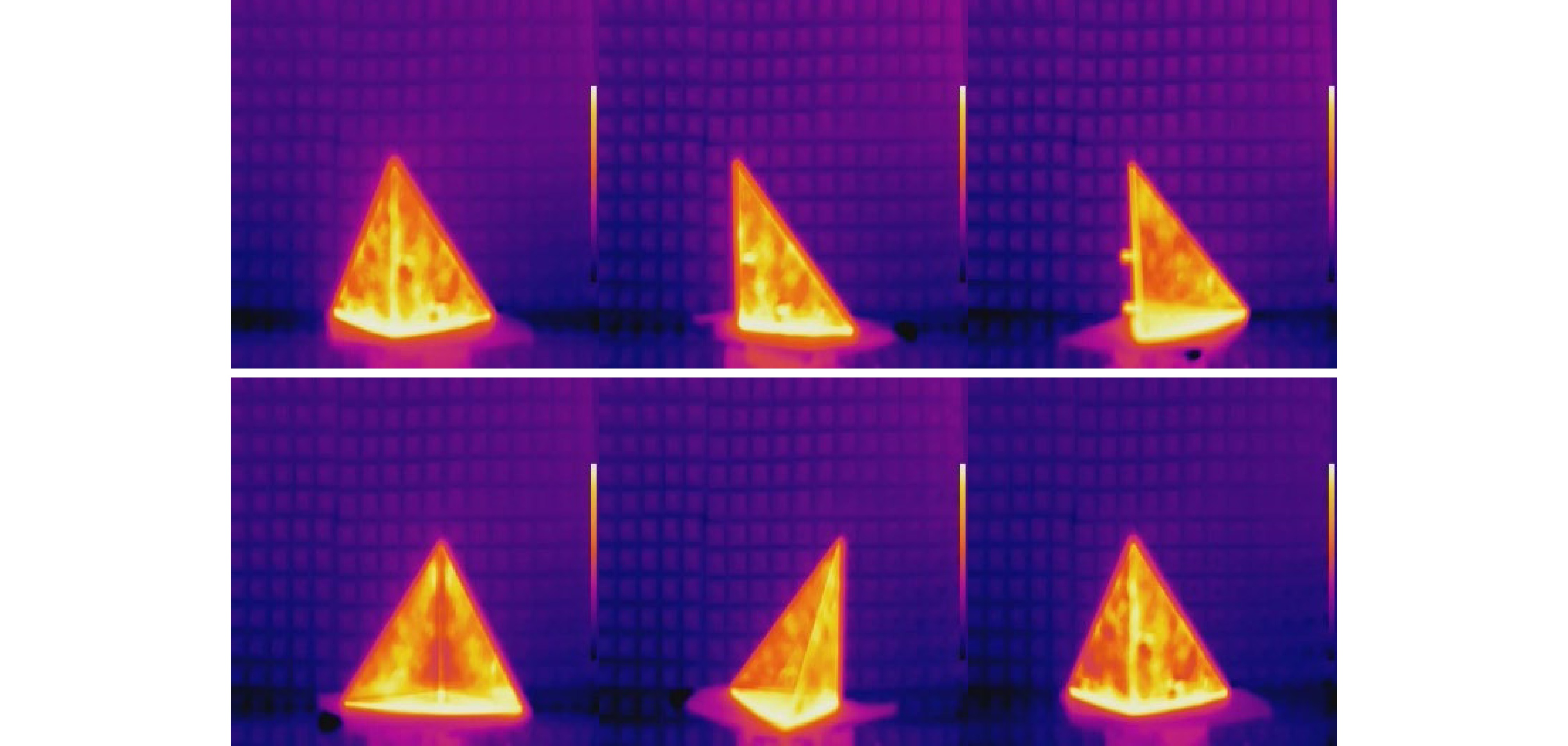
图 17 重建结果(每幅图的左图为采集的热像图，右图为相应的重建结果)。(a) 1.2 m下更换背景对角铁重建；(b) 1.2 m下添加干扰时对角铁重建；(c) 0.6 m下对立放的长方体铁制盒子重建；(d) 0.5 m下对横放的长方体的铝制盒子重建
Figure 17. Reconstruction results (the left image of each image shows the acquired thermal image, and the right image shows the corresponding reconstruction results). (a) Replacement of background diagonal iron reconstruction at 1.2 m; (b) Reconstruction of the angular iron with the addition of interference at 1.2 m; (c) Reconstruction of a rectangular iron box placed in opposition at 0.6 m; (d) Reconstruction of an aluminium box of a horizontal cuboid at 0.5 m
图 18 ArUco标记和可见光相机+热像仪方案(对比验证试验)
Figure 18. ArUco labeling and visible light camera + thermal imager solution (comparative validation tests)
表 1 标定参数
Table 1. Calibration parameters
重投影误差：0.2731 pixel 内参矩阵 $\left[ {\begin{array}{*{20}{c}} {1181.56613}&{0.00000}&{321.50320} \\ {0.00000}&{1180.47294}&{242.93282} \\ {0.00000}&{0.00000}&{1.00000} \end{array}} \right]$ 径向畸变 $ \left[ {\begin{array}{*{20}{c}} {0.16675001}&{0.80421873}&{ - 7.419377} \end{array}} \right] $ 切向畸变 $\left[ {\begin{array}{*{20}{c}} { - 0.00160773}&{ - 0.0024203} \end{array}} \right]$ 
下载: 导出CSV
表 2 联合标定参数
Table 2. Joint calibration parameters
平均重投影误差：0.1893 pixel 旋转矩阵 $\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.9984} \end{array}}&{\begin{array}{*{20}{c}} { - 0.0031} \end{array}}&{\begin{array}{*{20}{c}} { - 0.0573} \end{array}} \\ {\begin{array}{*{20}{c}} {0.0011} \end{array}}&{\begin{array}{*{20}{c}} {0.9994} \end{array}}&{\begin{array}{*{20}{c}} { - 0.0350} \end{array}} \\ {\begin{array}{*{20}{c}} {0.0574} \end{array}}&{\begin{array}{*{20}{c}} {0.0348} \end{array}}&{\begin{array}{*{20}{c}} {0.9977} \end{array}} \end{array}} \right]$ 平移矩阵 $\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 3.2557} \end{array}}&{\begin{array}{*{20}{c}} {54.4585} \end{array}}&{\begin{array}{*{20}{c}} {22.8751} \end{array}} \end{array}} \right]$
下载: 导出CSV
表 3 实验数据
Table 3. Experimental data
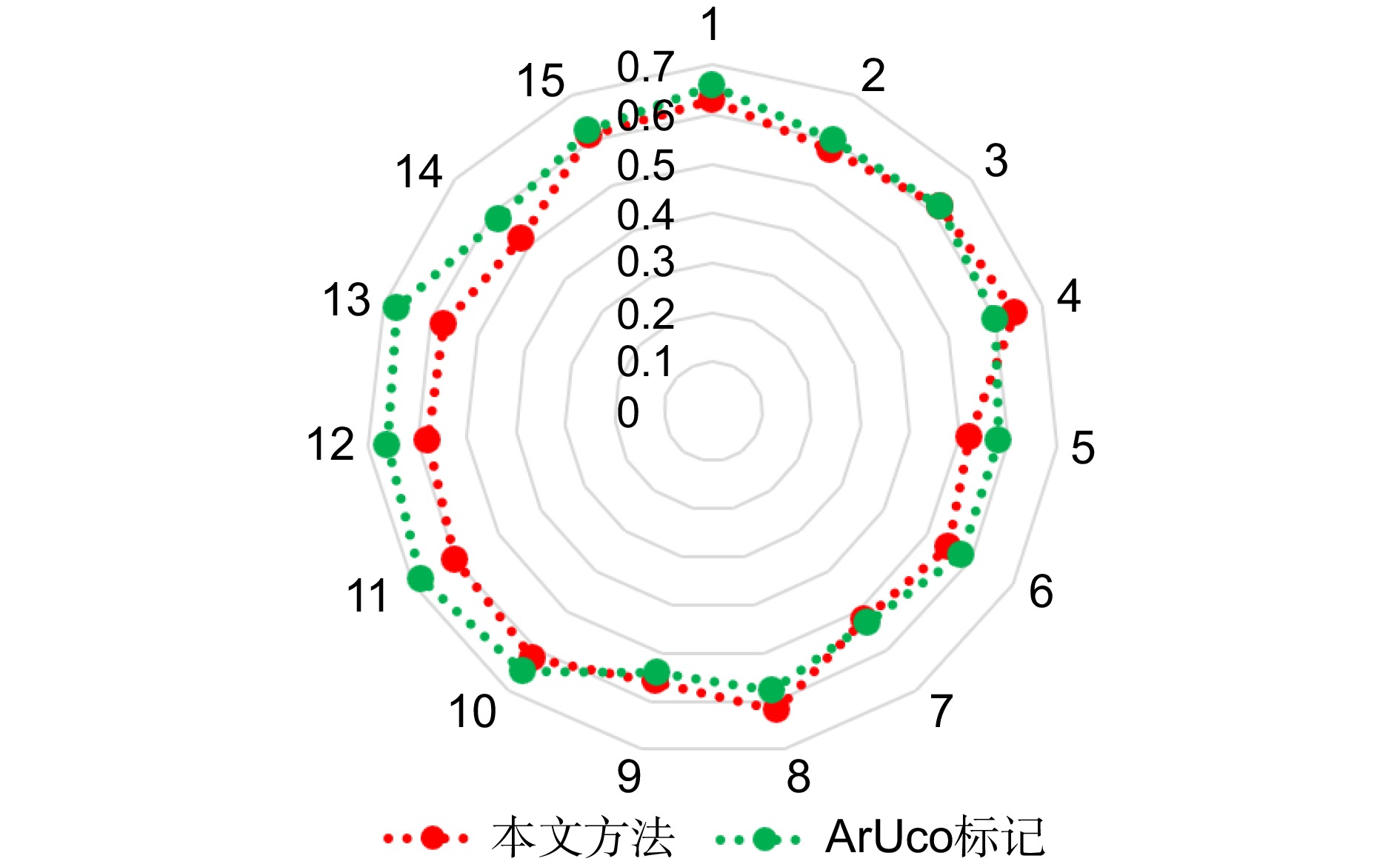
数据帧 本文方法 PNP法 可见光相机+热像仪方法 0 0.6342 0.6164 0.6621 1 0.5830 0.6210 0.6048 2 0.6138 0.5900 0.6241 3 0.6365 0.5946 0.6431 4 0.5242 0.6109 0.5364 5 0.5525 0.6005 0.5873 6 0.5246 0.6312 0.5300 7 0.6234 0.6413 0.5852 8 0.5687 0.6916 0.5468 9 0.6267 0.7354 0.6856 10 0.6354 0.6283 0.6564 11 0.6186 0.6150 0.6664 12 0.6235 0.6104 0.6715 13 0.5535 0.6137 0.5886 14 0.6112 0.6376 0.6274
下载: 导出CSV
表 4 实验数据处理
Table 4. Experimental data processing
最大误差/% 最小误差/% 平均误差/% 误差的方差 本文方法 8.6 1.0 4.3 0.001 PNP法 26.5 1.6 8.5 0.005
下载: 导出CSV
-
[1] 荆建行, 孔明东, 王强, 等. 基于红外热像仪的光学薄膜吸收测试方法[J]. 光电工程, 2021, 48(6): 210071. doi: 10.12086/oee.2021.210071
Jing J H, Kong M D, Wang Q, et al. Measurement of absorption loss of optical thin-film by infrared thermal imaging[J]. Opto-Electron Eng, 2021, 48(6): 210071. doi: 10.12086/oee.2021.210071
[2] 郑海君, 葛斌, 夏晨星, 等. 多特征聚合的红外-可见光行人重识别[J]. 光电工程, 2023, 50(7): 230136. doi: 10.12086/oee.2023.230136
Zheng H J, Ge B, Xia C X, et al. Infrared-visible person re-identification based on multi feature aggregation[J]. Opto-Electron Eng, 2023, 50(7): 230136. doi: 10.12086/oee.2023.230136
[3] 刘皓皎, 刘力双, 张明淳. 基于YOLOv5改进的红外目标检测算法[J]. 激光技术, 2024, 48(4): 534−541. doi: 10.7510/jgjs.issn.1001-3806.2024.04.011
Liu H J, Liu L S, Zhang M C. An improved infrared object detection algorithm based on YOLOv5[J]. Laser Technol, 2024, 48(4): 534−541. doi: 10.7510/jgjs.issn.1001-3806.2024.04.011
[4] Dlesk A, Vach K, Pavelka K. Photogrammetric co-processing of thermal infrared images and RGB images[J]. Sensors, 2022, 22(4): 1655. doi: 10.3390/s22041655
[5] 杨炎龙, 徐超. 一种人体体表三维温度场的融合重建方法[J]. 红外技术, 2022, 44(1): 33−40. doi: 10.11846/j.issn.1001-8891.2022.1.hwjs202201005
Yang Y L, Xu C. Fusion reconstruction method for 3D temperature fields on the human body surface[J]. Infrared Technol, 2022, 44(1): 33−40. doi: 10.11846/j.issn.1001-8891.2022.1.hwjs202201005
[6] 毕淳锴, 张远辉, 付铎. 基于多视角热像图序列的物体表面温度场重建[J]. 计量学报, 2024, 45(7): 997−1006. doi: 10.3969/j.issn.1000-1158.2024.07.09
Bi C K, Zhang Y H, Fu D. Surface temperature field reconstruction based on multi-view thermal image sequence[J]. Acta Metrol Sin, 2024, 45(7): 997−1006. doi: 10.3969/j.issn.1000-1158.2024.07.09
[7] 张远辉, 徐栢锐, 朱俊江, 等. 可见光与热像融合的三维温度模型重建[J]. 计量学报, 2022, 43(2): 256−263. doi: 10.3969/j.issn.1000-1158.2022.02.19
Zhang Y H, Xu B R, Zhu J J, et al. 3D temperature model reconstruction based on fusion of visible and thermal images[J]. Acta Metrol Sin, 2022, 43(2): 256−263. doi: 10.3969/j.issn.1000-1158.2022.02.19
[8] 张建华, 张天晶, 赵岩, 等. 面向室内动态场景的多传感视觉SLAM方法[J]. 信息与控制, 2022, 51(6): 641−650,661. doi: 10.13976/j.cnki.xk.2022.1436
Zhang J H, Zhang T J, Zhao Y, et al. Multi-sensor visual SLAM method for indoor dynamic scenes[J]. Inf Control, 2022, 51(6): 641−650,661. doi: 10.13976/j.cnki.xk.2022.1436
[9] Sentenac T, Bugarin F, Ducarouge B, et al. Automated thermal 3D reconstruction based on a robot equipped with uncalibrated infrared stereovision cameras[J]. Adv Eng Inf, 2018, 38: 203−215. doi: 10.1016/j.aei.2018.06.008
[10] Batchuluun G, Kang J K, Nguyen D T, et al. Deep learning-based thermal image reconstruction and object detection[J]. IEEE Access, 2021, 9: 5951−5971. doi: 10.1109/ACCESS.2020.3048437
[11] Cao Y P, Xu B B, Ye Z Y, et al. Depth and thermal sensor fusion to enhance 3D thermographic reconstruction[J]. Opt Express, 2018, 26(7): 8179−8193. doi: 10.1364/OE.26.008179
[12] Zhang Z Y. Flexible camera calibration by viewing a plane from unknown orientations[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 1999: 666–673. https://doi.org/10.1109/ICCV.1999.791289.
[13] Canny J. A Computational approach to edge detection[J]. IEEE Trans Pattern Anal Mach Intell, 1986, PAMI-8(6): 679−698. doi: 10.1109/TPAMI.1986.4767851
[14] Otsu N. A Threshold selection method from gray-level histograms[J]. IEEE Trans Syst Man Cybern, 1979, 9(1): 62−66. doi: 10.1109/TSMC.1979.4310076
[15] Han P F, Zhao G. CAD-based 3D objects recognition in monocular images for mobile augmented reality[J]. Comput Graph, 2015, 50: 36−46. doi: 10.1016/j.cag.2015.05.021
[16] Garrido-Jurado S, Muñoz-Salinas R, Madrid-Cuevas F J, et al. Automatic generation and detection of highly reliable fiducial markers under occlusion[J]. Pattern Recognition, 2014, 47(6): 2280−2292. doi: 10.1016/j.patcog.2014.01.005
[17] Lepetit V, Moreno-Noguer F, Fua P. EPnP: an accurate O(n) solution to the PnP problem[J]. Int J Comput Vis, 2009, 81(2): 155−166. doi: 10.1007/s11263-008-0152-6
-
点击扫一扫
图(22)
表(4)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
