E-mail Alert
RSS
-
摘要:
相位差法是常用的图像事后重建方法之一。为提高相位差法对太阳图像重建的鲁棒性，本文提出了基于低秩先验的改进的相位差法，即引入了图像核范数正则化到相位差模型中，并分别利用半二次分裂方法和BFGS求解图像子模型和相位子模型。在仿真退化的焦面和离焦面太阳图像上进行重建实验与分析，与基于Tikhonov正则化的经典相位差法相比，在无噪声和有噪声情况下基于低秩先验的相位差法在主观视觉效果和客观指标上均能够提高波前相位估计的精度，提高重建图像的质量。
Abstract:Phase diversity is one of the commonly used image post-reconstruction methods. In order to improve the robustness of phase diversity for solar image reconstruction, this paper proposes an improved phase diversity method based on the low-rank prior, i.e., the nuclear norm regularization of the image is introduced into the phase diversity model, and the image sub-model and the phase sub-model are solved by the half-quadratic splitting method and BFGS respectively. Reconstruction experiments and analysis are carried out on the simulated degraded focused and defocused solar images. Compared with the classical phase diversity based on Tikhonov regularization, the phase diversity based on low-rank prior can improve the accuracy of wavefront phase estimation and the quality of reconstructed images in terms of subjective visual effects and objective indexes in both the noise-free and noise-included cases.
-
Key words:
- phase diversity /
- low-rank prior /
- solar images
-
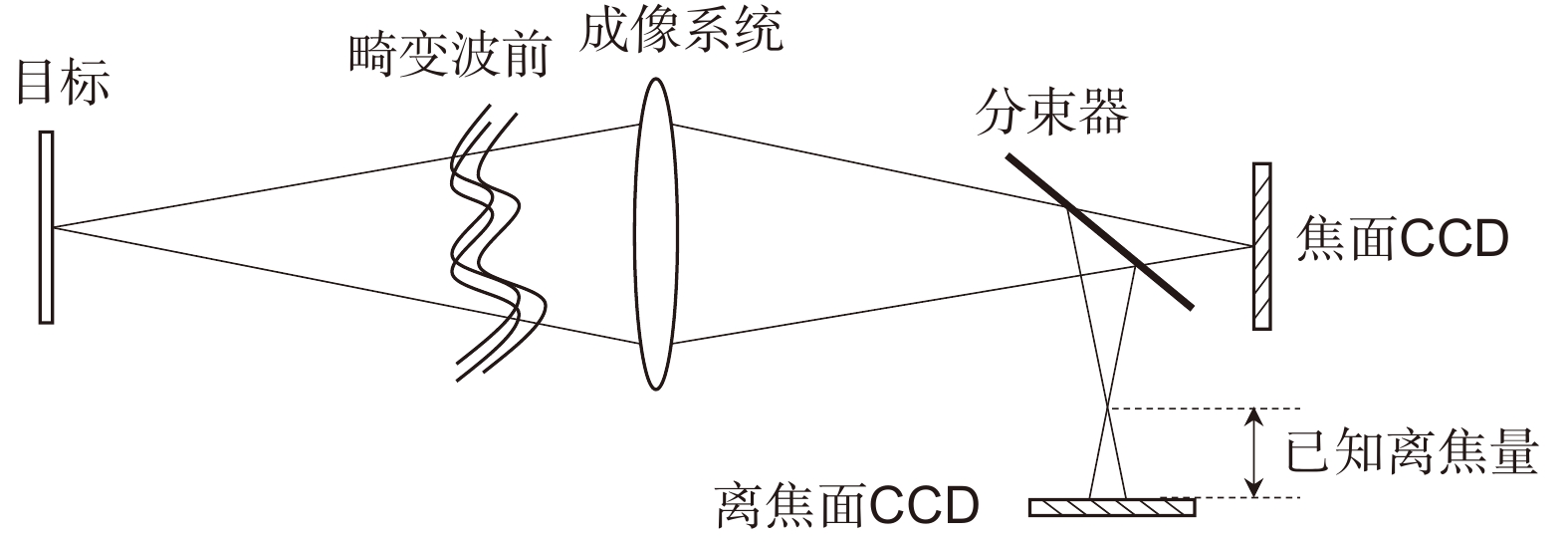
Overview: Atmospheric turbulence reduces the imaging resolution of ground-based optical telescopes and seriously affects astronomical observations. At present, the most effective solution to this problem is adaptive optics (AO) technology combined with image post-reconstruction. Most large-aperture solar telescopes at home and abroad are equipped with AO systems, and the collected solar (adaptive optics) images can be further reconstructed by blind deconvolution, phase diversity, speckle reconstruction, or deep learning. Among them, the phase diversity is to add one or more additional imaging channels in the imaging system and use a set of images (focused and defocused images) of different imaging channels of the same object collected at the same time to estimate the wavefront aberration, and then restore the object image based on the wavefront aberration.
Phase diversity (PD) is essentially a more constrained multi-channel blind deconvolution method with higher reliability. However, the traditional phase diversity has poor robustness and can be easily affected by image noise and initial value, which makes the optimization process fall into local minimum and even leads to a lot of ringing artifacts in the reconstructed image. For this problem, the common solution is to use multiple sets of focused and defocused images for phase diversity, i.e., the phase-diverse speckle (PDS). The complementarity of high-frequency information between multiple sets of focused and defocused images can reduce the influence of image noise and wavefront phase estimation errors in the iterative process of the algorithm. However, in some practical situations, it is inconvenient to obtain multiple sets of focused and defocused images in which the object remains stationary, so it is difficult to apply the phase-diverse speckle method.
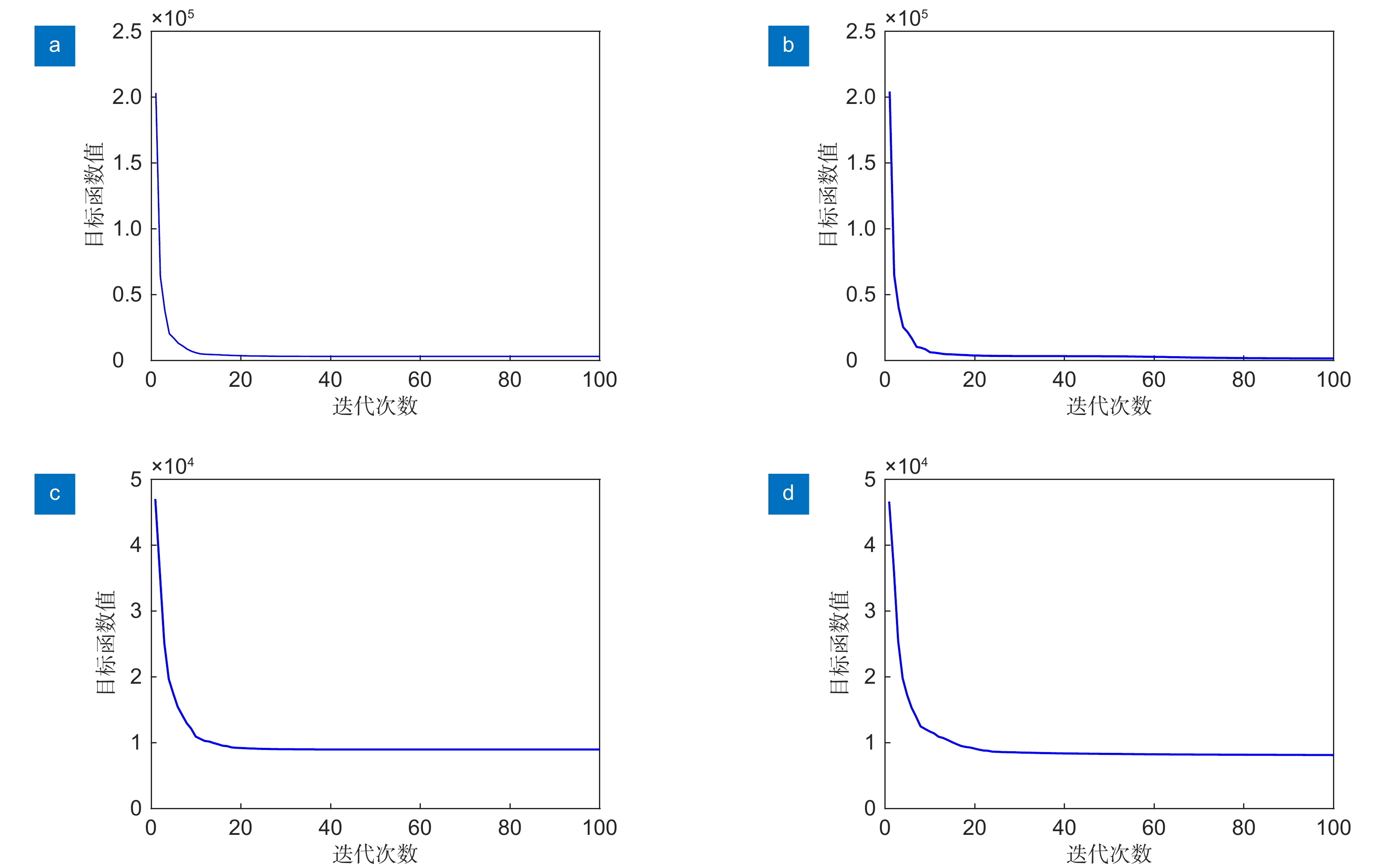
Inspired by the low-rank prior widely used in the robust principal component analysis (RPCA), noise and ringing artifacts are interference components that destroy the low-rank property of the original image. In order to improve the robustness of phase diversity for a single set of focused and defocused solar images, this paper proposes an improved phase diversity based on low rank prior, i.e., a new phase diversity model based on the nuclear norm regularization of the image is established, and the image sub-model and the phase sub-model are solved by the half-quadratic splitting method and BFGS respectively. Finally, reconstruction experiments and analysis are carried out on the simulated focused and defocused solar images. Compared with the classical phase diversity based on Tikhonov regularization, the phase diversity based on low rank prior can improve the accuracy of wavefront phase estimation and the quality of reconstructed images in terms of subjective visual effects and objective indexes in both the noise-free and noise-included cases.
-
-
图 2 仿真结果。(a) 原始目标图像；(b) 焦面图像；(c) 离焦面图像；(d) 焦面波前相位(rad)；(e) 焦面PSF；(f) 离焦面PSF
Figure 2. Simulation results. (a) Original object image; (b) Focused image; (c) Defocused image; (d) Wavefront phase of focused image (rad); (e) PSF of focused image; (f) PSF of defocused image
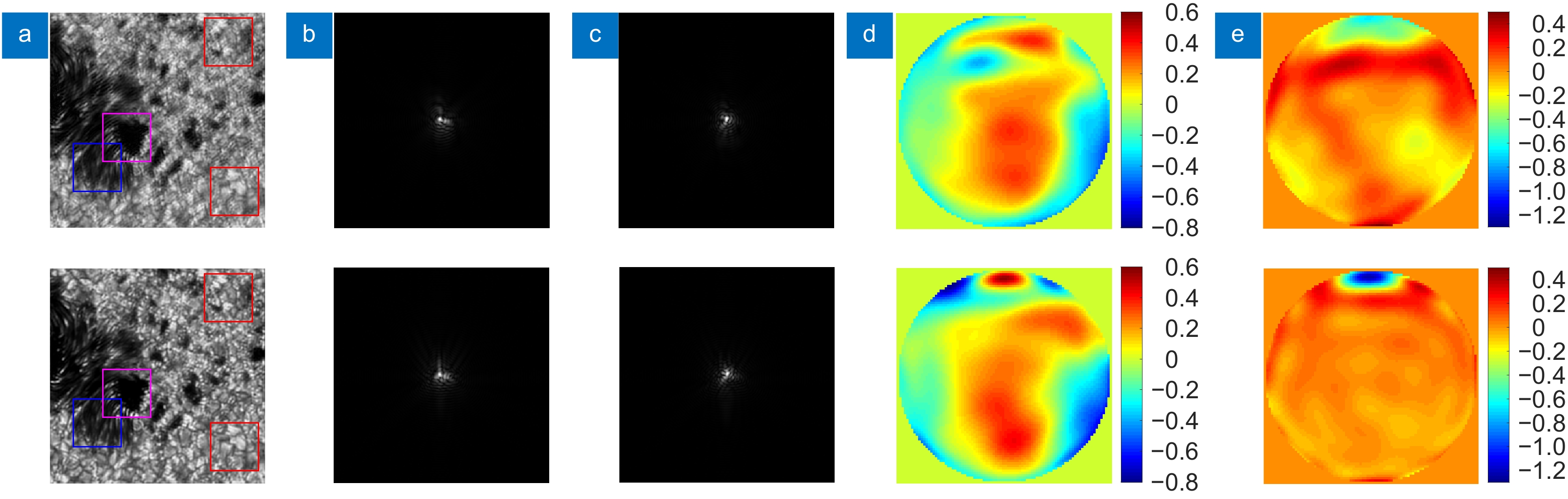
图 3 图像重建结果。第一行：Tikhonov；第二行：LR。(a) 列：重建图像；(b) 列：估计的焦面PSF；(c) 列：估计的离焦面PSF；(d) 列：估计的焦面波前相位(rad)；(e) 列：残余波前相位误差(rad)
Figure 3. Reconstruction results. Top line: Tikhonov; Bottom line: LR. (a) Column: reconstructed image; (b) Column: estimated PSF of focused image; (c) Column: estimated PSF of defocused image; (d) Column: estimated wavefront phase of focused image (rad); (e) Column: residual wavefront phase error (rad)
图 4 图像子区域重建结果。(a) 列：焦面图像；(b) 列：Tikhonov；(c) 列：LR；(d) 列：原始目标图像
Figure 4. Image subregion reconstruction results. (a) Column: focused image; (b) Column: Tikhonov; (c) Column: LR; (d) Column: original object image
图 5 仿真结果。(a) 原始目标图像；(b) 焦面图像；(c) 离焦面图像；(d) 焦面波前相位(rad)；(e) 焦面PSF；(f) 离焦面PSF
Figure 5. Simulation results. (a) Original object image; (b) Focused image; (c) Defocused image; (d) Wavefront phase of focused image; (e) PSF of focused image (rad); (f) PSF of defocused image
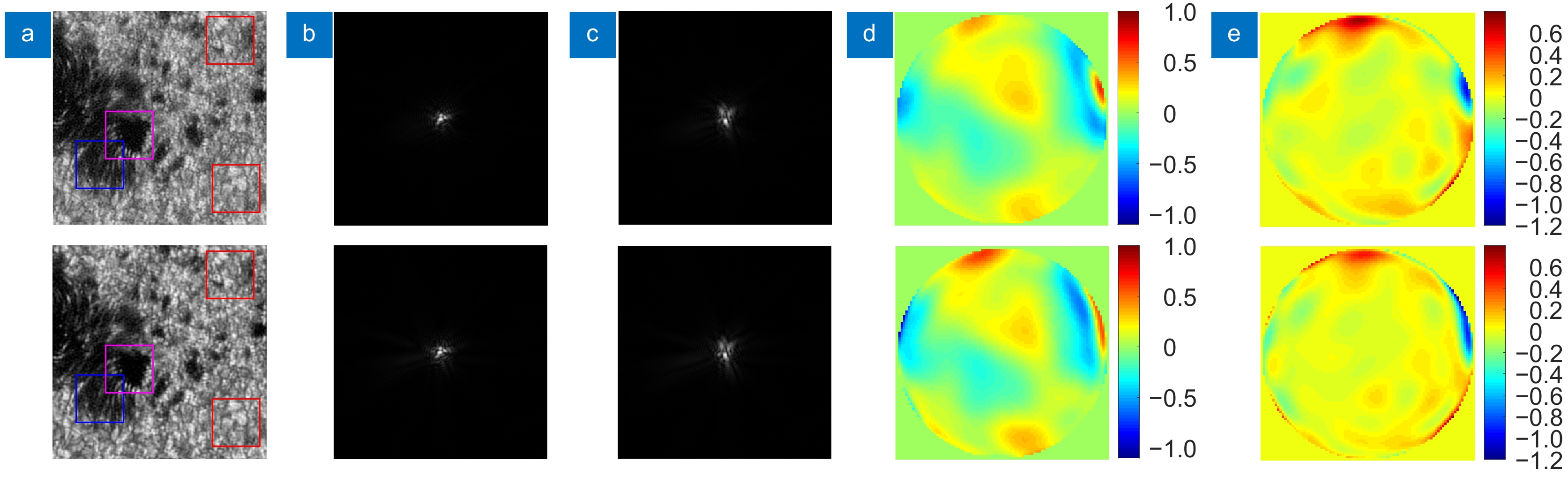
图 6 图像重建结果。第一行：Tikhonov；第二行：LR。(a) 列：重建图像；(b) 列：估计的焦面PSF；(c) 列：估计的离焦面PSF；(d) 列：估计的焦面波前相位；(e) 列：残余波前相位误差
Figure 6. Reconstruction results. Top line: Tikhonov; Bottom line: LR. (a) Column: reconstructed image; (b) Column: estimated PSF of focused image; (c) Column: estimated PSF of defocused image; (d) Column: estimated wavefront phase of focused image (rad); (e) Column: residual wavefront phase error (rad)
图 7 图像子区域重建结果。(a) 列：焦面图像；(b) 列：Tikhonov；(c) 列：LR；(d) 列：原始目标图像
Figure 7. Reconstruction results of subregion. (a) Column: focused image; (b) Column: Tikhonov; (c) Column: LR; (d) Column: original object image
图 8 不同权重参数下的重建图像。(a) λ = 1×10−5；(b) λ = 1×10−3；(c) λ = 1×10−2
Figure 8. Reconstructed images with different weight parameter values. (a) λ = 1×10−5; (b) λ = 1×10−3; (c) λ = 1×10−2
图 9 相位目标函数迭代曲线。(a) 无噪声情况，Tikhonov；(b) 无噪声情况，LR；(c) 有噪声情况，Tikhonov；(d) 有噪声情况，LR
Figure 9. Iteration curve of the phase objective function. (a) In the noise-free case, Tikhonov; (b) In the noise-free case, LR; (c) In the noise-included case, Tikhonov; (d) In the noise-included case, LR
表 1 无噪声情况下重建结果定量评价
Table 1. Quantitative evaluation of reconstruction results in the noise-free case
RMSE/波长 PSNR/dB SSIM 焦面图像 / 13.91 0.2166 Tikhonov 0.1756 18.54 0.5200 LR 0.1494 20.45 0.7494 
下载: 导出CSV
表 2 有噪声情况下重建结果定量评价
Table 2. Quantitative evaluation of reconstruction results in the noise-included case
RMSE/波长 PSNR/dB SSIM 焦面图像 / 14.72 0.2318 Tikhonov 0.1387 19.24 0.5603 LR 0.1293 19.80 0.6226
下载: 导出CSV
-
[1] 鲍华, 饶长辉, 田雨, 等. 自适应光学图像事后重建技术研究进展[J]. 光电工程, 2018, 45(3): 170730. doi: 10.12086/oee.2018.170730
Bao H, Rao C H, Tian Y, et al. Research progress on adaptive optical image post reconstruction[J]. Opto-Electron Eng, 2018, 45(3): 170730. doi: 10.12086/oee.2018.170730
[2] Miura N, Baba N. Segmentation-based multiframe blind deconvolution of solar images[J]. J Opt Soc A, 1995, 12(9): 1858−1866. doi: 10.1364/JOSAA.12.001858
[3] Löfdahl M G, Scharmer G B. Wavefront sensing and image restoration from focused and defocused solar images[J]. Astron Astrophys Suppl Ser, 1994, 107: 243−264.
[4] Seldin J H, Paxman R G. Phase-diverse speckle reconstruction of solar data[J]. Proc SPIE, 1994, 2302: 268−280. doi: 10.1117/12.188044
[5] 龙潇, 鲍华, 饶长辉, 等. 一种并行加速改进的快速相位解包裹算法[J]. 光电工程, 2020, 47(12): 200111. doi: 10.12086/oee.2020.200111
Long X, Bao H, Rao C H, et al. Improved fast phase unwrapping algorithm based on parallel acceleration[J]. Opto-Electron Eng, 2020, 47(12): 200111. doi: 10.12086/oee.2020.200111
[6] Von der Lühe O. Speckle imaging of solar small scale structure. I-methods[J]. Astron Astrophys, 1993, 268(1): 374−390.
[7] Ramos A A, de la Cruz Rodríguez J, Yabar A P. Real-time, multiframe, blind deconvolution of solar images[J]. Astron Astrophys, 2018, 620: A73. doi: 10.1051/0004-6361/201833648
[8] Wang S, Chen Q Q, He C Y, et al. Blind restoration of solar images via the channel sharing spatio-temporal network[J]. Astron Astrophys, 2021, 652: A50. doi: 10.1051/0004-6361/202140376
[9] Guo Y M, Zhong L B, Min L, et al. Adaptive optics based on machine learning: a review[J]. Opto-Electron Adv, 2022, 5(7): 200082. doi: 10.29026/oea.2022.200082
[10] Gonsalves R A, Chidlaw R. Wavefront sensing by phase retrieval[J]. Proc SPIE, 1979, 207: 32−39. doi: 10.1117/12.958223
[11] Gonsalves R A. Phase retrieval and diversity in adaptive optics[J]. Opt Eng, 1982, 21(5): 829. doi: 10.1117/12.7972989
[12] Paxman R G, Schulz T J, Fienup J R. Joint estimation of object and aberrations by using phase diversity[J]. J Opt Soc Am A, 1992, 9(7): 1072−1085. doi: 10.1364/JOSAA.9.001072
[13] Paxman R G, Seldin J H. Fine-resolution astronomical imaging with phase-diverse speckle[J]. Proc SPIE, 1993, 2029: 287−298. doi: 10.1117/12.162007
[14] Paxman R G, Seldin J H, Lofdahl M G, et al. Evaluation of phase-diversity techniques for solar-image restoration[J]. Astrophys J, 1996, 466: 1087. doi: 10.1086/177578
[15] Vogel C R, Chan T F, Plemmons R J. Fast algorithms for phase-diversity-based blind deconvolution[J]. Proc SPIE, 1998, 3353: 994−1005. doi: 10.1117/12.321720
[16] Lofdahl M G. Multi-frame blind deconvolution with linear equality constraints[J]. Proc SPIE, 2002, 4792: 146−155. doi: 10.1117/12.451791
[17] Van Noort M, Der Voort L R V, Löfdahl M G. Solar image restoration by use of multi-frame blind de-convolution with multiple objects and phase diversity[J]. Sol Phys, 2005, 228(1): 191−215. doi: 10.1007/s11207-005-5782-z
[18] Wu D S, Yang C L, Zhang P G, et al. Phase diversity technique with sparse regularization in liquid crystal adaptive optics system[J]. J Astron Telesc Instrum Syst, 2018, 4(4): 049007. doi: 10.1117/1.JATIS.4.4.049007
[19] Guo H Y, Xu Y J, Li Q, et al. Improved machine learning approach for wavefront sensing[J]. Sensors, 2019, 19(16): 3533. doi: 10.3390/s19163533
[20] Ma H M, Liu H Q, Qiao Y, et al. Numerical study of adaptive optics compensation based on convolutional neural networks[J]. Opt Commun, 2019, 433: 283−289. doi: 10.1016/j.optcom.2018.10.036
[21] Xin Q, Ju G H, Zhang C Y, et al. Object-independent image-based wavefront sensing approach using phase diversity images and deep learning[J]. Opt Express, 2019, 27(18): 26102−26119. doi: 10.1364/OE.27.026102
[22] Wu Y, Guo Y M, Bao H, et al. Sub-millisecond phase retrieval for phase-diversity wavefront sensor[J]. Sensors, 2020, 20(17): 4877. doi: 10.3390/s20174877
[23] Ramos A A, Olspert N. Learning to do multiframe wavefront sensing unsupervised: applications to blind deconvolution[J]. Astron Astrophys, 2021, 646: A100. doi: 10.1051/0004-6361/202038552
[24] Wright J, Ganesh A, Rao S, et al. Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization[C]//Proceedings of the 22nd International Conference on Neural Information Processing Systems, 2009: 2080–2088.
[25] Candès E J, Li X D, Ma Y, et al. Robust principal component analysis?[J]. J ACM, 2011, 58(3): 11. doi: 10.1145/1970392.1970395
[26] Krishnan D, Fergus R. Fast image deconvolution using hyper-Laplacian priors[C]//Proceedings of the 22nd International Conference on Neural Information Processing Systems, 2009: 1033–1041.
[27] Xu L, Lu C W, Xu Y, et al. Image smoothing via L0 gradient minimization[C]//Proceedings of the 2011 SIGGRAPH Asia Conference, 2011: 174. https://doi.org/10.1145/2024156.2024208.
[28] Cai J F, Candès E J, Shen Z W. A singular value thresholding algorithm for matrix completion[J]. SIAM J Optim, 2010, 20(4): 1956−1982. doi: 10.1137/080738970
-
点击扫一扫
图(10)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
