E-mail Alert
RSS
-
摘要:
为改进条纹投影动态三维测量系统性能，根据动态物体三维形貌测量的特点提出了两步法测量方案：1) 通过测量运动前物体或CAD模型，获得物体初始三维形貌及二维图像中特征点对应的三维坐标；2) 进行物体运动变化过程的三维测量。通过检测动态图像中的特征点，根据二维、三维坐标对应关系计算物体不同时刻的运动参数，再由初始形貌估计出物体的近似形貌，以此来计算该时刻条纹图的近似相位。然后结合该近似相位及实际条纹的截断相位计算得到展开相位，最后获得该时刻物体的三维形貌。与时间相位展开法相比，该方案在相同测量精度下提高了测量速度；而与空间相位展开法相比，该方案在相同测量速度下提高了测量可靠度，并且不受条纹不连续影响。采用DLP投影仪和高速摄像机搭建了静态、动态双模式三维测量系统，实现了1280×1024点及70 f/s的三维形貌测量。实验结果表明该方案不但可以对刚体运动物体进行测量，而且对非刚体运动物体，只要其形变引起的条纹变化不超过半个周期也能够测量。同时，提出的方法对相邻时刻物体位姿变化有较大的容限。
Abstract:A two-step scheme is proposed to improve the performance of dynamic 3D shape measurement according to its characteristics. 1) The initial 3D shape of the object and the corresponding 3D coordinates of feature points in the 2D image are obtained by measuring the static object or its CAD model. 2) Carry out the 3D measurement in the process of object motion and change. By detecting the feature points in the dynamic image, the motion parameters of the object at different times are calculated according to the corresponding relationship between two-dimensional and three-dimensional coordinates. Then the approximate shape of the object is estimated from the initial shape. The approximate phase of the fringe pattern at this time is calculated. Then, combined with the approximate phase and the wrapped phase of the actual fringe, the unwrapped phase is calculated, and the 3D shape of the object at that time is obtained. Compared with the temporal phase unwrapping method, the proposed scheme improves the measurement speed under the same measurement reliability. Compared with the spatial phase unwrapping method, this scheme improves the measurement reliability at the same measurement speed and is not affected by fringe discontinuity. A static and dynamic dual-mode 3D measurement system was built by using a DLP projector and high-speed camera. The 3D shape measurement of 1280×1024 points at 70 f/s is realized. The experimental results show that the scheme can measure not only the rigid moving object but also the non-rigid moving object, as long as the fringe change caused by its deformation does not exceed half a period. The proposed method has a large tolerance for the change of object pose at adjacent times as well.
-
Overview: In the deformation measurement of moving objects with fringe projection, such as the deformation of objects in high-speed flight and the measurement of the unconstrained facial expression changes, we pursue to project as few patterns as possible and obtain as high measurement accuracy as possible. Obtaining the unwrapped phase is one of the key steps in fringe projection 3D measurement, which generally needs the assistance of other information. The common methods are spatial phase unwrapping algorithm, temporal phase unwrapping algorithm, and multi-view geometric constraint. These methods solve the phase unwrapping problem well to some extent, but they have their limitations. The spatial phase unwrapping method is difficult to deal with spatially discontinuous or isolated regions. The temporal phase unwrapping method takes a long time and requires higher hardware at the same measurement speed. The multi-view geometric constraint method reduces the measurement area and increases the complexity and cost of the whole system. In most circumstances, the initial shape of the moving objects can be obtained. According to this fact, a two-step scheme is proposed to improve the performance of dynamic 3D shape measurement. 1) The initial 3D shape of the object and the corresponding 3D coordinates of feature points in the 2D image are obtained by measuring the static object or its CAD model. 2) Carry out the 3D measurement of object motion and change. By detecting the feature points in the dynamic image, the motion parameters of the object at different times are calculated according to the corresponding relationship between 2D and 3D coordinates. Then the approximate shape of the object is estimated from the initial shape. The approximate phase of the fringe pattern at this time is calculated. Then, combined with the approximate phase and the wrapped phase of the actual fringe, the unwrapped phase is calculated, and the 3D shape of the object at that time is obtained. Compared with the temporal phase unwrapping method, the proposed scheme improves the measurement speed under the same measurement reliability. Compared with the spatial phase unwrapping method, this scheme improves the measurement reliability at the same measurement speed and is not affected by fringe discontinuity. A static and dynamic dual-mode 3D measurement system was built by using a DLP projector and high-speed camera. The 3D shape measurement of 1280×1024 points at 70 f/s is realized. The experimental results show that the scheme is feasible and has a large tolerance for the change of the object pose at adjacent times.
-
1. 引 言
光学三维形貌测量技术由于其非接触、精度高等优点，在工业检测、安防、医疗、影视娱乐等方面具有广泛的运用，例如工件加工质量检测、物体高速运动中的形变测量、三维人脸识别中的信息获取、离子加速器癌症治疗中人体位姿的监测、影视制作中人脸三维表情的获取等。基于条纹相位测量[1-3]的三维测量技术(如相位测量轮廓术[4]、傅里叶变换轮廓术[5]、小波变换轮廓术[6]等)是其中重要的一类。傅里叶变换轮廓术、小波变换轮廓术等由于测量只需要一幅图像，能够实现动态三维形貌测量，但是测量精度不高。而相位测量轮廓术等需要多幅图像才能测量，在静态或准静态三维形貌测量方面能够获得高精度、高可靠的结果，但是在动态三维形貌测量方面尚存在较多需要改进、提高之处。
相位展开是条纹相位测量中的关键一步。在恢复物体三维形貌前首先要对截断相位进行展开。常见的有空间相位展开法、时间相位展开法和多视角几何约束法等。这些方法在某种程度上很好地解决了相位展开问题，但是它们各自存在局限。空间相位展开[7-8]法着重分析截断相位图空间分布特性来恢复相位的连续性，但是它很难处理空间上不连续或者孤立的区域。而时间相位展开法[9-10]借助额外的图案确定条纹次序，能够处理孤立区域问题，可靠性高，但是测量需要的时间长，相同测量速度情况下对硬件的要求更高。常见的时间相位展开法有双频[11]或多频(多波长)[12]相移技术、编码图案与相移技术结合的方法[13-15]等。多视角几何约束法[16-17]包括增设多个摄像机或者投影仪，提供多角度几何约束来展开相位。该类方法减小了测量区域，同时增加了整个系统的复杂性和成本。An等人[18]提出一种深度约束的方法，通过预先设定已知距离的虚拟参考平面，为截断相位提供级次信息。该方法不需要额外的图案投影，但是无法解决被测物体与参考平面相位差绝对值超过π的问题。后来Li等人[19]提出一种基于CAD模型的测量方法，将模型在被测对象深度方向进行分割，产生一系列虚拟参考平面辅助相位展开。但是，该方法的处理过程复杂。他们又提出了改进的方法[20]，通过场景中已知尺寸的物体提供绝对相位展开的线索。基于物体形貌约束，重建其三维形貌，借此创建最小相位平面，用于逐像素展开整个场景的相位。该方法可以实现运动物体的三维测量，但需要一个已知尺寸的物体且其与待测物体的相对位置有限制，造成了实际应用时的极大限制。
上述方法在各自适用场合取得了成功，但是还存在改进提升空间。目前条纹投影三维测量中普遍使用可编程数字投影仪，可以投影多种图案。这样，相同的硬件系统只要改变投影图案和处理算法就可以方便地实现多种测量方案。同时，不少被测物体(如生产线上的工件)是采用CAD设计的，其标准模型容易获得；另外，物体静态时的三维形貌也可以采用动态三维测量硬件系统，通过高精度、高可靠的测量方案获得。针对上述情况，本文提出了先验知识辅助的方法。这里的先验知识是指待测物体的近似三维形貌(可以通过CAD模型或预先测量获得)、物体二维图像中的特征点等信息。在不增加系统复杂性及投影图案数的同时，实现了可靠性与时间相位展开法接近的运动物体三维形貌测量。该方法允许测量过程中条纹有不连续或者孤立的部分，同时对物体运动中的形变量也有较大的容限。
2. 理论推导
2.1 测量原理
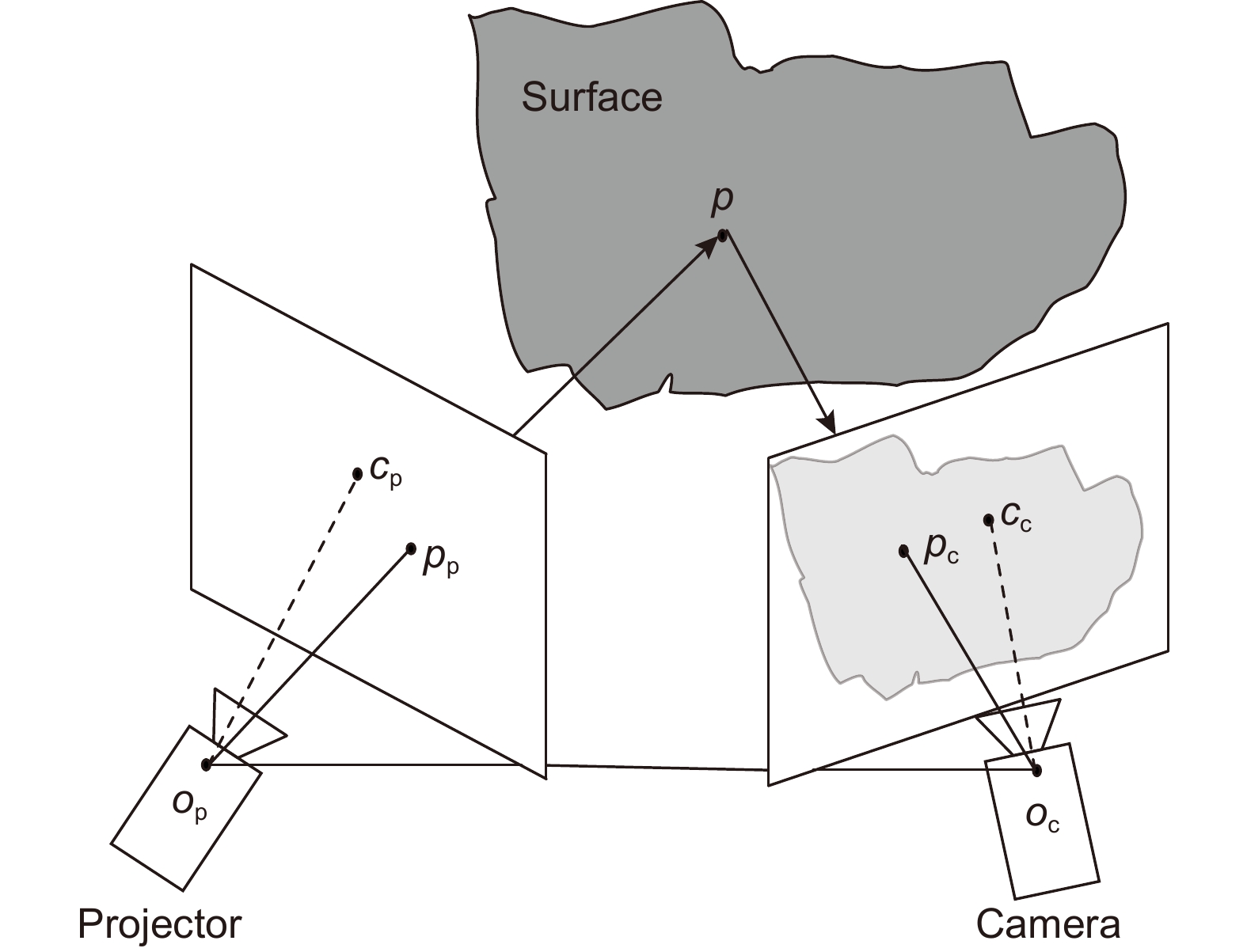
图1为测量系统结构示意图。系统主要由投影仪和摄像机组成。由投影仪投射正弦条纹到被测物体上，摄像机从另一视角拍摄受高度调制的变形条纹图。对变形条纹进行处理，获得物体三维形貌。
图 1. 条纹投影三维测量系统构成示意图Figure 1. Schematic diagram of fringe projection 3D measurement system structure采用整周期等间隔3步相移法时，该系统拍摄的变形条纹图可以表示为
Ii(u,v)=A(u,v)+B(u,v)⋅cos[π(u,v)−2(1−i)φ/3], i=0,1,2, (1) 这里的(u, v)为图像坐标，A(u,v)=2∑i=0Ii(u,v)/3为背景强度，B(u, v)为条纹幅度，φ(u, v)为条纹相位，
φ(u,v)=arctan{√3[I0(u,v)−I2(u,v)]2I1(u,v)−I0(u,v)−I2(u,v)}. (2) 根据式(2)计算的相位值由于反正切函数的性质而被截断在[−π,π)范围内，需要采用式(3)进行相位展开：
ϕ(u,v)=2k(u,v)π+φ(u,v), (3) 2.2 相位展开原理
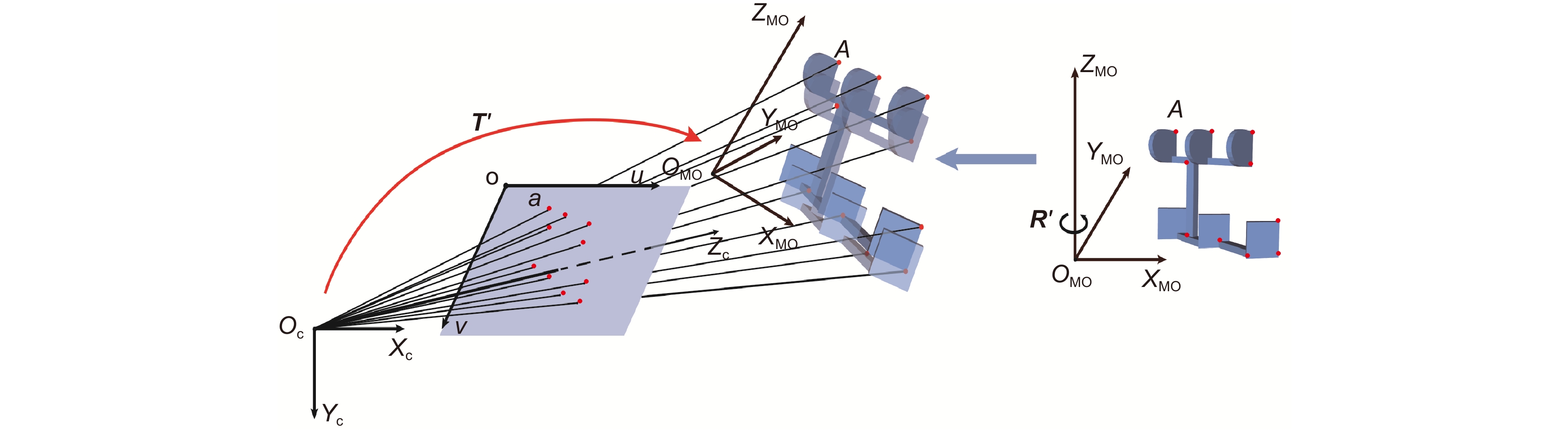
当待测物体的近似三维形貌、物体二维图像中的特征点等先验知识及摄像机内参数已知时，结合模型坐标系相对于摄像机坐标系的运动参数，根据测量系统原理对模型进行虚拟测量。通过虚拟测量获得与待测物相同位姿的模型的绝对相位分布。以其为参考，结合实际测量的截断相位求出待测物体的绝对相位。其中的一个关键问题是获得模型相对于摄像机坐标系的运动参数。根据摄像机成像模型，利用模型特征点三维坐标及其在二维图像中对应点的图像坐标能够获得该参数。
图2为所提方法中模型运动参数估计的原理图，图中a为A的像。采用针孔模型表示摄像机的成像模型，则成像关系表示为
s[uv1]=[fu0u000fvv000010][XcYcZc1]=M1[XcYcZc1], (4) 式中： [XcYcZc]T为物体表面采样点在摄像机坐标系中的坐标，s为比例因子，fu、fv分别是u、v方向上的归一化焦距，M1称为摄像机内参数矩阵。模型与待测物体位姿相同相当于将模型进行旋转、平移，使模型与待测物体重合。可以用下式表示：
[XcYcZc1]=[R′T′0T1][XMOYMOZMO1], (5) 式中：R′为旋转矩阵，T′为平移向量，[XMOYMOZMO]T为模型坐标。将式(5)代入式(4)得：
s[uv1]=M1[R′T′0T1][XMOYMOZMO1]. (6) 只要图像中三维特征点的像足够多(至少6个空间点的像)，在摄像机内参数已知的情况下，能够求解旋转矩阵及平移向量。实际应用中，由于二维图像中特征点获取的误差等，直接求解R′和T′误差较大。在得到初始值后，利用Levenberg-Marquardt方法进行迭代优化获得运动参数最优解。
将投影仪看作是逆向工作的摄像机，则可以使用与摄像机同样的方法处理三维空间到投影仪图像平面的变换关系。在获得运动参数后，我们将预先获得的三维模型数据进行变换使之与待测物体重合，再用摄像机和投影仪对模型成像。模型在投影仪中的像可表示为
s[upvp1]=M1p[RT0T1][R′T′0T1][XMOYMOZMO1], (7) 式中：(up, vp)为投影仪图像坐标，R和T分别为摄像机坐标系相对于投影仪坐标系的旋转矩阵和平移向量。分别计算出模型上的点成像在摄像机中的坐标(u, v)和投影仪中的坐标(up, vp)。如果摄像机和投影仪是水平摆放，采用竖向条纹，由式(8)得到参考相位图。如果摄像机和投影仪是垂直摆放，采用横向条纹，由式(9)得到参考相位图。
ϕr(u,v)=φ0+2πfup, (8) ϕr(u,v)=φ0+2πfvp, (9) 式中：φ0为条纹的初相位，f为条纹的频率。上述根据测量系统结构参数计算物体初始形貌旋转、平移后的相位过程被称为虚拟测量。得到参考相位后，每个像素对应的条纹级次k由式(10)获得：
k=round[ϕr(u,v)−φ(u,v)2π], (10) 式中：round[·]表示四舍五入取整。由式(10)可知，只要被测物体与参考模型差异引起的相位变化在(−π,π)内，就能够获得实际测量的绝对相位。这也意味着即使物体在运动中有形变(非刚体运动)，只要形变足够小，提出的方法也适用。
由上述展开相位获取过程可知，提出的方法只要投影3幅相移条纹就能够进行运动物体三维形貌测量。与时间相位展开法相比，所提方法减少了图案的投影数量，更适合动态物体测量，而测量可靠性与之接近。与空间相位展开法相比，所提方法投影图案数相同，但是可靠性高。只要实际测量物体与虚拟测量物体重合部分差异在允许范围内，即使物体形貌突变造成条纹不连续也能够正确展开相位。提出的方法不要求空间与时间上相位分布满足采样定理，与时空三维相位展开法相比，所提方法对相邻时刻物体位姿变化有较大的容限。
2.3 误差容限分析
为简化分析，采用如图3所示的测量系统原理示意图。图中P1P2为投影仪光轴，I1I2为摄像机光轴。基于其原理，利用相似三角形ΔADC 和ΔP2DI2，即可得到D点的高度h：
h(u,v)=¯AC(L/d)1+¯AC/d=LΔϕ(u,v)Δϕ(u,v)+2πf0d, (11) 式中：f0为条纹在参考平面上的频率。大多数情况下¯AC≪d，因此式(11)可进一步简化为
h(u,v)≈¯AC(Ld)=Δϕ(u,v)2πf0tanθ, (12) 式中：θ为投影仪与摄像机光轴夹角。只要参考模型与待测物体的相位差在(−π, π)区间内，二者的变形条纹级次相同。由式(12)得：
|Δh(u,v)|<12f0tanθ. (13) 由式(13)可知，误差容限随条纹频率升高而减小，随光轴夹角增加而减小。假设参考平面上条纹频率f0=1/5 mm−1，光轴夹角θ=30°，则高度误差容限约为±4.3 mm。
3. 实验结果
为验证所提方法的可行性，搭建了条纹投影动态三维测量系统。实验系统的硬件配置如下，摄像机(Mars 1300-210uc)的分辨率为1280 pixels×1024 pixels，投影仪(Lightcrafter 4500)的分辨率为1140 pixels×912 pixels。静态测量时采用3频外差法，动态测量时采用与静态测量时最高频率相同的条纹，条纹频率为32 (参考平面上条纹频率约为1/10 mm−1)，采用整周期等间隔3步相移测量相位。摄像机帧率为210 f/s，则动态三维数据的采集速度为70 f/s。选择CAD设计并用3D打印制作的特征分明的物体验证条纹不连续情况下所提方法的适用性。选择人脸进行非刚体运动物体的三维测量验证。
3.1 测量流程
所提方法的具体流程如下：
1) 采用3频外差法或从CAD模型获得待测物体参考模型。确定模型上的特征点并获得其三维坐标；
2) 投影3步相移条纹并拍摄，获得变形条纹图，计算背景强度图和截断相位图；
3) 获取背景强度图中被测对象的特征点；
4) 根据2D-3D特征点对应关系，计算出模型的运动参数；
5) 利用变换后模型的三维信息由式(6)~式(10)计算获得条纹级次；
6) 展开截断相位图，恢复三维形貌；
7) 重复2)~6)直到测量结束。
由流程可知，如果无CAD模型，只在开始时进行一次相对费时的三维扫描(投影、拍摄9幅条纹图)，在动态过程测量中每投影3幅条纹就能够获取1幅三维数据。由于采用了与传统方法相同的条纹及相移法，在保证精度及可靠度的同时，三维采集的速度得到了提高。
3.2 CAD设计物体测量结果
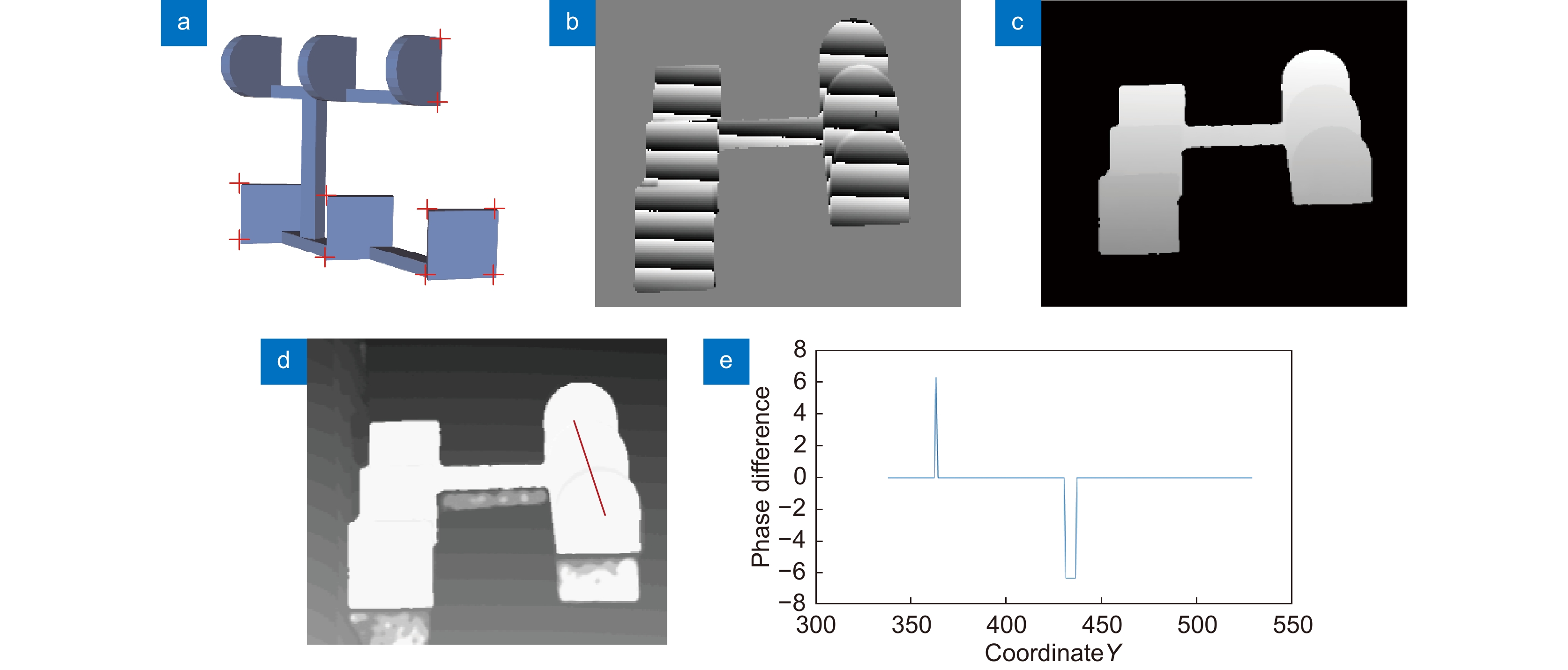
为了验证所提方法对测量中存在不连续部分的被测对象适用性，对采用CAD设计的如图4(a)所示的几何体进行了测量。该物体在测量过程中由于遮挡、阴影等，摄像机视角中条纹存在不连续部分。以3频外差法测量的结果为标准相位进行了比较。由于直角点检测的可靠性和准确性高，有助于提高物体运动参数的估计精度，这里选择它作为特征点。选择的特征点如图4(a)中十字叉所示，对其进行编号并从CAD模型中获得其三维坐标。测量时，从背景图中提取角点，根据对应编号特征点的三维坐标计算运动参数，进行相位展开。图4(b)为截断相位，图4(c)为所提方法展开的相位图，图4(d)为展开相位与标准相位之间的差值，图4(e)为4(d)中红线处的相位差。
3.3 非刚体运动实际物体测量结果
为验证所提方法对运动中伴随形变的物体测量适用性，对运动中的有表情变化的人脸进行了三维测量。采用3频外差法进行物体初始形貌测量。采用基于深度学习的人脸关键点检测算法[23]检测的结果作为运动参数估计的特征点。该算法标出了包括五官和外围轮廓的68个关键点。实际测量时，由于人脸表情变化导致的嘴巴部位关键点移动幅度较大，对于计算运动参数不利，因此嘴部的关键点不予考虑。平移运动几乎不影响特征点检测的准确性，而旋转有较大的影响。因此这里研究转动角度对关键点检测的影响情况。
首先进行了不同姿态准静态人脸三维形貌测量，同样用3频外差法测量的结果作为标准相位。从左右偏转、俯仰、侧倾这3个方向转动进行实验。图5(a)为实验过程中某一姿态的一幅变形条纹图，图5(b)为检测出的特征点，图5(c)为标准相位测量结果；图5(d)为本文方法计算的参考相位，图5(e)为参考相位与标准相位的差异图，图5(f)为5(e)图红线部分的截面图。可以看出相位差异远小于π，保证了相位的正确展开。通过实验，得到能够稳定展开相位的三个方向上的转动角度范围分别为：从正脸偏转左右均45°之内，俯仰上下均30°之内，侧倾顺时针逆时针均45°之内。
图 5. 某一姿态测量数据。(a) 变形条纹；(b) 特征点；(c) 标准相位；(d) 参考相位图；(e) 相位差值图；(f) (e)红线处截面图Figure 5. Measurement data at a certain posture. (a) Deformed fringe; (b) Feature points; (c) Standard phase; (d) Reference phase; (e) Difference between (d) and (c); (f) Cross-sections of red line in (e)接着对运动过程中伴随大幅度表情变化的人脸进行了测量实验，图6为部分测量结果。图6(a)为3频外差法获取的初始三维形貌，图6(b)~6(d)为运动中几个时刻的三维重构结果。可以看出，提出的方法在无姿态约束下，成功实现了对运动中有大幅表情变化的人脸测量。
4. 数据分析
从图4(b)可以看出，CAD设计的物体由于正方形平面间距离较大，各平面间的条纹不连续，连接左右两组平行平面的梁上与平面上的条纹也存在不连续之处，无法用空间相位展开法正确展开相位。从图4(e)可以看出，除边界附近存在相位展开错误外，其他地方都能正确展开相位，表明该方法不易受条纹不连续的影响。边界附近的错误主要是由于物体运动参数估计误差、噪音等共同作用造成了条纹级次计算错误。这类错误采用如下方法去除：1) 在虚拟测量相位图中进行边缘检测，得到相位不连续的边缘，并将其膨胀成一定厚度的区域，以将实际测量相位图中的边缘包含在内；2) 在背景强度图中对应的区域内进行边缘检测，并将边缘膨胀成一定厚度的新区域；3) 对展开的相位图操作，在每个对应的新区域中将相位从区域边界向区域中心展开，展到背景强度图中检测出边缘为止。展开过程中根据调制度高低避开区域中可靠度低部分。在非刚体运动物体测量实验中，从图5(c)可以看出参考相位与标准相位的差远远没有达到(−π，π)的边界，能够为展开截断相位图提供正确的条纹级次。从图6可以看出，提出的算法能够实现运动过程中伴随较大形变的物体三维形貌测量。图6中的三维结构看上去表面比较粗糙，存在空洞。这主要是因为结果没有任何滤波平滑，受摄像机噪音影响，表面法向量随机性较大。在视觉上，加上光照效果后细微的噪音被放大，噪音造成的实际形貌误差在0.2 mm以下。存在空洞主要是因为该部分反射率太低，如眼珠、头发等位置。
5. 结 论
本文提出了一种新的基于特征点及粗略模型等先验知识辅助的条纹投影动态三维形貌测量方法。该方法在保证原有测量精度、不增加系统硬件复杂性的情况下，投影最少的图案实现三维测量，并且有较大的误差容限。所提方法能够实现：CAD设计的物体，如生产线上工件形貌快速测量；运动中伴随形变的物体，如运动中有表情变化的人脸等测量。对于图像中特征信息弱的物体，本文方法将无法测量。
利益冲突：所有作者声明无利益冲突
-
图 1 条纹投影三维测量系统构成示意图
Figure 1. Schematic diagram of fringe projection 3D measurement system structure
图 5 某一姿态测量数据。(a) 变形条纹；(b) 特征点；(c) 标准相位；(d) 参考相位图；(e) 相位差值图；(f) (e)红线处截面图
Figure 5. Measurement data at a certain posture. (a) Deformed fringe; (b) Feature points; (c) Standard phase; (d) Reference phase; (e) Difference between (d) and (c); (f) Cross-sections of red line in (e)
图 6 运动过程中大幅度形变测量结果。(a) 初始三维形貌；(b) 时刻1形貌；(c) 时刻2形貌；(d) 时刻3形貌
Figure 6. Measurement results of large deformation during motion. (a) Initial 3D shape; (b) Shape of time 1; (c) Shape of time 2; (d) Shape of time 3
-
[1] Geng J. Structured-light 3D surface imaging: a tutorial[J]. Adv Opt Photon, 2011, 3(2): 128−160. doi: 10.1364/AOP.3.000128
[2] 李勇, 张广汇, 马利红, 等. 条纹投影动态三维表面成像技术综述[J]. 红外与激光工程, 2020, 49(3): 0303005. doi: 10.3788/IRLA202049.0303005
Li Y, Zhang G H, Ma L H, et al. Review of dynamic three-dimensional surface imaging based on fringe projection[J]. Infrared Laser Eng, 2020, 49(3): 0303005. doi: 10.3788/IRLA202049.0303005
[3] 应晓霖, 姚建云, 张晓松, 等. 采用LD的光源步进条纹投影三维测量系统[J]. 光电工程, 2021, 48(11): 210298. doi: 10.12086/oee.2021.210298
Ying X L, Yao J Y, Zhang X S, et al. Fringe projection based three-dimensional measurement system by the light-source-stepping method using LD[J]. Opto-Electron Eng, 2021, 48(11): 210298. doi: 10.12086/oee.2021.210298
[4] Srinivasan V, Liu H C, Halioua M. Automated phase-measuring profilometry of 3-D diffuse objects[J]. Appl Opt, 1984, 23(18): 3105−3108. doi: 10.1364/AO.23.003105
[5] Takeda M, Mutoh K. Fourier transform profilometry for the automatic measurement of 3-D object shapes[J]. Appl Opt, 1983, 22(24): 3977−3982. doi: 10.1364/AO.22.003977
[6] Zhong J G, Weng J W. Spatial carrier-fringe pattern analysis by means of wavelet transform: wavelet transform profilometry[J]. Appl Opt, 2004, 43(26): 4993−4998. doi: 10.1364/AO.43.004993
[7] Su X Y, Chen W J. Reliability-guided phase unwrapping algorithm: a review[J]. Opt Lasers Eng, 2004, 42(3): 245−261. doi: 10.1016/j.optlaseng.2003.11.002
[8] Zhao M, Huang L, Zhang Q C, et al. Quality-guided phase unwrapping technique: comparison of quality maps and guiding strategies[J]. Appl Opt, 2011, 50(33): 6214−6224. doi: 10.1364/AO.50.006214
[9] Huntley J M, Saldner H. Temporal phase-unwrapping algorithm for automated interferogram analysis[J]. Appl Opt, 1993, 32(17): 3047−3052. doi: 10.1364/AO.32.003047
[10] Zuo C, Huang L, Zhang M L, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review[J]. Opt Lasers Eng, 2016, 85: 84−103. doi: 10.1016/j.optlaseng.2016.04.022
[11] Cheng Y Y, Wyant J C. Two-wavelength phase shifting interferometry[J]. Appl Opt, 1984, 23(24): 4539−4543. doi: 10.1364/AO.23.004539
[12] Cheng Y Y, Wyant J C. Multiple-wavelength phase-shifting interferometry[J]. Appl Opt, 1985, 24(6): 804−807. doi: 10.1364/AO.24.000804
[13] 卢世江, 李勇, 王辉, 等. 含孤立物体场景的高速、高密度三维面形采集[J]. 光电工程, 2012, 39(1): 34−39. doi: 10.3969/j.issn.1003-501X.2012.01.007
Lu S J, Li Y, Wang H, et al. High-speed and dense 3D shape capture of scene consisting of spatially isolated objects[J]. Opto-Electron Eng, 2012, 39(1): 34−39. doi: 10.3969/j.issn.1003-501X.2012.01.007
[14] Zheng D L, Kemao Q, Da F P, et al. Ternary Gray code-based phase unwrapping for 3D measurement using binary patterns with projector defocusing[J]. Appl Opt, 2017, 56(13): 3660−3665. doi: 10.1364/AO.56.003660
[15] An Y T, Zhang S. Three-dimensional absolute shape measurement by combining binary statistical pattern matching with phase-shifting methods[J]. Appl Opt, 2017, 56(19): 5418−5426. doi: 10.1364/AO.56.005418
[16] Li Z W, Zhong K, Li Y F, et al. Multiview phase shifting: a full-resolution and high-speed 3D measurement framework for arbitrary shape dynamic objects[J]. Opt Lett, 2013, 38(9): 1389−1391. doi: 10.1364/OL.38.001389
[17] Guo X P, Zhao H, Jia P P, et al. Multiview fringe matching profilometry in a projector–camera system[J]. Opt Lett, 2018, 43(15): 3618−3621. doi: 10.1364/OL.43.003618
[18] An Y T, Hyun J S, Zhang S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system[J]. Opt Express, 2016, 24(16): 18445−18459. doi: 10.1364/OE.24.018445
[19] Li B W, Bell T, Zhang S. Computer-aided-design-model-assisted absolute three-dimensional shape measurement[J]. Appl Opt, 2017, 56(24): 6770−6776. doi: 10.1364/AO.56.006770
[20] Dai J F, An Y T, Zhang S. Absolute three-dimensional shape measurement with a known object[J]. Opt Express, 2017, 25(9): 10384−10396. doi: 10.1364/OE.25.010384
[21] 平乙杉, 刘元坤. 基于单应性矩阵的线结构光系统简易标定方法[J]. 光电工程, 2019, 46(12): 180677. doi: 10.12086/oee.2019.180677
Ping Y S, Liu Y K. An easy line-structured light system calibration method based on homography matrix[J]. Opto-Electron Eng, 2019, 46(12): 180677. doi: 10.12086/oee.2019.180677
[22] Li Y, Su X Y, Wu Q Y. Accurate phase–height mapping algorithm for PMP[J]. J Mod Opt, 2006, 53(14): 1955−1964. doi: 10.1080/09500340600720789
[23] Ren S Q, Cao X D, Wei Y C, et al. Face alignment at 3000 FPS via regressing local binary features[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, 2014: 1685–1692.
期刊类型引用(3)
1. 邵金凤，倪育博，孟召宗，高楠，高宇森，杨泽青，张国锋，尹伟，赵洪伟，张宗华. 基于离焦二值显示和条纹投影的复合表面三维测量方法. 光电工程. 2024(04): 90-102 . 
本站查看
2. 张波涛，李正强，华超豪，谢佳龙，吕强. 基于多视角融合的手眼协同超视野目标测量与3D重建. 光电工程. 2024(10): 113-127 . 本站查看
3. 王思远，刘元坤，于馨. 基于光流像素匹配的扫描显微相位测量轮廓术. 光电工程. 2024(11): 38-48 . 本站查看
其他类型引用(1)
-
下载:
点击扫一扫
图(7)
计量
- 文章访问数: 6067
- PDF下载数: 900
- 施引文献: 4
