-
摘要
针对有限元分析中自适应网格划分面临的计算精度与效率协同优化难题,本研究提出基于注意力融合机制的GTF-Net框架。该模型创新融合图注意力网络与Transformer架构,通过多头交叉注意力模块实现局部几何特征与全局物理场的动态耦合,增强对奇异场及复杂边界的表征能力。经光波导传输和贝塞尔函数双案例验证,相较传统Scikit-FEM (skFem)方法,GTF-Net在保持计算效率优势的同时,梯度误差标准差分别降低85.9%和23.8%。结果表明,该框架通过非线性特征映射显著提升网格分布与物理场变化的匹配度,为解决工程计算中的自适应网格优化问题提供深度学习新方案。
-
关键词:
- 自适应网格细化 /
- GATv2-Transformer融合网络 /
- 有限元分析 /
- 深度学习
Abstract
To address the challenge of balancing the computational accuracy and efficiency in adaptive finite element meshing, this study proposes a GTF-Net model based on the attention fusion mechanism. The model combines the graph attention network with the Transformer architecture, dynamically couples local geometric features with the global physical field through a multi-head cross-attention module, and enhances the representation of singular fields and complex boundaries. The verification of two case studies of waveguide transmission and Bessel equation shows that compared with the traditional Scikit-FEM (skFem) method, GTF-Net improves computational efficiency while reducing the standard deviation of gradient error by 85.9% and 23.8%, respectively. The results show that the model significantly improves the fit between mesh distribution and physical field changes through nonlinear feature mapping, providing a novel deep learning solution for adaptive mesh optimization in engineering calculations.
-
Overview
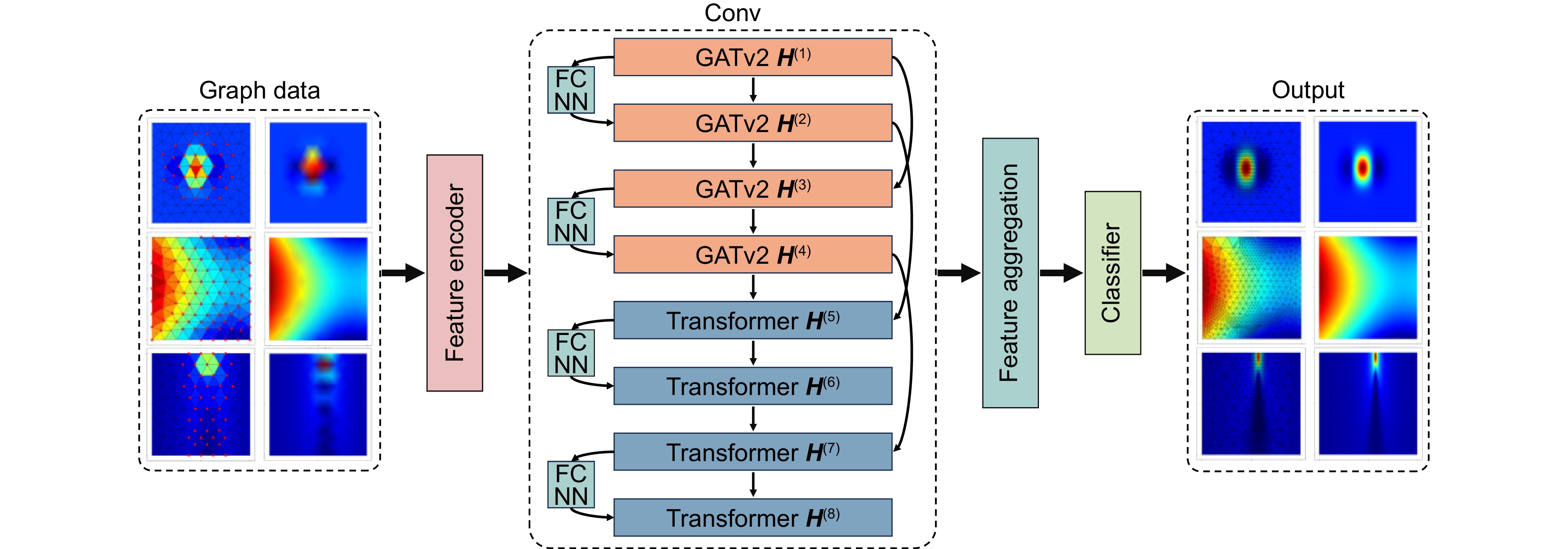
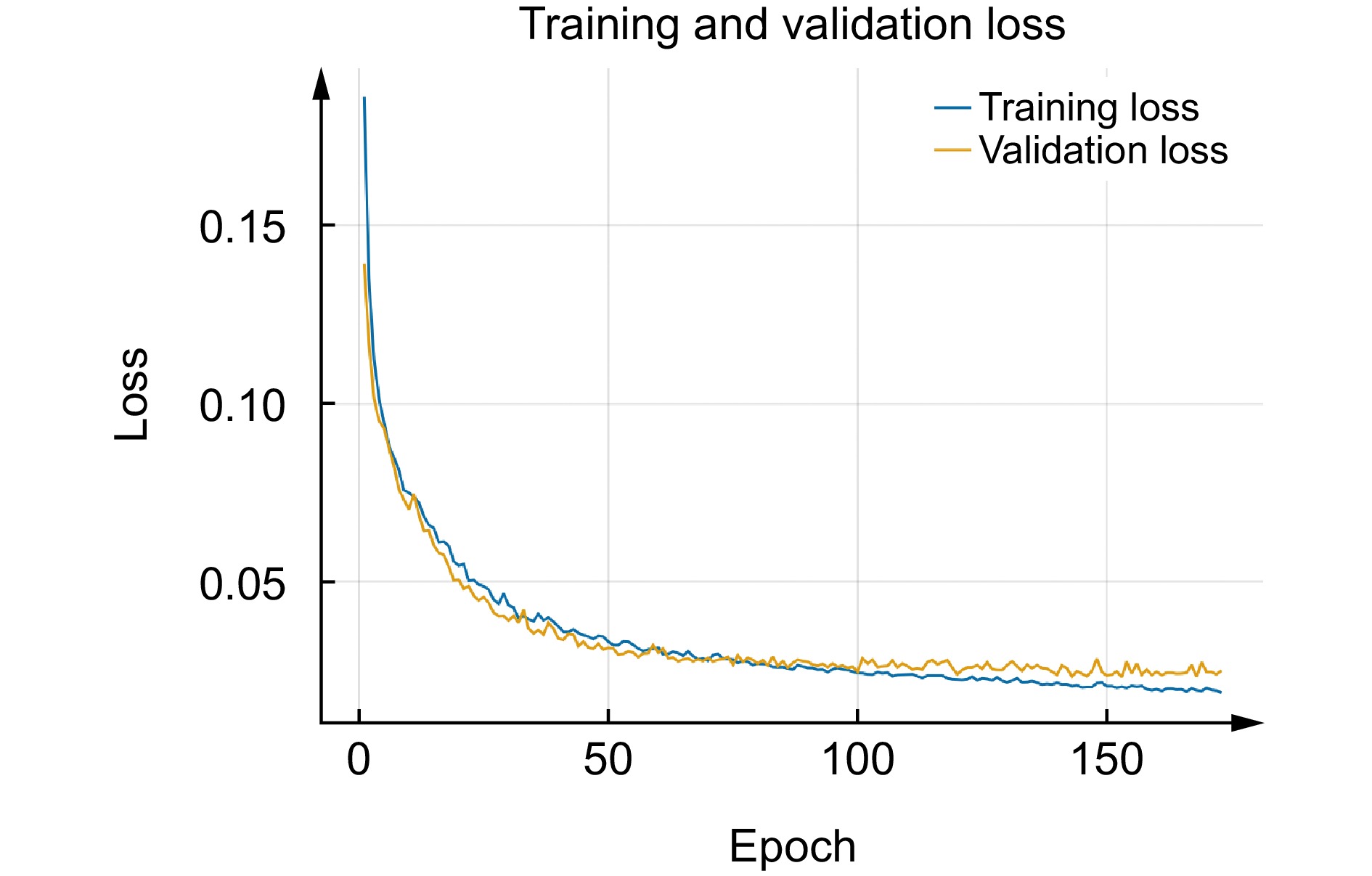
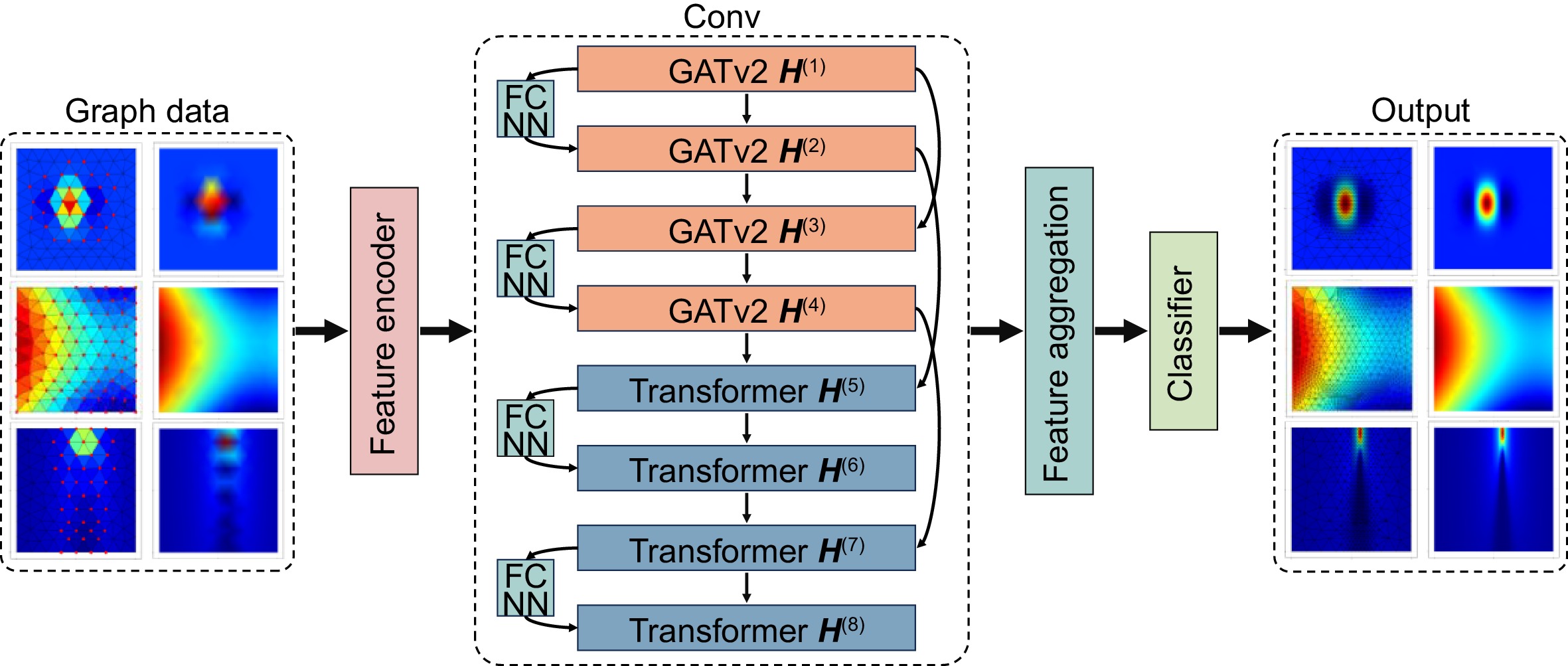
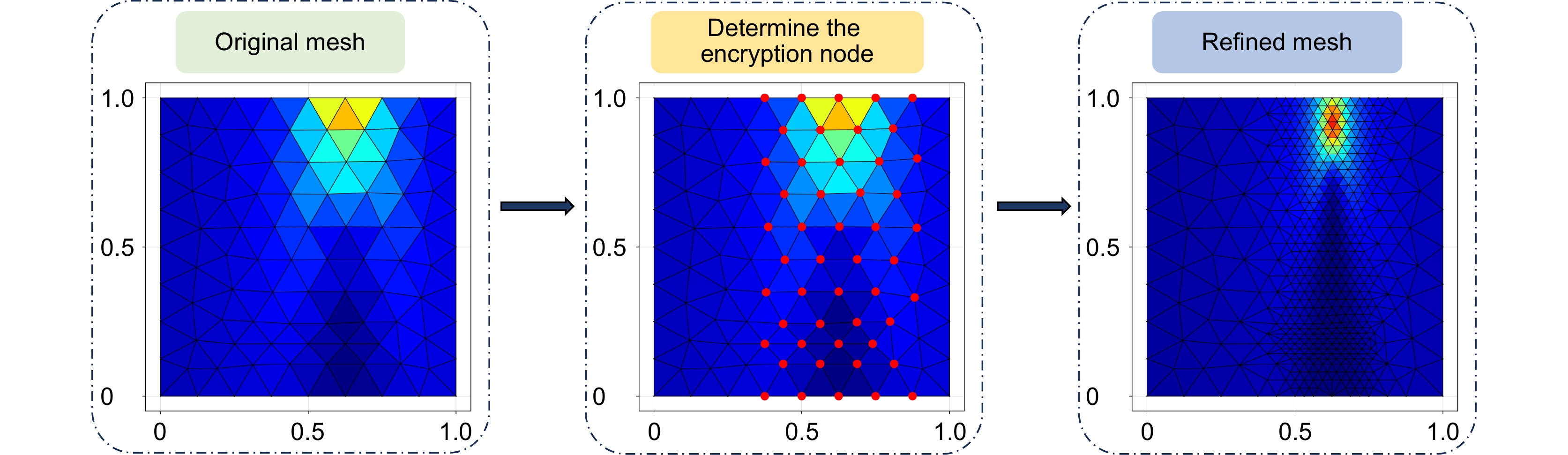
Overview: In the fields of engineering and computational science, finite element analysis is a commonly used numerical simulation tool. Its accuracy and efficiency directly affect the reliability and computational cost of engineering design. However, traditional adaptive mesh refinement technology faces certain challenges in the pursuit of high-precision and high-efficiency collaborative optimization. Especially when dealing with engineering problems with singular fields or complex boundary conditions, traditional iterative methods often show the problems such as uneven gradient error distribution and slow convergence. These limitations not only affect the accuracy of the calculation results, but also limit the application of finite element analysis in complex problems. To address the above problems, this study proposes an adaptive mesh partitioning framework based on the attention fusion mechanism, namely GATv2-Transformer fusion network (GTF-Net). This method transforms the mesh partitioning problem into a node classification problem. Each mesh node is regarded as a node in the graph, and the edges between nodes represent the relationship between units. The relationship between mesh units is modeled using graph neural networks, thereby achieving adaptive adjustment of mesh partitioning. Graph neural networks automatically adjust the mesh structure by learning these relationships. The network innovatively combines the graph attention mechanism with the Transformer architecture, and realizes the dynamic coupling of local geometric features and global physical fields through multi-head cross attention modules, effectively improving the representation ability of complex environments. The analytical solution of multiple equations is introduced into the network training, and a multi-task learning objective is constructed to ensure the generalization performance of the model under different physical field characteristics. The typical optical waveguide transmission problem example and the solution results of the first-kind Bessel function show that compared with the traditional skFem method, GTF-Net has improved the calculation speed while reducing the standard deviation of the gradient error by more than 20% (the Bessel function case is reduced by 23.8%, and the optical waveguide case is reduced by 85.9%). The experimental results show that the network significantly improves the matching degree between the grid density distribution and the physical field changes through nonlinear mapping of the feature space, and the method has a certain generalization ability and can adapt to different types of problems and application scenarios. This method provides a new deep learning solution for adaptive finite element analysis in engineering calculations, and also opens up a new technical path for the development of data-driven intelligent finite element analysis.
-

-
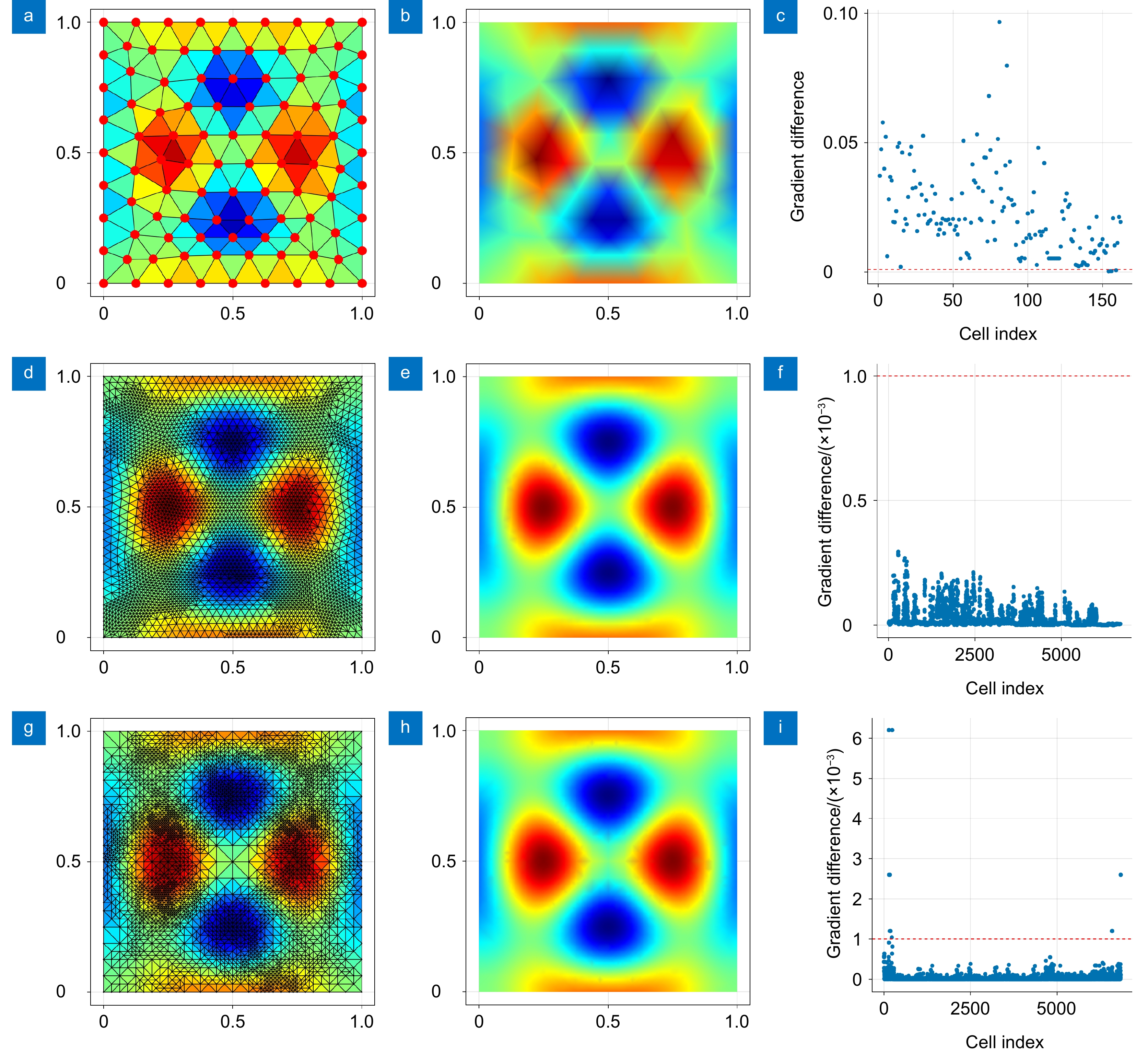
图 4 贝塞尔函数。(a)初始网格;(b)解场(初始网格);(c)梯度误差分布(初始网格);(d) GTF-Net网格;(e)解场(GTF-Net网格);(f)误差梯度分布(GTF-Net网格);(g) skFem网格;(h)解场(skFem网格);(i)梯度误差分布(skFem网格)
Figure 4. Bessel's equations. (a) Original mesh; (b) Solution field (original mesh); (c) Gradient error distribution (original mesh); (d) GTF-Net mesh; (e) Solution field (GTF-Net mesh); (f) Error gradient distribution (GTF-Net mesh); (g) skFem mesh; (h) Solution field (skFem mesh); (i) Gradient error distribution (skFem mesh)
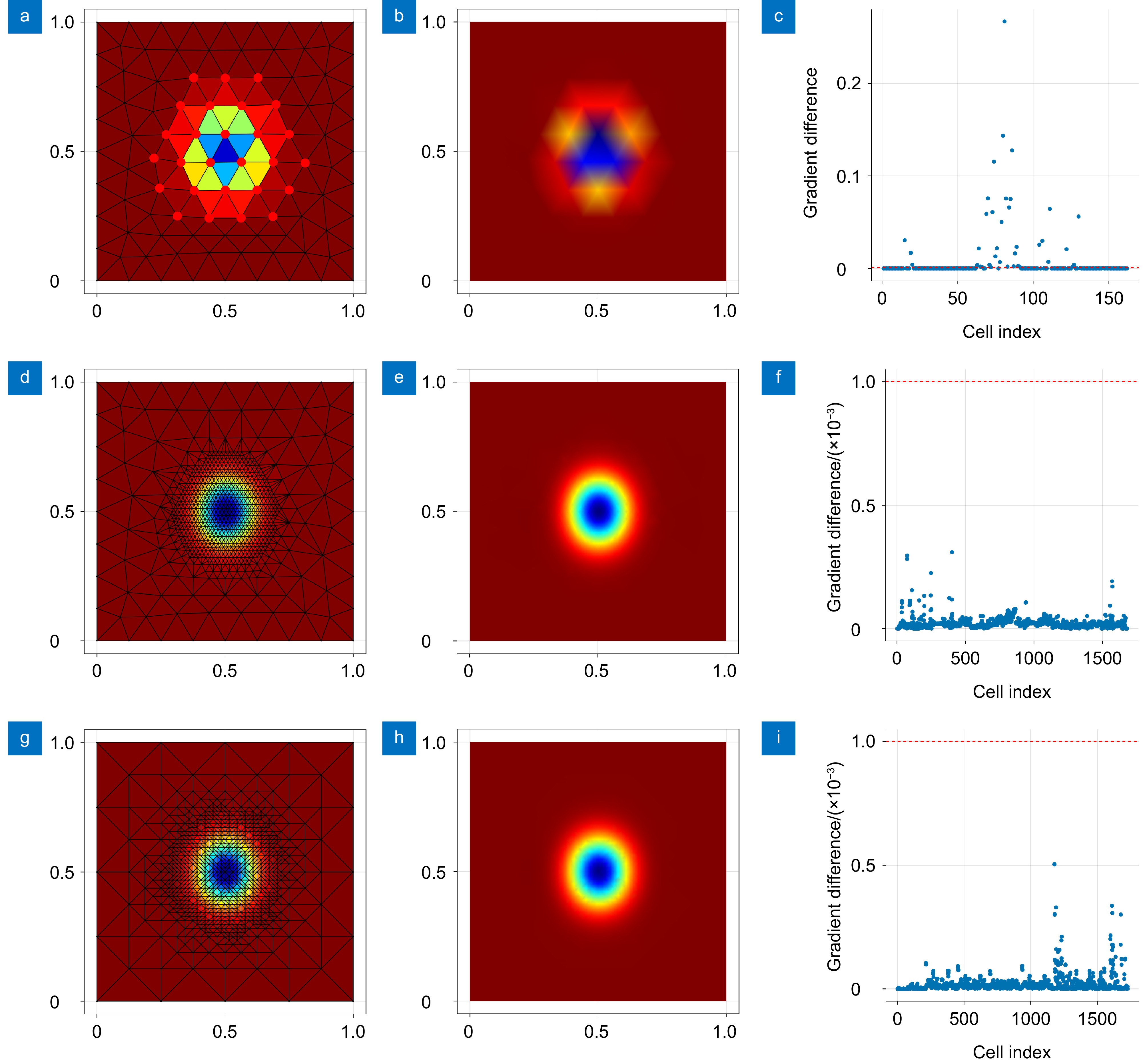
图 5 光波导的求解。 (a)初始网格;(b)解场(初始网格);(c)梯度误差分布(初始网格);(d) GTF-Net网格;(e)解场(GTF-Net网格);(f)误差梯度分布(GTF-Net网格);(g) skFem网格;(h)解场(skFem网格);(i)梯度误差分布(skFem网格)
Figure 5. Solving optical waveguide. (a) Original mesh; (b) Solution field (original mesh); (c) Gradient error distribution (original mesh); (d) GTF-Net mesh; (e) Solution field (GTF-Net mesh); (f) Error gradient distribution (GTF-Net mesh); (g) skFem mesh; (h) Solution field (skFem mesh); (i) Gradient error distribution (skFem mesh)
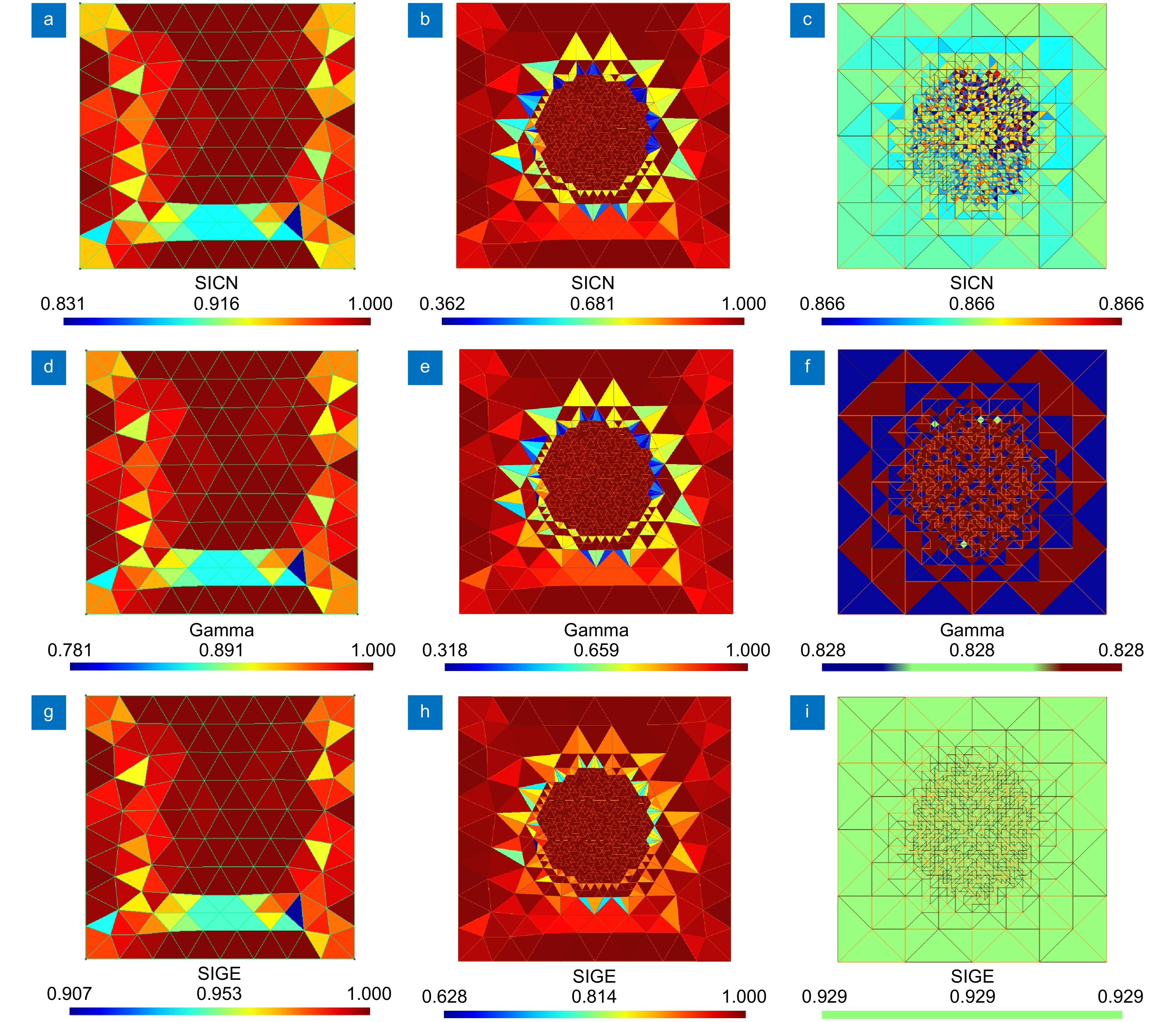
图 6 不同网格单元质量分布图。(a)初始网格单元SICN值分布;(b) GTF-Net网格单元SICN值分布;(c) skFem网格单元SICN值分布;(d)初始网格单元Gamma值分布;(e) GTF-Net网格单元Gamma值分布;(f) skFem网格单元Gamma值分布;(g)初始网格单元SIGE值分布;(h) GTF-Net网格单元SIGE值分布;(i) skFem网格单元SIGE值分布
Figure 6. Quality distribution of different mesh cells. (a) SICN value distribution of original mesh cells; (b) SICN value distribution of GTF-Net mesh cells; (c) SICN value distribution of skFem mesh cells; (d) Gamma value distribution of original mesh cells; (e) Gamma value distribution of GTF-Net mesh cells; (f) Gamma value distribution of skFem mesh cells; (g) SIGE value distribution of original mesh cells; (h) SIGE value distribution of GTF-Net mesh cells; (i) SIGE value distribution of skFem mesh cells
算法1 自适应网格训练数据生成方法 输入:非结构化网格mesh,生成样本的数量n_samples,用于节点标记的阈值tolerance,输出图类型graph_type 输出:网格列表graph_list,标签列表label_list 01. 使用随机函数创建初始网格图 02. 初始化graph_list和label_list 03. FOR 1:n_samples: 04. 复制基础网格并更新为新的随机函数 05. 计算单元梯度差 06. 初始化节点标签为0 07. IF 梯度差>阈值: 08. 标记节点标签为1 09. END IF 10. 按照图类型分类,添加到网格列表 11. END FOR 12. 返回 网格列表,标签列表 表 1 训练数据生成方法中部分随机函数
Table 1. Part of random function in training data generation method
Function name Description plane_wave( ) Generate two-dimensional plane wave, using cosine function to represent the propagation of electromagnetic waves. cylindrical_wave( ) Generate cylindrical wave, where the wave intensity is related to the radial distance from the source point, described using Bessel function. random_waveguide_field() Generate random waveguide field, providing random refractive index and waveguide parameter. gaussian_beam( ) Generate Gaussian beam, calculate the radial distance, and adjust the beam width based on propagation distance. random_interface_field( ) Generate random interface field, selecting random interface types and Gaussian beams as base field. step_interface( ) Define step interface, determining the change in dielectric constant of material at boundary position. periodic_interface( ) Define periodic interface, producing periodic material structure. multipole_field( ) Define multipole field, using Bessel function and angle to describe multipoles of different orders. evanescent_wave( ) Define evanescent wave, primarily decaying in the y-direction. 表 2 不同神经网络框架参数设置
Table 2. Parameter setting for different neural network frameworks
Parameter GTF-Net TF-Net GATv2-Net Feature encoder Dense Dense Dense Transformer layer 4-layer TransformerConv 8-layer TransformerConv None GATv2 layer 4-layer GATv2Conv None 8-layer GATv2Conv Skip connections 4 dense skip connections 4 dense skip connections 4 dense skip connections Layer normalization 8-layer LayerNorm 8-layer LayerNorm 8-layer LayerNorm Feature aggregation Dense -> ReLU -> Dropout Dense -> ReLU -> Dropout Dense -> ReLU -> Dropout Classifier Dense Dense Dense Activation function ReLU, Sigmoid ReLU, Sigmoid ReLU, Sigmoid Dropout 0.1 0.1 0.1 表 3 GTF-Net 与其他方法的性能比较
Table 3. Performance comparison of GTF-Net with other methods
Network MSE/% Accuracy/% F1-Score/% GTF-Net 1.52 97.9 96.4 TF-Net 1.86 97.5 95.7 GATv2-Net 3.12 95.9 94.2 表 4 GTF-Net网格与其他方法的误差比较
Table 4. Error comparison between GTF-Net Grid and other methods
Mesh Bessel equations Original mesh Number of
nodesNumber of
elementsStandard
deviationTime/s Ratio/% Number of
nodesNumber of
elementsStandard
deviationTime/s Ratio/% Original mesh 98 162 0.016 — — 98 162 0.031 — — skFem 3474 6842 2.384×10−4 5.46 — 873 1728 3.379×10−5 6.43 — GTF-Net 3489 6825 3.353×10−5 3.51 35.74 874 1714 2.573×10−5 2.58 59.91 表 5 不同网格的单元质量分析
Table 5. Element quality analysis of different meshes
Quality parameter Original mesh GTF-Net mesh skFem mesh SICN 0.9736 (0.8311->1) 0.9644 (0.362->1) 0.866 (0.866->0.866) Gamma 0.9685 (0.7812->1) 0.9622 (0.3179->1) 0.8284 (0.8284->0.8284) SIGE 0.9884 (0.9068->1) 0.9874 (0.6281->1) 0.9292 (0.9292->0.9292) -
参考文献
[1] Pasciak J E. The mathematical theory of finite element methods (Susanne C. Brenner and L. Ridgway Scott)[J]. SIAM Rev, 1995, 37(3): 472−473. doi: 10.1137/1037111
[2] Salminen T, Lehtinen K E J, Seppänen A. Application of the finite element method to the multicomponent general dynamic equation of aerosols[J]. J Aerosol Sci, 2023, 174: 106260. doi: 10.1016/j.jaerosci.2023.106260
[3] Barth T, Ohlberger M. Finite volume methods: foundation and analysis[M]//Stein E, de Borst R, Hughes T J R. Encyclopedia of Computational Mechanics. Chichester: John Wiley, 2004: 1–60. https://doi.org/10.1002/0470091355.ecm010.
[4] Berger M J, Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations[J]. J Comput Phys, 1984, 53(3): 484−512. doi: 10.1016/0021-9991(84)90073-1
[5] Perera R, Agrawal V. Dynamic and adaptive mesh-based graph neural network framework for simulating displacement and crack fields in phase field models[J]. Mech Mater, 2023, 186: 104789. doi: 10.1016/j.mechmat.2023.104789
[6] Zhao Y X, Li H R, Zhou H S, et al. A review of graph neural network applications in mechanics-related domains[J]. Artif Intell Rev, 2024, 57(11): 315. doi: 10.1007/s10462-024-10931-y
[7] Economon T D, Palacios F, Copeland S R, et al. SU2: an open-source suite for multiphysics simulation and design[J]. AIAA J, 2016, 54(3): 828−846. doi: 10.2514/1.J053813
[8] Marburg S, Nolte B. Computational Acoustics of Noise Propagation in Fluids-Finite and Boundary Element Methods[M]. Berlin, Heidelberg: Springer, 2008. https://doi.org/10.1007/978-3-540-77448-8.
[9] Verfürth R. A posteriori error estimation and adaptive mesh-refinement techniques[J]. J Comput Appl Math, 1994, 50(1-3): 67−83. doi: 10.1016/0377-0427(94)90290-9
[10] Xie L J, Chen J J, Liang Y, et al. Geometry-based adaptive mesh generation for continuous and discrete parametric surfaces[J]. J Inf Comput Sci, 2012, 9(8): 2327−2344.
[11] Möller M, Kuzmin D. Adaptive mesh refinement for high‐resolution finite element schemes[J]. Int J Numer Methods Fluids, 2006, 52(5): 545−569. doi: 10.1002/fld.1183
[12] Triantafyllidis D G, Labridis D P. A finite-element mesh generator based on growing neural networks[J]. IEEE Trans Neural Netw, 2002, 13(6): 1482−1496. doi: 10.1109/TNN.2002.804223
[13] Jilani H, Bahreininejad A, Ahmadi M T. Adaptive finite element mesh triangulation using self-organizing neural networks[J]. Adv Eng Softw, 2009, 40(11): 1097−1103. doi: 10.1016/j.advengsoft.2009.06.008
[14] Bohn J, Feischl M. Recurrent neural networks as optimal mesh refinement strategies[J]. Comput Math Appl, 2021, 97: 61−76. doi: 10.1016/j.camwa.2021.05.018
[15] Zhang Z Y, Wang Y X, Jimack P K, et al. MeshingNet: a new mesh generation method based on deep learning[C]//Proceedings of the 20th International Conference on Computational Science, Amsterdam, 2020: 186–198. https://doi.org/10.1007/978-3-030-50420-5_14.
[16] Wu Z H, Pan S R, Chen F W, et al. A comprehensive survey on graph neural networks[J]. IEEE Trans Neural Netw Learn Syst, 2020, 32(1): 4−24. doi: 10.1109/TNNLS.2020.2978386
[17] 张丽英, 孙海航, 孙玉发, 等. 基于图卷积神经网络的节点分类方法研究综述[J]. 计算机科学, 2024, 51(4): 95−105. doi: 10.11896/jsjkx.230600071
Zhang L Y, Sun H H, Sun Y F, et al. Review of node classification methods based on graph convolutional neural networks[J]. Comput Sci, 2024, 51(4): 95−105. doi: 10.11896/jsjkx.230600071
[18] Kim M, Lee J, Kim J. GMR-Net: GCN-based mesh refinement framework for elliptic PDE problems[J]. Eng Comput, 2023, 39(5): 3721−3737. doi: 10.1007/s00366-023-01811-0
[19] Khan A, Yamada M, Chikane A, et al. GraphMesh: geometrically generalized mesh refinement using GNNs[C]//Proceedings of the 24th International Conference on Computational Science, Malaga, 2024: 120–134. https://doi.org/10.1007/978-3-031-63775-9_9.
[20] Pelissier U, Parret-Fréaud A, Bordeu F, et al. Graph neural networks for mesh generation and adaptation in structural and fluid mechanics[J]. Mathematics, 2024, 12(18): 2933. doi: 10.3390/math12182933
[21] Peng J M, Chen X H, Liu J. 3DMeshNet: a three-dimensional differential neural network for structured mesh generation[J]. Graph Models, 2025, 139: 101257. doi: 10.1016/j.gmod.2025.101257
[22] Rowbottom J, Maierhofer G, Deveney T, et al. G-adaptivity: optimised graph-based mesh relocation for finite element methods[Z]. arXiv: 2407.04516, 2024.
[23] Freymuth N, Dahlinger P, Würth T, et al. Swarm reinforcement learning for adaptive mesh refinement[C]//Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, 2024: 3206.
[24] 梁礼明, 董信, 李仁杰, 等. 基于注意力机制多特征融合的视网膜病变分级算法[J]. 光电工程, 2023, 50(1): 220199. doi: 10.12086/oee.2023.220199
Liang L M, Dong X, Li R J, et al. Classification algorithm of retinopathy based on attention mechanism and multi feature fusion[J]. Opto-Electron Eng, 2023, 50(1): 220199. doi: 10.12086/oee.2023.220199
[25] 张红民, 田钱前, 颜鼎鼎, 等. GLCrowd: 基于全局-局部注意力的弱监督密集场景人群计数模型[J]. 光电工程, 2024, 51(10): 240174. doi: 10.12086/oee.2024.240174
Zhang H M, Tian Q Q, Yan D D, et al. GLCrowd: a weakly supervised global-local attention model for congested crowd counting[J]. Opto-Electron Eng, 2024, 51(10): 240174. doi: 10.12086/oee.2024.240174
[26] Scarselli F, Gori M, Tsoi A C, et al. The graph neural network model[J]. IEEE Trans Neural Netw, 2009, 20(1): 61−80. doi: 10.1109/TNN.2008.2005605
[27] 商雅名, 吴安彪, 袁野, 等. 基于个性化PageRank高阶邻域聚合的图神经网络增强[J]. 计算机工程, 2024. doi: 10.19678/j.issn.1000-3428.0068976
Shang Y M, Wu A B, Yuan Y, et al. Graph neural network enhancement based on personalized PageRank high-order neighborhood aggregation[J]. Comput Eng, 2024. doi: 10.19678/j.issn.1000-3428.0068976
[28] Brody S, Alon U, Yahav E. How attentive are graph attention networks?[C]//Proceedings of the 10th International Conference on Learning Representations, 2022: 1–26.
[29] Yun S, Jeong M, Kim R, et al. Graph transformer networks[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems, 2019: 1073.
[30] Geuzaine C, Remacle J F. Gmsh: a 3‐D finite element mesh generator with built‐in pre‐and post‐processing facilities[J]. Int J Numer Methods Eng, 2009, 79(11): 1309−1331. doi: 10.1002/nme.2579
[31] Gustafsson T, Mcbain G D. scikit-fem: a Python package for finite element assembly[J]. J Open Source Softw, 2020, 5(52): 2369. doi: 10.21105/joss.02369
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: