E-mail Alert
RSS
Design technology of the truss support structure of the ultra-low thermal deformation gravitational wave detection telescope
-
摘要
本文针对引力波探测望远镜超低热变形要求，提出了通过设计CFRP铺层改变材料热胀系数的方法，进而解决桁架支撑结构热变形问题。同时针对望远镜装调性能的要求，给出了结构的分段式设计方案。文章首先分析了CFRP的优势、现有的消热化的方式和国内外研究进展，确定了以CFRP为关键材料的三杆式望远镜的方案，并提出了设计指标。其次建立了“材料-热变形、桁架结构-热变形”数学模型，针对材料铺层和结构设计进行优化，给出了优化方案。然后将CFRP材料应用于支撑结构中，采用分段式主支撑结构设计方案，降低了结构加工装调的难度，最后对整体结构进行分析。分析结果表明：机械性能方面，结构基频和最大重力卸载变形满足主支撑结构的要求；热变形方面，基于CFRP铺层特定优化设计的结构方案热变形为普通铺层方案的27.15%、Invar材料支杆方案的6.42%、SiC支杆方案的11.50%和钛合金支杆方案的3.21%，即优化设计可显著降低结构热变形。
Abstract
This paper focuses on the ultra-low thermal deformation requirements of the main support structure of the gravitational wave detection telescope. It proposes a method to reduce the thermal deformation of the truss support structure by designing CFRP (carbon fiber reinforced polymer) layers to modify the material's thermal expansion coefficient. Additionally, to meet the alignment performance requirements of the telescope, a segmented design scheme for the structure is presented. The paper begins by analyzing the advantages of CFRP, existing methods of thermal dissipation, and the research progress both domestically and internationally. It determines the three-segment telescope design using CFRP as the support material and establishes design criteria. Next, mathematical models for "material-thermal deformation" and "truss structure-thermal deformation" are developed. Optimization is conducted for material layering and structural design, resulting in an optimized solution. Furthermore, CFRP materials are applied to the support structure, and a segmented main support structure design scheme is proposed to reduce the difficulty of structural processing and alignment. The overall structure is analyzed. The analysis results demonstrate that, in terms of mechanical performance, the overall structure's natural frequency and maximum gravity-unloading deformation meet the requirements of the main support structure. In terms of thermal deformation, the optimized design based on CFRP layering exhibits a thermal deformation that is 27.15% of the conventional layering scheme, 6.42% of the Invar material support rod scheme, 11.50% of the SiC support rod scheme, and 3.21% of the titanium alloy support rod scheme. This indicates that the optimized design can significantly reduce the structural thermal deformation.
-
Overview
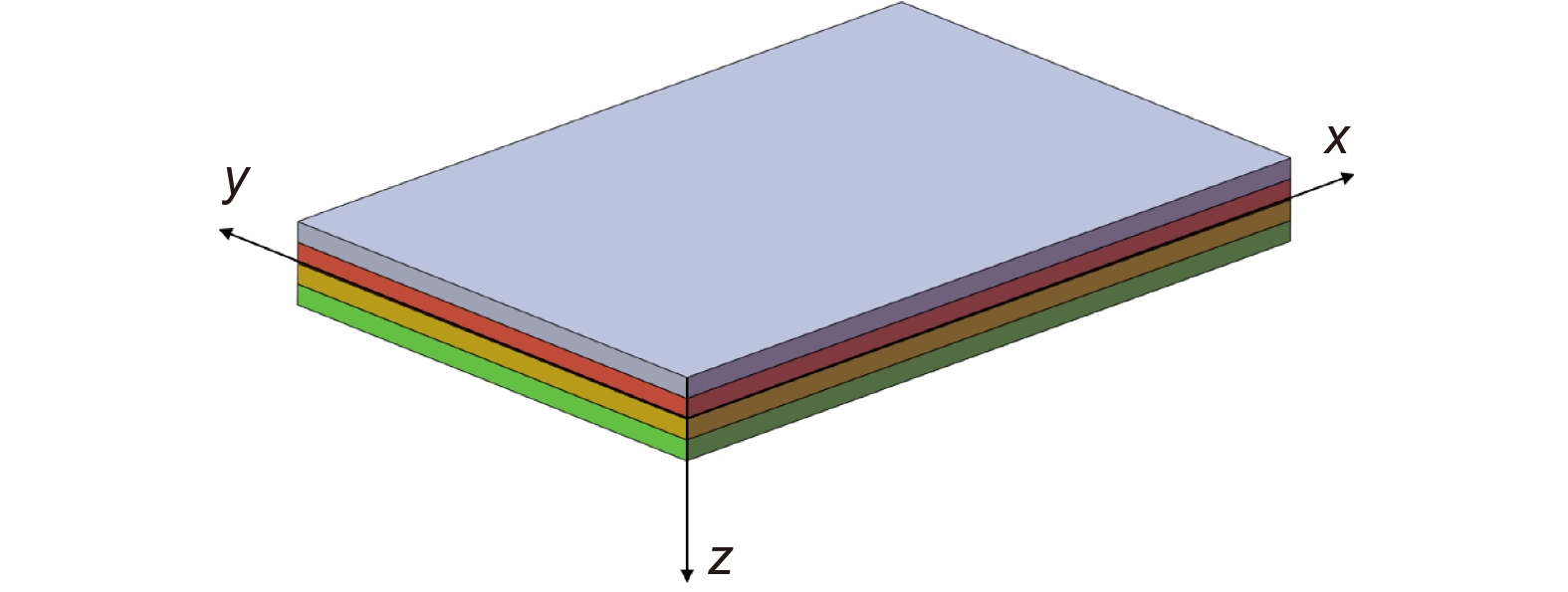
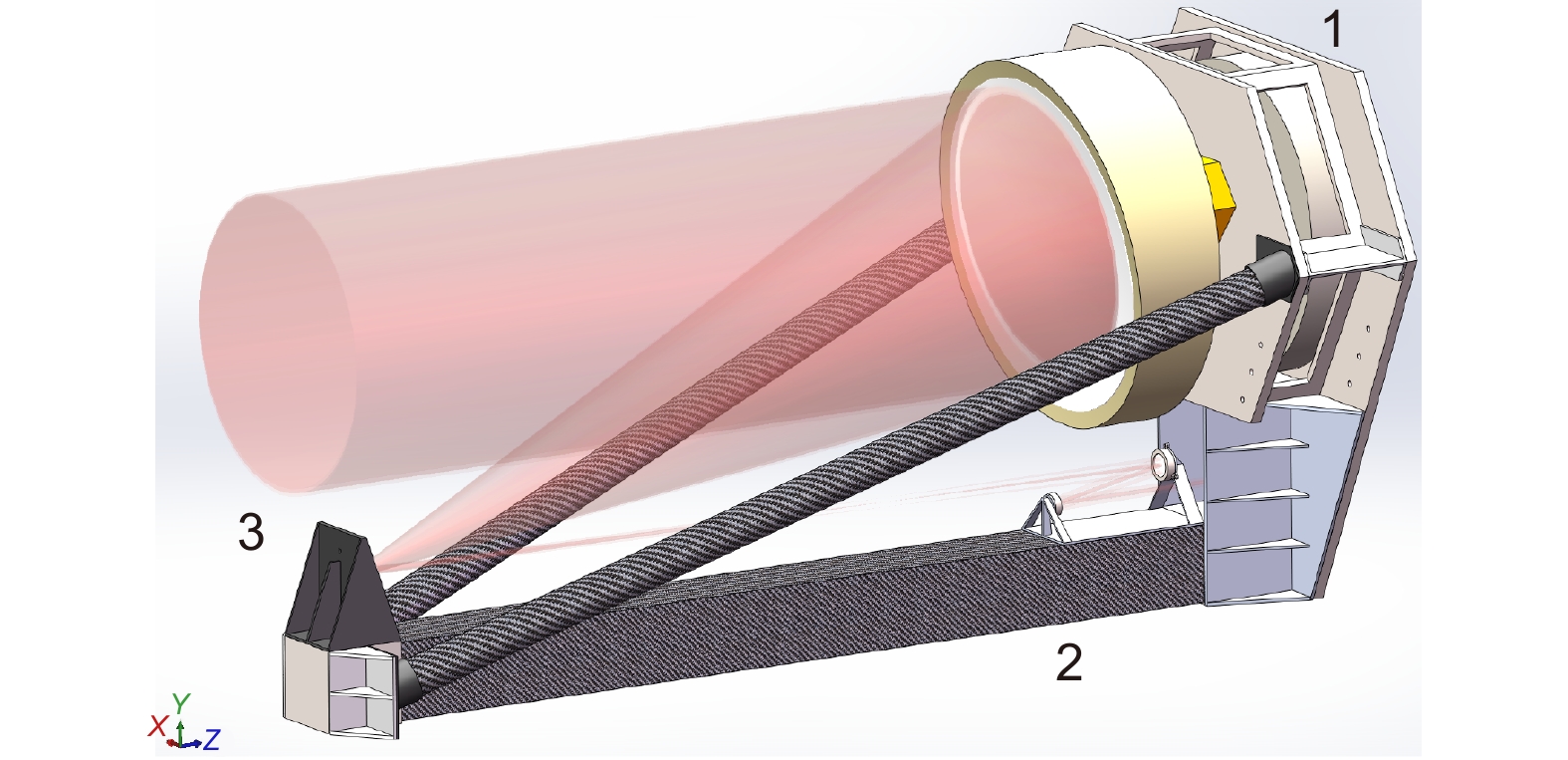
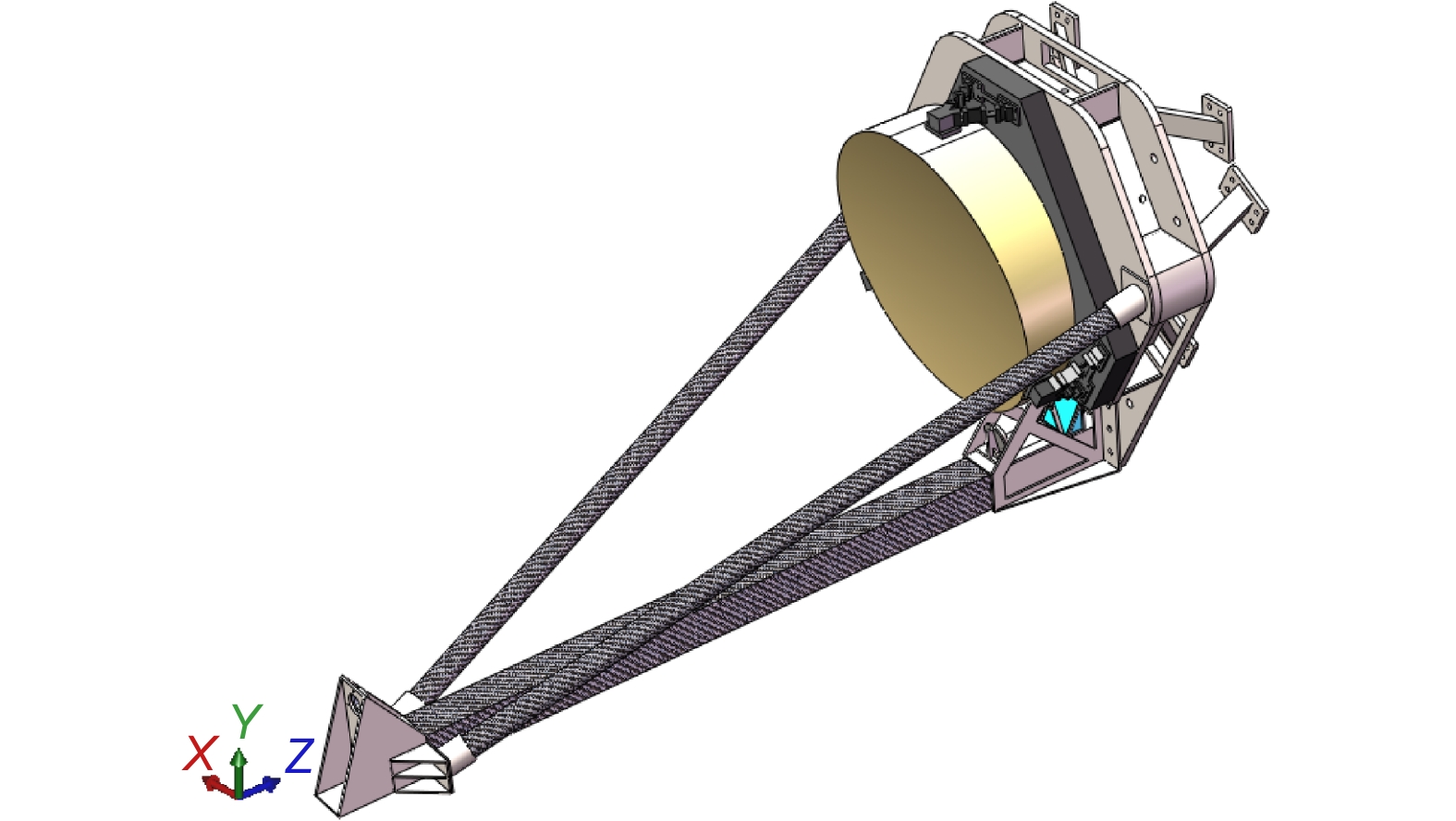
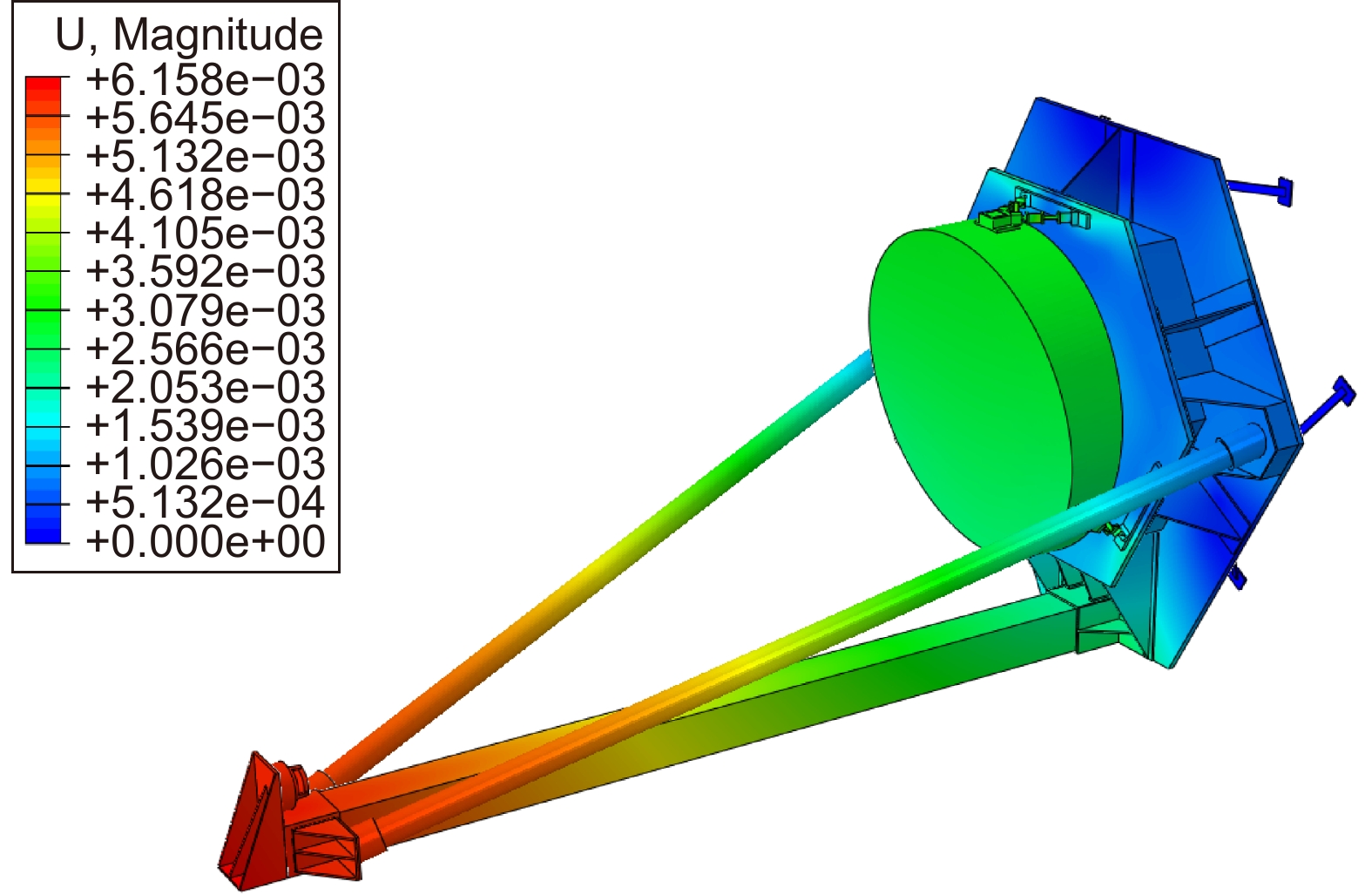
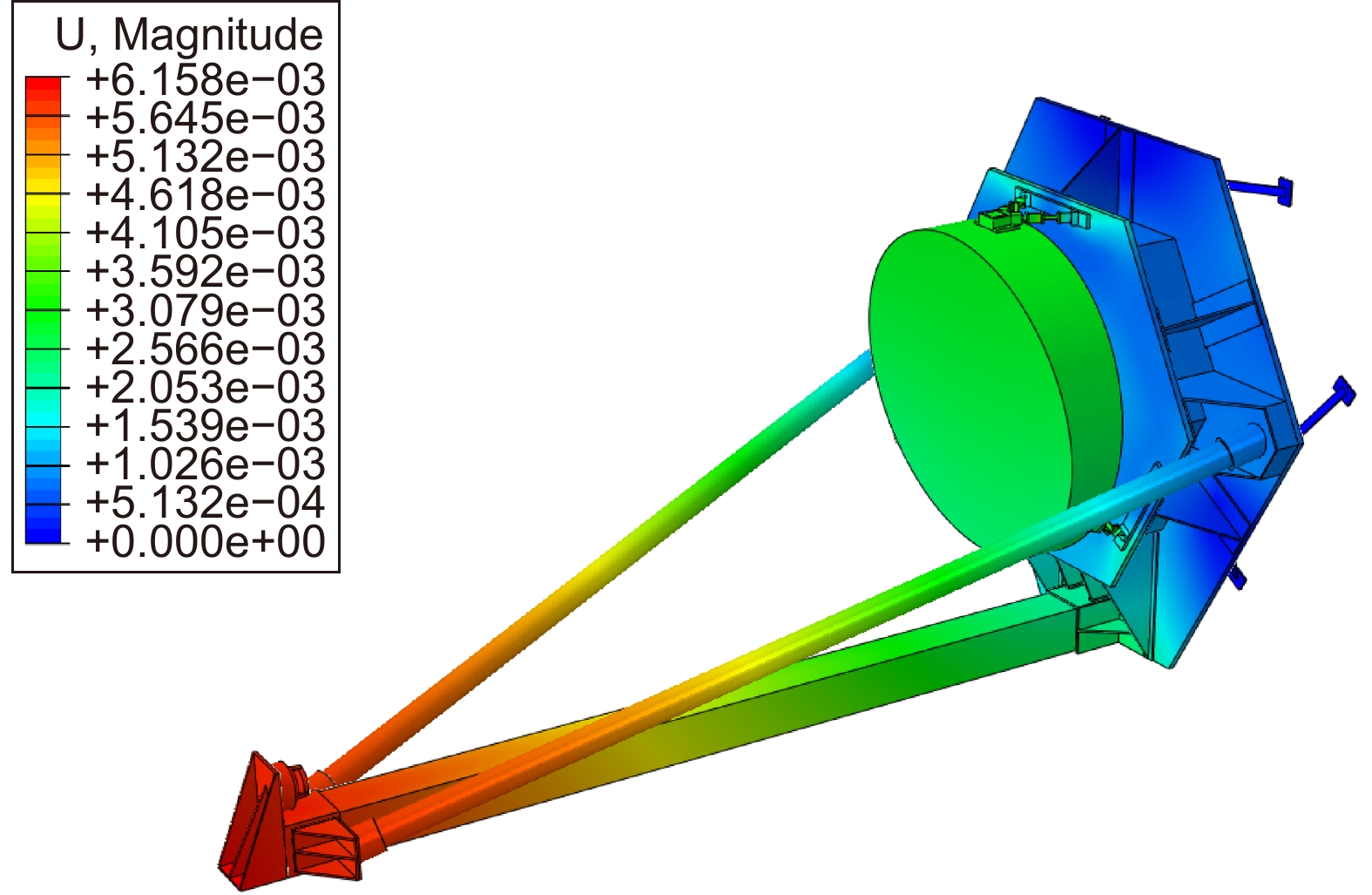
Overview: At the current stage, gravitational wave telescopes have stringent requirements for thermal deformation stability. Due to limitations in manufacturing processes and material properties, it is necessary to optimize the CFRP material and structural configuration to achieve the desired design. Based on the current progress in gravitational wave telescope design and the level of manufacturing processes, combined with a comparative analysis with advanced space-based telescopes domestically and internationally, it is deemed reasonable to set the thermal deformation design target for the support structure at α<1.0×10−7 /K. This paper primarily focuses on the following research aspects: 1) In order to reduce the overall thermal deformation of the structure to below 1×10−7 /K, it is necessary to ensure that the thermal expansion coefficient of the truss material meets this requirement. Therefore, the CFRP material layering scheme is optimized to reduce its longitudinal thermal expansion coefficient to below 1×10−7 /K, which is then used for the axial direction of the truss rods. 2) Provide a structural optimization scheme to observe whether the structure can meet the requirements of ΔT=10 K conditions for the relative rigid-body displacement between the primary and secondary mirrors, ensuring dz < 10 μm and dy < 5 μm. Additionally, check if weight, modal properties, gravitational unloading, and other aspects meet the standards. 3) Building upon this, discuss whether the use of CFRP material meeting the 1×10−7 /K level can satisfy the structural stability requirements after being incorporated into the structure as truss material. 4) Compare the advantages and design potential of CFRP with conventional telescope truss materials. Therefore, the paper first analyzes the advantages of CFRP, existing methods of thermal dissipation, and research progress both domestically and internationally. It establishes a design scheme for a three-rod telescope with CFRP as the support material and proposes design criteria. Mathematical models are then developed to describe the relationship between material properties and thermal deformation as well as truss structure thermal deformation. Optimization is performed on material layering and structural design, and an optimized solution is provided. Finally, CFRP material is applied to the support structure, a segmented main support structure design is presented to reduce manufacturing and alignment difficulties, and an overall structural analysis is conducted. The analysis results demonstrate that, in terms of mechanical performance, the truss structure has a weight of 6.7 kg and a fundamental frequency of 122.61 Hz. In terms of thermal deformation, the optimized design based on CFRP layering exhibits a thermal deformation that is 27.15% of the conventional layering scheme, 6.42% of the Invar material support rod scheme, 11.50% of the SiC support rod scheme, and 3.21% of the titanium alloy support rod scheme. This indicates that the optimized design can significantly reduce the structural thermal deformation.
-
-
图 1 单层CFRP示意图。方向1为面内纤维方向，简称纵向；方向2与方向1面内垂直，简称横向
Figure 1. Single-layer CFRP schematic diagram. Direction 1 corresponds to the in-plane fiber direction referred to as the longitudinal direction；Direction 2 is perpendicular to direction 1 within the plane referred to as the transverse direction
图 3 天琴望远镜三段式设计：1)主承力板；2)主支撑三杆；3)副镜支撑装调背板
Figure 3. Three-stage design of the TianQin telescope: 1) Main load-bearing plate; 2) Three main support rods; 3) Sub-mirror support adjustment backplate
图 6 CFRP材料热膨胀有限元仿真：以最优设计—铺层方式6为例
Figure 6. Finite element simulation of thermal expansion of CFRP material — taking laying method 6 as an example
图 8 实体单元模型(左)；桁架杆单元模型(中)；理论模型(右)
Figure 8. Solid model (left); truss structure model (middle); theoretical model (right)
图 9 实体仿真结果和桁架杆仿真结果—以间隔dz方向热变形为例
Figure 9. Solid simulation and truss simulation result — example of thermal deformation in the dz direction
图 10 对结构热变形的参数优化结果
Figure 10. Optimization results for structural thermal deformations
图 11 第一阶振型：沿Y方向摆动，122.61 Hz
Figure 11. First mode: oscillation along the Y direction, 122.61 Hz
图 12 第二阶振型：沿X方向摆动，128.47 Hz
Figure 12. Second mode: oscillation along the X direction, 128.47 Hz
图 13 热变形有限元分析—以铺层1为例
Figure 13. Element analysis of thermal deformation of truss support structure — example with layer 1
图 15 主次镜间隔相对热变形为12 pm/$ \sqrt{{\rm{Hz}}} $
Figure 15. The relative thermal deformation in the M1-M2 separation direction is 12 pm/$\sqrt{{\rm{Hz}}} $
表 1 常见望远镜样机主支撑结构备选材料
Table 1. Candidate materials for truss support structure of telescope prototype
材料 密度/(kg/m3) 工程常数 线胀系数/(10−6/K) 钛合金 $ {\rho =4430} \; $ $E $=114 ${\rm{GPa}}, \nu$=0.34 $ {\alpha =8.8} $ 碳化硅 $ {\rho =3210} \; $ $E $=466 ${\rm{GPa}},$ $ \nu $=0.21 $ {\alpha =2.4} $ Zerodur $ {\rho =2530} \; $ $E $=91 ${\rm{GPa}},$ $ \nu $=0.24 $ {\alpha =0.05} $ 常规Invar合金 $ {\rho =8110} \; $ $E $=148 ${\rm{GPa}},$ $ \nu $=0.30 $ {\alpha =4.30} $ 定制Invar合金 $ {\rho =8150} \; $ $E $=144 ${\rm{GPa}},$ $ \nu $=0.30 $ {\alpha =0.63} $ CFRP1*
M40J(3k)/wp-s3000单层板[21]$ {\rho =1596} \; $ $E $1=231 ${\rm{GPa}}, $$ {\nu }_{12} $=0.26
$E $2=7.76 ${\rm{GPa}}$
$G $12=4.3 ${\rm{GPa}}$
$G $23=2.8 ${\rm{GPa}},$$ {{\alpha }}_{{1}}{=-0.481} $
$ {{\alpha }}_{{2}}{=35.841} $CFRP2*
T800H/M21单层板[22]$ {\rho =1590} \; $ $E $1=134.7 ${\rm{GPa}}, $$ {\nu }_{12} $=0.369
$E $2=7.70 ${\rm{GPa}} $
G12=4.2 ${\rm{GPa}} $
$G $23=2.5 ${\rm{GPa}} $$ {{\alpha }}_{{1}}{=-0.31} $
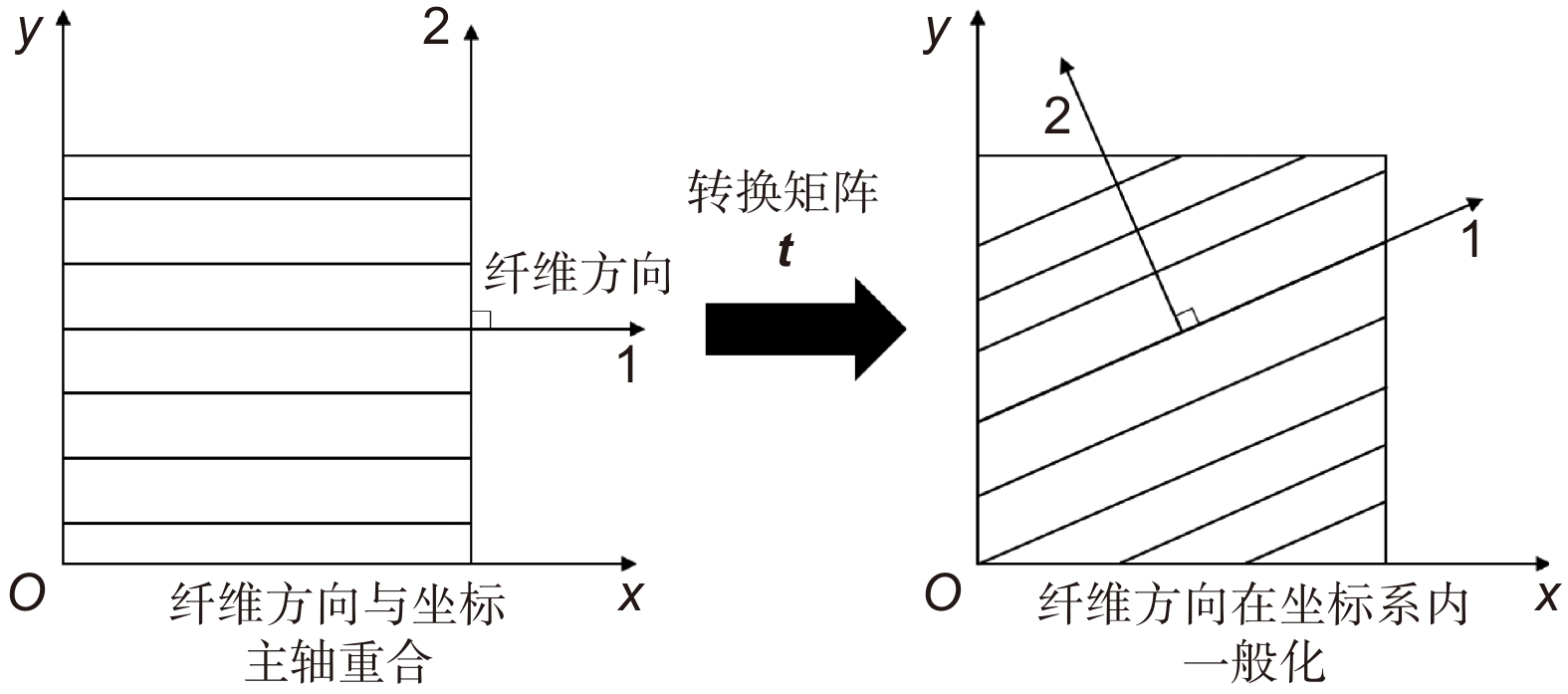
$ {{\alpha }}_{{2}}{=31.8} $
下载: 导出CSV
表 2 备选CFRP铺层方式
Table 2. Alternative CFRP layup methods
序号 铺层方式 $ {\alpha }_{x-{\rm{CFRP}}} $$ /({10}^{-7}/\mathrm{K}) $ $ {\alpha }_{y-{\rm{CFRP}}} $$ /({10}^{-7}/\mathrm{K}) $ 1 $ {\left[\pm 45/0/90/0/90/45/-45/90/0\right]}_{s} $ $ 9.817 $ $ 9.817 $ 2 $ {\left[\pm 45/90/0/-45/0/45/0/90/0\right]}_{s} $ $ 3.555 $ $ 18.90 $ 3 $ {\left[\pm 45/60/0/-45/90/45/0/-60/0\right]}_{s} $ $ 5.518 $ $ 14.99 $ 4 $ {\left[37.08/-59.45/31.38/-57.01/-16.64/16.64/57.01/-31.38/59.45/-37.08\right]}_{s} $ $ 1.205 $ $ 20.87 $ 5 $ {\left[32.61/-53.67/37.04/-56.86/-32.65/32.65/56.86/-37.04/53.67/-32.61\right]}_{s} $ $ 0.826 $ $ 20.28 $ 6 $ {\left[-30.49/-51.63/36.10/-60.38/-30.44/30.44/60.38/-36.10/51.63/30.49\right]}_{s} $ $ 0.069 $ $ 21.69 $
下载: 导出CSV
表 3 理论模型计算结果与仿真结果对比
Table 3. Comparison of theoretical model calculation results with simulation results
铺层方案 $ {\alpha }_{x-{\rm{CFRP}}}/({10}^{-7}/\mathrm{K}) $
(理论结果)$ {\alpha }_{x-{\rm{CFRP}}}/({10}^{-7}/\mathrm{K}) $
(仿真结果)相对误差/$\% $ 1 $ 9.817 $ $ 9.817 $ 0 2 $ 5.518 $ $ 5.518 $ 0 3 $ 6.713 $ $ 6.713 $ 0 4 $ 1.205 $ $ 1.199 $ $0.42$ 5 $ 0.826 $ $ 0.821 $ $0.63$ 6 $ 0.069 $ $ 0.065 $ $6.10$
下载: 导出CSV
表 4 望远镜样机主支撑结构设计要求
Table 4. Design requirements for main support structure of telescope prototype
指标项目 输入条件 性能要求 1.结构重量 固有性质 $< 7.5 \;{\rm{kg} }$(仅支架) 2.模态特性 固有性质 $fre{q}_{1} > 80\;{\rm{Hz}}$ 3.重力卸载 任意方向 $\mathrm{\Delta } {\textit{z} } _{{\rm{M}}\mathrm{1,2} } < 10 { {\rm{\text{ μ} } } }\mathrm{m}$
$\mathrm{\Delta }{y}_{{\rm{M}}\mathrm{1,2} } < 10 \rm{\text{ μ} }\mathrm{m}$
$\mathrm{\Delta }{T}_{{\rm{M}}\mathrm{1,2} }^{x} < 30\mathrm{\text{ μ} }\mathrm{r}\mathrm{a}\mathrm{d}$4.大尺度热变形 周期内环境温变$ \mathrm{\Delta }t=10\; \mathrm{K} $ ${\rm{d} } {\textit{z} } _{ {\rm{M} }\mathrm{1,2} } < 10\text{ μ} {\rm{m} } , {\rm{d} }{y}_{ {\rm{M} }\mathrm{1,2} } < 5\text{ μ} {\rm{m}}$ 5.热变形稳定性(极限) ${ {S} }_{\mathrm{\Delta }t} < 10\mathrm{\text{ μ} } \mathrm{K}/\sqrt{ { \rm{Hz} } } $
$(10 \;{\rm{mHz}} \sim 0.1 \;{\rm{Hz}}) $$ {{S}}_{\mathrm{\Delta }{l}_{M\mathrm{1,2}}} < 1.0 \; \mathrm{p}\mathrm{m}/\sqrt{ { \rm{Hz}}} $
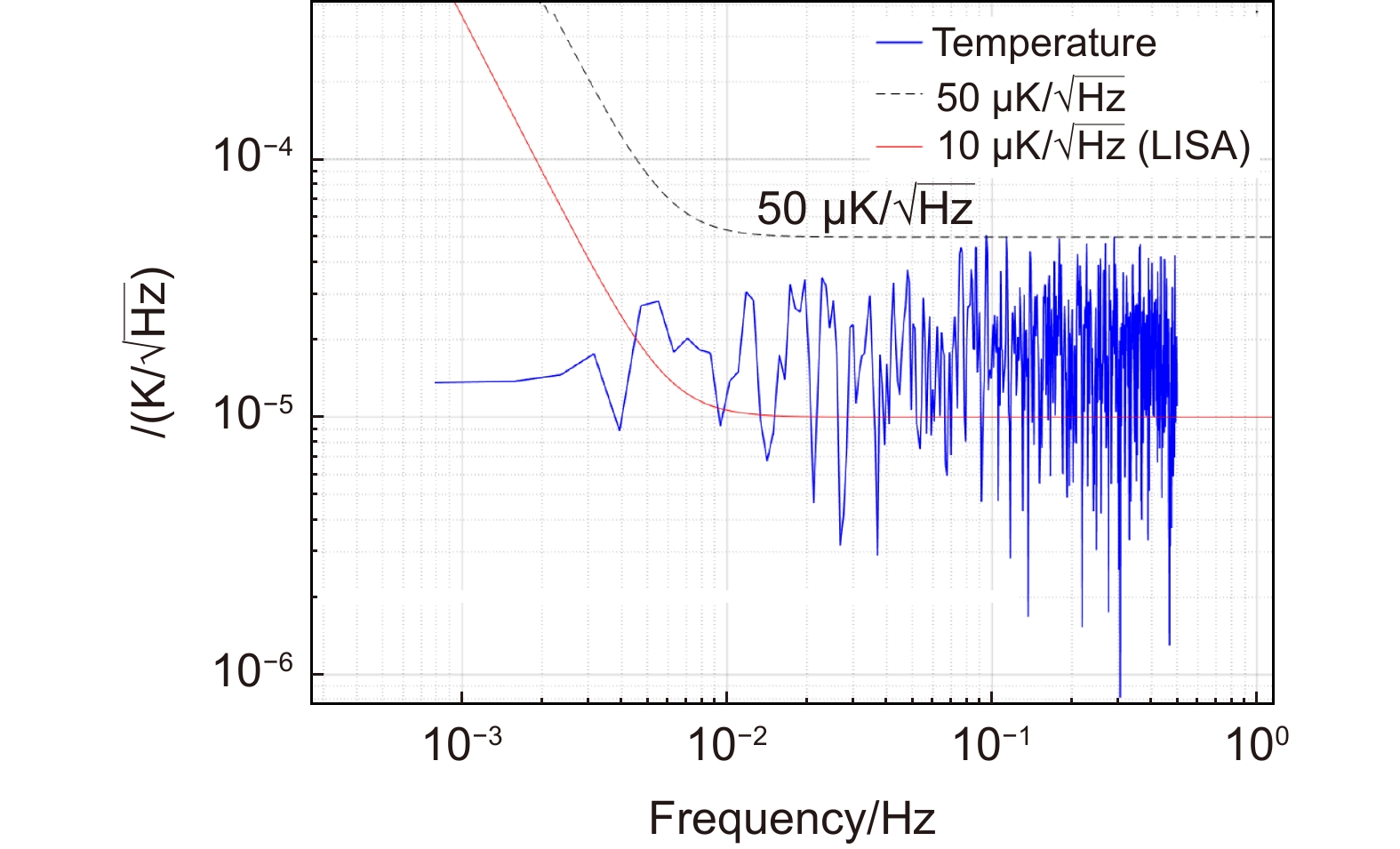
对应$ {\alpha }_ {\textit{z}} < 1\times {10}^{-7}/\; \mathrm{K} $6.热变形稳定性(常规) ${ {S} }_{\mathrm{\Delta }t} < 50\mathrm{\text{ μ} } \mathrm{K}/\sqrt{ { \rm{Hz} } }$
$ (10\; {\rm{mHz}} \sim 0.1 \;{\rm{Hz}}) $$ {{S}}_{\mathrm{\Delta }{l}_{M\mathrm{1,2}}} < 0.4 \; \mathrm{p}\mathrm{m}/\sqrt{ { \rm{Hz}}} $
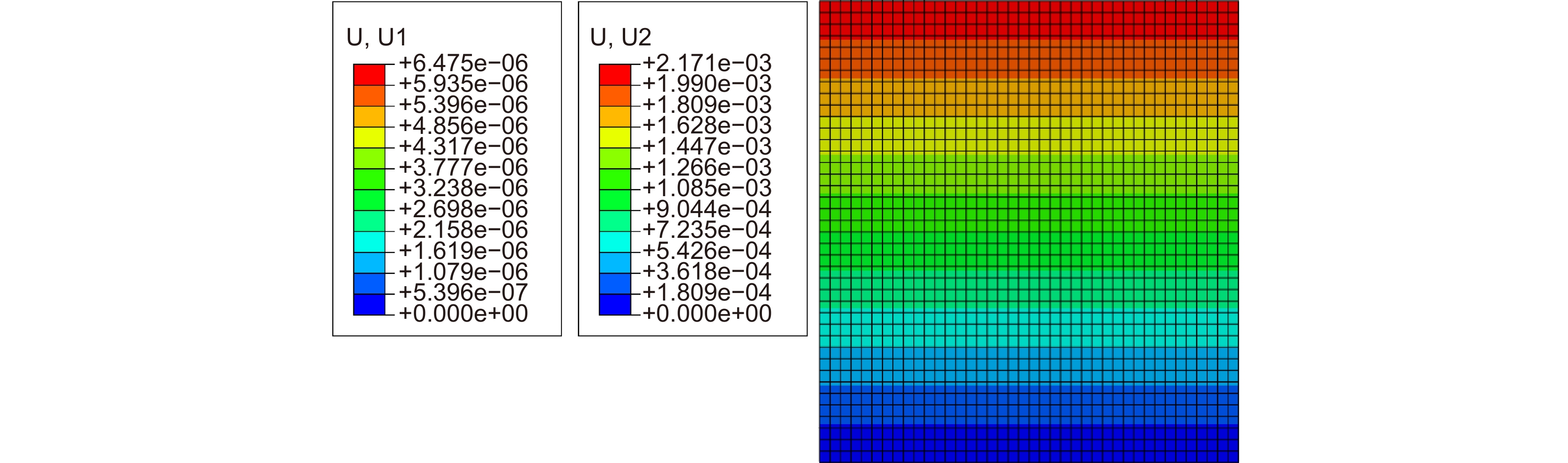
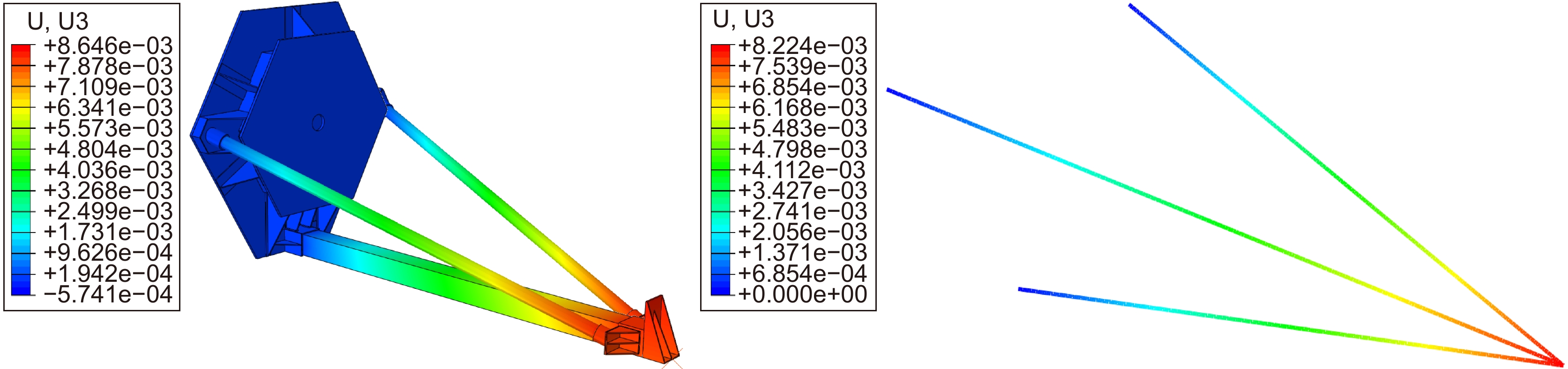
对应$ {\alpha }_ {\textit{z}} < 1\times {10}^{-8}/\; \mathrm{K} $
下载: 导出CSV
表 5 三种模型之间对比验证
Table 5. Comparison and verification among the three models
铺层序号 理论模型/$\text{ μm} $ 桁架模型/$\text{ μm} $ 实体单元模型/$\text{ μm} $ 间隔z $ 8.224 $ $8.224$ $8.646$ 偏心y $4.556$ $4.556$ $4.124$
下载: 导出CSV
表 6 重力卸载变形分析
Table 6. Gravity unloading deformation analysis
重力卸载方向 设计要求 分析结果 沿Z方向卸载 $ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x} < 30\text{ μrad}$$ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2}=0.38\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2}=-2.66\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x}=-0.16\text{ μrad}$沿Y方向卸载 $ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x} < 30\text{ μrad}$$ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2}=-2.57\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2}=-5.47\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x}=-2.31\text{ μrad}$沿X方向卸载 $ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{x}_{M1-M2} < 10\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x} < 30\text{ μrad}$$ \mathrm{\Delta }{ {\textit{z}} }_{M1-M2}=0.02\text{ μm} $
$ \mathrm{\Delta }{y}_{M1-M2}=-0.04\text{ μm} $
$ \mathrm{\Delta }{x}_{M1-M2}=5.91\text{ μm} $
$ \mathrm{\Delta }{T}_{M1-M2}^{x}=0.03\text{ μrad}$
下载: 导出CSV
表 7 不同选材之间结构热变形对比结果
Table 7. Comparison results of structural thermal deformation between different materials
主支撑结构选材 稳定性结果@$\text{10} \; {\rm{m}}{{\rm{Hz}} \sim 0.1 \; {\rm{Hz}}}$/$(\rm{ pm}/\sqrt{ {\rm{Hz} } })$ 对应结构热膨胀系数${\alpha }_{ {\textit{z}} }$/K CFRP支杆-铺层4-优化铺层方案 $ 12.0 $ $ 3.31\times {10}^{-7} $ CFRP支杆-铺层1-各向同性铺层 $ 44.2 $ $ 12.19\times {10}^{-7} $ SiC支杆 $ 104.3 $ $ 28.77\times {10}^{-7} $ Invar-42支杆 $ 186.8 $ $ 51.52\times {10}^{-7} $ 钛合金支杆 $ 373.6 $ $ 103.05\times {10}^{-7} $
下载: 导出CSV
-
参考文献
[1] 罗俊, 艾凌皓, 艾艳丽, 等. 天琴计划简介[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
Luo J, Ai L H, Ai Y L, et al. A brief introduction to the TianQin project[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
[2] 范纹彤, 赵宏超, 范磊, 等. 空间引力波探测望远镜系统技术初步分析[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020b111
Fan W T, Zhao H C, Fan L, et al. Preliminary analysis of space gravitational wave detection telescope system technology[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020b111
[3] Livas J C, Arsenovic P, Crow J A, et al. Telescopes for space-based gravitational wave missions[J]. Opt Eng, 2013, 52(9): 091811. doi: 10.1117/1.OE.52.9.091811
[4] Escudero Sanz I, Heske A, Livas J C. A telescope for LISA–the laser interferometer space antenna[J]. Adv Opt Technol, 2018, 7(6): 395−400. doi: 10.1515/aot-2018-0044
[5] 李文雄, 申军立, 吴清文, 等. 空间红外望远镜无热化支撑结构形式综述[J]. 红外, 2022, 43(6): 1−11. doi: 10.3969/j.issn.1672-8785.2022.06.001
Li W X, Shen J L, Wu Q W, et al. Overview of athermalized supporting structures for space infrared telescopes[J]. Infrared, 2022, 43(6): 1−11. doi: 10.3969/j.issn.1672-8785.2022.06.001
[6] 申碧云, 高明. 红外光学系统被动式无热化设计方法[J]. 电光与控制, 2012, 19(6): 70−73,78. doi: 10.3969/j.issn.1671-637X.2012.06.017
Shen B Y, Gao M. Passive optical athermalization design for infrared optical system[J]. Electron Opt Control, 2012, 19(6): 70−73,78. doi: 10.3969/j.issn.1671-637X.2012.06.017
[7] Verlaan A L, Hogenhuis H, Pijnenburg J, et al. LISA telescope assembly optical stability characterization for ESA[J]. Proc SPIE, 2017, 10564: 105640K. doi: 10.1117/12.2309058
[8] 张丽敏, 王富国, 安其昌, 等. Bipod柔性结构在小型反射镜支撑中的应用[J]. 光学 精密工程, 2015, 23(2): 438−443. doi: 10.3788/OPE.20152302.0438
Zhang L M, Wang F G, An Q C, et al. Application of Bipod to supporting structure of minitype reflector[J]. Opit Precis Eng, 2015, 23(2): 438−443. doi: 10.3788/OPE.20152302.0438
[9] 王永, 姚太克, 周烽, 等. 望远镜副镜的三自由度并联支撑构型研究与运动分析[J]. 光学 精密工程, 2013, 21(11): 2860−2869. doi: 10.3788/OPE.20132111.2860
Wang Y, Yao T K, Zhou F, et al. Type synthesis of 3-DOF parallel support system for telescope secondary mirror[J]. Opit Precis Eng, 2013, 21(11): 2860−2869. doi: 10.3788/OPE.20132111.2860
[10] Umińska A A, Kulkarni S, Sanjuan J, et al. Ground testing of the LISA telescope[J]. Proc SPIE, 2021, 11820: 118200I. doi: 10.1117/12.2594605
[11] Kulkarni S, Umińska A, Gleason J, et al. Ultrastable optical components using adjustable commercial mirror mounts anchored in a ULE spacer[J]. Appl Opt, 2020, 59(23): 6999−7003. doi: 10.1364/AO.395831
[12] Yang L, Wei L, Zhang L. Thermal compensation design of truss structure for large-scale off-axis three-mirror space telescope[J]. Opt Eng, 2019, 58(2): 023109. doi: 10.1117/1.OE.58.2.023109
[13] Schuldt T, Gohlke M, Spannagel R, et al. Sub-nanometer heterodyne interferometry and its application in dilatometry and industrial metrology[J]. Int J Optomechatroni, 2009, 3(3): 187−200. doi: 10.1080/15599610903144153
[14] Cordero J, Heinrich T, Schuldt T, et al. Interferometry based high-precision dilatometry for dimensional characterization of highly stable materials[J]. Meas Sci Technol, 2009, 20(9): 095301. doi: 10.1088/0957-0233/20/9/095301
[15] Koyanagi J, Arao Y, Utsunomiya S, et al. High accurate space telescope mirror made by light and thermally stable CFRP[J]. J Solid Mech Mater Eng, 2010, 4(11): 1540−1549. doi: 10.1299/jmmp.4.1540
[16] Sanjuán J, Preston A, Korytov D, et al. Carbon fiber reinforced polymer dimensional stability investigations for use on the laser interferometer space antenna mission telescope[J]. Rev Sci Instrum, 2011, 82(12): 124501. doi: 10.1063/1.3662470
[17] 胡守伟, 张勇, 王跃飞, 等. 三十米中国未来巨型望远镜主桁架结构的概念设计[J]. 光电工程, 2022, 49(6): 210402. doi: 10.12086/oee.2022.210402
Hu S W, Zhang Y, Wang Y F, et al. Concept design for the main structure of 30 m Chinese future giant telescope[J]. Opto-Electron Eng, 2022, 49(6): 210402. doi: 10.12086/oee.2022.210402
[18] Spannagel R, Hamann I, Sanjuan J, et al. Dilatometer setup for low coefficient of thermal expansion materials measurements in the 140 K-250 K temperature range[J]. Rev Sci Instrum, 2016, 87(10): 103112. doi: 10.1063/1.4965813
[19] Zhengchun D, Mengrui Z, Zhiguo W, et al. Design and application of composite platform with extreme low thermal deformation for satellite[J]. Compos Struct, 2016, 152: 693−703. doi: 10.1016/j.compstruct.2016.05.073
[20] Zhu X L, He R J, Lu X F, et al. A optimization technique for the composite strut using genetic algorithms[J]. Mater Des (1980–2015), 2015, 65: 482−488. doi: 10.1016/j.matdes.2014.09.039
[21] 张辰, 韦娟芳, 马小飞, 等. 空间超高频遥感反射器热变形优化及零膨胀材料的制备[J]. 复合材料学报, 2019, 36(4): 795−800. doi: 10.13801/j.cnki.fhclxb.20180529.001
Zhang C, Wei J F, Ma X F, et al. Optimization of thermal deformation of ultrahigh frequency remote sensing reflector and manufacture of a zero-expansion composite[J]. Acta Mater Compos Sin, 2019, 36(4): 795−800. doi: 10.13801/j.cnki.fhclxb.20180529.001
[22] Marín L, Trias D, Badalló P, et al. Optimization of composite stiffened panels under mechanical and hygrothermal loads using neural networks and genetic algorithms[J]. Compos Struct, 2012, 94(11): 3321−3326. doi: 10.1016/j.compstruct.2012.04.024
-
访问统计
点击扫一扫
图(16)
表(7)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
