An optimized high-performance technique for adaptive optics static aberration correction
-
摘要
非共光路误差是限制自适应光学系统(adaptive optics, AO)的成像性能达到衍射极限的关键因素,同时AO系统共光路部分也会不可避免地引入静态像差,尤其是在自适应光学系统与望远镜配合使用进行科学观测时。因此,本文提出了一种基于焦面优化的改进型AO系统静态像差校正技术。该方法通过迭代优化算法将单模光纤生成的完美点扩散函数复制到自适应光学系统中来校正系统中的静态像差。相比于我们之前提出的焦面校正法,本文提出的改进型焦面优化技术获得全局优化结果的速度更快,并且在系统初始静态误差极大的情况下,拥有更好的校正性能。当部署于天文或其他需要高质量成像的自适应光学系统中时,该改进型焦面优化技术相较于传统校正法也更加便捷。
Abstract
For adaptive optics (AO) systems, Non-Common Path Aberration (NCPA) is considered as a critical issue to limit its diffraction-limited imaging performance and the static aberration will inevitably be introduced in the common path of the AO system inevitably at the same time, especially when it is coupled to telescopes intended for scientific observation. This paper presents an optimized focal-plane-based static aberration correction technique, which can copy a perfect point-spread function (PSF) generated by a single-mode fiber to the AO system via iteration optimization algorithm and static aberration in the AO system can be rapidly corrected. Compared with the focal-plane approach we proposed before, this optimized approach can achieve a global optimization result rapidly and deliver better performance when the AO system has a large initial static wavefront error. This technique can be implemented more conveniently in the AO system than other traditional correction methods for achieving an extremely high imaging performance in astronomy or other fields.
-
Key words:
- adaptive optics /
- aberration correction /
- high angular resolution
-
Overview
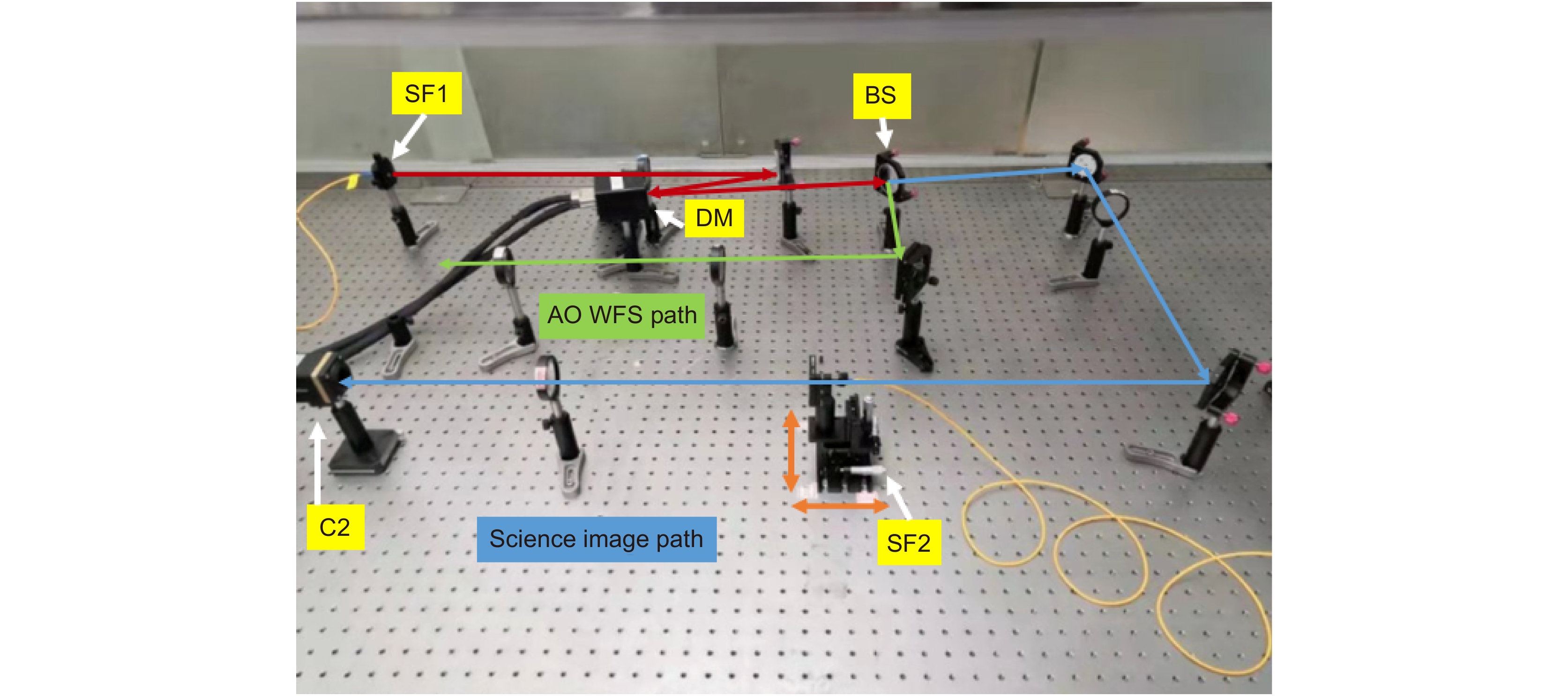
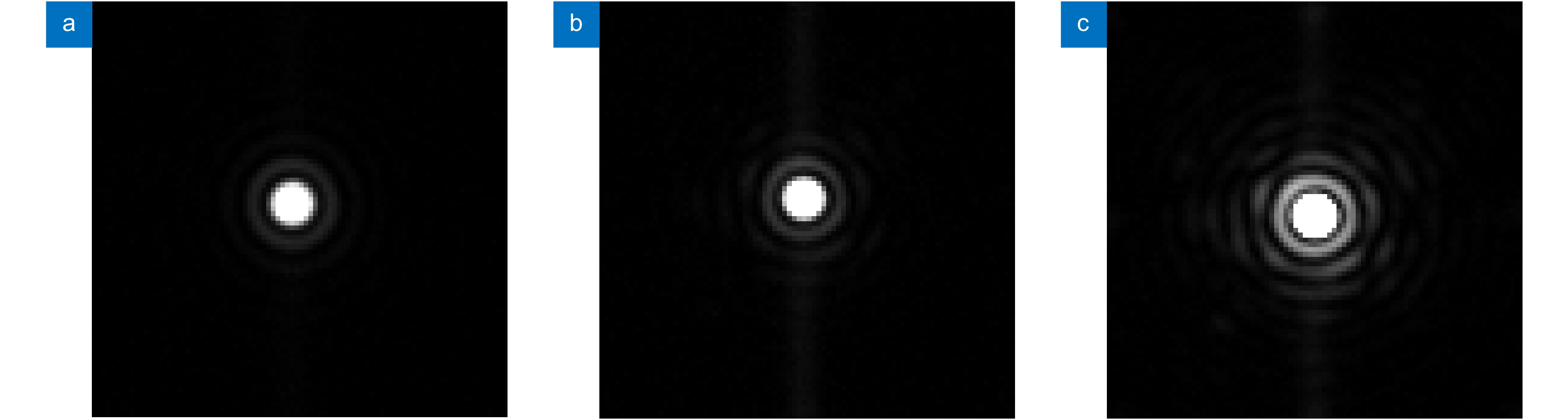
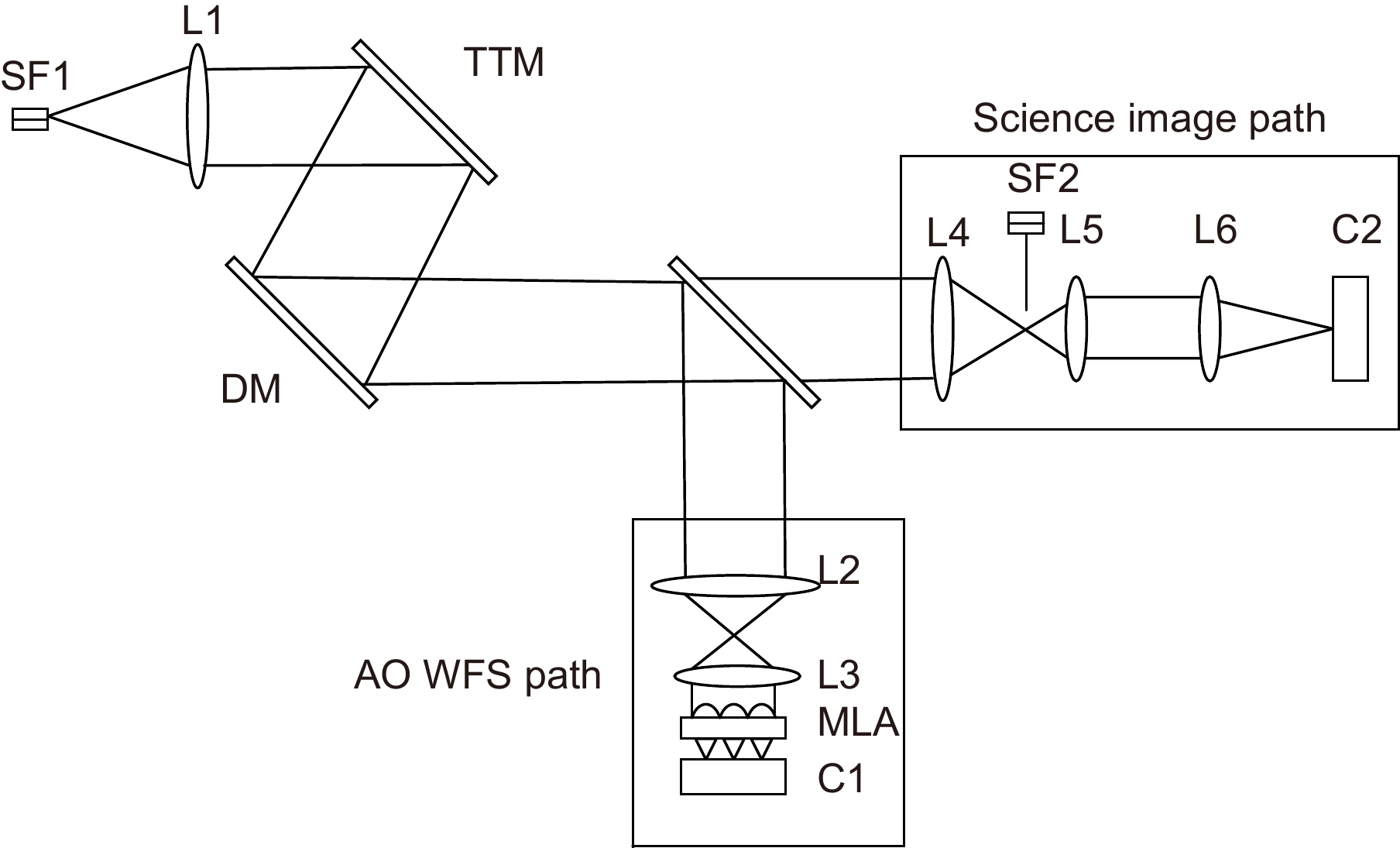
Overview: Non-Common Path Aberration (NCPA) is introduced by the physical separation between the science camera path and the wavefront sensor path. At the same time, the static aberration will also be introduced in common path of the AO system. They must be effectively corrected, especially when the AO system is implemented in astronomy or other fields for achieving high-performance imaging. Therefore, we proposed a sample but effective optimized focal-plane-based static aberration correction technique. The correction system is similar to the conventional AO system, except that only one lens and a single-mode fiber are temporarily added in the science image path for generating perfect reference point speared function (PSF). Since the existence of static aberration, any difference between the AO PSF and reference perfect PSF will be an indication of associated aberrations that need to be corrected. If the PSF of the AO system can be optimized to be the same as reference perfect PSF, aberration will be effectively corrected. For achieving this optimization result, the reference perfect PSF will be recorded in advance, and then iteration optimization algorithm will optimize the AO system’s PSF by directly controlling the deformable mirror (DM) with the model of reference PSF, which means copy the reference PSF to the AO system. In addition, we also designed new metrics functions for getting global optimization result rapidly and steadily. The laboratory experiments indicates that this proposed technique can successfully reduce the AO system’s root means square (RMS) from initial value of 109nm to final value of 7 nm and the Strehl Ratio (SR) can be raised from 0.305 to 0.995 accordingly. In conclusion, thte proposed optimized correction technique has the following advantages: 1) Correction system is easy to be deployed and can be flexibly implemented to different types of the AO systems that need extremely high-performance imaging in astronomy or other fields such as biology and medicine. 2) The hardware requirements of correction system are small, which means a low cost. Compared with the conventional AO system, only one more lens is needed temporarily in science image path and it will be removed after finishing correction. 3) The final correction performance is much better than traditional NCPA methods and the method we proposed in 2012, especially when the AO system has a large initial static wavefront error. 4) With the guidance of reference perfect PSF, the whole optimization speed is rapid and the global optimization will be achieved steadily, instead of trapping in local optimization result. This work is demonstrated to be a promising technique, it will be integrated into our coronagraph system for high-contrast imaging of exoplanets in our next study.
-

-
Table 1. Experiment results of different metric functions
Metric function RMS/nm SR Time/min Jo 55 0.739 140 Jlg 28 0.924 60 J 7 0.995 40 -
参考文献
[1] Baudoz P, Mas M, Galicher R, et al. Focal plane wavefront sensor sensitivity for ELT planet finder[J]. Proc SPIE, 2010, 7736: 77365S. doi: 10.1117/12.858272
[2] Wallace J K, Rao S, Jensen-Clem R M, et al. Phase-shifting Zernike interferometer wavefront sensor[J]. Proc SPIE, 2011, 8126: 81260F. doi: 10.1117/12.892843
[3] Campbell E W, Bauman B J, Sweider D R, et al. High-accuracy calibration of an adaptive optics system using a phase-shifting diffraction interferometer[J]. Proc SPIE, 1999, 3762: 237−244. doi: 10.1117/12.363579
[4] Gonsalves R A. Phase retrieval and diversity in adaptive optics[J]. Opt Eng, 1982, 21(5): 215829.
[5] Lamb M, Correia C, Sauvage J F, et al. Exploring the operational effects of phase diversity for the calibration of non-common path errors on NFIRAOS[J]. Proc SPIE, 2016, 9909: 99096E.
[6] Wallace J K, Burruss R S, Bartos R D, et al. The Gemini Planet Imager calibration wavefront sensor instrument[J]. Proc SPIE, 2010, 7736: 77365D.
[7] Hinkley S, Oppenheimer B R, Zimmerman N, et al. A new high contrast imaging program at Palomar observatory[J]. Publ Astron Soc Pac, 2011, 123(899): 74−86. doi: 10.1086/658163
[8] Ren D Q, Penn M, Wang H M, et al. A portable solar adaptive optics system[J]. Proc SPIE, 2009, 7438: 74380P. doi: 10.1117/12.824457
[9] Ren D Q, Dong B. Demonstration of portable solar adaptive optics system[J]. Opt Eng, 2012, 51(10): 101705. doi: OptEng
[10] Yamamoto S. Development of inspection robot for nuclear power plant[C]//Proceedings 1992 IEEE International Conference on Robotics and Automation, Nice, 1992, 2: 1559‒1566.
[11] Ren D Q, Dong B, Zhu Y T, et al. Correction of non–common-path error for extreme adaptive optics[J]. Publ Astron Soc Pac, 2012, 124(913): 247−253. doi: 10.1086/664947
[12] Vorontsov M A, Carhart G W, Ricklin J C. Adaptive phase-distortion correction based on parallel gradient-descent optimization[J]. Opt Lett, 1997, 22(12): 907−909. doi: 10.1364/OL.22.000907
[13] Vorontsov M A, Sivokon V P. Stochastic parallel-gradient-descent technique for high-resolution wave-front phase-distortion correction[J]. J Opt Soc Am A, 1998, 15(10): 2745−2758. doi: 10.1364/JOSAA.15.002745
[14] Vorontsov M A, Yu M. Compensation of distant phase-distorting layers. II. Extended-field-of-view adaptive receiver system[J]. J Opt Soc Am A, 2004, 21(9): 1659−1668. doi: 10.1364/JOSAA.21.001659
[15] Petit C, Sauvage J F, Costille A, et al. SAXO: the extreme adaptive optics system of SPHERE (I) system overview and global laboratory performance[J]. J Astron Telesc Instrum Syst, 2016, 2(2): 025003. doi: 10.1117/1.JATIS.2.2.025003
[16] Fusco T, Sauvage J F, Petit C, et al. Final performance and lesson-learned of SAXO, the VLT-SPHERE extreme AO: from early design to on-sky results[J]. Proc SPIE, 2014, 9148: 91481U.
[17] Liu Y, Ma J Q, He T, et al. Hybrid simulated annealing-hill climbing algorithm for fast aberration correction without wavefront sensor[J]. Opt Precis Eng, 2012, 20(2): 213−219. doi: 10.3788/OPE.20122002.0213
[18] Burke D, Patton B, Huang F, et al. Adaptive optics correction of specimen-induced aberrations in single-molecule switching microscopy[J]. Optica, 2015, 2(2): 177−185. doi: 10.1364/OPTICA.2.000177
[19] Sauvage J F, Fusco T, Rousset G, et al. Fine calibration and pre-compensation of non-common path aberrations for high performance AO system[J]. Proc SPIE, 2005, 5903: 59030B.
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: