Source optimization based on adaptive nonlinear particle swarm method in lithography
-
摘要
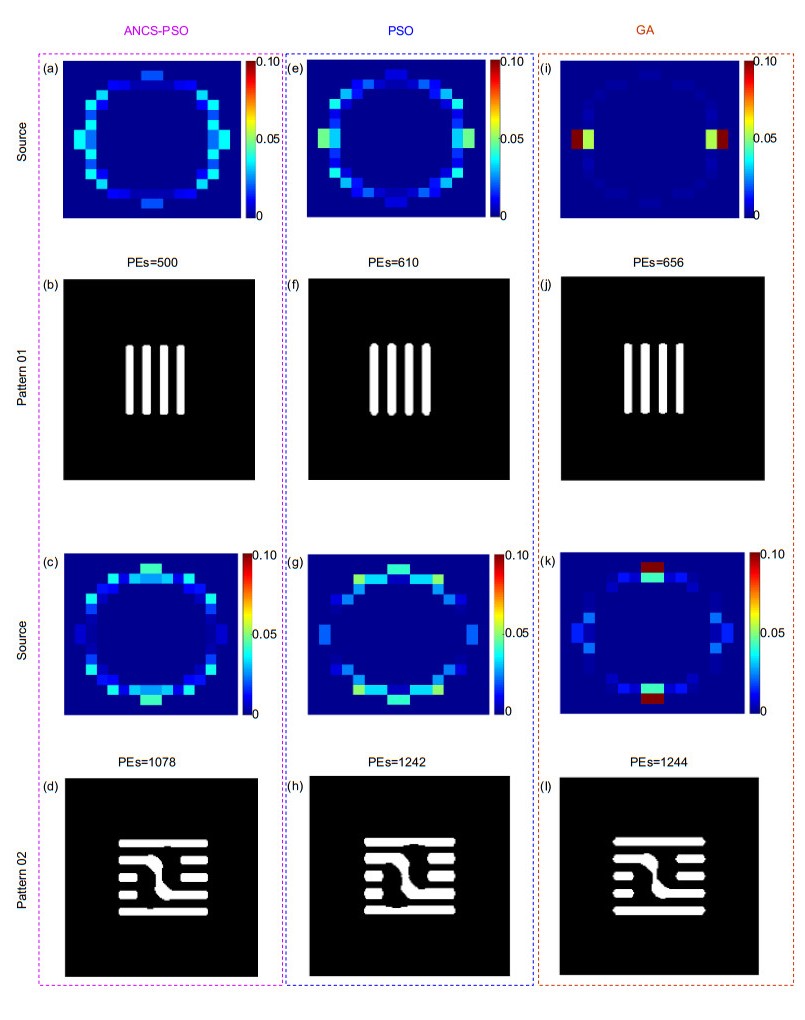
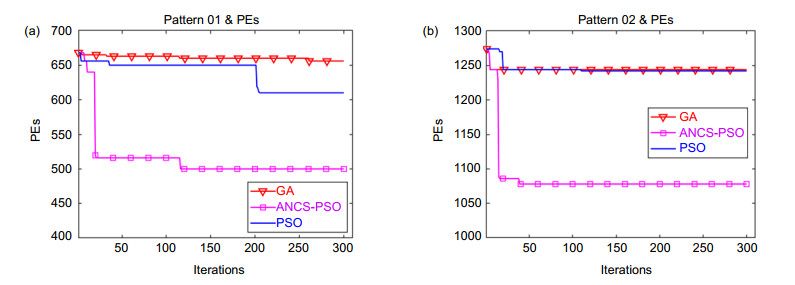
光刻光源优化作为必不可少的分辨率增强技术之一,能够提高先进光刻成像质量。在先进光刻领域,光源优化的收敛效率和优化能力是至关重要的。粒子群优化算法作为一种全局优化算法,自适应控制策略可以提高粒子的全局搜索能力,非线性控制策略可以扩大粒子搜索范围。本文提出一种基于自适应非线性控制策略的粒子群优化算法,将光刻光源优化问题转换成多变量评价函数求解。对简单周期光栅图形和不规则图形进行成像优化仿真,通过粒子群优化算法的全局迭代特性优化光源形貌。利用图形误差(PEs)作为多变量评价函数,对迭代300次的仿真结果进行评价,两种仿真图形的PEs分别降低52.2%和35%。与传统粒子群优化算法和遗传算法相比,该方法不仅能提高成像质量,而且具有更高的收敛效率。
Abstract
As an essential resolution enhancement technique, source optimization can improve the quality of advanced lithography. In the field of advanced lithography, the convergence efficiency and optimization ability of the source optimization are very important. Particle swarm optimization (PSO) is a global optimization algorithm. The adaptive control strategy can improve the global search ability of particles, and the nonlinear control strategy can expand the search range of particles. In this paper, a PSO algorithm based on adaptive nonlinear control strategy (ANCS) is proposed to solve the problem of source optimization by transforming it into a multivariable evaluation function. The image optimization simulation is carried out with a brief periodic grating image and an irregular image, and the source shape is optimized by the global iteration property of the proposed method. By using the pattern errors (PEs) as a multivariate merit function, the results of 300 iterations are evaluated, and the PEs of the two kinds of simulation patterns are reduced by 52.2% and 35%, respectively. Compared with the traditional PSO algorithm and genetic algorithm, the proposed method not only improves the imaging quality, but also has higher convergence efficiency.
-
Overview
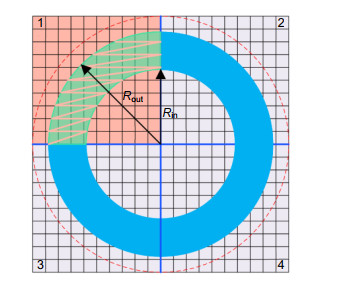
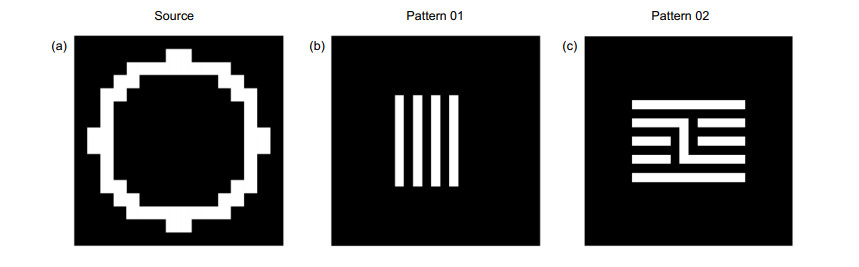
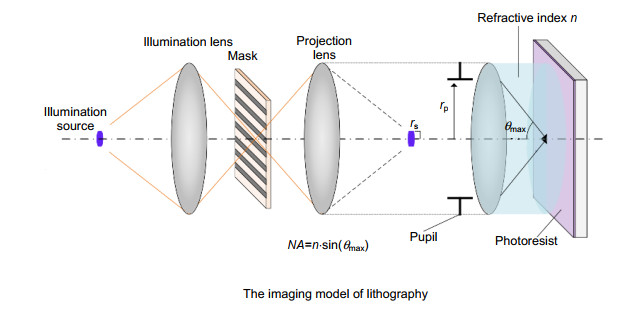
Overview: With the continuous reduction of critical dimension (CD) of semiconductors, lithography technology has gradually become a key technology in the field of integrated circuit manufacturing. Resolution enhancement technologies (RETs) is to improve the resolution of lithography by modifying the incident angle of the light source and the mask mode under the premise that the wavelength and numerical aperture (NA) remain the same. Due to the influence of experimental conditions, such as temperature, assembly tolerance, and other factors, the aberration is introduced, leading to the deformation of the aerial image. In addition, the optical proximity effect (OPE) will be introduced, if the CD of the pattern is smaller than the illumination wavelength. Therefore, it is very important to solve the above problems to improve the imaging quality and image fidelity. Recently, many researchers have proposed the optimization algorithm based on pixelated representation of illumination source for inverse lithography optimization. This method has not only achieved high modulation and flexibility, but also has great advantages in improving lithography resolution. In this paper, a particle swarm optimization algorithm (PSO) combing with adaptive nonlinear control strategy (ANCS) is proposed to optimize the shape of lithography illumination source based on pixel representation. According to the unique symmetry characteristics of the light source, the light source is characterized by equal separation and dispersion, which can reduce the optimization complexity and improve the iteration efficiency. A simple grating array pattern and a complex and irregular grating array pattern are selected to verify the simulation results, and the pattern errors (PEs) between the photoresist pattern and the ideal pattern are used as the cost function to evaluate the simulation results. The effectiveness of the improved algorithm is verified by simulation of the two grating structures. In order to verify the superiority of ANCS-PSO, it is compared with the traditional particle swarm optimization algorithm and genetic algorithm. The simulation results show that the errors of the two kinds of simulation patterns are reduced by Pattern 01: 52.2%, 41.7%, 37.4%, and Pattern 02: 35 %, 25.3%, 25.3%, respectively, which effectively improves the photoresist image assurance. The comparison of the simulation results of the three algorithms shows that the proposed method not only has higher iteration efficiency, but also has more advantages in improving the quality of lithographic imaging and image fidelity.
-

-
-
参考文献
[1] Wong A K K. Resolution Enhancement Techniques in Optical Lithography[M]. Bellingham, Washington: SPIE Press, 2001.
[2] Melville D, Rosenbluth A E, Waechter A, et al. Computational lithography. 2011.
[3] Liebmann L W. Resolution enhancement techniques in optical lithography: It's not just a mask problem[J]. Proc SPIE, 2001, 4409: 23-32. doi: 10.1117/12.438332
[4] Mack C. Fundamental Principles of Optical Lithography[M]. Chichester, West Sussex: Wiley, 2007.
[5] Peng Y, Zhang J Y, Wang Y, et al. High performance source optimization using a gradient-based method in optical lithography[C]//2010 11th International Symposium on Quality Electronic Design, San Jose, CA, USA, 2010: 108-113.
[6] Rosenbluth A E, Seong N. Global optimization of the illumination distribution to maximize integrated process window[J]. Proc SPIE, 2006, 6154: 61540H.
[7] Ma X, Arce G R. Pixel-based simultaneous source and mask optimization for resolution enhancement in optical lithography[J]. Opt Express, 2009, 17(7): 5783-5793. doi: 10.1364/OE.17.005783
[8] Peng Y, Zhang J Y, Wang Y, et al. Gradient-based source and mask optimization in optical lithography[J]. IEEE Trans Image Process, 2011, 20(10): 2856-2864. doi: 10.1109/TIP.2011.2131668
[9] Jia N N, Lam E Y. Pixelated source mask optimization for process robustness in optical lithography[J]. Opt Express, 2011, 19(20): 19384-19398. doi: 10.1364/OE.19.019384
[10] Li J, Lam E Y. Robust source and mask optimization compensating for mask topography effects in computational lithography[J]. Opt Express, 2014, 22(8): 9471-9485. doi: 10.1364/OE.22.009471
[11] Shen Y J, Peng F, Zhang Z R. Semi-implicit level set formulation for lithographic source and mask optimization[J]. Opt Express, 2019, 27(21): 29659-29668. doi: 10.1364/OE.27.029659
[12] Ma X, Zheng X Q, Arce G R. Fast inverse lithography based on dual-channel model-driven deep learning[J]. Opt Express, 2020, 28(14): 20404-2042. doi: 10.1364/OE.396661
[13] Ma X, Wang Z Q, Lin H J, et al. Optimization of lithography source illumination arrays using diffraction subspaces[J]. Opt Express, 2018, 26(4): 3738-3755. doi: 10.1364/OE.26.003738
[14] Fühner T, Erdmann A, Farkas R, et al. Genetic algorithms to improve mask and illumination geometries in lithographic imaging systems[C]//Applications of Evolutionary Computing, Coimbra, Portugal, 2004: 208-218.
[15] Born M, Wolf E. Principles of Optics[M]. Cambridge: Cambridge University Press, 2001.
[16] Saleh B E A, Rabbani M. Simulation of partially coherent imagery in the space and frequency domains and by modal expansion[J]. Appl Opt, 1982, 21(15): 2770-2777. doi: 10.1364/AO.21.002770
[17] Zhang Z N, Li S K, Wang X Z, et al. Source mask optimization for extreme-ultraviolet lithography based on thick mask model and social learning particle swarm optimization algorithm[J]. Opt Express, 2021, 29(4): 5448-5465. doi: 10.1364/OE.418242
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: