E-mail Alert
RSS
Co-simulation of optical chaotic secure communication systems in MATLAB and OptiSystem
-
摘要:
基于两个具有平行结构的电光时延反馈环，本文设计了一种电光强度混沌通信系统。通过混沌注入混沌的方式来产生更加复杂的混沌波形，增强混沌复杂程度以及通信系统的保密性。在本次设计中，采用MATLAB与OptiSystem协同的方式来对该系统进行仿真，解决了OptiSystem不能模拟光学反馈环路的问题。由OptiSystem中成熟的激光器和二进制序列生成模块为系统提供能量与输入信号，由MATLAB程序实现电光时延反馈环，并在OptiSystem中完成信号在光纤链路中的传输。文章介绍了如何利用MATLAB与OptiSystem实现混沌系统的协同仿真，并通过数值模拟表明，提出的用于模拟光学反馈环路的方法具有可行性，设计的混沌系统的性能与理论值吻合，证明了该混沌生成方式的可行性。
-
关键词:
- 混沌 /
- 混沌加密 /
- 电光时延 /
- MATLAB /
- OptiSystem
Abstract:An electro-optic intensity chaotic communication system is designed by combining two electro-optic delay feedback loops with parallel structures. By injecting chaos into chaos, a more complex chaotic waveform is generated to enhance the chaotic complexity and the communication system confidentiality. In this design, MATLAB and OptiSystem software are used to simulate the system, which solves the problem that OptiSystem software can't simulate the optical feedback loop. The mature laser and binary sequence generation modules in OptiSystem software provide energy and input signals for the system. The electro-optic delay feedback loops are realized by the MATLAB program, and the signal transmission in optical fibers is completed in the OptiSystem software. The article introduces how to use MATLAB and OptiSystem software to realize the co-simulation of chaotic systems. Numerical simulations show that the proposed method is feasible to simulate the optical feedback loop, and the simulation results are in good agreement with the theoretical values, which prove that the chaotic signal is generated.
-
Key words:
- chaos /
- chaotic encryption /
- electro-optic delay /
- MATLAB /
- OptiSystem
-
Overview: With the increase in demand for communication capacity, speed, and confidentiality, optical fiber communication has become an important way of information transmission. However, during the transmission process, there is a risk of being eavesdropped on by illegal receivers. Therefore, it is very necessary to encrypt the signal transmitted in optical fibers. Chaotic secure communication is the physical hardware encryption based on chaotic signals. With the chaotic signal has the advantages of aperiodic, continuous broadband spectrum, noise-like, and unpredictable long-term, information is hidden in chaotic signals for transmission, and the transmitted information is demodulated by the chaotic waveform synchronized with the transmitter at the receiver. Chaotic secure communication has a great application prospect in the secure communication field and has attracted extensive attention from researchers at home and abroad.
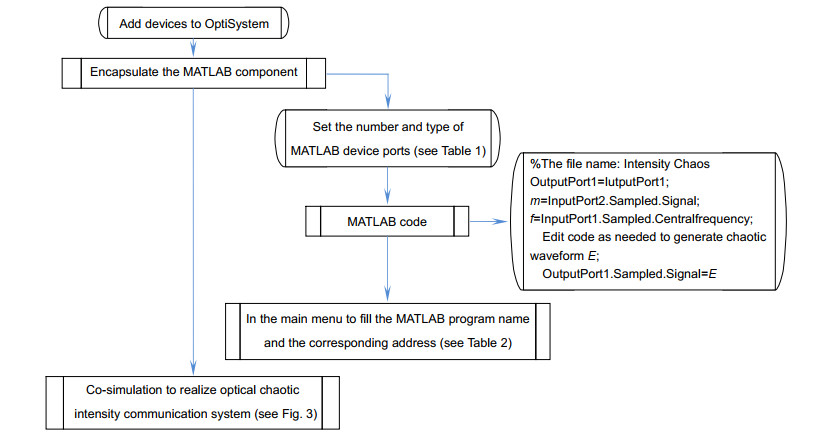
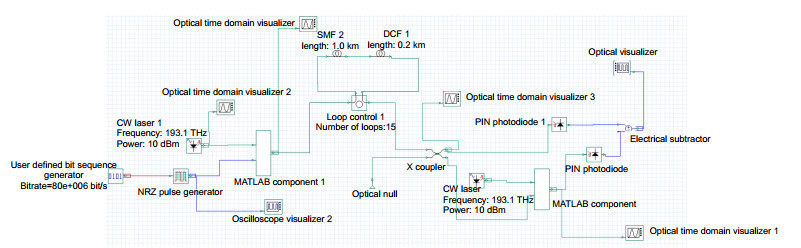
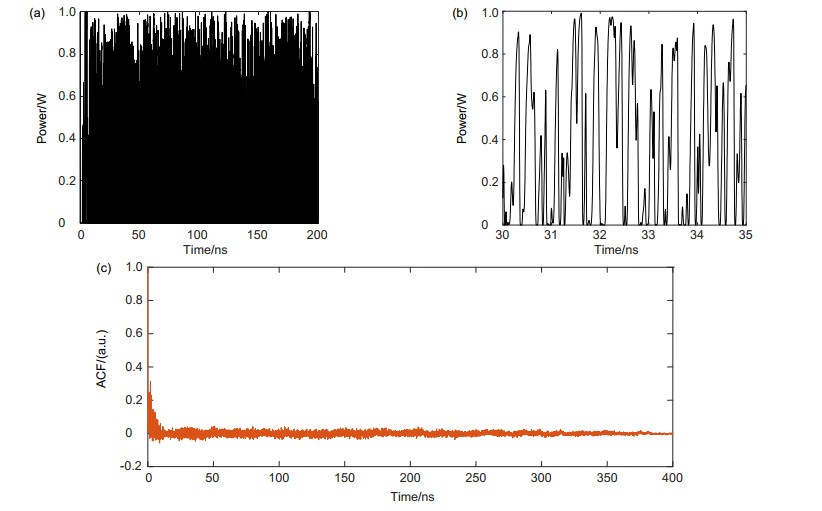
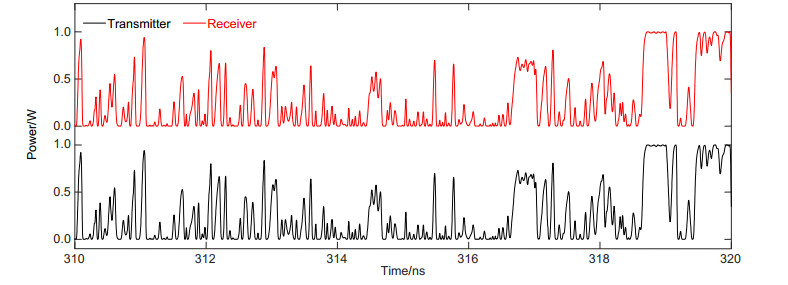
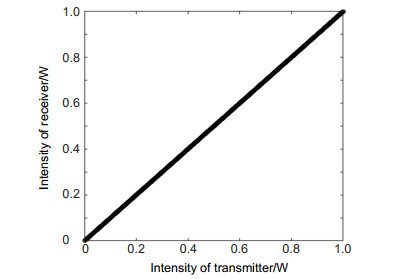
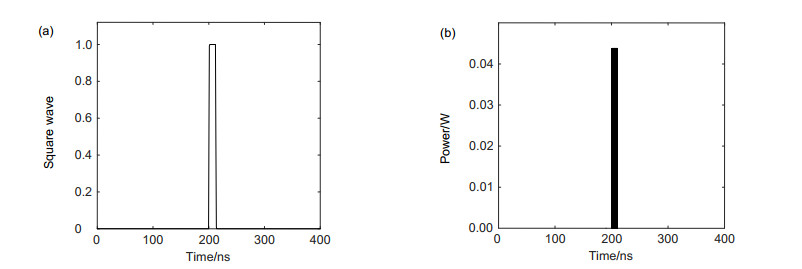
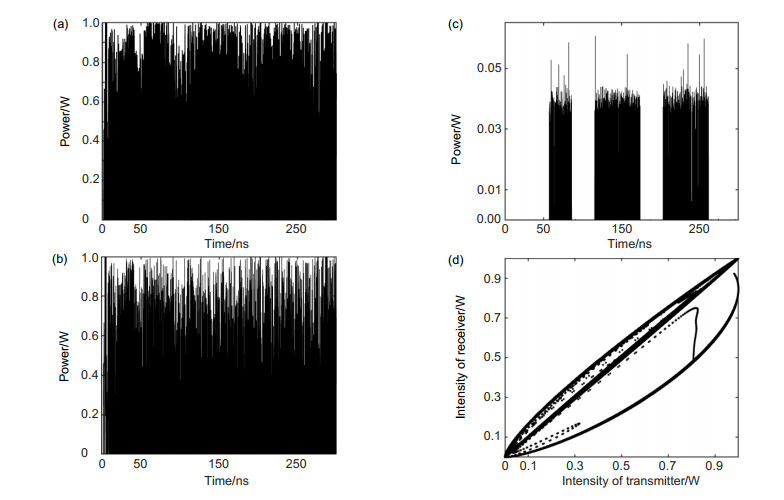
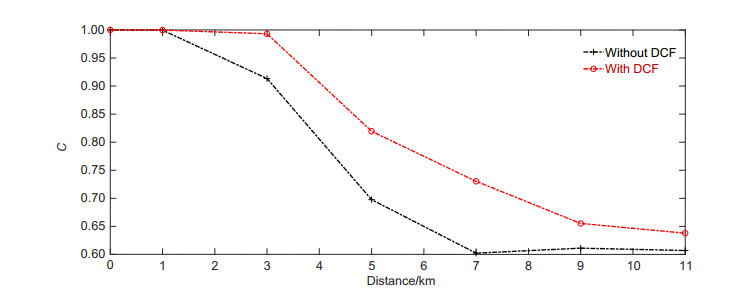
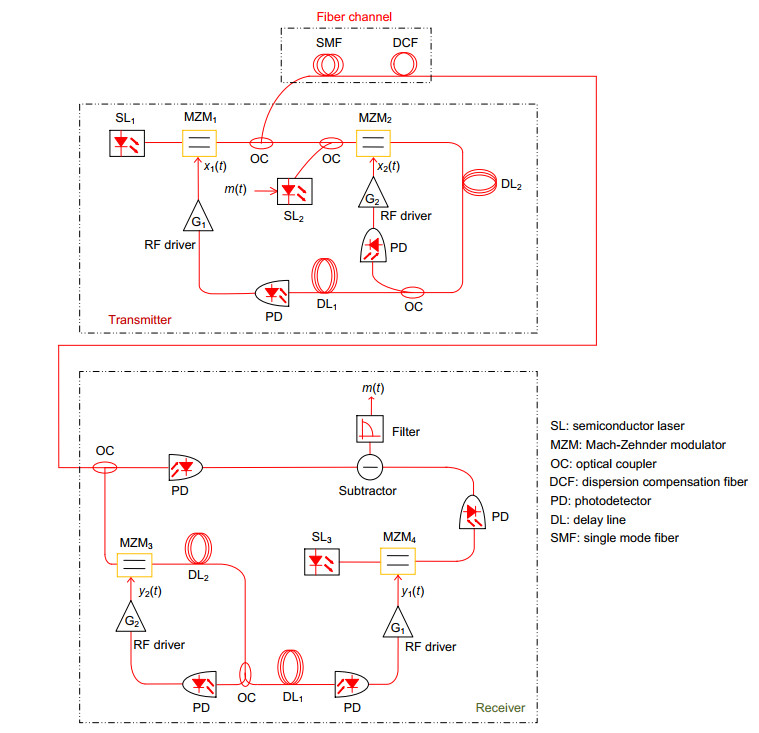
Based on two parallel electro-optic delay feedback loops, an electro-optic intensity chaotic system is designed in this paper. By injecting chaos into chaos, more complex chaotic waveforms can be generated to enhance the chaotic complexity and the communication system confidentiality. In this design, MATLAB and OptiSystem are used to simulate the system, which solves the difficulty that OptiSystem could not simulate the optical feedback loop. Combining MATLAB's numerical calculation capabilities with OptiSystem's simulation capabilities, an intensity chaotic device with two electro-optic delay feedback loops has been successfully constructed. The mature laser and binary sequence generation modules in OptiSystem provide energy and input signals to the system. The electro-optic delay feedback loop is realized by the MATLAB program, and the signal transmission in the optical fiber link is completed in OptiSystem. The simulation results show that the generated chaotic sequence has amplitude randomness, and the high and low pulse amplitudes follow each other, which can effectively conceal information. The chaotic sequence at the transmitter and receiver has synchronization and robustness. In the case of no information loading, the chaotic sequence intensity at both ends completely fits y=x. When an external disturbance is introduced, the synchronization solution of the delayed chaotic dynamics at both ends can still be maintained well and it has a certain anti-interference ability. These properties ensure that the system could be used for information encryption operation effectively, and the relationships between the transmission distance and the chaos synchronization at both ends under different compensation situations have been studied. The simulation results are in good agreement with the theoretical values, which proves the feasibility of the chaotic generation method and provides ideas for the subsequent research and simulation on chaotic generation schemes.
-
-
图 1 具有两个电光时延反馈环的强度混沌装置图
Figure 1. Intensity chaos device with two electro-optic time delay feedback loops
图 3 MATLAB与OptiSystem协同仿真具有两个电光时延反馈环的强度混沌装置图
Figure 3. MATLAB and OptiSystem co-simulation of an intensity chaos device with two electro-optic time delay feedback loops
图 4 MATLAB与OptiSystem协同仿真产生的混沌波形。
Figure 4. Chaos waveform generated by MATLAB and OptiSystem co-simulation. (a) Chaotic waveform; (b) Zoomed figure of the chaotic waveform; (c) Autocorrelation of the chaotic waveform
图 5 某段时间内，发射端与接收端的波形功率对比图
Figure 5. Power comparison chart of the waveform at the transmitter and receiver in a certain period of time
图 6 发射端与接收端的混沌强度拟合图
Figure 6. Chaotic intensity fitting diagram of the transmitter and receiver
图 7 系统鲁棒性研究。(a) 发射端引入的扰动；(b) 接收端的同步误差
Figure 7. System robustness research. (a) Disturbance introduced by the transmitter; (b) Synchronization error at the receiver
图 8 (a) 发射端混沌波形；(b) 接收端混沌波形；(c) 恢复出的信息；(d) 发射端与接收端混沌强度散点图
Figure 8. (a) Chaotic waveform of the transmitter; (b) Chaotic waveform of the receiver; (c) Recovered information; (d) Scatter plot of chaotic intensity of the transmitter and receiver
图 9 不同补偿情况下，传输距离与互相关函数之间的关系
Figure 9. The relationship between transmission distance and cross-correlation function under different compensation conditions
表 1 发射端MATLAB元件端口参数
Table 1. MATLAB component port parameters of the transmitter
Ports Parameters Inputs Number of input ports 2 Signal type (input 1) Optical Signal type (input 2) Electrical Outputs Number of output ports 1 Signal type (output 1) Optical 
下载: 导出CSV
表 2 MATLAB元件Main菜单设置
Table 2. Main menu settings of MATLAB components
Menu Setting Load MATLAB √ Run command Intensity Chaos MATLAB search path Path corresponding to Intensity Chaos
下载: 导出CSV
-
[1] 颜森林. 激光混沌并行串联同步及其在中继器保密通信系统中的应用[J]. 物理学报, 2019, 68(17): 170502. doi: 10.7498/aps.68.20190212
Yan S L. Chaotic laser parallel series synchronization and its repeater applications in secure communication[J]. Acta Phys Sin, 2019, 68(17): 170502. doi: 10.7498/aps.68.20190212
[2] 吴琼琼, 马子洋, 李启华, 等. 高速混沌光通信研究进展[J]. 光通信技术, 2021, 45(1): 22-27.
Wu Q Q, Ma Z Y, Li Q H, et al. Research progress of high speed chaotic optical communication[J]. Opt Commun Technol, 2021, 45(1): 22-27.
[3] Argyris A, Syvridis D, Larger L, et al. Chaos-based communications at high bit rates using commercial fibre-optic links[J]. Nature, 2005, 438(7066): 343-346. doi: 10.1038/nature04275
[4] Jacquot M, Lavrov R, Larger L. Nonlinear delayed differential optical phase feedback for high performance chaos communications[C]//Conference on Lasers and Electro-Optics 2010. San Jose, USA, 2010. doi: 10.1364/CLEO.2010.CFC6.
[5] 义理林, 柯俊翔. 混沌保密光通信研究进展[J]. 通信学报, 2020, 41(3): 168-181.
Yi L L, Ke J X. Research progress of chaotic secure optical communication[J]. J Commun, 2020, 41(3): 168-181.
[6] Yang Z, Yi L L, Ke J X, et al. Chaotic optical communication over 1000 km transmission by coherent detection[J]. J Lightwave Technol, 2020, 38(17): 4648-4655. doi: 10.1109/JLT.2020.2994155
[7] 刘小磊, 熊雪娟. 基于Optisystem的光电色散补偿技术的性能分析[J]. 电子测量技术, 2017, 40(11): 114-119.
Liu X L, Xiong X J. Performance analysis of photoelectric dispersion compensation technology based on Optisystem[J]. Electr Measur Technol, 2017, 40(11): 114-119.
[8] Ikeda K. Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system[J]. Opt Commun, 1979, 30(2): 257-261. doi: 10.1016/0030-4018(79)90090-7
[9] Kouomou Y C, Colet P, Larger L, et al. Mismatch-induced bit error rate in optical chaos communications using semiconductor lasers with electrooptical feedback[J]. IEEE J Quantum Electron, 2005, 41(2): 156-163. doi: 10.1109/JQE.2004.839686
[10] Nguimdo R M, Colet P, Larger L, et al. Digital key for chaos communication performing time delay concealment[J]. Phys Rev Lett, 2011, 107(3): 034103. doi: 10.1103/PhysRevLett.107.034103
[11] Hizanidis J, Deligiannidis S, Bogris A, et al. Enhancement of chaos encryption potential by combining all-optical and electrooptical chaos generators[J]. IEEE J Quantum Electron, 2010, 46(11): 1642-1649. doi: 10.1109/JQE.2010.2055837
[12] Nguimdo R M, Colet P, Mirasso C. Electro-optic delay devices with double feedback[J]. IEEE J Quantum Electron, 2010, 46(10): 1436-1443. doi: 10.1109/JQE.2010.2050055
[13] Shahzadi R, Anwar S M, Qamar F, et al. Secure EEG signal transmission for remote health monitoring using optical chaos[J]. IEEE Access, 2019, 7: 57769-57778. doi: 10.1109/ACCESS.2019.2912548
[14] Li Q L, Chen D W, Bao Q, et al. Numerical investigations of synchronization and communication based on an electro-optic phase chaos system with concealment of time delay[J]. Appl Opt, 2019, 58(7): 1715-1722. doi: 10.1364/AO.58.001715
[15] Wang L S, Mao X X, Wang A B, et al. Scheme of coherent optical chaos communication[J]. Opt Lett, 2020, 45(17): 4762-4765. doi: 10.1364/OL.390846
[16] Nguimdo R M, Colet P. Electro-optic phase chaos systems with an internal variable and a digital key[J]. Opt Express, 2012, 20(23): 25333-25344. doi: 10.1364/OE.20.025333
[17] Lavrov R, Jacquot M, Larger L. Nonlocal nonlinear electro-optic phase dynamics demonstrating 10 Gb/s chaos communications[J]. IEEE J Quantum Electron, 2010, 46(10): 1430-1435. doi: 10.1109/JQE.2010.2049987
-
点击扫一扫
图(9)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
