E-mail Alert
RSS
-
摘要
图像盲复原旨在无参考的情况下准确估计模糊核并恢复潜在的清晰图像。现有研究成果表明，利用全变分模型对高阶图像梯度先验约束进行描述可以有效抑制复原图像中产生的阶梯效应。本文在实验观察和研究的基础上，提出了采用稀疏先验约束模型对盲复原过程进行正则化的方法，以获得更佳的图像复原效果。该方法利用图像高阶梯度的稀疏性，通过与低阶梯度相结合来构造混合梯度正则项。同时，在正则项中引入基于图像熵的自适应因子，来调节迭代优化过程中两类梯度先验的比例，以此获得更好的收敛性。仿真与实验证明，与现有图像盲复原先进方法相比，本文方法具有更优越的图像复原性能。
Abstract
Blind image restoration aims to accurately estimate the blur kernel and the wanted clear image with no-reference. Existing researches show that the use of the Total Variation to model the high-order image gradient prior constraints can effectively suppress the blocking artifact generated in the restored image. On the basis of experimental observation and research, this paper proposes to use the sparse prior constraint model to regularize the blind restoration process to obtain a better image restoration performance. Our method makes use of the sparsity of the high-order gradient of the image and combines it with the low-order gradient to construct the mixed gradient regularization term. At the same time, an adaptive factor based on image entropy is introduced to adjust the ratio of the two types of gradient priors in the iterative optimization process so as to obtain better convergence. Simulated and experimental results prove that compared with the existing state-of-the-art methods of blind image restoration, the proposed method has superior image restoration performance.
-
Key words:
- blind image restoration /
- high-order gradient /
- sparse prior /
- adaption
-
Overview
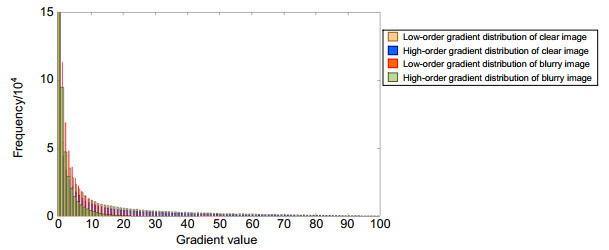
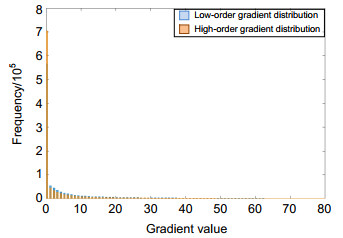
Overview: Blind image restoration is widely used to improve the quality of degraded images with no-reference. Its main purpose is to accurately estimate the blur kernel and the wanted clear image. In the blind restoration research based on high-order image gradient priors, most of the existing works employ the total variation to model the gradient prior constraints. This class of method can effectively suppress the blocking artifact in the restored image. On the basis of experimental observation and research, this paper proposes to use the sparse prior constraint model to regularize the blind restoration process to obtain a better image restoration performance. On the one hand, by looking into the histogram of high-order and low-order gradients of a natural image, it can be found that the sparsity of high-order gradients is even more salient than that of low-order gradients. On the other hand, the existing researches show that the use of sparse priors to describe a heavy-tailed distribution of low-order gradients helps to restore the significant edges of the have image while effectively suppressing noise and ringing effects. Therefore, this work proposes to combine the low-order and high-order gradient priors into a new sparse regularization term so as to benefit from both types of gradient priors. In the meantime, an interesting experimental finding is introduced in this work that different degrees of image blur favor different ratios of the two types of gradient priors which are beneficial to obtain the optimal solution. Therefore, to obtain better iteration convergence, an adaptive factor ω based on image entropy is introduced to adjust the ratio of the two types of gradient priors in the iterative optimization process. Since it is hard to model the parameter ωmathematically, the expression of ω is determined by manually parameter adjustment and statistically data fitting in this work. The overall iterative optimization process is developed in a coarse-to-fine manner, and the split Bergman method is employed to deal with the non-convex problem of each minimization subtask. Finally, to analyze the performance of the proposed blind image restoration method, the ablation study was firstly conducted to demonstrate the efficiency of the employed strategies. Then, on the BSDS image dataset (simulated dataset) and the GOPRO image dataset (real blurred dataset), the proposed method was compared with the existing state-of-the-art image restoration methods. Experimental results show that our method can recover sharper edges and smoother details as well as introduce less unwanted artifacts, and our method is at a relatively leading level not only in subjective visual effects but also in performance evaluation indicators. All the above advantages demonstrate that the proposed method has superior image restoration performance.
-
-
图 1 自然图像高阶梯度分布和低阶梯度分布。由水平梯度和垂直梯度可得到相似结论，图中仅对水平梯度分布进行展示
Figure 1. The distributions of the low-order and high-order gradient maps of clear natural images. This regularity exists in both horizontal and vertical directions and only the horizontal gradient distribution is presented for example
图 2 不同比例梯度约束下的图像复原效果。
Figure 2. The restoration performance over different ratios of gradient regularizations.
图 3 清晰图像和退化图像的高阶梯度分布和低阶梯度分布对比
Figure 3. An example of the variations of image gradients from clear to blurry (Please zoom in for a better view)
图 4 消融实验复原效果
Figure 4. An example of ablation experiment of the proposed regularization scheme
图 5 不同方法在合成数据集上的复原结果
Figure 5. Examples of qualitative comparisons on the BSDS dataset[22]. Columns from top to bottom: blurry image, Li, Nah, Krishnan, Xu and Jia, Hosseini, and ours
图 6 不同方法在真实数据集上的实验结果
Figure 6. An example of real-life blurry image from the GOPRO dataset[11]. Columns from left to right: blurry image, Li, Nah, Krishnan, Xu & Jia, Hosseini and ours
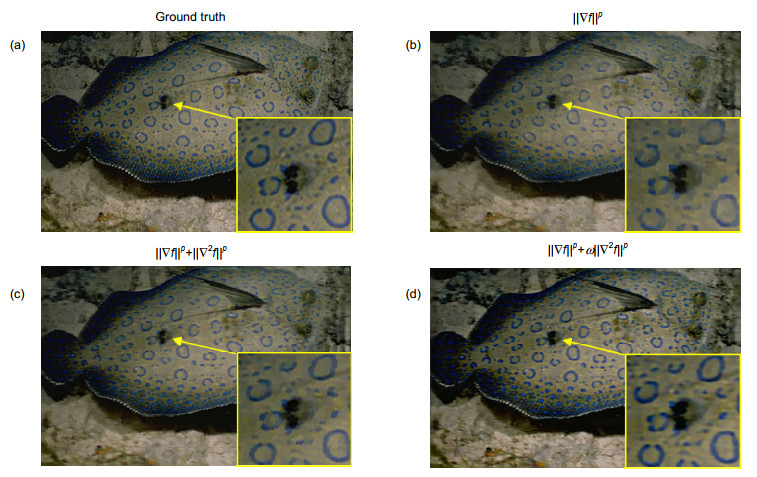
表 1 消融实验算法性能比较
Table 1. The average performance of ablation study. The best performed ones are marked in bold
Measure Blurred ||▽f||p ||▽f||p+||▽2f||p ||▽f||p+ω||▽2f||p SSIM 0.5436 0.7110 0.7407 0.8280 PSNR 25.1436 26.0087 26.6255 26.7176 
下载: 导出CSV
表 2 不同方法在合成数据集上的实验结果
Table 2. Average deconvolution performance on dataset[22]. The best performed ones are marked in bold
下载: 导出CSV
表 3 不同方法在真实数据集上的实验结果
Table 3. Average deconvolution performance on dataset[9]. The best performed ones are marked in bold
下载: 导出CSV
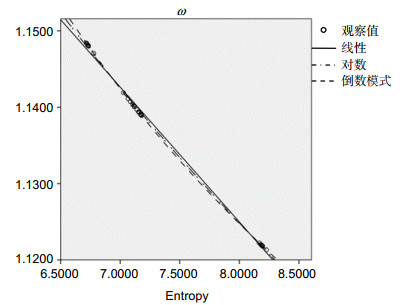
表 4 模型总计及参数评估
Table 4. Model overview and parameter estimation
方程式 模型摘要 参数评估 R2 F df1 df2 显著性 常数 b1 线性 0.937 10925.397 1 30 0.000 1.266 -0.018 对数 0.969 43365.874 1 30 0.000 1.400 -0.133 倒数模式 1.000 41328226.327 1 30 0.000 1.001 0.990 因变量: ω自变量：E(Entropy)
下载: 导出CSV
-
参考文献
[1] Weiss Y, Freeman W T. What makes a good model of natural images?[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1-8.
[2] Levin A, Weiss Y, Durand F, et al. Understanding and evaluating blind deconvolution algorithms[C]//Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition, 2009: 1964-1971.
[3] Fergus R, Singh B, Hertzmann A, et al. Removing camera shake from a single photograph[J]. ACM Trans Graph, 2006, 25(3): 787-794. doi: 10.1145/1141911.1141956
[4] Shan Q, Jia J Y, Agarwala A. High-quality motion deblurring from a single image[J]. ACM Trans Graph, 2008, 27(3): 1-10.
[5] Cho S, Lee S. Fast motion deblurring[J]. ACM Trans Graph, 2009, 28(5): 1-8. http://www.dbpia.co.kr/article/2579382
[6] Levin A, Weiss Y, Durand F, et al. Efficient marginal likelihood optimization in blind deconvolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2011: 20-25.
[7] Xu L, Zheng S C, Jia J Y. Unnatural L0 sparse representation for natural image deblurring[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition, 2013: 1107-1114.
[8] Wang K, Shen Y, Xiao L, et al. Blind motion deblurring based on fused ℓ0-ℓ1 regularization[C]//Proceedings of the 8th International Conference on Image and Graphics, 2015: 1-10.
[9] Kotera J, Šroubek F, Milanfar P. Blind deconvolution using alternating maximum a posteriori estimation with heavy-tailed priors[C]//Proceedings of the 15th International Conference on Computer Analysis of Images and Patterns, 2013: 59-66.
[10] 周海蓉, 田雨, 饶长辉. 稀疏先验型的大气湍流退化图像盲复原[J]. 光电工程, 2020, 47(7): 190040. doi: 10.12086/oee.2020.190040
Zhou H R, Tian Y, Rao C H. Blind restoration of atmospheric turbulence degraded images by sparse prior model[J]. Opto-Electron Eng, 2020, 47(7): 190040. doi: 10.12086/oee.2020.190040
[11] Nah S, Kim T H, Lee K M. Deep multi-scale convolutional neural network for dynamic scene deblurring[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, 2017: 257-265.
[12] Tao X, Gao H Y, Shen X Y, et al. Scale-recurrent network for deep image deblurring[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 8174-8182.
[13] Yan R M, Shao L. Blind image blur estimation via deep learning[J]. IEEE Trans Image Process, 2016, 25(4): 1910-1921. http://ieeexplore.ieee.org/document/7420686/
[14] Zhang J W, Pan J S, Ren J, et al. Dynamic scene deblurring using spatially variant recurrent neural networks [C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 2521-2529.
[15] Xu X Y, Pan J S, Zhang Y J, et al. Motion blur kernel estimation via deep learning[J]. IEEE Trans Image Process, 2018, 27(1): 194-205. doi: 10.1109/TIP.2017.2753658
[16] Li Y L, Tofighi M, Geng J Y, et al. Efficient and interpretable deep blind image deblurring via algorithm unrolling[J]. IEEE Trans Comput Imaging, 2020, 6: 666-681. doi: 10.1109/TCI.2020.2964202
[17] Lv X G, Song Y Z, Wang S X, et al. Image restoration with a high-order total variation minimization method[J]. Appl Math Mod, 2013, 37(16-17): 8210-8224. doi: 10.1016/j.apm.2013.03.028
[18] 穆绍硕, 张解放. 基于快速l1-范数稀疏表示和TGV的超分辨算法研究[J]. 光电工程, 2019, 46(11): 180499. doi: 10.12086/oee.2019.180499
Mu S S, Zhang J F. An anisotropic edge total generalized variation energy super-resolution based on fast l1-norm dictionary edge representations[J]. Opto-Electron Eng, 2019, 46(11): 180499. doi: 10.12086/oee.2019.180499
[19] Goldstein T, Osher S. The split Bregman method for ℓ1-regularized problems[J]. SIAM J Imaging Sci, 2009, 2(2): 323-343. doi: 10.1137/080725891
[20] Krishnan D, Fergus R. Fast image deconvolution using hyper-laplacian priors[C]//Proceedings of the 22nd International Conference on Neural Information Processing Systems, 2009: 1033-1041.
[21] Perrone D, Favaro P. Total variation blind deconvolution: the devil is in the details[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, 2014: 2909-2916.
[22] Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]//Proceedings of the Eighth IEEE International Conference on Computer Vision. ICCV 2001, 2001: 416-423.
[23] Krishnan D, Tay T, Fergus R. Blind deconvolution using a normalized sparsity measure[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, 2011: 233-240.
[24] Hosseini M S, Plataniotis K N. Convolutional deblurring for natural imaging[J]. IEEE Trans Image Process, 2019, 29: 250-264. http://ieeexplore.ieee.org/document/8782833/
-
访问统计
点击扫一扫
图(8)
表(5)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
