E-mail Alert
RSS
Mode field diameter measurement of single mode fiber using Bessel function fitting method based on variable aperture in far field
-
摘要
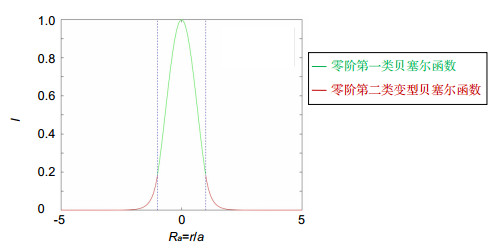
模场直径作为单模光纤的一个重要参数，远场可变孔径法是GB.15972.45-2008中推荐的测量方法。本文分析了单模光纤中传播光场的分布，其中光场的模式行为是亥姆霍兹方程的解，理论上应满足贝塞尔函数。对此，本文基于远场可变孔径法提出一种利用贝塞尔函数拟合光纤出射光场分布，进而由拟合得到的模场分布曲线计算模场直径。与目前常用的远场可变孔径法相比，在测量数据正常时，本方法与常用方法测量精度相当。当测量数据存在误差时，本方法仍能保证测量结果的稳定性与准确性。
Abstract
The mode field diameter is an important parameter of single-mode fiber, and the GB.15972.45-2008 recommends using the far-field variable aperture method to measure it. This paper analyzes the distribution of the propagating light field in a single-mode fiber. The mode behavior of the light field is the solution of the Helmholtz equation, which in theory should satisfy the Bessel function. In this regard, a method using Bessel function to fit the optical field distribution of the fiber based on the far-field variable aperture method is proposed, and the mode field diameter is calculated from the fitted mode field distribution curve. Compared with the commonly used far-field variable aperture method, when the measurement data is normal, this method has the same measurement accuracy. When there are errors in the measurement data, this method can still ensure the stability and accuracy of the measurement results.
-
Overview
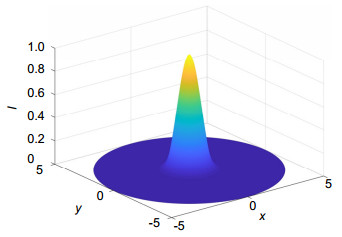
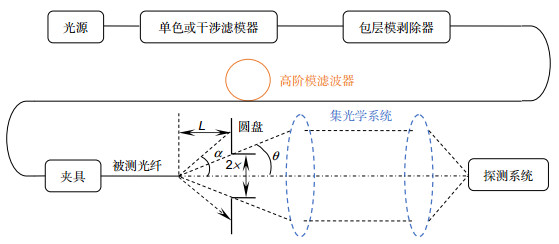
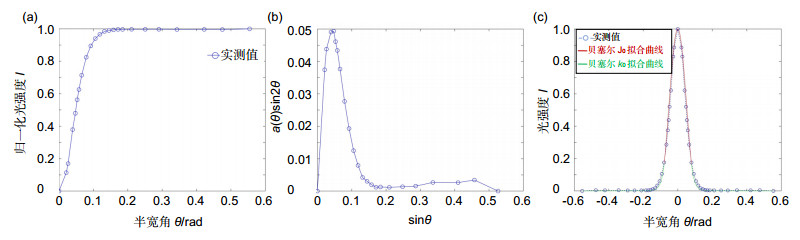
Overview: As an important parameter of single-mode fiber, the mode field diameter is used to describe the mode field distribution of the fundamental mode in the cross section of the single-mode fiber. The far field variable aperture method is recommended in GB.15972.45-2008 for the measurement of mode field diameter. In the process of measurement, the method is easily affected by the fact that the center of the fiber is not aligned with the center of the pervious hole or the cutting effect of the fiber is not good, which will result in the decrease of measurement accuracy. The transmission of light in a fiber is essentially the transmission of electromagnetic waves in a closed medium, and its solution should satisfy Maxwell's equations, where the mode behavior of light field is the solution of the Helmholtz equation, which theoretically should satisfy the Bessel function. Based on the far field variable aperture method, this paper presents a method to calculate the diameter of the optical field by fitting the distribution of the optical field of the fiber through Bessel function. Main steps are as follows: the first step is to preprocess the optical power data obtained by the far field variable aperture method. In the second step, two Bessel functions are used to fit the measured data respectively to obtain the real mode field distribution curve. In the third step, the Bessel curve obtained by fitting is used to obtain the mode field diameter through the Petermann (Ⅱ) formula. Taking G.652 fiber as an example, under normal measurement conditions, the measurement results of the standard instrument using the standard far-field variable aperture method are 9.210 μm and 9.208 μm. This shows that this method can achieve the same precision level as the standard method. When the measurement conditions are abnormal (error data), an error data appears in the measurement data, and the measurement results of the two methods are 9.765 μm and 9.199 μm, with the relative deviation of 6.02% and 0.09%. In two error data, the measurement results of the two methods are 10.042 μm and 9.152 μm, with the relative deviation of 9.03% and 0.62%. The subsequent results have been tested for many times, all of which show that the measurement results of this method have good accuracy and stability. This method is a meaningful supplement to the far field variable aperture method proposed in GB.15972.45-2008. At the same time, it replaces the expensive near-field infrared camera by a single photodetector combined with a variable aperture, and it realizes the mode field acquisition function of near-field infrared camera, which greatly improves the cost performance of the mode field diameter measurement instrument.
-
-
图 3 G.652光纤在1310 nm工作波长下模场分布函数
Figure 3. The mode field distribution function of G.652 fiber at 1310 nm working wavelength
图 4 远场可变孔径法测量原理图
Figure 4. Principle diagram of remote field variable aperture measurement
图 5 正常情况下模场直径测量结果图。
Figure 5. Measurement results of modulus field diameter under normal conditions. (a) Light intensity distribution of OFM tester; (b) Graph of the integral function a(θ)sin2θ~sinθ; (c) Fitting results of Bessel function modulus field distribution
图 6 异常情况下模场直径测量结果图。
Figure 6. Measurement results of modulus field diameter under abnormal conditions. (a) Light intensity distribution of OFM tester; (b) Graph of the integral function a(θ)sin2θ~sinθ; (c) Fitting results of Bessel function modulus field distribution
表 1 在1310 nm波长下不同型号单模光纤两种测量方法的测量结果比较
Table 1. Comparison of measurement results in two measurement methods at 1310 nm wavelength
测试组 G.652单模光纤 G.655单模光纤 wOFM/mm wBessel/mm wOFM/mm wBessel/mm 1 9.21 9.208 7.78 7.794 2 9.22 9.221 7.79 7.806 3 9.19 9.192 7.77 7.804 4 9.21 9.209 7.81 7.819 5 9.2 9.204 7.8 7.808 平均值 9.206 9.207 7.79 7.806 最大偏差 0.016 0.015 0.02 0.015 
下载: 导出CSV
表 2 在1310 nm波长下存在误差情况两种测量方法的测量结果比较
Table 2. Comparison of measurement results of the two methods in case of error at 1310 nm wavelength
被测光纤 测试方法 测试最佳模场直径/mm 1孔存在偏差(mm)/相对偏差 2孔存在偏差(mm)/相对偏差 3孔存在偏差(mm)/相对偏差 G.652光纤 wOFM 9.21 9.765/6.02% 10.042/9.03% 10.501/14.01% wBessel 9.208 9.199/0.09% 9.152/0.62% 9.042/1.82% G.655光纤 wOFM 7.78 8.247/6.00% 8.492/8.95% 8.912/14.34% wBessel 7.794 7.782/0.15% 7.763/0.40% 7.630/2.10%
下载: 导出CSV
-
参考文献
[1] Paul B K, Islam S, Sen S, et al. Low material loss and dispersion flattened fiber for single mode THz-wave transmission applications[J]. Results Phys, 2018, 11: 638-642. doi: 10.1016/j.rinp.2018.09.050
[2] Chen X, Himmelreich J E, Hurley J E, et al. Universal fiber for short-distance optical communications[J]. J Lightw Technol, 2019, 37(2): 389-395. doi: 10.1109/JLT.2018.2886954
[3] Han J W, Zhang J. Elasto-optical correction of bend loss for Ge-free fibers with large-effective-area and ultra-low-loss[J]. Opt Fiber Technol, 2020, 54: 102120. doi: 10.1016/j.yofte.2019.102120
[4] Ohashi M, Shibata N, Sato K. Mode field diameter measurement conditions in single-mode fibres[J]. Electron Lett, 1989, 25(8): 493-495. doi: 10.1049/el:19890338
[5] Hoo Y L, Jin W, Ju J, et al. Loss analysis of single-mode fiber/photonic-crystal fiber splice[J]. Microw Opt Technol Lett, 2004, 40(5): 378-380. doi: 10.1002/mop.11387
[6] 王建江, 何霖, 顾灵卫, 等. 光纤内应力对低损耗单模光纤衰减影响的改善[J]. 光纤与电缆及其应用技术, 2020(1): 31-32, 35. https://www.cnki.com.cn/Article/CJFDTOTAL-GYYD202001009.htm
Wang J J, He L, Gu L W, et al. Improvement of the influence of fiber internal stress on the attenuation of low-loss single-mode fiber[J]. Opt Fiber Electric Cable Their Appl, 2020(1): 31-32, 35. https://www.cnki.com.cn/Article/CJFDTOTAL-GYYD202001009.htm
[7] 续贝贝, 席丽霞, 张晓光, 等. 色散测量样机的设计与实验验证[J]. 光学学报, 2019, 39(2): 0206004. https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201902007.htm
Xu B B, Xi L X, Zhang X G, et al. Design and experimental verification of dispersion measurement prototype[J]. Acta Opt Sin, 2019, 39(2): 0206004. https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201902007.htm
[8] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 光纤试验方法规范第45部分: 传输特性和光学特性的测量方法和试验程序模场直径: GB/T 15972.45-2008[S]. 北京: 中国标准出版社, 2008.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of China. Specifications for optical fibre test methods - part 45: measurement methods and test procedures for transmission and optical characteristics - mode field diameter: GB/T 15972.45-2008[S]. Beijing: China Standard Press, 2008.
[9] Michtchenko A, Nava M F. Far field technique applied in single mode optical fibers for studying of modal field diameter[C]//2006 3rd International Conference on Electrical and Electronics Engineering, 2006: 1-3.
[10] 杨高波, 徐铁峰, 宋玉兰, 等. 两种快速测量单模光纤模场半径的方法及装置[J]. 光学仪器, 2004, 26(3): 59-63. doi: 10.3969/j.issn.1005-5630.2004.03.012
Yang G B, Xu T F, Song Y L, et al. Two methods and devices for quick measuring the mode-field radius of single-mode optical fibers[J]. Opt Instrum, 2004, 26(3): 59-63. doi: 10.3969/j.issn.1005-5630.2004.03.012
[11] Parker A J. Near field measurement of fiber mode field diameters: effects of defocusing[J]. IEEE Trans Instrum Meas, 1995, 44(2): 458-460. doi: 10.1109/19.377879
[12] Ohashi M, Miyoshi Y, Kubota H, et al. Longitudinal fiber parameter measurements of multi-core fiber using OTDR[J] Opt Express, 2014, 22(24): 30137-30147. doi: 10.1364/OE.22.030137
[13] 熊婷婷, 戴唯一, 王莲萍, 等. 采用后向散射法对B6类光纤模场直径的测量[J]. 光纤与电缆及其应用技术, 2018(3): 11-13, 20. https://www.cnki.com.cn/Article/CJFDTOTAL-GYYD201803003.htm
Xiong T T, Dai W Y, Wang L P, et al. Application of back-scattering method on the measurement of MFD of B6 optical fiber[J]. Opt Fiber Electric Cable Their Appl, 2018(3): 11-13, 20. https://www.cnki.com.cn/Article/CJFDTOTAL-GYYD201803003.htm
[14] Nakamura A, Okamoto K, Koshikiya Y, et al. Effective mode field diameter for LP11 mode and its measurement technique[J]. IEEE Photonics Technol Lett, 2016, 28(22): 2553-2556. doi: 10.1109/LPT.2016.2605639
[15] Matsui T, Sakamoto T, Nakajima K. Effective mode-field diameter measurement for few-mode fibers[C]//2017 25th Optical Fiber Sensors Conference (OFS), 2017: 1-4.
[16] 徐圣杰, 孙林波. 使用双向后向散射技术模拟单模光纤模场直径测试[J]. 现代传输, 2020(1): 70-73. https://www.cnki.com.cn/Article/CJFDTOTAL-YXCS202001022.htm
Xu S J, Sun L B. Using two-way backscattering technology to simulate the mode field diameter test of single-mode fiber[J]. Mod Transm, 2020(1): 70-73. https://www.cnki.com.cn/Article/CJFDTOTAL-YXCS202001022.htm
[17] 光纤多参数测试仪用户手册[M]. 上海: 上海电缆研究所, 2013.
SECRI. OFM Optical Fiber Multi-Parameter Tester User Manual[M]. Shanghai: Shanghai Cable Research Institute, 2013. SECRI. OFM
[18] 李一鸣, 涂建坤, 项华中, 等. 光纤灰度分布的高斯函数拟合法测量光纤几何参数[J]. 光电工程, 2020, 47(4): 190247. doi: 10.12086/oee.2020.190247
Li Y M, Tu J K, Xiang H Z, et al. Measurement of optical fiber geometry parameters by gray distribution fitting with Gaussian function[J]. Opto-Electron Eng, 2020, 47(4): 190247. doi: 10.12086/oee.2020.190247
[19] 欧攀. 高等光学仿真(MATLAB版): 光波导, 激光[M]. 2版. 北京: 北京航空航天大学出版社, 2014: 129-134.
Ou P. Advanced Optics Simulation (MATLAB Version)-Optical Waveguide, Laser[M]. 2nd ed. Beijing: Beihang University Press, 2014: 129-134.
[20] 郭福源, 李连煌, 王明华. 介质平面光波导TE0模模场分布的高斯近似[J]. 中国激光, 2008, 35(2): 235-239. doi: 10.3321/j.issn:0258-7025.2008.02.016
Guo F Y, Li L H, Wang M H. Gaussian approximation for mode field distribution of dielectric planar waveguide TE0 mode[J]. Chin J Lasers, 2008, 35(2): 235-239. doi: 10.3321/j.issn:0258-7025.2008.02.016
[21] 宋小鹿, 李兵斌, 王石语, 等. 一种测量激光光强按角度分布的新方法[J]. 半导体光电, 2007, 28(4): 572-575. doi: 10.3969/j.issn.1001-5868.2007.04.032
Song X L, Li B B, Wang S Y, et al. A new measurement of light intensity distribution with divergence[J]. Semicond Optoelectron, 2007, 28(4): 572-575. doi: 10.3969/j.issn.1001-5868.2007.04.032
[22] Miyagi K, Namihira Y, Razzak S M A, et al. Measurements of mode field diameter and effective area of photonic crystal fibers by far-field scanning technique[J]. Opt Rev, 2010, 17(4): 388-392. doi: 10.1007/s10043-010-0072-x
-
访问统计
点击扫一扫
图(6)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
