E-mail Alert
RSS
A high-precision centroid detecting method based on two-dimension orthogonal gratings
-
摘要
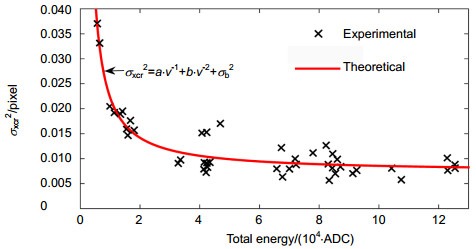
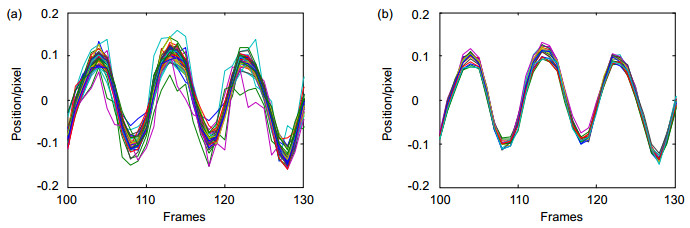
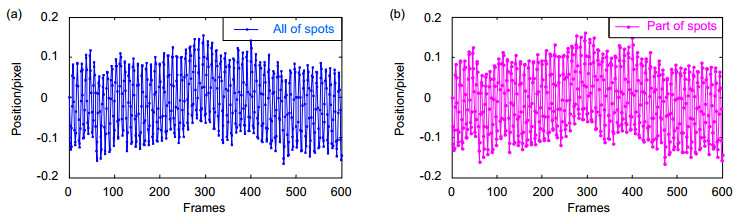
为了探测高精度的远场光斑质心，本文提出了一种多光斑质心探测方法。该方法利用二维正交的衍射光栅，将远场单光斑扩展为多光斑阵列，通过增加探测光斑的输入信息量，提高质心探测精度。实验结果表明，远场多光斑质心探测精度比单光斑质心探测精度提高了近4倍，单个光斑质心探测误差均方根(RMS)为0.0385 pixels，16个多光斑阵列平均质心探测误差RMS为0.0099 pixels。相对于传统的质心探测方法，本文所采用的远场多光斑质心探测方法更为简便。
Abstract
In order to detect high-precision far-field spots centroid, a multiple spots centroid detecting method is proposed. Using two-dimension orthogonal diffraction gratings, a single spot on the far-field focal plane is developed into a multiple spots array. By increasing the input information of the far-field detected spots, the centroid detection accuracy can be improved. The experimental results show that the centroid detecting accuracy of multiple spots is 4 times larger than that of single spot. The root mean square (RMS) of single spot centroid detecting error is 0.0385 pixels and the RMS of 16 spots centroid detecting error is 0.0099 pixels. Compared with the conventional method of the centroid detecting, the far-field multiple spots centroid detecting method proposed is simpler and more convenient.
-
Key words:
- optical test /
- diffraction grating /
- centroid detection /
- far-field spot /
- random noise
-
Overview
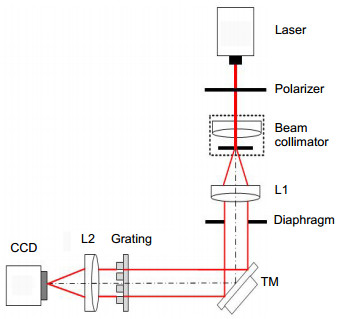
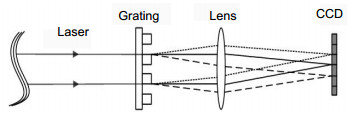
Abstract: In order to improve the detection accuracy of far-field spots centroid, a new optical path structure on the basis of a two-dimension orthogonal diffraction grating is proposed. Using two orthogonal one-dimension diffraction gratings, a single spot on the far-field focal plane is developed into a multiple spots array. A corresponding experimental setup was built to compare the centroid detection accuracy of the new method and the conventional method under the same experiment conditions. The experimental results show that by increasing the input information of the far-field detected spots, the centroid detection accuracy can be improved. First, the far-field imaging principle of the two-dimension orthogonal diffraction gratings is introduced. In this paper, the beam splitting characteristic of the two-dimensional diffraction grating is used to improve the detection accuracy of the incidence optical axis. The two-dimensional diffraction grating is composed of two orthogonal one-dimensional diffraction gratings. The incidence beam is divided into number of beams with the same phase and different intensity. A set of diffraction spots, which has different intensities but has the same ranks distance and distribution, are formed. These images are captured by the CCD camera. Second, the spot centroid detecting error is analyzed in theory and results show that the centroid random error is one of the main errors source. Third, the formula to decrease the centroid detecting random error based on far-field multiple spots is established. By increasing the input information of the far-field detected spots, the centroid detection accuracy can be improved. Finally, the experiments of centroid detecting are carried out. The experimental results show that the centroid detecting accuracy of multiple spots is 4 times larger than that of single spot. The root mean square of single spot centroid detecting error is 0.0385 pixels and the RMS of 16 spots centroid detecting error is 0.0099 pixels. In conclusion, a modified method with a two-dimensional orthogonal diffraction grating is proposed to improve the detection accuracy of far-field spots centroid. The basic principle of proposed method and the processing of the new method are described. The experimental setup with the diffraction grating is also illustrated in detail. It is only necessary to place the diffraction grating in the front of image lens, and the structure is simple. Under the same condition, the experiments are done to validate the high-precision centroid detection. Compared with the far-field single spot centroid detecting method, the far-field multiple spots centroid detecting method proposed is simpler and more convenient, especially for the optical axis alignment with bigger axis offset. It can be used as optical axis detection in an adaptive optics system.
-
-
图 2 基于衍射光栅的质心探测实验光路示意图.
Figure 2. Schematic diagram of centroid detecting based on diffraction gratings.
图 4 质心探测误差RMS与光斑总能量之间的关系.
Figure 4. Relationship between centroid RMS and spots total energy.
图 5 光斑质心相对位置曲线. (a)全部子光斑. (b)去除质心误差较大的光斑.
Figure 5. Serial position curve of centroid. (a) All the spot. (b) After removing large centroid error.
图 6 光斑平均质心探测误差对比. (a)全部子光斑. (b)筛选后的部分光斑.
Figure 6. Comparison results of the mean centroid detecting error. (a) All the spots. (b) Part of spots.
表 1 不同光斑数量下质心探测精度的实验RMS值与理论RMS值对比结果.
Table 1. Comparison results between experimental and theoretical RMS values of centroid detecting precision under different spots numbers.
Serial number Number of spot Experimental RMS/pixel Theoretical RMS/pixel 1 1 0.0385 —— 2 4 0.0201 0.0192 3 8 0.0134 0.0136 4 16 0.0099 0.0096 
下载: 导出CSV
-
参考文献
[1] Tyson R K. Principles of adaptive optics[M]. Boston: Academic Press, 1991: 121–122.
[2] 沈锋, 姜文汉.弱光波前传感器质心计算的新方法[J].强激光与粒子束, 1999, 11(1): 27–30. http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY901.008.htm
Shen Feng, Jiang Wenhan. Gaussian fitting method for esti-mating subaperture centroids of shack-Hartmann wavefront sensor at low light levels[J]. High Power Laser and Particle Beams, 1999, 11(1): 27–30. http://www.cnki.com.cn/Article/CJFDTOTAL-QJGY901.008.htm
[3] Jiang Wenhan, Xian Hao, Shen Feng. Detection error of Shack-Hartmann wavefront sensors[J]. Proceedings of SPIE, 1997, 3126: 534–544. doi: 10.1117/12.279060
[4] 任剑峰, 饶长辉, 李明全.一种Hartmann-Shack波前传感器图像的自适应阈值选取方法[J].光电工程, 2002, 29(1): 1–5. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gdgc200201000&dbname=CJFD&dbcode=CJFQ
Ren Jianfeng, Rao Changhui, Li Mingquan. An adaptive threshold selection method for Hartmann-Shack wavefront sensor[J]. Opto-Electronic Engineering, 2002, 29(1): 1–5. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gdgc200201000&dbname=CJFD&dbcode=CJFQ
[5] 梁春, 廖文和, 沈建新, 等. Hartmann-Shack波前传感器的自适应质心探测方法[J].中国激光, 2009, 36(2): 430–434. http://www.opticsjournal.net/abstract.htm?aid=OJ0902230000455B8EaG
Liang Chun, Liao Wenhe, Shen Jianxin, et al. An adaptive detecting centroid method for Hartmann-Shack wavefront sensor[J]. Chinese Journal of Lasers, 2009, 36(2): 430–434. http://www.opticsjournal.net/abstract.htm?aid=OJ0902230000455B8EaG
[6] Prieto P M, Vargas-Martı́n F, Goelz S, et al. Analysis of the performance of the Hartmann-Shack sensor in the human eye[J]. Journal of the Optical Society of America A, 2000, 17(8): 1388–1398. doi: 10.1364/JOSAA.17.001388
[7] Baik S H, Park S K, Kim C J, et al. A center detection algorithm for Shack-Hartmann wavefront sensor[J]. Optics & Laser Technology, 2007, 39(2): 262–267. https://www.sciencedirect.com/science/article/pii/S0030399205001659
[8] 李晶, 巩岩, 呼新荣, 等.哈特曼-夏克波前传感器的高精度质心探测方法[J].中国激光, 2014, 41(3): 0316002. http://www.opticsjournal.net/abstract.htm?id=OJ140226000127RnUqWt
Li Jing, Gong Yan, Hu Xinrong, et al. A high-precision centroid detecting method for Hartmann-Shack wavefront sensor[J]. Chinese Journal of Lasers, 2014, 41(3): 0316002. http://www.opticsjournal.net/abstract.htm?id=OJ140226000127RnUqWt
[9] 程利群, 王晓曼, 景文博.利用标记分水岭法实现夏克-哈特曼波前传感器质心探测[J].光学精密工程, 2014, 22(6): 1494–1499. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxjmgc201406013
Cheng Liqun, Wang Xiaoman, Jing Wenbo. Centroid detection of Shack-Hartmann wave-front sensor by marked watershed method[J]. Optics and Precision Engineering, 2014, 22(6): 1494–1499. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxjmgc201406013
[10] 张艳艳, 许文涛, 陈苏婷.稀疏表示的夏克-哈特曼波前传感器信号提取[J].光电工程, 2016, 43(4): 48–54. http://doi.wanfangdata.com.cn/10.3969/j.issn.1003-501X.2016.04.008
Zhang Yanyan, Xu Wentao, Chen Suting. The extraction of signal in Shack-Hartmann wavefront sensor based on sparse representation[J]. Opto-Electronic Engineering, 2016, 43(4): 48–54. http://doi.wanfangdata.com.cn/10.3969/j.issn.1003-501X.2016.04.008
[11] Luo Qun, Huang Linhai, Gu Naiting, et al. Experimental study of a modified phase diversity with a diffraction grating[J]. Optics Express, 2012, 20(11): 12059–12066. doi: 10.1364/OE.20.012059
[12] 贺元兴, 李新阳.基于衍射光栅的远场焦斑测量新方法[J].中国激光, 2012, 39(2): 0208001. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jjzz201202027&dbname=CJFD&dbcode=CJFQ
He Yuanxing, Li Xinyang. Far-field focal spot measurement based on diffraction grating[J]. Chinese Journal of Lasers, 2012, 39(2): 0208001. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jjzz201202027&dbname=CJFD&dbcode=CJFQ
[13] Ma Xiaoyu, Rao Changhui, Zheng Hanqing. Error analysis of CCD-based point source centroid computation under the background light[J]. Optics Express, 2009, 17(10): 8525–8541. doi: 10.1364/OE.17.008525
[14] Li Chaohong, Xian Hao, Jiang Wenhan, et al. Wavefront error caused by centroid position random error[J]. Journal of Modern Optics, 2008, 55(1): 127–133. doi: 10.1080/09500340701321990
[15] Cao Genrui, Yu Xin. Accuracy analysis of a Hartmann-Shack wavefront sensor operated with a faint object[J]. Optical Engineering, 1994, 33(7): 2331–2335. doi: 10.1117/12.169716
-
访问统计
点击扫一扫
图(6)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
