-
摘要
为了消弱滑模控制高频抖振,提出一种新型开关切换函数,代替传统的符号函数。以多自由度串联机器人的动力学模型为研究对象,利用该新型开关切换函数,设计了一种滑模控制律,并证明多自由度机器人滑模控制系统渐近稳定。两自由度机器人滑模控制的仿真实验表明,两个关节都实现了较高的角位置和角速度跟踪精度,并且动态响应较快。同时,与采用符号函数作为开关切换函数的机器人滑模控制系统相比,有效消弱了滑模控制量的高频抖振。该新型开关切换函数具有通用性,适用于机载光电稳定平台、导弹制导等其它滑模控制系统。

Abstract
A novel switching function which replaces the sign function is presented in order to reduce high frequency chattering of the sliding model control. The dynamics model of multi-DOF serial robot manipulators is studied. A sliding control law with this novel switching function is designed and the asymptotic stability of the sliding model control of robot manipulators is proved. The simulation experiments of the sliding model control of 2-DOF robot manipulators illustrate that two links have higher angular position tracking accuracy and speed tracking accuracy. Moreover, its dynamic response is faster. The sliding model control system with the novel switching function reduces high frequency chattering effectively compared with the sliding model control system with the sign function. This novel switching function can be used on other sliding model control systems, for instance, the airborne electro-optical stabilized platform and missile guidance.
-
Overview

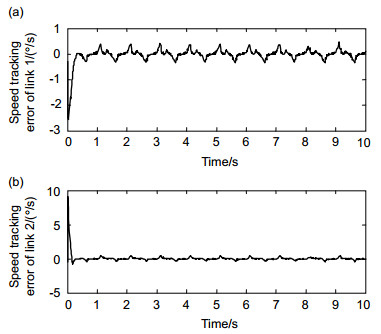
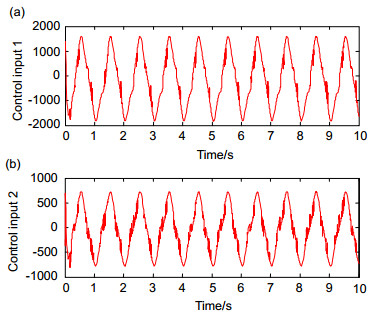
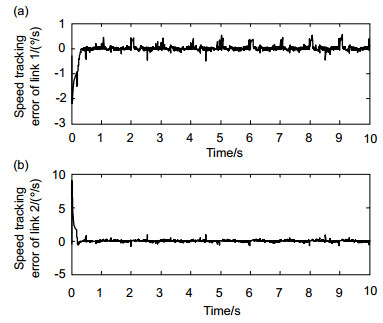
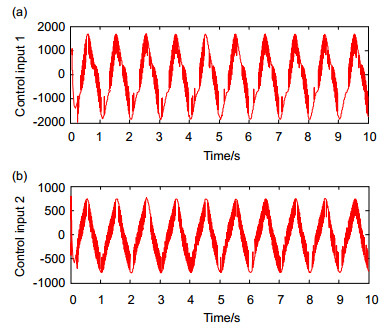
Abstract: The high frequency chattering of the sliding model control system affects the control accuracy and increases energy consumption. It perhaps stimulates the uncertainty dynamics with the high frequency and causes the system instability. The control input discontinuity caused by the sign function is the main reason for the high frequency chattering in the sliding model control system. A novel switching function which replaces the sign function is presented in order to reduce high frequency chattering of the sliding model control. It is a special continuous power function in the neighborhood of the origin, which refrains from the high frequency chattering phenomena of the control input. When the absolute value of the error is smaller, the gain in the function is greater. When the absolute value of the error is greater, the gain in the function is smaller. Firstly, the dynamics mathematics model of multi-DOF serial robot manipulators with the parameters uncertainties and external disturbance is studied. Secondly, a multi-order sliding control law for robot manipulators with the novel switching function is constructed, and the asymptotic stability of the sliding model control system of robot manipulators is proved by using the Lyapunov function. Finally, the sine signal tracking simulation experiments of the sliding model control of 2-DOF robot manipulators with the novel switching function are conducted, which are compared with those of the sliding model control with the sign function. The desired angular position signal of link 1 and link 2 is q1d=cos(2πt) and q2d=sin(2πt) respectively. The maximum angular position tracking error of link 1 is 0.013° and that of link 2 is 0.0065° besides the original values. The maximum angular speed tracking error of link 1 is 0.46°/s and that of link 2 is 0.45°/s besides the original values. The experiment results illustrate that two links of robot manipulators obtain higher angular position tracking accuracy and speed tracking accuracy. Moreover, dynamic response of the control system is faster. The sliding model control system with the novel switching function reduces high frequency chattering effectively compared with the sliding model control system with the sign function. So the angular speed of two links has much less high frequency chattering. The novel switching function can reduce high frequency chattering phenomena of the sliding model control system which achieves better tracking performances. This switching function can be used on other sliding model control systems, for instance, the airborne electro-optical stabilized platform, numerical control machine and missile guidance, etc.
-

-
参考文献
[1] 刘金琨.滑模变结构控制MATLAB仿真:基本理论与设计方法[M]. 3版.北京:清华大学出版社, 2015: 2–17.
Liu Jinkun. Sliding mode control design and MATLAB simulation: the basic theory and design method[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 2–17.
[2] 王长旭, 孟中, 韩松伟, 等.基于卡尔曼滤波滑模控制的伺服系统设计仿真[J].光电工程, 2010, 37(2): 22–26. http://www.cqvip.com/QK/90982A/201002/32957158.html
Wang Changxu, Meng Zhong, Han Songwei, et al. Design and simulation of servo system based on Kalman filtering sliding mode control[J]. Opto-Electronic Engineering, 2010, 37(2): 22–26. http://www.cqvip.com/QK/90982A/201002/32957158.html
[3] 武志鹏, 陈兴林, 刘川.光刻机工件台宏微系统的滑模变结构控制[J].光电工程, 2011, 38(9): 50–54. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201109010
Wu Zhipeng, Chen Xinglin, Liu Chuan. Sliding mode control of macro-micro system for wafer stage of lithography[J]. Opto-Electronic Engineering, 2011, 38(9): 50–54. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201109010
[4] 周涛.基于反双曲正弦函数的转台伺服系统滑模控制[J].光电工程, 2015, 42(6): 39–44. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201506007
Zhou Tao. Sliding mode control of a three-axis turntable with inverse hyperbolic sine functions[J]. Opto-Electronic Engineering, 2015, 42(6): 39–44. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201506007
[5] 周涛.光电平台伺服系统自抗扰滑模控制[J].光电工程, 2012, 39(9): 35–41. http://www.cqvip.com/QK/90982A/201209/43424273.html
Zhou Tao. An active disturbance rejection and sliding mode control of an opto-electronic platform servo system[J]. Opto-Electronic Engineering, 2012, 39(9): 35–41. http://www.cqvip.com/QK/90982A/201209/43424273.html
[6] Neila M B R, Tarak D. Adaptive terminal sliding mode control for rigid robotic manipulators[J]. International Journal of Automation and Computing, 2011, 8(2): 215–220. doi: 10.1007/s11633-011-0576-2
[7] Soltanpour M R, Otadolajam P, Khooban M H. Robust control strategy for electrically driven robot manipulators: adaptive fuzzy sliding mode[J]. IET Science, Measurement & Technology, 2015, 9(3): 322–334. http://ieeexplore.ieee.org/document/7089391
[8] Ferrara A, Incremona G P. Design of an integral suboptimal second-order sliding mode controller for the robust motion control of robot manipulators[J]. IEEE Transactions on Control Systems Technology, 2015, 23(6): 2316–2325. doi: 10.1109/TCST.2015.2420624
[9] Capisani L M, Ferrara A, Magnani L. Design and experimental validation of a second-order sliding-mode motion controller for robot manipulators[J]. International Journal of Control, 2009, 82(2): 365–377. doi: 10.1080/00207170802112591
[10] 付涛, 王大镇, 弓清忠, 等.改进神经网络自适应滑模控制的机器人轨迹跟踪控制[J].大连理工大学学报, 2014, 54(5): 523–530. doi: 10.7511/dllgxb201405007
Fu Tao, Wang Dazhen, Gong Qingzhong, et al. Robot trajectory tracking control of improved neural network adaptive sliding mode control[J]. Journal of Dalian University of Technology, 2014, 54(5): 523–530. doi: 10.7511/dllgxb201405007
[11] 田慧慧, 苏玉鑫.机器人系统终端滑模重复学习轨迹跟踪控制[J].控制与决策, 2014, 29(7): 1291–1296. http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201407023.htm
Tian Huihui, Su Yuxin. Terminal sliding mode repetitive learning tracking control of robotic manipulators[J]. Control and Decision, 2014, 29(7): 1291–1296. http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201407023.htm
[12] 姜寅令, 于显利.机器人多模型反演滑模控制策略研究[J].吉林大学学报(信息科学版), 2014, 32(4): 418–422. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ccydxyxb201404015
Jiang Yinling, Yu Xianli. Multi-model back-stepping sliding mode control of robotic manipulators[J]. Journal of Jilin University (Information Science Edition), 2014, 32(4): 418–422. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ccydxyxb201404015
[13] 刘金琨.滑模变结构控制MATLAB仿真:先进控制系统设计方法[M]. 3版.北京:清华大学出版社, 2015: 143–178.
Liu Jinkun. Sliding mode control design and MATLAB simulation: the design method of advanced control system[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 143–178.
[14] 韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京:国防工业出版社, 2008: 202–206.
Han Jingqing. Active disturbance rejection control technique: the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 202–206.
[15] 周涛.基于一种新型趋近律的自适应滑模控制[J].控制与决策, 2016, 31(7): 1135–1138. http://www.cnki.com.cn/Article/CJFDTotal-KZYC201607031.htm
Zhou Tao. Adaptive sliding control based on a new reaching law[J]. Control and Decision, 2016, 31(7): 1135–1138. http://www.cnki.com.cn/Article/CJFDTotal-KZYC201607031.htm
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: