E-mail Alert
RSS
An on-orbit calibration model for wide field of view star sensor based on the vector observations
-
摘要:
针对大视场星敏感器的在轨标定问题，提出了一种基于矢量观测的检校新模型。将3个罗德里格参数代替欧拉角，作为外方位参数与畸变参数、内方位参数一起求解，简化了运算。采用仿真星图分析了模型的性能，结果表明，该模型较采用欧拉角的传统标定模型精度更高，在星点位置噪声方差为0.05 pixels的情况下，仍能准确解算出星敏感器参数，其星内角距的统计偏差为0.483″，x、y方向的残差绝对均值分别为0.019 pixels、0.016 pixels，且算法的参数设置简单，无需计算初值。将检校模型应用于ZY-3号卫星星敏感器的检校，结果表明模型可以有效提高检校的精度。建议在实际应用中采用精度更高的星点中心计算算法。
Abstract:Focused on the on-orbit calibration problem of the wide field of view star sensor, a novel calibration model based on vector observations is proposed. The model uses 3 Rodrigues parameters, instead of Euler angles, as the exterior parameters to simplify the calculation, and complete the joint solution with intrinsic parameters and third order distortion parameters. Simulation shows that it has a higher accuracy than the traditional model with Euler angles. In case of a standard deviation of 0.05 pixels star point error, the model can still accurately calculate the camera parameters and the angle error after calibration is 0.483 arcsecond, and the mean residual errors are 0.019 pixels in x direction and 0.016 pixels in y direction. Furthermore, the initial parameters are simpler and there is no need to set initial values. Its accuracy is further verified by actual star maps of ZY-3 satellite, and result shows that it can improve the calibration accuracy largely. To further improve the calibration accuracy, higher precision centroid algorithm is recommended in actual applications.
-
Key words:
- calibration /
- wide field of view star sensor /
- vector observations /
- Rodrigues parameters /
- Euler angles
-
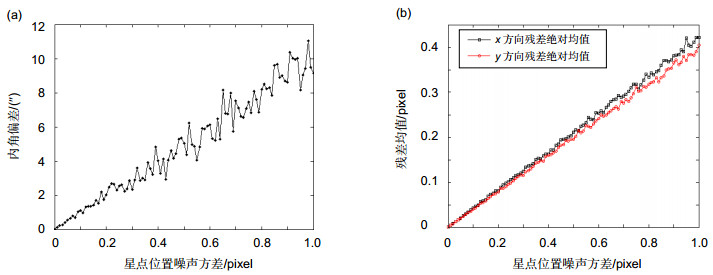
Abstract: It is urgent to develop high precision calibration model for wide field of view star sensor. It is hard to calculate the camera parameters precisely by using the traditional methods because of large optical aberration. Focused on the on-orbit calibration problem of the wide field of view star sensor, a novel calibration model based on vector observations is proposed. Rodriguez matrix is introduced into the model, and 3 Rodrigues parameters instead of Euler angles, are represented as the exterior parameters to simplify the calculation. The distortion parameters are extended to third order in order to describe the distortion more precisely. Then a joint calculation of intrinsic parameters, exterior parameters and distortion parameters are completed by the model. The performance of the model is analyzed by simulation star map, and result shows that the model has a higher accuracy than the traditional model with Euler angles. In case of a standard deviation of 0.05 pixels star point error, the model can still accurately calculate the camera parameters, and the angle error after calibration is 0.483 arcsecond, and the mean residual errors are 0.019 pixels in x direction and 0.016 pixels in y direction, respectively. Furthermore, the initial parameters are simpler and there is no need to set initial value, and no precise prior attitude information is needed in the calibration process, which will be of great convenience for the practical applications. Its accuracy is further verified by actual star maps of ZY-3 satellite, and result shows that the statistical deviation of star angle after the calibration is 2.376 arcsecond, and the mean residual errors are 0.257 pixels in x direction and 0.151 pixels in y direction respectively, which improve the calibration accuracy largely. Further research on precision analysis is conducted as well. The main procedure is as bellow: Firstly, the Gaussian white noise with the standard deviation of 0 to 1 pixel by steps of 0.01 pixels is added to the star point position, and then the mean value of precision indexes of 100 experiments is calculated. The result shows that the star extraction precision of actual star map is about 0.20 pixels to 0.33 pixels, and to further improve the calibration accuracy, higher precision centroid algorithm is recommended in actual applications.
-
-
图 1 检校后 x, y 方向上的残差.
Figure 1. The residual errors in x and y directions after calibration.
图 2 星点误差对检校精度的影响. (a)星点误差对星内角距的统计偏差的影响. (b)星点误差对的x、y方向残差的影响.
Figure 2. The star position error's influence on calibration accuracy. (a) The star position error's influence on star angle error. (b) The star position error's influence on the residual errors in x and y directions.
表 1 检校用的恒星.
Table 1. The stars for calibration.
No. x/pixel y/pixel α(°) δ(°) 1 115.166 814.399 258.11589 10.585082 2 3.734 652.121 258.66189 14.390443 3 38.602 836.754 259.65416 10.864146 4 139.553 602.085 255.78290 14.091733 5 459.400 750.400 251.45787 8.582668 6 331.474 727.382 253.50179 10.165241 7 534.690 543.263 248.15061 11.487774 8 309.088 783.887 254.41608 9.374997 9 550.415 388.333 246.35411 14.033067 10 461.188 140.669 245.47989 19.15328 11 316.533 83.949 247.55464 21.489563 12 659.203 150.599 242.01874 17.046961 13 784.641 957.652 247.72833 1.983676 14 817.723 139.217 239.11437 15.657291 15 933.545 83.001 236.54715 15.421685 
下载: 导出CSV
表 2 ZY-3号卫星星敏感器的检校结果.
Table 2. The calibration results of star sensor on ZY-3 satellite.
参数 k1 k2 k3 x0/pixel y0/pixel f/pixel 检校值 -4.656e-09 -1.444e-14 3.546e-20 526.437 512.662 2887.444
下载: 导出CSV
表 3 本文模型与传统标定模型的标定参数结果对比.
Table 3. The comparison between the calibrations proposed in the paper and the traditional model.
参数 k1 k2 k3 x0/pixel y0/pixel f/pixel 迭代次数 真实值 3e-8 1e-13 1e-20 512 512 2886.5 / 本文模型的检校值 2.807e-08 1.150e-13 -6.147e-20 511.926 512.072 2886.484 5 传统模型的检校值 2.774e-08 1.089e-13 -4.621 e-20 512.309 512.058 2886.898 5
下载: 导出CSV
表 4 本文模型与传统标定模型的标定精度对比.
Table 4. The comparison of the calibration accuracy.
检校模型 △R/(") Mean_abs(x)/pixel Mean_abs(y)/pixel 本文模型 0.483 0.019 0.016 传统模型 0.573 0.025 0.021
下载: 导出CSV
表 5 检校参数应用结果.
Table 5. The application results of the calibration parameters.
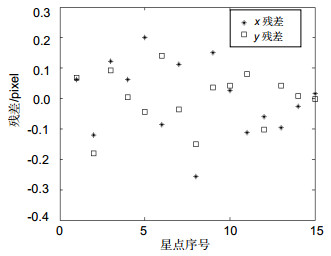
No. △R/(″) Mean_abs(x)/pixel Mean_abs(y)/pixel 1 0.507 0.021 0.022 2 0.708 0.022 0.019 3 0.755 0.015 0.018 4 0.734 0.028 0.019 5 0.662 0.022 0.020 6 0.751 0.022 0.018 7 0.632 0.022 0.018 8 0.477 0.025 0.015 9 0.698 0.022 0.024 10 0.554 0.025 0.020
下载: 导出CSV
-
[1] 孙高飞, 张国玉, 郑茹, 等.星敏感器标定方法的研究现状与发展趋势[J].长春理工大学学报(自然科学版), 2010, 33(4): 8–14. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ccgxjmjxxyxb201004003
Sun Gaofei, Zhang Guoyu, Zheng Ru, et al. Star sensor calibration research and development[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2010, 33(4): 8–14. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ccgxjmjxxyxb201004003
[2] 李欣璐, 杨进华, 张刘, 等.带有恒星自行校正的星敏感器定姿[J].光电工程, 2015, 42(2): 35–40. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201502006
Li Xinlu, Yang Jinhua, Zhang Liu, et al. Attitude determination of the star sensor with the star proper motion correction[J]. Opto-Electronic Engineering, 2015, 42(2): 35–40. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201502006
[3] Shuster M D, Chitre D M, Niebur D P. In-flight estimation of spacecraft attitude sensor accuracies and alignments[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(4): 339–343. doi: 10.2514/3.19772
[4] Ju G. Autonomous star sensing, pattern identification, and attitude determination for spacecraft: an analytical and experimental study[D]. Texas: Texas A & M University, 2001: 99–131.
[5] Samaan M A. Toward faster and more accurate star sensors using recursive centroiding and star identification[D]. Texas: Texas A&M University, 2003: 25–29.
[6] 邢飞, 董瑛, 武延鹏, 等.星敏感器参数分析与自主校正[J].清华大学学报(自然科学版), 2005, 45(11): 1484–1488. doi: 10.3321/j.issn:1000-0054.2005.11.012
Xing Fei, Dong Ying, Wu Yanpeng, et al. Star tracker parametric analysis for autonomous calibration[J]. Journal of Tsinghua University (Science and Technology), 2005, 25(11): 1484–1488. doi: 10.3321/j.issn:1000-0054.2005.11.012
[7] 郝雪涛, 张广军, 江洁.星敏感器模型参数分析与校准方法研究[J].光电工程, 2005, 32(3): 5–8. http://www.cqvip.com/QK/90982A/200503/15244757.html
Hao Xuetao, Zhang Guangjun, Jiang Jie. Star Sensor model parameter analysis and calibration method[J]. Opto-Electronic Engineering, 2005, 32(3): 5–8. http://www.cqvip.com/QK/90982A/200503/15244757.html
[8] 谢俊峰, 龚健雅, 江万寿.一种改进的恒星相机在轨检校方法[J].测绘科学, 2009, 34(2): 121–123. http://d.wanfangdata.com.cn/Periodical_chkx200902041.aspx
Xie Junfeng, Gong Jianya, Jiang Wanshou. An improved on-orbit calibration method for stellar camera[J]. Science of Surveying and Mapping, 2009, 34(2): 121–123. http://d.wanfangdata.com.cn/Periodical_chkx200902041.aspx
[9] 申娟, 张广军, 魏新国.基于卡尔曼滤波的星敏感器在轨校准方法[J].航空学报, 2010, 31(6): 1220–1224. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201006017
Shen Juan, Zhang Guangjun, Wei Xinguo. On-orbit calibration of star sensor based on kalman filter[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1220–1224. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201006017
[10] 原玉磊. 鱼眼相机恒星法检校技术研究[D]. 郑州: 解放军信息工程大学, 2012: 206–214.
Yuan Yulei. Research on fish-eye camera stellar calibration technology[D]. Zhengzhou: PLA Information Engineering Uni-versity, 2012: 206–214.
[11] Wei Xinguo, Zhang Guangjun, Fan Qiaoyun, et al. Star sensor calibration based on integrated modelling with intrinsic and extrinsic parameters[J]. Measurement, 2014, 55: 117–125. doi: 10.1016/j.measurement.2014.04.026
[12] Wang Shuang, Geng Yunhai, Jin Rongyu. A novel error model of optical systems and an on-orbit calibration method for star sensors[J]. Sensors, 2015, 15(12): 31428–31441. doi: 10.3390/s151229863
[13] Xiong Kun, Wei Xinguo, Zhang Guangjun, et al. High-accuracy star sensor calibration based on intrinsic and extrinsic parameter decoupling[J]. Optical Engineering, 2015, 54(3): 034112. doi: 10.1117/1.OE.54.3.034112
[14] 詹银虎, 郑勇, 张超, 等.鱼眼相机矢量观测检校模型及其应用[J].测绘学报, 2016, 45(3): 332–338. doi: 10.11947/j.AGCS.2016.20150080
Zhan Yinhu, Zheng Yong, Zhang Chao, et al. Fish-eye camera calibration model based on vector observations and its application[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 332–338. doi: 10.11947/j.AGCS.2016.20150080
[15] 曾文宪, 陶本藻.三维坐标转换的非线性模型[J].武汉大学学报•信息科学版, 2003, 28(5): 566–568. http://www.docin.com/p-352861358.html
Zeng Wenxian, Tao Benzao. Non-linear adjustment model of three-dimensional coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 566–568. http://www.docin.com/p-352861358.html
[16] 原玉磊, 蒋理兴, 刘灵杰.罗德里格矩阵在坐标系转换中的应用[J].测绘科学, 2010, 35(2): 178–179, 119. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chkx201002061
Yuan Yulei, Jiang Lixing, Liu Lingjie. Applications of Lodrigues matrix in coordinates transformation[J]. Science of Surveying and Mapping, 2010, 35(2): 178–179, 119. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chkx201002061
-
点击扫一扫
图(2)
表(5)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
