E-mail Alert
RSS
Integrating hierarchical semantic networks with physical models for MRI reconstruction
-
摘要
为缓解核磁共振成像(MRI)中的长时间采集困境，大数据驱动下的算法与模型融合已成为实现高质量MRI重建的重要手段。然而，现有方法多集中于视觉特征的提取，忽视稳健重建所需的深层次语义信息。为此，提出一种联合分层语义网络与物理模型网络的模型驱动架构，旨在提升重建性能的同时维持计算效率。该架构包含四个关键模块：上下文提取模块，用于捕获丰富的上下文特征以降低背景干扰；多尺度聚合模块，通过整合多尺度信息保留粗细解剖细节；语义图推理模块，建模语义关系以增强组织区分度并抑制伪影；双尺度注意力模块，强化不同细节层级上的关键特征表达。这种层次化且语义感知的设计有效减少混叠伪影，并显著提升图像保真度。实验结果表明，在涵盖不同采样率的多样化数据集上，所提方案在定量评估和视觉质量方面均优于现有方法。例如，在IXI数据集四倍径向加速的实验中，所提方法的峰值信噪比达到48.15 dB，平均领先最新的对比算法1.00 dB，同时实现更高的加速比并保持可靠的图像重建效果。
Abstract
To address the challenge of prolonged acquisition times in magnetic resonance imaging (MRI), data-driven algorithms and the model integration have emerged as crucial approaches for achieving high-quality MRI reconstruction. However, existing methods predominantly focus on visual feature extraction while neglecting deep semantic information critical for robust reconstruction. To bridge this gap, this study proposes a model-driven architecture that synergistically combines hierarchical semantic networks with physical model networks, aiming to enhance reconstruction performance while maintaining computational efficiency. The architecture comprises four core modules: a context extraction module to capture rich contextual features and mitigate background interference; a multi-scale aggregation module integrating multi-scale information to preserve coarse-to-fine anatomical details; a semantic graph reasoning module to model semantic relationships for improved tissue differentiation and artifact suppression; a dual-scale attention module to enhance critical feature representation across different detail levels. This hierarchical and semantic-aware design effectively reduces aliasing artifacts and significantly improves image fidelity. Experimental results demonstrate that the proposed method outperforms state-of-the-art approaches in both quantitative metrics and visual quality across diverse datasets with varying sampling rates. For instance, in 4× radial acceleration experiments on the IXI dataset, our approach achieved a peak signal-to-noise ratio (PSNR) of 48.15 dB, surpassing the latest comparison algorithms by approximately 1.00 dB on average, while enabling higher acceleration rates and maintaining reliable reconstruction outcomes.
-
Key words:
- MRI acceleration /
- contextual information /
- model-guided approaches /
- semantic reasoning
-
Overview
Overview: Magnetic resonance imaging (MRI) is a critical tool in biomedical research and clinical practice due to its exceptional soft tissue contrast and non-invasive, radiation-free imaging capabilities. However, its prolonged acquisition times (resulting from sequential k-space sampling) limit its efficiency in clinical workflows, patient comfort, and applicability in time-sensitive or large-scale screening scenarios. To address this challenge, undersampled k-space reconstruction techniques, particularly compressive sensing (CS), have been widely adopted. While CS leverages signal sparsity and prior knowledge to preserve image quality, aggressive undersampling often introduces aliasing artifacts, which complicates accurate reconstruction. Traditional model-driven methods, which rely on handcrafted priors (such as, sparsity, total variation, low-rank constraints), struggle to adapt to the complexity of real-world MRI data distributions. Meanwhile, deep learning approaches, despite their success in feature learning, often neglect physical degradation mechanisms. Additionally, they fail to capture semantic-level features necessary for distinguishing anatomical structures and suppressing artifacts.
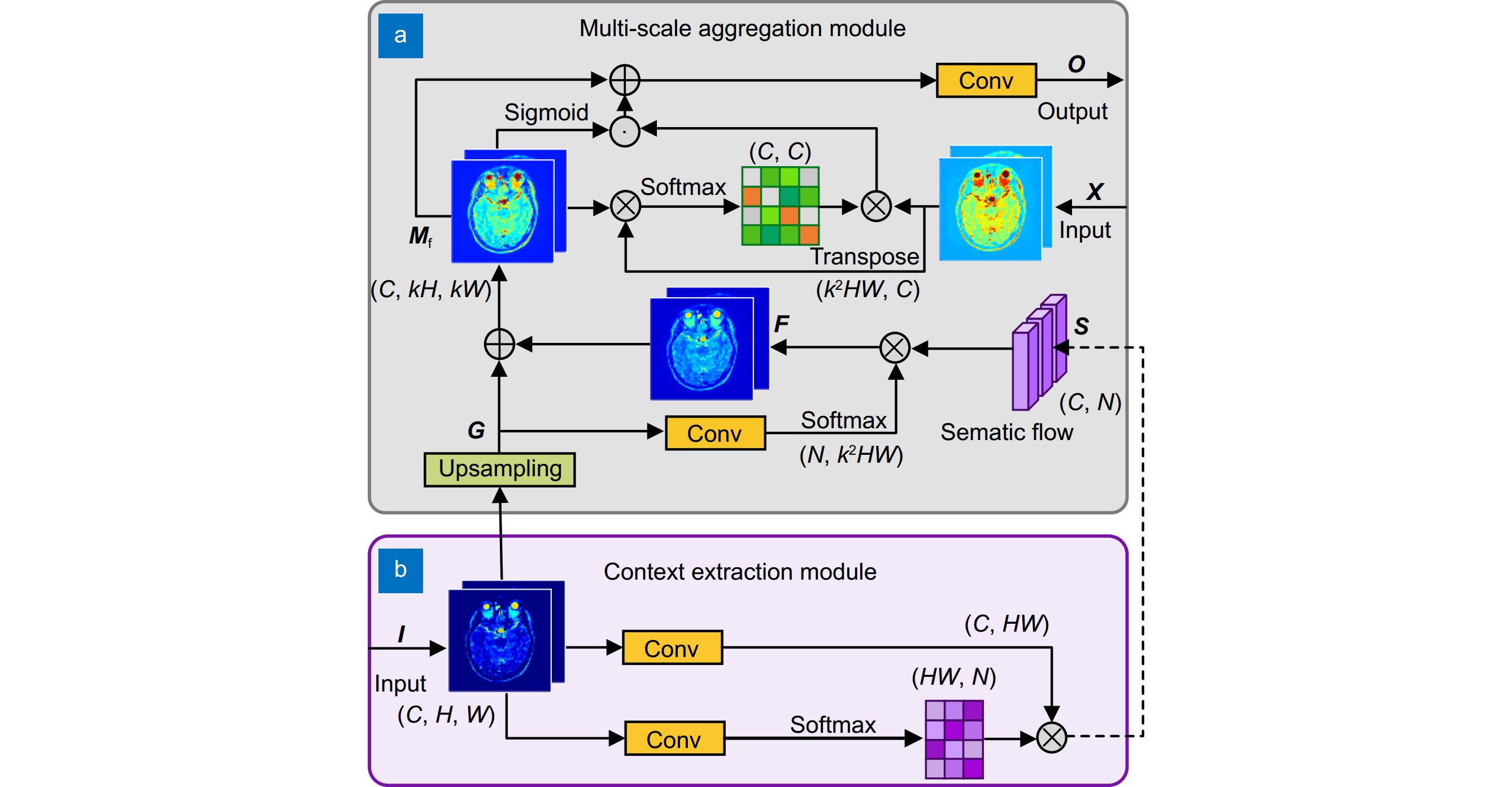
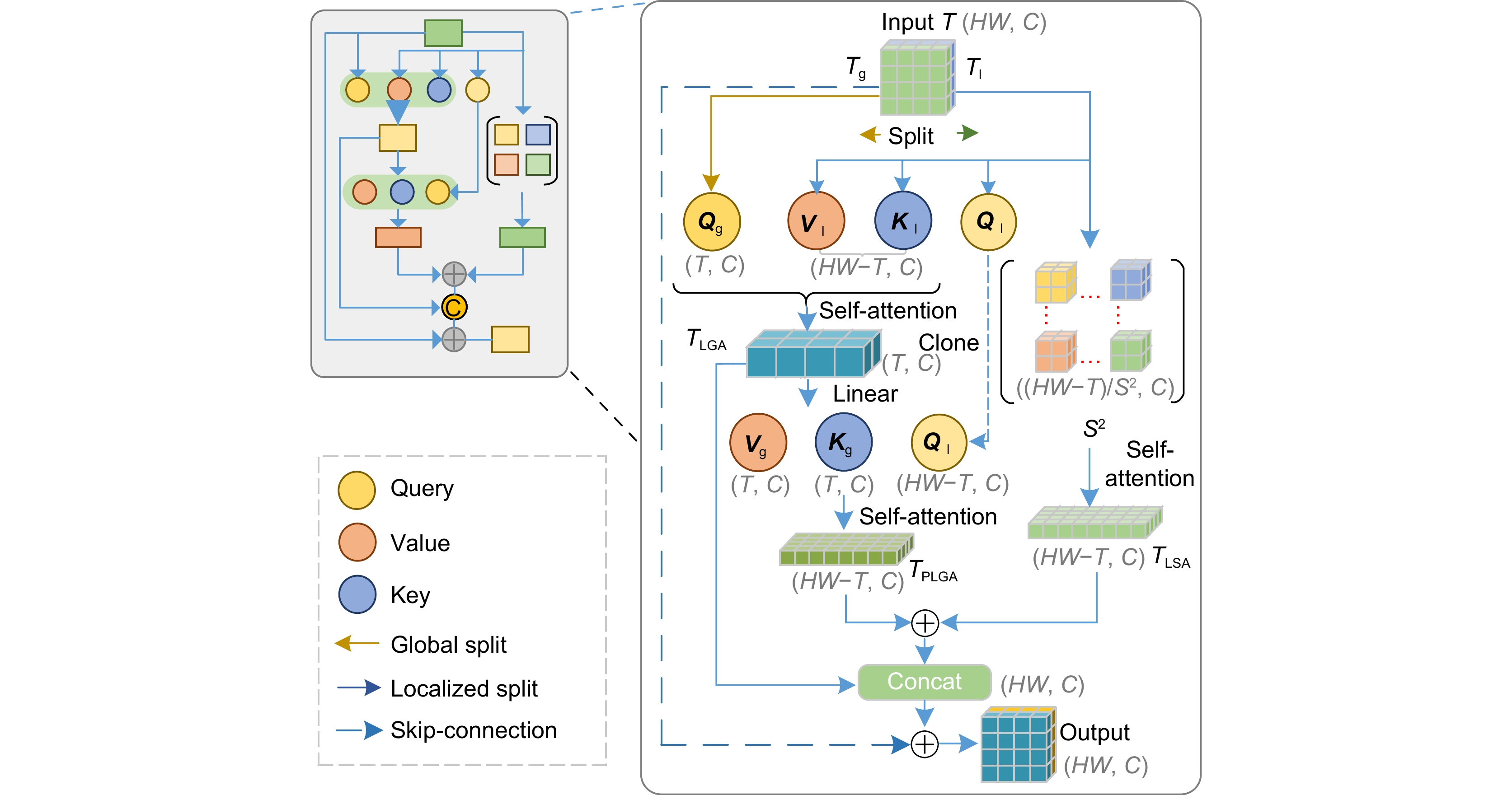
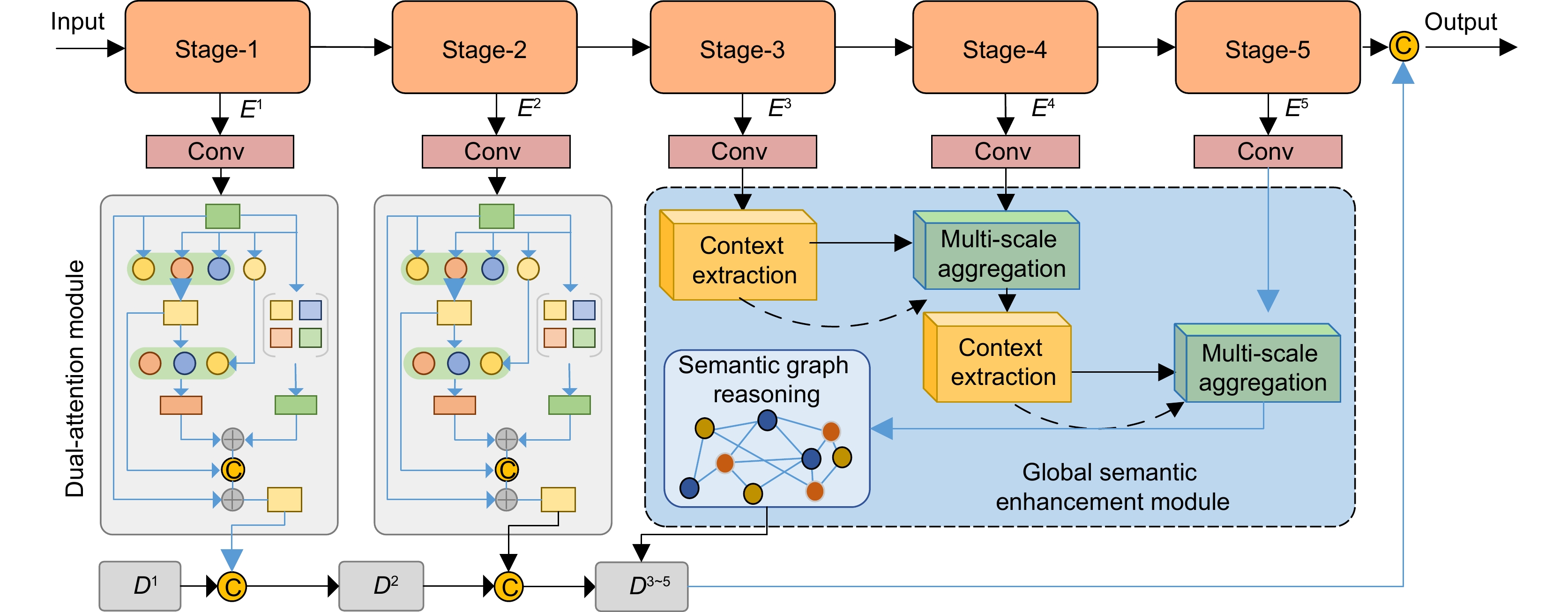
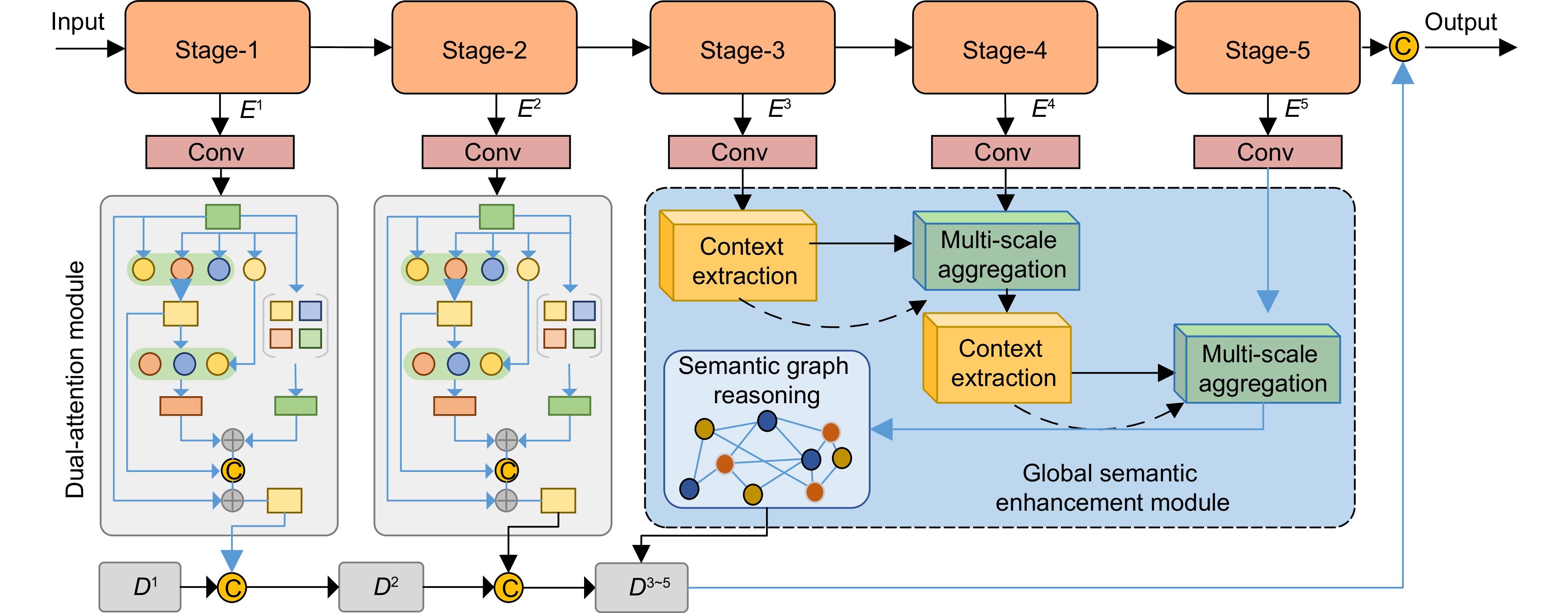
Recent efforts aim to bridge model-driven and data-driven paradigms, but existing methods remain constrained by rigid feature representations, inadequate multi-scale context integration, and insufficient semantic reasoning. For example, the prior models prioritize shallow visual features over deeper anatomical semantics, limiting their ability to generalize across diverse tissue types and reconstruct high-fidelity images under extreme undersampling. To address these limitations, this paper proposes a physics-informed hierarchical semantic network (PHSN), an innovative framework that unifies physical signal principles with semantic-aware deep learning. The architecture integrates four core modules: 1) a context extraction module to capture spatial dependencies across scales; 2) a scale-aggregation module for hierarchical feature fusion; 3) a semantic graph reasoning module to model tissue-specific relationships and enhance artifact suppression via graph-based inference; 4) a dual-scale attention module to prioritize anatomical details at both coarse (global structure) and fine (local tissue) spatial levels. The overall framework is illustrated in Fig. 7.
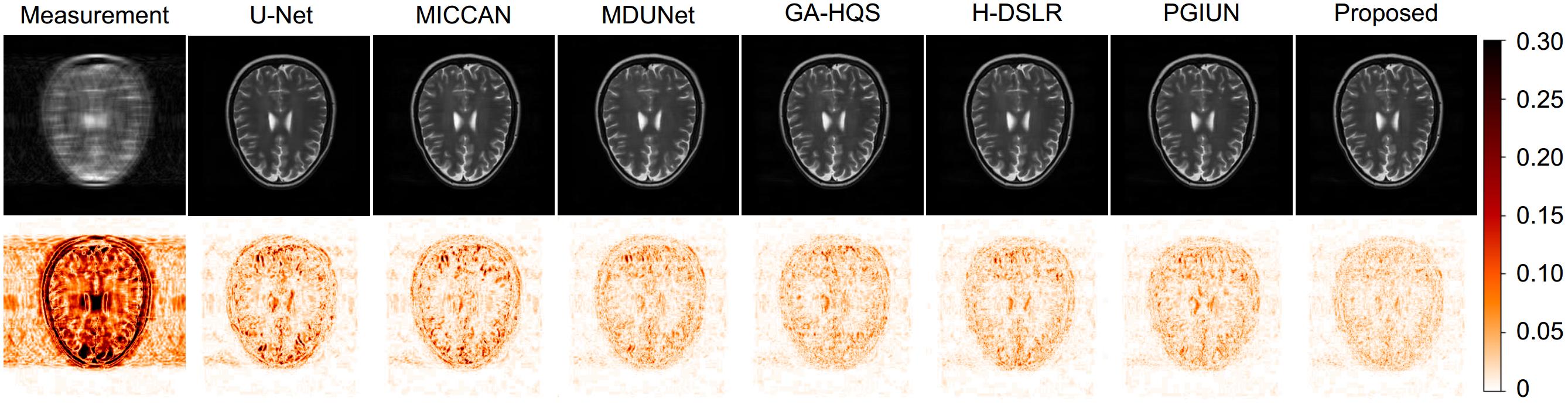
By embedding physical k-space sampling constraints into hierarchical feature learning and explicitly modeling semantic relationships, PHSN achieves robust reconstruction under high acceleration factors (e.g., 8-fold) while preserving diagnostic image fidelity. Comprehensive experiments on diverse datasets (e.g., IXI) demonstrate that the proposed method outperforms state-of-the-art approaches in suppressing artifacts, maintaining anatomical accuracy, and balancing acceleration efficiency with clinical reliability. The framework’s hierarchical design enables adaptive feature optimization across scales, effectively mitigating aliasing artifacts and improving visibility of complex anatomical structures. This study advances MRI reconstruction by integrating interpretable physics-based constraints with data-driven semantic understanding, offering a pathway toward faster, higher-quality imaging for clinical and research applications.
-
-
图 2 网络组成模块。(a) 多尺度聚合模块；(b) 上下文提取模块
Figure 2. Network composition module. (a) Multi-scale aggregation module; (b) Context extraction module
图 5 IXI数据集上使用随机掩膜进行8×加速下的重建结果
Figure 5. Reconstruction results using random masking for 8× acceleration on the IXI dataset
图 6 在IXI数据集上使用随机掩膜进行4倍和8倍加速下的验证损失
Figure 6. Validation loss using random masking for 4-fold and 8-fold acceleration on IXI dataset
表 1 径向、随机、等分三种掩码在4
$ \times $ $ \times $ Table 1. Numerical results under three kinds of masks: radial, random and equidistant, and acceleration rates of 4× and 8×
Dataset Ratio Mask Metric U-Net MICCAN MDUNet GA-HQS H-DSLR PGIUN Ours
IXI4× Radial PSNR 34.04 41.62 45.87 45.28 45.30 47.08 48.15 SSIM 0.971 0.990 0.992 0.993 0.993 0.995 0.996 Random PSNR 31.18 35.42 37.45 37.07 35.98 37.97 39.12 SSIM 0.953 0.972 0.978 0.980 0.981 0.984 0.989 Equispaced PSNR 30.12 33.48 34.96 35.46 33.63 35.50 35.65 SSIM 0.944 0.964 0.968 0.977 0.965 0.977 0.978 8× Radial PSNR 29.74 32.82 35.48 34.13 34.50 36.26 36.42 SSIM 0.934 0.958 0.977 0.968 0.971 0.980 0.981 Random PSNR 29.05 31.68 34.02 33.58 31.96 34.07 34.11 SSIM 0.931 0.949 0.959 0.962 0.955 0.964 0.968 Equispaced PSNR 27.90 29.98 31.33 31.29 29.80 31.63 31.75 SSIM 0.921 0.939 0.951 0.940 0.938 0.943 0.953 fastMRI 4× Radial PSNR 28.59 30.11 30.18 30.82 30.22 30.96 31.09 SSIM 0.828 0.861 0.879 0.873 0.865 0.873 0.881 Random PSNR 27.86 29.03 30.09 39.98 29.01 30.01 30.15 SSIM 0.810 0.830 0.843 0.848 0.831 0.849 0.851 Equispaced PSNR 27.16 28.11 28.53 28.51 28.23 28.53 28.62 SSIM 0.779 0.795 0.809 0.807 0.786 0.803 0.826 8× Radial PSNR 26.42 27.41 28.01 27.91 27.28 28.01 28.16 SSIM 0.723 0.745 0.764 0.789 0.741 0.791 0.816 Random PSNR 26.38 27.26 27.65 27.79 27.04 27.75 27.81 SSIM 0.754 0.771 0.739 0.781 0.762 0.792 0.803 Equispaced PSNR 26.21 26.96 27.31 27.33 26.84 27.29 27.34 SSIM 0.743 0.745 0.747 0.767 0.752 0.768 0.783 
下载: 导出CSV
表 2 计算复杂度和运行时间分析结果
Table 2. Computational complexity and runtime analysis results
Method Params./M Flops/G Inference/ms U-Net 7.756 11.2 21 MICCAN 2.622 36.6 34 MDUNet 1.800 90.7 49 GA-HQS 6.100 120.2 63 H-DSLR 1.650 85.3 44 PGIUN 1.250 74.8 53 Ours 1.530 86.3 57
下载: 导出CSV
表 3 多线圈重建实验结果
Table 3. Multi-coil reconstruction contrast results
Ratio Mask Method PSNR/dB SSIM NRMSE $ 4 \times $ Equispaced U-Net 25.78 0.877 0.763 H-DSLR 31.54 0.942 0.212 MoDL 29.12 0.919 0.304 PGIUN 30.01 0.926 0.307 Ours 32.70 0.958 0.190 $ 6 \times $ Random U-Net 32.35 0.946 0.222 H-DSLR 40.84 0.986 0.073 MoDL 39.63 0.977 0.081 PGIUN 38.50 0.976 0.095 Ours 41.35 0.990 0.062
下载: 导出CSV
表 4 模块消融实验结果
Table 4. Module ablation experiment results
No. Contextual extraction Multiscale aggregation Semantic graph reasoning Dual-scale attention IXI Complexity PSNR/dB SSIM Param./M FLOPs/G 1 √ 30.01 0.901 4.20 55.30 2 √ 30.25 0.912 5.10 66.12 3 √ √ 31.10 0.921 6.50 72.45 4 √ √ 31.95 0.931 6.80 80.32 5 √ √ 32.50 0.940 7.15 85.20 6 √ √ √ 33.75 0.950 7.85 95.00 7 √ √ √ √ 35.65 0.976 8.17 102.12
下载: 导出CSV
-
参考文献
[1] 张子建, 王天义, 徐欣, 等. 偏振激光照明对多层薄膜结构成像对比度影响[J]. 光电工程, 2023, 50(7): 230089. doi: 10.12086/oee.2023.230089
Zhang Z J, Wang T Y, Xu X, et al. Effect of polarized laser illumination on imaging contrast of multilayer thin film structure[J]. Opto-Electron Eng, 2023, 50(7): 230089. doi: 10.12086/oee.2023.230089
[2] 张子建, 徐欣, 王吉祥, 等. 光片荧光显微镜研究进展[J]. 光电工程, 2023, 50(5): 220045. doi: 10.12086/oee.2023.220045
Zhang Z J, Xu X, Wang J X, et al. Review of the development of light sheet fluorescence microscopy[J]. Opto-Electron Eng, 2023, 50(5): 220045. doi: 10.12086/oee.2023.220045
[3] Abraham E, Zhou J X, Liu Z W. Speckle structured illumination endoscopy with enhanced resolution at wide field of view and depth of field[J]. Opto-Electron Adv, 2023, 6(7): 220163. doi: 10.29026/oea.2023.220163
[4] 严福华. 深度学习MRI重建算法的临床应用和发展前景[J]. 磁共振成像, 2023, 14(5): 8−10. doi: 10.12015/issn.1674-8034.2023.05.002
Yan F H. The clinical application and development prospect of deep learning MRI reconstruction algorithm[J]. Chin J Magn Reson Imaging, 2023, 14(5): 8−10. doi: 10.12015/issn.1674-8034.2023.05.002
[5] Lustig M, Donoho D, Pauly J M. Sparse MRI: the application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6): 1182−1195. doi: 10.1002/mrm.21391
[6] Liu J S, Qin C, Yaghoobi M. High-fidelity MRI reconstruction using adaptive spatial attention selection and deep data consistency prior[J]. IEEE Trans Comput Imaging, 2023, 9: 298−313. doi: 10.1109/TCI.2023.3258839
[7] Sandino C M, Cheng J Y, Chen F Y, et al. Compressed sensing: from research to clinical practice with deep neural networks: shortening scan times for magnetic resonance imaging[J]. IEEE Signal Process Mag, 2020, 37(1): 117−127. doi: 10.1109/MSP.2019.2950433
[8] Goujon A, Neumayer S, Bohra P, et al. A neural-network-based convex regularizer for inverse problems[J]. IEEE Trans Comput Imaging, 2023, 9: 781−795. doi: 10.1109/TCI.2023.3306100
[9] Hou R Z, Li F, Zhang G X. Truncated residual based plug-and-play ADMM algorithm for MRI reconstruction[J]. IEEE Trans Comput Imaging, 2022, 8: 96−108. doi: 10.1109/TCI.2022.3145187
[10] Xie J F, Zhang J, Zhang Y B, et al. PUERT: probabilistic under-sampling and explicable reconstruction network for CS-MRI[J]. IEEE J Sel Top Signal Process, 2022, 16(4): 737−749. doi: 10.1109/JSTSP.2022.3170654
[11] Li P, Chen W G, Ng M K. Compressive total variation for image reconstruction and restoration[J]. Comput Math Appl, 2020, 80(5): 874−893. doi: 10.1016/j.camwa.2020.05.006
[12] Xu H H, Jiang J W, Feng Y C, et al. Tensor completion via hybrid shallow-and-deep priors[J]. Appl Intell, 2023, 53(13): 17093−17114. doi: 10.1007/s10489-022-04331-4
[13] Sandilya M, Nirmala S R. Compressed sensing MRI reconstruction using convolutional dictionary learning and Laplacian prior[M]//Senjyu T, Mahalle P, Perumal T, et al. IOT with Smart Systems: Proceedings of ICTIS 2021, Volume 2. Singapore: Springer, 2022: 661–669. https://doi.org/10.1007/978-981-16-3945-6_65.
[14] Zhang X M, Ma J W, Zhang H. Curvature-regularized manifold for seismic data interpolation[J]. Geophysics, 2023, 88(1): WA37−WA53. doi: 10.1190/geo2022-0002.1
[15] Jiang J W, He Z H, Quan Y Q, et al. PGIUN: physics-guided implicit unrolling network for accelerated MRI[J]. IEEE Trans Comput Imaging, 2024, 10: 1055−1068. doi: 10.1109/TCI.2024.3422840
[16] Pramanik A, Aggarwal H K, Jacob M. Deep generalization of structured low-rank algorithms (Deep-SLR)[J]. IEEE Trans Med Imaging, 2020, 39(12): 4186−4197. doi: 10.1109/TMI.2020.3014581
[17] Chen Y W, He Y, Ye H, et al. Unified deep learning model for predicting fundus fluorescein angiography image from fundus structure image[J]. J Innov Opt Health Sci, 2024, 17(3): 2450003. doi: 10.1142/S1793545824500032
[18] Geng C H, Jiang M F, Fang X, et al. HFIST-Net: high-throughput fast iterative shrinkage thresholding network for accelerating MR image reconstruction[J]. Comput Methods Programs Biomed, 2023, 232: 107440. doi: 10.1016/j.cmpb.2023.107440
[19] Zhang J, Zhang Z Y, Xie J F, et al. High-throughput deep unfolding network for compressive sensing MRI[J]. IEEE J Sel Top Signal Process, 2022, 16(4): 750−761. doi: 10.1109/JSTSP.2022.3170227
[20] Arabi H, Zeng G D, Zheng G Y, et al. Novel adversarial semantic structure deep learning for MRI-guided attenuation correction in brain PET/MRI[J]. Eur J Nucl Med Mol Imaging, 2019, 46(13): 2746−2759. doi: 10.1007/s00259-019-04380-x
[21] Panić M, Aelterman J, Crnojević V, et al. Sparse recovery in magnetic resonance imaging with a Markov random field prior[J]. IEEE Trans Med Imaging, 2017, 36(10): 2104−2115. doi: 10.1109/TMI.2017.2743819
[22] Ke Z W, Huang W Q, Cui Z X, et al. Learned low-rank priors in dynamic MR imaging[J]. IEEE Trans Med Imaging, 2021, 40(12): 3698−3710. doi: 10.1109/TMI.2021.3096218
[23] Abdullah S, Arif O, Mehmud T, et al. Compressed sensing MRI reconstruction using low dimensional manifold model[C]//Proceedings of 2019 IEEE EMBS International Conference on Biomedical & Health Informatics, 2019: 1–4. https://doi.org/10.1109/BHI.2019.8834498.
[24] Wang J, Zong Y, He Y, et al. Domain adaptation-based automated detection of retinal diseases from optical coherence tomography images[J]. Curr Eye Res, 2023, 48(9): 836−842. doi: 10.1080/02713683.2023.2212878
[25] Jethi A K, Murugesan B, Ram K, et al. Dual-Encoder-Unet for fast MRI reconstruction[C]//Proceedings of 2020 IEEE 17th International Symposium on Biomedical Imaging Workshops, 2020: 1–4. https://doi.org/10.1109/ISBIWorkshops50223.2020.9153453.
[26] Lee D, Yoo J, Tak S, et al. Deep residual learning for accelerated MRI using magnitude and phase networks[J]. IEEE Trans Biomed Eng, 2018, 65(9): 1985−1995. doi: 10.1109/TBME.2018.2821699
[27] 王钟贤, 王志文, 张中洲, 等. PFONet: 一种用于加速MRI的渐进式聚焦导向双域重建网络[J]. 四川大学学报(自然科学版), 2024, 61(5): 053004. doi: 10.19907/j.0490-6756.2024.053004
Wang Z X, Wang Z W, Zhang Z Z, et al. PFONet: a progressive focus-oriented dual-domain reconstruction network for accelerated MRI[J]. J Sichuan Univ (Nat Sci Ed), 2024, 61(5): 053004. doi: 10.19907/j.0490-6756.2024.053004
[28] Korkmaz Y, Yurt M, Dar S U H, et al. Deep MRI reconstruction with generative vision transformers[C]//Proceedings of the 4th International Workshop Machine Learning for Medical Image Reconstruction, 2021: 54–64. https://doi.org/10.1007/978-3-030-88552-6_6.
[29] Aggarwal H K, Mani M P, Jacob M. MoDL: model-based deep learning architecture for inverse problems[J]. IEEE Trans Med Imaging, 2019, 38(2): 394−405. doi: 10.1109/TMI.2018.2865356
[30] Yang G, Zhang L, Zhou M, et al. Model-guided multi-contrast deep unfolding network for MRI super-resolution reconstruction[C]//Proceedings of the 30th ACM International Conference on Multimedia, 2022: 3974–3982.
[31] Zhang X H, Lian Q S, Yang Y C, et al. A deep unrolling network inspired by total variation for compressed sensing MRI[J]. Digital Signal Process, 2020, 107: 102856. doi: 10.1016/j.dsp.2020.102856
[32] Huang Q Y, Yang D, Wu P X, et al. MRI reconstruction via cascaded channel-wise attention network[C]//Proceedings of 2019 IEEE 16th International Symposium on Biomedical Imaging, 2019: 1622–1626. https://doi.org/10.1109/ISBI.2019.8759423.
[33] Jiang J W, Wu J, Quan Y Q, et al. Memory-augmented dual-domain unfolding network for MRI reconstruction[C]//Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing, 2024: 1651–1655. https://doi.org/10.1109/ICASSP48485.2024.10446091.
[34] Jiang J W, Chen J C, Xu H H, et al. GA-HQS: MRI reconstruction via a generically accelerated unfolding approach[C]//Proceedings of 2023 IEEE International Conference on Multimedia and Expo, 2023: 186–191. https://doi.org/10.1109/ICME55011.2023.00040.
[35] Xin B Y, Phan T, Axel L, et al. Learned half-quadratic splitting network for MR image reconstruction[C]//Proceedings of the 5th International Conference on Medical Imaging with Deep Learning, 2022: 1403–1412.
[36] Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM J Imaging Sci, 2009, 2(1): 183−202. doi: 10.1137/080716542
[37] Chen J C, Jiang J W, Wu F, et al. Null space matters: range-null decomposition for consistent multi-contrast MRI reconstruction[C]//Proceedings of the 38th AAAI Conference on Artificial Intelligence, 2024: 1081–1090. https://doi.org/10.1609/aaai.v38i2.27869.
[38] Li Y, Gupta A. Beyond grids: learning graph representations for visual recognition[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018: 9245–9255.
[39] Cheng S, Wang Y Z, Huang H B, et al. NBNet: noise basis learning for image denoising with subspace projection[C]//Proceedings of 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021: 4896–4906. https://doi.org/10.1109/CVPR46437.2021.00486.
[40] Zbontar J, Knoll F, Sriram A, et al. fastMRI: an open dataset and benchmarks for accelerated MRI[Z]. arXiv: 1811.08839, 2018. https://doi.org/10.48550/arXiv.1811.08839.
[41] Uecker M, Lai P, Murphy M J, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA[J]. Magn Reson Med, 2014, 71(3): 990−1001. doi: 10.1002/mrm.24751
-
访问统计
点击扫一扫
图(7)
表(4)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
