E-mail Alert
RSS
Repetitive-control-based high-frequency disturbance suppression method in tip-tilt correction
-
摘要
扰动抑制尤其是超过闭环带宽外的高频扰动抑制是实现倾斜校正系统高精度稳定控制的核心。重复控制具有周期性的轨迹跟踪和扰动抑制的良好性能，应用于高精度系统的稳定控制。对倾斜校正系统的高频扰动抑制问题进行分析，并研究基于重复控制的高频扰动抑制性能。针对传统重复控制器存在的固有频率漂移和水床放大问题，研究设计一种基于Youla参数化的梳状重复控制器来抑制超过闭环带宽外的高频扰动。针对重复控制阶次取整数时仅对特定频率点有效，尤其在大部分高频区域会因扰动波动和不确定导致控制器失效的问题，优化设计一种全通型的分数阶延时滤波器用在倾斜校正系统中抑制可至Nyquist频率的任意频率点的高频扰动。最后，针对难以抑制的非周期结构振动抑制问题，设计并行式重复控制方案并讨论该方案在应对多个非周期扰动抑制时的鲁棒稳定性和有效性。
Abstract
Disturbance suppression, especially high-frequency disturbance suppression beyond the closed-loop bandwidth, is the core of realizing high-precision stability control for tip-tilt correction systems. Repetitive control has good performance of periodic trajectory tracking and disturbance suppression, which is applied to the stability control of high-precision systems. The high-frequency disturbance suppression problem of the tip-tilt correction system is analyzed in this paper, and the performance of high-frequency disturbance suppression based on repetitive control is summarized. To solve the problems of natural frequency drift and waterbed amplification in traditional repetitive controllers, a comb-like repetitive controller based on Youla parameterization is designed to suppress high-frequency disturbances beyond the closed-loop bandwidth. In order to solve the problem that the integer-order repetitive control is only effective for specific frequency points, especially in most high frequency regions, the controller will fail due to disturbance fluctuations and uncertainty, an all-pass frit-order delay filter is optimized to suppress the high frequency disturbance at any frequency point up to Nyquist frequency in the tip-tilt correction system. Finally, a parallel repetitive control scheme is designed to suppress the vibration of aperiodic structures which is difficult to suppress, and its robust stability and effectiveness are discussed.
-
Overview
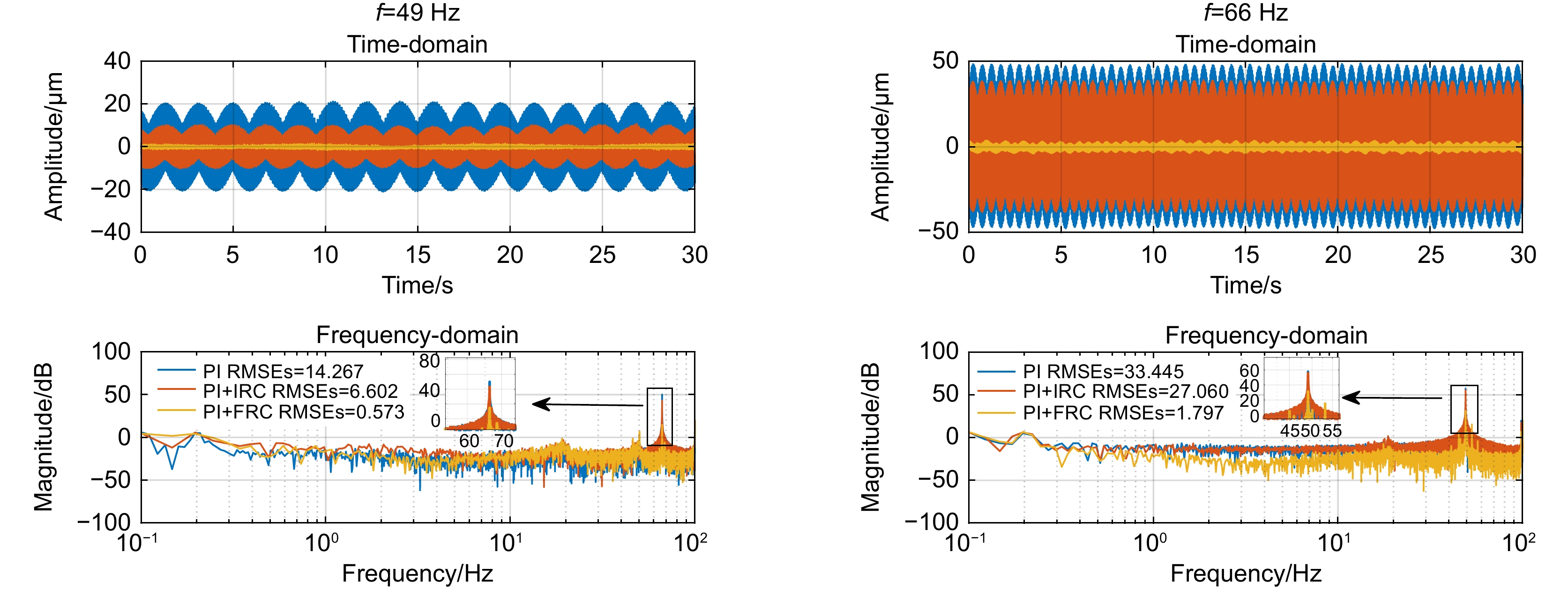
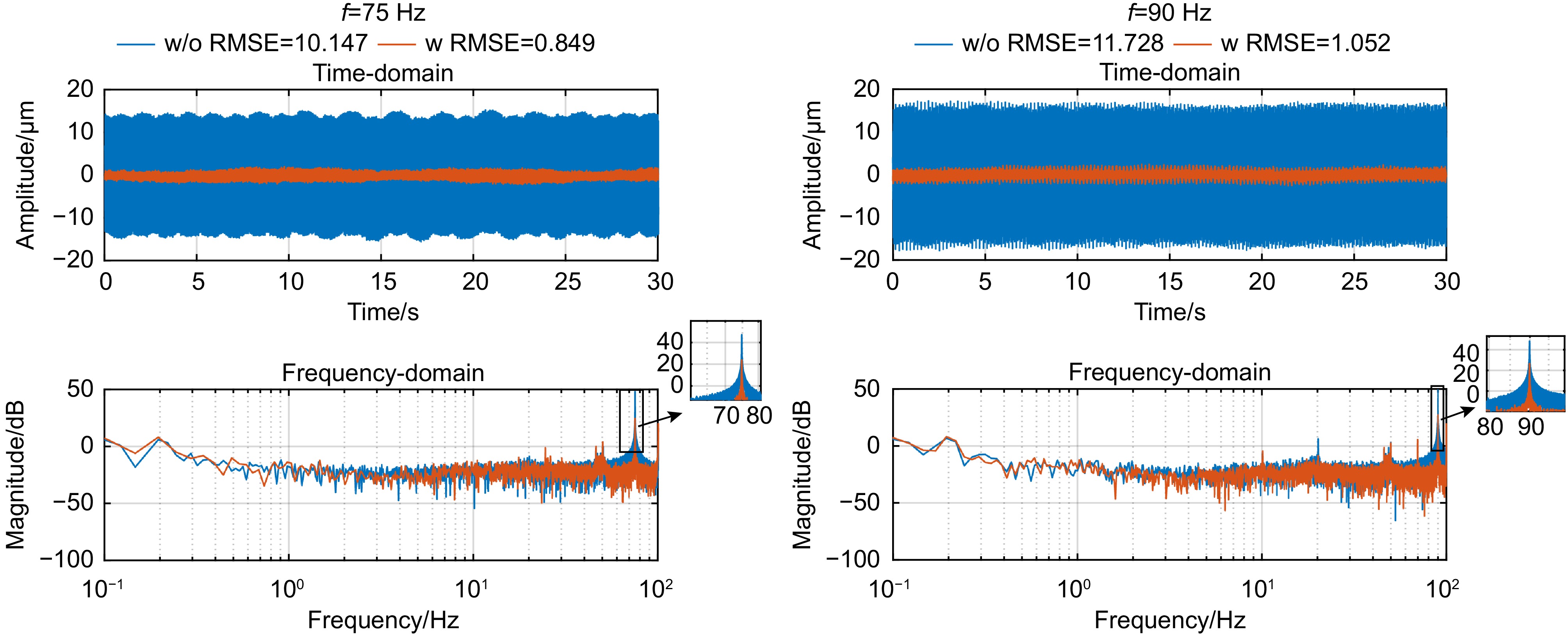
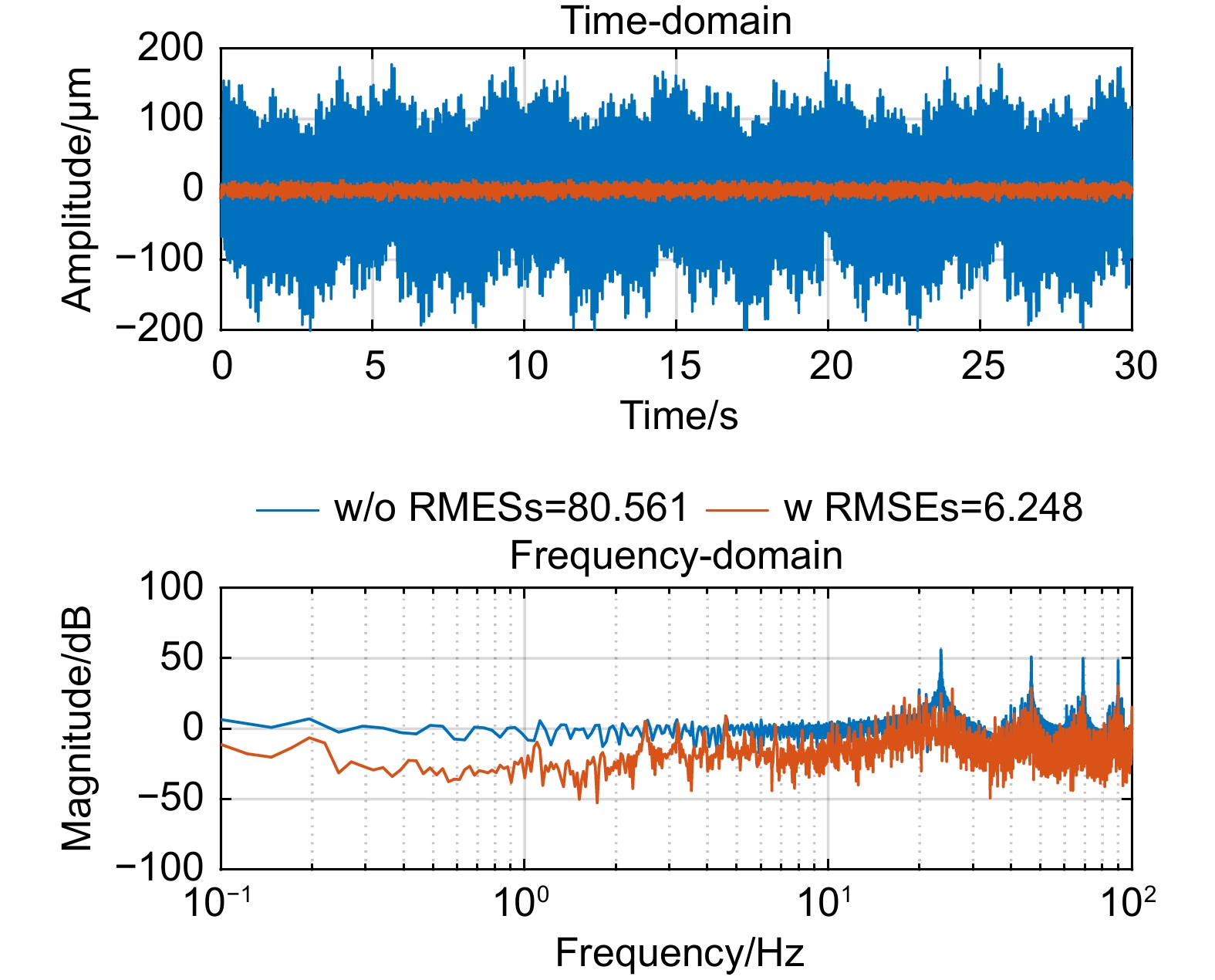
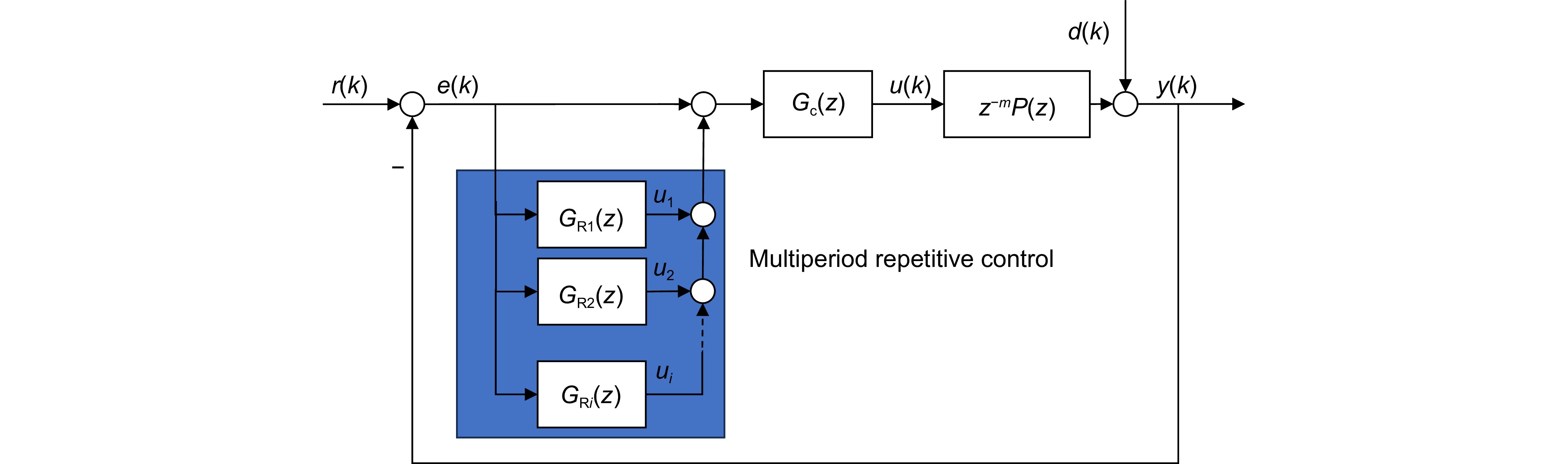
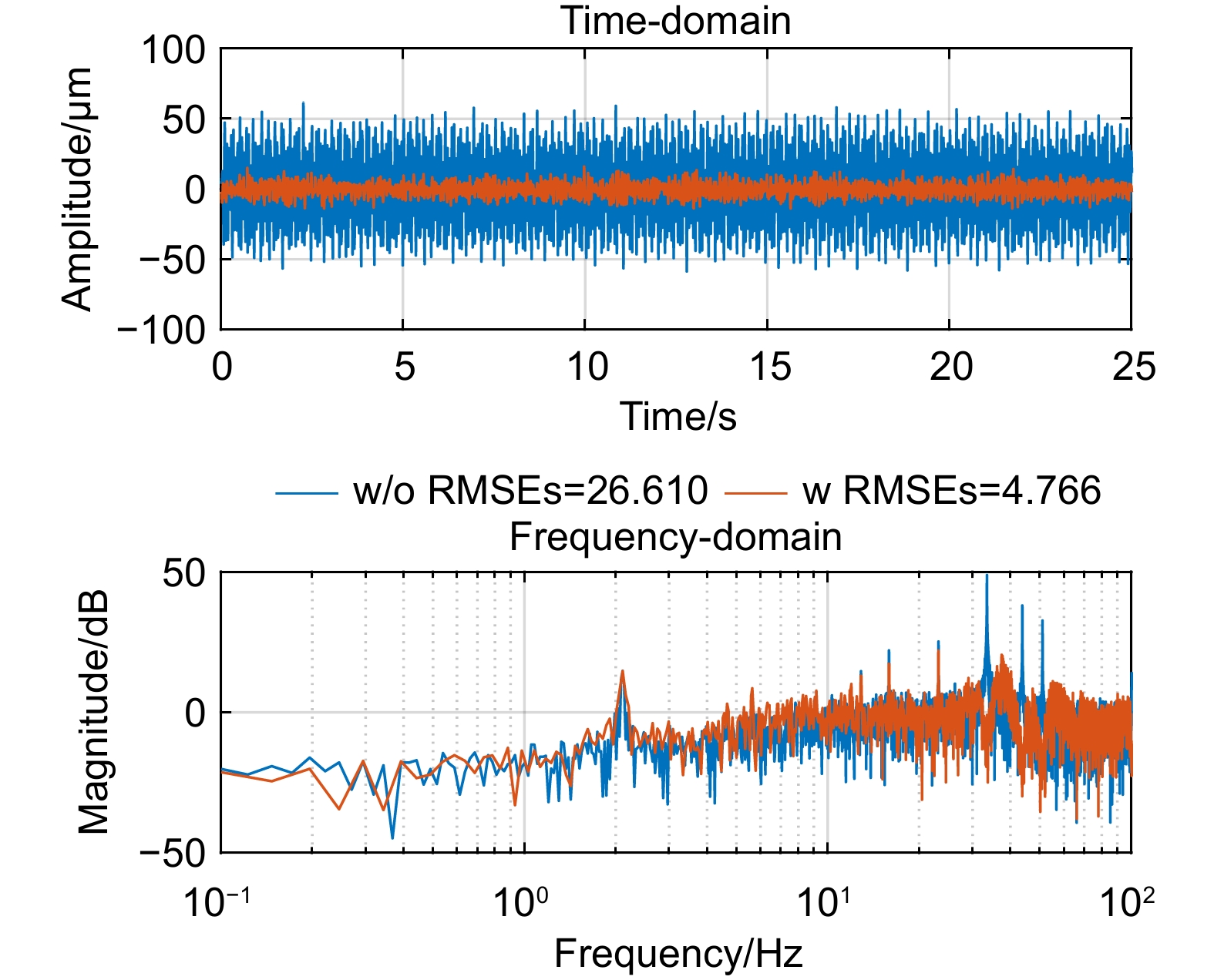
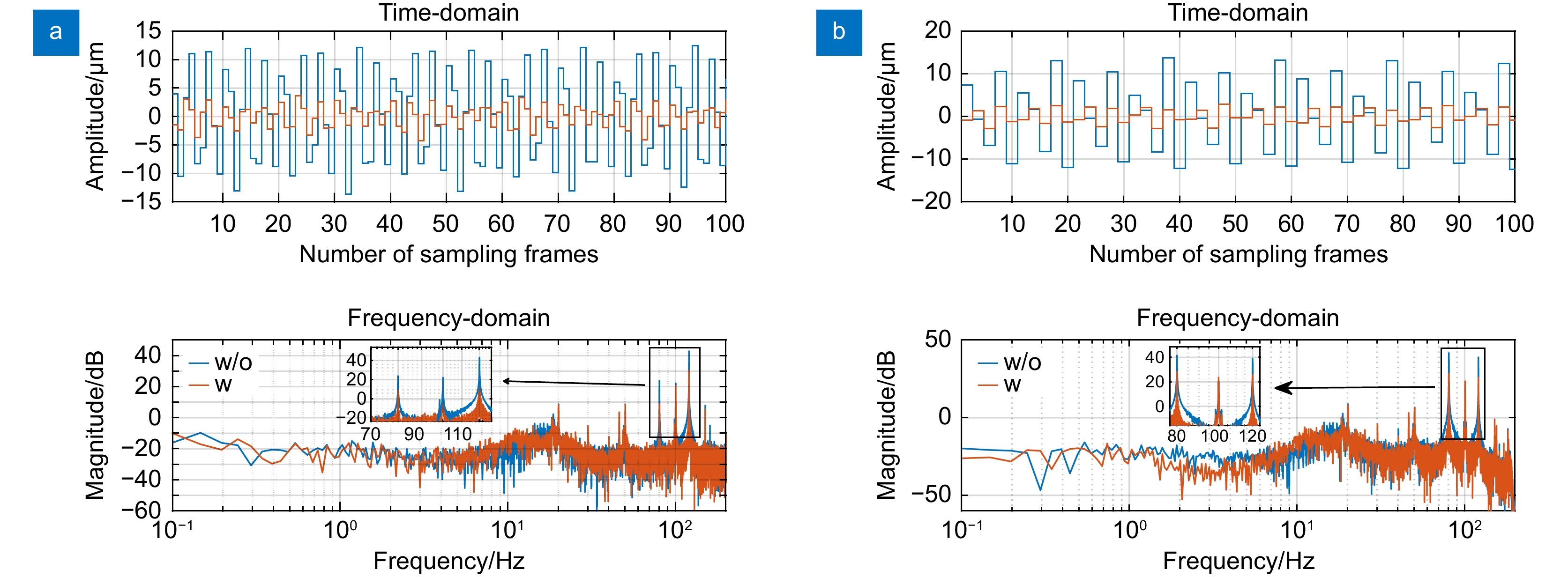
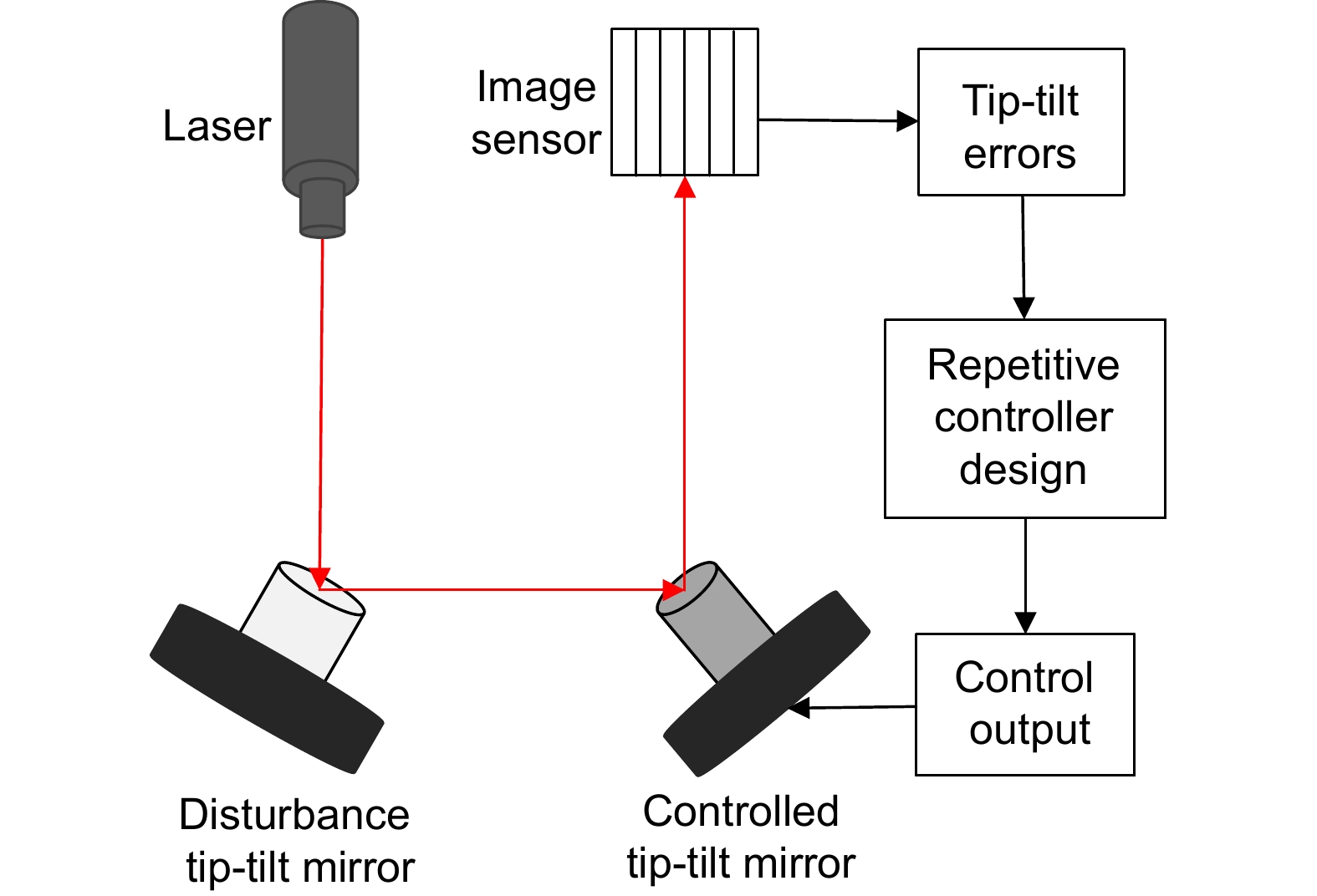
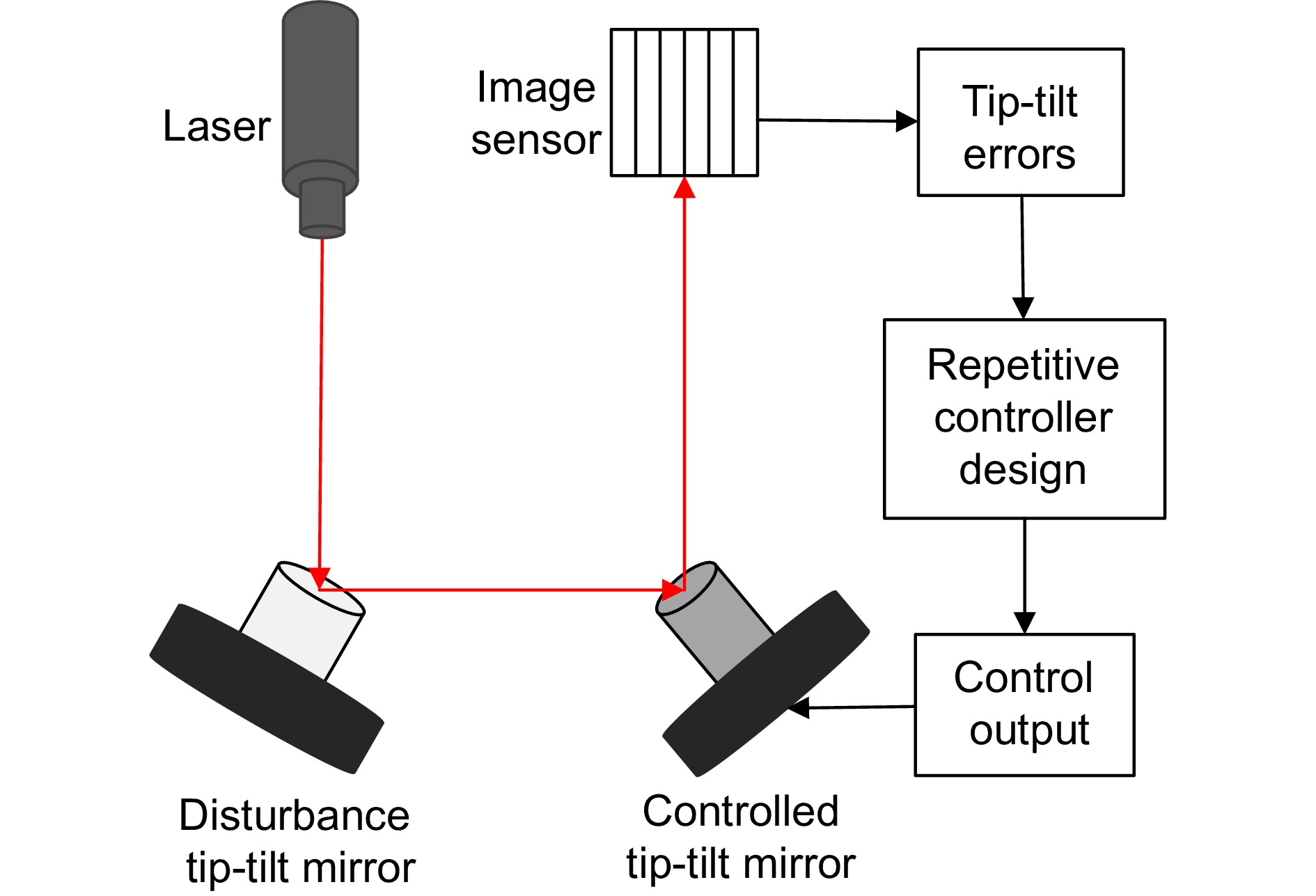
Overview: In optical telescope systems, the control accuracy with tip-tilt correction systems as a fine tracking link is improved to the level of micro radian or even sub-micro radian. Disturbance suppression, especially high-frequency disturbance suppression outside the closed-loop bandwidth, is the key to achieving high precision stability control of tip-tilt correction systems, so as to approach the diffraction limit of the telescope system. Repetitive control has good performance of periodic trajectory tracking and disturbance suppression and is widely applied to improve the control performance of high-precision control systems, such as nanopositioning stages, power inventers, and hard disk drive systems. Therefore, repetitive control is a promising algorithm for high-frequency disturbance suppression. Firstly, this paper analyzes the problem of high-frequency disturbance suppression of tip-tilt correction systems and summarizes the performance of high-frequency interference suppression based on repetitive control. To solve the problem of natural frequency drift and waterbed amplification of traditional repetitive controllers, a comb-like repetitive controller based on Youla parameterization is designed to suppress high-frequency interference outside the closed-loop bandwidth. In the optimal design of the controller, time delays are compensated by the delay characteristic of the repetitive controller to improve the stability of the closed-loop system in suppressing high-frequency disturbance. In addition, in order to solve the problem that the integer-order repetitive controller is only effective for certain frequency points, especially in most high frequency regions, the controller fails due to interference fluctuations and uncertainties, an all-pass fractional delay filter is optimized, which can suppress high-frequency disturbance at any frequency point up to the Nyquist frequency in the tip-tilt correction system. An additional delay compensation factor is designed to preserve the notch characteristic of the repetitive controller in high-frequency domains and improve the system's stability. Finally, a parallel repetitive control scheme is designed for the non-periodic structure vibration which is difficult to suppress, and its robust stability and effectiveness are discussed. A series of experiments were designed to suppress a single peak disturbance, and the results show that repetitive control suppresses any frequency disturbance up to the Nyquist frequency. Furthermore, the experimental results of multiple periodic and aperiodic disturbance suppression prove that the repetitive controller is superior in dealing with multiple high-frequency disturbances beyond the closed-loop bandwidth. In general, these proposed repetitive controllers have good performance in improving the high-frequency disturbance suppression ability of the tip-tilt correction system, and these algorithms are also suitable for other high-precision control systems in the future.
-
-
图 5 是否补偿延时的灵敏度传递函数对比
Figure 5. Comparison of sensitivity transfer function whether time delay is compensated or not
图 7 是否添加重复控制器时的倾斜误差
Figure 7. Tip-tilt errors with/without adding the repetitive controller
图 8 不同α值下一阶分数阶延时滤波器的Bode图
Figure 8. Bode diagram of first-order fractional delay filters with different α
图 9 不同分数阶滤波器参数下分数阶$ F( {\textit{z}}) $的幅值响应
Figure 9. Amplitude response of $ F( {\textit{z}}) $ with different fractional filter parameters
图 10 不同控制器时的灵敏度传递函数
Figure 10. The sensitivity transfer function with different controllers
图 12 有无添加分数阶重复控制器的倾斜误差
Figure 12. Tip-tilt errors with/without fractional repetitive controllers
图 13 重复控制器抑制周期扰动时的倾斜误差
Figure 13. Tip-tilt errors with/without the repetitive controller for periodic disturbances
图 15 重复控制器抑制非周期扰动时的倾斜误差
Figure 15. Tip-tilt errors with/without the repetitive controller for non-periodic disturbances
图 16 重复控制器抑制超高频扰动时的倾斜误差
Figure 16. Tip-tilt errors with/without the repetitive controller for ultra-high frequency disturbance
-
参考文献
[1] Glück M, Pott J U, Sawodny O. Piezo-actuated vibration disturbance mirror for investigating accelerometer-based Tip-Tilt reconstruction in large telescopes[J]. IFAC-PapersOnLine, 2016, 49(21): 361−366. doi: 10.1016/j.ifacol.2016.10.581
[2] 黄林海, 凡木文, 周睿, 等. 大口径压电倾斜镜模型辨识与控制[J]. 光电工程, 2018, 45(3): 170704. doi: 10.12086/oee.2018.170704
Huang L H, Fan M W, Zhou R, et al. System identification and control for large aperture fast-steering mirror driven by PZT[J]. Opto-Electron Eng, 2018, 45(3): 170704. doi: 10.12086/oee.2018.170704
[3] 罗勇, 刘凯凯, 杨帆, 等. 快反镜系统滑模复合分层干扰观测补偿控制[J]. 光电工程, 2023, 50(4): 220330. doi: 10.12086/oee.2023.220330
Luo Y, Liu K K, Yang F, et al. Observation and compensation control of sliding mode compound layered interference for the fast steering mirror system[J]. Opto-Electron Eng, 2023, 50(4): 220330. doi: 10.12086/oee.2023.220330
[4] 刘鑫, 李新阳, 杜睿. 压电倾斜镜迟滞非线性建模及逆补偿控制[J]. 光电工程, 2020, 47(4): 180654. doi: 10.12086/oee.2020.180654
Liu X, Li X Y, Du R. Modeling and inverse compensation control of hysteresis nonlinear characteristics of piezoelectric steering mirror[J]. Opto-Electron Eng, 2020, 47(4): 180654. doi: 10.12086/oee.2020.180654
[5] Tumarina M, Ryazanskiy M, Jeong S, et al. Design, fabrication and space suitability tests of wide field of view, ultra-compact, and high resolution telescope for space application[J]. Opt Express, 2018, 26(3): 2390−2399. doi: 10.1364/OE.26.002390
[6] Wang X, Su X Q, Liu G Z, et al. Laser beam jitter control of the link in free space optical communication systems[J]. Opt Express, 2021, 29(25): 41582−41599. doi: 10.1364/OE.443411
[7] Guesalaga A, Neichel B, O’Neal J, et al. Mitigation of vibrations in adaptive optics by minimization of closed-loop residuals[J]. Opt Express, 2013, 21(9): 10676−10696. doi: 10.1364/OE.21.010676
[8] Tang T, Niu S X, Ma J G, et al. A review on control methodologies of disturbance rejections in optical telescope[J]. Opto-Electron Adv, 2019, 2(10): 190011. doi: 10.29026/oea.2019.190011
[9] Sanfedino F, Preda V, Pommier-Budinger V, et al. Robust active mirror control based on hybrid sensing for spacecraft line-of-sight stabilization[J]. IEEE Trans Control Syst Technol, 2021, 29(1): 220−235. doi: 10.1109/TCST.2020.2970658
[10] 唐涛, 马佳光, 陈洪斌, 等. 光电跟踪系统中精密控制技术研究进展[J]. 光电工程, 2020, 47(10): 200315. doi: 10.12086/oee.2020.200315
Tang T, Ma J G, Chen H B, et al. A review on precision control methodologies for optical-electric tracking control system[J]. Opto-Electron Eng, 2020, 47(10): 200315. doi: 10.12086/oee.2020.200315
[11] 吴红梅, 王琛, 冯念, 等. 特征扰动频率辨识的自适应倾斜扰动抑制技术[J]. 光电工程, 2023, 50(10): 230177. doi: 10.12086/oee.2023.230177
Wu H M, Wang C, Feng N, et al. Adaptive Tip-Tilt disturbance suppression technique for characteristic disturbance frequency identification[J]. Opto-Electron Eng, 2023, 50(10): 230177. doi: 10.12086/oee.2023.230177
[12] 阮勇, 徐田荣, 杨涛, 等. 具有延迟特性的倾斜镜系统中速度-位置控制方法[J]. 光电工程, 2020, 47(12): 200006. doi: 10.12086/oee.2020.200006
Ruan Y, Xu T R, Yang T, et al. Position-rate control for the time delay control system of Tip-Tilt mirror[J]. Opto-Electron Eng, 2020, 47(12): 200006. doi: 10.12086/oee.2020.200006
[13] 周睿, 张强, 廖勇, 等. 混合自适应滤波的光束抖动控制技术研究[J]. 激光与光电子学进展, 2021, 58(13): 1314004. doi: 10.3788/LOP202158.1314004
Zhou R, Zhang Q, Liao Y, et al. Research on beam jitter control technology base on hybrid adaptive filter[J]. Laser Optoelectron Prog, 2021, 58(13): 1314004. doi: 10.3788/LOP202158.1314004
[14] Wen L, Xu T R, Ruan Y, et al. Disturbance feedforward control of Tip-Tilt mirror with gyro measuring for large-amplitude vibration rejection[J]. IEEE Sens J, 2022, 22(16): 16351−16358. doi: 10.1109/JSEN.2022.3190134
[15] 王玉, 边启慧, 廖军, 等. 惯性稳定万向架中基于SBG惯导的捷联控制技术[J]. 光电工程, 2023, 50(5): 220238. doi: 10.12086/oee.2023.220238
Wang Y, Bian Q H, Liao J, et al. Strapdown inertial stabilization technology based on SBG inertial navigation in inertial stabilization gimbal[J]. Opto-Electron Eng, 2023, 50(5): 220238. doi: 10.12086/oee.2023.220238
[16] Fan Y F, Tan U X. Design of a feedforward-feedback controller for a piezoelectric-driven mechanism to achieve high-frequency nonperiodic motion tracking[J]. IEEE/ASME Trans Mechatron, 2019, 24(2): 853−862. doi: 10.1109/TMECH.2019.2899069
[17] 徐田荣, 阮勇, 赵志强, 等. 基于误差的观测器在光电跟踪系统中的应用(英文)[J]. 光电工程, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
Xu T R, Ruan Y, Zhao Z Q, et al. Error-based observer control of an optic-electro tracking control system[J]. Opto-Electron Eng, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
[18] Mooren N, Witvoet G, Oomen T. Gaussian process repetitive control: Beyond periodic internal models through kernels[J]. Automatica, 2022, 140: 110273. doi: 10.1016/j.automatica.2022.110273
[19] 牛帅旭, 蒋晶, 唐涛, 等. 望远镜中扰动抑制的Youla控制器优化设计[J]. 光电工程, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
Niu S X, Jiang J, Tang T, et al. Optimal design of Youla controller for vibration rejection in telescopes[J]. Opto-Electron Eng, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
[20] Zou Z X, Zhou K L, Wang Z, et al. Fractional-order repetitive control of programmable AC power sources[J]. IET Power Electron, 2014, 7(2): 431−438. doi: 10.1049/iet-pel.2013.0429
[21] Liu T Q, Wang D W. Parallel structure fractional repetitive control for PWM inverters[J]. IEEE Trans Ind Electron, 2015, 62(8): 5045−5054. doi: 10.1109/TIE.2015.2402117
[22] Feng Z, Ming M, Ling J, et al. Fractional delay filter based repetitive control for precision tracking: design and application to a piezoelectric nanopositioning stage[J]. Mech Syst Signal Process, 2022, 164: 108249. doi: 10.1016/j.ymssp.2021.108249
[23] Feng N, Ruan Y, Xu T R, et al. Enhanced observer-based repetitive control for Tip-Tilt disturbance rejections beyond control bandwidth in optical-stabilized systems[J]. IEEE Photonics J, 2023, 15(1): 7800207. doi: 10.1109/JPHOT.2023.3240694
[24] Li L L, Aphale S S, Zhu L M. Enhanced odd-harmonic repetitive control of nanopositioning stages using spectrum-selection filtering scheme for high-speed raster scanning[J]. IEEE Trans Autom Sci Eng, 2021, 18(3): 1087−1096. doi: 10.1109/TASE.2020.2995444
[25] Zhang Q F, Guo H H, Liu Y C, et al. Robust plug-in repetitive control for speed smoothness of cascaded-PI PMSM drive[J]. Mech Syst Signal Process, 2022, 163: 108090. doi: 10.1016/j.ymssp.2021.108090
[26] Li L L, Huang W W, Wang X Y, et al. Dual-notch-based repetitive control for tracking lissajous scan trajectories with piezo-actuated nanoscanners[J]. IEEE Trans Instrum Meas, 2022, 71: 4503612. doi: 10.1109/TIM.2022.3169561
[27] Nie K, Xue W C, Zhang C, et al. Disturbance observer-based repetitive control with application to optoelectronic precision positioning system[J]. J Franklin Inst, 2021, 358(16): 8443−8469. doi: 10.1016/j.jfranklin.2021.08.042
[28] Tang T, Niu S X, Yang T, et al. Vibration rejection of Tip-Tilt mirror using improved repetitive control[J]. Mech Syst Signal Process, 2019, 116: 432−442. doi: 10.1016/j.ymssp.2018.06.060
[29] Li L L, Gu G Y, Zhu L M. Fractional repetitive control of nanopositioning stages for tracking high-frequency periodic inputs with nonsynchronized sampling[J]. Rev Sci Instrum, 2019, 90(5): 055108. doi: 10.1063/1.5088673
[30] Zhou K L, Tang C, Chen Y X, et al. A generic multi-frequency repetitive control scheme for power converters[J]. IEEE Trans Ind Electron, 2023, 70(12): 12680−12688. doi: 10.1109/TIE.2023.3239855
[31] Cui P L, Zhang G X, Liu Z Y, et al. A second-order dual mode repetitive control for magnetically suspended rotor[J]. IEEE Trans Ind Electron, 2020, 67(6): 4946−4956. doi: 10.1109/TIE.2019.2927184
[32] Li L L, Chen Z Z, Aphale S S, et al. Fractional repetitive control of nanopositioning stages for high-speed scanning using low-pass FIR variable fractional delay filter[J]. IEEE/ASME Trans Mechatron, 2020, 25(2): 547−557. doi: 10.1109/TMECH.2020.2969222
[33] Chen D, Zhang J M, Qian Z M. An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability[J]. IEEE Trans Ind Electron, 2013, 60(2): 814−823. doi: 10.1109/TIE.2012.2205364
[34] Li L L, Fleming A J, Yong Y K, et al. High performance raster scanning of atomic force microscopy using Model-free Repetitive Control[J]. Mech Syst Signal Process, 2022, 173: 109027. doi: 10.1016/j.ymssp.2022.109027
[35] Feng N, Ruan Y, Tang T. Youla parameterization-based fractional repetitive control of arbitrary frequency disturbance rejections for line-of-sight stabilization[J]. IEEE Trans Ind Electron, 2024, 71(8): 9460−9469. doi: 10.1109/TIE.2023.3317840
[36] Ye J, Liu L G, Xu J B, et al. Frequency adaptive proportional-repetitive control for grid-connected inverters[J]. IEEE Trans Ind Electron, 2021, 68(9): 7965−7974. doi: 10.1109/TIE.2020.3016247
[37] Chen S N, Zhao Q S, Ye Y Q, et al. Using IIR filter in fractional order phase lead compensation PIMR-RC for grid-tied inverters[J]. IEEE Trans Ind Electron, 2023, 70(9): 9399−9409. doi: 10.1109/TIE.2022.3212433
[38] Blanken L, Bevers P, Koekebakker S, et al. Sequential multiperiod repetitive control design with application to industrial wide-format printing[J]. IEEE/ASME Trans Mechatron, 2020, 25(2): 770−778. doi: 10.1109/TMECH.2020.2967305
[39] Feng N, Ruan Y, Bian Q H, et al. High-frequency multiperiod wideband vibration rejections of piezoelectric tip-tilt mirror using parallel odd-harmonic repetitive control[J]. Mech Syst Signal Process, 2025, 224: 111958. doi: 10.1016/j.ymssp.2024.111958
[40] Chen Y X, Zhou K L, Tang C, et al. Fractional-order multiperiodic odd-harmonic repetitive control of programmable AC power sources[J]. IEEE Trans Power Electron, 2022, 37(7): 7751−7758. doi: 10.1109/TPEL.2022.3147062
-
访问统计
下载:
点击扫一扫
图(17)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
