E-mail Alert
RSS
Research on the all-Stokes vector measurement and correction method via elastic-optic difference frequency modulation
-
摘要
为实现全Stokes矢量的高精度测量，提出一种双弹光调制器(photoelectric modulator, PEM)的互差频调制全Stokes矢量测量方法。利用两种不同频率的PEM对入射光进行差频调制，被测偏振矢量与PEM相位延迟幅值同时被调制在不同的差频分量中。通过奇次差频分量相除操作，可实时获得PEM相位延迟幅值。结合不同差频分量，精确获得被测光Stokes矢量。该方法可减小PEM测量系统中相位延迟幅值波动引入的误差。理论及实验分析结果显示，测得Stokes矢量方差在10−5量级，该方法将对高精度偏振测量提供支撑。
Abstract
To achieve high-precision measurement of the all-Stokes vector, a mutual differential frequency modulation approach for dual photo-elastic modulators (photoelectric modulator, PEM) in all-Stokes vector measurement was proposed. The incident light was differently frequency modulated by two PEMs of different frequencies. The measured polarization vector and the phase delay amplitude of the PEM were simultaneously modulated at different differential frequency components. The phase delay amplitude of the PEM was obtained in real time by dividing the odd differential frequency components, and the Stokes vector of the measured light was accurately obtained by combining different differential frequency components. This method reduced the error introduced by the fluctuation of the phase delay amplitude in the PEM measurement system. Theoretical and experimental analyses were conducted, and the results showed that the variance of the measured Stokes vector was 10−5. This method will provide support for high-precision polarization measurement.
-
Overview
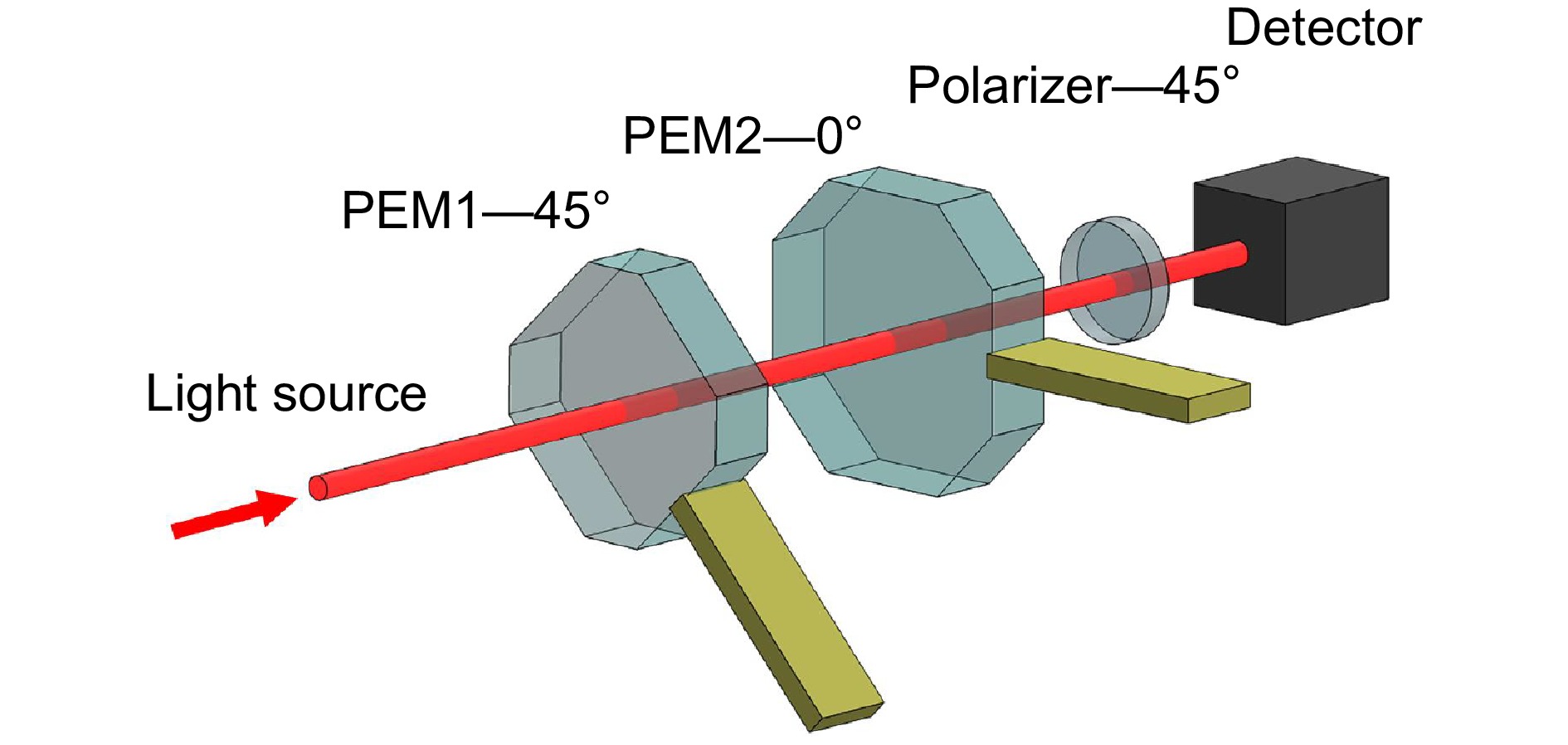
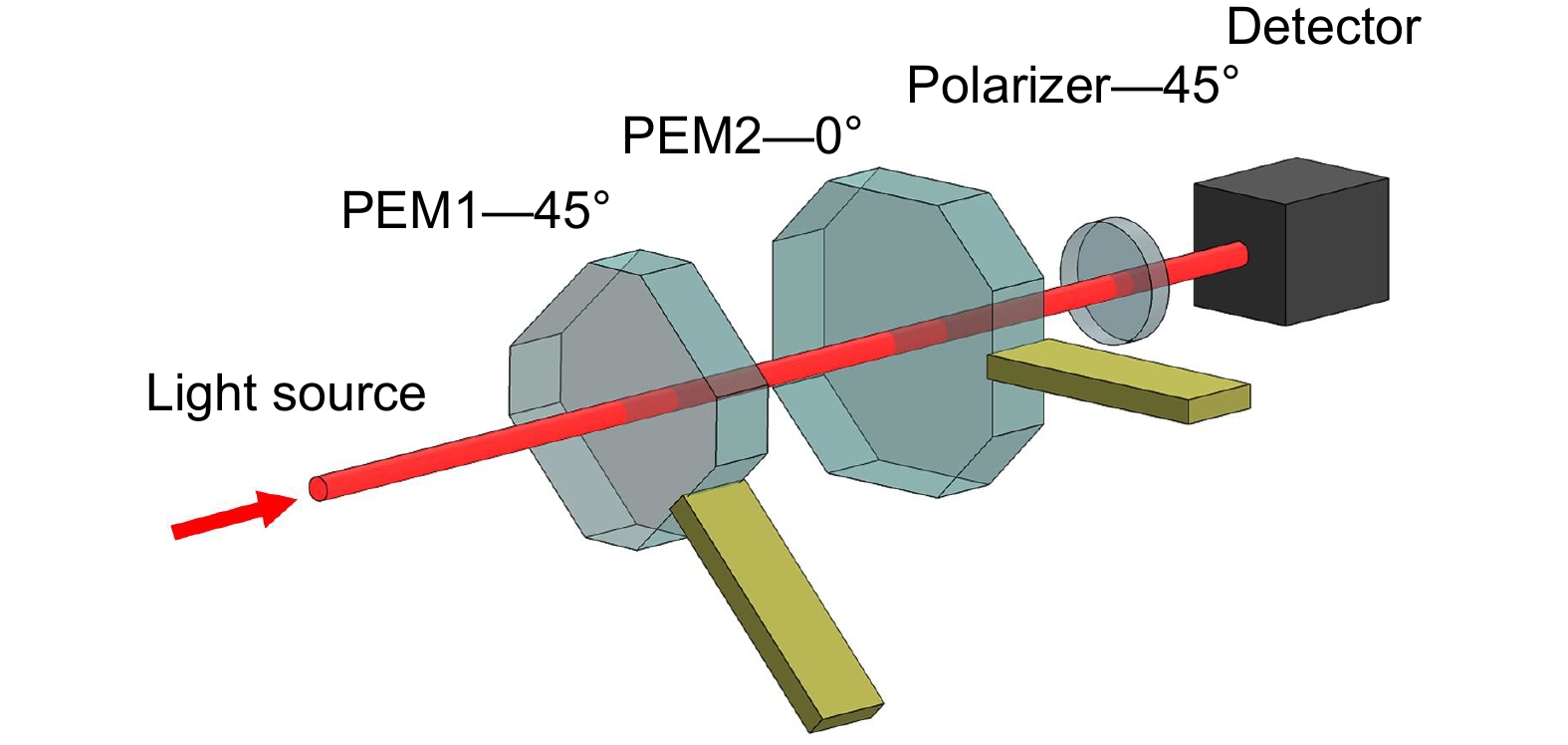
Overview: The comprehensive measurement of all-Stokes vector is of paramount importance across various scientific disciplines such as optics, light scattering theory, atmospheric science, and quantum mechanics, where understanding and applying light-matter interactions is crucial. Traditional methods often employ linear polarizers and quarter-wave plates to analyze polarized light, requiring mechanical rotation of the polarizer and measurement of light intensity at different angles to calculate the Stokes vector. Although these methods are simple and cost-effective, they may be limited in terms of measurement precision and speed. Another approach utilizes the snapshot Stokes measurement technique with a Dammer grating, which divides the incident beam into four beams, modulates them with wave plates and a linear polarizer, and captures the results with a CCD, enabling rapid measurement of the beam's Stokes vector. However, the design of Dammer gratings is often tailored to specific beam polarization states, and their adaptability to varying states is somewhat limited. Photoelectric modulation (PEM) technology offers a novel solution by modulating light with PEMs at frequency superpositions, generating high-frequency components carrying the measured polarization state information, and acquiring all four Stokes parameters simultaneously using lock-in amplification techniques. We proposed a new method for high-precision all-Stokes vector measurement based on dual PEMs. This technique leveraged two PEMs with different modulation frequencies to heterodyne modulate the incident light. We simultaneously modulated the measured polarization parameters with the phase delay amplitudes of the two PEMs in distinct beat frequency components. Through phase-locking and dividing the odd-order beat frequency components, the phase delay amplitudes of the two PEMs were obtained in real-time. By combining different beat frequency components with the DC component, the four parameters of the measured light's Stokes vector were precisely acquired and normalized. This method simplifies the complexity of mechanical rotation in traditional measurement methods and reduces measurement errors introduced by phase delay amplitude fluctuations in dual-PEM systems. Theoretically, the Mueller matrix is used to describe the polarization changes of light propagating through the system, and based on this, the expression for the outgoing light's Stokes vector can be calculated. Experimental measurements using known polarization states of light validate the theoretical analysis, with results showing that the variance of the measured Stokes vector is on the order of 10−5, indicating that this technique can provide technical support for high-precision polarization measurements. The high-precision measurement capabilities are of significant practical importance for applications requiring accurate polarization information, such as remote sensing, optical imaging, and physical research, enabling precise control and measurement of the polarization state of light and advancing related scientific fields.
-
-
图 1 PEM电压驱动控制。(a) PEM控制结构；(b)压电效应仿真结构
Figure 1. PEM voltage drive control. (a) PEM control structure; (b) Piezoelectric effect simulation structure
图 2 弹光差频调制Stokes测量基本原理图
Figure 2. Basic principle diagram of hetero-dyne modulation Stokes measurement
图 3 弹光差频调制Stokes测量装置
Figure 3. Elastic optical difference frequency modulation Stokes measuring device
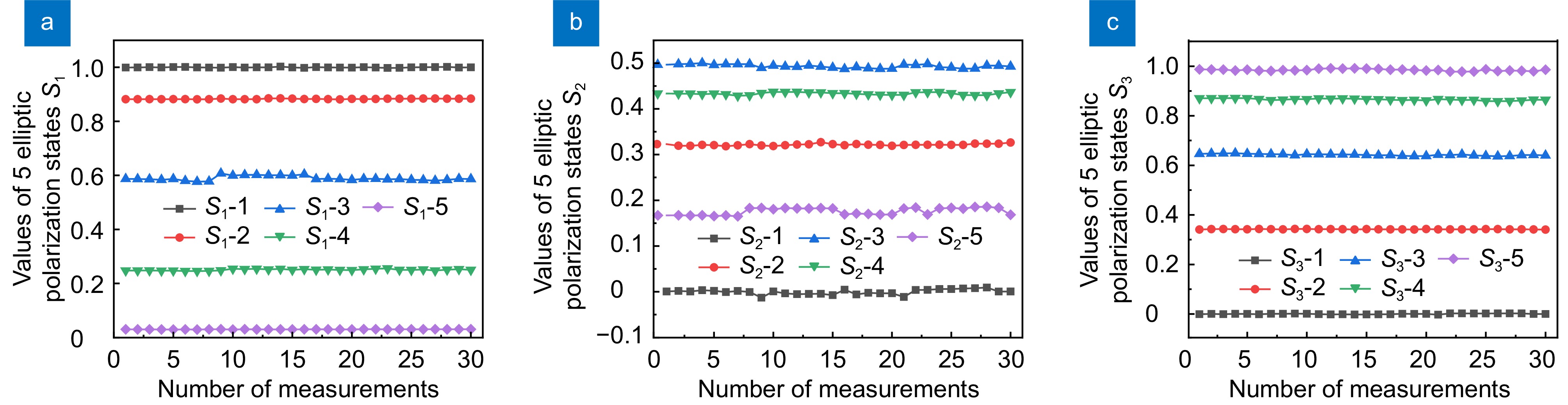
图 4 椭圆偏振光的Stokes矢量测量结果。(a)测量不同椭圆偏振光的S1值；(b)测量不同椭圆偏振光的S2值；(c)测量不同椭圆偏振光的S3值
Figure 4. Stokes vector measurement results of elliptically polarized light. (a) S1 for different elliptically polarized light is measured; (b) S2 for different elliptically polarized light is measured; (c) S3 for different elliptically polarized light is measured
表 1 5组不同椭圆偏振光的测量数据方差
Table 1. Variance of measured data of 5 different elliptically polarized light
Parameter Polarization state 1 Ppolarization state 2 Polarization stadte 3 Polarization state 4 Polarization state 5 S1 $ 1.0\times {10}^{-5} $ $ 1.1\times {10}^{-6} $ $ 1.9\times {10}^{-5} $ $ 7.2\times {10}^{-6} $ $ 1.9\times {10}^{-7} $ S2 $ 2.7\times {10}^{-5} $ $ 3.1\times {10}^{-6} $ $ 1.6\times {10}^{-5} $ $ 7.4\times {10}^{-6} $ $ 9.8\times {10}^{-6} $ S3 $ 2.3\times {10}^{-6} $ $ 5.7\times {10}^{-7} $ $ 1.1\times {10}^{-5} $ $ 1.3\times {10}^{-5} $ $ 1.4\times {10}^{-5} $ 
下载: 导出CSV
-
参考文献
[1] 戴万田, 王锦津, 谢欣, 等. 偏振探测技术的应用需求发展研究[J]. 光电技术应用, 2023, 38(5): 6−12,82. doi: 10.3969/j.issn.1673-1255.2023.05.003
Dai W T, Wang J J, Xie X, et al. Requirements and development of polarization detection technology[J]. Electro-Opt Technol Appl, 2023, 38(5): 6−12,82. doi: 10.3969/j.issn.1673-1255.2023.05.003
[2] 罗海波, 张俊超, 盖兴琴, 等. 偏振成像技术的发展现状与展望(特邀)[J]. 红外与激光工程, 2022, 51(1): 20210987. doi: 10.3788/IRLA20210987
Luo H B, Zhang J C, Gai X Q, et al. Development status and prospects of polarization imaging technology (Invited)[J]. Infrared Laser Eng, 2022, 51(1): 20210987. doi: 10.3788/IRLA20210987
[3] Dai P Z, Yao D, Ma T X, et al. Analysis of polarization detector performance parameters on polarization 3D imaging accuracy[J]. Sensors, 2023, 23(11): 5129. doi: 10.3390/s23115129
[4] Pierangeli D, Conti C. Single-shot polarimetry of vector beams by supervised learning[J]. Nat Commun, 2023, 14(1): 1831. doi: 10.1038/s41467-023-37474-0
[5] Yi S Y, Kim D, Na J, et al. Spin-weighted spherical harmonics for polarized light transport[J]. ACM Trans Graph, 2024, 43(4): 127. doi: 10.1145/3658139
[6] Sun Z Q, Huang Y H, Bao Y L, et al. Polarized remote sensing: a note on the stokes parameters measurements from natural and man-made targets using a spectrometer[J]. IEEE Trans Geosci Remote Sens, 2017, 55(7): 4008−4021. doi: 10.1109/TGRS.2017.2686485
[7] Adhiya A, Shah M, Pandya A, et al. A simple device for simultaneous measurement of Stokes polarization parameters[J]. IEEE Trans Instrum Meas, 2023, 72: 7001606. doi: 10.1109/TIM.2023.3235451
[8] Zuo J W, Bai J, Choi S, et al. Chip-integrated metasurface full-Stokes polarimetric imaging sensor[J]. Light Sci Appl, 2023, 12(1): 218. doi: 10.1038/s41377-023-01260-w
[9] Guo X Y, Li P, Zhong J Z, et al. Stokes meta-hologram toward optical cryptography[J]. Nat Commun, 2022, 13(1): 6687. doi: 10.1038/s41467-022-34542-9
[10] Hu Y Q, Jiang Y T, Zhang Y, et al. Achromatic full Stokes polarimetry metasurface for full-color polarization imaging in the visible range[J]. Nano Lett, 2024, 24(41): 13018−13026. doi: 10.1021/acs.nanolett.4c03785
[11] 徐参军, 赵劲松, 蔡毅, 等. 红外偏振成像的几种技术方案[J]. 红外技术, 2009, 31(5): 262−266. doi: 10.3969/j.issn.1001-8891.2009.05.005
Xu C J, Zhao J S, Cai Y, et al. Several schemes of infrared polarization imaging[J]. Infrared Technol, 2009, 31(5): 262−266. doi: 10.3969/j.issn.1001-8891.2009.05.005
[12] 唐凡春, 步扬, 吴芳, 等. 基于达曼光栅的快照式斯托克斯偏振测量方法[J]. 光学学报, 2023, 43(13): 1312002. doi: 10.3788/AOS221731
Tang F C, Bu Y, Wu F, et al. Snapshot Stokes polarimetry method based on Dammann grating[J]. Acta Opt Sin, 2023, 43(13): 1312002. doi: 10.3788/AOS221731
[13] 李坤钰, 王志斌, 李克武, 等. 双弹光调制广义偏振测量的数字锁相数据处理研究[J]. 光学技术, 2023, 49(1): 51−56,96. doi: 10.13741/j.cnki.11-1879/o4.2023.01.011
Li K Y, Wang Z B, Li K W, et al. Research on digital phase locked data processing of generalized polarization measurement with dual photoelastic modulation[J]. Opt Tech, 2023, 49(1): 51−56,96. doi: 10.13741/j.cnki.11-1879/o4.2023.01.011
[14] 王立福, 王志斌, 李晓, 等. 弹光调制偏振Stokes参量测量及误差分析[J]. 激光技术, 2014, 38(2): 255−259. doi: 10.7510/jgjs.issn.1001-3806.2014.02.023
Wang L F, Wang Z B, Li X, et al. Measurement of the polarization Stokes parameters based on photoelastic-modulation and its error analysis[J]. Laser Technol, 2014, 38(2): 255−259. doi: 10.7510/jgjs.issn.1001-3806.2014.02.023
[15] 武燕婷, 熊伟, 李超波. 光弹调制器研究综述及原理验证[J]. 压电与声光, 2021, 43(3): 352−358. doi: 10.11977/j.issn.1004-2474.2021.03.013
Wu Y T, Xiong W, Li C B. Review and principle verification of photoelastic modulator[J]. Piezoelectr Acoustoopt, 2021, 43(3): 352−358. doi: 10.11977/j.issn.1004-2474.2021.03.013
[16] 周军. 光弹调制器应用的Mueller矩阵分析[J]. 常熟高专学报, 2001, 15(4): 19−22. doi: 10.3969/j.issn.1008-2794.2001.04.007
Zhou J. Mueller matrix analysis of photoelastic modulator[J]. J Changshu Coll, 2001, 15(4): 19−22. doi: 10.3969/j.issn.1008-2794.2001.04.007
[17] Xing T L, Veetil S P, Lin Q, et al. Elliptically polarized light photoelasticity based on LCD[J]. Opt Express, 2023, 31(17): 28161−28173. doi: 10.1364/OE.492084
[18] Li K W, Wang S, Wang L M, et al. Research on rapid and high-sensitivity ellipsometry employing multi-harmonic terms of dual cascade photoelastic modulators[J]. Opt Lasers Eng, 2024, 178: 108235. doi: 10.1016/j.optlaseng.2024.108235
[19] 张瑞, 薛鹏, 李克武, 等. 一种双PEM偏振态分析精确修正装置及方法: 115683563A[P]. 2023-02-03.
Zhang R, Xue P, Li K W, et al. Double-PEM polarization state analysis accurate correction device and method: 115683563A[P]. 2023-02-03.
[20] 杨军营, 韩培高, 魏莹莹. 无频响影响的光弹调制器定标新方法[J]. 中国激光, 2024, 51(8): 0804007. doi: 10.3788/CJL231410
Yang J Y, Han P G, Wei Y Y. New calibration method for photoelastic modulator without frequency response[J]. Chin J Lasers, 2024, 51(8): 0804007. doi: 10.3788/CJL231410
[21] 刘梓良, 王志斌, 李克武, 等. 一种弹光调制器精确定标微系统设计[J]. 光学技术, 2022, 48(1): 8−13. doi: 10.13741/j.cnki.11-1879/o4.2022.01.001
Liu Z L, Wang Z B, Li K W, et al. A precise calibration microsystem for photoelastic modulator[J]. Opt Tech, 2022, 48(1): 8−13. doi: 10.13741/j.cnki.11-1879/o4.2022.01.001
-
访问统计
点击扫一扫
图(5)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
