E-mail Alert
RSS
-
摘要:
基于双平面模型的四维光场表示形式，光场相机以牺牲图像空间分辨率为代价，实现了三维场景空间信息和角度信息的同步记录。为了提高光场图像的空间分辨率，本文搭建了基于双路引导更新机制的光场图像超分辨率重建网络。网络前端以不同形式的图像阵列为输入，构建残差串并联卷积实现了空间、角度信息解耦合。针对解耦合后的空间、角度信息，设计了双路引导更新模块，采用逐级增强、融合、再增强的方式，完成空间信息与角度信息的交互引导迭代更新。最后将逐级更新后的角度信息送入简化后的残差特征蒸馏模块，实现数据重建。对比实验表明，所提网络在有效控制复杂度的基础上，获得了更好的超分性能。
Abstract:Based on the four-dimensional representation of the two-plane model, the light field camera captures spatial and angular information of the three-dimensional scene simultaneously at the expense of image spatial resolution. To improve the spatial resolution of light field images, a two-way guided updating network for light field image super-resolution is built in this work. In the front of the network, different forms of image arrays are used as inputs, and the residual series and parallel convolution are constructed to realize the decoupling of spatial and angular information. Aiming at the decoupled spatial information and angular information, a two-way guide updating module is designed, which adopts step-by-step enhancement, fusion, and re-enhancement methods to complete the interactive guidance iterative update of spatial and angular information. Finally, the step-by-step updated angular information is sent to the simplified residual feature distillation module to realize data reconstruction. Many experimental results have confirmed that our proposed method achieves state-of-the-art performance while effectively controlling complexity.
-
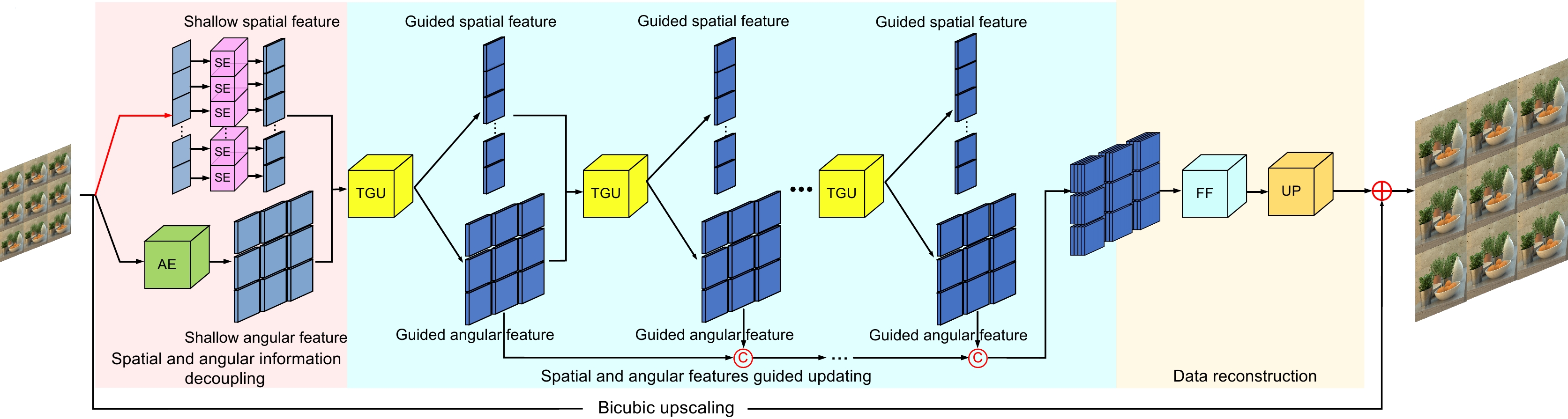
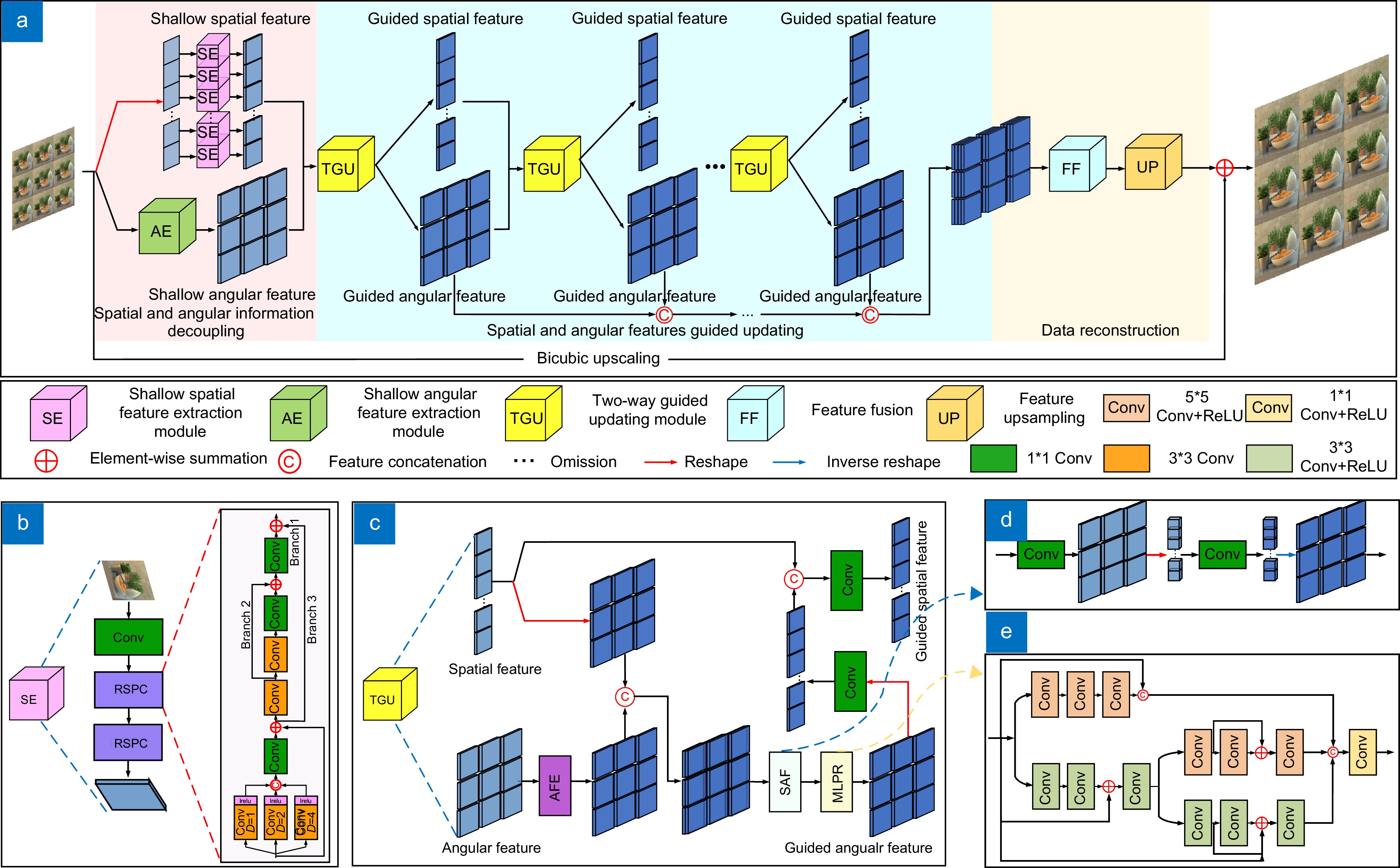
Overview: Based on the two-plane representation model, the light field camera captures both spatial and angular information of a three-dimensional scene, which causes the spatial resolution decline of the light field image. To improve the spatial resolution, a two-way guided updating super-resolution network is constructed in this work. In the shallow layers of the network, a double-branch structure is adopted. A series-parallel convolution (RSPC) block based on the atrous spatial pyramid is designed in each branch to decouple the spatial and angular information from different forms of image arrays. Then, based on the ideas of enhancement, fusion, and re-enhancement, a two-way guide updating (TGU) module is designed to complete the iterative update of the decoupled spatial and angular information. Finally, the updated angular information at different layers is fed into the simplified residual feature distillation (SRFD) module to realize data reconstruction and upsampling. Based on effectively controlling complexity, this network adopts a two-way guided updating mechanism to collect light field features of different levels, achieving better super-resolution results. The design concepts for each part of the network are as follows:
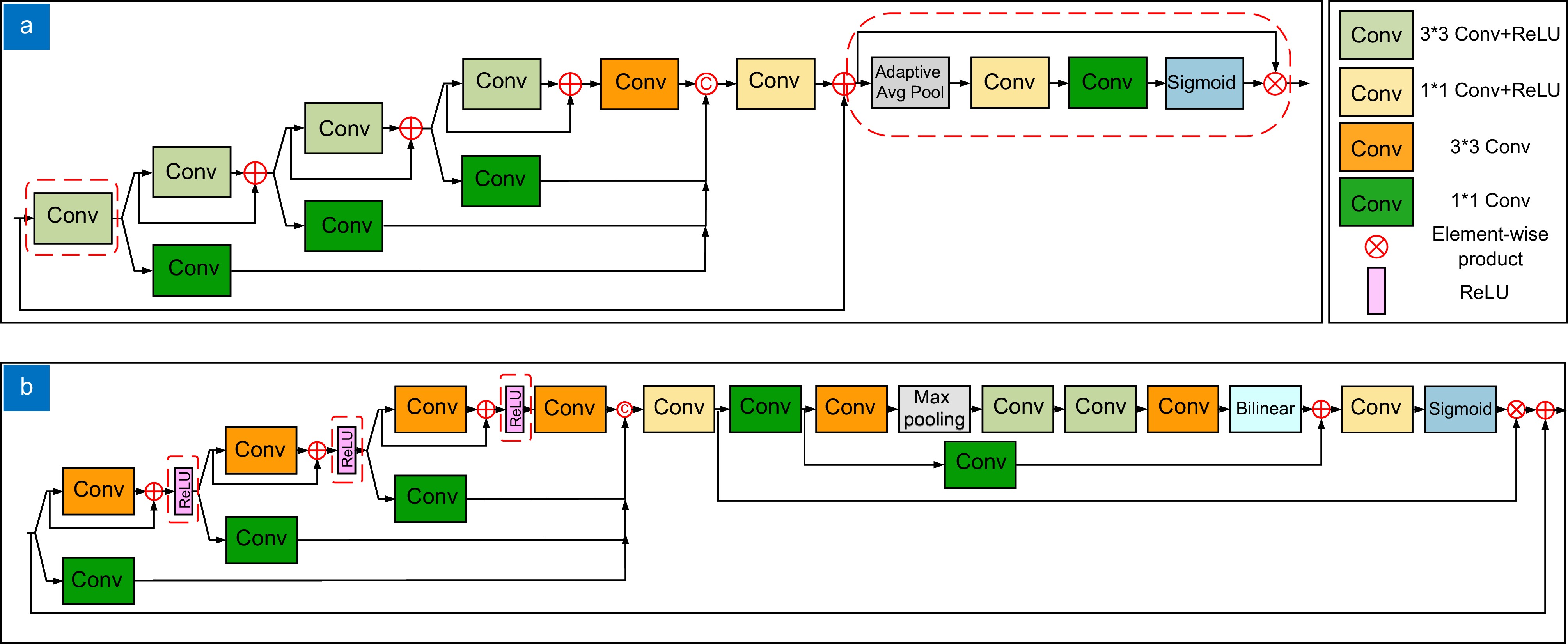
1) When decoupling spatial information and angular information, different forms of image arrays are used as inputs to extract the inherent features of each sub-aperture image and the overall parallax structure of the 4D light field through the RSPC block. The RSPC initially employs three atrous convolutions with varying atrous rates in parallel to achieve feature extraction at different levels. Subsequently, it cascades three convolutions of differing sizes to enhance feature extraction. Finally, a residual structure is introduced to mitigate network degradation.
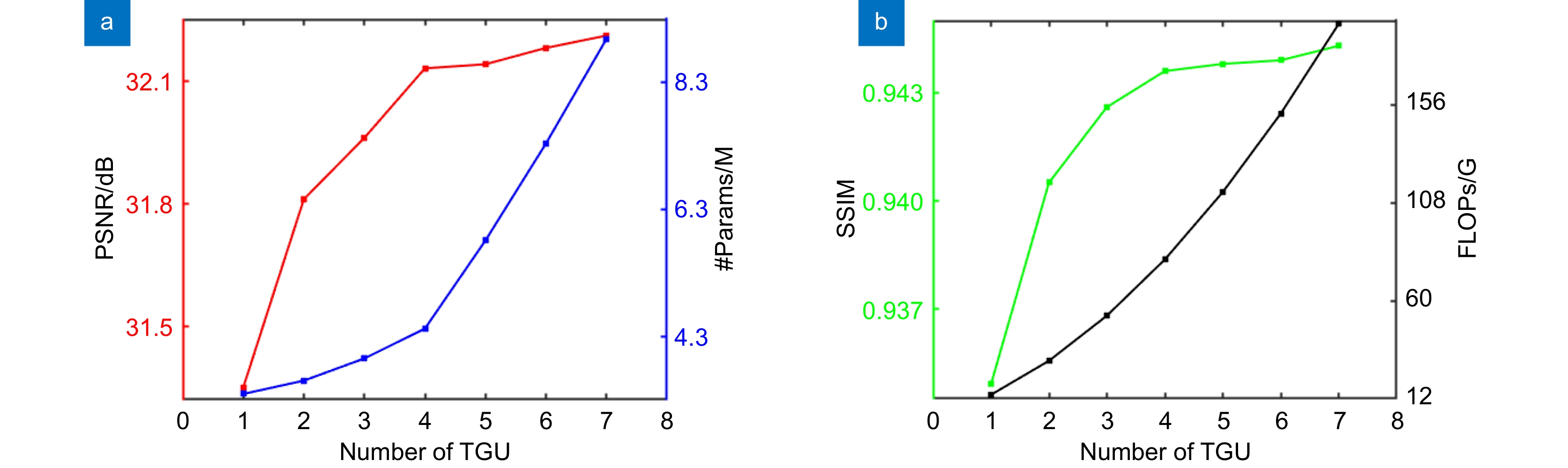
2) In the middle part of the network, TGU module is repeatedly used to iteratively update the decoupled spatial information and angular information. The angular features are first enhanced by TGU module, then fuse with the spatial features and feed into a multi-level perception residual module to obtain the updated angular features. The updated angular features are integrated with the original spatial features, then channel reduction is performed to obtain the updated spatial features.
3) The SRFD module is presented to facilitate data reconstruction. In comparison to the residual feature distillation (RFD) network, SRFD uses channel attention to replace the CCA layer in the RFD, which results in fewer parameters and better performance.
Numerous experimental results on public light field datasets have confirmed that our proposed method achieves state-of-the-art performance both in qualitative analysis and quantitative evaluation.
-
-
图 1 LF-TGUnet结构图。(a)整体网络结构图；(b) SE模块；(c) TGU模块； (d) SAF模块；(e) MLPR模块
Figure 1. An overview of our diagram. (a) Overall network architecture diagram; (b) SE module; (c) TGU module; (d) SAF module; (e) MLPR module
图 2 SFRD与FRD对比。 (a) SRFD模块； (b) RFD模块
Figure 2. Comparison between SFRD and FRD. (a) SRFD module; (b) RFD module
图 3 “Origima”与“Bicycle”场景的2倍超分的视觉效果对比
Figure 3. Visual results of the “Origima” and “Bicycle” scene with 2×SR
图 4 “Bedroom”与“LEGO Knights”场景的4倍超分的视觉效果对比
Figure 4. Visual results of the “Bedroom” and “LEGO Knights” scene with 4×SR
图 5 2倍超分任务下5×5子孔径图像PSNR值分布的可视化
Figure 5. A visualization of PSNR distribution among different perspectives on 5×5 LFs for 2×SR
图 6 各个模块的变体。(a) RSPC无并联卷积；(b) RSPC无串联卷积；(c) RSPC无残差结构；(d) 单支路TGU
Figure 6. Variations of each module. (a) RSPC w/o parallel convolution; (b) RSPC w/o series convolution; (c) RSPC w/o residual; (d) Half TGU
图 7 TGU个数的最优选择。(a) PSNR、网络参数量随TGU个数增长的曲线；(b) SSIM、FLOPs随TGU个数增长的曲线
Figure 7. Optimal selection of the number of TGUs. (a) PSNR and the number of parameters values increase with the number of TGUs; (b) SSIM and FLOPs values increase with the number of TGUs
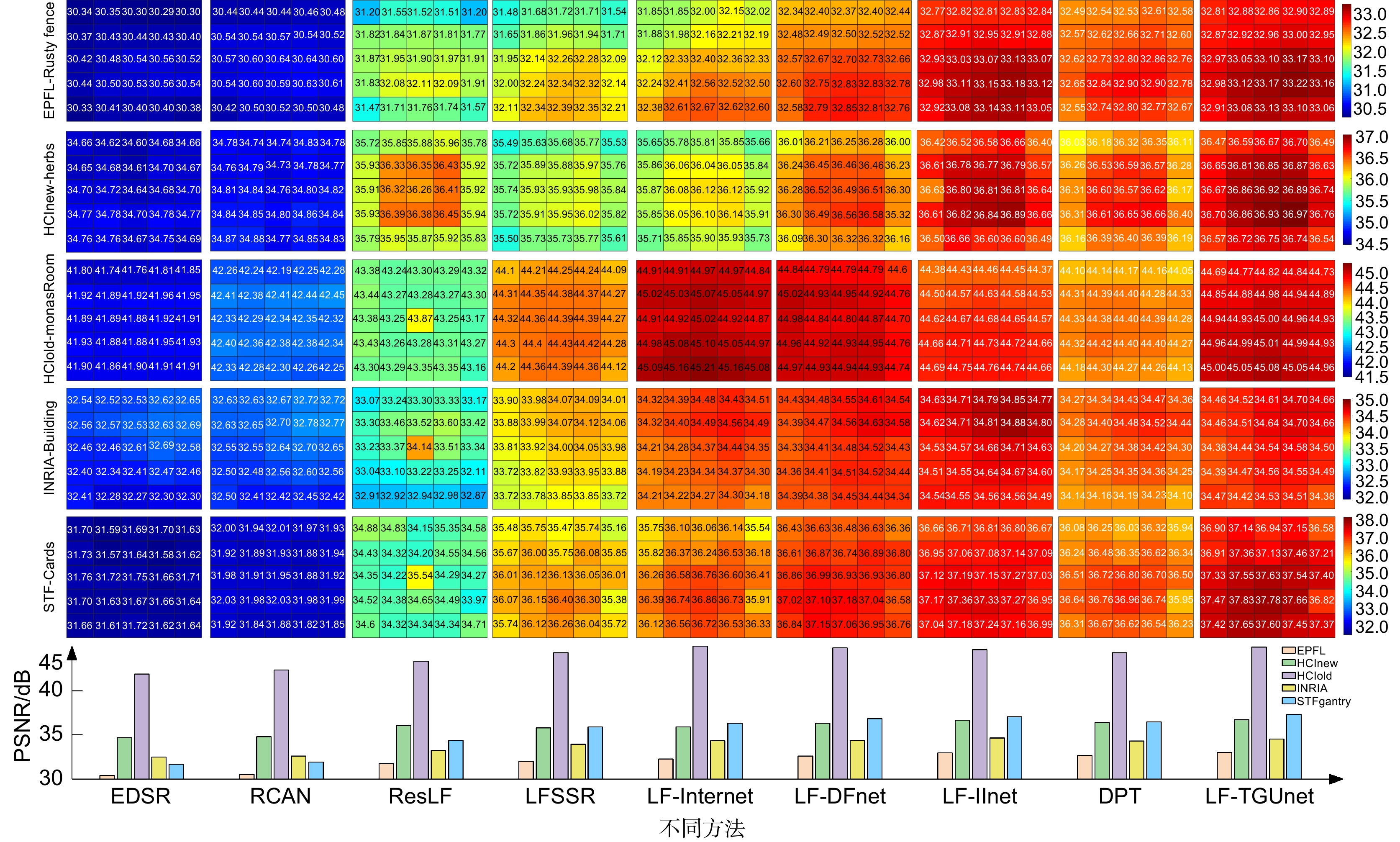
表 1 2倍超分和4倍超分任务下不同算法得到超分图像的PSNR/SSIM值
Table 1. PSNR/SSIM values by different methods for 2×SR and 4×SR
Method Scale Dataset Average EPFL HCInew HCIold INRIA STFgantry bicubic 2× 29.74/0.9376 31.89/0.9356 37.69/0.9785 31.33/0.9577 31.06/0.9498 32.34/0.9518 EDSR[32] 2× 33.09/0.9631 34.83/0.9594 41.01/0.9875 34.97/0.9765 36.29/0.9819 36.04/0.9728 RCAN[33] 2× 33.16/0.9635 34.98/0.9602 41.05/0.9875 35.01/0.9769 36.33/0.9825 36.11/0.9741 ResLF[15] 2× 32.75/0.9672 36.07/0.9715 42.61/0.9922 34.57/0.9784 36.89/0.9873 36.58/0.9793 LFSSR[12] 2× 33.69/0.9748 36.86/0.9753 43.75/0.9939 35.27/0.9834 38.07/0.9902 37.53/0.9835 LF-Internet[21] 2× 34.14/0.9761 37.28/0.9769 44.45/0.9945 35.80/0.9846 38.72/0.9916 38.08/0.9847 LF-DFnet[20] 2× 34.44/0.9766 37.44/0.9786 44.23/0.9943 36.36/0.9841 39.61/0.9935 38.42/0.9854 LF-IInet[22] 2× 34.68 /0.977137.74/0.9789 44.84/0.9948 36.57/0.9853 39.86/0.9935 38.74/0.9859 DPT[20] 2× 34.48/0.9759 37.35/0.9770 44.31/0.9943 36.40/0.9843 39.52/0.9928 38.41/0.9849 LF-ADEnet[17] 2× 34.58/0.9772 37.92/0.9796 44.84/0.9948 36.59 /0.985440.11/0.9939 38.81/0.9862 LF-MDFnet[18] 2× 34.62/ 0.9844 37.37/0.9772 44.06/0.9823 36.23/0.9791 39.42/0.9923 38.34/0.9831 LF-TGUnet 2× 34.67/0.9776 37.80/0.9791 44.78/ 0.9948 36.46/ 0.9857 39.95/0.9936 38.73/ 0.9862 bicubic 4× 25.14/0.8324 27.61/0.8517 32.42/0.9344 26.82/0.8867 25.93/0.8452 27.58/0.8661 EDSR[32] 4× 27.84/0.8858 29.60/0.8874 35.18/0.9538 29.66/0.9259 28.70/0.9075 30.20/0.9121 RCAN[33] 4× 27.88/0.8863 29.63/0.8880 35.20/0.9540 29.76/0.9273 28.90/0.9110 30.27/0.9133 ResLF[15] 4× 27.46/0.8899 29.92/0.9011 36.12/0.9651 29.64/0.9339 28.99/0.9214 30.43/0.9223 LFSSR[12] 4× 28.27/0.9080 30.72/0.9124 36.70/0.9690 30.31/0.9446 30.15/0.9385 31.23/0.9345 LF-Internet[21] 4× 28.67/0.9143 30.98/0.9165 37.11/0.9715 30.64/0.9486 30.53/0.9426 31.59/0.9387 LF-DFnet[13] 4× 28.77/0.9165 31.23/0.9196 37.32/0.9718 30.83/0.9503 31.15/0.9494 31.86/0.9415 LF-IInet[22] 4× 29.11/0.9194 31.36/0.9211 37.62/0.9737 31.08/0.9516 31.21/0.9495 32.08/0.9431 DPT[20] 4× 28.93/0.9167 31.19/0.9186 37.39/0.9720 30.96/0.9502 31.14/0.9487 31.92/0.9412 LF-ADEnet[17] 4× 28.81/0.9190 31.30/0.9206 37.39/0.9725 30.81/0.9513 31.15/0.9494 31.86/0.9429 LF-MDFnet[18] 4× 28.70/0.9049 31.41/0.9146 37.42/ 0.9856 30.86/0.9521 30.86/0.9365 31.85/0.9387 LF-TGUnet 4× 28.96/0.9189 31.42/0.9215 37.63 /0.973431.28/0.9529 31.36/0.9511 32.13/0.9436 
下载: 导出CSV
表 2 不同算法的参数量、每秒浮点运算次数与运行时间对比
Table 2. Comparisons of the number of parameters (#Params), FLOPs, and running time
Method EDSR[32] RCAN[33] ResLF[15] LFSSR[12] LF-Internet[21] LF-DFnet[13] LF-IInet[22] DPT[20] LF-ADEnet[17] LF-MDFnet[18] LF-TGUnet #Params/M 2× 38.62 15.31 6.35 0.81 4.80 3.94 4.84 3.73 12.74 5.37 4.37 4× 38.89 15.36 6.79 1.61 5.23 3.99 4.89 3.78 12.80 5.42 4.42 FLOPs/G 2× 39.56×25 15.59×25 37.06 25.70 47.46 57.22 56.16 57.44 238.92 135.65 78.84 4× 40.66×25 15.65×25 39.70 128.44 50.10 57.31 57.42 58.64 240.51 136.91 80.11 Running time
/s2× 0.44 13.10 2.95 0.21 1.45 1.73 0.55 7.56 4.85 3.53 3.02 4× 0.29 3.54 0.95 0.16 0.47 0.55 0.21 2.06 1.75 1.77 0.81
下载: 导出CSV
表 3 各模块的有效性验证
Table 3. Validity verification of each module
Case 1 Case 2 Case 3 Case 4 Case 5 Case 6 Case 7
(LF-TGUnet)Spatial and
angular information
decouplingRPSC w/o parallel
convolution√ RPSC w/o series
convolution√ RPSC w/o residual √ RSPC √ √ √ √ Spatial and
angular features
guided updatinghalf TGU √ TGU √ √ √ √ √ √ TGU w/o MLPR √ MLPR √ √ √ √ √ √ Data reconstruction RFD √ SRFD √ √ √ √ √ √ #Params/M 4.30 4.34 4.42 4.46 4.41 5.70 4.42 Dataset EPFL 28.83/0.9184 29.01/ 0.9196 25.26/0.8324 27.82/0.8856 28.87/0.9195 29.18 /0.917528.96/0.9189 HCInew 31.40/0.9214 31.40/ 0.9216 27.71/0.8517 29.64/0.8869 31.37/0.9212 31.23/0.9193 31.42 /0.9215HCIold 37.55/0.9730 37.57/0.9731 32.58/0.9344 35.12/0.9536 37.51/0.9732 37.30/0.9720 37.63/0.9734 INRIA 30.89/0.9512 30.97/0.9516 26.95/0.8867 29.79/0.9264 31.02/0.9520 31.08/0.9505 31.28/0.9529 STFgantry 31.35/0.9510 31.35/0.9511 26.09/0.8452 28.78/0.9091 31.29/ 0.9512 31.07/0.9486 31.36 /0.9511Average (PSNR/SSIM) 32.00/0.9430 32.06/0.9434 27.72/0.8701 30.23/0.9123 32.01/0.9434 31.97/0.9416 32.13/0.9436 Deviation −0.13/−0.0006 −0.07/−0.0002 −4.41/−0.0735 −1.90/−0.0313 −0.12/−0.0002 −0.16/−0.0020 0/0
下载: 导出CSV
-
[1] Van Duong V, Huu T N, Yim J, et al. Light field image super-resolution network via joint spatial-angular and epipolar information[J]. IEEE Trans Comput Imaging, 2023, 9: 350−366. doi: 10.1109/TCI.2023.3261501
[2] Wang C C, Zang Y S, Zhou D M, et al. Robust multi-focus image fusion using focus property detection and deep image matting[J]. Expert Syst Appl, 2024, 237: 121389. doi: 10.1016/j.eswa.2023.121389
[3] Sakem A, Ibrahem H, Kang H S. Learning epipolar-spatial relationship for light field image super-resolution[C]// Proceedings of 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Vancouver, 2023: 1336–1345. https://doi.org/10.1109/CVPRW59228.2023.00140.
[4] Cui Z L, Sheng H, Yang D, et al. Light field depth estimation for non-Lambertian objects via adaptive cross operator[J]. IEEE Trans Circuits Syst Video Technol, 2024, 34 (2): 1199−1211. doi: 10.1109/TCSVT.2023.3292884
[5] Chao W T, Wang X C, Wang Y Q, et al. Learning sub-pixel disparity distribution for light field depth estimation[J]. IEEE Trans Comput Imaging, 2023, 9: 1126−1138. doi: 10.1109/TCI.2023.3336184
[6] Wang Y Q, Wang L G, Wu G C, et al. Disentangling light fields for super-resolution and disparity estimation[J]. IEEE Trans Pattern Anal Mach Intell, 2023, 45 (1): 425−443. doi: 10.1109/TPAMI.2022.3152488
[7] Ding Y Q, Chen Z, Ji Y, et al. Light field-based underwater 3D reconstruction via angular re-sampling[J]. IEEE Trans Comput Imaging, 2023, 9: 881−893. doi: 10.1109/TCI.2023.3319983
[8] 张志俊, 吴庆阳, 邓亦锋, 等. 基于霍夫变换的结构光场3维成像方法[J]. 激光技术, 2023, 47 (4): 492−499. doi: 10.7510/jgjs.issn.1001-3806.2023.04.008
Zhang Z J, Wu Q Y, Deng Y F, et al. Structured light field 3-D imaging method based on Hough transform[J]. Laser Technol, 2023, 47 (4): 492−499. doi: 10.7510/jgjs.issn.1001-3806.2023.04.008
[9] Gao W, Fan S L, Li G, et al. A thorough benchmark and a new model for light field saliency detection[J]. IEEE Trans Pattern Anal Mach Intell, 2023, 45 (7): 8003−8019. doi: 10.1109/TPAMI.2023.3235415
[10] Chen G, Fu H Z, Zhou T, et al. Fusion-embedding Siamese network for light field salient object detection[J]. IEEE Trans Multimedia, 2024, 26: 984−994. doi: 10.1109/TMM.2023.3274933
[11] Chen Y L, Li G Y, An P, et al. Light field salient object detection with sparse views via complementary and discriminative interaction network[J]. IEEE Trans Circuits Syst Video Technol, 2024, 34 (2): 1070−1085. doi: 10.1109/TCSVT.2023.3290600
[12] Yeung H W F, Hou J H, Chen X M, et al. Light field spatial super-resolution using deep efficient spatial-angular separable convolution[J]. IEEE Trans Image Process, 2019, 28 (5): 2319−2330. doi: 10.1109/TIP.2018.2885236
[13] Wang Y Q, Yang J G, Wang L G, et al. Light field image super-resolution using deformable convolution[J]. IEEE Trans Image Process, 2021, 30: 1057−1071. doi: 10.1109/TIP.2020.3042059
[14] Yoon Y, Jeon H G, Yoo D, et al. Learning a deep convolutional network for light-field image super-resolution[C]//Proceedings of 2015 IEEE International Conference on Computer Vision Workshop, Santiago, 2015: 24–32. https://doi.org/10.1109/ICCVW.2015.17.
[15] Zhang S, Lin Y F, Sheng H. Residual networks for light field image super-resolution[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, 2019: 11046–11055. https://doi.org/10.1109/CVPR.2019.01130.
[16] Jin J, Hou J H, Chen J, et al. Light field spatial super-resolution via deep combinatorial geometry embedding and structural consistency regularization[C]//Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, 2020: 2260–2269. https://doi.org/10.1109/CVPR42600.2020.00233.
[17] 吕天琪, 武迎春, 赵贤凌. 角度差异强化的光场图像超分网络[J]. 光电工程, 2023, 50 (2): 220185. doi: 10.12086/oee.2023.220185
Lv T Q, Wu Y C, Zhao X L. Light field image super-resolution network based on angular difference enhancement[J]. Opto-Electron Eng, 2023, 50 (2): 220185. doi: 10.12086/oee.2023.220185
[18] Chan K H, Im S K. Light-field image super-resolution with depth feature by multiple-decouple and fusion module[J]. Electron Lett, 2024, 60 (1): e13019. doi: 10.1049/ell2.13019
[19] Liang Z Y, Wang Y Q, Wang L G, et al. Angular‐flexible network for light field image super‐resolution[J]. Electron Lett, 2021, 57 (24): 921−924. doi: 10.1049/ell2.12312
[20] Wang S Z, Zhou T F, Lu Y, et al. Detail-preserving transformer for light field image super-resolution[C]//Proceedings of the 36th AAAI Conference on Artificial Intelligence, Vancouver, 2022: 2522–2530. https://doi.org/10.1609/aaai.v36i3.20153.
[21] Wang Y Q, Wang L G, Yang J G, et al. Spatial-angular interaction for light field image super-resolution[C]// Proceedings of the 16th European Conference on Computer Vision, Glasgow, 2020: 290–308. https://doi.org/10.1007/978-3-030-58592-1_18.
[22] Liu G S, Yue H J, Wu J M, et al. Intra-inter view interaction network for light field image super-resolution[J]. IEEE Trans Multimedia, 2023, 25: 256−266. doi: 10.1109/TMM.2021.3124385
[23] 李玉龙, 陈晔曜, 崔跃利, 等. LF-UMTI: 基于多尺度空角交互的无监督多曝光光场图像融合[J]. 光电工程, 2024, 51 (6): 240093. doi: 10.12086/oee.2024.240093
Li Y L, Chen Y Y, Cui Y L, et al. LF-UMTI: unsupervised multi-exposure light field image fusion based on multi-scale spatial-angular interaction[J]. Opto-Electron Eng, 2024, 51 (6): 240093. doi: 10.12086/oee.2024.240093
[24] 武迎春, 王玉梅, 王安红, 等. 基于边缘增强引导滤波的光场全聚焦图像融合[J]. 电子与信息学报, 2020, 42 (9): 2293−2301. doi: 10.11999/JEIT190723
Wu Y C, Wang Y M, Wang A H, et al. Light field all-in-focus image fusion based on edge enhanced guided filtering[J]. J Electron Inf Technol, 2020, 42 (9): 2293−2301. doi: 10.11999/JEIT190723
[25] Wu Y C, Wang Y M, Liang J, et al. Light field all-in-focus image fusion based on spatially-guided angular information[J]. J Vis Commun Image Represent, 2020, 72: 102878. doi: 10.1016/j.jvcir.2020.102878
[26] Liu J, Tang J, Wu G S. Residual feature distillation network for lightweight image super-resolution[C]//Proceedings of 2020 European Conference on Computer Vision Workshops, Glasgow, 2020: 41–55. https://doi.org/10.1007/978-3-030-67070-2_2.
[27] Rerabek M, Ebrahimi T. New light field image dataset[C]//Proceedings of the 8th International Conference on Quality of Multimedia Experience, Lisbon, 2016.
[28] Honauer K, Johannsen O, Kondermann D, et al. A dataset and evaluation methodology for depth estimation on 4D light fields[C]//Proceedings of the 13th Asian Conference on Computer Vision, Taipei, China, 2017, 10113 : 19–34. https://doi.org/10.1007/978-3-319-54187-7_2.
[29] Wanner S, Meister S, Goldluecke B. Datasets and benchmarks for densely sampled 4D light fields[C]// Proceedings of the 18th International Workshop on Vision, Lugano, 2013: 225–226.
[30] Le Pendu M, Jiang X R, Guillemot C. Light field inpainting propagation via low rank matrix completion[J]. IEEE Trans Image Process, 2018, 27 (4): 1981−1993. doi: 10.1109/TIP.2018.2791864
[31] Vaish V, Adams A. The (new) Stanford light field archive[EB/OL]. [2024-3-15]. http://lightfield.stanford.edu/.
[32] Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, 2017: 136–144. https://doi.org/10.1109/CVPRW.2017.151.
[33] Zhang Y L, Li K P, Li K, et al. Image super-resolution using very deep residual channel attention networks[C]//Proceedings of the 15th European Conference on Computer Vision, Munich, 2018: 286–301. https://doi.org/10.1007/978-3-030-01234-2_18.
-
点击扫一扫
图(8)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
