E-mail Alert
RSS
Design of an orbital angular momentum demultiplexing system based on off-axis cascaded metasurfaces
-
摘要:
设计超表面系统时，实际制作的超表面效率与理论设计效率相差较大，常会存在超表面调制效率不足产生的杂散光，这些杂散光作为背景噪声在级联超表面系统中的影响会逐级放大，影响系统功能。为了降低有限效率的超表面对系统性能的影响，本文提出了一种基于离轴级联超表面的轨道角动量解复用系统设计方法。这一工作通过加入离轴相位设计，有效消除了级联超表面系统中因超表面效率降低所产生的杂散光。利用FDTD (时域有限差分)仿真软件进行计算和验证，结果表明，离轴级联超表面系统能有效减少因调制效率不足而产生的杂散光，与同轴系统相比，实现了最大串扰降低4.15 dB以及平均80%的杂散光消除，展现出较大的性能优势。
Abstract:When designing metasurface systems, the actual efficiency of the metasurface is much different from the theoretical design efficiency. This can lead to stray light caused by insufficient modulation efficiency of the metasurfaces, which acts as background noise and is magnified in cascaded metasurface systems step by step, affecting system functionality. To reduce the impact of metasurfaces with limited efficiency on system performance, this paper proposes a design method for an orbital angular momentum demultiplexing system based on off-axis cascaded metasurfaces. By incorporating an off-axis phase design, the stray light generated by the reduced efficiency of the metasurface in a cascaded metasurface system is effectively eliminated. Using FDTD (finite difference time domain) simulation software for calculation and validation, the results demonstrate that the off-axis cascaded metasurface system can effectively reduce stray light caused by insufficient modulation efficiency. Compared to the on-axis system, it achieves a maximum reduction in crosstalk of 4.15 dB and an average of 80% stray light elimination, showing a significant performance advantage.
-
Key words:
- metasurface /
- off-axis /
- cascade /
- orbital angular momentum
-
Overview: Optical orbital angular momentum (OAM) has garnered widespread attention in the fields of high-speed optical communication and quantum communication due to its characteristic of spatial orthogonality. The beam carrying OAM has a spiral phase structure exp(ilθ) in the spatial phase distribution, where the topological charge l can take any integer, which can theoretically provide an infinite number of channels, thus greatly enhancing the capacity of the communication system. As an array of miniature planar structures composed of sub-wavelength structures, the metasurface, with its unique planar structure and precise control of light waves, shows great application potential in promoting miniaturization and integration of space OAM communication systems. When designing metasurface systems, factors such as electromagnetic coupling between metasurface unit structures and insufficient processing precision can lead to the actual efficiency of the metasurface are much different from the theoretical design efficiency. This can often result in stray light due to insufficient modulation efficiency of the metasurface, and the influence of these stray light as background noise in the cascade metasurfaces system will be magnified step by step, affecting the system function. In order to improve the modulation efficiency of metasurface, researchers often use genetic algorithms, topology optimization, and machine learning to design more efficient metasurface structures or use higher precision machining processes to fabricate metasurface. However, these methods are often accompanied by complex computing processes and high manufacturing price costs, which largely limit the widespread use of metasurface in practical optical systems. To reduce the impact of metasurface with limited efficiency on system performance and to decrease the demand for fabricating high-efficiency metasurface structures in high signal-to-noise ratio metasurface systems, based on the coordinate transformation method proposed by Berkhout et al, this paper proposes a design method for an orbital angular momentum demultiplexing system based on off-axis cascaded metasurfaces. By introducing an off-axis design, this work effectively separates the stray light produced in cascaded metasurface systems due to reduced metasurface efficiency. Compared to traditional methods of improving system performance by optimizing the modulation efficiency of metasurface structure, the approach presented in this paper avoids complex structural optimization and the fabrication process of high-efficiency metasurfaces, while also significantly improving optical performance. This design method can be extended to the cascade of multi-level metasurfaces to solve the problem of limiting the number of layers of cascaded super-surfaces, which is of potential application value and significance for the miniaturization and integration of optical systems.
-
-
图 1 (a)同轴与(b)离轴级联超表面轨道角动量解复用系统示意图
Figure 1. Schematic of (a) on-axis and (b) off-axis cascade metasurface OAM demultiplexing system
图 2 (a)单元结构偏振转化率随波长变化曲线；(b) 单元结构偏振转化率随离轴角度变化曲线
Figure 2. (a) Polarization conversion efficiency of a unitary structure as a function of wavelength; (b) Polarization conversion efficiency of a unitary structure as a function of off-angle
图 3 (a)同轴级联超表面轨道角动量解复用系统中信号光与杂散光示意图；(b)解复用系统信噪比随超表面偏振转化率变化曲线
Figure 3. (a) Schematic of signal/noise in OAM demultiplexing system based on on-axis cascaded metasurface; (b) SNR of demultiplexing system as a function of polarization conversion efficiency
图 4 (a)离轴级联超表面轨道角动量解复用系统中信号光与杂散光示意图；(b)解复用系统信噪比随超表面偏振转换率以及离轴角度的变化曲线图
Figure 4. (a) Schematic of signal/noise in OAM demultiplexing system based on off-axis cascaded metasurface; (b) SNR of demultiplexing system as a function of polarization conversion efficiency and off-angle
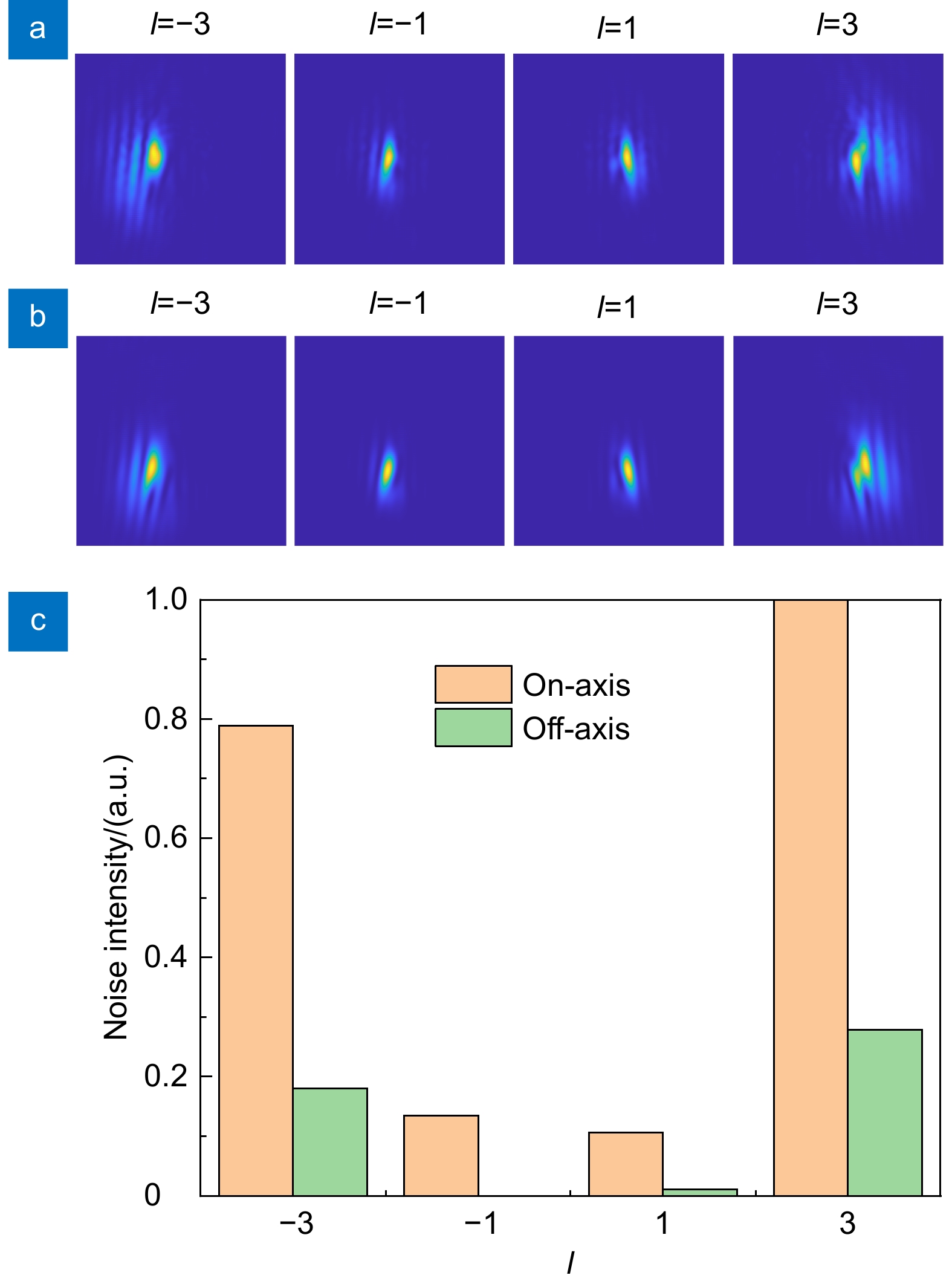
图 5 (a)同轴与(b)离轴系统中不同OAM状态(l = ±1, ±3)对应的的出射光强分布图；(c) 同轴与离轴系统中不同OAM状态(l = ±1, ±3)出射场范围内归一化杂散光强度
Figure 5. (a) On-axis and (b) off-axis , intensity profiles corresponding to different OAM states (l = ±1, ±3); (c) Normalized noise intensities in the range of outgoing field for different OAM states (l = ±1, ±3) in on-axis and off-axis system
-
[1] García-Escartín J C, Chamorro-Posada P. Quantum multiplexing with the orbital angular momentum of light[J]. Phys Rev A, 2008, 78(6): 062320. doi: 10.1103/PhysRevA.78.062320
[2] Yan Y, Xie G D, Lavery M P J, et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing[J]. Nat Commun, 2014, 5: 4876. doi: 10.1038/ncomms5876
[3] Willner A E, Huang H, Yan Y, et al. Optical communications using orbital angular momentum beams[J]. Adv Opt Photonics, 2015, 7(1): 66−106. doi: 10.1364/AOP.7.000066
[4] Yuan X Y, Xu Q, Lang Y H, et al. Tailoring spatiotemporal dynamics of plasmonic vortices[J]. Opto-Electron Adv, 2023, 6(4): 220133. doi: 10.29026/oea.2023.220133
[5] Allen L, Beijersbergen M W, Spreeuw R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Phys Rev A, 1992, 45(11): 8185−8189. doi: 10.1103/PhysRevA.45.8185
[6] Allen L, Padgett M J, Babiker M. IV the orbital angular momentum of light[J]. Prog Opt, 1999, 39: 291−372. doi: 10.1016/S0079-6638(08)70391-3
[7] Pendry J B, Schurig D, Smith D R. Controlling electromagnetic fields[J]. Science, 2006, 312(5781): 1780−1782. doi: 10.1126/science.1125907
[8] Yu N F, Capasso F. Flat optics with designer metasurfaces[J]. Nat Mater, 2014, 13(2): 139−150. doi: 10.1038/nmat3839
[9] Luo X G, Pu M B, Ma X L, et al. Taming the electromagnetic boundaries via metasurfaces: from theory and fabrication to functional devices[J]. Int J Antennas Propag, 2015, 2015: 204127. doi: 10.1155/2015/204127
[10] 张飞, 郭迎辉, 蒲明博, 等. 基于非对称光子自旋—轨道相互作用的超构表面[J]. 光电工程, 2020, 47(10): 200366. doi: 10.12086/oee.2020.200366
Zhang F, Guo Y H, Pu M B, et al. Metasurfaces enabled by asymmetric photonic spin-orbit interactions[J]. Opto-Electron Eng, 2020, 47(10): 200366. doi: 10.12086/oee.2020.200366
[11] Yu N F, Genevet P, Kats M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333−337. doi: 10.1126/science.1210713
[12] Li Y, Li X, Chen L W, et al. Orbital angular momentum multiplexing and demultiplexing by a single metasurface[J]. Adv Opt Mater, 2017, 5(2): 1600502. doi: 10.1002/adom.201600502
[13] Berkhout G C G, Lavery M P J, Courtial J, et al. Efficient sorting of orbital angular momentum states of light[J]. Phys Rev Lett, 2010, 105(15): 153601. doi: 10.1103/PhysRevLett.105.153601
[14] Lavery M P J, Robertson D J, Berkhout G C G, et al. Refractive elements for the measurement of the orbital angular momentum of a single photon[J]. Opt Express, 2012, 20(3): 2110−2115. doi: 10.1364/OE.20.002110
[15] Ruffato G, Massari M, Parisi G, et al. Test of mode-division multiplexing and demultiplexing in free-space with diffractive transformation optics[J]. Opt Express, 2017, 25(7): 7859−7868. doi: 10.1364/OE.25.007859
[16] Ruffato G, Massari M, Romanato F. Compact sorting of optical vortices by means of diffractive transformation optics[J]. Opt Lett, 2017, 42(3): 551−554. doi: 10.1364/OL.42.000551
[17] Ruffato G, Girardi M, Massari M, et al. A compact diffractive sorter for high-resolution demultiplexing of orbital angular momentum beams[J]. Sci Rep, 2018, 8(1): 10248. doi: 10.1038/s41598-018-28447-1
[18] Ruffato G, Capaldo P, Massari M, et al. Total angular momentum sorting in the telecom infrared with silicon Pancharatnam-Berry transformation optics[J]. Opt Express, 2019, 27(11): 15750−15764. doi: 10.1364/OE.27.015750
[19] Ruffato G, Massari M, Girardi M, et al. Non-paraxial design and fabrication of a compact OAM sorter in the telecom infrared[J]. Opt Express, 2019, 27(17): 24123−24134. doi: 10.1364/OE.27.024123
[20] Cheng J P, Sha X B, Zhang H, et al. Ultracompact orbital angular momentum sorter on a CMOS chip[J]. Nano Lett, 2022, 22(10): 3993−3999. doi: 10.1021/acs.nanolett.2c00572
[21] Wang B M, Wen Y H, Zhu J B, et al. Sorting full angular momentum states with Pancharatnam-Berry metasurfaces based on spiral transformation[J]. Opt Express, 2020, 28(11): 16342−16351. doi: 10.1364/OE.393859
[22] Li Y, Hong M H. Diffractive efficiency optimization in metasurface design via electromagnetic coupling compensation[J]. Materials (Basel), 2019, 12(7): 1005. doi: 10.3390/ma12071005
[23] Yang Z Y, Wang Z K, Wang Y X, et al. Generalized Hartmann-Shack array of dielectric metalens sub-arrays for polarimetric beam profiling[J]. Nat Commun, 2018, 9(1): 4607. doi: 10.1038/s41467-018-07056-6
[24] Chen R, Zhou Y, Chen W J, et al. Multifunctional metasurface: coplanar embedded design for metalens and nanoprinted display[J]. ACS Photonics, 2020, 7(5): 1171−1177. doi: 10.1021/acsphotonics.9b01795
[25] Fan Y L, Xu Y K, Qiu M, et al. Phase-controlled metasurface design via optimized genetic algorithm[J]. Nanophotonics, 2020, 9(12): 3931−3939. doi: 10.1515/nanoph-2020-0132
[26] Huang M, Zheng B, Cai T, et al. Machine–learning-enabled metasurface for direction of arrival estimation[J]. Nanophotonics, 2022, 11(9): 2001−2010. doi: 10.1515/nanoph-2021-0663
[27] Ji W Y, Chang J, Xu H X, et al. Recent advances in metasurface design and quantum optics applications with machine learning, physics-informed neural networks, and topology optimization methods[J]. Light Sci Appl, 2023, 12(1): 169. doi: 10.1038/s41377-023-01218-y
[28] Xu M F, Pu M B, Sang D, et al. Topology-optimized catenary-like metasurface for wide-angle and high-efficiency deflection: from a discrete to continuous geometric phase[J]. Opt Express, 2021, 29(7): 10181−10191. doi: 10.1364/OE.422112
[29] Nishijima Y, Balčytis A, Naganuma S, et al. Kirchhoff’s metasurfaces towards efficient photo-thermal energy conversion[J]. Sci Rep, 2019, 9(1): 8284. doi: 10.1038/s41598-019-44781-4
[30] Xu Z J, Dong Y, Tseng C K, et al. CMOS-compatible all-Si metasurface polarizing bandpass filters on 12-inch wafers[J]. Opt Express, 2019, 27(18): 26060−26069. doi: 10.1364/OE.27.026060
[31] Meng W J, Hua Y L, Cheng K, et al. 100 Hertz frame-rate switching three-dimensional orbital angular momentum multiplexing holography via cross convolution[J]. Opto-Electron Sci, 2022, 1(9): 220004. doi: 10.29026/oes.2022.220004
[32] Zheng G X, Mühlenbernd H, Kenney M, et al. Metasurface holograms reaching 80% efficiency[J]. Nat Nanotechnol, 2015, 10(4): 308−312. doi: 10.1038/nnano.2015.2
[33] Pancharatnam S. Generalized theory of interference, and its applications: part I. Coherent pencils[J]. Proc Indian Acad Sci-Sec A, 1956, 44(5): 247−262. doi: 10.1007/BF03046050
[34] Berry M V, Dennis M R. Polarization singularities in isotropic random vector waves[J]. Proc R Soc Lond A Math Phys Sci, 2001, 457(2005): 141−155. doi: 10.1098/rspa.2000.0660
[35] Li S Q, Li X Y, Zhang L, et al. Efficient optical angular momentum manipulation for compact multiplexing and demultiplexing using a dielectric metasurface[J]. Adv Opt Mater, 2020, 8(8): 1901666. doi: 10.1002/adom.201901666
[36] Mirhosseini M, Malik M, Shi Z M, et al. Efficient separation of the orbital angular momentum eigenstates of light[J]. Nat Commun, 2013, 4: 2781. doi: 10.1038/ncomms3781
[37] Wen Y H, Chremmos I, Chen Y J, et al. Spiral transformation for high-resolution and efficient sorting of optical vortex modes[J]. Phys Rev Lett, 2018, 120(19): 193904. doi: 10.1103/PhysRevLett.120.193904
-
下载:
点击扫一扫
图(6)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
