E-mail Alert
RSS
Review of nonlinearity correction of frequency modulated continuous wave LiDAR measurement technology
-
摘要:
现代测量技术中，频率调制连续波激光雷达结合了传统雷达和激光干涉测量的优点，凭借其非接触性、测量范围大、分辨率高和抗干扰能力强等特性，在大尺寸空间精密测量、微小测量以及生物计量等领域发挥着至关重要的作用。但实际应用中，激光光源的频率调制不能呈现出完全线性，使得频率调制连续波激光雷达技术的测量精度严重下降。所以，如何抑制激光的调频非线性带来的影响成为频率调制连续波激光雷达测量领域的一项研究热点。本文介绍了频率调制连续波激光雷达的工作原理，根据频率调制非线性校正方案的不同，针对性地介绍和分析了四种应用较为广泛和部分特殊的非线性校正方法，并进行了总结和展望。
Abstract:In modern measurement technology, frequency modulation continuous wave LiDAR combines the advantages of traditional radar and laser interferometry and plays an important role in the fields of the large-size space precision measurement, micro-distance measurement, and three-dimensional imaging with its characteristics such as non-contact, large measurement range, high resolution, and strong anti-jamming capability. However, in practical application, the frequency modulation of the laser light source can’t be completely linear, which greatly reduces the measurement accuracy of the frequency modulation continuous wave LiDAR technology. Therefore, how to suppress the effects of the laser frequency modulation nonlinearity has become a hot research topic in the field of frequency modulation continuous wave LiDAR measurement. This paper introduces the basic principle of the frequency modulation continuous wave LiDAR, and introduces four widely used nonlinear correction methods and some special nonlinear correction methods according to the different nonlinear correction schemes of the frequency modulation, and makes summaries and prospects.
-
Key words:
- frequency modulation continuous wave /
- LiDAR /
- interferometry /
- nonlinear correction
-
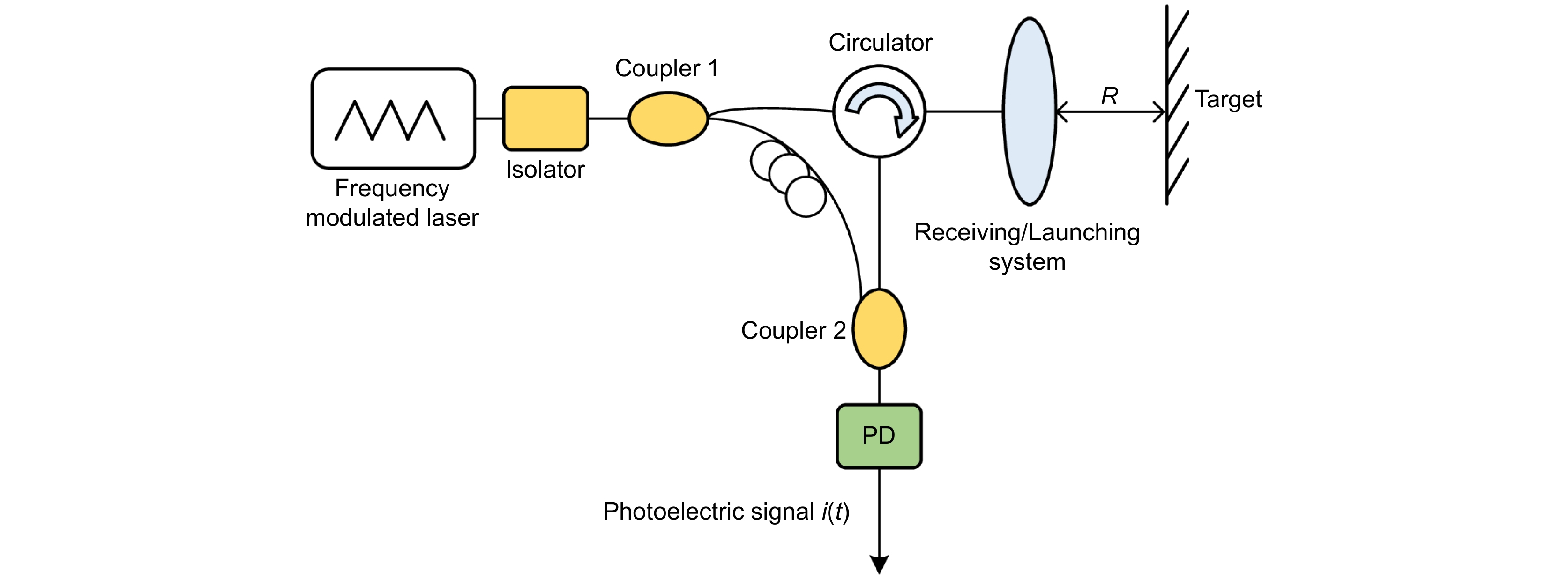
Overview: In the 1980s, Skolnik from Switzerland proposed a theoretical model of frequency modulation continuous wave (FMCW), and single-mode semiconductor lasers were also gradually used by researchers, which led to the formation of the frequency modulated continuous wave (FMCW) LiDAR. Frequency modulation continuous wave LiDAR is a kind of laser detection and ranging, which belongs to coherent detection. FMCW LiDAR combines the advantages of traditional radar and laser interferometry and has the advantages of large measurement range, high precision, high sensitivity, fast speed, high resolution, no distance blind zone, low transmission power, strong anti-interference ability, and no need to cooperate with targets. It is widely used in various fields such as large-scale and precision equipment manufacturing, atmospheric exploration, aerospace, and the 3D imaging because of these advantages.
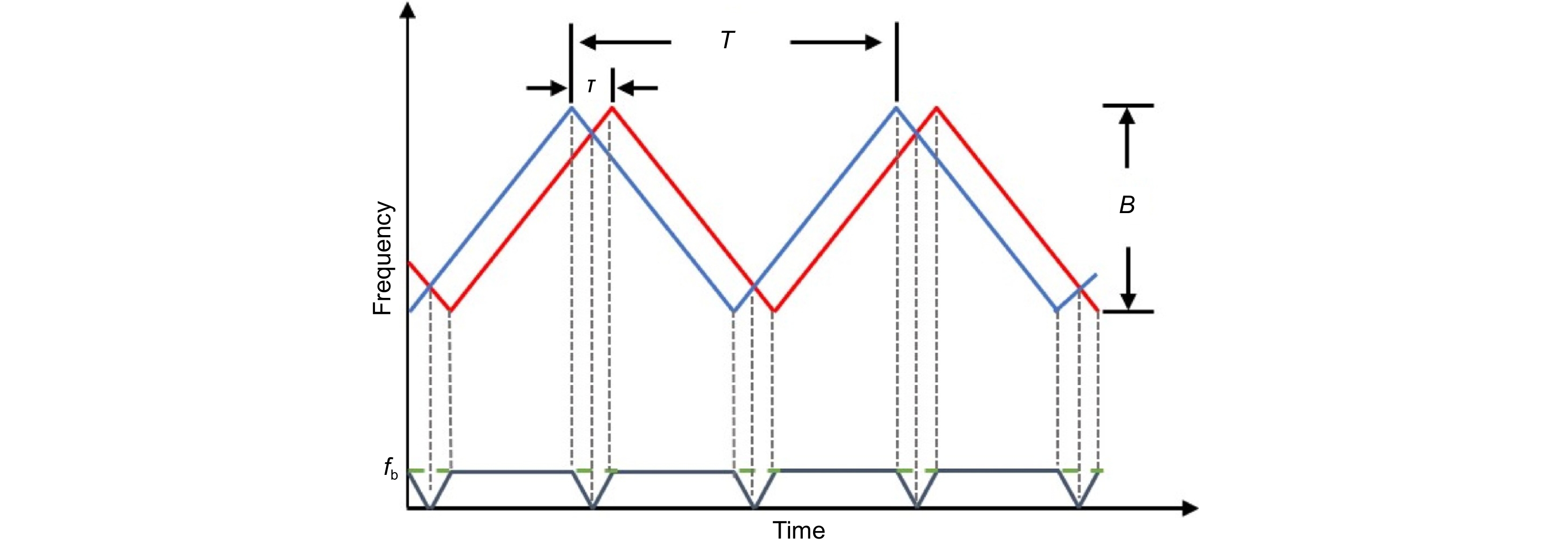
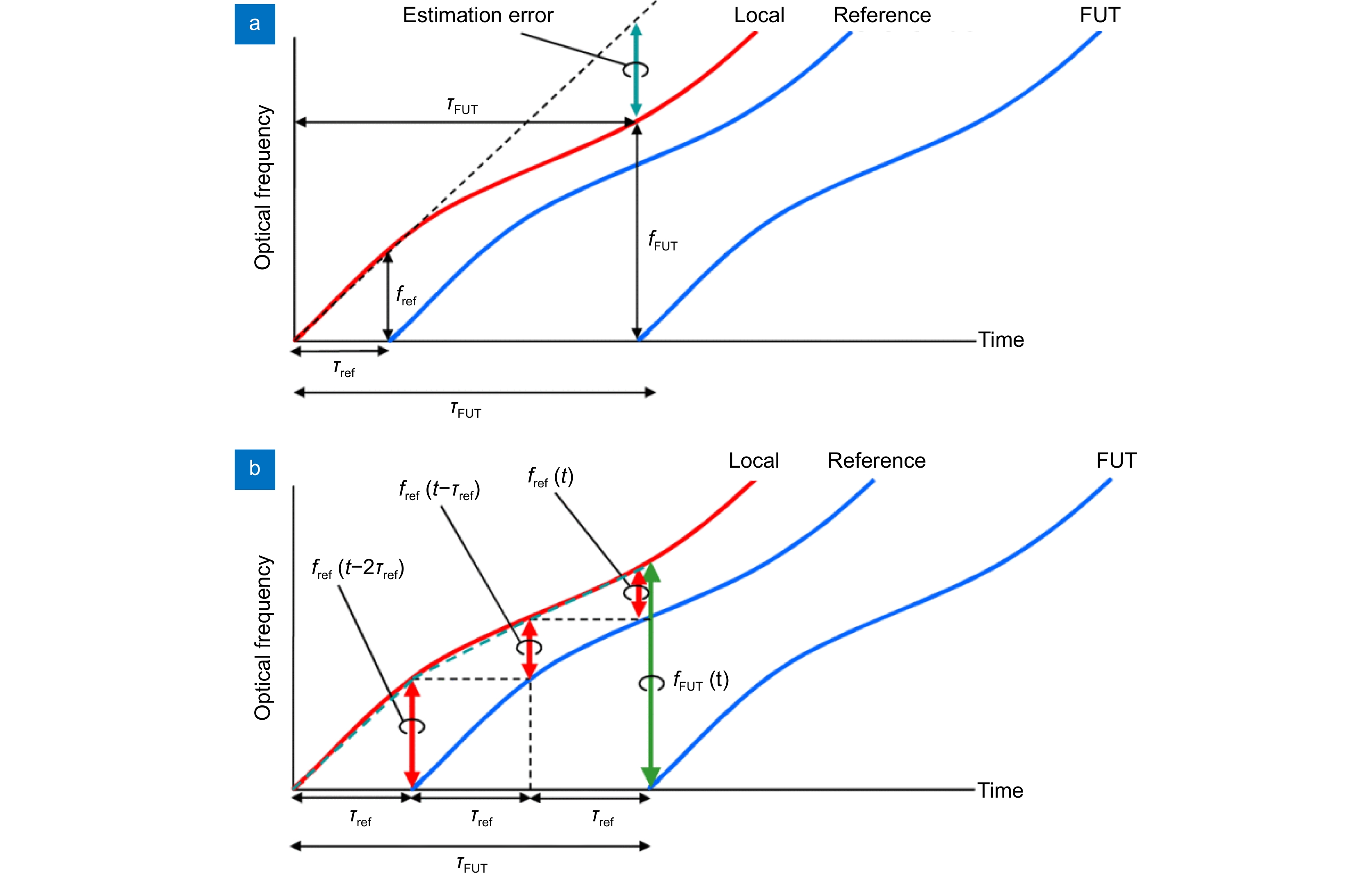
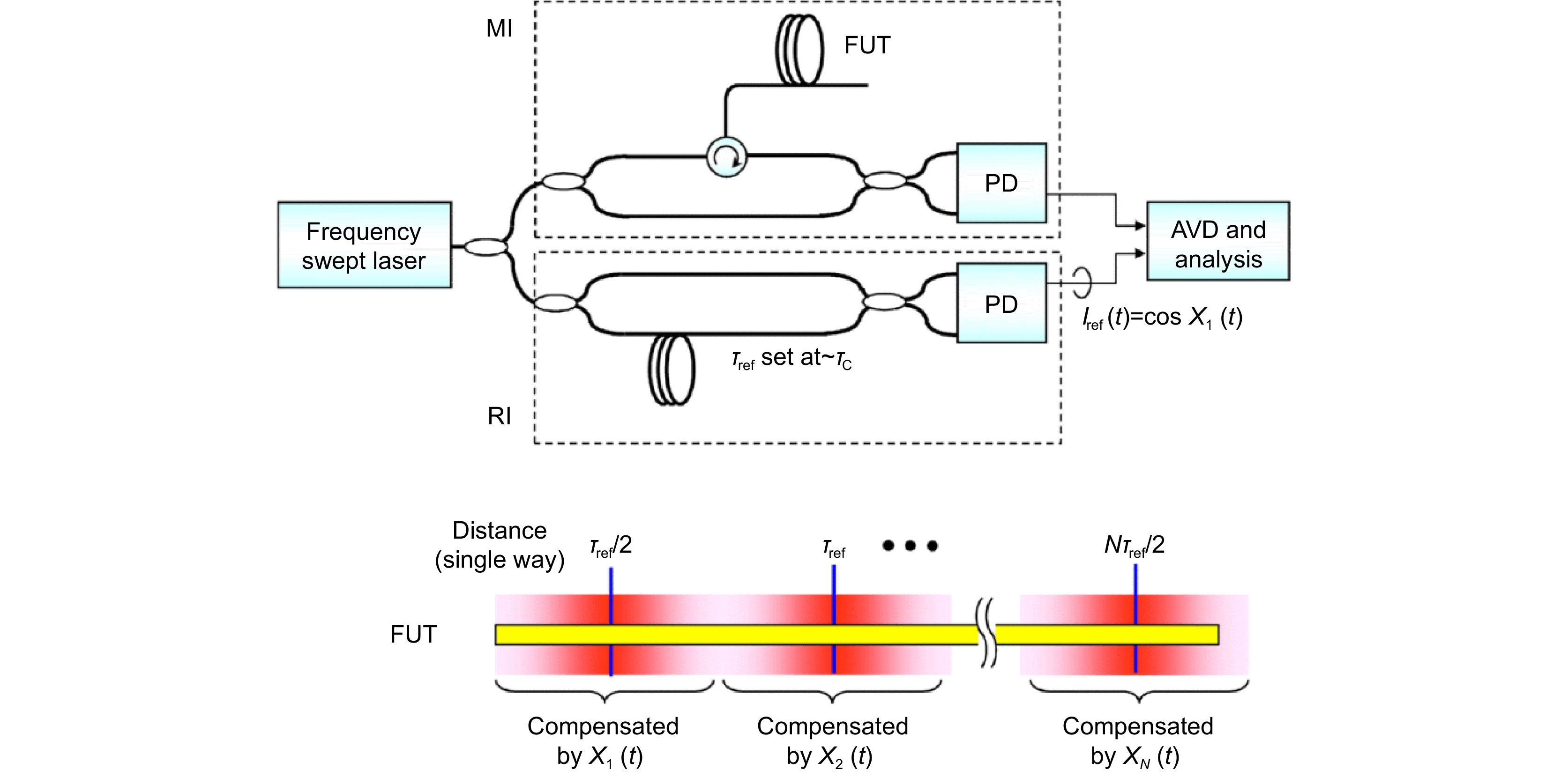
In principle, the FMCW LiDAR ranging system uses the interference of the frequency linearly modulated laser emission signal and echo signal to form a stable beat signal, then calculate the target’s distance based on the frequency or phase of the beat signal. Therefore, the FMCW LiDAR ranging system has very strict requirements on the linearity of frequency modulation. However, the frequency modulation of laser light source can’t be completely linear in practical application, seriously affecting the ranging accuracy, and resolution. This makes the nonlinearity correction of the FM become the research focus of the FMCW LiDAR ranging systems. According to the different correction schemes, we can summarize the methods of frequency modulation nonlinear correction into frequency sweep active linearization based on the phase-locked loop feedback, equal optical frequency interval resampling, optical frequency comb correction method, phase ratio method, and some other special correction methods, such as on-chip modulator-based approaches. These nonlinear correction methods have their advantages and disadvantages. And this paper introduces and analyzes the principles and research progress of these methods.
Although the FMCW LiDAR measurement technology has gradually matured, further exploration and research is still needed. At present, most of the nonlinear correction methods focus on the optical system and signal processing, but we hope to solve the problem from the design of the laser itself, and make further improvements in its mechanical structure, circuit design, and temperature control to avoid subsequent complicated work. In order to achieve true intelligence, on the one hand, we need to improve the efficiency of measurement (especially three-dimensional imaging). On the other hand, we must strive to miniaturize and integrate the FMCW LiDAR measurement system to bring more convenience and wider application scenarios.
-
-
图 1 2006~2021年FMCW的发文量和被引频次
Figure 1. The quantity of papers and times cited of FMCW from 2006 to 2021
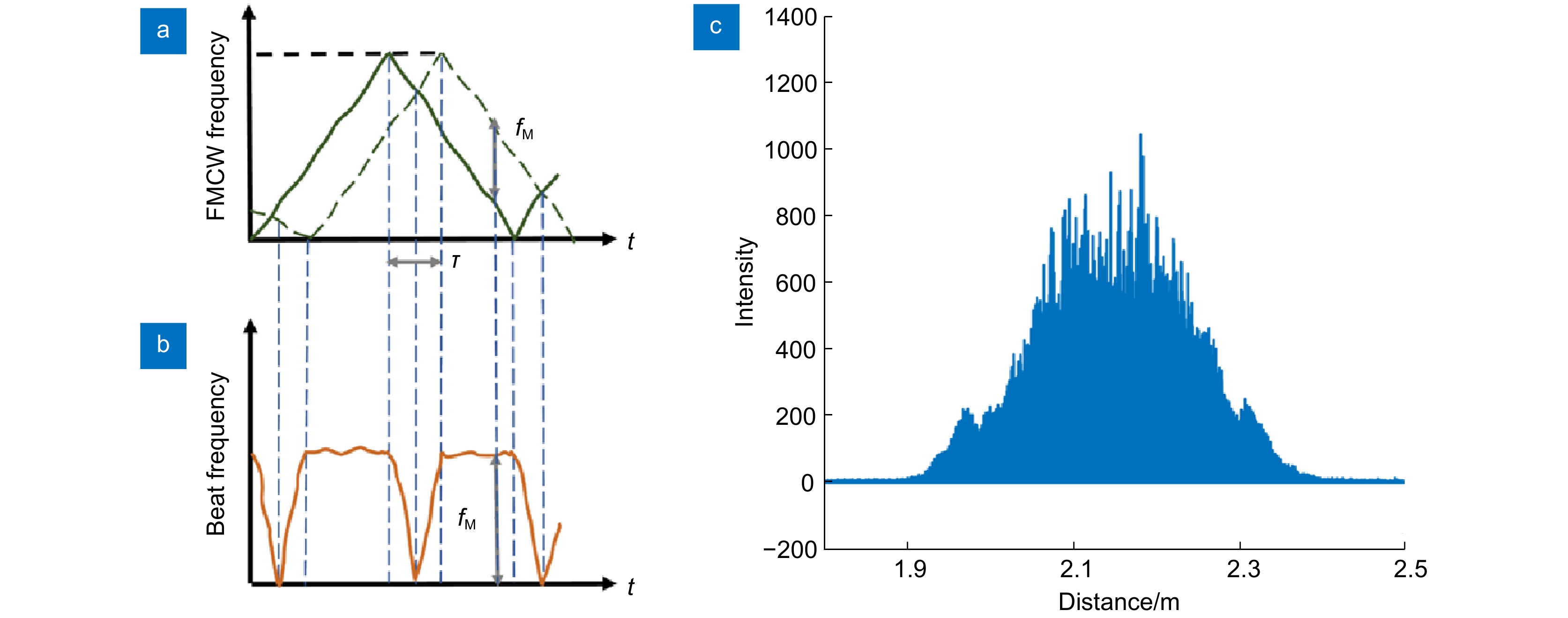
图 4 调频非线性对测距结果的影响。(a) FMCW信号的时频图；(b) 波动拍频信号的时频图；(c) 未经非线性校准的测距信号频谱图[15]
Figure 4. Influence of FM nonlinearity on ranging results. (a) Time-frequency graph of the FMCW signal; (b) Time-frequency graph of the fluctuant beat signal; (c) A broadened distance spectrum obtained by FFT on the ranging signal without nonlinear calibration[15]
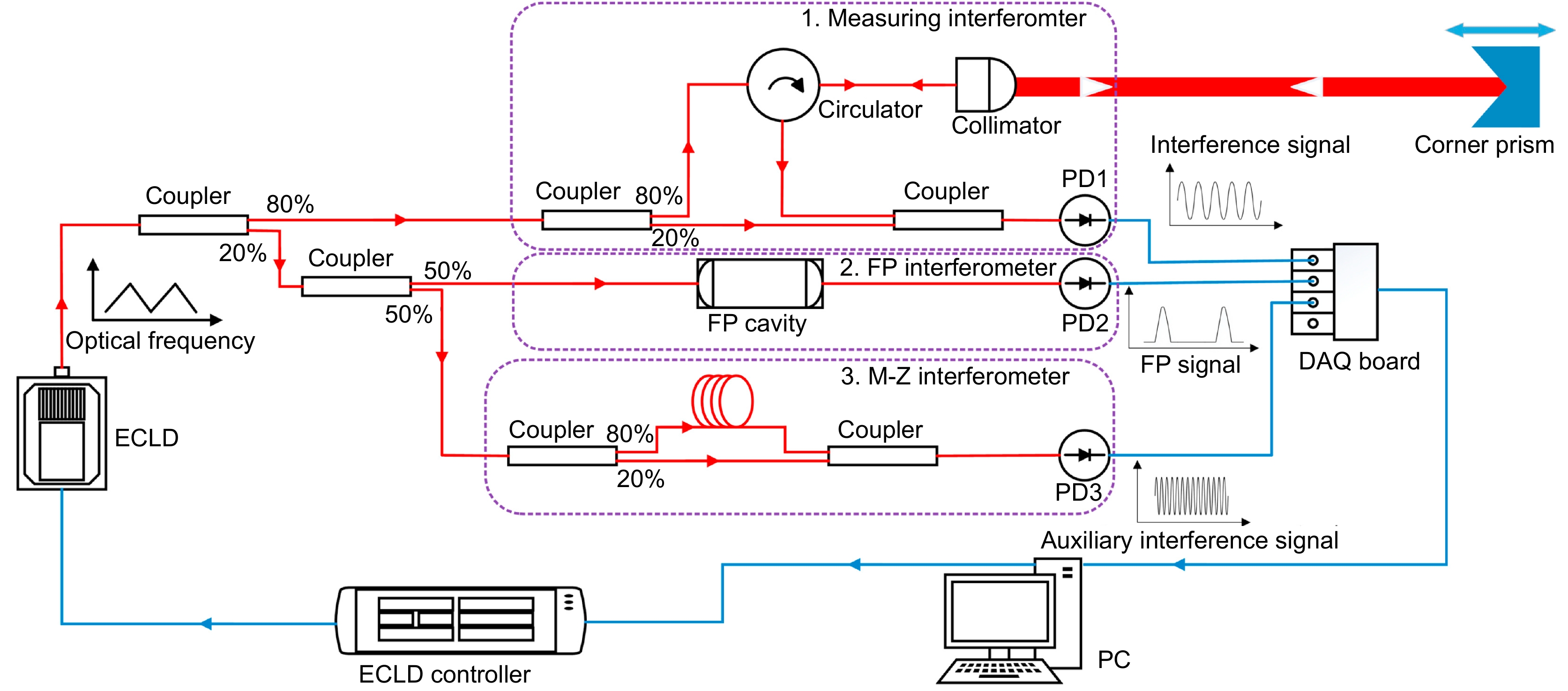
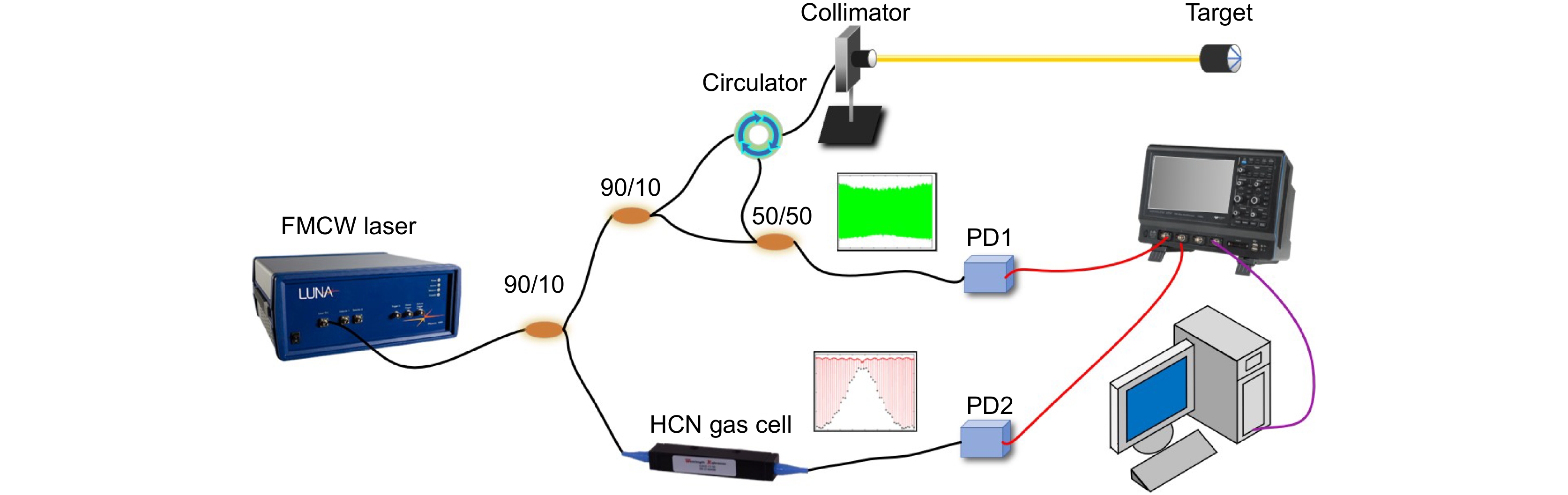
图 5 (a) 使用自外差技术进行宽带光学频率线性化的实验装置；(b) 上图：40次连续测量的距离误差，误差标准差为86 nm；下图：目标的相对距离测量，以步长为10 μm移动超过 100 μm[17]
Figure 5. (a) Experimental setup for broadband optical frequency chirp linearization using the self-heterodyne technique; (b) Top: range peak centers for 40 consecutive measurements. The standard deviation of the errors is 86 nm. Bottom: relative range measured as the target was manually moved over 100 μm in 10 μm increments[17]
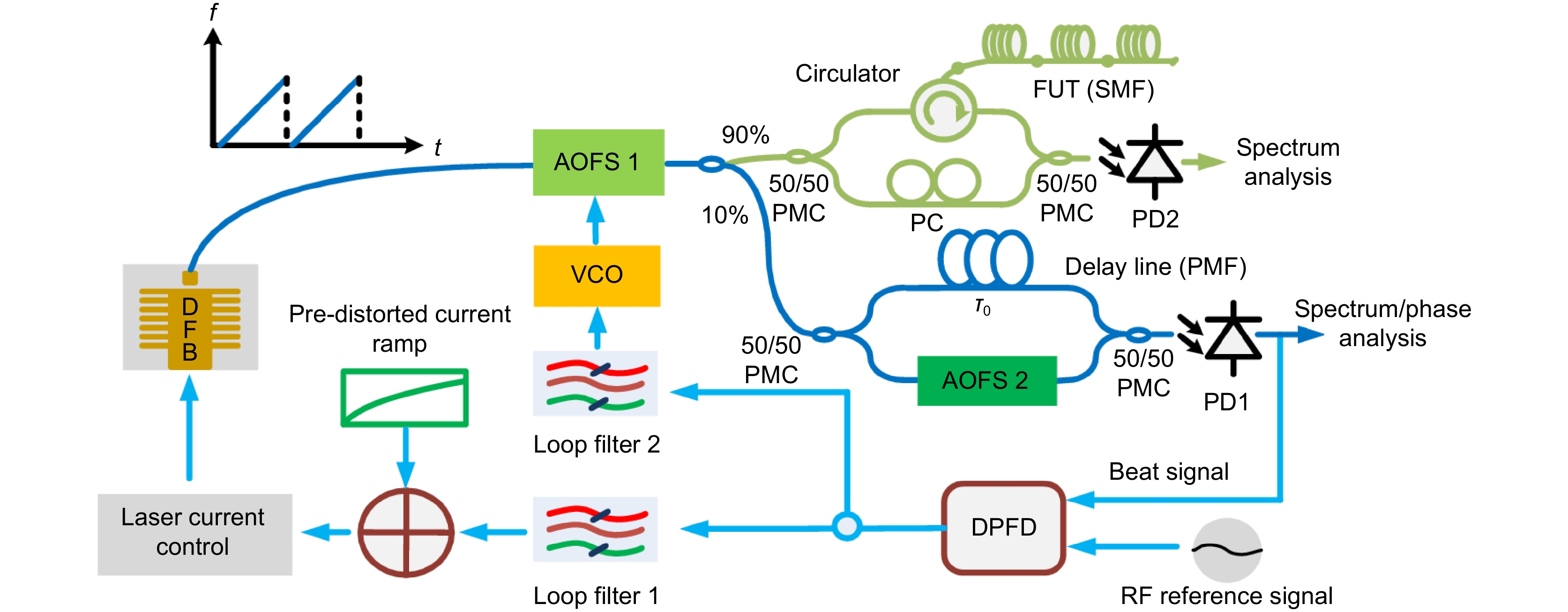
图 6 (a) 用于生成精确宽带线性啁啾的光电反馈回路；(b) 环路锁定时环路光电探测器输出的测量光谱图，对应于100 GHz/ms 的光扫描速率；(c) 在1 ms持续时间内测量的光电探测器输出的傅里叶变换[18]
Figure 6. (a) Optoelectronic feedback loop for the generation of accurate broadband linear chirps; (b) Measured spectrogram of the output of the loop photodetector when the loop is in lock, corresponding to an optical sweep rate of 100 GHz/ms; (c) Fourier transform of the photodetector output measured over a 1 ms duration[18]
图 9 等光频间隔重采样测距原理图
Figure 9. Schematic of distance measurement with equal optical frequency interval resampling
图 13 一种单通道检测的调频非线性校正的新硬件结构。
Figure 13. A new hardware structure for correcting FM nonlinearity with only a single detection channel.
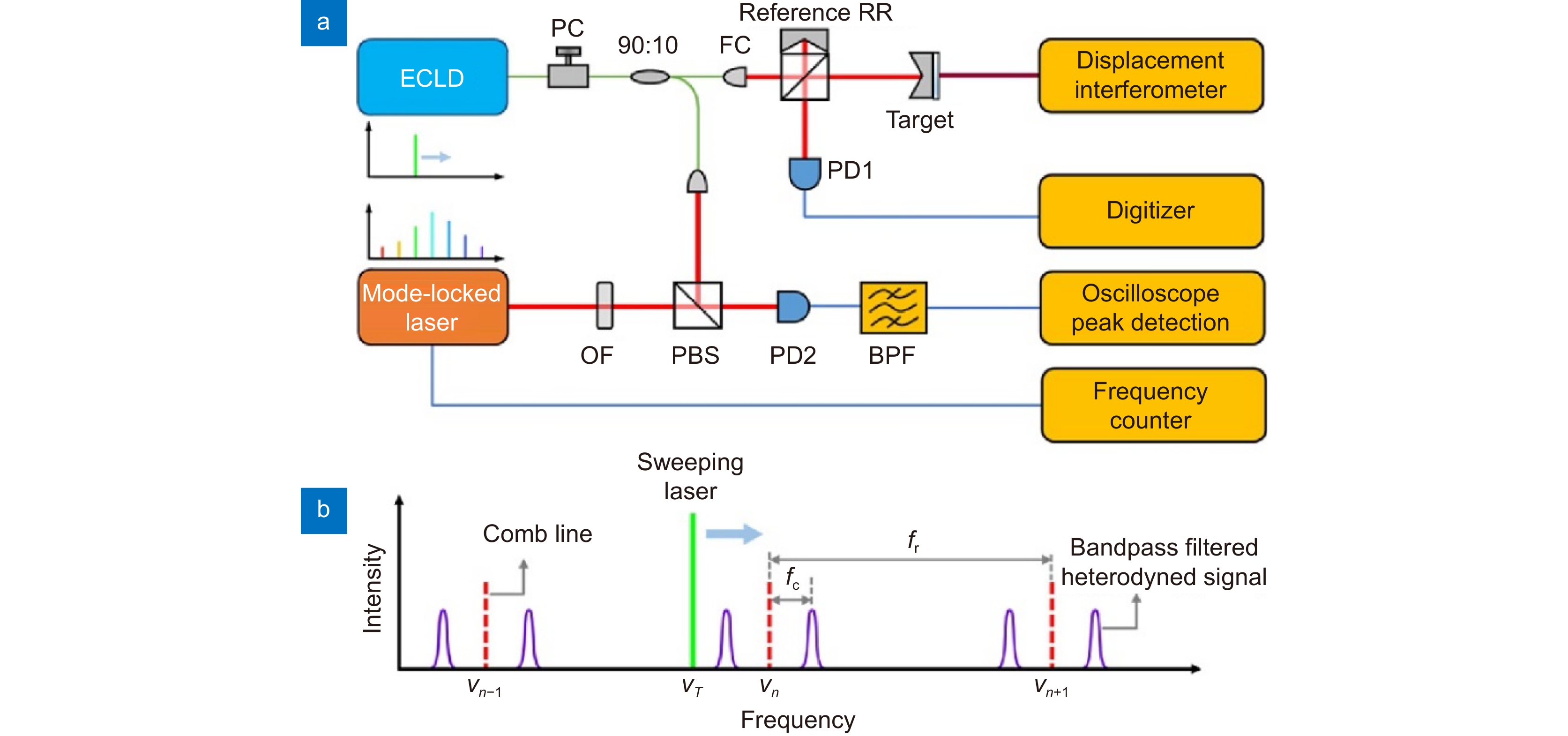
图 14 (a) 实验装置。基于MEMS的ECL以1 ms的周期在1 THz上进行正弦扫描。该系统根据自由运行的频率梳测量，同时记录激光雷达外差信号和瞬时ECL频率；(b) 测得的激光雷达信号的波形图。峰值幅度对应于fFMCW(t)；(c) ECL瞬时频率，vECL(t)−v0；(d) 单次0.5 ms长扫描和~10 nW~100 nW返回功率的拉丝铝表面的距离信号；(e) 放大图说明了ΔR = 0.9c/(2B) = 130 μm的未变迹、带宽受限分辨率，尽管扫描速率高达3400 THz/s[45]
Figure 14. (a) Experimental setup. A MEMS-based ECL is swept sinusoidally over 1 THz with a 1 ms period. The system simultaneously records the ladar heterodyne signal and the instantaneous ECL frequency, as measured against a free-running frequency comb; (b) Sonogram of the measured ladar signal. The peak amplitude corresponds to fFMCW(t); (c) Instantaneous ECL frequency, vECL(t)−v0; (d) Range signal to the brushed Al surface for a single 0.5 ms long sweep and ~10 nW~100 nW return power; (e) Expanded view illustrating the unapodized, bandwidth-limited resolution of ΔR = 0.9c/(2B) = 130 μm, despite the sweep rate of up to 3400 THz/s[45]
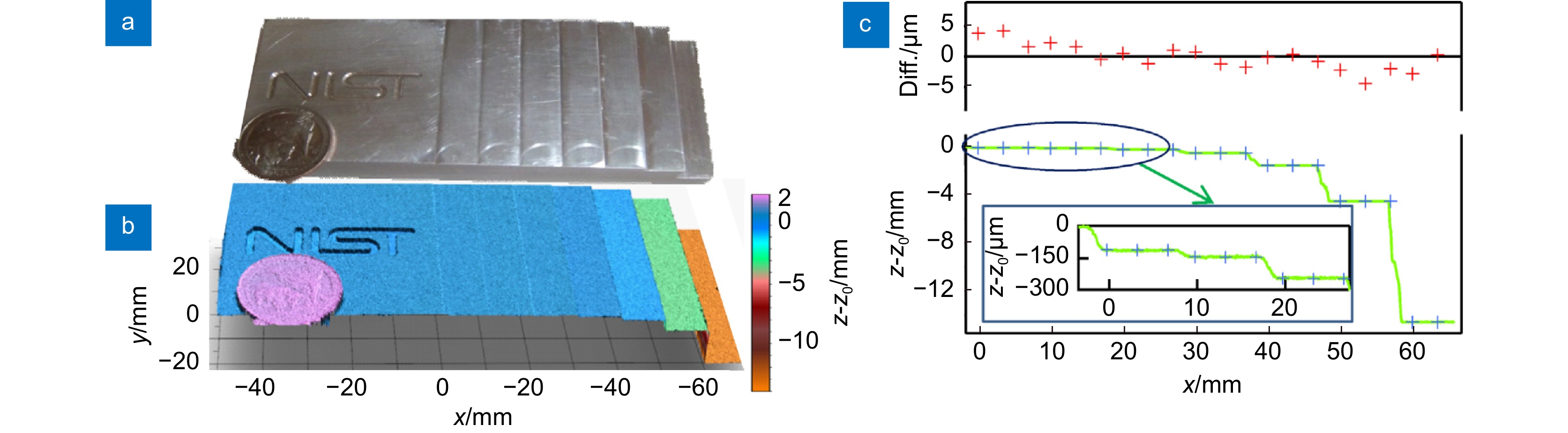
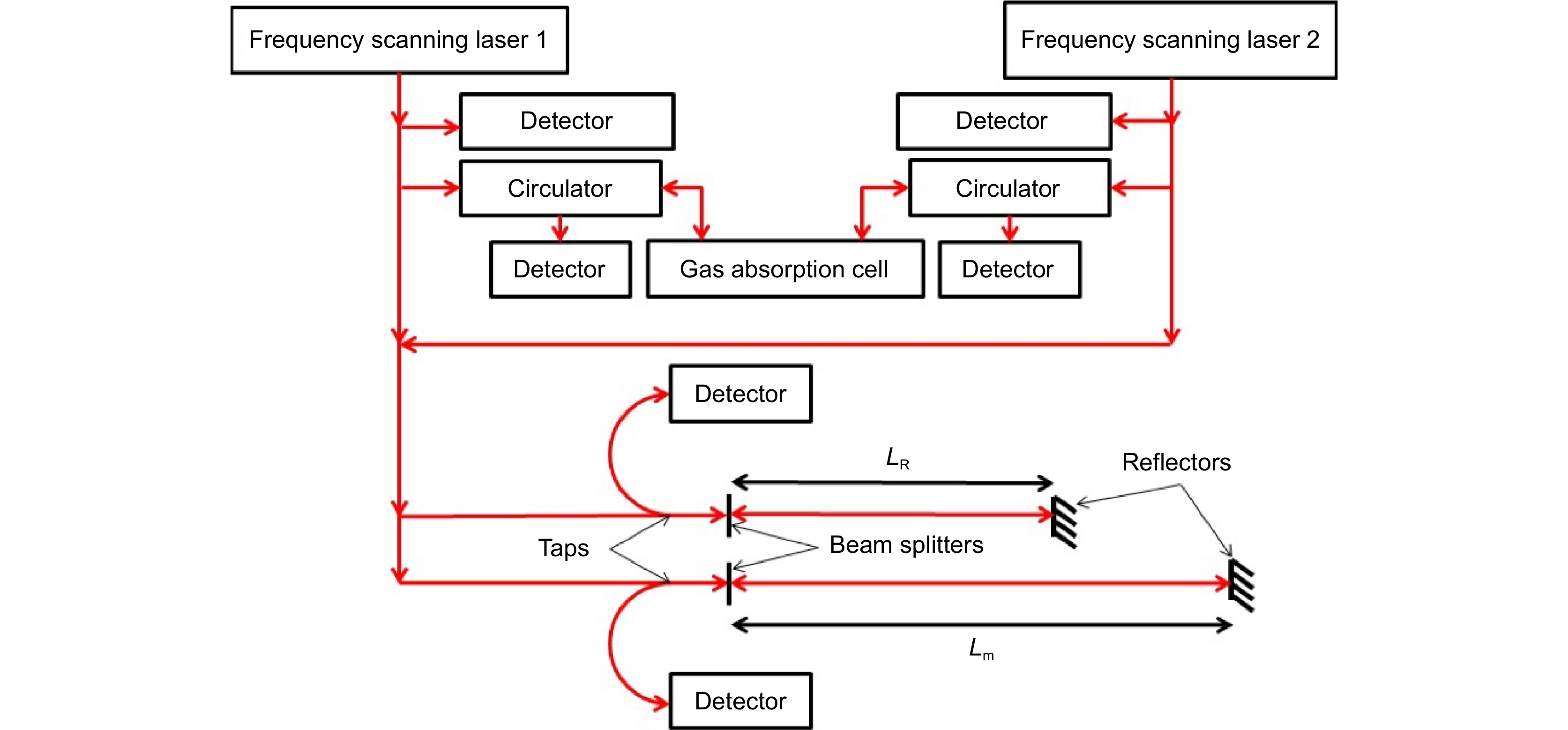
图 15 (a) 一个带NIST标志的阶梯式铝块和一个25美分的硬币；(b) 由FMCW LiDAR系统在z0= 4.760 m测量得到的三维假彩图；(c) 从三维图像中提取的截面(绿色轨迹)与用坐标测量机(CMM)进行测量的结果(蓝色叉线)对比图，误差(红色叉线)标准差低于 2 μm[46]
Figure 15. (a) Photograph of an Al-step block with the NIST logo imprinted and a quarter located on the lower left corner; (b) False colored, 3D surface image of the step block, along with a quarter on the bottom left, measured by our FMCW LADAR system at a stand-off of z0= 4.760 m; (c) The FMCW LADAR image (green trace) is compared to an average of 12 measurement points taken with a CMM (blue crosses). The error (red crosses) has a standard deviation below 2 μm[46]
图 16 (a) 利用窄带通滤波器标定瞬时频率的测量示意图；(b) 扫频激光，梳线和带通滤波器的频率位置示意图。
Figure 16. (a) Measurement schematic diagram of instantaneous frequency calibration with narrow bandpass filter; (b) Illustration of frequency positions of the sweeping laser, comb lines, and the bandpass filter.
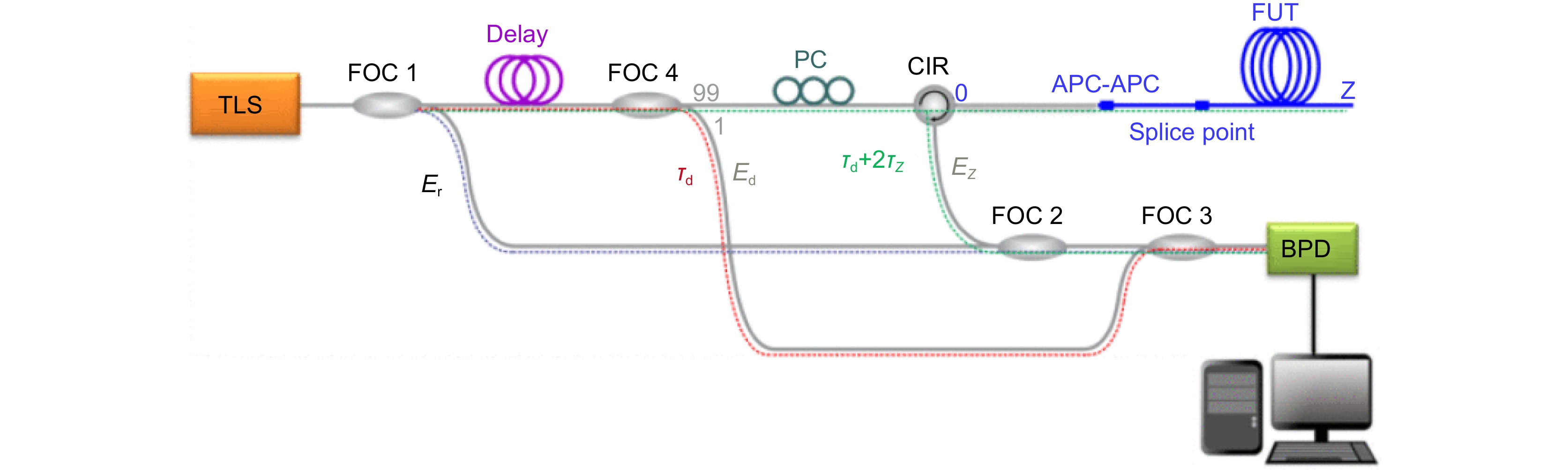
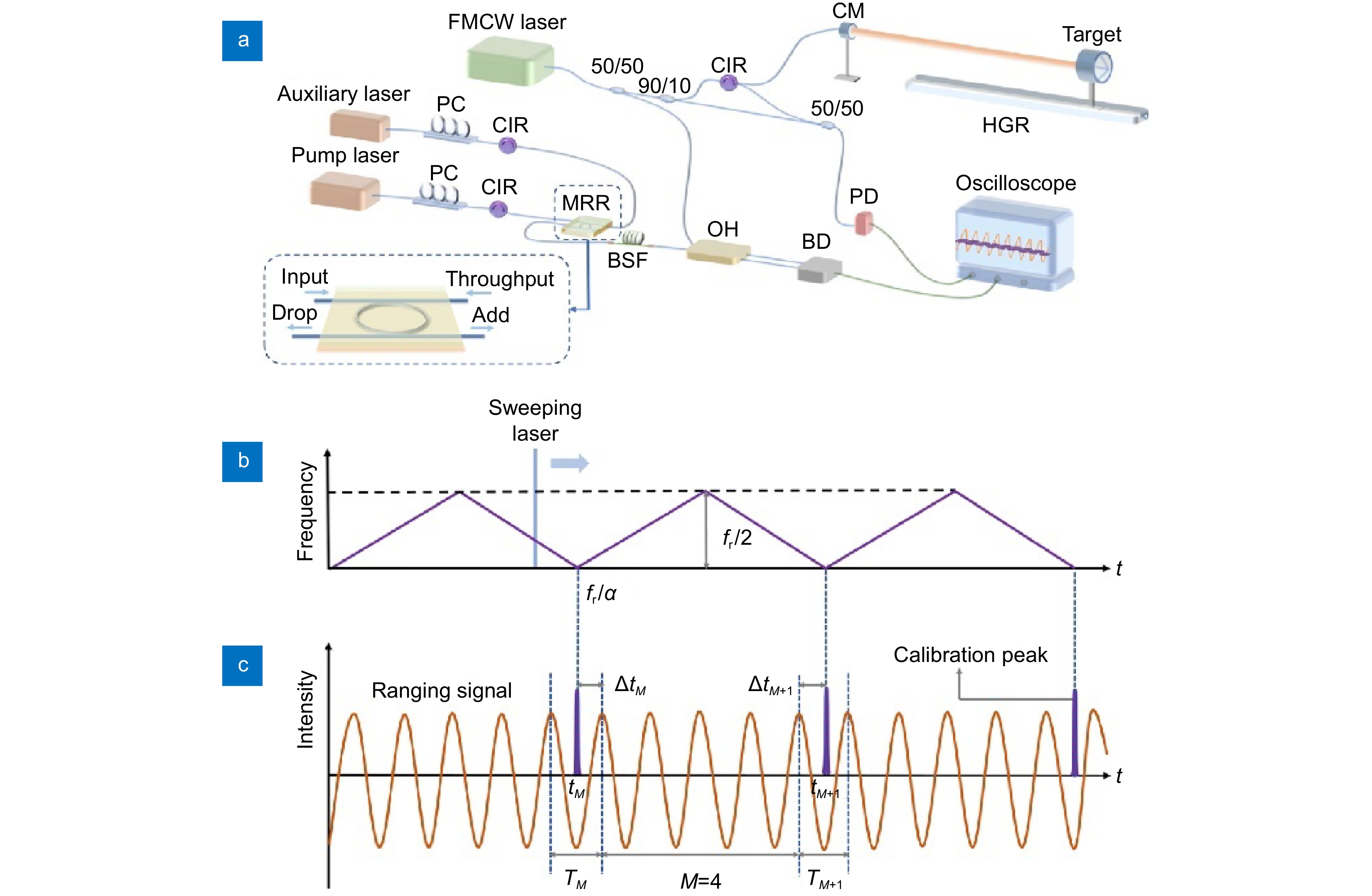
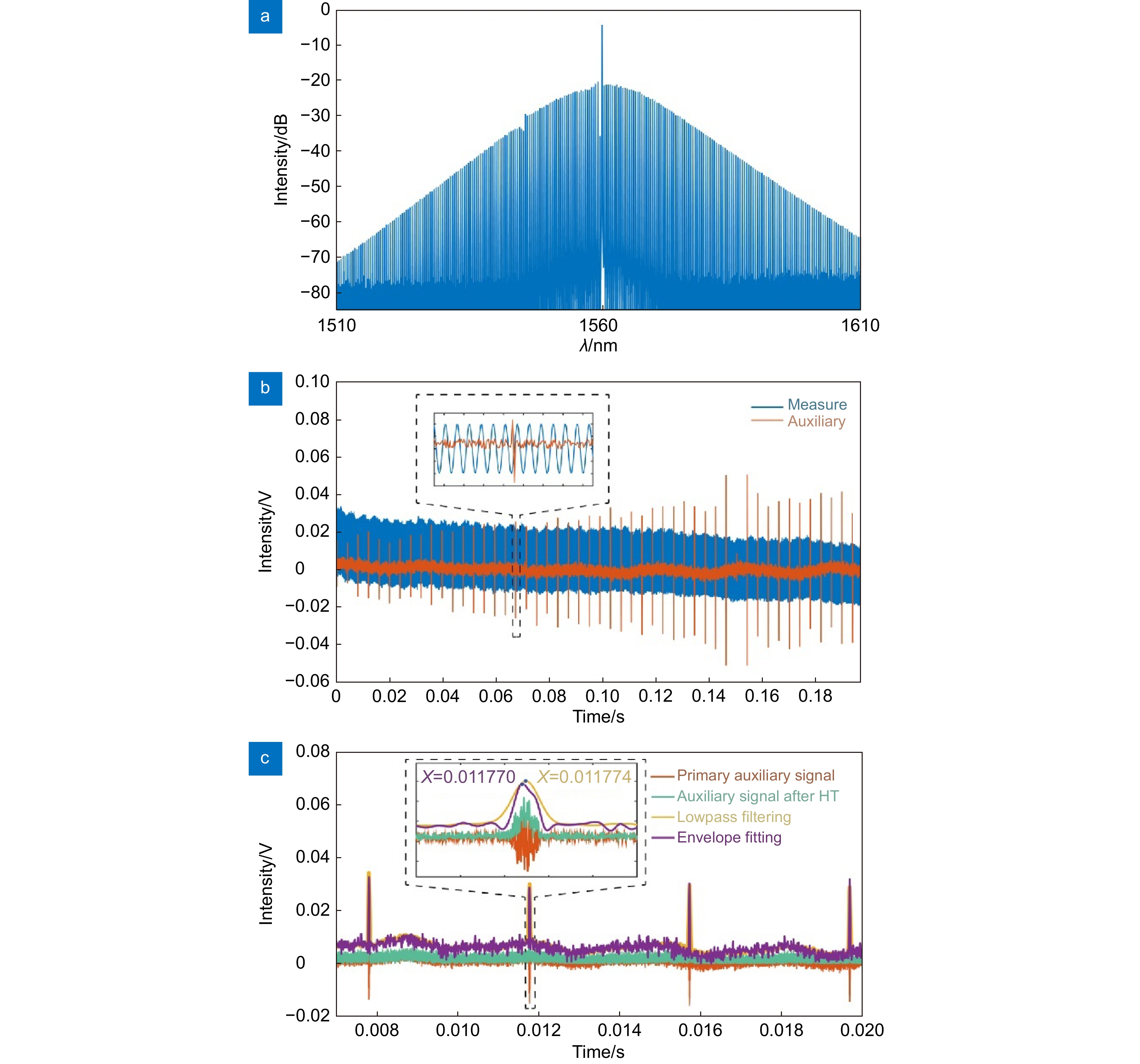
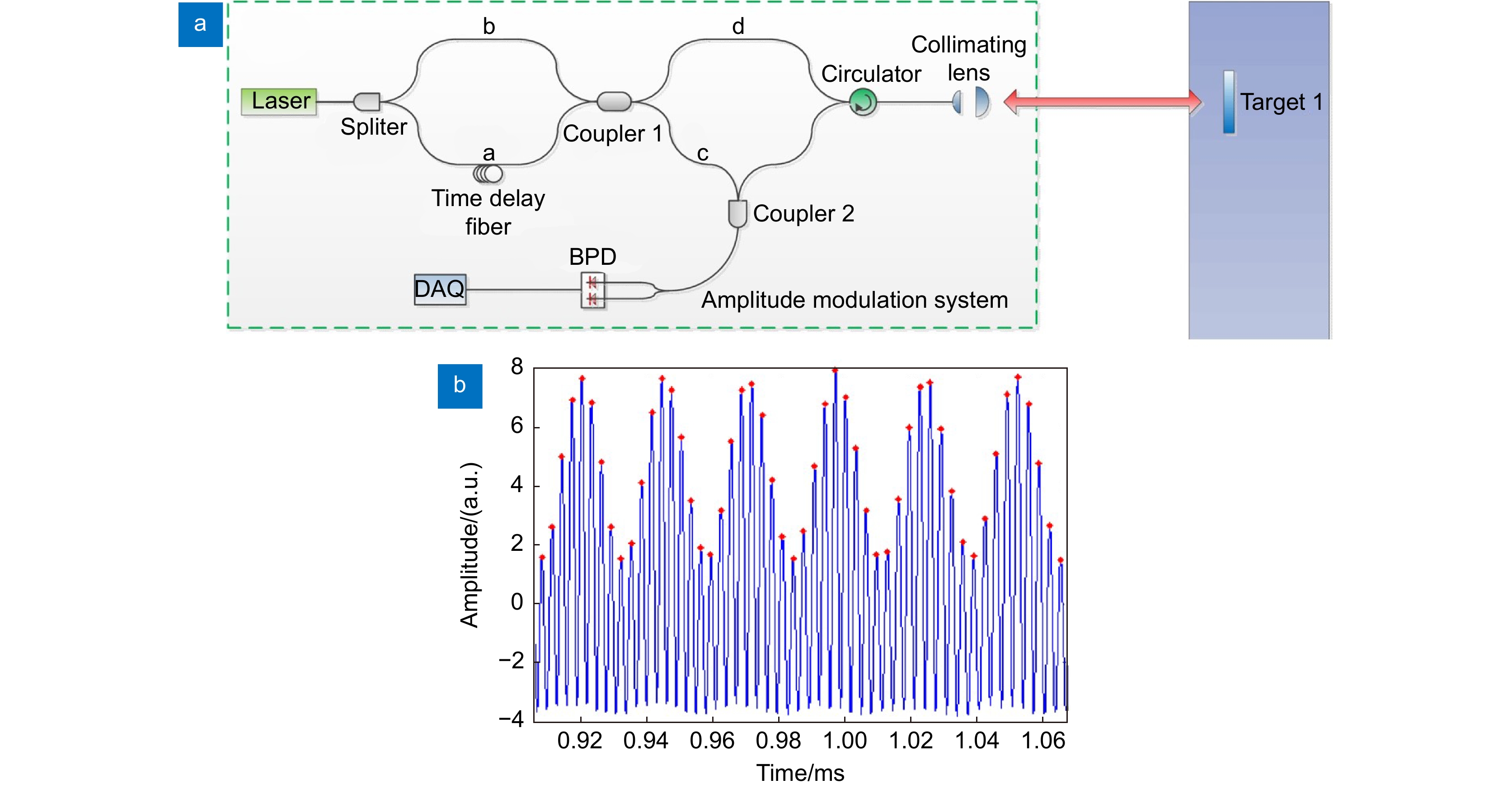
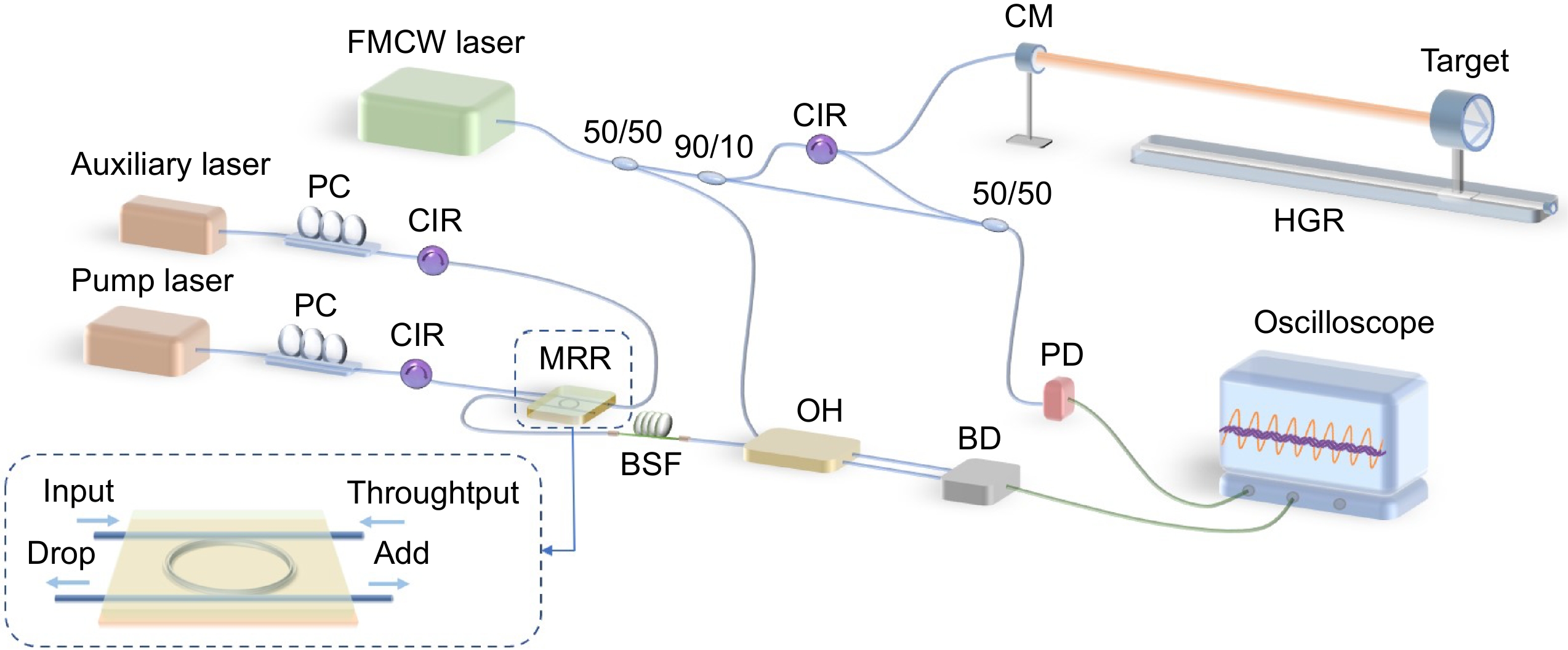
图 18 (a) 滤波后孤子梳的光谱；(b) 测距信号和辅助信号的时域图；(c) 提取辅助信号中的校准峰值位置。图中包含了原始辅助信号和经过希尔伯特变换(HT)的复包络信号，以及对复包络信号进行低通滤波和包络拟合处理后的波形[15]
Figure 18. (a) Spectral of the soliton comb after filtering; (b) Time-domain graph of the ranging signal and auxiliary signal; (c) Extraction of calibration peak positions in the auxiliary signal. The figure contains the original auxiliary signal and the complex envelope signal through Hilbert transform (HT), as well as the waveform processed by low-pass filtering and envelope fitting for the complex envelope signal[15]
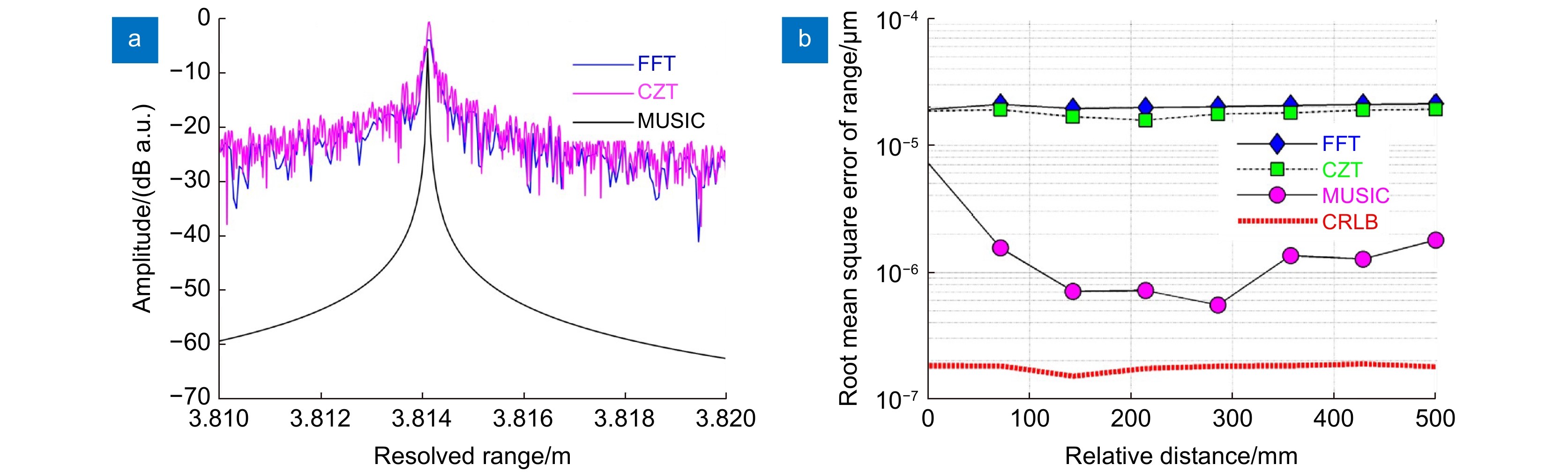
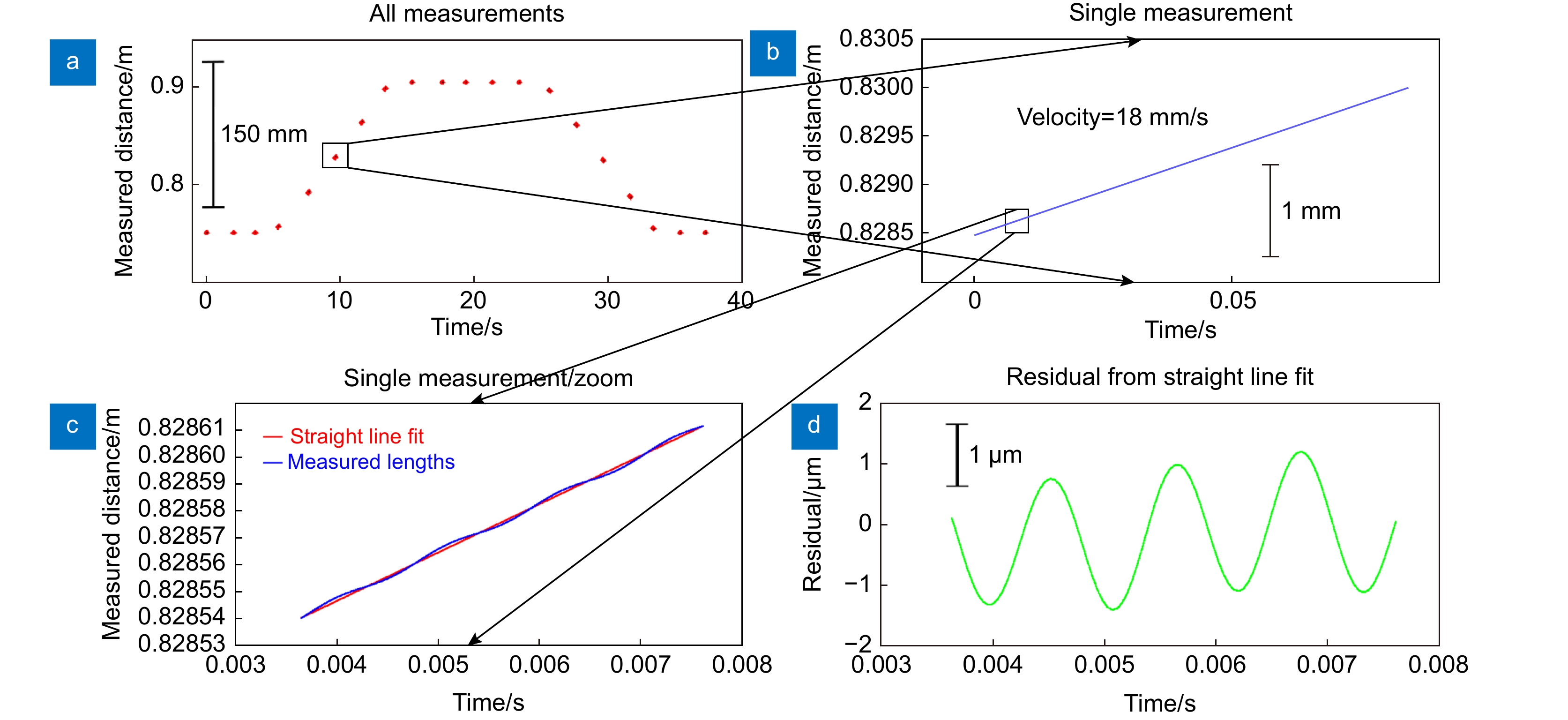
图 20 (a) 测量干涉仪的多次扫描，目标在线性运动平台上；(b) 以最快的线性运动平台速度进行单次扫描；(c) 以直线拟合放大(a)；(d)，(c)拟合直线的残差[52]
Figure 20. (a) Multiple scans of a measurement interferometer with the target on a linear motion stage; (b) Single scan at fastest linear motion stage speed; (c) Zoom in of (a) with a straight line fit; (d) Residual to the straight line fit in (c)[52]
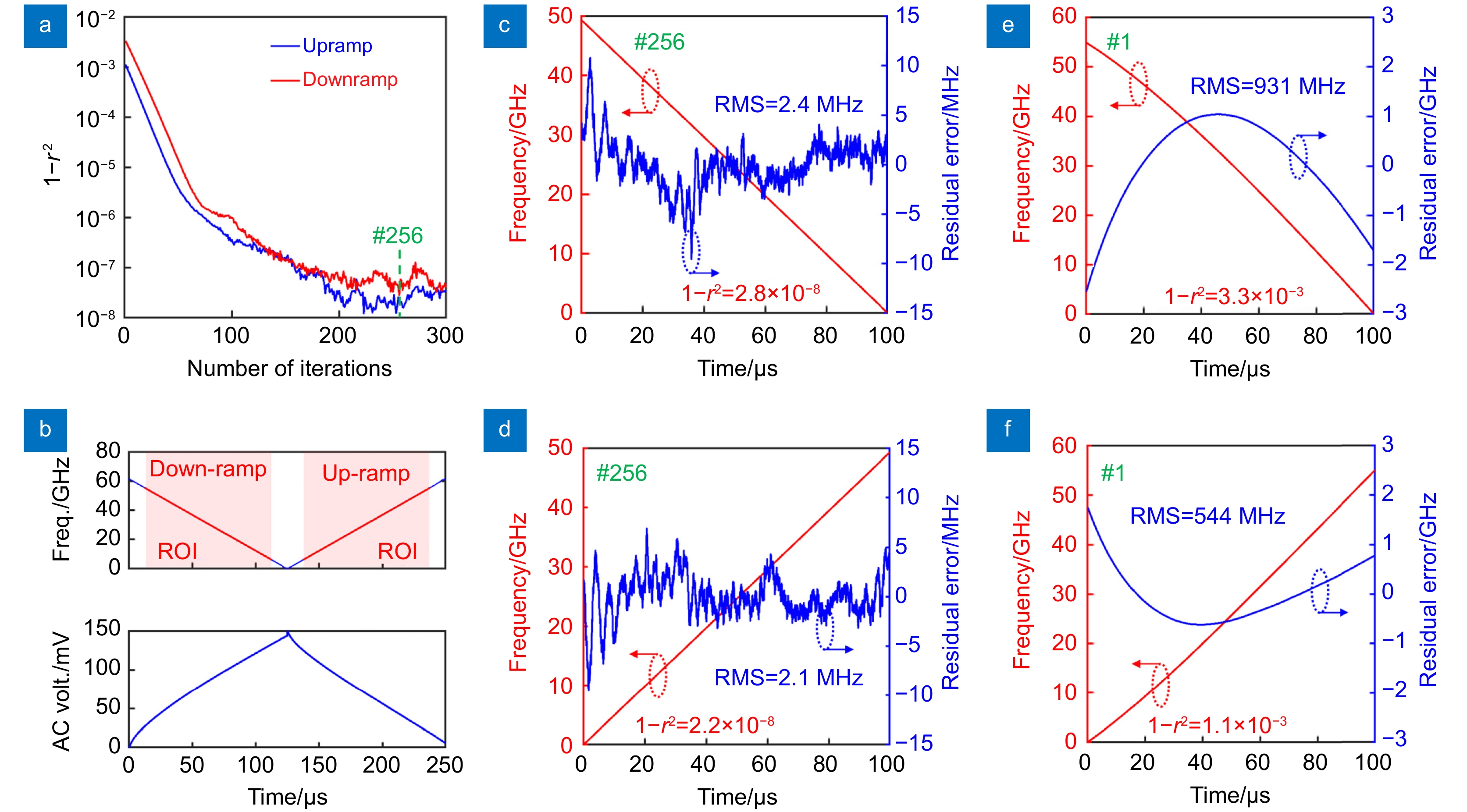
图 26 ILC对VCSEL激光扫频线性化的实验结果。(a) 残余非线性与迭代次数的关系；(b) 第256次迭代的激光频率扫描和相应的驱动电压波形。ROI用红色标记；(c)，(d) 第256次迭代的ROI中的向下和向上斜坡激光频率扫描和残余误差；(e)，(f) 用于比较的第一次迭代的向下和向上斜坡激光频率扫描和剩余误差[58]
Figure 26. Experimental results of laser frequency sweep linearization of VCSEL by ILC. (a) Residual nonlinearity versus the number of iterations; (b) Laser frequency sweep and the corresponding drive voltage waveforms at the 256th iteration. The ROI is labeled by red color; (c), (d) The down- and up-ramp laser frequency sweeps and residual errors in the ROIs of the 256th iteration; (e), (f) The down- and up-ramp laser frequency sweeps and residual errors of the 1st iteration for comparison[58]
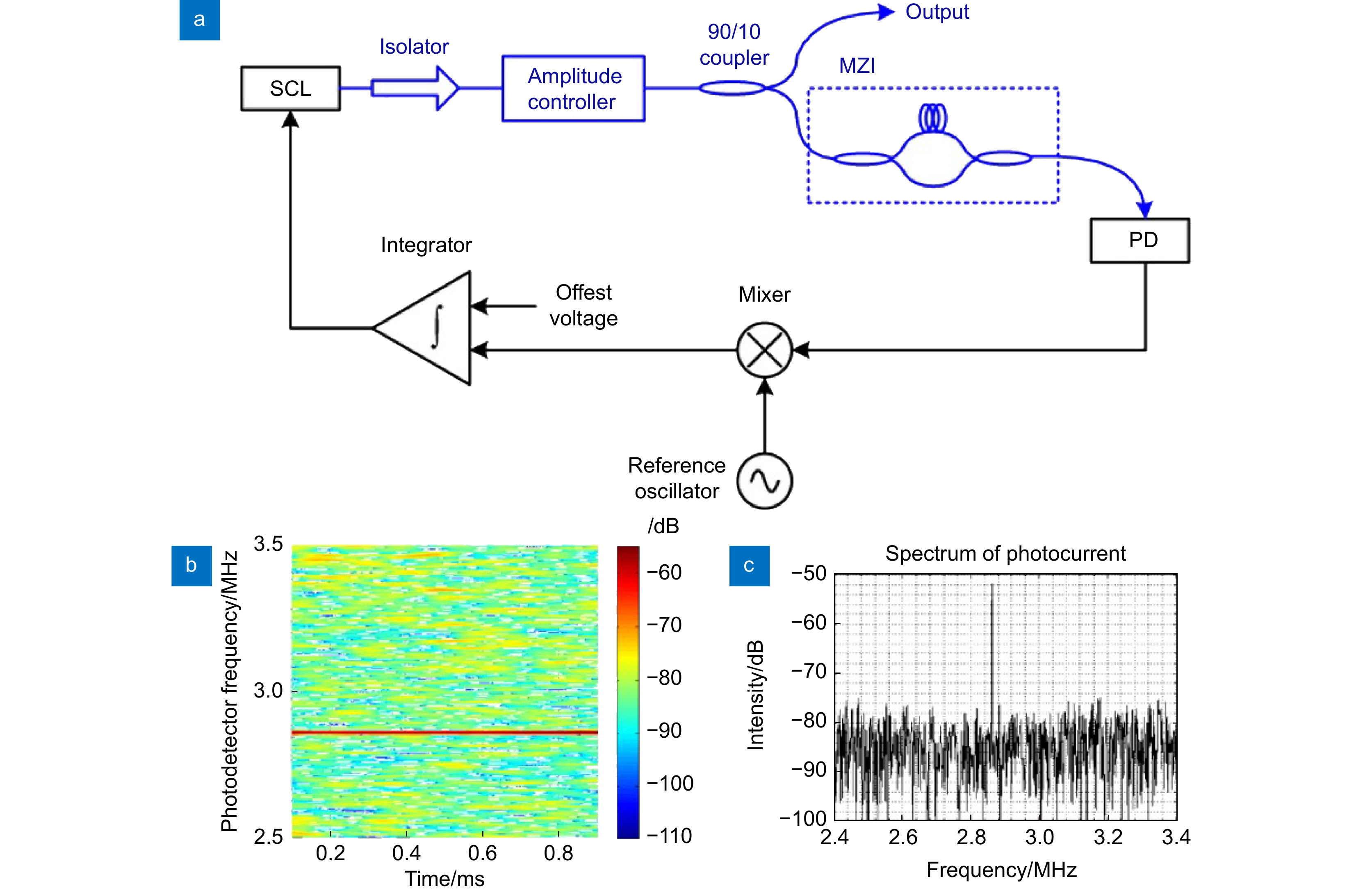
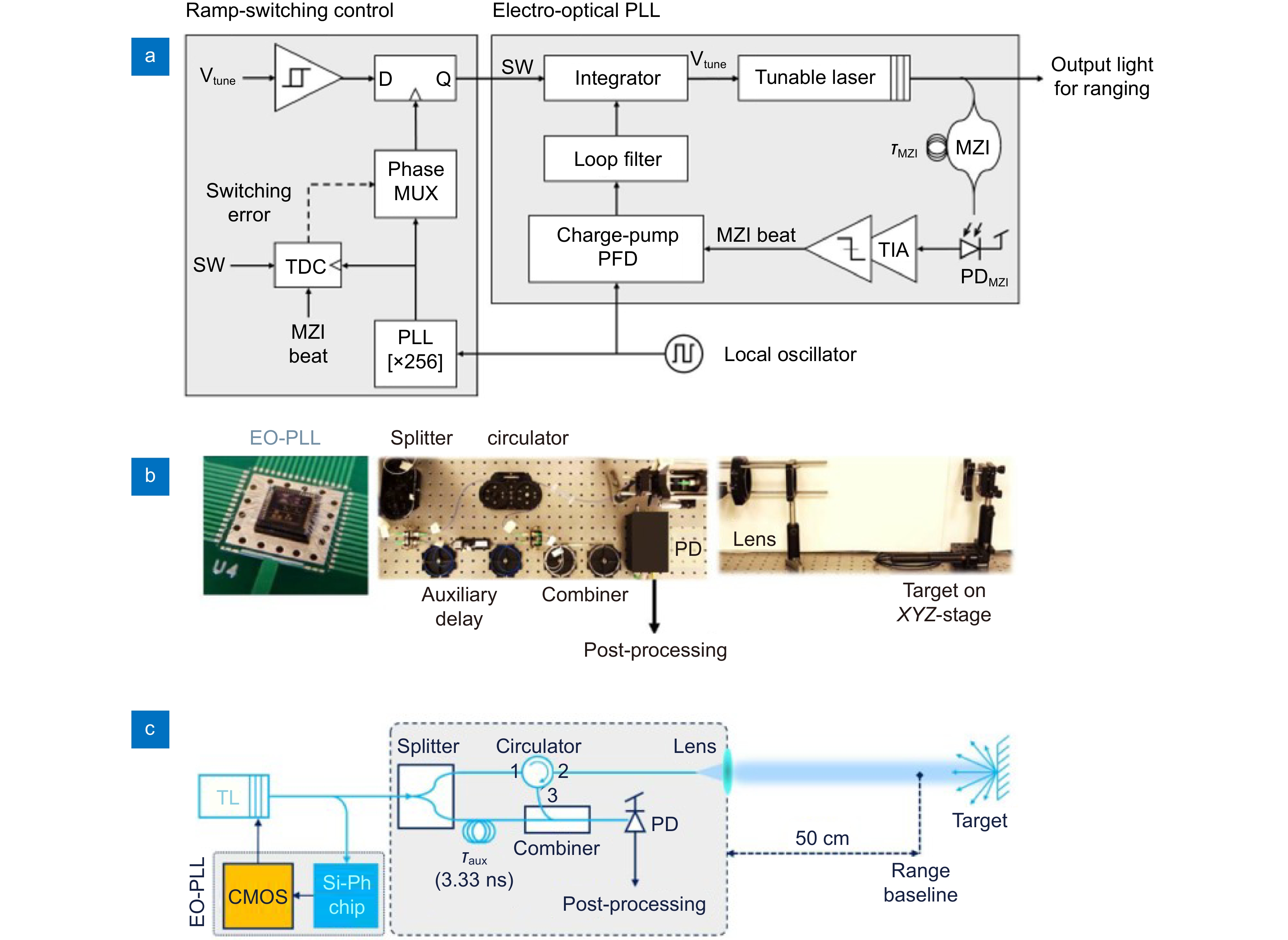
图 27 (a) 基于FMCW的LiDAR系统的示意图。AWG：任意波形发生器；DFB：分布式反馈激光器；PC：偏振控制器；MZM：Mach-Zehnder调制器；BPD：平衡光电探测器；DAQ：数据采集卡。实线表示光路，虚线表示电子路；(b) 光调制后的主激光器(红色)、没有光注入的从激光器(黑色)和注入锁定后的从激光器(蓝色)的光谱[59]
Figure 27. (a) The sketch diagram of the proposed FMCW-based LiDAR system. AWG: arbitrary waveform generator; DFB: distributed feedback laser; PC: polarization controller; MZM: Mach-Zehnder modulator; BPD: balanced photodetector; DAQ: data acquisition card. Solid line means light path and dash line means electronic path; (b) The optical spectra of the master laser after optical modulation (red), the slave laser without the optical injection (black), and the slave laser after the injection-locked (blue)[59]
图 30 基于HCN气体吸收池的FMCW激光雷达测距系统
Figure 30. FMCW LiDAR ranging system based on HCN gas cell
表 1 四种FMCW激光雷达测量的非线性校正技术重要参数和实验结果对比
Table 1. Comparison of parameters and experimental results of nonlinear correction techniques for FMCW LiDAR
非线性校正技术 锁相反馈控制线性化[17] 等光频间隔重采样[31] 光频梳校正法[46] 相位比值法[52] 频率调制范围/THz 4.8 3.52 ~1 7.49 & 5.30 频率调制速度/(THz/s) 6 1 3.4 PHz/s 6.24 THz/s & 4.42 THz/s 线性度标准差/kHz 170 --- --- --- 距离分辨率/μm 31 50 130 --- 实验所测距离/m 1.5 8.7 10.5 20 测量标准差 86 nm --- 10 μm --- 相对测量不确定度 --- --- --- 0.41×10-6 (k=2)* *k=2是指高斯概率分布假设中的置信水平为2σ 
下载: 导出CSV
-
[1] 宦克为, 郑峰, 石晓光, 等. 基于调频连续波原理的三维成像激光雷达系统[J]. 长春理工大学学报(自然科学版), 2008, 31(4): 61−64.
Huan K W, Zheng F, Shi X G, et al. The system of 3D LADAR base on FM/CW principles[J]. J Changchun Univ Sci Technol (Nat Sci Ed), 2008, 31(4): 61−64.
[2] Lee J, Kim Y J, Lee K, et al. Time-of-flight measurement with femtosecond light pulses[J]. Nat Photonics, 2010, 4(10): 716−720. doi: 10.1038/nphoton.2010.175
[3] Whyte R, Streeter L, Cree M J, et al. Application of lidar techniques to time-of-flight range imaging[J]. Appl Opt, 2015, 54(33): 9654−9664. doi: 10.1364/AO.54.009654
[4] Jang I G, Lee S H, Park Y H. A parallel-phase demodulation-based distance-measurement method using dual-frequency modulation[J]. Appl Sci, 2019, 10(1): 293. doi: 10.3390/app10010293
[5] Jang Y S, Park J, Jin J H. Sub-100-nm precision distance measurement by means of all-fiber photonic microwave mixing[J]. Opt Express, 2021, 29(8): 12229−12239. doi: 10.1364/OE.421719
[6] Nicolaescu R, Rogers C, Piggott A Y, et al. 3D imaging via silicon-photonics-based LIDAR[J]. Proc SPIE, 2021, 11691: 116910G.
[7] Zhang X B Q, Kong M, Guo T T, et al. Frequency modulation nonlinear correction and range-extension method based on laser frequency scanning interference[J]. Appl Opt, 2021, 60(12): 3446−3451. doi: 10.1364/AO.420663
[8] Zhang F M, Yi L P, Qu X H. Simultaneous measurements of velocity and distance via a dual-path FMCW lidar system[J]. Opt Commun, 2020, 474: 126066. doi: 10.1016/j.optcom.2020.126066
[9] Piracha M U, Nguyen D, Ozdur I, et al. Simultaneous ranging and velocimetry of fast moving targets using oppositely chirped pulses from a mode-locked laser[J]. Opt Express, 2011, 19(12): 11213−11219. doi: 10.1364/OE.19.011213
[10] Kakuma S. Frequency-modulated continuous-wave laser radar using dual vertical-cavity surface-emitting laser diodes for real-time measurements of distance and radial velocity[J]. Opt Rev, 2017, 24(1): 39−46. doi: 10.1007/s10043-016-0294-7
[11] Cheng X R, Liu J C, Jia L H, et al. Precision and repeatability improvement in frequency-modulated continuous-wave velocity measurement based on the splitting of beat frequency signals[J]. Opt Express, 2021, 29(18): 28582−28596. doi: 10.1364/OE.433637
[12] DiLazaro T, Nehmetallah G. Large-volume, low-cost, high-precision FMCW tomography using stitched DFBs[J]. Opt Express, 2018, 26(3): 2891−2904. doi: 10.1364/OE.26.002891
[13] Hariyama T, Sandborn P A M, Watanabe M, et al. High-accuracy range-sensing system based on FMCW using low-cost VCSEL[J]. Opt Express, 2018, 26(7): 9285−9297. doi: 10.1364/OE.26.009285
[14] Hillger P, Grzyb J, Jain R, et al. Terahertz imaging and sensing applications with silicon-based technologies[J]. IEEE Trans Terahertz Sci Technol, 2019, 9(1): 1−19. doi: 10.1109/TTHZ.2018.2884852
[15] Jia L H, Wang Y, Wang X Y, et al. Nonlinear calibration of frequency modulated continuous wave LIDAR based on a microresonator soliton comb[J]. Opt Lett, 2021, 46(5): 1025−1028. doi: 10.1364/OL.415524
[16] Iiyama K, Wang L T, Hayashi K I. Linearizing optical frequency-sweep of a laser diode for FMCW reflectometry[J]. J Lightwave Technol, 1996, 14(2): 173−178. doi: 10.1109/50.482260
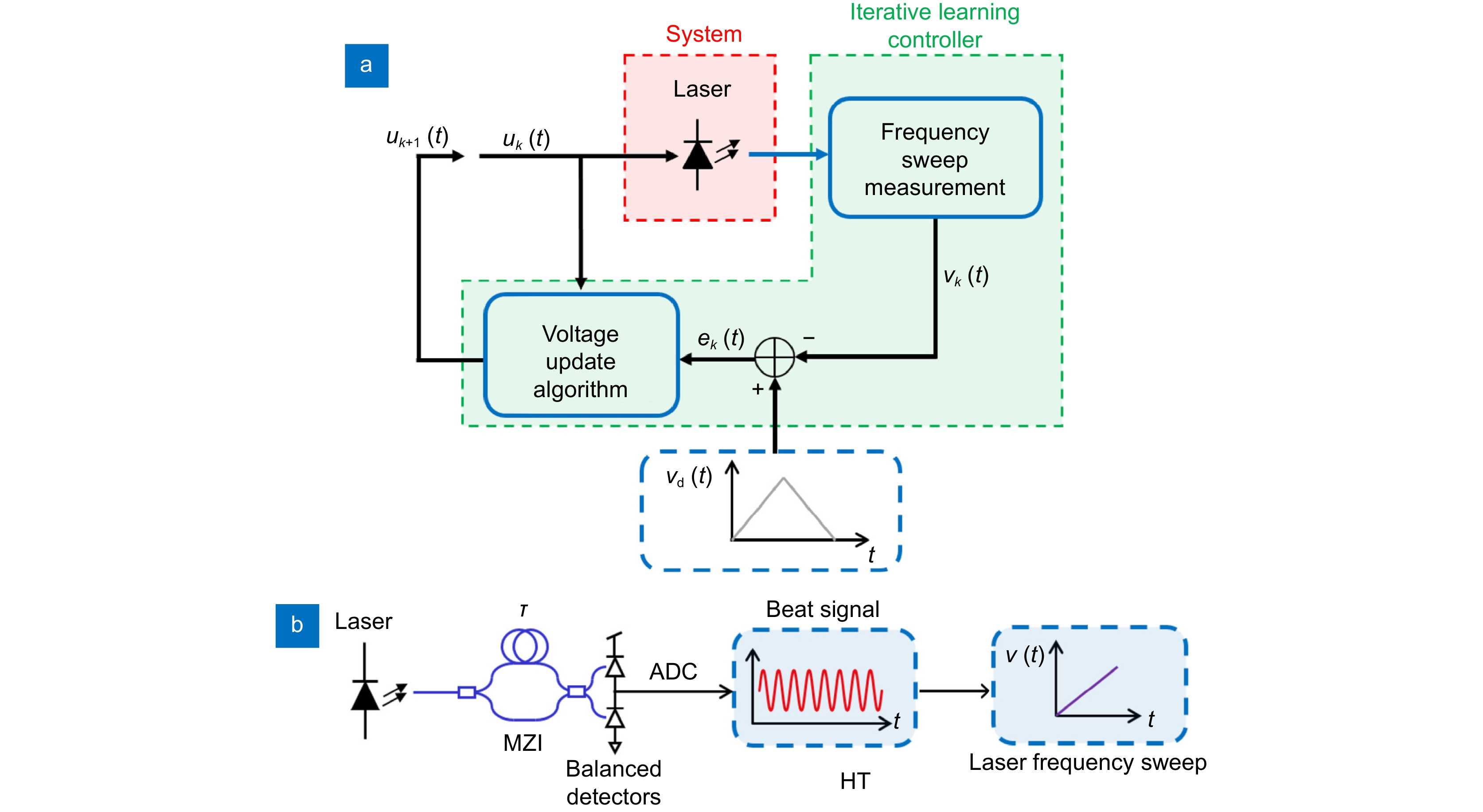
[17] Roos P A, Reibel R R, Berg T, et al. Ultrabroadband optical chirp linearization for precision metrology applications[J]. Opt Lett, 2009, 34(23): 3692−3694. doi: 10.1364/OL.34.003692
[18] Satyan N, Vasilyev A, Rakuljic G, et al. Precise control of broadband frequency chirps using optoelectronic feedback[J]. Opt Express, 2009, 17(18): 15991−15999. doi: 10.1364/OE.17.015991
[19] Satyan N, Vasilyev A, Rakuljic G, et al. Phase-locking and coherent power combining of broadband linearly chirped optical waves[J]. Opt Express, 2012, 20(23): 25213−25227. doi: 10.1364/OE.20.025213
[20] Behroozpour B, Sandborn P A M, Quack N, et al. Electronic-photonic integrated circuit for 3D microimaging[J]. IEEE J Solid-State Circuits, 2017, 52(1): 161−172. doi: 10.1109/JSSC.2016.2621755
[21] Qin J, Zhou Q, Xie W L, et al. Coherence enhancement of a chirped DFB laser for frequency-modulated continuous-wave reflectometry using a composite feedback loop[J]. Opt Lett, 2015, 40(19): 4500−4503. doi: 10.1364/OL.40.004500
[22] Qin J, Zhang L, Xie W L, et al. Ultra-long range optical frequency domain reflectometry using a coherence-enhanced highly linear frequency-swept fiber laser source[J]. Opt Express, 2019, 27(14): 19359−19368. doi: 10.1364/OE.27.019359
[23] Meng Y X, Xie W L, Feng Y X, et al. Dynamic range enhanced optical frequency domain reflectometry using dual-loop composite optical phase-locking[J]. IEEE Photon J, 2021, 13(4): 7100307.
[24] 卢炤宇, 葛春风, 王肇颖, 等. 频率调制连续波激光雷达技术基础与研究进展[J]. 光电工程, 2019, 46(7): 190038.
Lu Z Y, Ge C F, Wang Z Y, et al. Basics and developments of frequency modulation continuous wave LiDAR[J]. Opto-Electron Eng, 2019, 46(7): 190038.
[25] Barber Z W, Babbitt W R, Kaylor B, et al. Accuracy of active chirp linearization for broadband frequency modulated continuous wave ladar[J]. Appl Opt, 2010, 49(2): 213−219. doi: 10.1364/AO.49.000213
[26] Glombitza U, Brinkmeyer E. Coherent frequency-domain reflectometry for characterization of single-mode integrated-optical waveguides[J]. J Lightwave Technol, 1993, 11(8): 1377−1384. doi: 10.1109/50.254098
[27] Rosenfeldt H, Knothe C, Cierullies J, et al. Evolution of amplitude and dispersion spectra during fiber Bragg grating fabrication[C]//Proceedings of the Bragg Gratings, Photosensitivity, and Poling in Glass Waveguides 2001, Stresa, 2001: BWA4.
[28] Ahn T J, Lee J Y, Kim D Y. Suppression of nonlinear frequency sweep in an optical frequency-domain reflectometer by use of Hilbert transformation[J]. Appl Opt, 2005, 44(35): 7630−7634. doi: 10.1364/AO.44.007630
[29] Ahn T J, Kim D Y. Analysis of nonlinear frequency sweep in high-speed tunable laser sources using a self-homodyne measurement and Hilbert transformation[J]. Appl Opt, 2007, 46(13): 2394−2400. doi: 10.1364/AO.46.002394
[30] Moore E D, McLeod R R. Correction of sampling errors due to laser tuning rate fluctuations in swept-wavelength interferometry[J]. Opt Express, 2008, 16(17): 13139−13149. doi: 10.1364/OE.16.013139
[31] Shi G, Zhang F M, Qu X H, et al. High-resolution frequency-modulated continuous-wave laser ranging for precision distance metrology applications[J]. Opt Eng, 2014, 53(12): 122402. doi: 10.1117/1.OE.53.12.122402
[32] Pan H, Zhang F M, Shi C Z, et al. High-precision frequency estimation for frequency modulated continuous wave laser ranging using the multiple signal classification method[J]. Appl Opt, 2017, 56(24): 6956−6961. doi: 10.1364/AO.56.006956
[33] Shi G, Wang W, Zhang F M. Precision improvement of frequency-modulated continuous-wave laser ranging system with two auxiliary interferometers[J]. Opt Commun, 2018, 411: 152−157. doi: 10.1016/j.optcom.2017.11.062
[34] 曲兴华, 职广涛, 张福民, 等. 利用信号拼接提高调频连续波激光测距系统的分辨力[J]. 光学 精密工程, 2015, 23(1): 40−47. doi: 10.3788/OPE.20152301.0040
Qu X H, Zhi G T, Zhang F M, et al. Improvement of resolution of frequency modulated continuous wave laser ranging system by signal splicing[J]. Opt Precis Eng, 2015, 23(1): 40−47. doi: 10.3788/OPE.20152301.0040
[35] Xiong X T, Qu X H, Zhang F M. Error correction for FSI-based system without cooperative target using an adaptive filtering method and a phase-matching mosaic algorithm[J]. Appl Sci, 2018, 8(10): 1954. doi: 10.3390/app8101954
[36] Zhang F M, Li Y T, Pan H, et al. Vibration compensation of the frequency-scanning-interferometry-based absolute ranging system[J]. Appl Sci, 2019, 9(1): 147. doi: 10.3390/app9010147
[37] Pan H, Qu X H, Zhang F M. Micron-precision measurement using a combined frequency-modulated continuous wave ladar autofocusing system at 60 meters standoff distance[J]. Opt Express, 2018, 26(12): 15186−15198. doi: 10.1364/OE.26.015186
[38] Badar M, Lu P, Buric M, et al. Integrated auxiliary interferometer for self-correction of nonlinear tuning in optical frequency domain reflectometry[J]. J Lightwave Technol, 2020, 38(21): 6097−6103. doi: 10.1109/JLT.2020.3007703
[39] Yüksel K, Wuilpart M, Mégret P. Analysis and suppression of nonlinear frequency modulation in an optical frequency-domain reflectometer[J]. Opt Express, 2009, 17(7): 5845−5851. doi: 10.1364/OE.17.005845
[40] 包为政, 张福民, 曲兴华. 基于等光频细分重采样的调频干涉测距方法[J]. 激光技术, 2020, 44(1): 1−6. doi: 10.7510/jgjs.issn.1001-3806.2020.01.001
Bao W Z, Zhang F M, Qu X H. Laser ranging method of frequency modulation interference based on equal optical frequency subdivision resampling[J]. Laser Technol, 2020, 44(1): 1−6. doi: 10.7510/jgjs.issn.1001-3806.2020.01.001
[41] Jiang S, Liu B, Wang H C. FMCW laser ranging method based on a frequency multiplier[J]. Appl Opt, 2021, 60(4): 918−922. doi: 10.1364/AO.412633
[42] Adler D C, Chen Y, Huber R, et al. Three-dimensional endomicroscopy using optical coherence tomography[J]. Nat Photonics, 2007, 1(12): 709−716. doi: 10.1038/nphoton.2007.228
[43] 姚艳南, 张福民, 曲兴华. 基于硬件的等光频间隔采样及频谱分析方法[J]. 光学学报, 2016, 36(12): 1212003. doi: 10.3788/AOS201636.1212003
Yao Y N, Zhang F M, Qu X H. Hardware-based equispaced-phase resampling nonlinearity correction algorithm and spectral analysis method[J]. Acta Opt Sin, 2016, 36(12): 1212003. doi: 10.3788/AOS201636.1212003
[44] Barber Z W, Giorgetta F R, Roos P A, et al. Characterization of an actively linearized ultrabroadband chirped laser with a fiber-laser optical frequency comb[J]. Opt Lett, 2011, 36(7): 1152−1154. doi: 10.1364/OL.36.001152
[45] Baumann E, Giorgetta F R, Coddington I, et al. Comb-calibrated frequency-modulated continuous-wave ladar for absolute distance measurements[J]. Opt Lett, 2013, 38(12): 2026−2028. doi: 10.1364/OL.38.002026
[46] Baumann E, Giorgetta F R, Deschênes J D, et al. Comb-calibrated laser ranging for three-dimensional surface profiling with micrometer-level precision at a distance[J]. Opt Express, 2014, 22(21): 24914−24928. doi: 10.1364/OE.22.024914
[47] Yu W H, Pfeiffer P, Morsali A, et al. Comb-calibrated frequency sweeping interferometry for absolute distance and vibration measurement[J]. Opt Lett, 2019, 44(20): 5069−5072. doi: 10.1364/OL.44.005069
[48] Xie W L, Meng Y X, Feng Y X, et al. Optical linear frequency sweep based on a mode-spacing swept comb and multi-loop phase-locking for FMCW interferometry[J]. Opt Express, 2021, 29(2): 604−614. doi: 10.1364/OE.410405
[49] Kippenberg T J, Gaeta A L, Lipson M, et al. Dissipative Kerr solitons in optical microresonators[J]. Science, 2018, 361(6402): eaan8083. doi: 10.1126/science.aan8083
[50] Twayana K, Ye Z C, Helgason Ó B, et al. Frequency-comb-calibrated swept-wavelength interferometry[J]. Opt Express, 2021, 29(15): 24363−24372. doi: 10.1364/OE.430818
[51] Diddams S A, Vahala K, Udem T. Optical frequency combs: coherently uniting the electromagnetic spectrum[J]. Science, 2020, 369(6501): eaay3676. doi: 10.1126/science.aay3676
[52] Dale J, Hughes B, Lancaster A J, et al. Multi-channel absolute distance measurement system with sub ppm-accuracy and 20 m range using frequency scanning interferometry and gas absorption cells[J]. Opt Express, 2014, 22(20): 24869−24893. doi: 10.1364/OE.22.024869
[53] Ito F, Fan X Y, Koshikiya Y. Long-range coherent OFDR with light source phase noise compensation[J]. J Lightwave Technol, 2012, 30(8): 1015−1024. doi: 10.1109/JLT.2011.2167598
[54] Prellinger G, Meiners-Hagen K, Pollinger F. Spectroscopically in situ traceable heterodyne frequency-scanning interferometry for distances up to 50 m[J]. Meas Sci Technol, 2015, 26(8): 084003. doi: 10.1088/0957-0233/26/8/084003
[55] Prellinger G, Meiners-Hagen K, Pollinger F. Dynamic high-resolution spectroscopic frequency referencing for frequency sweeping interferometry[J]. Surf Topogr:Metrol Prop, 2016, 4(2): 024012. doi: 10.1088/2051-672X/4/2/024012
[56] Zhang T, Qu X H, Zhang F M. Nonlinear error correction for FMCW ladar by the amplitude modulation method[J]. Opt Express, 2018, 26(9): 11519−11528. doi: 10.1364/OE.26.011519
[57] Liu Z, Liu Z G, Deng Z W, et al. Interference signal frequency tracking for extracting phase in frequency scanning interferometry using an extended Kalman filter[J]. Appl Opt, 2016, 55(11): 2985−2992. doi: 10.1364/AO.55.002985
[58] Zhang X S, Pouls J, Wu M C. Laser frequency sweep linearization by iterative learning pre-distortion for FMCW LiDAR[J]. Opt Express, 2019, 27(7): 9965−9974. doi: 10.1364/OE.27.009965
[59] Dong Y K, Zhu Z D, Tian X N, et al. Frequency-modulated continuous-wave LIDAR and 3D imaging by using linear frequency modulation based on injection locking[J]. J Lightwave Technol, 2021, 39(8): 2275−2280. doi: 10.1109/JLT.2021.3050772
[60] Cole D B, Sorace-Agaskar C, Moresco M, et al. Integrated heterodyne interferometer with on-chip modulators and detectors[J]. Opt Lett, 2015, 40(13): 3097−3100. doi: 10.1364/OL.40.003097
[61] Aflatouni F, Abiri B, Rekhi A, et al. Nanophotonic coherent imager[J]. Opt Express, 2015, 23(4): 5117−5125. doi: 10.1364/OE.23.005117
[62] Lippok N, Coen S, Nielsen P, et al. Dispersion compensation in Fourier domain optical coherence tomography using the fractional Fourier transform[J]. Opt Express, 2012, 20(21): 23398−23413. doi: 10.1364/OE.20.023398
[63] Bradu A, Israelsen N M, Maria M, et al. Recovering distance information in spectral domain interferometry[J]. Sci Rep, 2018, 8(1): 15445. doi: 10.1038/s41598-018-33821-0
[64] 许新科, 刘国栋, 刘炳国, 等. 基于光纤色散相位补偿的高分辨率激光频率扫描干涉测量研究[J]. 物理学报, 2015, 64(21): 219501. doi: 10.7498/aps.64.219501
Xu X K, Liu G D, Liu B G, et al. High-resolution laser frequency scanning interferometer based on fiber dispersion phase compensation[J]. Acta Phys Sin, 2015, 64(21): 219501. doi: 10.7498/aps.64.219501
[65] Lu C, Liu G D, Liu B G, et al. Method based on chirp decomposition for dispersion mismatch compensation in precision absolute distance measurement using swept-wavelength interferometry[J]. Opt Express, 2015, 23(25): 31662−31671. doi: 10.1364/OE.23.031662
[66] Liu G D, Xu X K, Liu B G, et al. Dispersion compensation method based on focus definition evaluation functions for high-resolution laser frequency scanning interference measurement[J]. Opt Commun, 2017, 386: 57−64. doi: 10.1016/j.optcom.2016.10.052
[67] Pan H, Qu X H, Shi C Z, et al. Resolution-enhancement and sampling error correction based on molecular absorption line in frequency scanning interferometry[J]. Opt Commun, 2018, 416: 214−220. doi: 10.1016/j.optcom.2018.02.006
[68] Swinkels B L, Bhattacharya N, Braat J J M. Correcting movement errors in frequency-sweeping interferometry[J]. Opt Lett, 2005, 30(17): 2242−2244. doi: 10.1364/OL.30.002242
[69] Krause B W, Tiemann B G, Gatt P. Motion compensated frequency modulated continuous wave 3D coherent imaging ladar with scannerless architecture[J]. Appl Opt, 2012, 51(36): 8745−8761. doi: 10.1364/AO.51.008745
[70] Lu C, Liu G D, Liu B G, et al. Absolute distance measurement system with micron-grade measurement uncertainty and 24 m range using frequency scanning interferometry with compensation of environmental vibration[J]. Opt Express, 2016, 24(26): 30215−30224. doi: 10.1364/OE.24.030215
[71] Wang R R, Wang B N, Xiang M S, et al. Vibration compensation method based on instantaneous ranging model for triangular FMCW ladar signals[J]. Opt Express, 2021, 29(11): 15918−15939. doi: 10.1364/OE.423289
[72] Wang R R, Wang B N, Wang Y C, et al. Time-varying vibration compensation based on segmented interference for triangular FMCW LiDAR signals[J]. Remote Sens, 2021, 13(19): 3803. doi: 10.3390/rs13193803
[73] Riemensberger J, Lukashchuk A, Karpov M, et al. Massively parallel coherent laser ranging using a soliton microcomb[J]. Nature, 2020, 581(7807): 164−170. doi: 10.1038/s41586-020-2239-3
[74] Fitch C R, Baltušis A, Marko I P, et al. Carrier recombination properties of low-threshold 1.3 μm quantum dot lasers on silicon[J]. IEEE J Sel Top Quantum Electron, 2022, 28(1): 1900210.
[75] Komljenovic T, Huang D N, Pintus P, et al. Photonic integrated circuits using heterogeneous integration on silicon[J]. Proc IEEE, 2018, 106(12): 2246−2257. doi: 10.1109/JPROC.2018.2864668
[76] Kaur P, Boes A, Ren G H, et al. Hybrid and heterogeneous photonic integration[J]. APL Photon, 2021, 6(6): 061102. doi: 10.1063/5.0052700
[77] Komljenovic T, Liang L J, Chao R L, et al. Widely-tunable ring-resonator semiconductor lasers[J]. Appl Sci, 2017, 7(7): 732. doi: 10.3390/app7070732
[78] Huang D N, Tran M A, Guo J, et al. High-power sub-kHz linewidth lasers fully integrated on silicon[J]. Optica, 2019, 6(6): 745−752. doi: 10.1364/OPTICA.6.000745
[79] Jones R, Doussiere P, Driscoll J B, et al. Heterogeneously integrated InP\/silicon photonics: fabricating fully functional transceivers[J]. IEEE Nanotechnol Mag, 2019, 13(2): 17−26. doi: 10.1109/MNANO.2019.2891369
[80] Thomas S, Bredendiek C, Jaeschke T, et al. A compact, energy-efficient 240 GHz FMCW radar sensor with high modulation bandwidth[C]//Proceedings of 2016 German Microwave Conference (GeMiC), Bochum, Germany, 2016: 397–400.
[81] Su Y P, Huang C Y, Chen S J. A 24-GHz fully integrated CMOS transceiver for FMCW radar applications[J]. IEEE J Solid-State Circuits, 2021, 56(11): 3307−3317. doi: 10.1109/JSSC.2021.3095137
[82] Isaac B J, Song B W, Pinna S, et al. Indium phosphide photonic integrated circuit transceiver for FMCW LiDAR[J]. IEEE J Sel Top Quantum Electron, 2019, 25(6): 8000107.
[83] Spencer D T, Drake T, Briles T C, et al. An optical-frequency synthesizer using integrated photonics[J]. Nature, 2018, 557(7703): 81−85. doi: 10.1038/s41586-018-0065-7
[84] Sun J, Timurdogan E, Yaacobi A, et al. Large-scale nanophotonic phased array[J]. Nature, 2013, 493(7431): 195−199. doi: 10.1038/nature11727
[85] Hulme J C, Doylend J K, Heck M J R, et al. Fully integrated hybrid silicon two dimensional beam scanner[J]. Opt Express, 2015, 23(5): 5861−5874. doi: 10.1364/OE.23.005861
[86] Hutchison D N, Sun J, Doylend J K, et al. High-resolution aliasing-free optical beam steering[J]. Optica, 2016, 3(8): 887−890. doi: 10.1364/OPTICA.3.000887
[87] Li Z Y, Chen B S, Na Q X, et al. Wide-steering-angle high-resolution optical phased array[J]. Photon Res, 2021, 9(12): 2511−2518. doi: 10.1364/PRJ.437846
-
点击扫一扫
图(31)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
