E-mail Alert
RSS
Color image multi-scale guided depth image super-resolution reconstruction
-
摘要:
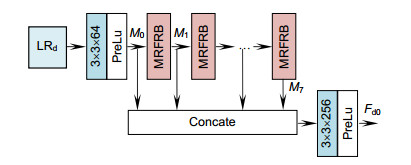
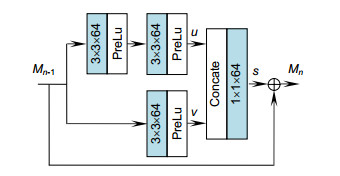
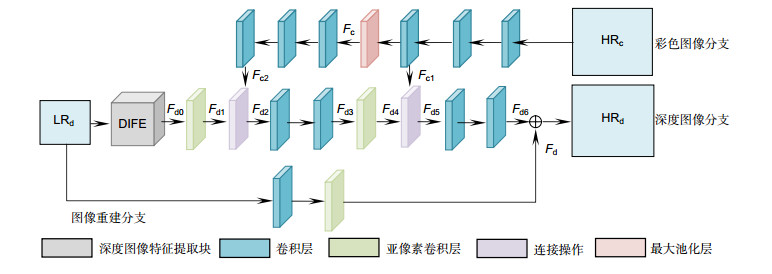
为获得更优的深度图像超分辨率重建结果，本文构建了彩色图像多尺度引导深度图像超分辨率重建卷积神经网络。该网络使用多尺度融合方法实现高分辨率(HR)彩色图像特征对低分辨率(LR)深度图像特征的引导，有益于恢复图像细节信息。在对LR深度图像提取特征的过程中，构建了多感受野残差块(MRFRB)提取并融合不同感受野下的特征，然后将每一个MRFRB输出的特征连接、融合，得到全局融合特征。最后，通过亚像素卷积层和全局融合特征，得到HR深度图像。实验结果表明，该算法得到的超分辨率图像缓解了边缘失真和伪影问题，有较好的视觉效果。
Abstract:In order to obtain better super-resolution reconstruction results of depth images, this paper constructs a multi-scale color image guidance depth image super-resolution reconstruction convolutional neural network. In this paper, the multi-scale fusion method is used to realize the guidance of high resolution (HR) color image features to low resolution (LR) depth image features, which is beneficial to the restoration of image details. In the process of extracting features from LR depth images, a multiple receptive field residual block (MRFRB) is constructed to extract and fuse the features of different receptive fields, and then connect and fuse the features of each MRFRB output to obtain global fusion features. Finally, the HR depth image is obtained through sub-pixel convolution layer and global fusion features. The experimental results show that the super-resolution image obtained by this method alleviates the edge distortion and artifact problems, and has better visual effects.
-
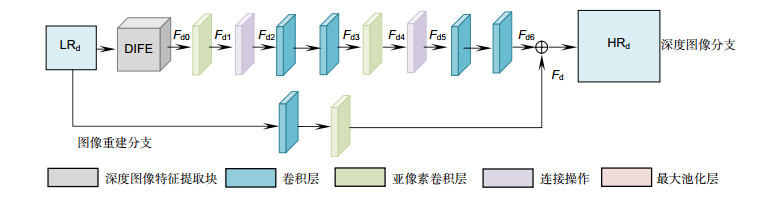
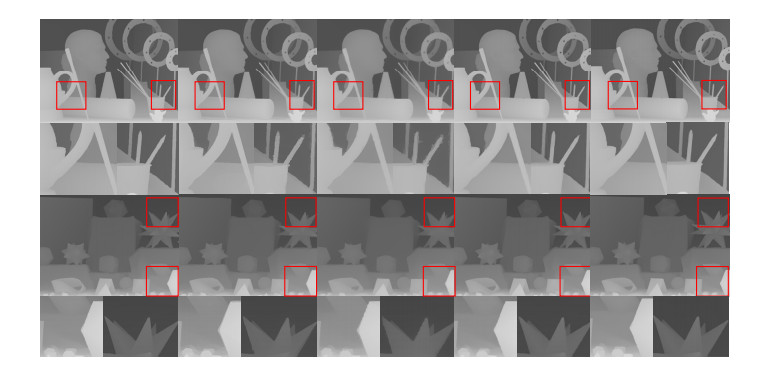
Overview: In recent years, as the demand for depth information in the field of computer vision has expanded, the acquisition of high-resolution depth images has become crucial. However, due to the limitations of hardware conditions such as sensors, the depth image resolution obtained by the depth camera is generally not high, and it is difficult to meet the practical application requirements. For example, the PMD Camcube camera has a resolution of only 200×200, and Microsoft's Kinect camera has a resolution of only 640×480. If the resolution of the depth image is increased by improving the hardware facilities, the cost will increase, and there are some technical problems that are difficult to overcome, so the depth image resolution is usually improved by a software processing method. In order to obtain better super-resolution reconstruction results of depth images, this paper constructs a multi-scale color image guidance depth image super-resolution reconstruction convolutional neural network. The network consists of three branches: a color image branch, a depth image branch, and an image reconstruction branch. The relationship between high resolution (HR) color image and low resolution (LR) depth image of the same scene is corresponding. Super-resolution reconstruction of LR depth image guided by HR color image of the same scene is conducive to restoring high-frequency information of LR depth image. So the LR depth image super-resolution reconstruction can be guided by the same scene HR color image to obtain more excellent reconstruction results. Because different structural information in the image has different scales, so the multi-scale fusion method is used to realize the guidance of HR color image features to LR depth image features, which is beneficial to the restoration of image details. For the depth image super-resolution reconstruction problem, the input LR depth image is highly correlated with the output HR depth image, so if the features of the LR depth image can be fully extracted, a better reconstruction result will be obtained. Thus in the process of extracting features from LR depth images, this paper constructs a multi-receptive residual block to extract and fuse the features of different receptive fields, and then connect and fuse the features of each multiple receptive field residual block output to obtain global fusion features. Finally, the HR depth image is obtained through sub-pixel convolution layer and global fusion features. The experimental results on different data sets show that the super-resolution image obtained by this algorithm can alleviate the problem of edge distortion and artifacts, and has better visual effect.
-
-
图 1 当超分辨率重建倍数r为4时的网络结构
Figure 1. Network structure when super-resolution reconstruction multiple r is 4
图 5 有无彩色图像引导在Middlebury数据集上的实验结果的定性比较。
Figure 5. Qualitative comparison of experimental results on the data set at Middlebury with and without color image guidance.
图 6 不同方法在Middlebury数据集上的超分辨率重建结果。
Figure 6. Super-resolution reconstruction results on the Middlebury dataset by different methods.
表 1 有无彩色图像引导在Middlebury数据集上的实验结果的定量比较
Table 1. Quantitative comparison of experimental results on the data set at Middlebury with and without color image guidance
RMSE SSIM Art Books Moebius Art Books Moebius Bicubic 3.8564 1.5789 1.4005 0.9683 0.9899 0.9888 Mandal[6] 2.6869 1.2520 1.1255 0.9854 0.9934 0.9925 Kim[25] 1.7986 0.7560 0.7657 0.9934 0.9966 0.9962 Without color 1.6267 0.7586 0.7448 0.9949 0.9969 0.9966 Ours 1.6000 0.7484 0.7244 0.9951 0.9969 0.9967 注：粗体字表示最优值，下划线标识次优值。 
下载: 导出CSV
表 2 不同的方法在Middlebury数据集A上重建结果的定量分析(RMSE)
Table 2. Quantitative analysis of reconstruction results on dataset A of Middlebury by different methods (RMSE)
Art Books Moebius X2 X4 X8 X2 X4 X8 X2 X4 X8 Bicubic 2.5837 3.8564 5.5279 1.0319 1.5789 2.2682 0.9303 1.4005 2.0578 Mandal[6] 1.7502 2.6869 6.0125 0.6152 1.2520 2.6268 0.7046 1.1255 2.2823 Liu[11] 2.3406 3.4221 4.6056 1.1873 1.6225 2.2459 1.0183 1.5159 2.1717 Kiechle[12] 1.1414 1.8789 2.8130 0.5541 0.8137 1.2378 0.6037 0.8497 1.5094 Li[13] 2.9834 4.0422 5.3825 1.2582 1.8400 2.4619 1.2400 1.7089 2.2352 Park[14] 2.9923 4.2771 6.4019 1.2339 1.8707 2.6495 1.1248 1.6981 2.5554 Dong[23] 1.1330 2.0170 3.8290 0.5230 0.9350 1.7260 0.5370 0.9130 1.5790 Hui[24] 0.8130 1.6270 2.7690 0.4170 0.7240 1.0720 0.4130 0.7410 1.1380 Kim[25] 1.0208 1.7986 3.0044 0.4553 0.7560 1.2075 0.4769 0.7657 1.1854 Lai[26] 0.7568 2.0198 3.3320 0.4470 0.8653 1.3639 0.4367 0.8843 1.3811 Ours 0.6306 1.6000 2.6063 0.4197 0.7484 1.0917 0.3905 0.7244 1.0864 注：粗体字表示最优值，下划线标识次优值。
下载: 导出CSV
表 3 不同的方法在Middlebury数据集B上重建结果的定量分析(RMSE)
Table 3. Quantitative analysis of reconstruction results on dataset B of Middlebury by different methods (RMSE)
Cones Venus Tsukuba X2 X4 X2 X4 X2 X4 Bicubic 2.5418 3.8659 1.3370 1.9364 5.8185 8.5637 Mandal[6] 1.9663 3.3027 0.7919 1.3592 4.4127 7.0468 Chen[10] — 3.1742 — 0.9955 — 6.3472 Liu[11] 2.6181 4.5441 1.1619 1.5082 5.6176 7.9656 Kiechle[12] 1.7212 3.2005 0.6102 0.8758 3.6626 6.1629 Li[13] 3.6702 5.5222 1.2277 1.7814 6.3763 9.0654 Park[14] 4.1455 6.3944 1.2662 1.8346 6.9523 9.8982 Dong[23] 1.4840 3.5850 0.4560 0.7890 3.2750 7.9390 Hui[24] 1.1000 2.7700 0.2590 0.4220 2.4720 4.9960 Kim[25] 1.3261 2.6033 0.5517 0.8808 3.0955 5.0385 Lai[26] 0.9976 2.7728 0.3855 1.1368 2.0191 5.3103 Ours 0.8688 2.5339 0.2516 0.7055 1.8346 4.5424 注：粗体字表示最优值，下划线标识次优值。
下载: 导出CSV
表 4 不同的方法在Middlebury数据集A上重建结果的定量分析(SSIM)
Table 4. Quantitative analysis of reconstruction results on data set A of Middlebury by different methods (SSIM)
Art Books Moebius X2 X4 X8 X2 X4 X8 X2 X4 X8 Bicubic 0.9870 0.9683 0.9438 0.9956 0.9899 0.9833 0.9950 0.9888 0.9812 Mandal[6] 0.9943 0.9854 0.9407 0.9980 0.9934 0.9830 0.9969 0.9925 0.9788 Liu[11] 0.9902 0.9810 0.9706 0.9939 0.9910 0.9868 0.9942 0.9897 0.9834 Kiechle[12] 0.9971 0.9931 0.9863 0.9980 0.9965 0.9938 0.9975 0.9955 0.9920 Li[13] 0.9842 0.9742 0.9653 0.9936 0.9897 0.9870 0.9924 0.9884 0.9851 Park[14] 0.9847 0.9704 0.9546 0.9944 0.9895 0.9857 0.9937 0.9884 0.9836 Kim[25] 0.9974 0.9934 0.9833 0.9984 0.9966 0.9931 0.9983 0.9962 0.9921 Lai[26] 0.9984 0.9918 0.9795 0.9986 0.9962 0.9926 0.9986 0.9955 0.9909 Ours 0.9988 0.9951 0.9881 0.9985 0.9969 0.9944 0.9988 0.9967 0.9938 注：粗体字表示最优值，下划线标识次优值。
下载: 导出CSV
表 5 不同的方法在Middlebury数据集B上重建结果的定量分析(SSIM)
Table 5. Quantitative analysis of reconstruction results on dataset B of Middlebury by different methods (SSIM)
Cones Venus Tsukuba X2 X4 X2 X4 X2 X4 Bicubic 0.9814 0.9585 0.9935 0.9861 0.9700 0.9295 Mandal[6] 0.9877 0.9713 0.9979 0.9934 0.9829 0.9553 Chen[10] — 0.9711 — 0.9897 — 0.9599 Liu[11] 0.9761 0.9473 0.9941 0.9919 0.9665 0.9461 Kiechle[12] 0.9904 0.9757 0.9983 0.9970 0.9904 0.9733 Li[13] 0.9633 0.9331 0.9951 0.9919 0.9618 0.9341 Park[14] 0.9633 0.9300 0.9943 0.9893 0.9589 0.9177 Kim[25] 0.9935 0.9826 0.9980 0.9963 0.9931 0.9781 Lai[26] 0.9952 0.9803 0.9988 0.9947 0.9956 0.9749 Ours 0.9960 0.9834 0.9993 0.9973 0.9970 0.9834 注：粗体字表示最优值，下划线标识次优值。
下载: 导出CSV
-
[1] Palacios J M, Sagüés C, Montijano E, et al. Human-computer interaction based on hand gestures using RGB-D sensors[J]. Sensors, 2013, 13(9): 11842-11860. doi: 10.3390/s130911842
[2] Nguyen T N, Huynh H H, Meunier J. 3D reconstruction with time-of-flight depth camera and multiple mirrors[J]. IEEE Access, 2018, 6: 38106-38114. doi: 10.1109/ACCESS.2018.2854262
[3] Yamamoto S. Development of inspection robot for nuclear power plant[C]//Proceedings of 1992 IEEE International Conference on Robotics and Automation, Nice, France, 1992: 1559-1566.
[4] Kolb A, Barth E, Koch R, et al. Time-of-flight cameras in computer graphics[J]. Computer Graphics Forum, 2010, 29(1): 141-159.
[5] Xie J, Feris R S, Yu S S, et al. Joint super resolution and denoising from a single depth image[J]. IEEE Transactions on Multimedia, 2015, 17(9): 1525-1537. doi: 10.1109/TMM.2015.2457678
[6] Mandal S, Bhavsar A, Sao A K. Noise adaptive super-resolution from single image via non-local mean and sparse representation[J]. Signal Processing, 2017, 132: 134-149. doi: 10.1016/j.sigpro.2016.09.017
[7] Aodha O M, Campbell N D F, Nair A, et al. Patch based synthesis for single depth image super-resolution[C]//Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 2012: 71-84.
[8] Li J, Lu Z C, Zeng G, et al. Similarity-aware patchwork assembly for depth image super-resolution[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 2014: 3374-3381.
http://www.researchgate.net/publication/286594554_Similarity-Aware_Patchwork_Assembly_for_Depth_Image_Super-resolution?ev=auth_pub [9] Xie J, Feris R S, Sun M T. Edge-guided single depth image super resolution[J]. IEEE Transactions on Image Processing, 2016, 25(1): 428-438. http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0214835112/
[10] Chen B L, Jung C. Single depth image super-resolution using convolutional neural networks[C]//Proceedings of 2018 IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, AB, Canada, 2018: 1473-1477.
[11] Liu W, Chen X G, Yang J, et al. Robust color guided depth map restoration[J]. IEEE Transactions on Image Processing, 2017, 26(1): 315-327. doi: 10.1109/TIP.2016.2612826
[12] Kiechle M, Hawe S, Kleinsteuber M. A joint intensity and depth co-sparse analysis model for depth map super-resolution[C]//Proceedings of 2013 International Conference on Computer Vision, Sydney, NSW, Australia, 2013: 1545-1552.
[13] Li Y, Min D B, Do M N, et al. Fast guided global interpolation for depth and motion[C]//Proceedings of the 14th European Conference on Computer Vision. Amsterdam, The Netherlands, 2016: 717-733.
http://link.springer.com/chapter/10.1007/978-3-319-46487-9_44 [14] Park J, Kim H, Tai Y W, et al. High quality depth map upsampling for 3D-tof cameras[C]//Proceedings of 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 2011: 1623-1630.
[15] 李伟, 张旭东.基于卷积神经网络的深度图像超分辨率重建方法[J].电子测量与仪器学报, 2017, 31(12): 1918-1928.
Li W, Zhang X D. Depth image super-resolution reconstruction based on convolution neural network[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(12): 1918-1928.
[16] Xiao Y, Cao X, Zhu X Y, et al. Joint convolutional neural pyramid for depth map super-resolution[Z]. arXiv: 1801.00968, 2018.
[17] Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. doi: 10.1109/5.726791
[18] Scharstein D, Szeliski R, Zabih R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[C]//Proceedings of 2001 IEEE Workshop on Stereo and Multi-Baseline Vision, Kauai, HI, USA, 2001: 131-140.
[19] Richardt C, Stoll C, Dodgson N A, et al. Coherent spatiotemporal filtering, upsampling and rendering of rgbz videos[J]. Computer Graphics Forum, 2012, 31(2): 247-256. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1111/j.1467-8659.2012.03003.x
[20] Lu S, Ren X F, Liu F. Depth enhancement via low-rank matrix completion[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 2014: 3390-3397.
[21] Handa A, Whelan T, McDonald J, et al. A benchmark for RGB-D visual odometry, 3D reconstruction and SLAM[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 2014: 1524-1531.
[22] He K M, Zhang X Y, Ren S Q, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 2015: 1026-1034.
http://www.researchgate.net/publication/319770272_Delving_Deep_into_Rectifiers_Surpassing_Human-Level_Performance_on_ImageNet_Classification [23] Dong C, Loy C C, He K M, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. doi: 10.1109/TPAMI.2015.2439281
[24] Hui T W, Loy C C, Tang X O. Depth map super-resolution by deep multi-scale guidance[C]//Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 353-369.
http://link.springer.com/chapter/10.1007/978-3-319-46487-9_22 [25] Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 1646-1654.
http://ieeexplore.ieee.org/document/7780551/ [26] Lai W S, Huang J B, Ahuja N, et al. Deep Laplacian pyramid networks for fast and accurate super-resolution[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 2017: 624-632.
-
点击扫一扫
图(6)
表(5)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
