Measurement of optical fiber geometry parameters by gray distribution fitting with Gaussian function
-
摘要:
光纤的几何参数影响着光纤的光学传输和机械性能等,是衡量光纤质量的重要指标。近场光分布法是国标GB 15972.20-2008中推荐的几何参数测量方法。该方法在对光纤纤芯的测量中需对光纤通光照明,以区分纤芯和包层的边界。通光的纤芯端面是一个边缘并不清晰的发光亮斑,因而无法准确判断纤芯与包层的真实边缘。本文分析了光纤内光传播模场的分布,理论上光纤模场电磁矢量的解满足贝塞尔函数,但在近似情况下也可以用高斯函数代表光纤模场分布。因此本文利用高斯函数拟合光纤纤芯端面灰度分布,进而由拟合后的高斯函数得到纤芯与包层的真实边缘。本方法是对国标GB15972.20-2008的测量方法的进一步完善。实验测量结果表明,当光纤的切割效果不佳或成像质量较差时,模场灰度分布的高斯函数拟合法仍能保证测量的重复精度和测量数据的稳定性。
Abstract:The geometry parameters of optical fiber affect the optical transmission and mechanical properties, which are the important indexes to measure the quality of fiber. Near-field light distribution method is recommended in GB15972.20-2008 for the measurement of geometry parameters. In order to distinguish the boundary between fiber core and cladding, the method needs to illuminate the fiber. The end face of the fiber core is a bright spot with unclear edge, so the true edge of the core and cladding cannot be accurately judged. In this paper, the distribution of mode field in optical fiber is analyzed. Theoretically, the solution of electromagnetic vector of mode field satisfies Bessel function, but Gaussian function can also be used under approximate conditions. Therefore, Gaussian function is used to fit the distribution of the fiber core in this paper, and the real edge of the fiber core and cladding can be obtained from the Gaussian function after fitting. This method is a further improvement on the measurement method of GB15972.20-2008. The experimental results show that when the cutting effect of the fiber is not good or the imaging quality is poor, the Gaussian function method fitting with mode distribution can still ensure the repeatability of the measurement and the stability of the measured data.
-
Key words:
- optical fiber geometry parameters /
- mode distribution /
- Gaussian function /
- edge detect
-

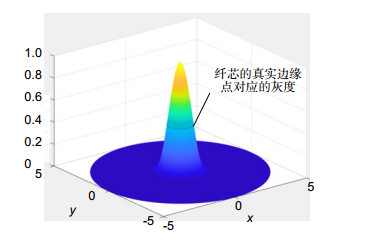
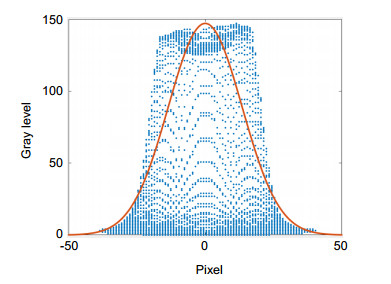
Overview: The geometry parameters of optical fiber affect the optical transmission and mechanical properties of optical fiber. The near-field optical distribution method is a measurement method recommended in GB15972.20-2008. The main parameters to be measured include the diameter of cladding and core, the roundness of cladding and core, and the concentricity of cladding and core. In order to distinguish the boundary between fiber core and cladding, the fiber core should be illuminated during the measurement of the geometry parameters. Actually, the end face of fiber core is a bright spot with unclear edges, so it is impossible to accurately judge the true edges of fiber core, which will bring errors to the measurement of geometry parameters of fiber core. In this paper, the distribution of optical mode field in fiber was analyzed. Theoretically, the solution of electromagnetic vector of optical fiber mode field satisfies Bessel function, but Gaussian function can also be used to approximately describe the distribution of optical fiber mode field.
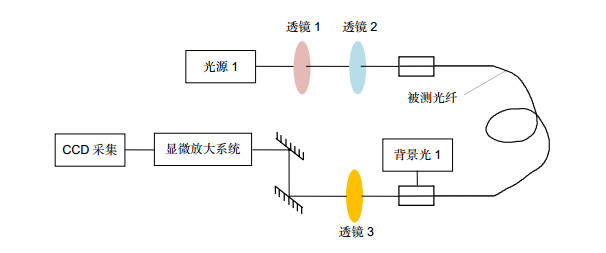
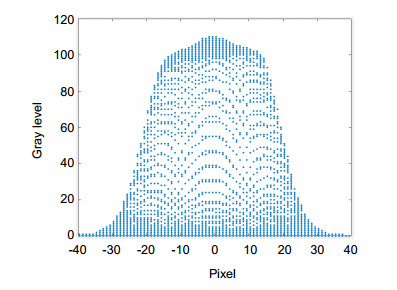
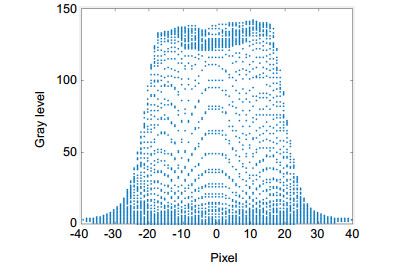
Therefore, Gaussian function was used to fit the gray distribution of fiber core, and the true edge of fiber core was obtained from the Gaussian function. Gaussian function fitting method mainly includes the following three steps. The first step is to obtain the image of the end face of the optical fiber by CCD and conduct appropriate image preprocessing. The image contrast is stronger and more conducive to subsequent gray data extraction by image preprocessing. The second step is to find the best Gaussian function by the fitting with gray data of the image. 3D fitting with all the gray data of fiber core end face can effectively filter out error data and reflect the true mode field distribution of fiber core. The third step is to find the true edge of the fiber core through the best-fitting Gaussian function, and fit the edge data with elliptical curves. Finally, the geometry parameters of the fiber core will be obtained. For the measurement of cladding geometry parameters, because of the high contrast of the edge, Canny operator can be directly used to extract the edge of the cladding. The cladding geometry parameters with high precision can be obtained by elliptical curves fitting.
The real edge of optical fiber core can be accurately obtained by Gaussian function fitting, and the error points in the image can be effectively filtered through fitting, so as to improve the measurement accuracy of optical fiber geometry parameters. Taking fiber core data as an example, the data of diameter and roundness measured by the standard instrument are 8.420 μm and 0.670%, respectively. When cutting effect of fiber end face or lighting condition is poor, the instrument data change to 9.044 μm and 1.457%, while the data measured in this paper are 8.425 μm and 0.480%, respectively.
-

-
表 1 正常条件下FGM-5几何参数测试仪的测量结果
Table 1. Data measured by FGM-5 under normal conditions
实验组数 包层直径/μm 包层不圆度/% 纤芯直径/μm 纤芯不圆度/% 芯—包同心度/μm 1 125.073 0.116 8.421 0.865 0.241 2 125.094 0.117 8.409 0.335 0.236 3 125.120 0.118 8.431 0.666 0.246 4 125.101 0.098 8.449 0.616 0.247 5 125.093 0.102 8.388 0.868 0.221 平均值 125.096 0.110 8.420 0.670 0.238 最大偏差 0.024 0.012 0.032 0.335 0.017 表 2 正常条件的高斯函数拟合法测量结果
Table 2. Data measured by Gaussian function fitting under normal conditions
实验组数 包层直径/μm 包层不圆度/% 纤芯直径/μm 纤芯不圆度/% 芯—包同心度/μm 1 125.081 0.108 8.379 0.116 0.226 2 125.101 0.114 8.368 0.423 0.247 3 125.125 0.111 8.413 0.102 0.238 4 125.108 0.122 8.413 0.096 0.244 5 125.097 0.114 8.412 0.269 0.237 平均值 125.102 0.114 8.397 0.201 0.238 最大偏差 0.023 0.008 0.029 0.222 0.013 表 3 非正常成像条件下FGM-5仪的测量数据
Table 3. Data measured by FGM-5 under abnormal conditions
实验组数 包层直径/μm 包层不圆度/% 纤芯直径/μm 纤芯不圆度/% 芯—包同心度/μm 1 124.832 0.077 9.092 1.529 0.288 2 124.83 0.094 9.037 1.148 0.302 3 124.869 0.089 9.037 1.754 0.302 4 124.862 0.095 9.045 0.837 0.283 5 124.837 0.091 9.01 2.016 0.278 平均值 124.846 0.089 9.044 1.457 0.291 最大偏差 0.023 0.012 0.048 0.62 0.013 表 4 非正常成像条件下高斯函数拟合法的测量结果
Table 4. Data measured by Gaussian function fitting under abnormal conditions
实验组数 包层直径/μm 包层不圆度/% 纤芯直径/μm 纤芯不圆度/% 芯—包同心度/μm 1 124.874 0.084 8.427 0.570 0.305 2 124.857 0.072 8.410 0.295 0.300 3 124.897 0.069 8.428 0.380 0.314 4 124.885 0.078 8.416 0.736 0.310 5 124.862 0.055 8.442 0.421 0.320 平均值 124.875 0.072 8.425 0.480 0.310 最大偏差 0.022 0.016 0.017 0.256 0.011 -
[1] Ekici C, Dinleyici M S. A practical approach for optical characterization of a film coated on the optical fiber[J]. Optical Fiber Technology, 2017, 36: 382-386. doi: 10.1016/j.yofte.2017.05.015
[2] Zhang H, Kuschmierz R, Czarske J. Miniaturized interferometric 3-D shape sensor using coherent fiber bundles[J]. Optics and Lasers in Engineering, 2018, 107: 364-369. doi: 10.1016/j.optlaseng.2018.04.011
[3] 张晓娟, 赵建林, 侯建平.一种新型高双折射光子晶体光纤[J].物理学报, 2007, 56(8): 4668-4676. doi: 10.3321/j.issn:1000-3290.2007.08.055
Zhang X J, Zhao J L, Hou J P. A novel photonic crystal fiber with high birefringence[J]. Acta Physica Sinica, 2007, 56(8): 4668-4676. doi: 10.3321/j.issn:1000-3290.2007.08.055
[4] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.光纤试验方法规范第20部分: 尺寸参数的测量方法和试验程序光纤几何参数: GB/T 15972.20-2008[S].北京: 中国标准出版社, 2008.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Management Committee. Specifications for optical fibre test methods-Part 20: measurement methods and test procedures for dimensions-fiber geometry: GB/T 15972.20-2008[S]. Beijing: China Standard Press, 2008.
[5] 陈磊, 陈进榜, 陆润华.光纤几何参数的自动检测仪[J].光学学报, 2001, 21(10): 1245-1248. doi: 10.3321/j.issn:0253-2239.2001.10.021
Chen L, Chen J B, Lu R H. Automatic measurement of optical fiber geometric parameters[J]. Acta Optica Sinica, 2001, 21(10): 1245-1248. doi: 10.3321/j.issn:0253-2239.2001.10.021
[6] 赵新彦, 陈陶, 丁志雄.光纤端面参数自动化测量系统的研究[J].光学仪器, 2009, 31(4): 1-6. doi: 10.3969/j.issn.1005-5630.2009.04.001
Zhao X Y, Chen T, Ding Z X. Research on automatic measurement system for fiber end-face parameters[J]. Optical Instruments, 2009, 31(4): 1-6. doi: 10.3969/j.issn.1005-5630.2009.04.001
[7] Chang Y Y, Wang L A. Silicon cored fiber diameter measurement[C]//Proceedings of 2015 International Conference on Optical MEMS and Nanophotonics, 2015: 1-2.
[8] 林延东, 李平, 李熙.连续变孔径法单模光纤模场直径(MFD)测量的数据处理[J].现代计量测试, 1999(5): 29-31, 36. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199900707538
Lin Y D, Li P, Li X. Data processing method for MFD measurement by means of continuous variable aperture far field[J]. Modern Measurement and Test, 1999(5): 29-31, 36. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199900707538
[9] Gander W, Golub G H, Strebel R. Least-squares fitting of circles and ellipses[J]. BIT Numerical Mathematics, 1994, 34(4): 558-578. doi: 10.1007/BF01934268
[10] 殷爱娥, 姜仲玄, 张一龙.光纤折射率剖面的折射近场法测量的研究[J].光学学报, 1989, 9(2): 181-185. doi: 10.3321/j.issn:0253-2239.1989.02.014
Yin A E, Jiang Z X, Zhang Y L. Refracted near-field technique for the measurement of optical fiber refractive index profiles[J]. Acta Optica Sinica, 1989, 9(2): 181-185. doi: 10.3321/j.issn:0253-2239.1989.02.014
[11] 高迎春.基于折射近场法测量光纤折射率分布的仿真研究[D].哈尔滨: 哈尔滨工程大学, 2012.
Gao Y C. Simulation of measuring the optical fiber refractive index profiles by refraction near-field method[D]. Harbin: Harbin Engineering University, 2012.
[12] 孙会刚, 储九荣, 钟力生, 等.塑料光纤折射率分布的测量方法[J].光纤与电缆及其应用技术, 2001(4): 12-16. doi: 10.3969/j.issn.1006-1908.2001.04.004
Sun H G, Chu J R, Zhong L S, et al. Measurement of refractive-index profile of plastic optical fibers[J]. Optical Fiber & Electric Cable, 2001(4): 12-16. doi: 10.3969/j.issn.1006-1908.2001.04.004
[13] 李春生, 李琳莹, 杨世信, 等.单模光纤模场直径标准研究[J].现代传输, 2013(2): 72-76. doi: 10.3969/j.issn.1673-5137.2013.02.008
Li C X, Li L Y, Yang S X, et al. Study on mode field diameter standard of single-mode optical fiber[J]. Modern Transmission, 2013(2): 72-76. doi: 10.3969/j.issn.1673-5137.2013.02.008
[14] 沈奶连, 涂建坤, 王建财, 等.光纤几何参数测试仪的研究与设计[J].现代传输, 2008, 34(6): 51-54. doi: 10.3969/j.issn.1673-5137.2008.06.020
Shen N L, Tu J K, Wang J C, et al. Research and design of optical fiber geometry testing instrument[J]. Modern Transmission, 2008, 34(6): 51-54. doi: 10.3969/j.issn.1673-5137.2008.06.020
[15] 欧攀.高等光学仿真(MATLAB版)--光波导, 激光[M]. 2版.北京:北京航空航天大学出版社, 2014.
Ou P. Advanced Optical Simulation (MATLAB Version)-Optical Waveguide, Laser[M]. 2nd ed. Beijing: Beihang University Press, 2014.
[16] 郭福源, 李连煌, 王明华.介质平面光波导TE0模模场分布的高斯近似[J].中国激光, 2008, 35(2): 235-239. doi: 10.3321/j.issn:0258-7025.2008.02.016
Guo F Y, Li L H, Wang M H. Gaussian approximation for mode field distribution of dielectric planar waveguide TE0 mode[J]. Chinese Journal of Lasers, 2008, 35(2): 235-239. doi: 10.3321/j.issn:0258-7025.2008.02.016
[17] 宋小鹿, 李兵斌, 王石语, 等.一种测量激光光强按角度分布的新方法[J].半导体光电, 2007, 28(4): 572-575. doi: 10.3969/j.issn.1001-5868.2007.04.032
Song X L, Li B B, Wang S Y, et al. A new measurement of light intensity distribution with divergence[J]. Semiconductor Optoelectronics, 2007, 28(4): 572-575. doi: 10.3969/j.issn.1001-5868.2007.04.032
[18] Marcuse D. Gaussian approximation of the fundamental modes of graded-index fibers[J]. Journal of the Optical Society of America, 1978, 68(1): 103-109. doi: 10.1364/JOSA.68.000103
[19] 李一鸣, 涂建坤, 项华中, 等.用Canny算子和二值化滤波的光纤几何参数测量[J].光学技术, 2018, 44(5): 513-518. http://d.old.wanfangdata.com.cn/Periodical/gxjs201805001
Li Y M, Tu J K, Xiang H Z, et al. Measurement of optical fiber geometric parameters with Canny operator and binaryzation filtering[J]. Optical Technique, 2018, 44(5): 513-518. http://d.old.wanfangdata.com.cn/Periodical/gxjs201805001
[20] 李一鸣, 郑刚, 涂建坤, 等.任意椭圆函数拟合法测量光纤几何参数[J].光电工程, 2019, 46(5): 180319. doi: 10.12086/oee.2019.180319
Li Y M, Zheng G, Tu J K, et al. Measurement of optical fiber geometry with arbitrary ellipse curve fitting[J]. Opto-Electronic Engineering, 2019, 46(5): 180319. doi: 10.12086/oee.2019.180319
[21] 刘为, 唐春晖, 马秀梅, 等.缺陷光纤端面几何参数的测量[J].光通信研究, 2013(6): 35-38. doi: 10.3969/j.issn.1005-8788.2013.06.011
Liu W, Tang C H, Ma X M, et al. Measurement of geometric parameters of defective fiber ends[J]. Study on Optical Communications, 2013(6): 35-38. doi: 10.3969/j.issn.1005-8788.2013.06.011
[22] 穆丹丹, 朱永田, 张凯.天文光纤机械扰模器调制环形光场的实验研究[J].应用光学, 2012, 33(5): 996-1001. http://d.old.wanfangdata.com.cn/Periodical/yygx201205033
Mu D D, Zhu Y T, Zhang K. Modulation of annular light distribution by mechanical fiber scrambler[J]. Journal of Applied Optics, 2012, 33(5): 996-1001. http://d.old.wanfangdata.com.cn/Periodical/yygx201205033
-


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: