E-mail Alert
RSS
Convolution theorems for the linear canonical sine and cosine transform and its application
-
摘要:
针对奇、偶信号的去噪问题，提出了一种基于线性正则正(余)弦变换卷积定理的乘性滤波器设计方法。在现有线性正则变换域卷积理论的基础上，研究了两类线性正则正(余)弦变换卷积定理，利用所得卷积定理，通过合理选择滤波函数，设计了一类基于卷积定理的线性正则正(余)弦变换域带限信号的乘性滤波模型，并对算法的复杂度进行分析。研究表明，这种滤波模型特别适合处理奇、偶信号，并能有效降低乘积滤波的计算复杂度，提高运算效率。
-
关键词:
- 线性正则变换 /
- 线性正则正(余)弦变换 /
- 卷积定理 /
- 滤波
Abstract:For the denoising problem of odd and even signals, a multiplicative filter design method based on the convolution theorem of the linear canonical sine and cosine transform is proposed. Two kinds of convolution theorems associated with the linear canonical sine and cosine transform based on the existing linear canonical transform domain convolution theory are derived. Using this two convolution theorems, two kinds of the multiplicative filtering models of the band-limited signal are designed by choosing an appropriate filter function in linear canonical sine and cosine transform domain. And the complexity of these schemes is analyzed. The results indicate that these filtering models are particularly suitable for handling odd and even signals, and can effectively improve computational efficiency by reducing computational complexity.
-
Overview: In the modern optical signal processing domain, the collected signals must be denoised before the signal is analyzed and processed. The multiplicative filtering is one of the effective denoising methods in signal processing field based on the convolution theorem. The classical convolution theorem shows that the convolution of the two signals in time domain is leads to simple multiplication of their Fourier transforms in the Fourier transform domain. But Fourier transform is a holistic transformation based on the time domain or frequency domain, which is not suitable for modern optical signal processing.
As generalization of the Fourier transform and the fractional Fourier transform, Linear canonical transform has become a one of the powerful tools for modern optical signal analysis and processing, and has achieved fruitful research results in recent years. In order to further reduce computation and improve computing efficiency, convolution theory and application based on linear canonical transform has become one of the hot topic research in modern optical signal processing. Therefore, this paper will mainly focus on the research of convolution theory and application based on canonical sine transform and canonical cosine transform which have very close relations with the linear canonical transform, and have important role in signal processing, optics and other fields. Because canonical sine transform has no even eigenfunction and canonical cosine transform have no odd eigenfunction, therefore, it is much more efficient to use the canonical sine transform to deal with the odd signal and use the canonical cosine transform to deal with the even signal. Moreover, the complexity of the canonical sine transform and canonical cosine transform is one half of the complexities of the linear canonical transform, then, it is more suitable for engineering applications.
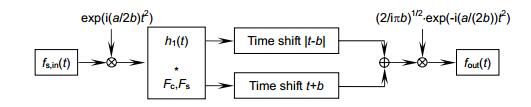
Hence, for the denoising problem of odd and even signals, a multiplicative filter design method based on the convolution theorem of the canonical sine and cosine transform is proposed. Two kinds of the convolution theorems associated with the canonical sine and cosine transform based on the existing linear canonical transform domain convolution theory are derived. Using this two convolution theorems, a kind of the multiplicative filtering model of the band-limited signal is designed by choosing an appropriate filter function in canonical sine and cosine transform domain. And the complexity of this scheme is analyzed. The results indicate that this filtering model is particularly suitable for handling odd and even signals, and can effectively improve computational efficiency by reducing computational complexity.
-
-
图 1 线性正则正(余)弦变换的带通乘积滤波器
Figure 1. The bandpass multiplicative filter in the CST or CCT domain
图 2 线性正则正弦变换的带通乘积滤波器的时域实现
Figure 2. The method to achieve the bandpass multiplicative filters in the CST domain by convolution in the time domain
-
[1] Akay O, Boudreaux-Bartels G F. Fractional convolution and correlation via operator methods and an application to detection of linear FM signals[J]. IEEE Transactions on Signal Processing, 2001, 49(5): 979-993. doi: 10.1109/78.917802
[2] Mustard D. Uncertainty principles invariant under the fractional Fourier transform[J]. The ANZIAM Journal, 1991, 33(2): 180-191.
[3] Shinde S, Gadre V M. An uncertainty principle for real signals in the fractional Fourier transform domain[J]. IEEE Transactions on Signal Processing, 2001, 49(11): 2545-2548. doi: 10.1109/78.960402
[4] 李红, 李明伟.编码曝光相机设计与实现[J].光电工程, 2016, 43(9): 72-77. http://www.oee.ac.cn/CN/abstract/abstract1771.shtml
Li H, Li M W. Design and implementation of coded exposure camera[J]. Opto-Electronic Engineering, 2016, 43(9): 72-77. http://www.oee.ac.cn/CN/abstract/abstract1771.shtml
[5] 葛明锋, 亓洪兴, 王雨曦, 等.高分辨力成像光谱仪光谱定标研究[J].光电工程, 2015, 42(12): 14-19. doi: 10.3969/j.issn.1003-501X.2015.12.003 http://www.oee.ac.cn/CN/abstract/abstract1715.shtml
Ge M F, Qi H X, Wang Y X, et al. Spectral calibration for the high spectral resolution imager[J]. Opto-Electronic Engineering, 2015, 42(12): 14-19. doi: 10.3969/j.issn.1003-501X.2015.12.003 http://www.oee.ac.cn/CN/abstract/abstract1715.shtml
[6] Cooley J W, Tukey J W. An algorithm for the machine computation of complex Fourier series[J]. Mathematics of Computation, 1965, 19(90): 297-301. doi: 10.1090/S0025-5718-1965-0178586-1
[7] Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3): 241-265. doi: 10.1093/imamat/25.3.241
[8] 陶然, 齐林, 王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社, 2004.
Tao R, Qi L, Wang Y. Theory Applications of the Fractional Fourier transform[M]. Tsinghua University Press: China, 2004.
[9] 许天周, 李炳照.线性正则变换及其应用[M].北京:科学出版社, 2013.
Xu T Z, Li B Z. Linear Canonical Transform and Its Applications[M]. Beijing: Science Press, 2013.
[10] Sneddon I N. Fourier Transforms[M]. New York: McGraw-Hill, 1951.
[11] Deng B, Tao R, Wang Y. Convolution theorems for the linear canonical transform and their applications[J]. Science in China Series F: Information Sciences, 2006, 49(5): 592-603. doi: 10.1007/s11432-006-2016-4
[12] Wei D Y, Ran Q W, Li Y. A convolution and correlation theorem for the linear canonical transform and its application[J]. Circuits, Systems, and Signal Processing, 2012, 31(1): 301-312. doi: 10.1007/s00034-011-9319-4
[13] Wei D Y, Ran Q W, Li Y M. New convolution theorem for the linear canonical transform and its translation invariance property[J]. Optik, 2012, 123(16): 1478-1481. doi: 10.1016/j.ijleo.2011.08.054
[14] Wei D Y, Ran Q W, Li Y M, et al. A convolution and product theorem for the linear canonical transform[J]. IEEE Signal Processing Letters, 2009, 16(10): 853-856. doi: 10.1109/LSP.2009.2026107
[15] Shi J, Liu X P, Zhang N T. Generalized convolution and product theorems associated with linear canonical transform[J]. Signal, Image and Video Processing, 2014, 8(5): 967-974. doi: 10.1007/s11760-012-0348-7
[16] Feng Q, Li B Z. Convolution and correlation theorems for the two-dimensional linear canonical transform and its applications[J]. IET Signal Processing, 2016, 10(2): 125-132. doi: 10.1049/iet-spr.2015.0028
[17] Zhang Z C. New convolution structure for the linear canonical transform and its application in filter design[J]. Optik, 2016, 127(13): 5259-5263. doi: 10.1016/j.ijleo.2016.03.025
[18] Stern A. Sampling of linear canonical transformed signals[J]. Signal Processing, 2006, 86(7): 1421-1425. doi: 10.1016/j.sigpro.2005.07.031
[19] Tao R, Li B Z, Wang Y. Spectral analysis and reconstruction for periodic nonuniformly sampled signals in fractional Fourier domain[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3541-3547. doi: 10.1109/TSP.2007.893931
[20] Li B Z, Tao R, Wang Y. New sampling formulae related to linear canonical transform[J]. Signal Processing, 2007, 87(5): 983-990. doi: 10.1016/j.sigpro.2006.09.008
[21] Shi J, Sha X J, Zhang Q Y, et al. Extrapolation of bandlimited signals in linear canonical transform domain[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1502-1508. doi: 10.1109/TSP.2011.2176338
[22] Li B Z, Ji Q H. Sampling analysis in the complex reproducing kernel Hilbert space[J]. European Journal of Applied Mathematics, 2015, 26(1): 109-120. doi: 10.1017/S0956792514000357
[23] Wei D Y, Li Y M. The dual extensions of sampling and series expansion theorems for the linear canonical transform[J]. Optik, 2015, 126(24): 5163-5167. doi: 10.1016/j.ijleo.2015.09.226
[24] Stern A. Uncertainty principles in linear canonical transform domains and some of their implications in optics[J]. Journal of the Optical Society of America A, 2008, 25(3): 647-652. doi: 10.1364/JOSAA.25.000647
[25] Sharma K K, Joshi S D. Uncertainty principle for real signals in the linear canonical transform domains[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 2677-2683. doi: 10.1109/TSP.2008.917384
[26] Zhao J, Tao R, Li Y L, et al. Uncertainty principles for linear canonical transform[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2856-2858. doi: 10.1109/TSP.2009.2020039
[27] Xu G L, Wang X T, Xu X G. On uncertainty principle for the linear canonical transform of complex signals[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4916-4918. doi: 10.1109/TSP.2010.2050201
[28] Dang P, Deng G T, Qian T. A tighter uncertainty principle for linear canonical transform in terms of phase derivative[J]. IEEE Transactions on Signal Processing, 2013, 61(21): 5153-5164. doi: 10.1109/TSP.2013.2273440
[29] Shi J, Han M, Zhang N T. Uncertainty principles for discrete signals associated with the fractional Fourier and linear canonical transforms[J]. Signal, Image and Video Processing, 2016, 10(8): 1519-1525. doi: 10.1007/s11760-016-0965-7
[30] Pei S C, Ding J J. Fractional cosine, sine, and Hartley transforms[J]. IEEE Transactions on Signal Processing, 2002, 50(7): 1661-1680. doi: 10.1109/TSP.2002.1011207
[31] Paley R C, Wiener N. Fourier Transforms in the Complex Domain[M]. New York: American Mathematical Society, 1934.
[32] Churchill R V. Fourier Series and Boundary Value Problems[M]. New York: McGraw-Hill, 1941.
[33] Thao N X, Kakichev V A, Tuan V K. On the generalized convolutions for Fourier cosine and sine transforms[J]. East West Journal of Mathematics, 1998, 1(1): 85-90.
[34] Thao N X, Tuan V K, Hong N T. A Fourier generalized convolution transform and applications to integral equations[J]. Fractional Calculus and Applied Analysis, 2012, 15(3): 493-508.
[35] Thao N X, Khoa N M. On the generalized convolution with a weight function for the Fourier sine and cosine transforms[J]. Integral Transforms and Special Functions, 2006, 17(9): 673-685. doi: 10.1080/10652460500432071
[36] Thao N X, Tuan V K, Khoa N M. A generalized convolution with a weight function for the Fourier cosine and sine transforms[J]. Fractional Calculus and Applied Analysis, 2004, 7(3): 323-337.
[37] Thao N X, Khoa N M. On the convolution with a weight-function for the cosine-Fourier integral transform[J]. Acta Mathematica Vietnamica, 2004, 29(2): 149-162.
[38] Kakichev V A. On the convolution for integral transforms (in Russian)[J]. Vestsi Akademii Navuk BSSR, Seriya Fizika-Mathematics, 1967, 2: 48-57.
[39] Thao N X, Hai N T. Convolution for Integral Transforms and Their Applications[M]. Moscow: Russian Academy, 1997.
[40] Ganesan C, Roopkumar R. Convolution theorems for fractional Fourier cosine and sine transforms and their extensions to Boehmians[J]. Communications of the Korean Mathematical Society, 2016, 31(4): 791-809. doi: 10.4134/CKMS.c150244
[41] Feng Q, Li B Z. Convolution theorem for fractional cosine-sine transform and its application[J]. Mathematical Methods in the Applied Sciences, 2017, 40(10): 3651-3665. doi: 10.1002/mma.v40.10
[42] Lee B G. A new algorithm for computing the discrete cosine transform[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, 32(6): 1243-1245. doi: 10.1109/TASSP.1984.1164443
-
下载:
点击扫一扫
图(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
