E-mail Alert
RSS
Radar maneuvering target detection method based on fast and high resolution sparse fractional Fourier transform
-
摘要:
数据量的增加及新体制雷达的发展，对雷达探测技术提出了更高的要求。经典检测方法具有其优势，但同时也存在很多局限性，迫切需要创新雷达动目标检测方法以提升复杂背景和有限雷达资源条件下的雷达目标探测性能。该文介绍了稀疏傅里叶变换(SFT)的基本概念，在其基础上对稀疏分数阶傅里叶变换(SFRFT)的实现方法进行了系统描述。然后将SFRFT算法应用于雷达信号处理中，提出了基于快速高分辨稀疏FRFT的雷达机动目标检测算法，为雷达动目标探测能力的提高提供了新的思路。
-
关键词:
- 雷达信号处理 /
- 机动目标检测 /
- 稀疏傅里叶变换 /
- 稀疏分数阶傅里叶变换 /
- 稀疏时频分析
Abstract:With the increase of data volume and the rapid development of modern radar, more requirements are put forward for radar target detection technology. There are both advantages and limitations of classical radar detection methods. Innovative methods are urgently needed to improve the radar target detection performance under complex background and limited radar resources. The main purpose of this paper is to illustrate the implementation of sparse fractional Fourier transform (SFRFT), which is developed on the basis of sparse Fourier transform (SFT). Besides, the SFRFT algorithm is applied to radar signal processing and a SFRFT-based fast and high resolution detection method is proposed to improve the detection performance of radar maneuvering target. It is expected that the method can provide a new way for radar moving target detection.
-
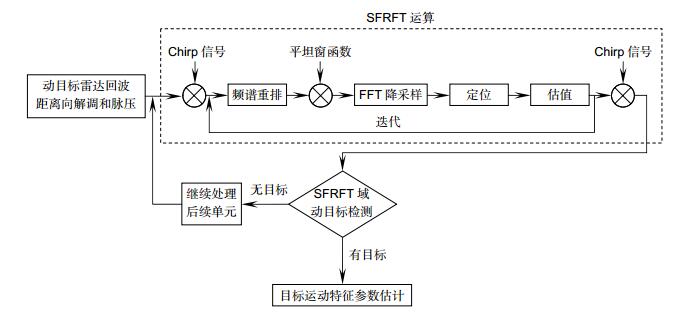
Overview: Fast and effective detection of moving targets within a complex environment is always a challenging subject in the field of radar signal processing, which is also important in both military and civil fields. What they have in common is that due to the strong background, low radar resolution, far range and other factors, the signal-to-noise/clutter ratio (SNR/SCR) is so low in both time and frequency domains that detection performance is seriously descended. In general, radar signals can be classified as a kind of nonstationary signals and their frequencies are changing over time, so time-frequency analysis methods are studied to improve the detection performance of nonstationary signals. Radar echo of moving target with constant acceleration can be modeled as a linear frequency modulation (LFM) signal in some circumstances. The fractional Fourier transform (FRFT), which is the generalised formula for the Fourier transform (FT), has a good energy concentration property of LFM signal and it is feasible to the moving target detection and parameter estimation in low SCR environment. However, due to the wide observation range of radar and large amount of echo data caused by the new system radar, more requirements are put forward for radar target detection technology. It is urgent to study the valid signal analysis methods with high time-frequency resolution and suitable for large data volumes. Hence, more effective and higher efficiency FRFT-based methods for moving target detection are desired to improve the radar moving target detection performance under complex background. Recently, a novel sub-linear algorithm for discrete Fourier transform (DFT) named sparse Fourier transform (SFT) was developed by Hassanieh et al. SFT is a new discrete Fourier transform algorithm for sparse signals, which is more efficient than the traditional fast Fourier transform (FFT). Assuming that a LFM signal has a sparse characteristic in the fractional domain, in order to improve the time-frequency analysis speed, professor Tao of Beijing Institute of Technology redesigned Pei's discrete FRFT (DFRFT) method on the basis of SFT and studied a new fast algorithm, namely sparse FRFT (SFRFT). So the complexity of DFRFT is further reduced. The radar echo of target can be regarded as a superposition of a few strong scattering center echoes, which has a property of sparsity. This paper illustrates the implementation of SFRFT, then the SFRFT algorithm is applied to radar signal processing and a SFRFT-based fast and high resolution maneuvering target detection method is proposed. The effectiveness of the detection method is validated by simulation results. It is proved that the SFRFT-based detection method can achieve low computational complexity with good clutter suppression and parameter estimation ability.
-
-
图 1 基于SFRFT动目标检测方法流程
Figure 1. Flowchart of SFRFT-based moving target detection method
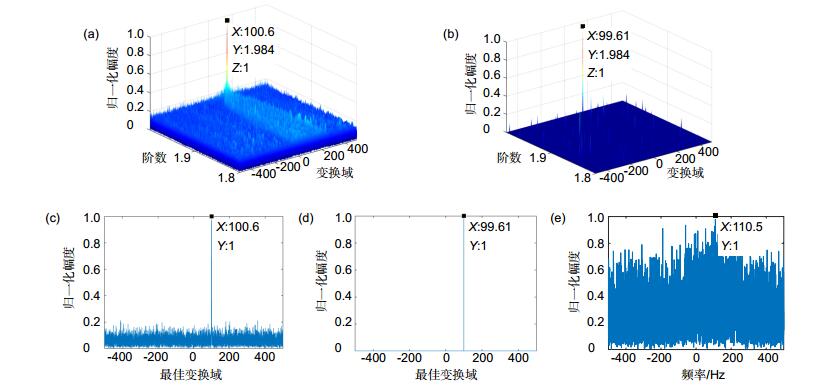
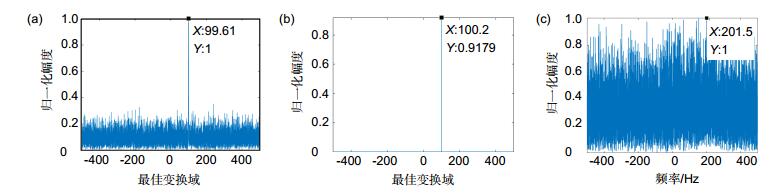
图 2 DFRFT、SFRFT、MTD处理结果对比(SNR=-3 dB)。(a) DFRFT处理结果；(b) SFRFT处理结果；(c) DFRFT最佳变换域(p=1.984)；(d) SFRFT最佳变换域(p=1.984)；(e) MTD结果
Figure 2. Comparison of DFRFT, SFRFT and MTD results (SNR=-3 dB). (a) Result of DFRFT; (b) Result of SFRFT; (c) The optimal transformation of DFRFT (p=1.984); (d) The optimal transformation of SFRFT (p=1.984); (e) Result of MTD
图 3 DFRFT、SFRFT、MTD处理结果对比(SNR=-5 dB)。(a) DFRFT最佳变换域(p=1.984)；(b) SFRFT最佳变换域(p=1.984)；(c) MTD结果
Figure 3. Comparison of DFRFT, SFRFT and MTD results (SNR=-5 dB). (a) The optimal transformation of DFRFT (p=1.984); (b) The optimal transformation of SFRFT (p=1.984); (c) Result of MTD
表 1 仿真参数说明
Table 1. Description of the simulation parameters
观测时长/s 采样频率/Hz 工作波长/m f0/Hz μ0/(Hz/s) 大值个数K 8.192 1000 0.03 100 40 1 
下载: 导出CSV
表 2 SFRFT、DFRFT、MTD检测性能比较(SNR=-3 dB)
Table 2. Detection performance comparison of SFRFT, DFRFT and MTD (SNR=-3 dB)
目标峰值 ${\hat f_0}/{\rm{Hz}}$ ${\hat \mu _0}/\left( {{\rm{Hz}}/{\rm{s}}} \right)$ Δf0/Hz Δμ0/(Hz/s) 计算时间*/ms SFRFT 1 99.61 39.7804 0.39 0.2196 49.5 DFRFT 1 100.6 39.7804 0.6 0.2196 62.8 MTD 1 110.5 —— 10.5 —— 29.4 *计算机配置：Intel Core i7-4790 3.6G Hz CPU；16G RAM；Matlab R2016a，计算时间为算法一次运算时间
下载: 导出CSV
-
[1] Zuo L, Li M, Zhang X W, et al. An efficient method for detecting slow-moving weak targets in sea clutter based on time-frequency iteration decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3659-3672. doi: 10.1109/TGRS.2012.2224665
[2] 陈小龙, 刘宁波, 王国庆, 等.基于高斯短时分数阶Fourier变换的海面微动目标检测方法[J].电子学报, 2014, 42(5): 971-977. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201405021
Chen X L, Liu N B, Wang G Q, et al. Gaussian short-time fractional Fourier transform based detection algorithm of target with micro-motion at sea[J]. Acta Electronica Sinica, 2014, 42(5): 971-977. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201405021
[3] Greco M, Stinco P, Gini F, et al. Impact of sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1502-1513. doi: 10.1109/TAES.2010.5545205
[4] Luo F, Zhang D T, Zhang B. The fractal properties of sea clutter and their applications in maritime target detection[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1295-1299. doi: 10.1109/LGRS.2013.2237750
[5] Chen X L, Song J, Guan J, et al. Moving target detection at sea based on fractal characters in FRFT domain[C]//Proceedings of 2011 IEEE Radar Conference, 2011: 1-5.
[6] 鲁溟峰, 倪国强, 白廷柱, 等.基于分数阶傅里叶变换的量化噪声抑制方法[J].北京理工大学学报, 2015, 35(12): 1285-1290. http://mall.cnki.net/magazine/Article/BJLG201512014.htm
Lu M F, Ni G Q, Bai T Z, et al. A novel method for suppressing the quantization noise based on fractional Fourier transform[J]. Transactions of Beijing Institute of Technology, 2015, 35(12): 1285-1290. http://mall.cnki.net/magazine/Article/BJLG201512014.htm
[7] Wu J M, Lu M F, Tao R, et al. Improved FRFT-based method for estimating the physical parameters from Newton's rings[J]. Optics and Lasers in Engineering, 2017, 91: 178-186. doi: 10.1016/j.optlaseng.2016.11.021
[8] Liu N, Tao R, Wang R, et al. Signal reconstruction from recurrent samples in fractional Fourier domain and its application in multichannel SAR[J]. Signal Processing, 2017, 131: 288-299. doi: 10.1016/j.sigpro.2016.08.008
[9] Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(2): 241-265.
[10] Guan J, Chen X L, Huang Y, et al. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter[J]. IET Radar, Sonar & Navigation, 2012, 6(5): 389-401.
[11] 陈小龙, 关键, 于晓涵, 等.基于短时稀疏时频分布的雷达目标微动特征提取及检测方法[J].电子与信息学报, 2017, 39(5): 1017-1023. http://www.cqvip.com/QK/95985X/201304/45400713.html
Chen X L, Guan J, Yu X H, et al. Radar micro-Doppler signature extraction and detection via short-time sparse time-frequency distribution[J]. Journal of Electronics & Information Technology, 2017, 39(5): 1017-1023. http://www.cqvip.com/QK/95985X/201304/45400713.html
[12] Hassanieh H, Indyk P, Katabi D, et al. Simple and practical algorithm for sparse Fourier transform[C]//Proceedings of the 23rd Annual ACM-SIAM Symposium on Discrete Algorithms, 2012: 1183-1194.
[13] Gilbert A C, Indyk P, Iwen M, et al. Recent developments in the sparse Fourier transform: A compressed Fourier transform for big data[J]. IEEE Signal Processing Magazine, 2014, 31(5): 91-100. doi: 10.1109/MSP.2014.2329131
[14] Hassanieh H, Indyk P, Katabi D, et al. Nearly optimal sparse Fourier transform[C]//Proceedings of the 44th Annual ACM Symposium on Theory of Computing, 2012: 563-577.
[15] Pei S C, Ding J J. Closed-form discrete fractional and affine Fourier transforms[J]. IEEE Transactions on Signal Processing, 2000, 48(5): 1338-1353. doi: 10.1109/78.839981
[16] Liu S H, Shan T, Tao R, et al. Sparse discrete fractional Fourier transform and its applications[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6582-6595. doi: 10.1109/TSP.2014.2366719
[17] Liu S H, Shan T, Zhang Y D, et al. A fast algorithm for multi-component LFM signal analysis exploiting segmented DPT and SDFrFT[C]//Proceedings of 2015 IEEE Radar Conference, 2015: 1139-1143.
[18] 陈小龙, 关键, 董云龙, 等.稀疏域海杂波抑制与微动目标检测方法[J].电子学报, 2016, 44(4): 860-867. http://mall.cnki.net/magazine/Article/DZXU201604015.htm
Chen X L, Guan J, Dong Y L, et al. Sea clutter suppression and micromotion target detection in sparse domain[J]. Acta Electronica Sinica, 2016, 44(4): 860-867. http://mall.cnki.net/magazine/Article/DZXU201604015.htm
-
点击扫一扫
图(3)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
