E-mail Alert
RSS
Research on wavefront measurement technology of space-based telescope using Shack-Hartmann wavefront sensor
-
摘要
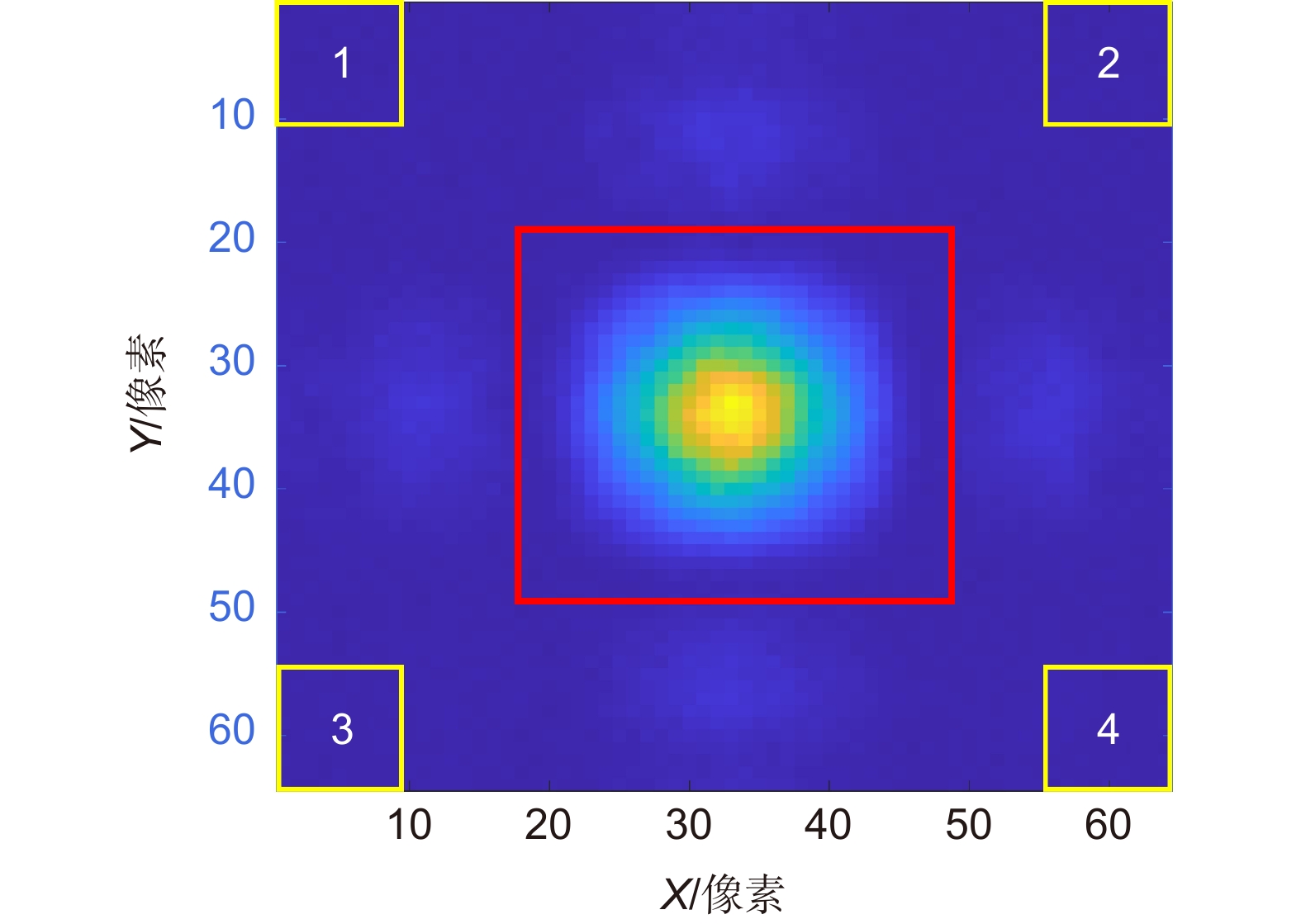
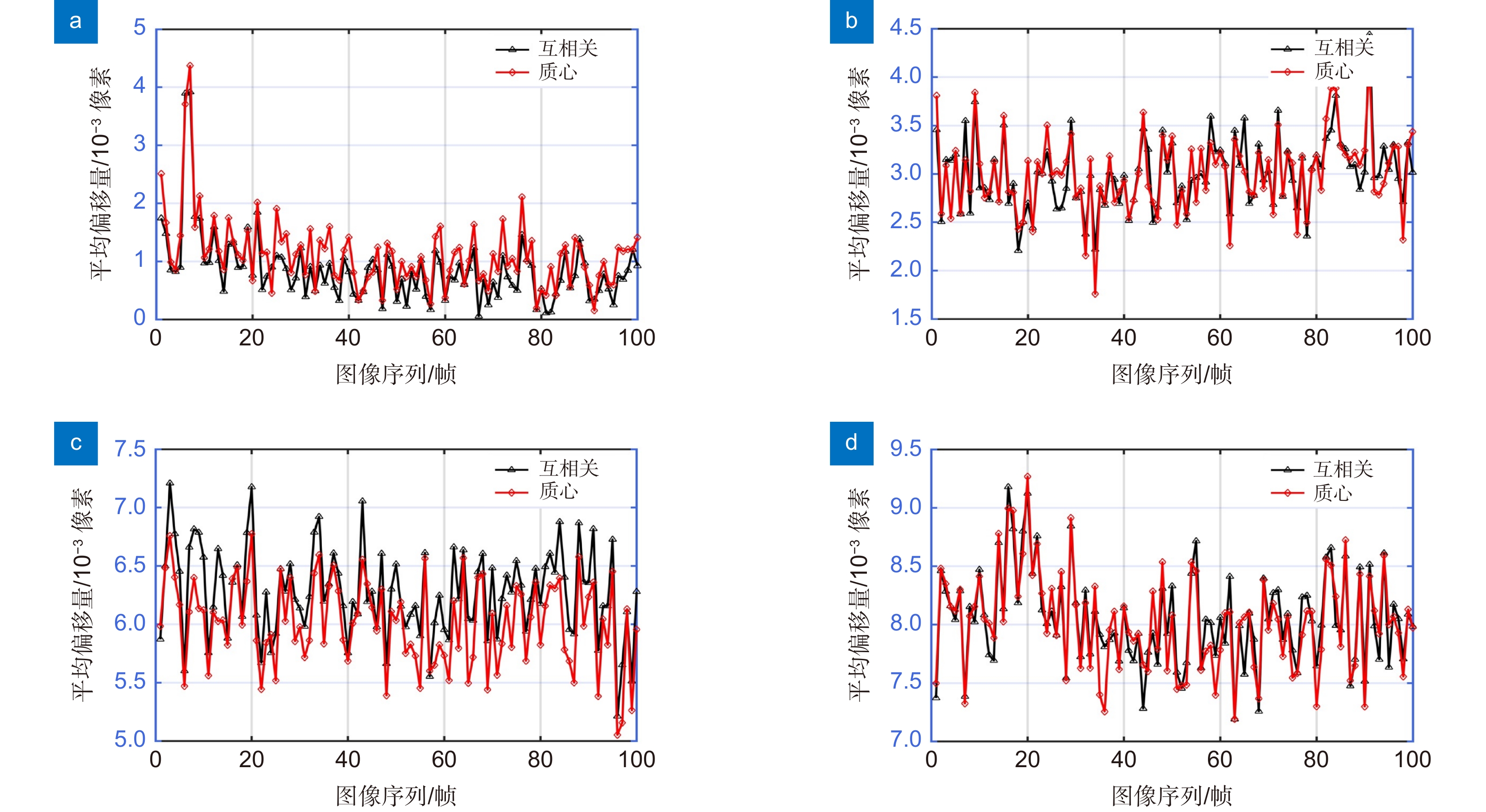
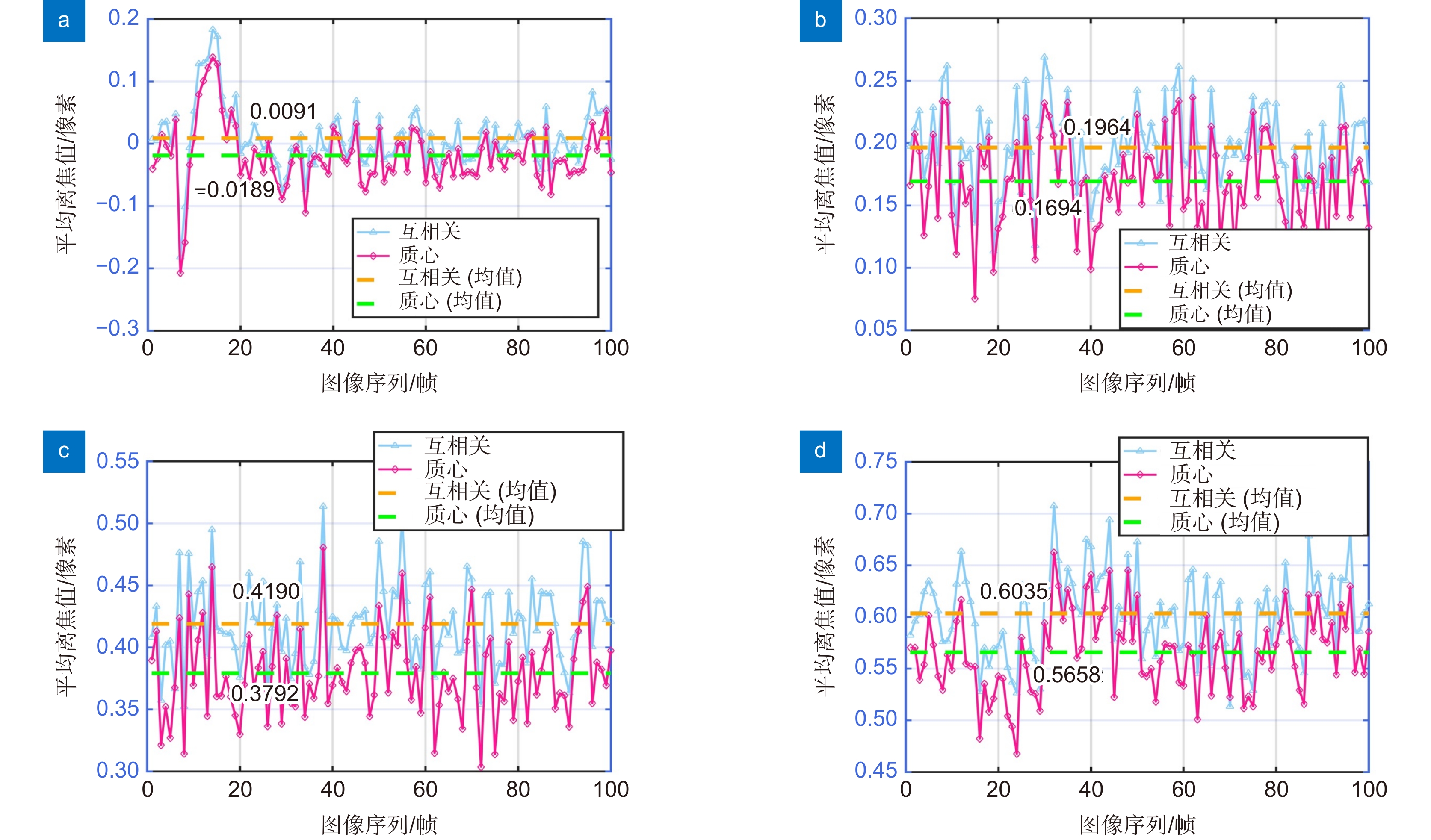
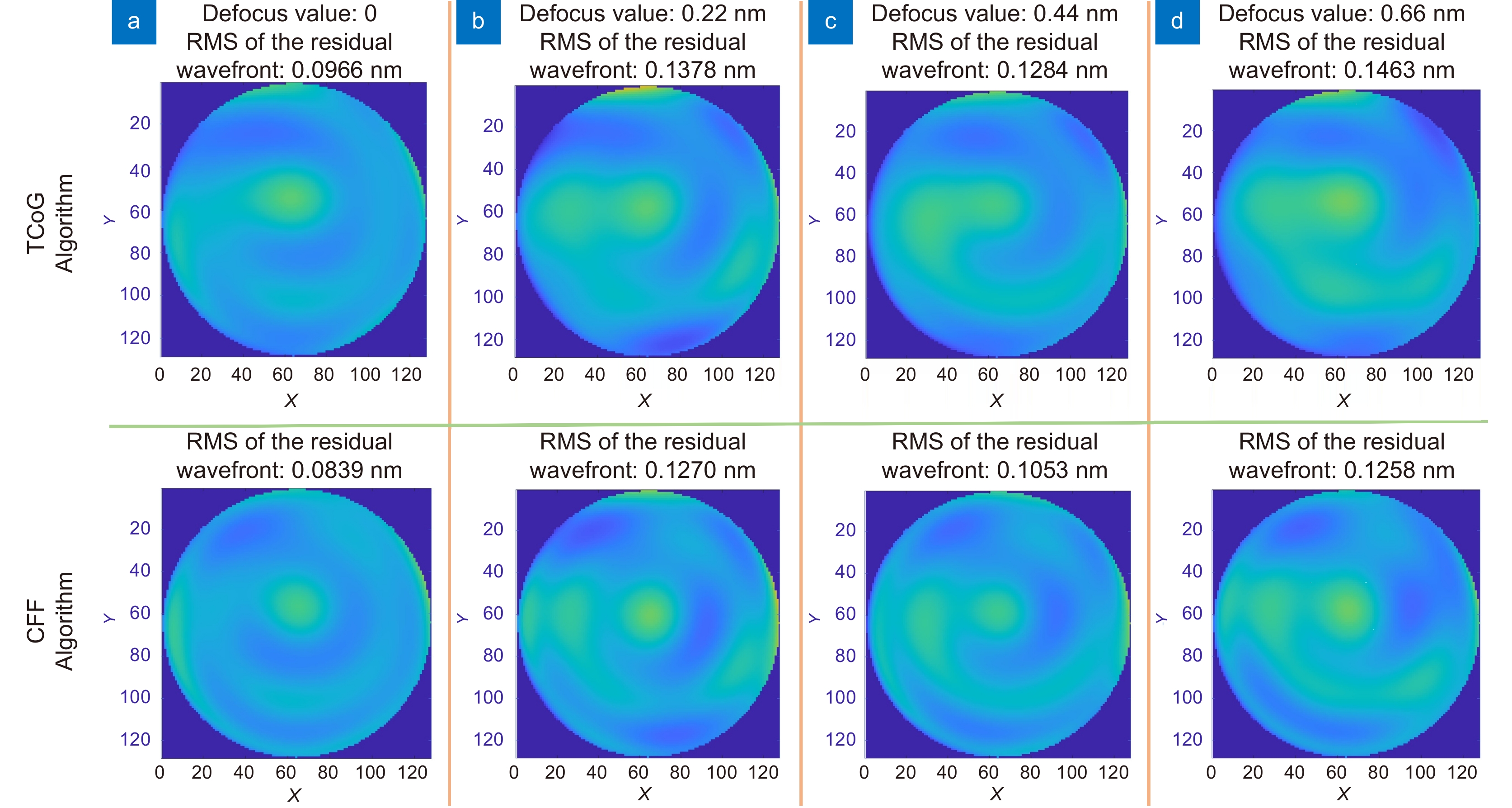
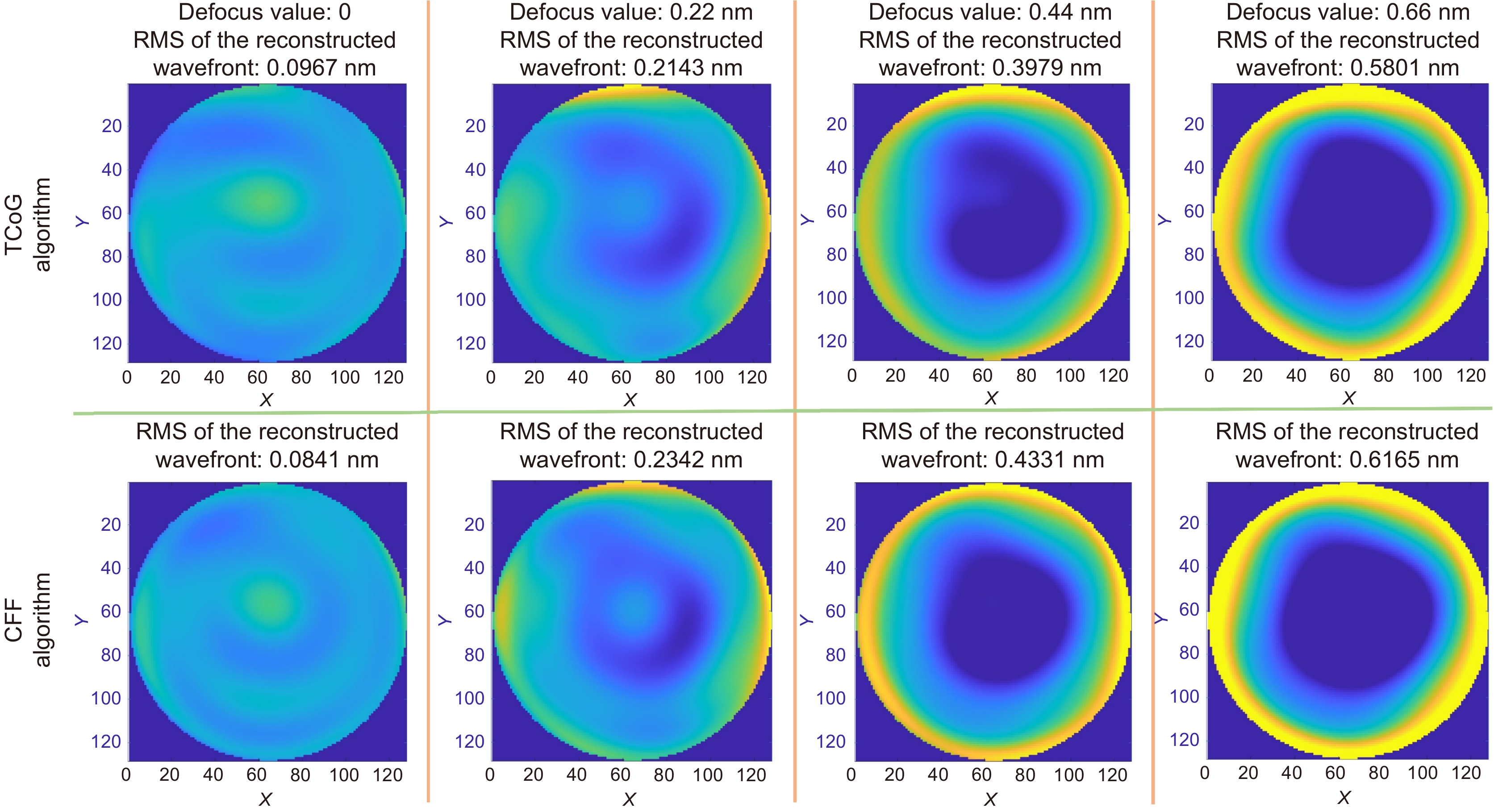
精确的测量和控制星载望远镜的波前像差是实现高效空间引力波探测的关键。本文提出了一种基于夏克-哈特曼波前传感器原理的星载望远镜波前像差测量方法，该方法采用经过频域阈值去噪处理后的频域上的互相关算法，使用子孔径数20×16、微透镜尺寸0.279 mm×0.279 mm、焦距34 mm的夏克-哈特曼波前传感器对算法的测量精确度进行验证。对实际点源图像生成已知RMS离焦值(0, 0.22, 0.44, 0.66 nm)，从而产生具有偏移量的点源图像。使用模式法进行波前复原后，计算复原波面和残余波面的RMS值，用于比较频域上的互相关算法和传统质心算法的测量精度。结果显示，随着实际离焦值的增加，质心算法的测量误差呈现上升趋势，分别为0.0966 nm, 0.1378 nm, 0.1284 nm和0.1463 nm。频域互相关算法可以使夏克-哈特曼波前像差均方根(RMS)误差分别减少13%, 7%, 18%和14%，为空间引力波星载望远镜地面波前像差的高精度测试提供了重要参考。
Abstract
Accurate measurement and control of wavefront aberrations in space-based telescopes are key to achieving efficient space gravitational wave detection. This paper presents a method for measuring wavefront aberrations of space-based telescopes based on the Shack-Hartmann wavefront sensor. This method employs a cross-correlation algorithm in the frequency domain after frequency domain threshold denoising. The measurement accuracy of the algorithm is verified using a Shack-Hartmann wavefront sensor with 20×16 sub-apertures, microlens dimensions of 0.279 mm×0.279 mm, and a focal length of 34 mm. Point source images with known defocus RMS values (0, 0.22, 0.44, and 0.66 nm) are generated, producing point source images with displacements. After wavefront reconstruction using the modal method, the RMS values of the reconstructed and residual wavefronts are calculated, comparing the measurement accuracy of the cross-correlation algorithm in the frequency domain with the traditional centroid algorithm. The results show that as the actual defocus value increases, the measurement error of the centroid algorithm presents an upward trend, respectively at 0.0966 nm, 0.1378 nm, 0.1284 nm, and 0.1463 nm. The cross-correlation algorithm in the frequency domain can increase the measurement accuracy by 13%, 7%, 18%, and 14% respectively, providing an important reference for the high-precision testing of wavefront aberrations of space gravitational wave space-based telescopes on the ground.
-
Overview
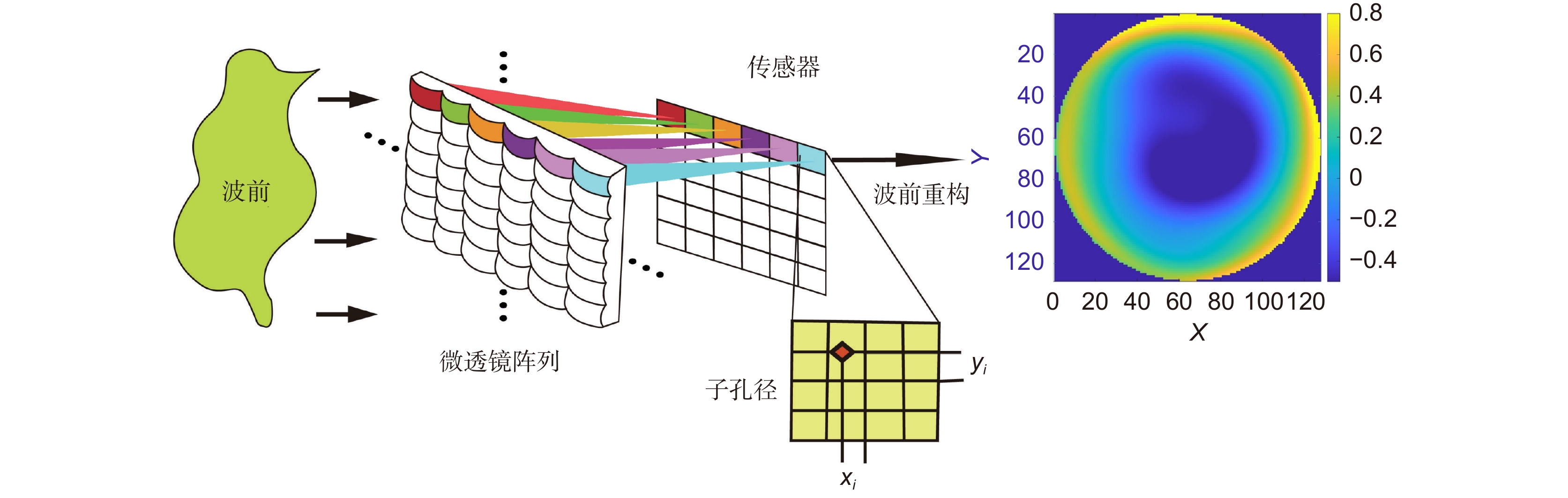
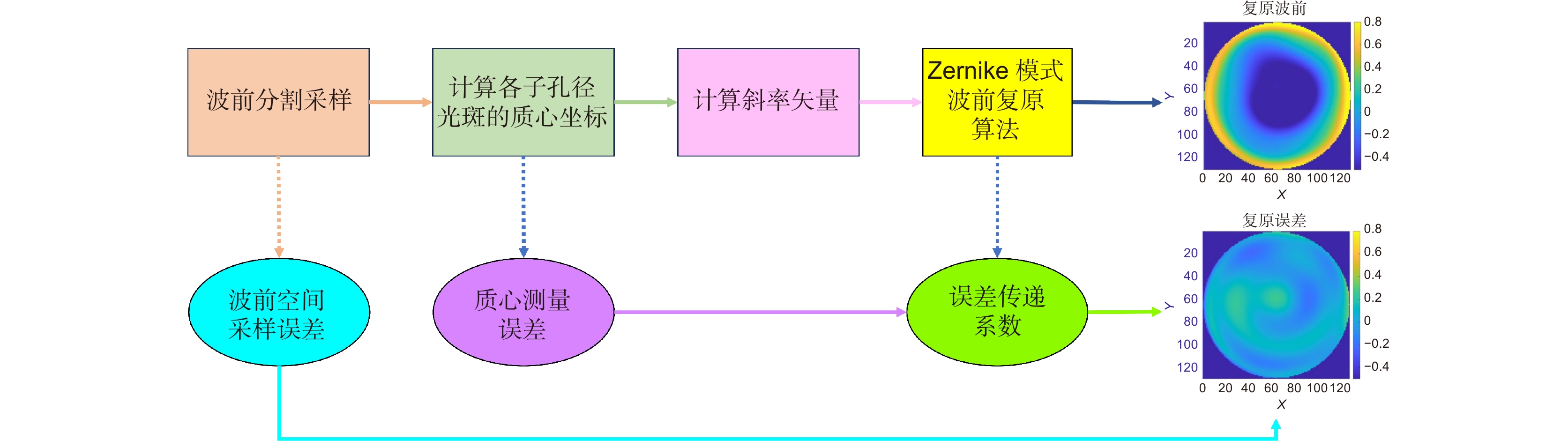
Overview: The successful detection of gravitational waves not only validate the general theory of relativity but also unveile previously undetectable cosmic events, opening new research directions for both physics and astronomy. Laser interferometers, characterized by their high sensitivity and broad frequency response, have become the primary method for gravitational wave detection. Due to the constraints imposed by terrestrial conditions, the frequency range for ground-based detection is quite limited, necessitating the exploration of space-based gravitational wave detection. Within this space-based detection framework, spaceborne telescopes serve as the core component. These telescopes require robust capabilities for interferometric laser transmission and reception, as well as high-precision tracking to accurately measure and detect gravitational wave events. Throughout their operation, these telescopes are affected by temperature variations in space, mechanical stresses or vibrations caused by launches or other space operations, thermal effects or expansions, and, over time, aging, degradation, or minor structural changes in the materials and components, all of which can result in wavefront aberrations. Such aberrations can directly influence the energy distribution and spatial position of the far-field light spot after being transmitted over hundreds of thousands of kilometers, subsequently limiting the interference quality and, in turn, the gravitational wave detection capability. To minimize the impact of wavefront aberrations on space-based gravitational wave detection, this paper introduces a frequency domain covariance algorithm for noise thresholding, replacing the threshold centroid algorithm for offset position estimation, and enhancing detection precision by incorporating multi-aperture multiplexing technology. By applying the frequency domain covariance algorithm and the threshold centroid algorithm to the slope measurement and wavefront reconstruction of actual point source images with added defocus values, we concluded that the former achieves higher measurement accuracy than the latter. The calculated defocus value and root mean square (RMS) of the residual wavefront further verified the computational precision of the relevant algorithms and their superior performance over the centroid algorithm. In comparison to the threshold centroid method, our approach exhibits greater accuracy in wavefront aberration measurement, achieving a precision of up to λ/3000. This study not only deepens our understanding of wavefront aberrations in gravitational wave detection but also paves the way for enhancing the precision and accuracy of gravitational wave detection.
-
-
图 1 天琴计划的星载望远镜的光学布局设计
Figure 1. Optical layout design of the spaceborne telescope for TianQin Project
图 6 点源图像的有效子孔径分布
Figure 6. Effective sub-aperture distribution of the point source image
图 7 单个子孔径图像及噪声计算区域(黄色框线内)和匹配区域(红色框线内)
Figure 7. Individual sub-aperture image and noise calculation region (within the yellow box) and matching region (within the red box)
图 8 互相关算法和质心算法在每帧图像上计算的平均斜率值。实际离焦值分别为 (a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0.66 nm
Figure 8. The average shift measured on each frame image by employing the CFF and the TCoG algorithm. Defocus values are (a) 0 nm, (b) 0.22 nm, (c) 0.44 nm and (d) 0.66 nm
图 9 互相关算法和质心算法波在每帧图像上生成的Zernike离焦值及平均值。实际离焦值分别为 (a) 0 nm， (b) 0.22 nm， (c) 0.44 nm， (d) 0.66 nm
Figure 9. Zernike defocus values, and their average calculated on each frame image by employing the CFF and the TCoG algorithm. Defocus values are (a) 0 nm, (b) 0.22 nm, (c) 0.44 nm and (d) 0.66 nm
图 10 互相关算法和质心算法通过复原后得到的平均复原波面。实际离焦值分别为 (a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0.66 nm
Figure 10. The average reconstructed wavefront using the CFF and the TCoG algorithm. Defocus values are (a) 0 nm, (b) 0.22 nm, (c) 0.44 nm and (d) 0.66 nm
图 11 互相关算法和质心算法通过复原后得到的残余波面。实际离焦值分别为 (a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0 .66 nm
Figure 11. The residual wavefront generated using the CFF and the TCoG algorithm. Defocus values are (a) 0 nm, (b) 0.22 nm, (c) 0.44 nm and (d) 0.66 nm
图 4 波前复原流程及复原误差的组成
Figure 4. The process of wavefront reconstruction and the composition of reconstruction error
表 1 微透镜阵列及相机参数
Table 1. Microlens array and camera parameters
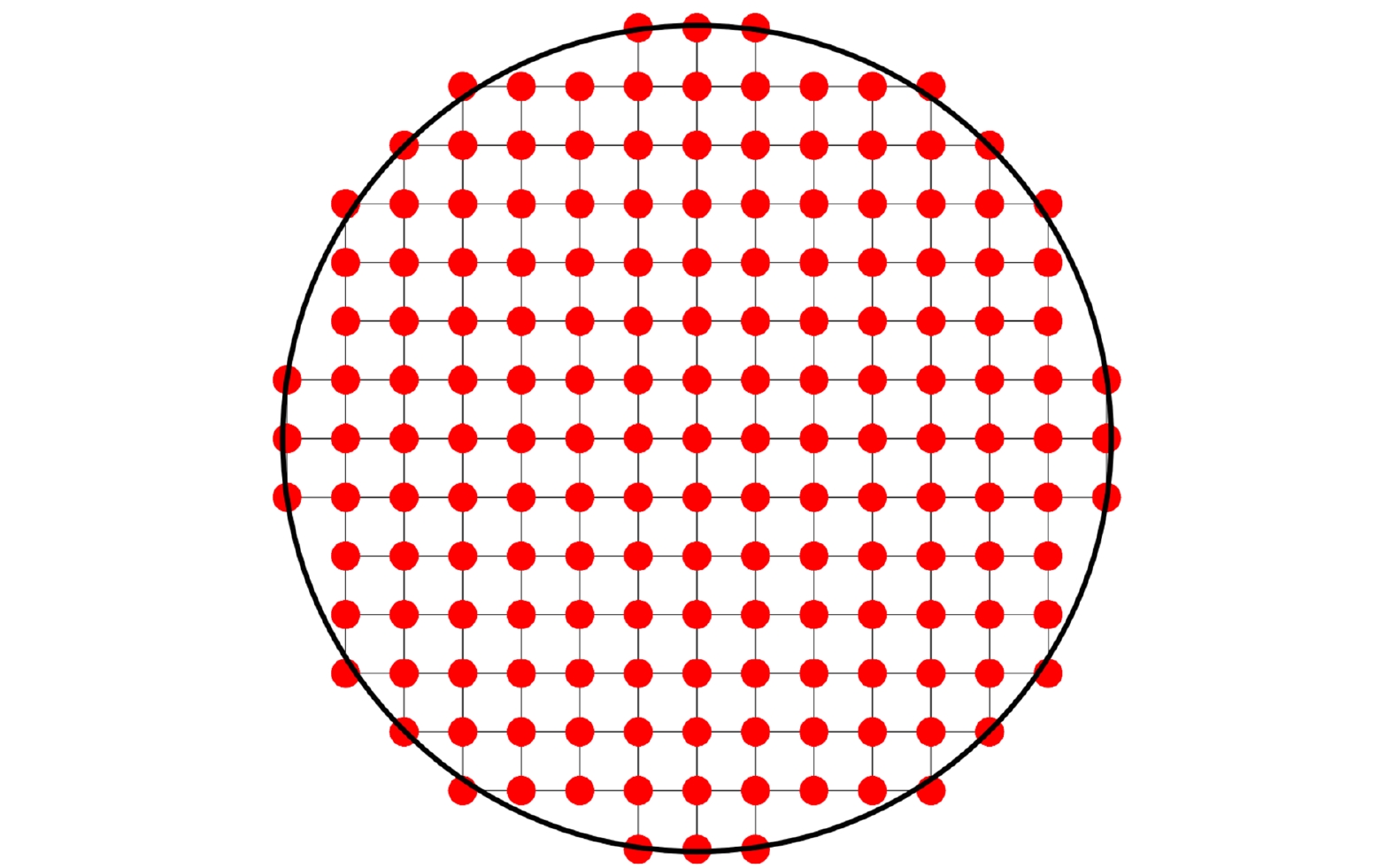
系统参数 值 波长 523 nm 相机位深 12 bits 像素尺寸 8.3 µm×8.3 µm 微透镜尺寸 0.279 mm×0.279 mm 焦距 34 mm 子孔径数 20×16 有效子孔径个数 140 
下载: 导出CSV
-
参考文献
[1] Thorne K S. Gravitational waves[Z]. arXiv: gr-qc/9506086, 1995. https://doi.org/10.48550/arXiv.gr-qc/9506086.
[2] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Phys Rev Lett, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102
[3] Bian L G, Cai R G, Cao S, et al. The gravitational-wave physics II: progress[J]. Sci China Phys, Mech Astron, 2021, 64(12): 120401. doi: 10.1007/s11433-021-1781-x
[4] Piccinni O J. Status and perspectives of Continuous Gravitational Wave searches[J]. Galaxies, 2022, 10(3): 72. doi: 10.3390/galaxies10030072
[5] Bailes M, Berger B K, Brady P R, et al. Gravitational-wave physics and astronomy in the 2020s and 2030s[J]. Nat Rev Phys, 2021, 3(5): 344−366. doi: 10.1038/s42254-021-00303-8
[6] Weber J. Detection and generation of gravitational waves[J]. Phys Rev, 1960, 117(1): 306−313. doi: 10.1103/PhysRev.117.306
[7] van Remortel N, Janssens K, Turbang K. Stochastic gravitational wave background: methods and implications[J]. Prog Part Nucl Phys, 2023, 128: 104003. doi: 10.1016/j.ppnp.2022.104003
[8] Abbott R, Abbott T D, Acernese F, et al. GWTC-3: compact binary coalescences observed by LIGO and Virgo during the second part of the third observing run[J]. Phys Rev X, 2023, 13(4): 041039. doi: 10.1103/PhysRevX.13.041039
[9] Aasi J, Abadie J, Abbott B P, et al. The characterization of Virgo data and its impact on gravitational-wave searches[J]. Class Quantum Grav, 2012, 29(15): 155002. doi: 10.1088/0264-9381/29/15/155002
[10] K Danzmann for the LISA Study Team. LISA-an ESA cornerstone mission for a gravitational wave observatory[J]. Class Quantum Grav, 1997, 14(6): 1399−1404. doi: 10.1088/0264-9381/14/6/002
[11] Luo J, Chen L S, Duan H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Class Quantum Grav, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010
[12] Kawamura S, Ando M, Seto N, et al. The Japanese space gravitational wave antenna: DECIGO[J]. Class Quantum Grav, 2011, 28(9): 094011. doi: 10.1088/0264-9381/28/9/094011
[13] Lu X Y, Tan Y J, Shao C G. Sensitivity functions for space-borne gravitational wave detectors[J]. Phys Rev, 2019, 100(4): 044042.
[14] Fan Z C, Zhao L J, Cao S Y, et al. High performance telescope system design for the TianQin project[J]. Class Quantum Grav, 2022, 39(19): 195017. doi: 10.1088/1361-6382/ac8b57
[15] Sankar S R, Livas J. Optical alignment and wavefront error demonstration of a prototype LISA telescope[J]. Class Quantum Grav, 2020, 37(6): 065005. doi: 10.1088/1361-6382/ab6adf
[16] Bates W J. A wavefront shearing interferometer[J]. Proc Phys Soc, 1947, 59(6): 940. doi: 10.1088/0959-5309/59/6/303
[17] 饶长辉, 朱磊, 张兰强, 等. 太阳自适应光学技术进展[J]. 光电工程, 2018, 45(3): 170733. doi: 10.12086/oee.2018.170733
Rao C H, Zhu L, Zhang L Q, et al. Development of solar adaptive optics[J]. Opto-Electron Eng, 2018, 45(3): 170733. doi: 10.12086/oee.2018.170733
[18] Roddier F, Roddier C, Roddier N. Curvature sensing: a new wavefront sensing method[J]. Proc SPIE, 1988, 976: 203−209. doi: 10.1117/12.948547
[19] Shatokhina I, Hutterer V, Ramlau R. Review on methods for wavefront reconstruction from pyramid wavefront sensor data[J]. J Astron Telesc, Instrum, Syst, 2020, 6(1): 010901. doi: 10.1117/1.JATIS.6.1.010901
[20] Li C H, Xian H, Rao C H, et al. Field-of-view shifted Shack-Hartmann wavefront sensor for daytime adaptive optics system[J]. Opt Lett, 2006, 31(19): 2821−2823. doi: 10.1364/OL.31.002821
[21] Zhang L Q, Bao H, Rao X J, et al. Ground-layer adaptive optics for the New Vacuum Solar Telescope: Instrument description and first results[J]. Sci China Phys, Mech Astron, 2023, 66(6): 269611. doi: 10.1007/s11433-022-2107-4
[22] 姜文汉, 鲜浩, 沈锋. 夏克-哈特曼波前传感器的探测误差[J]. 量子电子学报, 1998, 15(2): 218−227.
Jiang W H, Xian H, Shen F. Detecting error of Shack-Hartmann wavefront sensor[J]. Chin J Quantum Electron, 1998, 15(2): 218−227.
[23] Arines J, Ares J. Minimum variance centroid thresholding[J]. Opt Lett, 2002, 27(7): 497−499. doi: 10.1364/OL.27.000497
[24] Lardière O, Conan R, Clare R, et al. Compared performance of different centroiding algorithms for high-pass filtered laser guide star Shack-Hartmann wavefront sensors[J]. Proc SPIE, 2010, 7736: 821−835. doi: 10.1117/12.857742
[25] Ma X Y, Rao C H, Zheng H Q, et al. Error analysis of CCD-based point source centroid computation under the background light[J]. Opt Express, 2009, 17(10): 8525−8541. doi: 10.1364/oe.17.008525
[26] Smithson R C, Tarbell T D. Correlation tracking study for meter-class solar telescope on space shuttle[R]. Palo Alto: Lockheed Palo Alto Research Laboratory, 1977.
[27] Waldmann T A, Berkefeld T, von der Lühe II O. Turbulence profiling using wide field of view Hartmann-Shack wavefront sensors[J]. Proc SPIE, 2008, 7015: 70155O. doi: 10.1117/12.789553
[28] Miura N, Noto Y, Kato S, et al. Solar adaptive optics system using an electromagnetic deformable mirror[J]. Opt Rev, 2009, 16(5): 558−561. doi: 10.1007/s10043-009-0109-1
[29] Schewel J. Field Programmable Gate Arrays (FPGAs) for fast board development and reconfigurable computing[C]. Philadelphia, PA, United States: SPIE, 1995.
[30] Von Der Luehe O. A study of a correlation tracking method to improve imaging quality of ground-based solar telescopes[J]. Astron Astrophys, 1983, 119(1): 85−94.
[31] Poyneer L A. Correlation wave-front sensing algorithms for shack-hartmann-based adaptive optics using a point source[C]//Center for Adaptive Optics Spring Retreat, San Jose, 2003.
[32] Li X X, Li X Y, Wang C X. Improvement of correlation-based centroiding methods for point source Shack–Hartmann wavefront sensor[J]. Opt Commun, 2018, 411: 187−194. doi: 10.1016/j.optcom.2017.11.059
[33] Hu X C, Li X H, Wang Y, et al. Fundamentals of the orbit and response for TianQin[J]. Classical and Quantum Gravity, 2018, 35(9): 095008. doi: 10.1088/1361-6382/ac8b57.
[34] Zhao Y, Shen J, Fang C, et al. Tilt-to-length noise coupled by wavefront errors in the interfering beams for the space measurement of gravitational waves[J]. Opt Express, 2020, 28(17): 25545−25561. doi: 10.1364/OE.397097
[35] Chen Z W, Leng R K, Yan C X, et al. Analysis of telescope wavefront aberration and optical path stability in space gravitational wave detection[J]. Appl Sci, 2022, 12(24): 12697. doi: 10.3390/app122412697
[36] Platt B C, Shack R. History and principles of Shack-Hartmann wavefront sensing[J]. J Refract Surg, 2001, 17(5): S573−S557. doi: 10.3928/1081-597X-20010901-13
[37] Kong L, Zhu L, Rao C H. Development status on the real-time controller for solar multi-conjugate adaptive optics system[J]. Proc SPIE, 2016, 9682: 96820M. doi: 10.1117/12.2243804
[38] Thomas S, Fusco T, Tokovinin A, et al. Comparison of centroid computation algorithms in a Shack–Hartmann sensor[J]. Mon Not Roy Astron Soc, 2006, 371(1): 323−336. doi: 10.1111/j.1365-2966.2006.10661.x
[39] Löfdahl M G. Evaluation of image-shift measurement algorithms for solar Shack-Hartmann wavefront sensors[J]. Astron Astrophys, 2010, 524: A90. doi: 10.1051/0004-6361/201015331
[40] 陈林辉, 饶长辉. 点源信标相关哈特曼-夏克波前传感器光斑偏移测量误差分析[J]. 物理学报, 2011, 60(9): 090701. doi: 10.7498/aps.60.090701
Chen L H, Rao C H. Error analysis of correlating Shack-Hartmann wave-front sensor for a point source[J]. Acta Phys Sin, 2011, 60(9): 090701. doi: 10.7498/aps.60.090701
[41] Mugnier L M, Blanc A, Idier J. Phase diversity: a technique for wave-front sensing and for diffraction-limited imaging[J]. Adv Imaging Electron Phys, 2006, 141: 1−76. doi: 10.1016/S1076-5670(05)41001-0
[42] 李新阳, 姜文汉. 哈特曼夏克传感器的泽尼克模式波前复原误差[J]. 光学学报, 2002, 22(10): 1236−1240. doi: 10.3321/j.issn:0253-2239.2002.10.016
Li X Y, Jiang W H. Zernike modal wavefront reconstruction error of Hartmann-Shack wavefront sensor[J]. Acta Opt Sin, 2002, 22(10): 1236−1240. doi: 10.3321/j.issn:0253-2239.2002.10.016
[43] Cao G, Yu X. Accuracy analysis of a Hartmann-Shack wavefront sensor operated with a faint object[J]. Opt Eng, 1994, 33(7): 2331−2335. doi: 10.1117/12.169716
[44] 李新阳, 姜文汉, 王春红, 等. 湍流大气中哈特曼传感器的模式波前复原误差[J]. 强激光与粒子束, 2000, 12(3): 319−323.
Li X Y, Jiang W H, Wang C H, et al. Modal reconstruction error of the Hartmann sensor on measuring the atmosphere disturbed wavefront II[J]. High Power Laser Part Beams, 2000, 12(3): 319−323.
-
访问统计
点击扫一扫
图(12)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
