E-mail Alert
RSS
Adaptive tip-tilt disturbance suppression technique for characteristic disturbance frequency identification
-
摘要
为了抑制倾斜校正系统中的时变扰动，提出了一种基于特征扰动频率辨识的自适应扰动抑制方法。采用最小均方误差准则对闭环系统误差进行特征扰动频率辨识，以实现自适应控制器参数的在线调整，且将辨识的滤波参数与控制器调整并行化设计。同时提出频率分割的方法，将低频扰动以及高频扰动的抑制相结合，进一步提高了特征频率辨识速度以及简化设计流程，实现对闭环带宽内的扰动自适应抑制。所提出的方法在倾斜校正装置中进行了闭环验证，实验结果表明该方法能快速辨识特征扰动并自适应调节控制器，可以在单频或多频时变扰动下提升系统的闭环性能。
Abstract
In order to suppress the time-varying disturbance in the tip-tilt correction system, an adaptive disturbance suppression method based on characteristic disturbance frequency identification is proposed in this paper. The least mean square error criterion is used to identify the characteristic disturbance frequency of the closed-loop system error, and the identified filtering parameters and controller adjustment are designed in parallel. At the same time, a method based on frequency splitting is proposed: combining low-frequency disturbance with high-frequency disturbance suppression, which further improves the speed of characteristic frequency identification and simplifies the design process, and realizes adaptive disturbance suppression in the closed-loop bandwidth. The closed-loop verification of the proposed method is carried out in the tip-tilt correction device. The experimental results show that the method can quickly identify the characteristic disturbance and adaptively adjust the controller, which can improve the closed-loop performance of the system under single-frequency and multi-frequency time-varying disturbance.
-
Overview
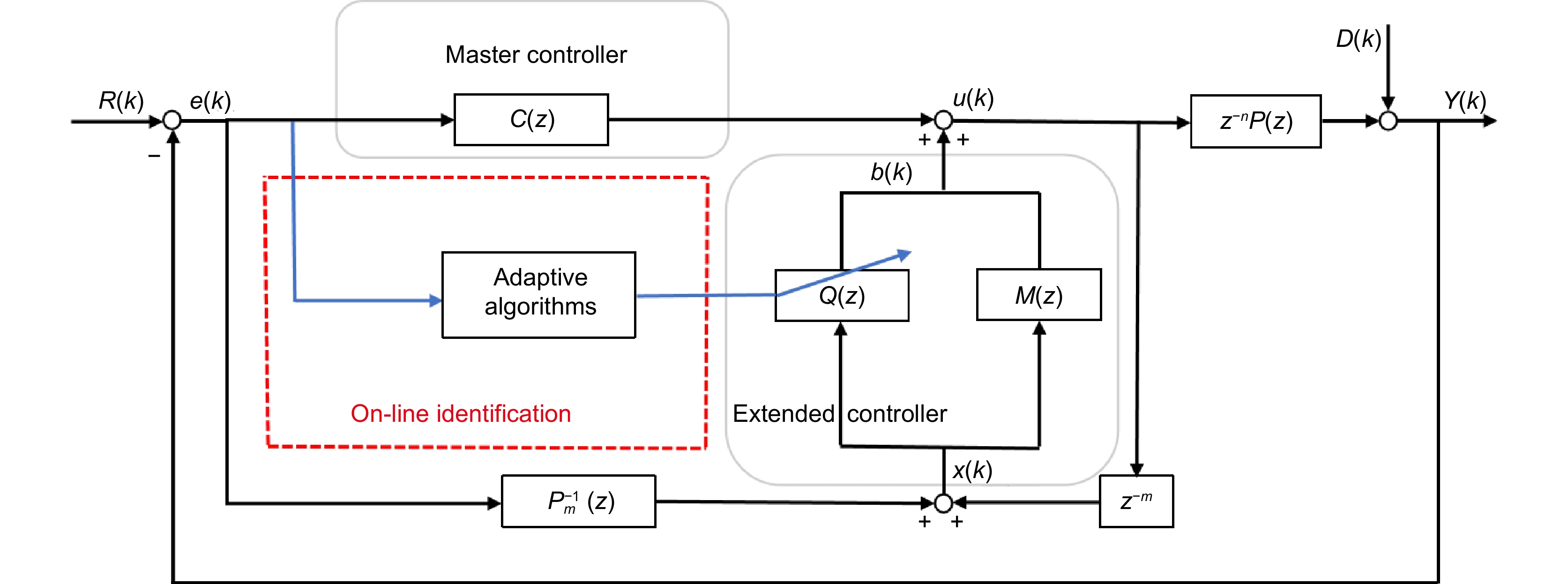
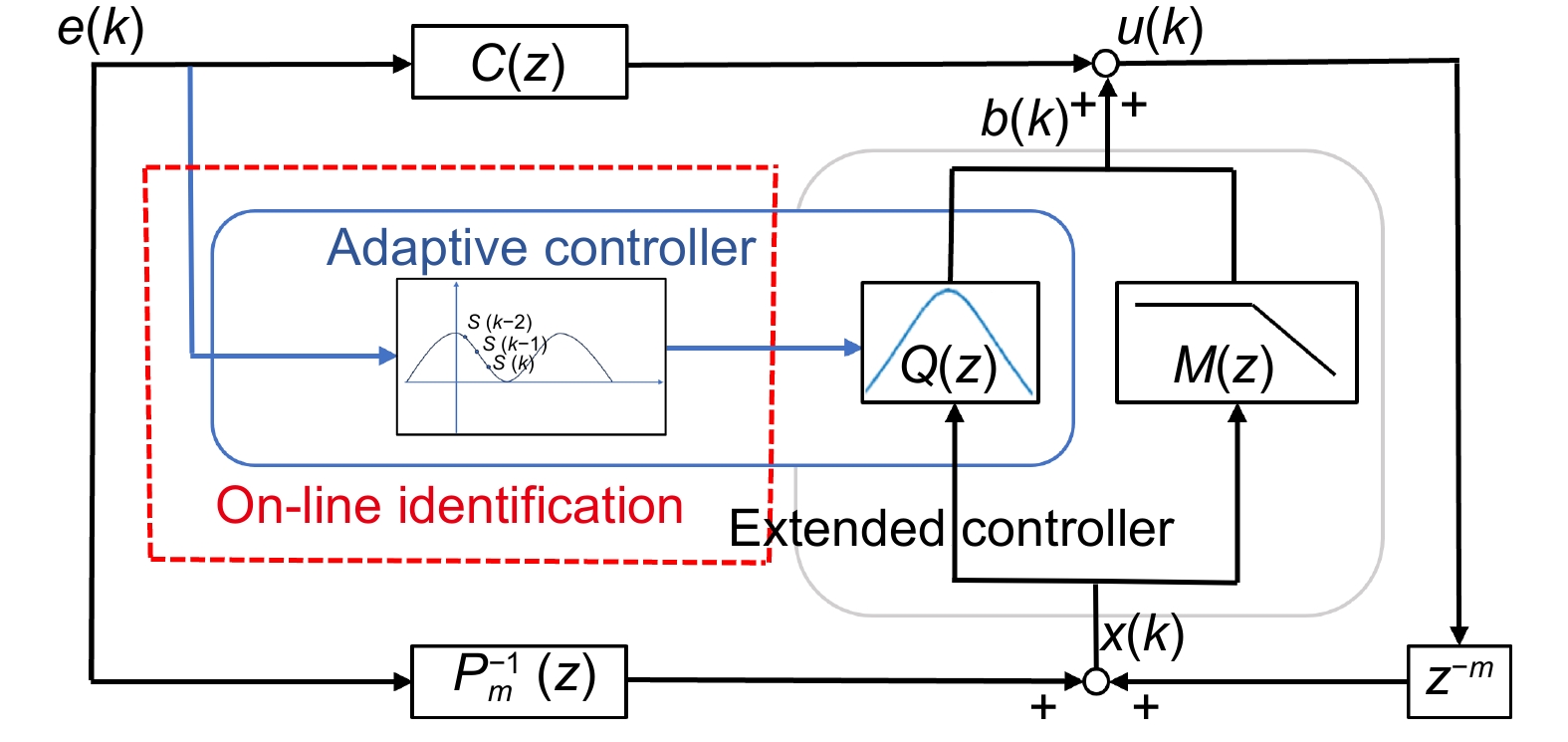
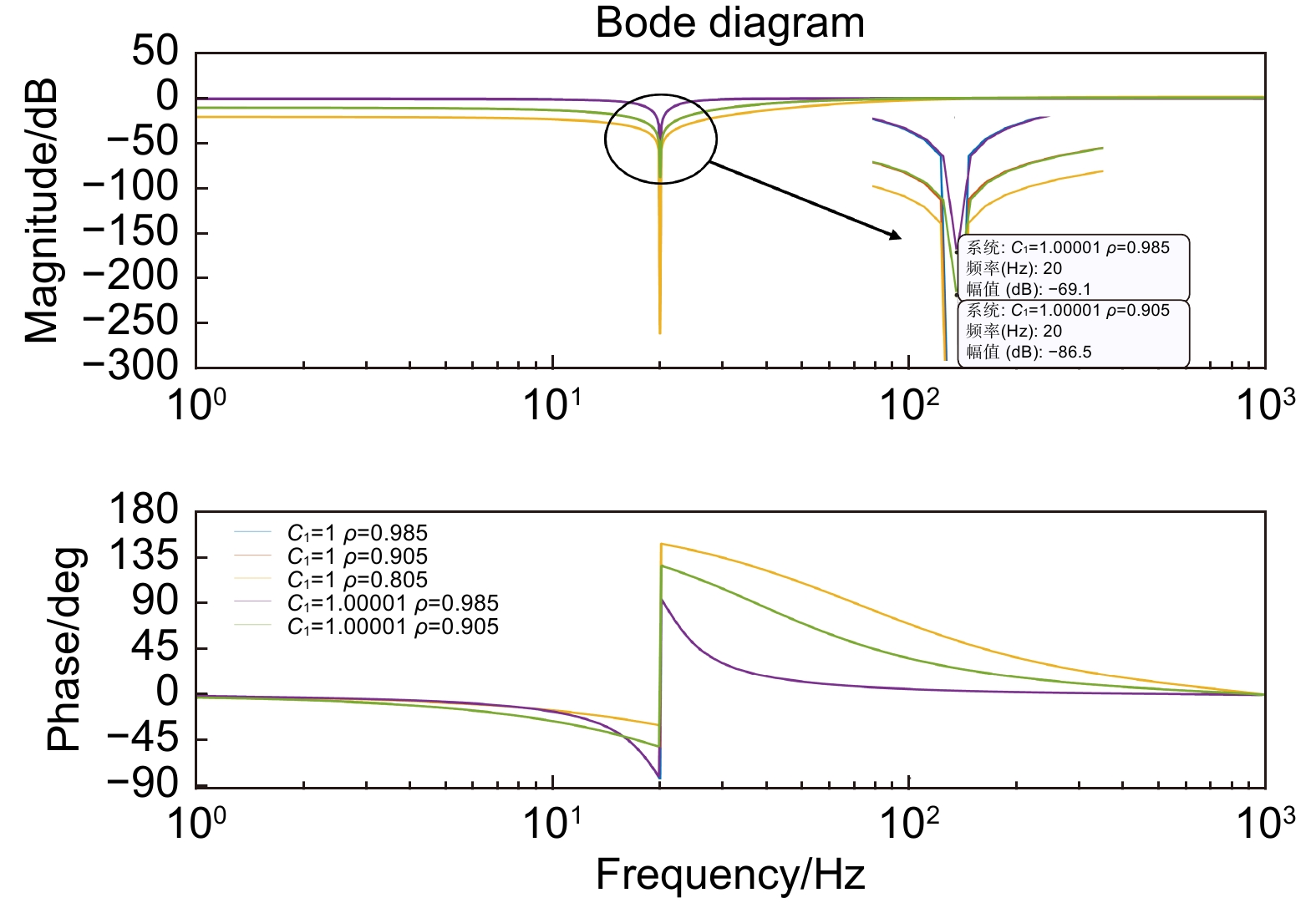
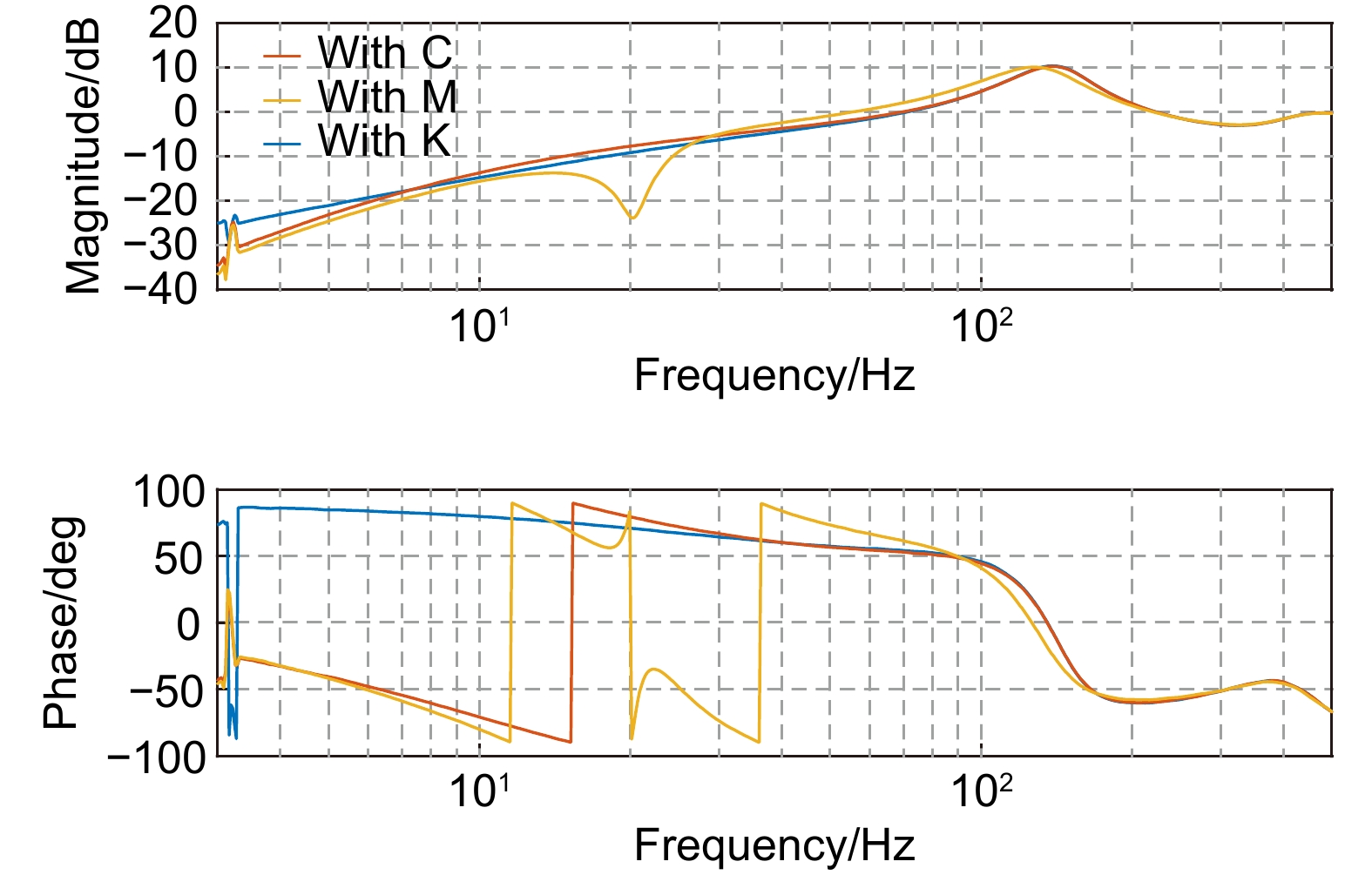
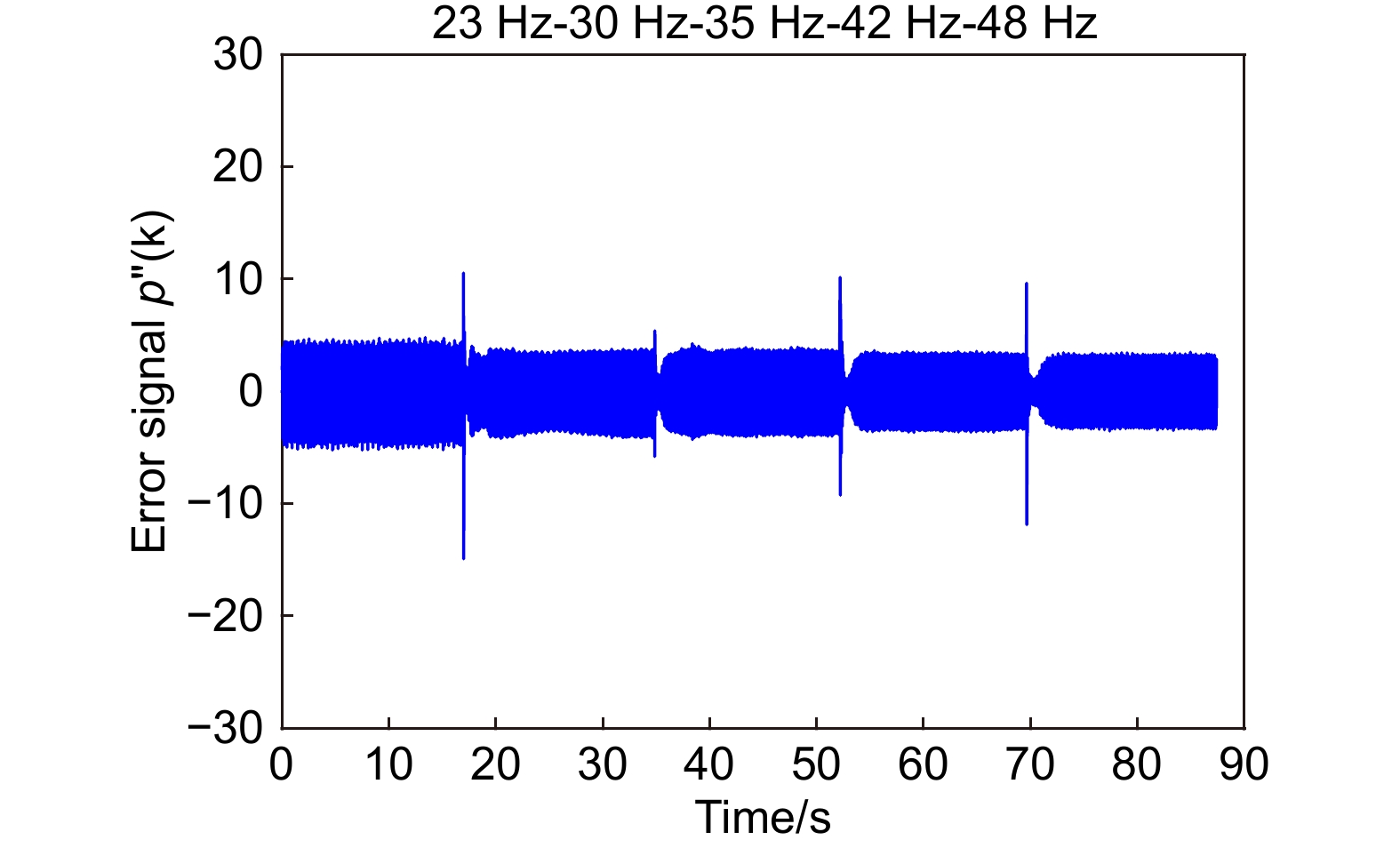
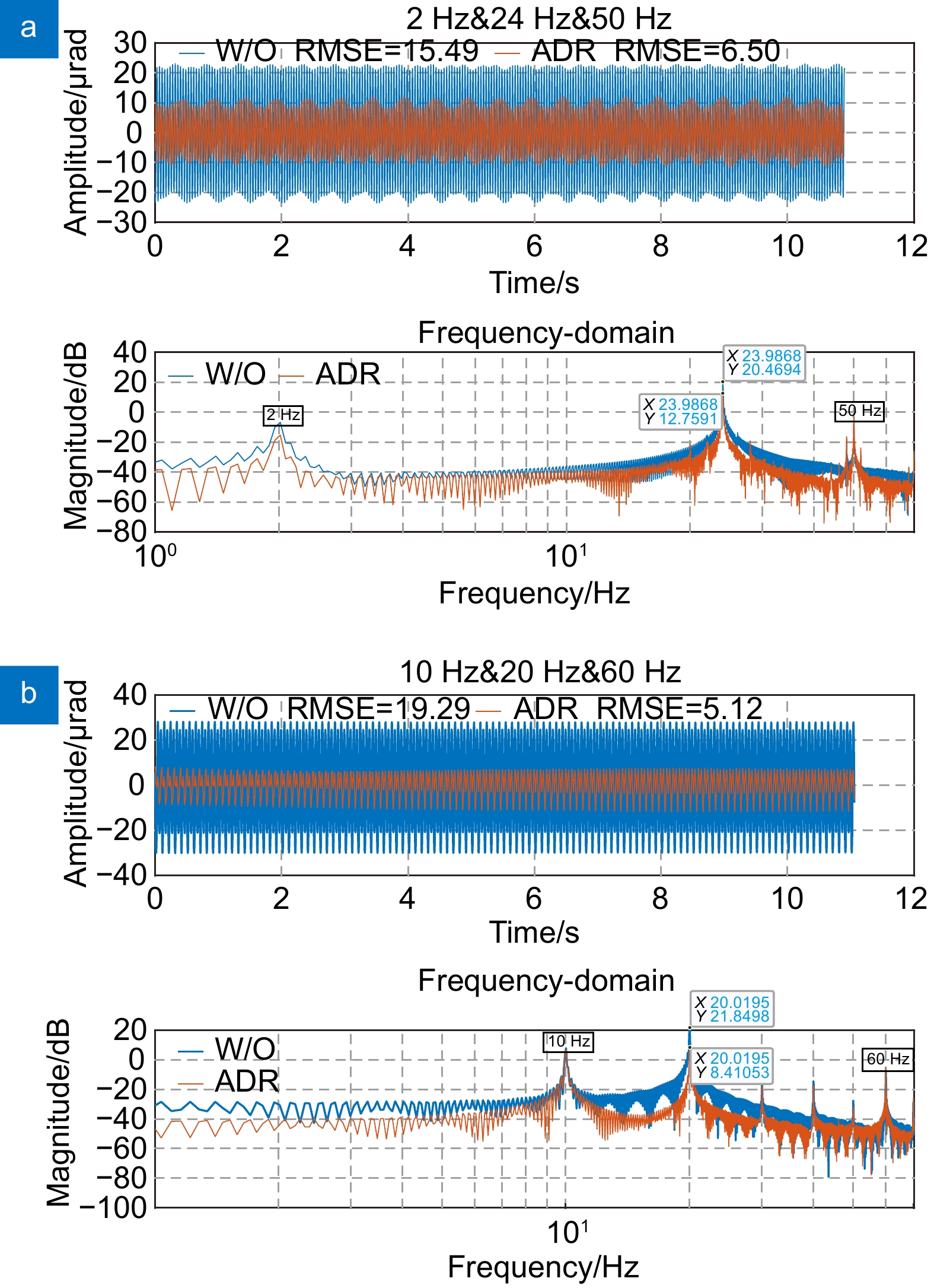
Overview: The tip-tilt correction system is widely used in precision optical systems, such as high-resolution telescopes and free space optical communications, to achieve image stabilization and beam stabilization. In these precision optical systems, the tip-tilt correction system is affected by disturbance during beam stabilization control, which generally have unknown time-varying characteristics. Therefore, fast adaptive suppression of time-varying disturbances is a task of great significance, so plentiful adaptive control algorithms have been proposed which is mainly composed of control structure and parameter identification algorithms. Most adaptive control identification algorithms are based on spectrum analysis, which is a full frequency domain search method and has a large amount of calculation. At present, the time domain identification algorithm based on least mean square error criterion is relatively simple and fast, which provides a guarantee for the rapid adjustment of controller parameters. In addition, adaptive algorithms based on linear quadratic Gaussian (LQG) control or adaptive Kalman filter require accurate modeling and many parameters for adjusting controller, which is complicated and time-consuming. However, the control algorithm based on Youla parameterization does not depend on the accurate model, and can directly adjust the internal model of the controller, which reduces the complexity of the adaptive controller and does not involve the redesign of the controller. Therefore, this paper proposes an adaptive disturbance rejection method combining characteristic disturbance frequency identification and Youla parameterized control. On the basis of the least mean square error criterion, this method uses the closed-loop system error to identify the characteristic disturbance frequency, so that to realize the online adjustment of the adaptive controller. Moreover, the identified filtering parameters and controller adjustment are designed in parallel, thereby reducing the time consumption of adaptive disturbance suppression. At the same time, the frequency segmentation method is applied to combine the low-frequency disturbance and the filter suppression of high-frequency disturbance, so as to realize the adaptive suppression of the disturbance within the closed-loop bandwidth. The experimental results show that the method can quickly identify the characteristic disturbance and adjust the relevant parameters of the controller, and can improve the closed-loop performance of the system under single-frequency time-varying disturbance and multi-frequency disturbance.
-
-
图 4 不同参数陷波器的幅频特性曲线
Figure 4. Amplitude-frequency characteristic curves of notch filters with different parameters
图 8 扰动连续变化时的估计误差
Figure 8. The estimation error when the disturbance changes continuously
图 9 扰动连续变化时倾斜误差的时域、频域图
Figure 9. Time domain and frequency domain diagram of tip-tilt error when disturbance changes continuously
图 10 抑制多频扰动的倾斜误差。(a)低频宽带扰动混合尖峰扰动；(b)尖峰扰动
Figure 10. Tip-tilt error of suppressing multifrequency disturbances. (a) Low-frequency broadband disturbance mixed spike disturbance; (b) Peak disturbance
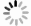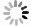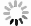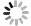
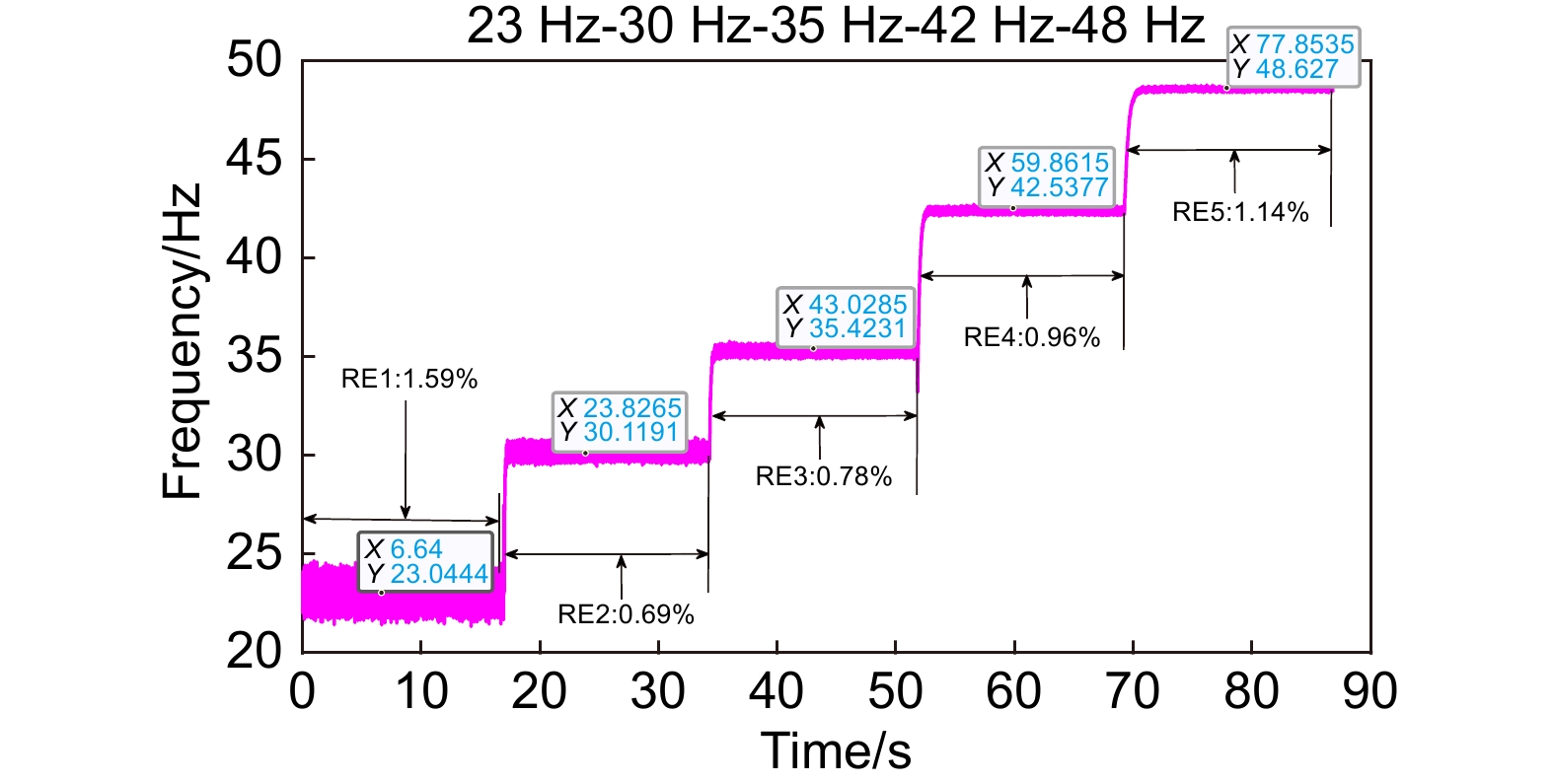
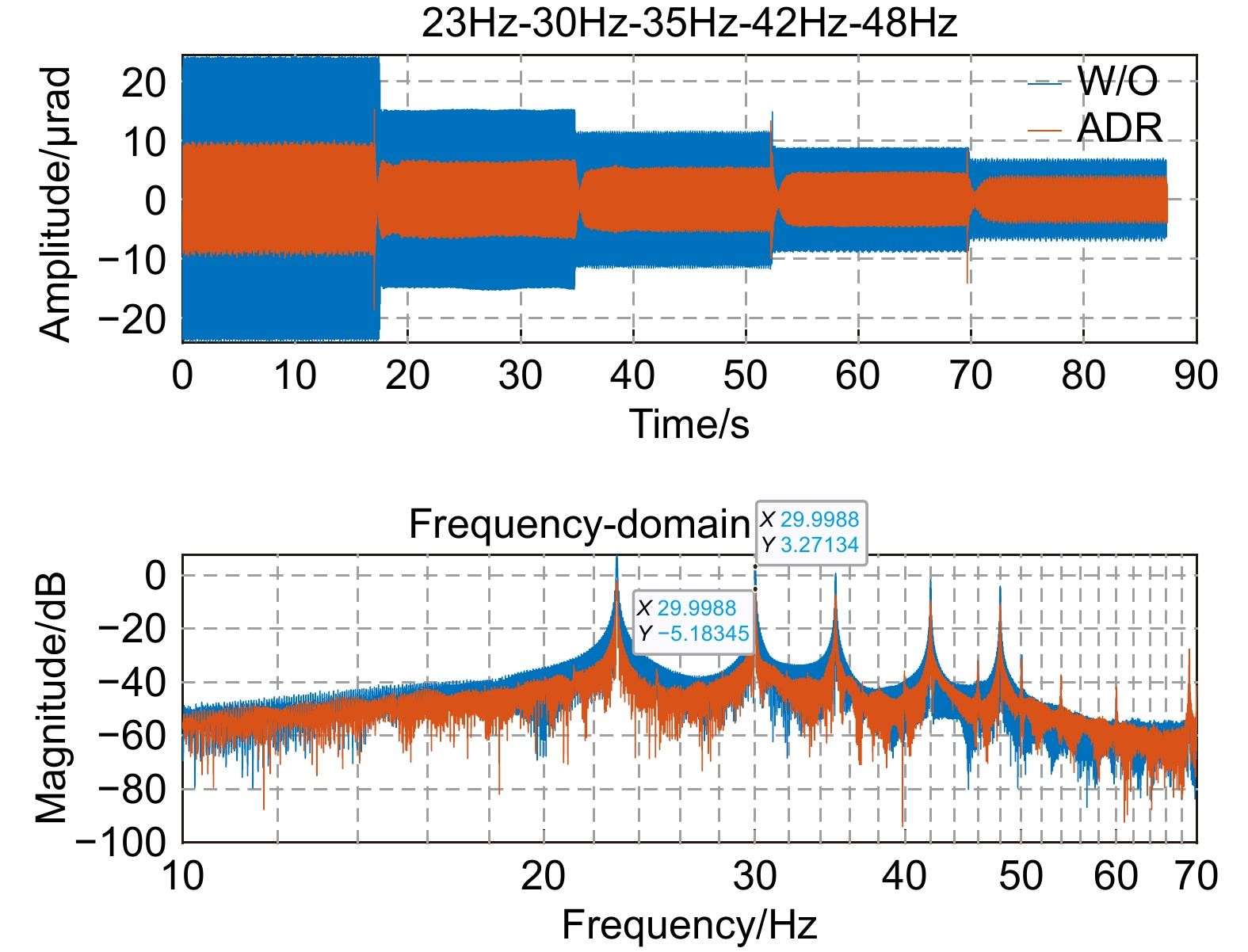
表 1 均方根误差
Table 1. Root-mean-square error
Frequency/Hz 23 30 35 42 48 PI/μrad 16.77 10.41 7.75 5.78 4.46 ADR/μrad 5.82 3.87 3.22 2.59 2.16 Ratio/% 65.3 62.8 58.5 55.2 51.6 
下载: 导出CSV
-
参考文献
[1] 牛帅旭, 蒋晶, 唐涛, 等. 望远镜中扰动抑制的Youla控制器优化设计[J]. 光电工程, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
Niu S X, Jiang J, Tang T, et al. Optimal design of Youla controller for vibration rejection in telescopes[J]. Opto-Electron Eng, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
[2] Wang X, Su X Q, Liu G Z, et al. Laser beam jitter control of the link in free space optical communication systems[J]. Opt Express, 2021, 29(25): 41582−41599. doi: 10.1364/OE.443411
[3] Zhu W, Rui X T. Adaptive control of a piezo-actuated steering mirror to restrain laser-beam jitter[J]. IEEE Trans Ind Electron, 2018, 66(10): 7873−7881. doi: 10.1109/TIE.2018.2885731
[4] Tang T, Niu S X, Ma J G, et al. A review on control methodologies of disturbance rejections in optical telescope[J]. Opto-Electron Adv, 2019, 2(10): 190011. doi: 10.29026/oea.2019.190011
[5] 王玉, 边启慧, 廖军, 等. 惯性稳定万向架中基于SBG惯导的捷联控制技术[J]. 光电工程, 2023, 50(5): 220238. doi: 10.12086/oee.2023.220238
Wang Y, Bian Q H, Liao J, et al. Strapdown inertial stabilization technology based on SBG inertial navigation in inertial stabilization gimbal[J]. Opto-Electron Eng, 2023, 50(5): 220238. doi: 10.12086/oee.2023.220238
[6] 张良总, 杨涛, 吴云, 等. 基于图像测量的Stewart平台双阶控制技术[J]. 光电工程, 2022, 49(8): 220019. doi: 10.12086/oee.2022.220019
Zhang L Z, Yang T, Wu Y, et al. Image measurement-based two-stage control of Stewart platform[J]. Opto-Electron Eng, 2022, 49(8): 220019. doi: 10.12086/oee.2022.220019
[7] 张伟明, 史泽林, 马德鹏. 光电稳像平台扰动力矩估计与自适应补偿[J]. 信息与控制, 2019, 48(5): 589−594,602. doi: 10.13976/j.cnki.xk.2019.9028
Zhang W M, Shi Z L, Ma D P. Disturbance torque estimate and adaptive compensation for optoelectronic stabilized platform[J]. Inf Control, 2019, 48(5): 589−594,602. doi: 10.13976/j.cnki.xk.2019.9028
[8] Wang J Y, Guo Y M, Kong L, et al. Automatic disturbance identification for linear quadratic Gaussian control in adaptive optics[J]. Mon Not R Astron Soc, 2020, 496(4): 5126−5138. doi: 10.1093/mnras/staa1698
[9] Ruan Y, Xu T R, Tang T, et al. Adaptive Youla–Kučera parametric control of unknown tip-tilt disturbance rejection in image stabilization systems[J]. Opt Lett, 2022, 47(11): 2670−2673. doi: 10.1364/OL.460716
[10] Pan J W, Chen Z, Wang Y, et al. Frequency separation based adaptive feedforward control for rejecting wideband vibration with application to hard disk drives[Z]. arXiv: 2012.05049, 2020. https://doi.org/10.48550/arXiv.2012.05049.
[11] Zheng M H, Tomizuka M. Adaptive frequency-shaped sliding mode control for narrow-band disturbance rejection[C]//2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 2016: 834–839. https://doi.org/10.1109/AIM.2016.7576872.
[12] Stuart Z K, El-Laham Y, Bugallo M F. Robust frequency and phase estimation for three-phase power systems using a bank of Kalman filters[J]. IEEE Signal Process Lett, 2021, 28: 1235−1239. doi: 10.1109/LSP.2021.3087464
[13] Tomar S, Sumathi P. Amplitude and frequency estimation of exponentially decaying sinusoids[J]. IEEE Trans Instrum Meas, 2018, 67(1): 229−237. doi: 10.1109/TIM.2017.2755998
[14] Zhu C, Fan Y, Chen J L. Resonance frequency identification of non-contact integrated permanent magnet vernier motor based on FFT[C]//2022 IEEE 3rd China International Youth Conference on Electrical Engineering (CIYCEE), 2022: 1–6. https://doi.org/10.1109/CIYCEE55749.2022.9959058.
[15] Serbes A. Fast and efficient sinusoidal frequency estimation by using the DFT coefficients[J]. IEEE Trans Commun, 2019, 67(3): 2333−2342. doi: 10.1109/TCOMM.2018.2886355
[16] Yang Z D, Huo L S, Wang J K, et al. Denoising low SNR percussion acoustic signal in the marine environment based on the LMS algorithm[J]. Measurement, 2022, 202: 111848. doi: 10.1016/j.measurement.2022.111848
[17] Yuan J P, An S, Pan X X, et al. A wave peak frequency tracking method based on two-stage recursive extended least squares identification algorithm[J]. IEEE Access, 2021, 9: 86514−86522. doi: 10.1109/ACCESS.2021.3057454
[18] Yuan Y, Qing M Y, Liang H Q. Average plain gradient based indirect frequency estimation using adaptive notch filter[C]//2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), 2020: 1–5. https://doi.org/10.1109/CCECE47787.2020.9255681.
[19] Wu W Y, Xiao Y G, Lin J H, et al. An efficient filter bank structure for adaptive notch filtering and applications[J]. IEEE/ACM Trans. Audio Speech Lang Process, 2021, 29: 3226−3241. doi: 10.1109/TASLP.2021.3120600
[20] Wu Z Z, Zhang M T, Chen Z Y, et al. Youla parameterized adaptive vibration suppression with adaptive notch filter for unknown multiple narrow band disturbances[J]. J Vibrat Control, 2019, 25(3): 685−694. doi: 10.1177/1077546318794539
[21] 徐田荣, 阮勇, 赵志强, 等. 基于误差的观测器在光电跟踪系统中的应用[J]. 光电工程, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
Xu T R, Ruan Y, Zhao Z Q, et al. Error-based observer control of an optic-electro tracking control system[J]. Opto-Electron Eng, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
[22] Ruan Y, Xu T R, Liu Y, et al. Error-based observation control of an image-based control loop for disturbance suppression in segmented lightweight large-scaled diffractive telescope (SLLDT)[J]. Opt Lasers Eng, 2022, 156: 107105. doi: 10.1016/j.optlaseng.2022.107105
[23] 王之昊, 张文喜, 伍洲, 等. 激光测振仪中最小均方误差前向预测器的研究[J]. 光电工程, 2022, 49(5): 210391. doi: 10.12086/oee.2022.210391
Wang Z H, Zhang W X, Wu Z, et al. Research on the forward predictor of minimum mean square error in laser vibrometer[J]. Opto-Electron Eng, 2022, 49(5): 210391. doi: 10.12086/oee.2022.210391
[24] 王雅丽, 虞莉娟, 张华军, 等. 基于自适应陷波器的电网频率估计方法[J]. 电测与仪表, 2018, 55(24): 121−127. doi: 10.3969/j.issn.1001-1390.2018.24.020
Wang Y L, Yu L J, Zhang H J, et al. Frequency estimation method for power grid based on adaptive notch filter[J]. Electr Meas Instrum, 2018, 55(24): 121−127. doi: 10.3969/j.issn.1001-1390.2018.24.020
-
访问统计
点击扫一扫
图(11)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
