E-mail Alert
RSS
-
摘要
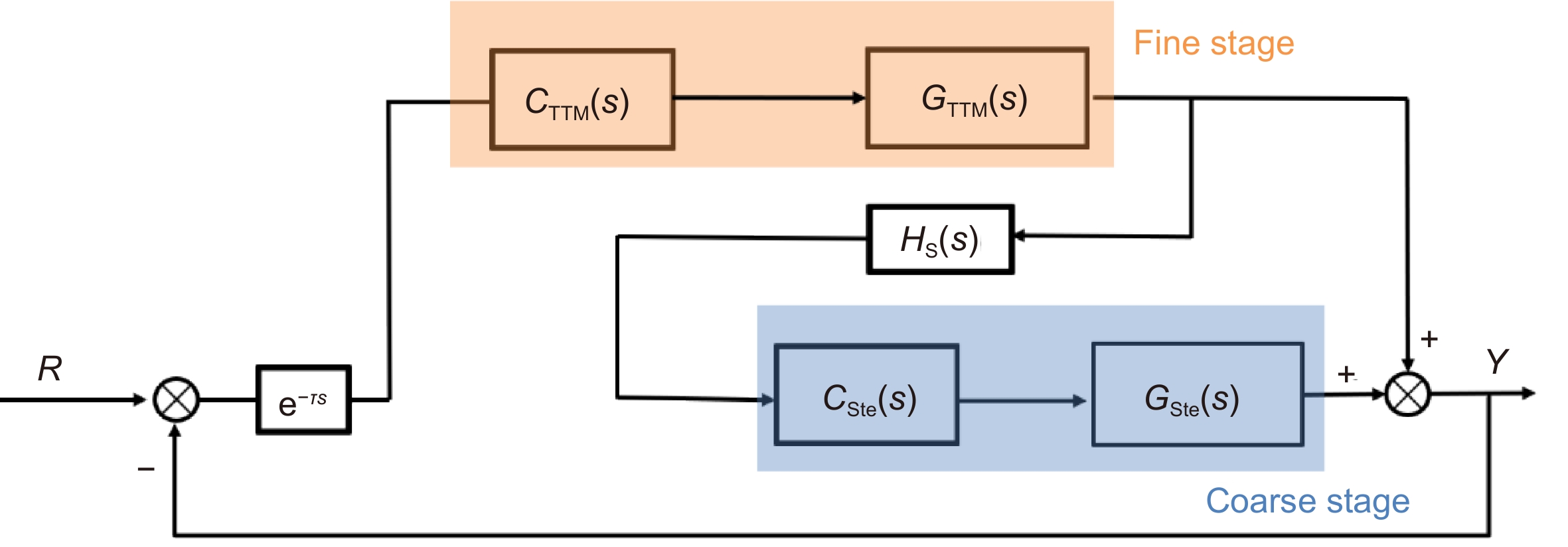
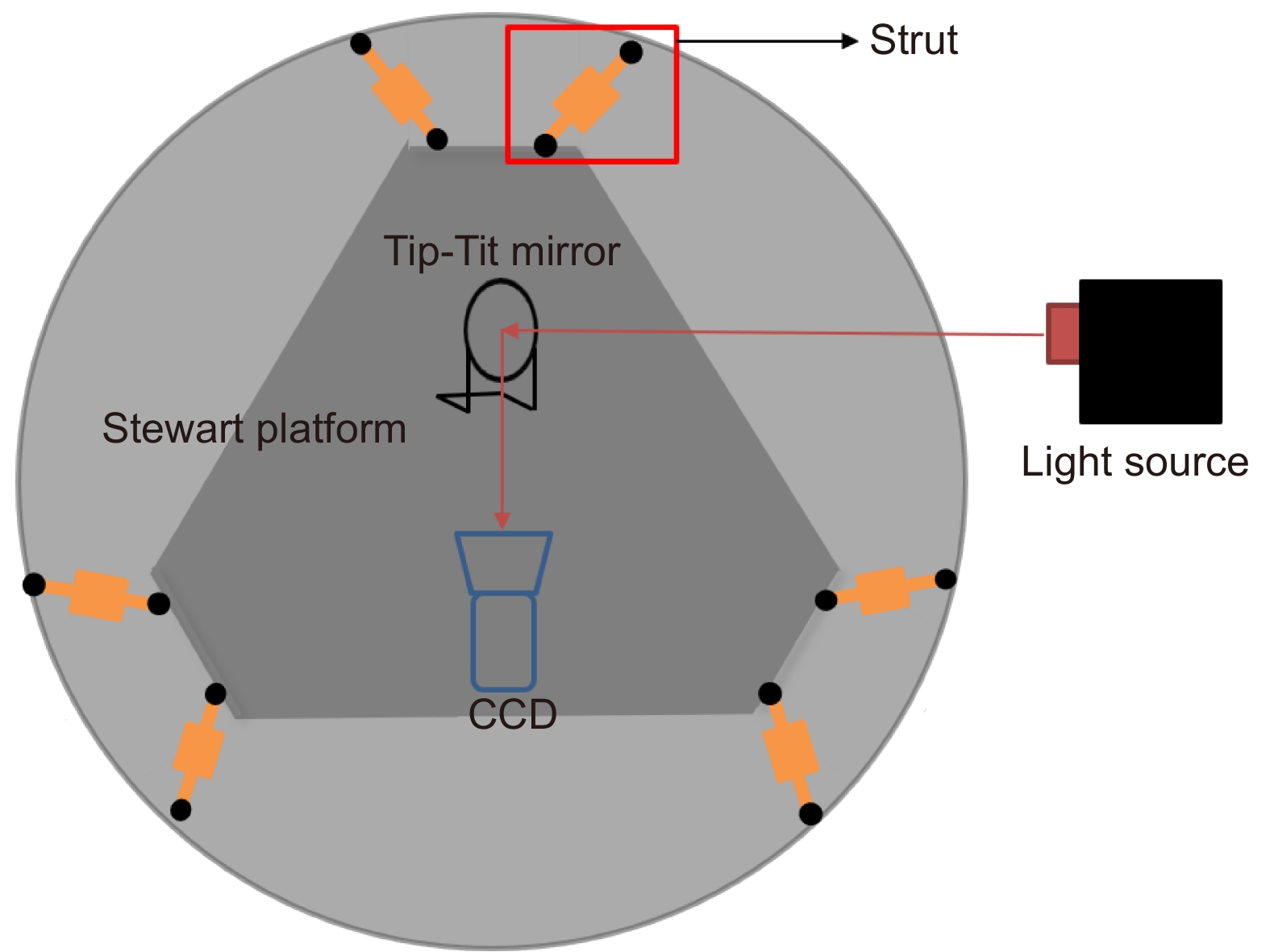
Stewart平台具有六自由度运动特性，既可用于隔振，也可用作跟踪平台。但是隔振功能要求系统带宽低，而跟踪功能则要求系统带宽高，二者的矛盾使得使用具有隔振功能的Stewart平台很难实现高精度跟踪。为了解决这一技术问题，引入高带宽的倾斜校正系统，构成双阶控制结构，以提高精度。传统的双阶控制需设计解耦环节，需要独立的测量传感器实现分级控制。本文提出了一种基于单传感器的控制方法，对传统的双阶结构进行改进，避免解耦环节，实现对Stewart-TTM高精度稳定闭环。为了进一步提高系统在带宽内的跟踪精度，设计PI-PI控制器经理论分析以及实验验证：基于单传感器测量的Stewart的双阶控制结构既能够满足隔振要求，又能够实现高精度跟踪控制。
Abstract
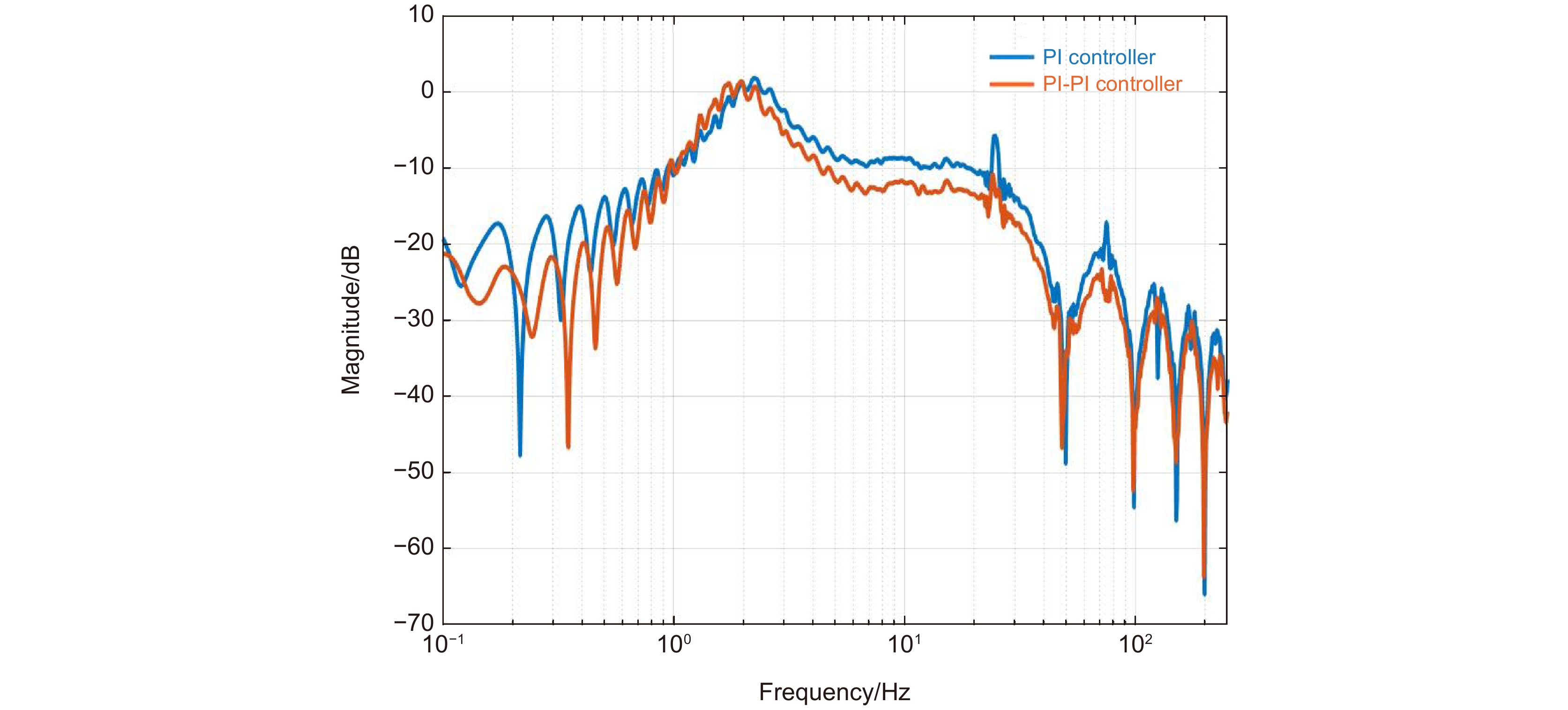
The Stewart platform has six degrees of freedom motion characteristics and can be used as both vibration isolation and tracking platform. However, the vibration isolation function requires low system bandwidth, while the tracking function requires high system bandwidth, which makes it difficult to achieve high precision tracking using the Stewart platform with vibration isolation function. To solve this technical problem, a high-bandwidth tilt correction system is introduced to form a two-stage control structure, so as to improve the accuracy. The traditional two-stage control needs to design decoupling link and independent measurement sensors to achieve hierarchical control. In this paper, a control method based on a single sensor is proposed to improve the traditional dual-order structure to avoid decoupling and achieve a high-precision closed-loop for the Stewart-TTM. In order to further improve the tracking accuracy of the system at low frequencies, a PI-PI controller is designed. Theoretical analysis and experimental verification show that the Stewart dual-stage control structure based on image measurement can not only meet the requirements of vibration isolation, but also achieve high-precision tracking control. Compared with the traditional PI controller, the PI-PI control proposed in the tilt correction system can effectively improve the tracking accuracy.
-
Key words:
- Stewart platform /
- two-stage system /
- PI-PI control
-
Overview
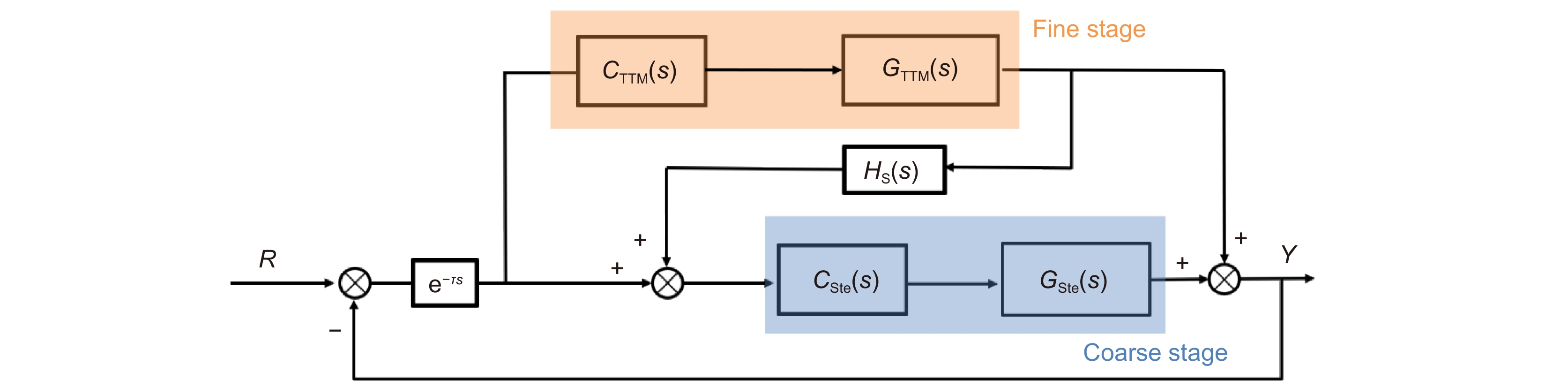
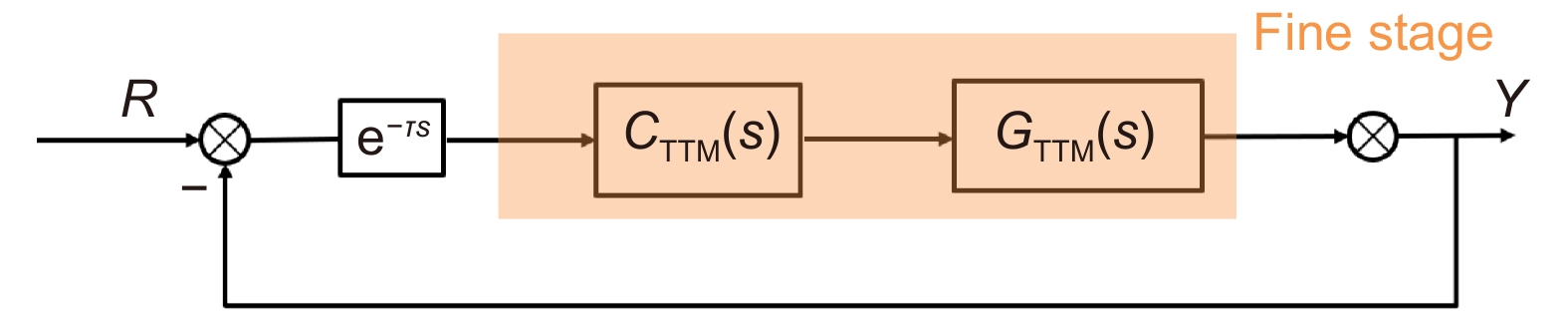
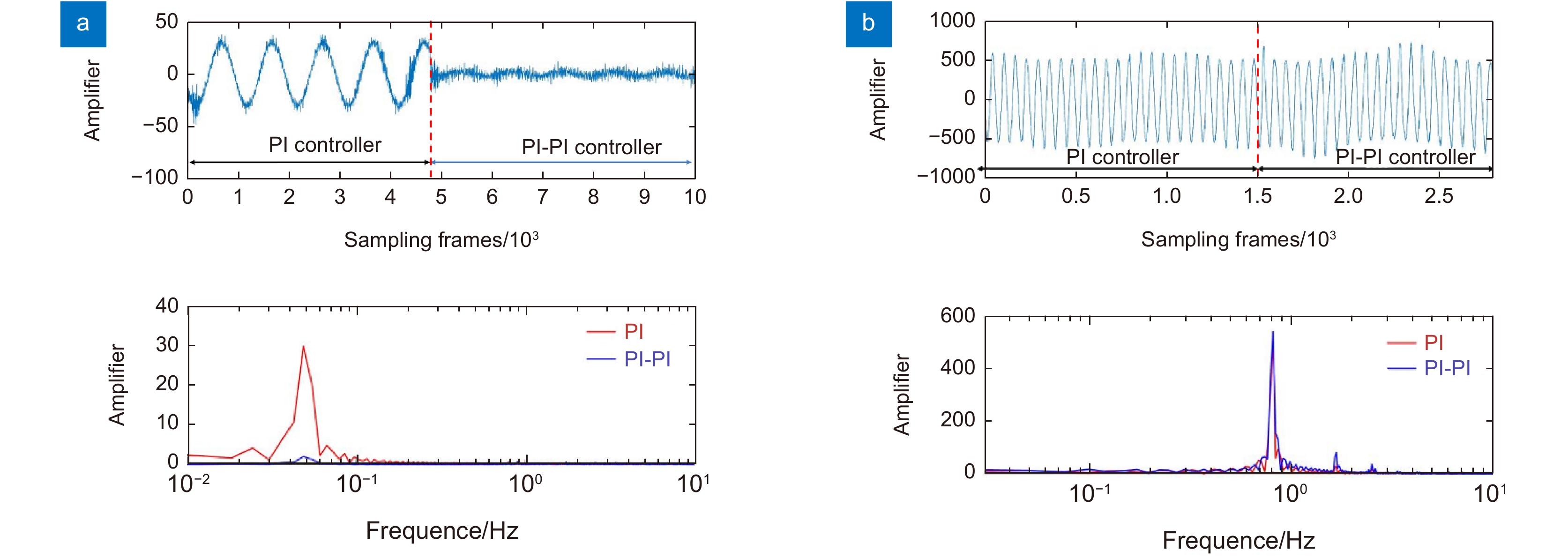
Overview: It is a trend of development to use the Stewart platform as a means of space. But the Stewart platform, which has a vibration ability and low system bandwidth, causing the tracking accuracy to be difficult to improve. In response to this problem, many scholars have proposed a two-stage control system, which is to design the system of a system that is far higher than the Stewart platform, which is used to curb the tracking error of the Stewart platform, thereby improving the tracking accuracy of the system. Tip-tit-mirror (TTM) bandwidth is very high, available in the intensive subsystem and the Stewart platform for two-stage control. When the system has only one CCD as a detector, it is necessary to design the decoupling link to make the system stable. But for the traditional two-order structure, it is difficult to design the decoupling element as the object of the probe. Therefore, this paper analyzes the traditional two-order structure and removes the redundant control structure. This paper also obtains the new structure based on the two-stage control of the position output and makes the decoupling link becomes easy. Through theoretical analysis, the accuracy of the system is mainly due to the ability of the precision subsystem to suppress the error of the rough system. The traditional controller of the advanced subsystem is the PI controller, which is extremely limited to the accuracy of the precision. The current research on the accuracy of the TTM tracking accuracy is mainly by introducing additional hardware devices, but this increases the uncertainty of the system stability. Therefore, the design of the PI-PI controller can effectively improve the tracking accuracy while increasing the cost of the system. After theoretical analysis and experimental verification, the PI-PI controller, compared to the PI controller, can improve the suppression ability of the error of the precision subsystem in the low frequencies. The double order structure control of the system and the Stewart platform is made up of the system, which makes the tracking precision of the system significantly improved, which is better solved the problem of the Stewart platform tracking precision that has the vibration function.
-
-
图 7 积分控制器和PI-PI控制误差抑制曲线仿真图
Figure 7. Integral controller and pi-pi control error suppression curve simulation diagram
图 9 PI与PI-PI控制器的误差抑制曲线对比
Figure 9. The error suppression curve of the PI and PI-PI controller is compared
图 10 双阶系统实验图。(a) f=0.05 Hz; (b) f=0.80 Hz
Figure 10. The two-stage system experiment. (a) f=0.05 Hz; (b) f=0.80 Hz
图 11 双阶控制中卸载量变化过程
Figure 11. The process of unloading quantization in two-stage control
图 12 单阶结构和双阶结构的跟踪误差对比。(a) 0.01 Hz；(b) 0.02 Hz；(c) 0.05 Hz
Figure 12. The tracking error of single-order structure and two-step structure is compared. (a) 0.01 Hz；(b) 0.02 Hz；(c) 0.05 Hz
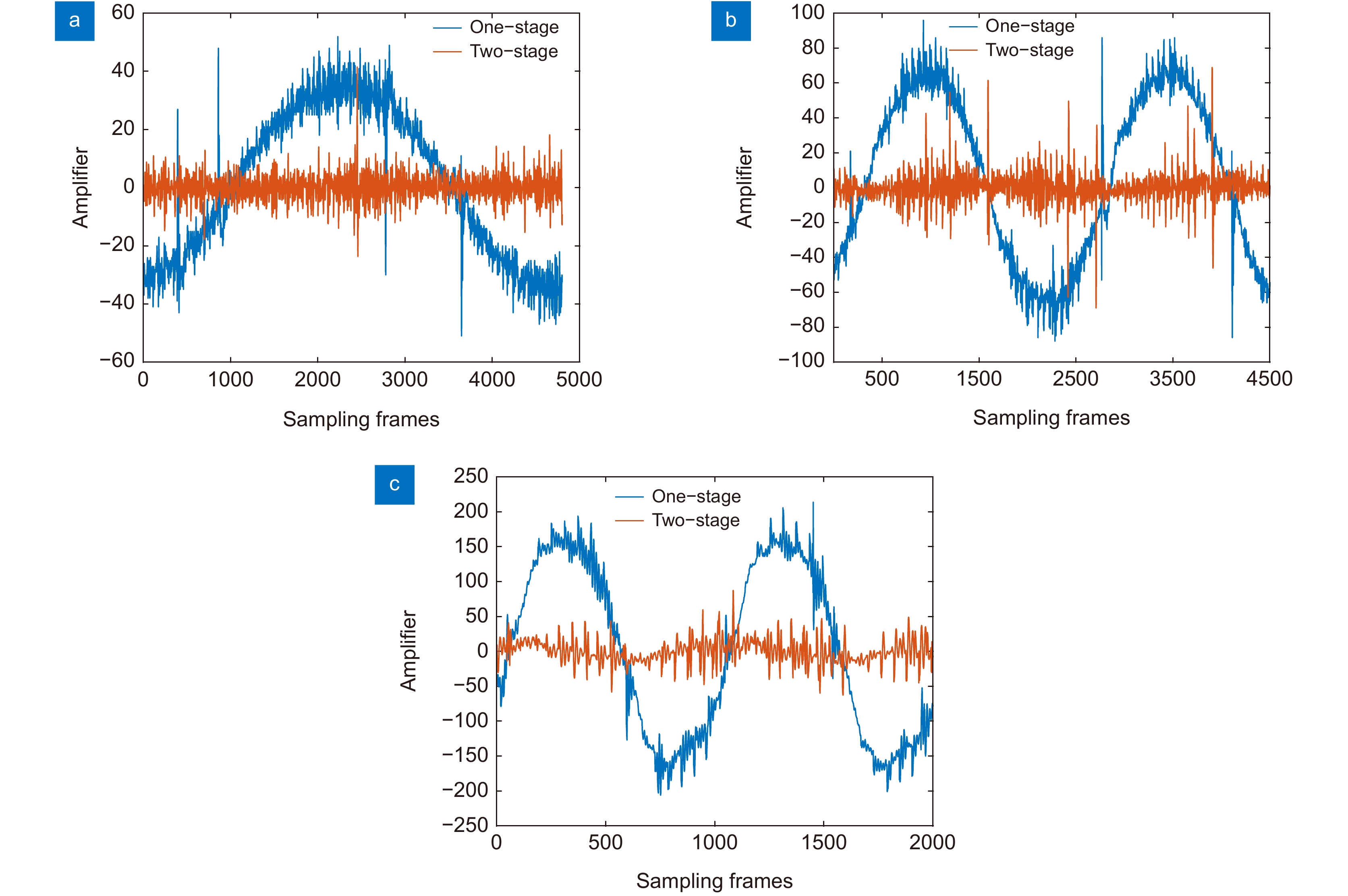
表 1 3种频率下单阶结构和双阶结构的跟踪误差RMS对比
Table 1. RMS comparison of tracking errors between single-order structure and double-order structure at three frequencies
Frequency/Hz Single-order structure/(′′) Double-order structure/(′′) 0.01 26.16005 3.172951 0.02 49.77028 5.876996 0.05 129.2003 14.38101 
下载: 导出CSV
-
参考文献
[1] 李林, 袁利, 王立, 等. 从哈勃太空望远镜剖析微振动对高性能航天器指向测量与控制系统的影响[J]. 光学精密工程, 2020, 28(11): 2478−2487. doi: 10.37188/OPE.20202811.2478
Li L, Yuan L, Wang L, et al. Influence of micro vibration on measurement and pointing control system of high-performance spacecraft from Hubble Space Telescope[J]. Opt Prec Eng, 2020, 28(11): 2478−2487. doi: 10.37188/OPE.20202811.2478
[2] Yun H, Liu L, Li Q, et al. Development of an isotropic Stewart platform for telescope secondary mirror[J]. Mech Syst Signal Process, 2019, 127: 328−344. doi: 10.1016/j.ymssp.2019.03.001
[3] Du Z J, Shi R C, Dong W. A piezo-actuated high-precision flexible parallel pointing mechanism: conceptual design, development, and experiments[J]. IEEE Trans Robot, 2014, 30(1): 131−137. doi: 10.1109/TRO.2013.2288800
[4] Zhang Y Z, Guan X. Active damping control of flexible appendages for spacecraft[J]. Aerosp Sci Technol, 2018, 75: 237−244. doi: 10.1016/j.ast.2017.12.027
[5] Thayer D, Campbell M, Vagners J, et al. Six-axis vibration isolation system using soft actuators and multiple sensors[J]. J Spacecr Rockets, 2002, 39(2): 206−212. doi: 10.2514/2.3821
[6] Wang C X, Xie X L, Chen Y H, et al. Investigation on active vibration isolation of a Stewart platform with piezoelectric actuators[J]. J Sound Vib, 2016, 383: 1−19. doi: 10.1016/j.jsv.2016.07.021
[7] Kong Y F, Huang H. Vibration isolation and dual-stage actuation pointing system for space precision payloads[J]. Acta Astronaut, 2018, 143: 183−192. doi: 10.1016/j.actaastro.2017.11.038
[8] Brugarolas P, Alexander J, Trauger J, et al. ACCESS pointing control system[J]. Proc SPIE, 2010, 7731(1): 77314V. doi: 10.1117/12.856518
[9] Yun H, Liu L, Li Q, et al. Investigation on two-stage vibration suppression and precision pointing for space optical payloads[J]. Aerosp Sci Technol, 2020, 96: 105543. doi: 10.1016/j.ast.2019.105543
[10] Tang T, Huang Y M, Fu C Y, et al. Acceleration feedback of a CCD-based tracking loop for fast steering mirror[J]. Opt Eng, 2009, 48(1): 013001. doi: 10.1117/1.3065500
[11] 阮勇, 徐田荣, 杨涛, 等. 具有延迟特性的倾斜镜系统中速度-位置控制方法[J]. 光电工程, 2020, 47(12): 200006. doi: 10.12086/oee.2020.200006
Ruan Y, Xu T R, Yang T, et al. Position-rate control for the time delay control system of tip-tilt mirror[J]. Opto-Electron Eng, 2020, 47(12): 200006. doi: 10.12086/oee.2020.200006
[12] 徐田荣, 阮勇, 赵志强, 等. 基于误差的观测器在光电跟踪系统中的应用(英文)[J]. 光电工程, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
Xu T R, Ruan Y, Zhao Z Q, et al. Error-based observer control of an optic-electro tracking control system[J]. Opto-Electron Eng, 2020, 47(11): 190713. doi: 10.12086/oee.2020.190713
[13] Tang T, Ma J G, Ge R. PID-I controller of charge coupled device-based tracking loop for fast-steering mirror[J]. Opt Eng, 2011, 50(4): 043002. doi: 10.1117/1.3567059
-
访问统计
点击扫一扫
图(13)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
