E-mail Alert
RSS
-
摘要
深度卷积神经网络最近在图像超分辨率方面展示了高质量的恢复效果。然而，现有的图像超分辨率方法大多只考虑如何充分利用训练集中固有的静态特性，却忽视了低分辨率图像本身的自相似特征。为了解决这些问题，本文设计了一种自相似特征增强的网络结构(SSEN)。具体来说，本文将可变形卷积嵌入到金字塔结构中并结合跨层次协同注意力，设计出了一个能够充分挖掘多层次自相似特征的模块，即跨层次特征增强模块。此外，本文还在堆叠的密集残差块中引入池化注意力机制，利用条状池化扩大卷积神经网络的感受野并在深层特征中建立远程依赖关系，从而深层特征中相似度较高的部分能够相互补充。在常用的五个基准测试集上进行了大量实验，结果表明，SSEN比现有的方法在重建效果上具有明显提升。
Abstract
Deep convolutional neural networks (DCNN) recently demonstrated high-quality restoration in the single image super-resolution (SISR). However, most of the existing image super-resolution methods only consider making full use of the inherent static characteristics of the training sets, ignoring the internal self-similarity of low-resolution images. In this paper, a self-similarity enhancement network (SSEN) is proposed to address above-mentioned problems. Specifically, we embedded the deformable convolution into the pyramid structure and combined it with the cross-level co-attention to design a module that can fully mine multi-level self-similarity, namely the cross-level feature enhancement module. In addition, we introduce a pooling attention mechanism into the stacked residual dense blocks, which uses a strip pooling to expand the receptive field of the convolutional neural network and establish remote dependencies within the deep features, so that the patches with high similarity in deep features can complement each other. Extensive experiments on five benchmark datasets have shown that the SSEN has a significant improvement in reconstruction effect compared with the existing methods.
-
Key words:
- super-resolution /
- self-similarity /
- feature enhancement /
- deformable convolution /
- attention /
- strip pooling
-
Overview
Overview: Single image super-resolution can not only be directly used in practical applications, but also benefits other tasks of computer vision, such as object detection and semantic segmentation. Single image super-resolution, with the goal of reconstructing an accurate high-resolution (HR) image from its observed low-resolution (LR) image counterpart, is a representative branch of image reconstruction tasks in the field of computer vision. Dong et al. firstly introduced a three-layer convolutional neural network to learn the mapping function between the bicubic-interpolated and HR image pairs, demonstrating the substantial performance improvements compared to those of conventional algorithms. Therefore, a series of single image super-resolution algorithms based on deep learning have been proposed. Although a great progress has been made in image super-resolution methods, existing convolutional neural network-based super-resolution models still have some limitations. First, most CNN-based super-resolution methods focus on designing deeper or wider networks to learn more advanced features of discriminability, but fail to make full use of the internal self-similarity information of the low-resolution images. In response to this problem, SAN introduced non-local networks and CS-NL proposed cross-scale non-local. Although these methods can take the advantage of self-similarity, they still need to consume a huge amount of memory to calculate the large relational matrix of each spatial location. Second, most methods do not make reasonable use of multi-level self-similarity. Even if some methods consider the importance of multi-level self-similarity, they do not have a good method to fuse them, so as to achieve a good image reconstruction effect.
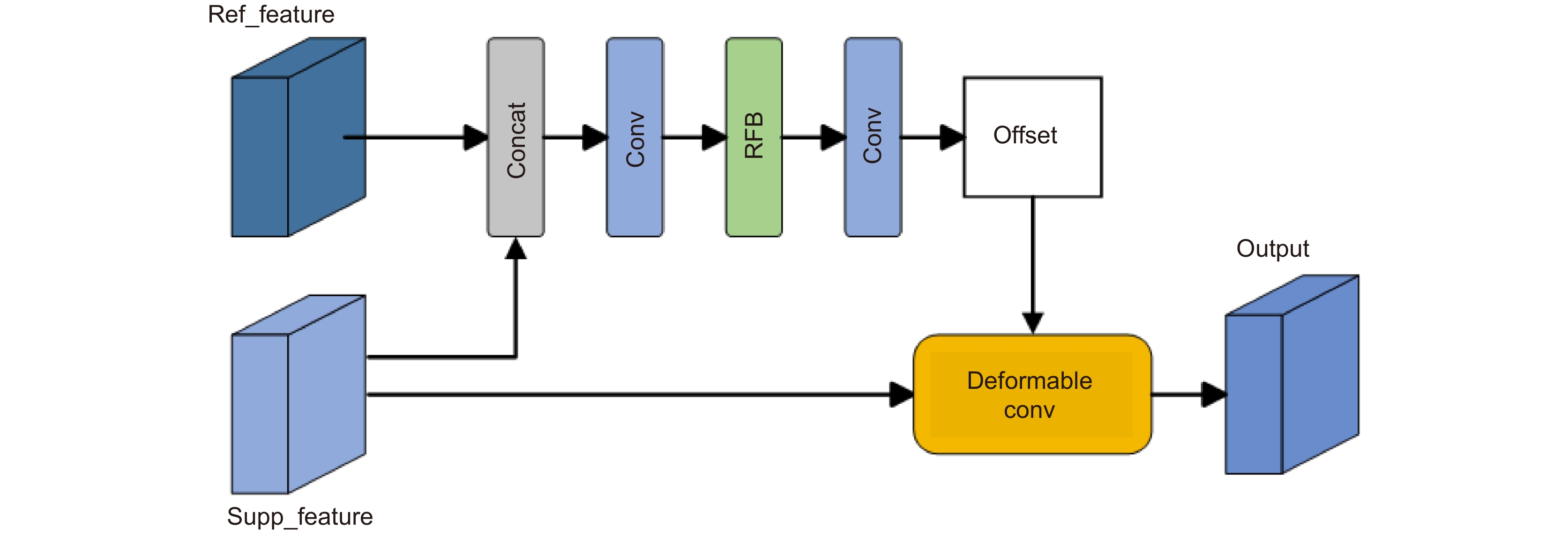
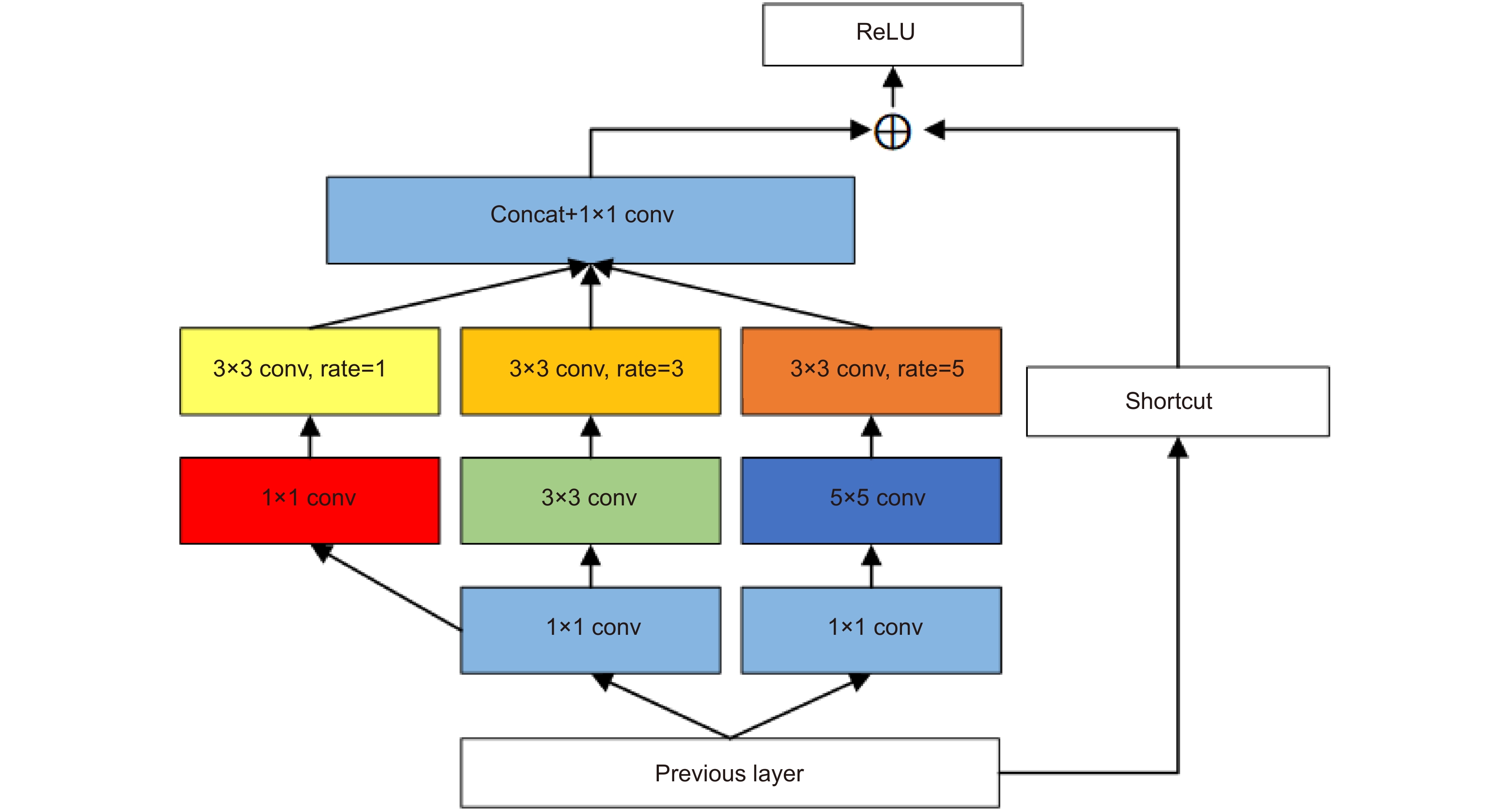
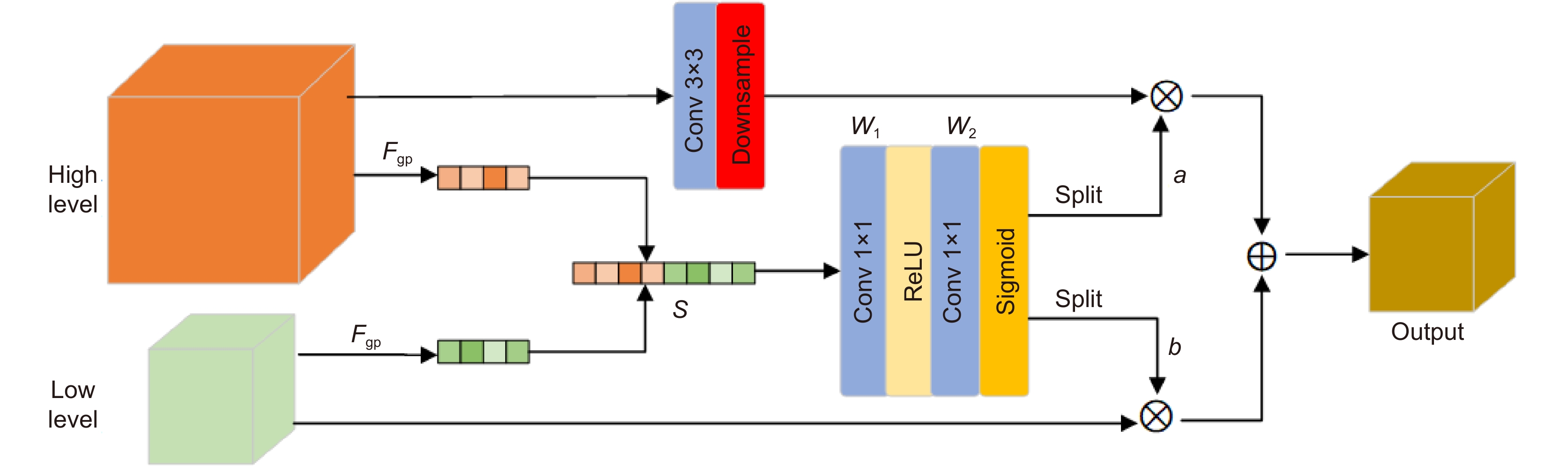
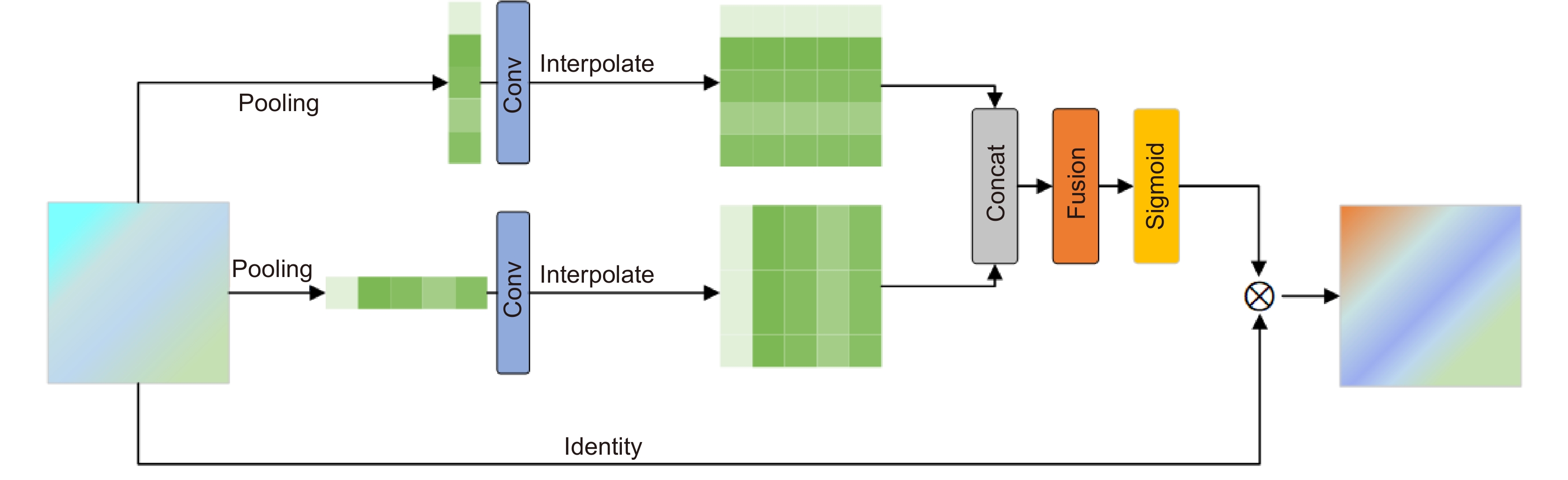
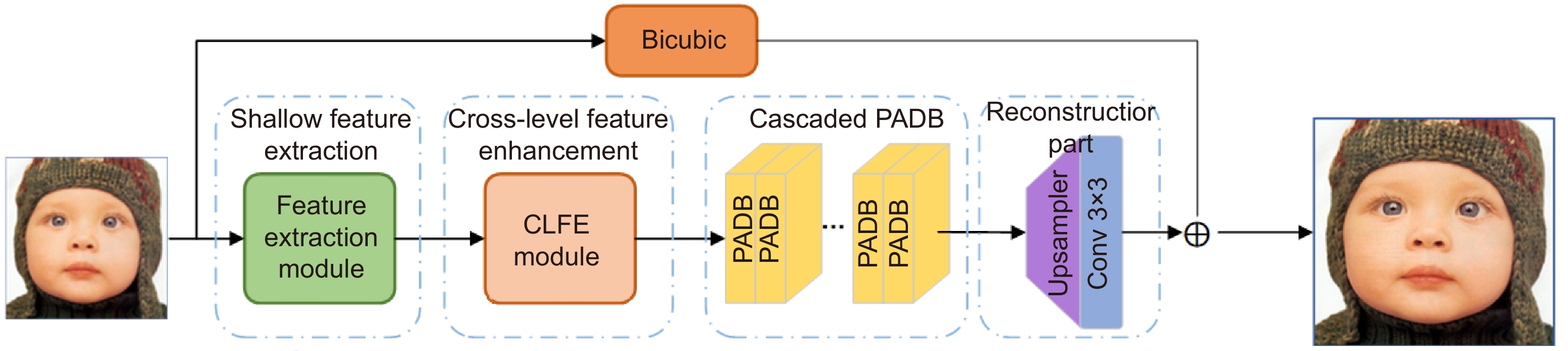
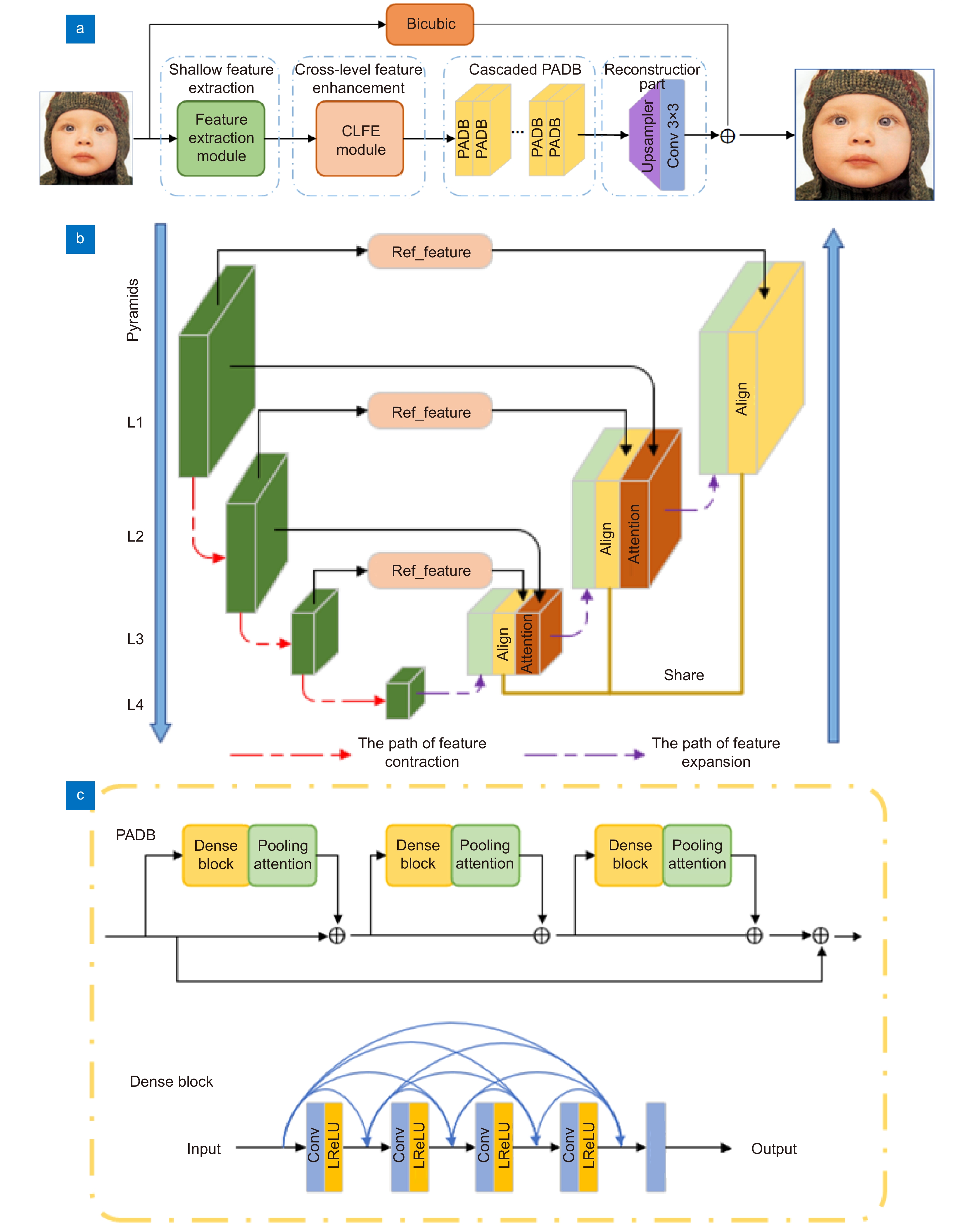
To solve these problems, we propose a self-similarity enhancement network (SSEN). We embedded deformable convolution into the pyramid structure to mine multi-level self-similarity in the low-resolution images, and then introduced the cross-level co-attention at each level of the pyramid to fuse them. Finally, the pooling attention mechanism was utilized to further explore the self-similarity in deep features. Compared with other models, our network mainly has the following differences. First, our network searches self-similarity using an offset estimator of deformable convolution. At the same time, we use the cross-level co-attention to enhance the ability of cross-level feature transmission in the feature pyramid structure. Second, most models capture global correlation by calculating pixel correlation through non-local networks. However, the pooled attention mechanism is used in our network to adaptively capture remote dependencies with low computational cost, which enhances the deep features of self-similarity, thus significantly improving the reconstruction effect. Extensive experiments on five benchmark datasets have shown that the SSEN has a significant improvement in reconstruction effect compared with the existing methods.
-
-
图 4 提出的跨层次协同注意力结构， 其中Fgp表示全局平均池化
Figure 4. The proposed Cross-Level Co-Attention architec-ture. "Fgp" denotes the global average pooling
图 6 数据集Urban100中“Img048”放大4倍的超分辨率结果
Figure 6. Super-resolution results of " Img048" in Urban100 dataset for 4× magnification
图 7 数据集Urban100中“Img092”放大4倍的超分辨率结果
Figure 7. Super-resolution results of " Img092" in Urban100 dataset for 4× magnification
图 8 数据集BSD100中“
223061 ”放大4倍的超分辨率结果Figure 8. Super-resolution results of "
223061 " in BSD100 dataset for 4× magnification
图 9 数据集BSD100中“
253027 ”放大4倍的超分辨率结果Figure 9. Super-resolution results of "
253027 " in BSD100 dataset for 4× magnification
图 10 跨层次特征增强模块和池化注意力密集块聚合分析每种组合的曲线均基于Set5，放大因子为4，共800 epoch
Figure 10. Convergence analysis on CLFE and PADB. The curves for each combination are based on the PSNR on Set5 with scaling factor 4× in 800 epochs.
表 1 在数据集Set5、Set14、BSD100、Urban100、Manga109上放大倍数分别为2、3、4的平均 PSNR(dB)和SSIM的结果比较
Table 1. The average results of PSNR/SSIM with scale factor 2×，3× and 4× on datasets Set5，Set14，BSD100，Urban100 and Manga109
Scale Method Set5 Set14 BSD100 Urban100 Manga109 PSNR/SSIM PSNR/SSIM PSNR/SSIM PSNR/SSIM PSNR/SSIM 2× Bicubic 33.66/0.9299 30.24/0.8688 29.56/0.8431 26.88/0.8409 30.80/0.9339 SRCNN[7] 36.66/0.9542 32.45/0.9067 31.36/0.8879 29.50/0.8946 35.60/0.9663 VDSR[8] 37.53/0.9590 33.05/0.9130 31.90/0.8960 30.77/0.9140 37.22/0.9750 M2SR[23] 38.01/0.9607 33.72/0.9202 32.17/0.8997 32.20/0.9295 38.71/0.9772 LapSRN[34] 37.52/0.9591 33.08/0.9130 31.80/0.8950 30.41/0.9100 37.27/0.9740 PMRN[35] 38.13/0.9609 33.85/0.9204 32.28/0.9010 32.59/0.9328 38.91/0.9775 OISR-RK2[37] 38.12/0.9609 33.80/0.9193 32.26/0.9006 32.48/0.9317 − DBPN[38] 38.09/0.9600 33.85/0.9190 32.27/0.9000 32.55/0.9324 38.89/0.9775 RDN[36] 38.24/0.9614 34.01/0.9212 32.34/0.9017 32.89/0.9353 39.18/0.9780 SSEN(ours) 38.11/0.9609 33.92/0.9204 32.28/0.9011 32.87/0.9351 39.06/0.9778 3× Bicubic 30.39/0.8682 27.55/0.7742 27.21/0.7385 24.46/0.7349 26.96/0.8546 SRCNN[7] 32.75/0.9090 29.28/0.8209 28.41/0.7863 26.24/0.7989 30.59/0.9107 VDSR[8] 33.66/0.9213 29.77/0.8314 28.82/0.7976 27.14/0.8279 32.01/0.9310 M2SR[23] 34.43/0.9275 30.39/0.8440 29.11/0.8056 28.29/0.8551 33.59/0.9447 LapSRN[34] 33.82/0.9227 29.79/0.8320 28.82/0.7973 27.07/0.8272 32.19/0.9334 PMRN[35]
OISR-RK2[37]34.57/0.9280
34.55/0.928230.43/0.8444
30.46/0.844329.19/0.8075
29.18/0.807528.51/0.8601
28.50/0.859733.85/0.9465
−RDN[36] 34.71/0.9296 30.57/0.8468 29.26/0.8093 28.80/0.8653 34.13/0.9484 SSEN(ours) 34.64/0.9289 30.53/0.8462 29.20/0.8079 28.66/0.8635 34.01/0.9474 4× Bicubic 28.42/0.8104 26.00/0.7027 25.96/0.6675 23.14/0.6577 24.89/0.7866 SRCNN[7] 30.48/0.8628 27.50/0.7513 26.90/0.7101 24.52/0.7221 27.58/0.8555 VDSR[8] 31.35/0.8838 28.02/0.7680 27.29/0.7260 25.18/0.7540 28.83/0.8870 M2SR[23] 32.23/0.8952 28.67/0.7837 27.60/0.7373 26.19/0.7889 30.51/0.9093 LapSRN[34] 31.54/0.8850 28.19/0.7720 27.32/0.7270 25.21/0.7551 29.09/0.8900 PMRN[35] 32.34/0.8971 28.71/0.7850 27.66/0.7392 26.37/0.7950 30.71/0.9107 OISR-RK2[37] 32.32/0.8965 28.72/0.7843 27.66/0.7390 26.37/0.7953 − DBPN[38] 32.47/0.8980 28.82 /0.786027.72 /0.740026.38/0.7946 30.91/0.9137 RDN[36] 32.47/0.8990 28.81 /0.7871 27.72/0.7419 26.61/0.8028 31.00/0.9151 SSEN(ours) 32.42 /0.8982 28.79 /0.7864 27.69/0.7400 26.49/0.7993 30.88/0.9132 
下载: 导出CSV
表 2 跨层次特征增强模块和池化注意力密集块在数据集Set5放大4倍下结果比较
Table 2. The results of cross-level and feature enhancement module and pooling attention dense block with scale factor 4× on Set5
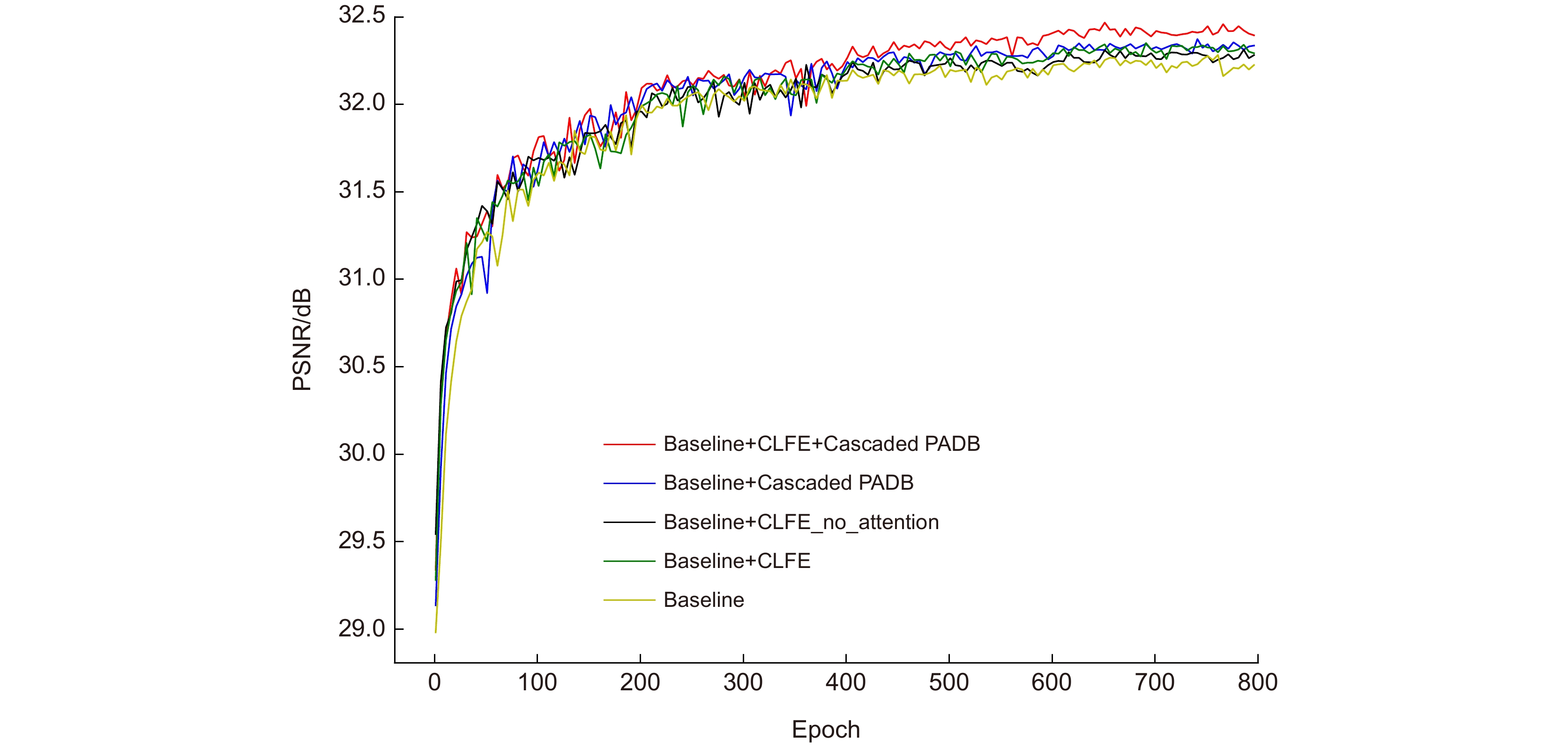
Baseline √ √ √ √ CLFE × √ × √ Cascaded PADB × × √ √ PSNR/dB 32.28 32.35 32.37 32.42 SSIM 0.8962 0.8971 0.8972 0.8982
下载: 导出CSV
表 3 模型大小和计算量在数据集Set14放大2倍情况下的比较，计算量表示乘法操作和加法操作的数目之和
Table 3. Model size and MAC comparison on Set14 (2×)， "MAC" denotes the number of multiply-accumulate operations
下载: 导出CSV
-
参考文献
[1] Zhang L, Wu X L. An edge-guided image interpolation algorithm via directional filtering and data fusion[J]. IEEE Trans Image Process, 2006, 15(8): 2226−2238. doi: 10.1109/TIP.2006.877407
[2] Li X Y, He H J, Wang R X, et al. Single image superresolution via directional group sparsity and directional features[J]. IEEE Trans Image Process, 2015, 24(9): 2874−2888. doi: 10.1109/TIP.2015.2432713
[3] Zhang K B, Gao X B, Tao D C, et al. Single image super-resolution with non-local means and steering kernel regression[J]. IEEE Trans Image Process, 2012, 21(11): 4544−4556. doi: 10.1109/TIP.2012.2208977
[4] 徐亮, 符冉迪, 金炜, 等. 基于多尺度特征损失函数的图像超分辨率重建[J]. 光电工程, 2019, 46(11): 180419.
Xu L, Fu R D, Jin W, et al. Image super-resolution reconstruction based on multi-scale feature loss function[J]. Opto-Electron Eng, 2019, 46(11): 180419.
[5] Huang J B, Singh A, Ahuja N. Single image super-resolution from transformed self-exemplars[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition, 2015: 5197–5206.
[6] 沈明玉, 俞鹏飞, 汪荣贵, 等. 多路径递归网络结构的单帧图像超分辨率重建[J]. 光电工程, 2019, 46(11): 180489.
Shen M Y, Yu P F, Wang R G, et al. Image super-resolution via multi-path recursive convolutional network[J]. Opto-Electron Eng, 2019, 46(11): 180489.
[7] Dong C, Loy C C, He K M, et al. Learning a deep convolutional network for image super-resolution[C]//Proceedings of the 13th European Conference on Computer Vision, 2014: 184–199.
[8] Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1646–1654.
[9] Hui Z, Gao X B, Yang Y C, et al. Lightweight image super-resolution with information multi-distillation network[C]//Proceedings of the 27th ACM International Conference on Multimedia, 2019: 2024–2032.
[10] Liu S T, Huang D, Wang Y H. Receptive field block net for accurate and fast object detection[C]//Proceedings of the 15th European Conference on Computer Vision, 2018: 404–419.
[11] Dai T, Cai J R, Zhang Y B, et al. Second-order attention network for single image super-resolution[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 11057–11066.
[12] Mei Y Q, Fan Y C, Zhou Y Q, et al. Image super-resolution with cross-scale non-local attention and exhaustive self-exemplars mining[C]//Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020: 5689–5698.
[13] Jaderberg M, Simonyan K, Zisserman A, et al. Spatial transformer networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015: 2017–2025.
[14] Hu J, Shen L, Sun G. Squeeze-and-excitation networks[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 7132–7141.
[15] Zhang Y L, Li K P, Li K, et al. Image super-resolution using very deep residual channel attention networks[C]//Proceedings of the 15th European Conference on Computer Vision, 2018: 294–310.
[16] Woo S, Park J, Lee J Y, et al. CBAM: convolutional block attention module[C]//Proceedings of the 15th European Conference on Computer Vision, 2018: 3–19.
[17] Sun K, Zhao Y, Jiang B R, et al. High-resolution representations for labeling pixels and regions[Z]. arXiv: 1904.04514, 2019. https://arxiv.org/abs/1904.04514.
[18] Newell A, Yang K Y, Deng J. Stacked hourglass networks for human pose estimation[C]//Proceedings of the 14th European Conference on Computer Vision, 2016: 483–499.
[19] Ke T W, Maire M, Yu S X. Multigrid neural architectures[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4067–4075.
[20] Chen Y P, Fan H Q, Xu B, et al. Drop an octave: reducing spatial redundancy in convolutional neural networks with octave convolution[C]//Proceedings of 2019 IEEE/CVF International Conference on Computer Vision, 2019: 3434–3443.
[21] Han W, Chang S Y, Liu D, et al. Image super-resolution via dual-state recurrent networks[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 1654–1663.
[22] Li J C, Fang F M, Mei K F, et al. Multi-scale residual network for image super-resolution[C]//Proceedings of the 15th European Conference on Computer Vision (ECCV), 2018: 527–542.
[23] Yang Y, Zhang D Y, Huang S Y, et al. Multilevel and multiscale network for single-image super-resolution[J]. IEEE Signal Process Lett, 2019, 26(12): 1877−1881. doi: 10.1109/LSP.2019.2952047
[24] Feng R C, Guan W P, Qiao Y, et al. Exploring multi-scale feature propagation and communication for image super resolution[Z]. arXiv: 2008.00239, 2020. https://arxiv.org/abs/2008.00239v2.
[25] Dai JF, Qi H Z, Xiong Y W, et al. Deformable convolutional networks[C]//Proceedings of 2017 IEEE International Conference on Computer Vision, 2017: 764–773.
[26] Zhu X Z, Hu H, Lin S, et al. Deformable ConvNets V2: more deformable, better results[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 9300–9308.
[27] Wang X T, Yu K, Wu S X, et al. ESRGAN: enhanced super-resolution generative adversarial networks[C]//Proceedings of 2018 European Conference on Computer Vision, 2018: 63–79.
[28] Hou Q B, Zhang L, Cheng M M, et al. Strip pooling: rethinking spatial pooling for scene parsing[C]//Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020: 4002–4011.
[29] Agustsson E, Timofte R. NTIRE 2017 challenge on single image super-resolution: dataset and study[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017: 1122–1131.
[30] Bevilacqua M, Roumy A, Guillemot C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]//Proceedings of the British Machine Vision Conference, 2012.
[31] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations[C]//Proceedings of the 7th International Conference on Curves and Surfaces, 2010: 711–730.
[32] Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]//Proceedings Eighth IEEE International Conference on Computer Vision, 2001: 416–423.
[33] Matsui Y, Ito K, Aramaki Y, et al. Sketch-based manga retrieval using manga109 dataset[J]. Multimed Tools Appl, 2017, 76(20): 21811−21838. doi: 10.1007/s11042-016-4020-z
[34] Lai W S, Huang J B, Ahuja N, et al. Deep laplacian pyramid networks for fast and accurate super-resolution[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, 2017: 5835–5843.
[35] Liu Y Q, Zhang X F, Wang S S, et al. Progressive multi-scale residual network for single image super-resolution[Z]. arXiv: 2007.09552, 2020. https://arxiv.org/abs/2007.09552v3.
[36] Zhang Y L, Tian Y P, Kong Y, et al. Residual dense network for image super-resolution[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 2472–2481.
[37] He X Y, Mo Z T, Wang P S, et al. ODE-inspired network design for single image super-resolution[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 1732–1741.
[38] Haris M, Shakhnarovich G, Ukita N. Deep back-projection networks for super-resolution[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018: 1664–1673.
[39] Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017: 1132–1140.
-
访问统计
点击扫一扫
图(12)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
