E-mail Alert
RSS
-
摘要
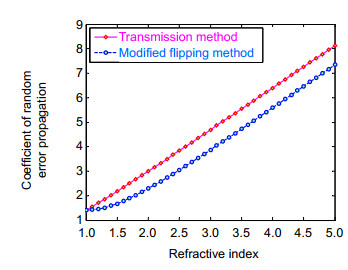
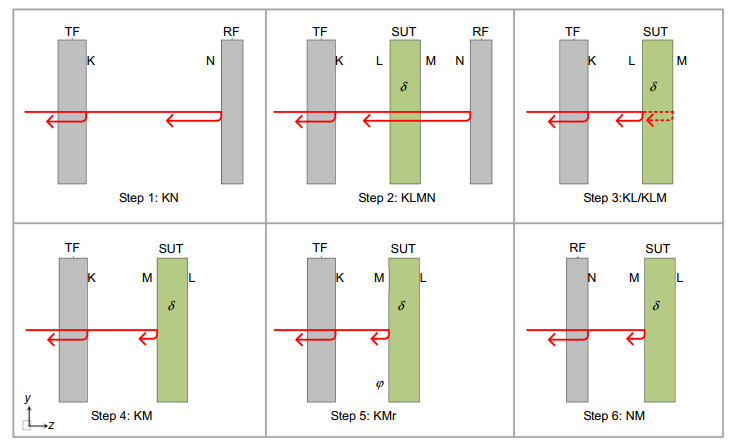
本文提出了一种改进六步翻转法，同时实现平行平板均匀性以及绝对面形的测量，结合相应的稀疏迭代算法，进一步实现高精度的均匀性和绝对面形误差的重构。通过相应的理论分析和实验验证工作，进一步证明了该方法的有效性和达到亚纳米级检测精度的能力。利用本文所提出的方法与传统绝对平面检测方法以及材料均匀性测量方法进行交叉对比，其中绝对平面测量结果之间差异优于1.7 nm RMS，均匀性测量精度差异不超过2.3 nm RMS。实验结果表明了两者具有高度一致性，同时具有较好的重复性，验证了文章提出的方法的准确性。并且根据不确定度分析表明，该方法与传统的透射法相比提高了测量精度。
Abstract
We describe a modified six-step method to simultaneously measure the inhomogeneity of sample plate and the planarity of the four surfaces in an absolute manner, along with a high-efficiency iterative algorithm for data reduction. Combined with the iterative algorithm, the errors of inhomogeneity and flatness can be estimated with pixel-level spatial resolution in a fast and effective manner. The simulation and experiments prove the validity of the method and the measurement capability of reaching sub-nanometer accuracy. The method presented in this paper is cross-compared with traditional absolute testing method and the method of inhomogeneity. The difference between absolute plane measurements is less than 1.7 nm RMS, and the difference of inhomogeneity measurement accuracy is less than 2.3 nm RMS. The experimental results show that these two methods are highly consistent and have good repeatability, which verifies the accuracy of the methods proposed in this paper. Uncertainty analysis indicates that the proposed method improves the measurement uncertainty, compared with the classical transmission method.
-
Key words:
- optical testing /
- interferometry /
- absolute test /
- uncertainty evaluation
-
Overview
Overview: For many international projects, such as EUV lithography, Synchrotron Radiation Facility and Inertial Confinement Fusion, there are a variety of optical materials that must be produced with excellent optical flatness and refractive index homogeneity. Inhomogeneity is a measure of the variation in the refractive index within a material. Several methods can be used to measure the inhomogeneity based on standard phase measuring interferometry, including liquid immersion method and transmission method. Since the use of liquid is inconvenient for some applications, many researchers turn to develop techniques that can separate surface deviation caused by inhomogeneity from system errors (i.e. absolute test techniques). Absolute measurement of surface is a complex process that involves multiple measurements. As to absolute measurement of inhomogeneity, transmission method is the most popular. The transmission method with four measurements is able to remove the error contributions of the surfaces of the sample plate, as well as the errors of the return flat and interferometer. Another straightforward method called "window-flipping method", measuring the rear surface of the window by flipping the window, can avoid this problem. But the flipping method inherently has a big uncertainty introduced by systematic effects—the surface error of transmission flat cannot be removed completely. With the aid of absolute test techniques (such as three-flat test), it is possible to measure the surface in advance and store them for later use. But it is also a complex process. To simplify the whole measurement process, it is necessary to measure the absolute planarity and inhomogeneity of the sample plate at the same time. In this paper, a modified six-step method to simultaneously measure the inhomogeneity of the sample plate and the four surfaces in an absolute manner is presented. Unlike the classical transmission method, the modified flipping method can test a polished sample that has no wedge between the two surfaces (such as parallel transparent plates). With the help of a high-efficiency iterative algorithm for data reduction, the errors of inhomogeneity and flatness are estimated with pixel-level spatial resolution in a fast and effective manner without using the polynomial fitting. The example experiments prove the validity of the method and the measurement capability of achieving sub-nanometer RMS accuracy. Uncertainty analysis suggests that the modified six-step flipping method improves the measurement uncertainty, compared with the classical four-step transmission method. Furthermore, this method can be effectively applied to measure high quality polished samples and extended to measure large optical materials at oblique incidence (such as large optics in Synchrotron Radiation Facility, Inertial Confinement Fusion, and giant telescopes).
-
-
图 1 样品SUT非均匀性测量以及K、L、M、N四个表面的绝对面形测量(TF透射标准平面、RF标准平面、SUT测试样品)的六步测量步骤
Figure 1. Six-step procedure for inhomogeneity evaluations, as well as absolute planarity measurements of the four surfaces K, L, M, N. (TF: Transmission flat, TF: Standard flat, SUT: Sample under test)
图 2 原始实验表面K、L、M、N的面形误差和由于样板不均匀而产生的面形误差
Figure 2. Example figure errors of original experimental surfaces K, L, M, N and figure error due to inhomogeneity of the sample plate
图 3 六步翻转试验的示例模拟实验结果(每次测量的测量噪声为0.1 nm RMS)
Figure 3. Example experimental results of simulation with six-step flipping test(the measurement noise of each measurement is 0.1 nm RMS)
图 4 (a) 通过迭代算法计算得到的K、L、M、N表面的面形误差和由于样板不均匀而产生的面形误差；(b) 各个表面对应的测量残差图
Figure 4. (a) Retrieved figure errors of surfaces K, L, M, N and figure error due to inhomogeneity of the sample plate by the iterative algorithm; (b) The associated measurement error maps with respect to the original surfaces
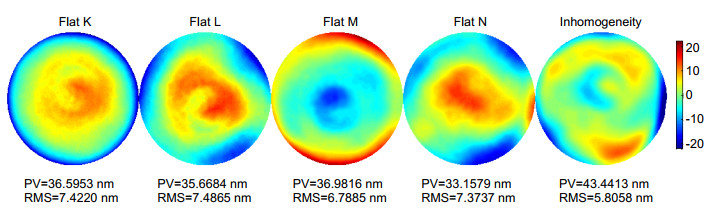
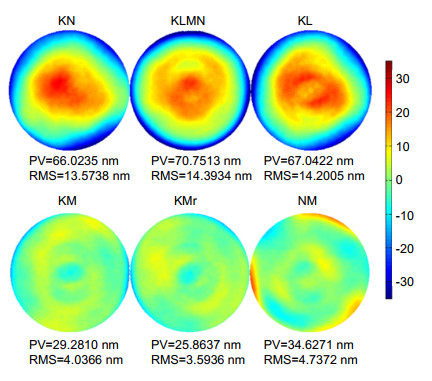
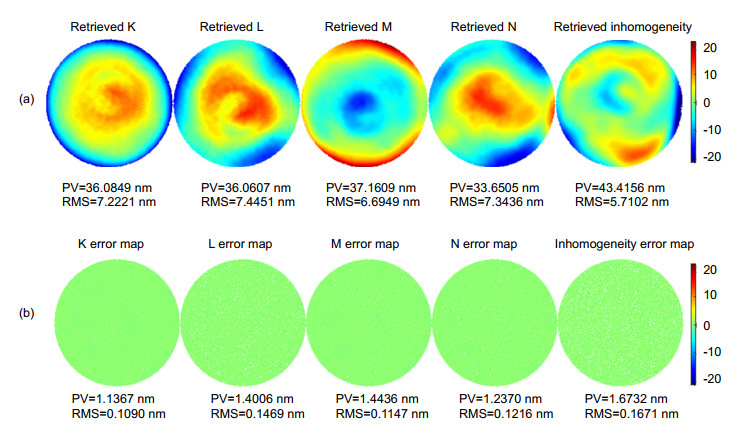
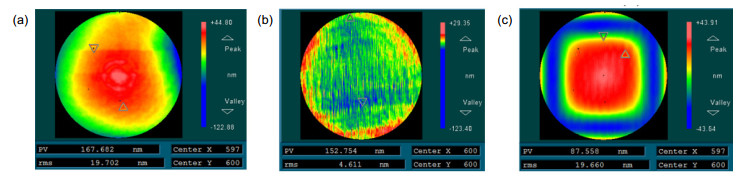
图 5 本文所提出改进的六步翻转法，计算出表面L绝对面形(RMS=18.61 nm) (a)；表面M绝对面形(RMS=4.87 nm) (b)和折射率不均匀性(RMS=19.47 nm) (c)引起的面形误差
Figure 5. Retrieved figure errors of (a) surface L (RMS= 18.61 nm), (b) surface M (RMS=4.87 nm), and (c) figure error due to inhomogeneity (RMS=19.47 nm) of the PPP by the proposed iterative algorithm
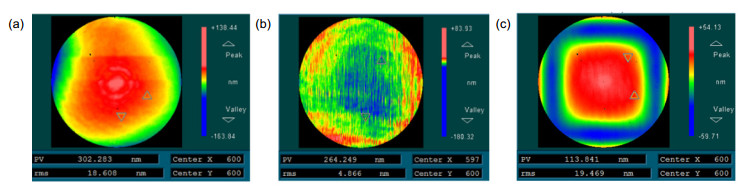
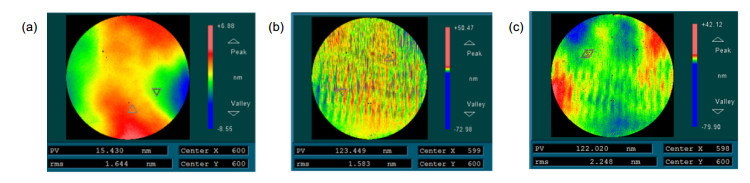
图 6 通过傅里叶变换相移干涉法(FTPSI)，计算得到(a)表面L绝对面形(RMS=19.71 nm)；(b) 表面M绝对面形(RMS=4.62 nm)和(c) 折射率不均匀性(RMS=19.67 nm)而引起的面形误差
Figure 6. Retrieved figure errors of (a) surface L (RMS=19.71 nm), (b) surface M (RMS=4.62 nm), and (c) figure error due to inhomogeneity (RMS=19.67 nm) of the PPP by the proposed iterative algorithm
-
参考文献
[1] Adachi I, Asuda M T, Nishiyama S. A testing of optical materials by the Twyman type interferometer[J]. Atti Fond Giorgio Ronchi Contrib 1st Nax Ottica, 1961, 16: 666-674.
[2] Guo Y W. A surface shape test method for a thin flat mirror[J]. Optik, 2018, 152: 116-126. doi: 10.1016/j.ijleo.2017.09.049
[3] Ai C, Wyant J C. Measurement of the inhomogeneity of a window[J]. Opt Eng, 1991, 30(9): 1399. doi: 10.1117/12.55928
[4] Roberts F E, Langenbeck P. Homogeneity evaluation of very large disks[J]. Appl Opt, 1969, 8(11): 2311-2314. doi: 10.1364/AO.8.002311
[5] Schwider J, Burow R, Elssner K E, et al. Homogeneity testing by phase sampling interferometry[J]. Appl Opt, 1985, 24(18): 3059-3061. doi: 10.1364/AO.24.003059
[6] 李强, 刘昂, 高波, 等. 光学材料光学不均匀性绝对测量误差分析[J]. 应用光学, 2013, 34(3): 463-468. doi: 10.5768/JAO201334.0303002
Li Q, Liu A, Gao B, et al. Error analysis of absolute test method of inhomogeneity of optical materials[J]. J Appl Opt, 2013, 34(3): 463-468. doi: 10.5768/JAO201334.0303002
[7] 张瑞, 陈磊, 朱文华, 等. 点源异位同步移相法检测平行平晶的光学均匀性[J]. 光子学报, 2018, 47(1): 0112002. doi: 10.3788/gzxb20184701.0112002
Zhang R, Chen L, Zhu W H, et al. Measuring optical homogeneity of parallel plates based on simultaneous phase-shifting by lateral displacement of point sources[J]. Acta Photonica Sin, 2018, 47(1): 0112002. doi: 10.3788/gzxb20184701.0112002
[8] 高波, 李强, 刘昂, 等. 基于短相干技术的光学平板折射率测量方法[J]. 中国激光, 2019, 46(8): 0804004. https://www.cnki.com.cn/Article/CJFDTOTAL-JJZZ201908022.htm
Gao B, Li Q, Liu A, et al. Measuring refractive index of transparent plate by low-coherent interference[J]. Chin J Lasers, 2019, 46(8): 0804004. https://www.cnki.com.cn/Article/CJFDTOTAL-JJZZ201908022.htm
[9] Evans C J, Hocken R J, Estler W T. Self-calibration: reversal, redundancy, error separation, and 'absolute testing'[J]. CIRP Ann, 1996, 45(2): 617-634. doi: 10.1016/S0007-8506(07)60515-0
[10] 侯溪, 张帅, 胡小川, 等. 超高精度面形干涉检测技术进展[J]. 光电工程, 2020, 47(8): 200209. doi: 10.12086/oee.2020.200209
Hou X, Zhang S, Hu X C, et al. The research progress of surface interferometric measurement with higher accuracy[J]. Opto-Electron Eng, 2020, 47(8): 200209. doi: 10.12086/oee.2020.200209
[11] Park J, Chen L F, Wang Q D, et al. Modified Roberts-Langenbeck test for measuring thickness and refractive index variation of silicon wafers[J]. Opt Express, 2012, 20(18): 20078-20089. doi: 10.1364/OE.20.020078
[12] Deck L L. Multiple-surface phase-shifting interferometry[J]. Proc SPIE, 2001, 4451: 424-431. doi: 10.1117/12.453640
[13] Mantel K, Schwider J. Interferometric homogeneity test using adaptive frequency comb illumination[J]. Appl Opt, 2013, 52(9): 1897-1912. doi: 10.1364/AO.52.001897
[14] 任寰, 马力, 刘旭, 等. 多表面干涉下的光学元件面形检测[J]. 光学精密工程, 2013, 21(5): 1144-1150. doi: 10.3788/OPE.20132105.1144
Ren H, Ma L, Liu X, et al. Optical element test with multiple surface interference[J]. Opt Precision Eng, 2013, 21(5): 1144-1150. doi: 10.3788/OPE.20132105.1144
[15] 徐建程, 石琦凯, 柴立群, 等. 三表面干涉条纹空域傅里叶分析[J]. 中国激光, 2006, 33(9): 1260-1264. doi: 10.3321/j.issn:0258-7025.2006.09.024
Xue J C, Shi Q K, Chai L Q, et al. Spatial fourier fringe analysis with single three-surface interferogram[J]. Chin J Lasers, 2006, 33(9): 1260-1264. doi: 10.3321/j.issn:0258-7025.2006.09.024
[16] Guo R H, Liao Z S, Li J X, et al. Optical homogeneity measurement of parallel plates by wavelength-tuning interferometry using nonuniform fast Fourier transform[J]. Opt Express, 2019, 27(9): 13072-13082. doi: 10.1364/OE.27.013072
[17] 陈贞屹, 赵文川, 张启灿, 等. 基于立体相位测量偏折术的预应力薄镜面形检测[J]. 光电工程, 2020, 47(8): 190435. doi: 10.12086/oee.2020.190435
Chen Z Y, Zhao W C, Zhang Q C, et al. Shape measurement of stressed mirror based on stereoscopic phase measuring deflectometry[J]. Opto-Electron Eng, 2020, 47(8): 190435. doi: 10.12086/oee.2020.190435
[18] Fritz S B. Absolute calibration of an optical flat[J]. Opt Eng, 1984, 23(4): 234379. doi: 10.1117/12.936799
[19] Quan H Y, Hou X, Wu F, et al. Absolute measurement of optical flats based on basic iterative methods[J]. Opt Express, 2015, 23(12): 16305-16319. doi: 10.1364/OE.23.016305
[20] Vannoni M V, Sordini A, Molesini G. Calibration of absolute planarity flats: generalized iterative approach[J]. Opt Eng, 2012, 51(8): 081510. doi: 10.1117/1.OE.51.8.081510
[21] Griesmann U. Three-flat test solutions based on simple mirror symmetry[J]. Appl Opt, 2006, 45(23): 5856-5865. doi: 10.1364/AO.45.005856
[22] 李宇琛, 韩森, 吴泉英, 等. 基于奇偶函数法的绝对检测实验研究[J]. 应用光学, 2017, 38(3): 469-475. doi: 10.5768/JAO201738.0303007
Li Y C, Han S, Wu Q Y, et al. Absolute test of flats based on even or odd functions[J]. J Appl Opt, 2017, 38(3): 469-475. doi: 10.5768/JAO201738.0303007
[23] Huan H Y, Xi H, Wu F. Evaluating surface repeatability for interferometric measurement: a comparative study[J]. Proc SPIE, 2016, 9684: 96842M. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=2564657
[24] Hou X, Yang P, Wu F, et al. Comparative experimental study on absolute measurement of spherical surface with two-sphere method[J]. Opt Lasers Eng, 2011, 49(7): 833-840. doi: 10.1016/j.optlaseng.2011.03.002
-
访问统计
下载:
点击扫一扫
图(8)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
