-
摘要
针对龙门架机器人末端执行机构只具有三个正交方向上的平移自由度的工作特性,参照传统手眼标定的两步法,设计了一种直接对3D视觉传感器的点云坐标系与机器人执行机构的工具坐标系进行手眼标定的方法。该方法只需要操作机器人进行两次正交的平移运动,采集三组标定板图片和对应点云数据,并通过执行机构的工具中心点(TCP)接触式测量出标定板上标志点的基坐标值,即可解算出手眼关系的旋转矩阵和平移矢量。该方法操作简单,标定板易于制作且成本低。采用XINJE龙门架机器人与3D视觉传感器搭建实验平台,实验结果表明,该方法具有良好的稳定性,适合现场标定,标定精度达到±0.2 mm。

Abstract
Aiming at the working characteristics of the end-effector of the gantry robot with only three translational degrees of freedom, a method for calibrating the point cloud coordinate system of the 3D vision sensor and the tool coordinate system of the robot actuator is designed, on the basis of the traditional two-step method of hand-eye calibration. In this method, only three calibration target pictures and three sets of point clouds are collected by two orthogonal translation movements of the robot, the rotation matrix and translation vector of the hand-eye relationship can be calibrated by measuring the base coordinates of mark points on the target through the TCP contact of the actuator. The method is simple to operate, and the calibration target is easy to make with low cost. The XINJE gantry robot and 3D vision sensor of structured light was used to build an experimental platform for experiments. The results show that the method has good stability and is suitable for field calibration, with calibration accuracy within ±0.2 mm
-
Key words:
- vision guidance /
- hand-eye calibration /
- gantry robot /
- 3D vision sensor /
- point cloud
-
Overview

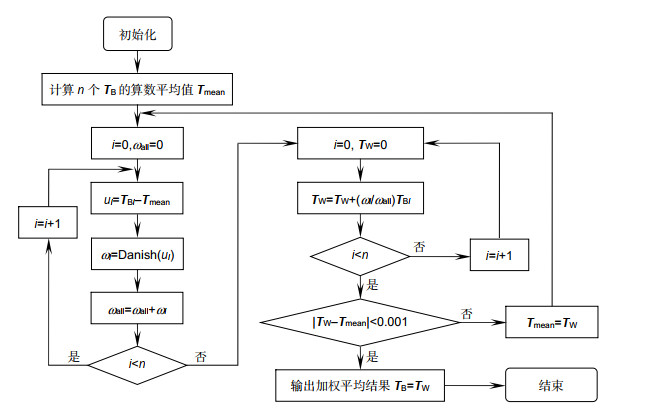
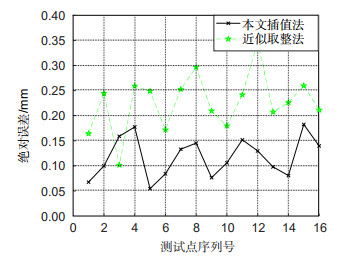
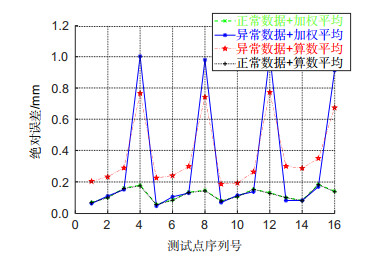
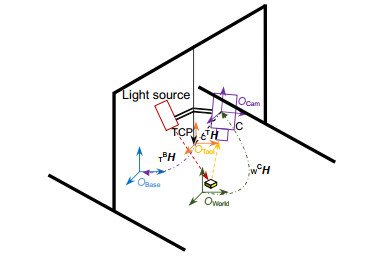
Overview: The gantry robot's actuator only has three translational degrees of freedom, which makes it impossible to operate the linkage between the camera and the actuator to rotate, so that the calibration information of different shooting angles cannot be obtained in the hand-eye calibration. In this paper, we improve the two-step calibration method of Tsai and design a new solution. In the first step of the proposed method, the robot actuator is operated for two orthogonal translational motions, and the matrix of hand-eye relationship can be calculated, according to the robot motion parameters and the data of the visual sensor. In the second step, the actuator is operated for contact measurement, and the base coordinates of at least one mark point on the calibration plate are measured by the TCP of the robot, which can calculate the translation vector of hand-eye relationship combined with the rotation matrix got by the first step, thus acquiring the complete hand-eye matrix. In this paper, a 3D structured light measuring instrument is used as the vision sensor. We introduce in detail the method of obtaining calibration data from the 3D vision sensor and use an interpolation method based on area ratio to calculate the exact correspondence between 2D image pixels and 3D point cloud coordinates. An effective optimization method is adopted to suppress the possible interference of industrial calibration. This method only needs to use the printed 2D calibration plate, which reduces the cost of calibration. At the same time, we give the image of the calibration plate. XINJE gantry robot and structured light 3D vision sensor were used to build the experimental platform for the real experiment. We sampled 16 test points and compared the absolute errors of the test points with the interpolation method or the weighted optimization method, and the experimental results show that the interpolation method can improve the precision, and the weighted optimization method can improve the anti-interference performance. When we use both optimization methods, the average absolute error of 16 test points is 0.119 mm and the maximum absolute error is 0.174 mm, indicating that this method meets the welding process requirements of industrial robots. To sum up, the method in this paper has the advantages of simple teaching, high precision, and applicability for field calibration. It provides useful ideas for hand-eye calibration of robots with limited degree of freedom and calibration of robots with 3D vision sensors.
-

-
表 1 不同干扰量下的标定结果
Table 1. Calibration results under different interference amounts
干扰点位置 无 4 3 4 1 3 4 1 2 3 4 干扰量/mm 无 Y+1 X-1 Y+1 X+0.5Y+0.5 Y-1 X+1 X+0.5Y+0.5 X+0.5Z-1 Y-1 X+1 CTR标定结果 $ \left[ \begin{array}{l} 0.99989{\rm{ }}\;0.01180{\rm{ }}\; - 0.00902\\ 0.01012{\rm{ }} - 0.99992\;{\rm{ }} - 0.00769\\ - 0.00911{\rm{ }}0.00760{\rm{ }} - 0.99993 \end{array} \right]$
CTT标定结果 $ \left[ {\begin{array}{*{20}{l}} {{\rm{114}}.{\rm{1502}}}\\ {{\rm{ - 218}}.{\rm{4688}}}\\ {{\rm{54}}.{\rm{2915}}} \end{array}} \right]$
$\left[ {\begin{array}{*{20}{l}} {{\rm{114}}.{\rm{1451}}}\\ {{\rm{ - 218}}.{\rm{4568}}}\\ {{\rm{54}}.{\rm{3208}}} \end{array}} \right] $
$ \left[ {\begin{array}{*{20}{l}} {{\rm{114}}.{\rm{1268}}}\\ {{\rm{ - 218}}.{\rm{4495}}}\\ {{\rm{54}}.{\rm{2906}}} \end{array}} \right]$
$\left[ {\begin{array}{*{20}{l}} {{\rm{114}}.{\rm{1495}}}\\ {{\rm{ - 218}}.{\rm{4418}}}\\ {{\rm{54}}.{\rm{2698}}}\end{array}} \right] $
$\left[ {\begin{array}{*{20}{l}} {{\rm{114}}.{\rm{6041}}}\\ {{\rm{ - 217}}.{\rm{9572}}}\\ {{\rm{54}}.{\rm{3115}}} \end{array}} \right] $
CTT与正常数据标定结果的误差 $\left[ {{\rm{000}}} \right] $
$\left[ \begin{array}{l} {\rm{0}}{\rm{.0051}}\\ {\rm{ - 0}}{\rm{.0120}}\\ {\rm{ - 0}}{\rm{.0293}} \end{array} \right] $
$ \left[ \begin{array}{l} {\rm{0}}{\rm{.0234}}\\ {\rm{ - 0}}{\rm{.0193}}\\ {\rm{0}}{\rm{.0009}} \end{array} \right]$
$ \left[ \begin{array}{l} {\rm{0}}{\rm{.0007}}\\ {\rm{ - 0}}{\rm{.0270}}\\ {\rm{0}}{\rm{.0217}} \end{array} \right]$
$ \left[ \begin{array}{l} {\rm{ - 0}}{\rm{.4539}}\\ {\rm{ - 0}}{\rm{.5116}}\\ {\rm{ - 0}}{\rm{.0200}} \end{array} \right]$
算法运行时间/ms 3 4 2 2 5 -
参考文献
[1] Liu S Y, Wang G R, Zhang H, et al. Design of robot welding seam tracking system with structured light vision[J]. Chin J Mech Eng, 2010, 23(4): 436-443. doi: 10.3901/CJME.2010.04.436
[2] Du Q J, Sun C, Huang X G. Motion control system design of a humanoid robot based on stereo vision[C]//The International Conference on Recent Trends in Materials and Mechanical Engineering, 2011: 178-181.
[3] Tsai R Y, Lenz R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Trans Robot Autom, 1989, 5(3): 345-358. doi: 10.1109/70.34770
[4] Park F C, Martin B J. Robot sensor calibration: solving AX=XB on the Euclidean group[J]. IEEE Trans Robot Autom, 1994, 10(5): 717-721. doi: 10.1109/70.326576
[5] Chen H H. A screw motion approach to uniqueness analysis of head-eye geometry[C]//Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1991: 145-151.
[6] Daniilidis K. Hand-eye calibration using dual quaternions[J]. Int J Robot Res, 1999, 18(3): 286-298. doi: 10.1177/02783649922066213
[7] Malm H, Heyden A. A new approach to hand-eye calibration[C]//Proceedings 15th International Conference on Pattern Recognition, 2000, 1: 525-529.
[8] Zhang H Q. Hand/eye calibration for electronic assembly robots[J]. IEEE Trans Robot Autom, 1998, 14(4): 612-616. doi: 10.1109/70.704231
[9] 叶溯, 叶玉堂, 刘娟秀, 等. 补强片自动贴片系统高精度手眼标定方法[J]. 应用光学, 2015, 36(1): 71-76. https://www.cnki.com.cn/Article/CJFDTOTAL-YYGX201501014.htm
Ye S, Ye Y T, Liu J X, et al. High-precision hand-eye calibration for automatic stiffness bonder[J]. J Appl Opt, 2015, 36(1): 71-76. https://www.cnki.com.cn/Article/CJFDTOTAL-YYGX201501014.htm
[10] 张召瑞, 张旭, 郑泽龙, 等. 融合旋转平移信息的机器人手眼标定方法[J]. 仪器仪表学报, 2015, 36(11): 2443-2450. doi: 10.3969/j.issn.0254-3087.2015.11.006
Zhang Z R, Zhang X, Zheng Z L, et al. Hand-eye calibration method fusing rotational and translational constraint information[J]. Chin J Sci Instrum, 2015, 36(11): 2443-2450. doi: 10.3969/j.issn.0254-3087.2015.11.006
[11] 陈丹, 白军, 石国良. 一种新的四自由度SCARA机器人手眼标定方法[J]. 传感器与微系统, 2018, 37(2): 72-75, 82. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201802020.htm
Chen D, Bai J, Shi G L. A new method of four DOF SCARA robot hand-eye calibration[J]. Transd Microsyst Technol, 2018, 37(2): 72-75, 82. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201802020.htm
[12] 邹劲松, 黄凯锋. 一种新的三维测量机器人手眼标定方法[J]. 计算机测量与控制, 2015, 23(7): 2270-2273. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201507009.htm
Zou J S, Huang K F. A new method of hand-eye calibration for robot measuring system[J]. Comput Meas Control, 2015, 23(7): 2270-2273. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201507009.htm
[13] 杜惠斌, 宋国立, 赵忆文, 等. 利用3D打印标定球的机械臂与RGB-D相机手眼标定方法[J]. 机器人, 2018, 40(6): 835-842. https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR201806008.htm
Du H B, Song G L, Zhao Y W, et al. Hand-eye calibration method for manipulator and RGB-D camera using 3D-printed ball[J]. Robot, 2018, 40(6): 835-842. https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR201806008.htm
[14] 林玉莹, 穆平安. 基于标准球的机器人手眼标定方法改进研究[J]. 软件导刊, 2019, 18(5): 41-43, 48. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201905010.htm
Lin Y Y, Mu P A. An improved hand-eye calibration method for robot based on standard ball[J]. Softw Guide, 2019, 18(5): 41-43, 48. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201905010.htm
[15] 郑健, 张轲, 罗志锋, 等. 基于空间直线约束的焊接机器人手眼标定[J]. 焊接学报, 2018, 39(8): 108-113. https://www.cnki.com.cn/Article/CJFDTOTAL-HJXB201808024.htm
Zheng J, Zhang K, Luo Z F, et al. Hand-eye calibration of welding robot based on the constraint of spatial line[J]. Trans China Weld Inst, 2018, 39(8): 108-113. https://www.cnki.com.cn/Article/CJFDTOTAL-HJXB201808024.htm
[16] 李明峰, 陆海芳, 赵湘玉. 对偶四元数法在稳健点云配准中的应用[J]. 测绘通报, 2019(9): 22-26.
Li M F, Lu H F, Zhao X Y. Application of dual quaternion method in robust point cloud registration[J]. Bull Surv Mapp, 2019(9): 22-26.
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: