E-mail Alert
RSS
Research on sparsity of frequency modulated signal in fractional Fourier transform domain
-
摘要
调频信号广泛应用于声纳、雷达、激光和新兴光学交叉研究领域，其紧致性(稀疏性)是调频信号采样、去噪、压缩等研究中面临的共性基础问题。本文致力于研究调频信号在分数傅里叶变换域的稀疏性，提出了一种最大奇异值法来估计调频信号的紧致分数傅里叶变换域。该方法利用调频信号幅度谱的最大奇异值来度量其紧致域，并应用鲸鱼优化算法来搜寻紧致域，有效改善了现有方法的不足。与MNM和MACF方法相比，本文方法给出了调频信号在分数傅里叶变换域更加稀疏的表征，具有更少的重要振幅数。最后，给出了该方法在调频信号滤波中的初步应用。
Abstract
Frequency modulated (FM) signal is extensively applied in sonar, radar, laser and emerging optical cross-research, its sparsity is a common basic issue for the sampling, denoising and compression of FM signal. This paper mainly studies the sparsity of FM signal in the fractional Fourier transform (FRFT) domain, and a maximum singular value method (MSVM) is proposed to estimate the compact FRFT domain of FM signal. This method uses the maximum singular value of amplitude spectrum of FM signal to measure the compact domain, and WOA is used to search the compact domain, which effectively improves the shortcomings of the existing methods. Compared with MNM and MACF, this method gives a sparser representation of FM signal in the FRFT domain, which has less number of significant amplitudes. Finally, the primary application of this method in the FM signal filtering is given.
-
Overview
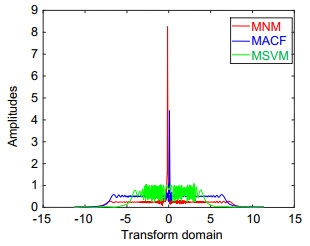
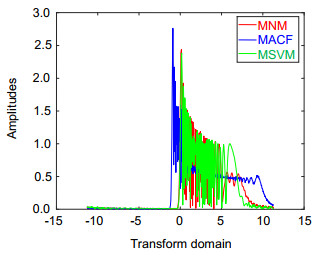
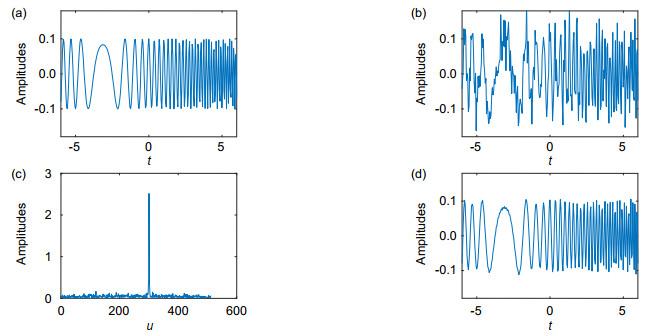
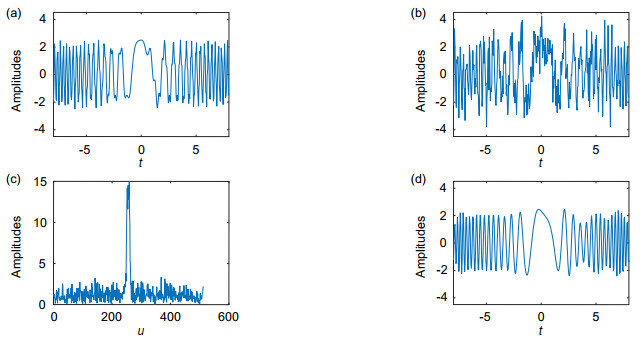
Overview:Frequency modulated (FM) signal is a typical non-stationary signal, which is widely used in sonar, radar, laser and other traditional fields. In recent years, it has been applied to the new field of optical intersection. Its sparsity is a common basic problem in the FM signal processing. Fractional Fourier transform (FRFT) uses the orthogonal chirp function to decompose signal and is unaffected by the cross terms, and thus is very suitable for analyzing and processing FM signal. Due to the advantages of FRFT in the FM signal processing, FRFT is also applied to explore the sparsity of FM signal. FRFT can represent the signal from any fractional domain between the time domain and the frequency domain. Therefore, there is at least one optimal fractional Fourier transform domain, which makes the FM signal have best sparsity in this optimal domain. This optimal domain is named as compact fractional Fourier transform domain. In the process of finding the compact fractional Fourier transform domain, the measurement and searching of optimal domain are two key points. On the basis of the above advantages, this paper is devoted to studying the sparsity of FM signal in fractional Fourier transform domain, and a sparse representation method of FM signal based on FRFT and singular value decomposition is proposed, called as maximum singular value method (MSVM). On the one hand, the maximum singular value of amplitude spectrum in FRFT domain is taken as the measurement of optimal domain, which makes MSVM has better sparsity and noise robustness. Since singular value decomposition can map high-dimensional data space to a relatively low-dimensional data space, and thus singular value decomposition effectively reduces the dimension of data processing. The larger the singular value of the amplitude spectrum, the better the sparsity of the FM signal in the corresponding fractional Fourier transform domain. Moreover, the singular value decomposition is a kind of decomposition method which can be applied to any matrix, and has a wider applicability. On the other hand, whale optimization algorithm is used to search optimal domain. Whale optimization algorithm is a new heuristic bionic algorithm, which imitates the behavior of humpback whales in searching, seizing and foraging. Because whale optimization algorithm is flexible and has no gradient limitation. It can effectively avoid falling into the local optimum, and effectively improve the shortcomings of the coarse-to-fine grid search and traversal search methods, and is not influenced by the search step size. The quantitative index is the number of significant amplitudes (NSA), the less NSA means better sparsity. By the simulation, compared with MACF and MNM, MSVM has less NSA in the compact fractional Fourier transform domain. It is concluded that the MSVM can give better sparsity of FM signal in the compact fractional Fourier transform domain. In the end, this paper presents the application of MSVM in the filter of linear FM signal, which basically achieves the filtering of noise and the maintenance of signal behavior.
-
-
图 1 双分量线性调频信号在时域和紧致分数傅里叶变换域中的表征
Figure 1. Representation of bi-component LFM signal in the time domain and compact FRFT domain
图 2 三种方法给出的线性调频信号在紧致分数傅里叶变换域中的表征
Figure 2. Representation of bi-component LFM signal in the compact FRFT domain for three methods
图 3 三种方法得到的二次调频信号在紧致分数傅里叶变换域中的表征
Figure 3. Representation of QFM signal in the compact FRFT domain for three methods
图 4 单分量线性调频信号的滤波。(a)原始信号；(b)加噪信号(SNR=5 dB)；(c)加噪信号在紧致分数傅里叶变换域的幅度谱；(d)滤波之后的信号
Figure 4. Filter of single component LFM signal. (a) Original signal; (b) Noisy signal (SNR=5 dB); (c) Amplitude spectrum of the noisy signal in the compact FRFT domain; (d) Filtered signal
图 5 双分量线性调频信号的滤波。(a)原始信号；(b)加噪信号(SNR=5 dB)；(c)加噪信号在紧致分数傅里叶变换域的幅度谱；(d)滤波之后的信号
Figure 5. Filter of bi-component LFM signal. (a) Original signal; (b) Noisy signal (SNR=5 dB); (c) Amplitude spectrum of the noisy signal in the compact FRFT domain; (d) Filtered signal
表 1 线性调频信号的估计结果比较
Table 1. Comparison of estimation results for LFM signal
衡量指标 α0 NSA {A0, k0, f0}, {A1, k1, f1} MNM MACF MSVM MNM MACF MSVM {0.1, 0.8, 5}, {0, 0, 0} 2.2455 2.2455 2.2454 3 3 3 {0.2, 0, 0.8}, {0.3, 0.7, 0} 2.1816 1.5708 1.9041 223 324 138 {5, 0.1, -0.3}, {8, 0.87, 0.3} 2.2777 2.2872 2.0055 217 239 140 {2, 0.1, 0.2}, {1, 0.4, -0.2} 1.6704 1.67 1.7714 100 100 70 {2, 0.5, -1/9}, {0.5, 9/5, 5/6} 2.0342 2.0345 2.0560 73 74 34 
下载: 导出CSV
表 2 二次调频信号的估计结果比较
Table 2. Comparison of estimation results for QFM signal
衡量指标
{A, σ, k, f}α0 NSA MNM MACF MSVM MNM MACF MSVM {0.5, 0.04, 0.4, 0.06} 2.0415 2.3510 1.9279 122 218 116 {4, 0.2, 0.03, 0.01} 2.0722 0.9106 1.5729 353 368 309 {0.2, 05, 0, 0.02} 2.2627 0.9416 1.5705 332 339 290 {2.3, 0.07, 0.05, 0} 2.2932 2.2777 1.5707 241 241 210 {3, 0.052, 0, 1} 1.9633 0.7858 1.6653 197 260 166
下载: 导出CSV
-
参考文献
[1] Pang C S, Shan T, Ran T, et al. Detection of high-speed and accelerated target based on the linear frequency modulation radar[J]. IET Radar, Sonar & Navigation, 2014, 8(1): 37-47. http://ieeexplore.ieee.org/document/6702408
[2] Xin H C, Bai X, Song Y E, et al. ISAR imaging of target with complex motion associated with the fractional Fourier transform[J]. Digital Signal Processing, 2018, 83: 332-345. doi: 10.1016/j.dsp.2018.09.012
[3] Liu N, Tao R, Wang R, et al. Signal reconstruction from recurrent samples in fractional Fourier domain and its application in multichannel SAR[J]. Signal Processing, 2017, 131: 288-299. doi: 10.1016/j.sigpro.2016.08.008
[4] Chen W J, Zhu D, Xie C X, et al. Photonics-based reconfigurable multi-band linearly frequency-modulated signal generation[J]. Optics Express, 2018, 26(25): 32491-32499. doi: 10.1364/OE.26.032491
[5] Zhou P, Zhang F Z, Pan S L. Generation of linear frequency-modulated waveforms by a frequency-sweeping optoelectronic oscillator[J]. Journal of Lightwave Technology, 2018, 36(18): 3927-3934. doi: 10.1109/JLT.2018.2854713
[6] Li S P, Xue M, Qing T, et al. Ultrafast and ultrahigh-resolution optical vector analysis using linearly frequency-modulated waveform and dechirp processing[J]. Optics Letters, 2019, 44(13): 3322-3325. doi: 10.1364/OL.44.003322
[7] Lu M F, Zhang F, Tao R, et al. Parameter estimation of optical fringes with quadratic phase using the fractional Fourier transform[J]. Optics and Lasers in Engineering, 2015, 74: 1-16. http://www.sciencedirect.com/science/article/pii/S0143816615001074
[8] Wu J M, Lu M F, Tao R, et al. Improved FRFT-based method for estimating the physical parameters from Newton's rings[J]. Optics and Lasers in Engineering, 2017, 91: 178-186. doi: 10.1016/j.optlaseng.2016.11.021
[9] Guo Z, Lu M F, Wu J M, et al. Fast FRFT-based method for estimating physical parameters from Newton's rings[J]. Applied Optics, 2019, 58(14): 3926-3931. doi: 10.1364/AO.58.003926
[10] An P, Bai F Z, Liu Z, et al. Measurement to radius of Newton's ring fringes using polar coordinate transform[J]. Journal of the European Optical Society-Rapid Publications, 2016, 12(1): 17. doi: 10.1186/s41476-016-0019-3
[11] 马金铭, 苗红霞, 苏新华, 等.分数傅里叶变换理论及其应用研究进展[J].光电工程, 2018, 45(6): 170747. doi: 10.12086/oee.2018.170747
Ma J M, Miao H X, Su X H, et al. Research progress in theories and applications of the fractional Fourier transform[J]. Opto-Electronic Engineering, 2018, 45(6): 170747. doi: 10.12086/oee.2018.170747
[12] 宋维斌, 张圣儒, 邓忆秋, 等.分数傅里叶变换域稀疏带限信号的模拟信息转换[J].光电工程, 2018, 45(6): 170740. doi: 10.12086/oee.2018.170740
Song W B, Zhang S R, Deng Y Q, et al. Analog to information conversion for sparse signals band-limited in fractional Fourier transform domain[J]. Opto-Electronic Engineering, 2018, 45(6): 170740. doi: 10.12086/oee.2018.170740
[13] 于晓涵, 陈小龙, 陈宝欣, 等.快速高分辨稀疏FRFT雷达机动目标检测方法[J].光电工程, 2018, 45(6): 170702. doi: 10.12086/oee.2018.170702
Yu X H, Chen X L, Chen B X, et al. Radar maneuvering target detection method based on fast and high resolution sparse fractional Fourier transform[J]. Opto-Electronic Engineering, 2018, 45(6): 170702. doi: 10.12086/oee.2018.170702
[14] Sejdić E, Djurović I, Stanković L. Fractional Fourier transform as a signal processing tool: An overview of recent developments[J]. Signal Processing, 2011, 91(6): 1351-1369. doi: 10.1016/j.sigpro.2010.10.008
[15] 仇兆炀, 陈蓉, 汪一鸣.基于FRFT的线性调频信号欠采样快速检测方法[J].电子学报, 2012, 40(11): 2165-2170. http://www.cnki.com.cn/Article/CJFDTotal-DZXU201211004.htm
Qiu Z Y, Chen R, Wang Y M. Fast detection of LFM signal based on FRFT and sub-nyquist sampling[J]. Acta Electronica Sinica, 2012, 40(11): 2165-2170. http://www.cnki.com.cn/Article/CJFDTotal-DZXU201211004.htm
[16] 许述文, 水鹏朗, 杨晓超.基于FRFT的非线性调频信号双特征检测方法[J].中国科学:信息科学, 2011, 41(10): 1200-1209. http://www.cnki.com.cn/Article/CJFDTotal-PZKX201110005.htm
Xu S W, Shui P L, Yang X C. Double-characters detection of nonlinear frequency modulated signals based on FRFT[J]. Science China: Information Sciences, 2011, 41(10): 1200-1209. http://www.cnki.com.cn/Article/CJFDTotal-PZKX201110005.htm
[17] 曲强, 金明录.基于自适应分数阶傅里叶变换的线性调频信号检测及参数估计[J].电子与信息学报, 2009, 31(12): 2937-2940. http://www.cnki.com.cn/Article/CJFDTotal-DZYX200912030.htm
Qu Q, Jin M L. Adaptive fractional Fourier transform based chirp signal detection and parameter estimation[J]. Journal of Electronics & Information Technology, 2009, 31(12): 2937-2940. http://www.cnki.com.cn/Article/CJFDTotal-DZYX200912030.htm
[18] Qi L, Tao R, Zhou S Y, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2004, 47(2): 184–198. doi: 10.1360/02yf0456
[19] Qu Q, Jin M L, Kim J M. FRFT based parameter estimation of the quadratic FM signal[J]. Chinese Journal of Electronics, 2010, 19(3): 463-467. http://www.cqvip.com/QK/86774X/201003/37118355.html
[20] Song J, Wang Y X, Liu Y F. Iterative interpolation for parameter estimation of LFM signal based on fractional Fourier transform[J]. Circuits, Systems, and Signal Processing, 2013, 32(3): 1489-1499. doi: 10.1007/s00034-012-9517-8
[21] 张树银, 郭英, 霍文俊, 等. LFM信号参数估计的FRFT-HOC方法[J].信号处理, 2013, 29(2): 165-170. http://www.cqvip.com/QK/92416X/20132/44971133.html
Zhang S Y, Guo Y, Huo W J, et al. FRFT-HOC based method of LFM parameter estimation[J]. Journal of Signal Processing, 2013, 29(2): 165-170. http://www.cqvip.com/QK/92416X/20132/44971133.html
[22] 翟木易, 邢丽坤, 李昕, 等.分数阶傅里叶变换在线性调频信号滤波中的应用[J].舰船电子工程, 2017, 37(12): 39-41, 45. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&filename=JCGC201712010
Zhai M Y, Xing L K, Li X, et al. Application of FRFT in LFM signal filtering[J]. Ship Electronic Engineering, 2017, 37(12): 39-41, 45. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&filename=JCGC201712010
[23] 刘建成, 刘忠, 王雪松, 等.高斯白噪声背景下的LFM信号的分数阶Fourier域信噪比分析[J].电子与信息学报, 2007, 29(10): 2337-2340. http://d.wanfangdata.com.cn/Periodical/dzkxxk200710013
Liu J C, Liu Z, Wang X S, et al. SNR analysis of LFM signal with Gaussian white noise in fractional Fourier transform domain[J]. Journal of Electronics & Information Technology, 2007, 29(10): 2337-2340. http://d.wanfangdata.com.cn/Periodical/dzkxxk200710013
[24] 金燕, 黄振, 陆建华.基于FRFT的线性调频多径信号分离算法[J].清华大学学报(自然科学版), 2008, 48(10): 1617-1620. http://www.cnki.com.cn/Article/CJFDTotal-QHXW200810023.htm
Jin Y, Huang Z, Lu J H. Separation of multi-path LFM signals based on fractional Fourier transform[J]. Journal of Tsinghua University (Science & Technology), 2008, 48(10): 1617-1620. http://www.cnki.com.cn/Article/CJFDTotal-QHXW200810023.htm
[25] Cowell D M J, Freear S. Separation of overlapping linear frequency modulated (LFM) signals using the fractional Fourier transform[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(10): 2324-2333. doi: 10.1109/TUFFC.2010.1693
[26] Stanković L J, Alieva T, Bastiaans M J. Time–frequency signal analysis based on the windowed fractional Fourier transform[J]. Signal Processing, 2003, 83(11): 2459-2468. doi: 10.1016/S0165-1684(03)00197-X
[27] Vijaya C, Bhat J S. Signal compression using discrete fractional Fourier transform and set partitioning in hierarchical tree[J]. Signal Processing, 2006, 86(8): 1976-1983. doi: 10.1016/j.sigpro.2005.09.025
[28] Serbes A, Durak L. Optimum signal and image recovery by the method of alternating projections in fractional Fourier domains[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(3): 675-689. doi: 10.1016/j.cnsns.2009.05.013
[29] Zheng L Y, Shi D M. Maximum amplitude method for estimating compact fractional Fourier domain[J]. IEEE Signal Processing Letters, 2010, 17(3): 293-296. doi: 10.1109/LSP.2009.2038511
[30] Serbes A. Compact fractional fourier domains[J]. IEEE Signal Processing Letters, 2017, 24(4): 427-431. doi: 10.1109/LSP.2017.2672860
[31] Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008
[32] Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2141-2150. doi: 10.1109/78.536672
[33] Klema V, Laub A. The singular value decomposition: Its computation and some applications[J]. IEEE Transactions on Automatic Control, 1980, 25(2): 164-176. doi: 10.1109/TAC.1980.1102314
-
访问统计
点击扫一扫
图(5)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
