E-mail Alert
RSS
-
摘要
复杂光学曲面的在位测量是当前精密工程领域面临的重要难题。偏折术对光学曲面的测量精度可与干涉仪相比，而且拥有更高的测量效率、稳定性及动态范围，因此具有广阔的应用前景。但是偏折测量本质上是一个标定问题，其测量精度直接取决于几何标定的可靠性。本文结合单点金刚石切削机床设计了原位偏折测量系统，采用机床中自带的气浮转台安装辅助反射镜，在两个姿态下进行光线追迹，通过数值优化计算各元件之间的相对位置，将标定精度提高一个数量级。根据反向投影偏差的统计规律，可有效分离工件的面形偏差与位姿误差。该方法有效利用了工件的名义面形信息，将传统的位置-面形单向映射转变为双向映射，显著提高了在位测量的灵活性与效率。对于复杂的自由曲面，采用子孔径拼接测量方法，对待测的局部区域发展了精准定位技术，有效保证了迭代重构过程的正确收敛。采用离轴抛物镜等光学曲面进行实验验证，所提出的偏折测量方法的精度优于150 nm RMS。
Abstract
The in-situ measurement of complex optical surfaces is a challenging task in precision engineering. The phase measuring deflectometry is a powerful measuring method for complex specular surfaces, and it has higher measuring efficiency, stability and dynamic range compared to interferometry. Consequently it is promising to widespread applications in various fields. Deflectometry is essentially a calibration problem, and the measuring accuracy is directly determined by the quality of geometrical calibration. An in-situ deflectometric measuring system is designed based on the single point diamond turning machine. A self-calibration method is developed to specify the relative positions of the camera and screen. Ray tracing is conducted at two positions of an auxiliary reflecting mirror, which is mounted on an air bearing spindle. The accuracy of the geometrical positions can be improved by an order of magnitude by minimizing the deviations of the traced points with respect to the true correspondences. According to the statistical properties of the deviations in reverse ray tracing, the form errors and the position errors can be separated, and the positioning error of the workpiece can be corrected accordingly. Henceforth, the nominal shape of the fabricated workpiece can be fully utilized, and the conventional one-way position-form mapping can be converted into a two-way mapping problem. As for the complex shapes, the whole surface can be covered by sub-aperture measurement. Precise localization of a local region under test is achieved by multi-position imaging, so that correct convergence of the iterative reconstruction process can be guaranteed. Several typical optical surfaces including an off-axis paraboloid mirror are measured, and the measuring accuracy of the proposed method is proved better than 150 nm RMS.
-
Key words:
- optical manufacturing /
- in-situ measurement /
- deflectometry /
- geometrical calibration /
- ray tracing
-
Overview
Overview: In recent years, the measurement of freeform optical surfaces has attracted intensive attention in precision engineering. Off-line measurement using laboratory instruments causes remounting errors and low manufacturing efficiency, thus high precision in-situ measurement technologies are required. The phase measuring deflectometry is a powerful measuring technique for complex specular surfaces. Its measurement accuracy is comparable with conventional interferometry, but with higher flexibility, stability and dynamic range.
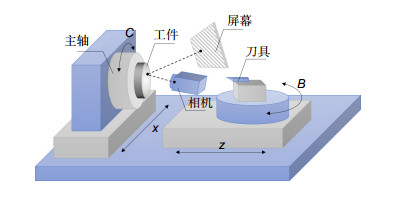
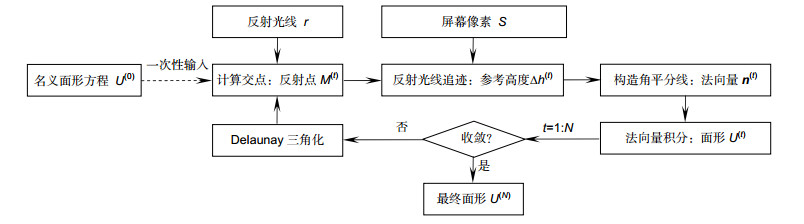
In this paper, an in-situ deflectometric measurement method is developed for the ultra-precision optical manufacturing with single point diamond turning. The measuring accuracy of deflectometry depends on the reliability of the geometrical positions between the camera, screen and workpiece, but it is difficult to conduct precise geometrical calibration using a third-party instrument in the situation of the in-situ measurement.
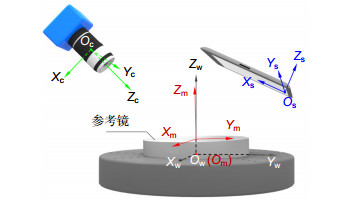
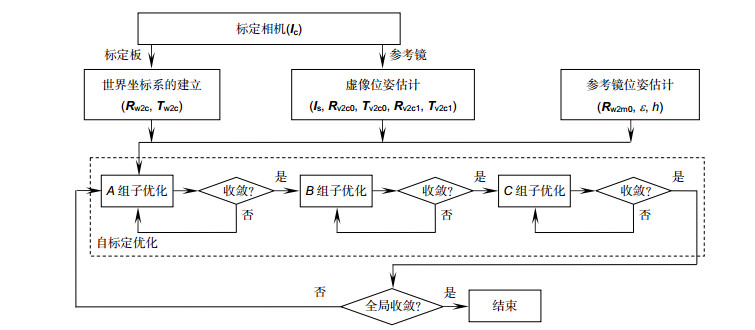
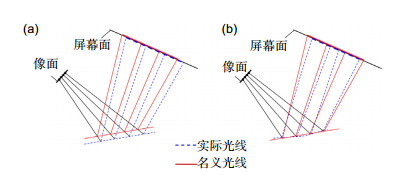
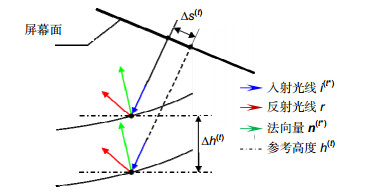
A self-calibration method is proposed to determine the positions of the camera and the screen. A world coordinate system is established by introducing a flat mirror without markers, rather than using high-precision metrological instruments. The rays are re-traced from the screen to the camera, and numerical optimization is performed on the global parameters, including the camera intrinsic parameters, the screen intrinsic parameters and the geometric transformations by minimizing sum of the squared tracing deviations. Only four images need to be captured, hereby reducing the operating complexity and improving the measuring efficiency.
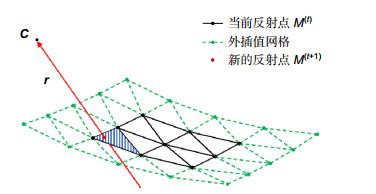
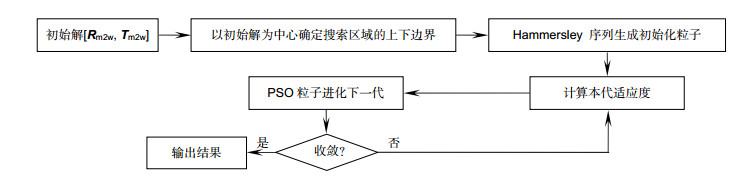
The behaviors of the position error and form error of the measured surface can be discriminated according to the statistical properties of the tracing deviations, and the axial position of the workpiece can be determined accordingly. By fully utilizing the nominal model, the conventional one-way position-form mapping is converted into a two-way mapping problem. Extra detections can in turn be avoided, and the measuring efficiency and range of freeform surfaces can be greatly improved. The whole aperture cannot be measured simultaneously due to the limit of the imaging scope of the camera used. A positioning method is proposed to specify the pose/location of the measured sub-aperture surface. Reverse ray-tracing from the camera to the screen via the measured surface is conducted, and a rotary stage carrying the workpiece is rotated to provide external constraints. The particle swarm optimization method is adopted to solve this problem.
Several typical optical surfaces including an off-axis paraboloid mirror are measured using the proposed deflectometric measuring method. Experimental results demonstrate that the measurement error is within 150 nm. The superior performance prove that this method is of significance for the technical development of ultra-precision intelligent manufacturing.
-
-
图 15 中空离轴抛物面镜的横纵变形条纹。
Figure 15. Deformed fringes of hollow off-axis paraboloid mirror.
图 16 中空离轴抛物面镜测量结果。
Figure 16. Measurement results of hollow off-axis paraboloid mirror.
表 1 工件位姿误差对投影偏差的影响
Table 1. Effect of workpiece position error on tracing deviations
工件姿态 tx ty tz θx θy A ↓ ↑ ↑ ← ↓ B ← ↑ ↑ ↓ → C ↑ ↓ ↑ → ↑ 
下载: 导出CSV
表 2 中空离轴抛物镜的技术指标
Table 2. Specifications of hollow off-axis paraboloid mirror
参数 数值/mm 母焦距 45 口径 30 离轴量 51.96 基高 0
下载: 导出CSV
表 3 各像差项对相对差异RMS的贡献度
Table 3. Contributions of aberration factors to the RMS of relative difference
Zernike项 Z5，
45°初级像散Z6，
0°初级像散Z7，
y轴初级彗差Z8，
x轴初级彗差Z9，
0°三叶差Z10，
45°三叶差Z11，
初级球差Z5~Z11，
共计误差/nm 48.18 127.65 17.84 27.55 6.96 0.41 3.61 139.23
下载: 导出CSV
-
参考文献
[1] Huang L, Idir M, Zuo C, et al. Review of phase measuring deflectometry[J]. Optics and Lasers in Engineering, 2018, 107: 247-257. doi: 10.1016/j.optlaseng.2018.03.026
[2] Niu Z Q, Xu X Y, Zhang X C, et al. Efficient phase retrieval of two-dimensional phase-shifting fringe patterns using geometric constraints of deflectometry[J]. Optics Express, 2019, 27(6): 8195-8207. doi: 10.1364/OE.27.008195
[3] Xu Y J, Gao F, Jiang X Q. Enhancement of measurement accuracy of optical stereo deflectometry based on imaging model analysis[J]. Optics and Lasers in Engineering, 2018, 111: 1-7. doi: 10.1016/j.optlaseng.2018.07.007
[4] Xiao Y L, Su X Y, Chen W J, et al. Three-dimensional shape measurement of aspheric mirrors with fringe reflection photogrammetry[J]. Applied Optics, 2012, 51(4): 457-464. doi: 10.1364/AO.51.000457
[5] Liu Y, Huang S J, Zhang Z H, et al. Full-field 3D shape measurement of discontinuous specular objects by direct phase measuring deflectometry[J]. Scientific Reports, 2017, 7(1): 10293. doi: 10.1038/s41598-017-11014-5
[6] Su P, Wang Y H, Burge J H, et al. Non-null full field X-ray mirror metrology using SCOTS: a reflection deflectometry approach[J]. Optics Express, 2012, 20(11): 12393-12406. doi: 10.1364/OE.20.012393
[7] Zhang X C, Xu X Y, Niu Z Q, et al. Precise positioning in the in-situ deflectometric measurement of optical surfaces[J]. Proceedings of SPIE, 2019, 11102: 111020S.
[8] Graves L R, Choi H, Zhao W C, et al. Model-free deflectometry for freeform optics measurement using an iterative reconstruction technique[J]. Optics Letters, 2018, 43(9): 2110-2113. doi: 10.1364/OL.43.002110
[9] Zhang Z Y. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. doi: 10.1109/34.888718
[10] Xu X Y, Zhang X C, Niu Z Q, et al. Self-calibration of in-situ monoscopic deflectometric measurement in precision optical manufacturing[J]. Optics Express, 2019, 27(5): 7523-7536. doi: 10.1364/OE.27.007523
[11] Li S Q, Xu C, Xie M. A robust O(n) solution to the perspective-n-point problem[J]. IEEE Transactions on Software Engineering, 2012, 34(7): 1444-1450. http://ieeexplore.ieee.org/document/6143946
[12] Xu X Y, Zhang X C, Niu Z Q, et al. Extra-detection-free monoscopic deflectometry for the in situ measurement of freeform specular surfaces[J]. Optics Letters, 2019, 44(17): 4271-4274. doi: 10.1364/OL.44.004271
[13] O'Rourker J. Computational Geometry in C[M]. 2nd ed. Cambridge: Cambridge University Press, 1994.
[14] Kennedy J. Particle swarm optimization[M]//Sam-mut C, Webb G I. Encyclopedia of Machine Learning. Boston, MA: Springer, 2010: 760-766.
[15] Zhang X C, Jiang X Q, Scott P J. A reliable method of minimum zone evaluation of cylindricity and conicity from coordinate measurement data[J]. Precision Engineering, 2011, 35(3): 484-489. doi: 10.1016/j.precisioneng.2011.03.002
[16] Wong T T, Luk W S, Heng P A. Sampling with hammersley and halton points[J]. Journal of Graphics Tools, 1997, 2(2): 9-24. doi: 10.1080/10867651.1997.10487471
[17] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73. doi: 10.1109/4235.985692
[18] Huang R, Su P, Horne T, et al. Optical metrology of a large deformable aspherical mirror using software configurable optical test system[J]. Optical Engineering, 2014, 53(8): 085106. doi: 10.1117/1.OE.53.8.085106
-
访问统计
点击扫一扫
图(16)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
