E-mail Alert
RSS
Shape measurement of stressed mirror based on stereoscopic phase measuring deflectometry
-
摘要
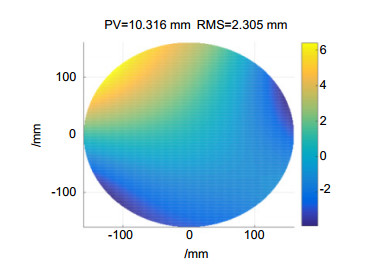
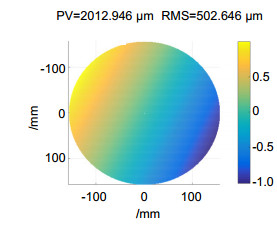
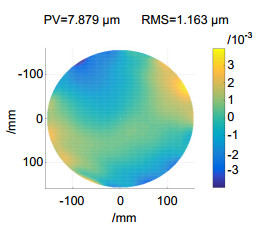
应力抛光技术通过在镜面上施加预定载荷，将包括自由曲面在内的非球面转化为球面进行加工，对加工镜面的形变进行精准检测是实现高精度应力抛光的关键。利用立体相位测量偏折术对预应力薄镜进行镜面面形和形变检测，获得被测镜表面的连续相位分布，结合表面法线唯一性与梯度分布积分，最终得到被测镜的高度分布和面形。模拟了系统误差成分，同时采用旋转平均法对系统误差进行标定去除，保证和提高了测量精度。对一块口径320 mm，球面半径5200 mm的预应力薄镜面形和变形量进行测量，静态测量结果与三坐标机测量结果对比，动态应变测量结果与有限元仿真结果对比，分别一致吻合，表明本文方法具备微米级的测量精度，相比于干涉仪和三坐标机更适用于大面形变化的预应力薄镜检测。
Abstract
Stressed polishing technology transforms aspheric fabrication into spherical fabrication by applying predetermined loads on the surface of the mirror. The key to achieve high precision of stressed polishing is to test the surface deformation with high precision. Stereoscopic phase measuring deflectometry was used to test the surface topography and the deformation of stressed mirror. After obtained unwrapped phase distribution, and combined with normal consistency constraint and gradient integral algorithm, the height distribution was finally obtained. Composition of systematic errors were simulated. Also, the errors were calibrated and removed by N-step averaging method in this system, which improved the measuring precision. In this paper, the surface topography and the deformation of a stressed mirror with a diameter of 320 mm, spherical radius of 5200 mm were measured. The measuring results were consistent with the corresponding result of CMM and finite element simulation, indicating that this proposed method is on the level of micron in terms of accuracy and more suitable for the test of stressed mirror compared with interferometer and CMM.
-
Overview
Overview: Stressed polishing technology was firstly proposed by Jerry E.Nelson in 1980, considered as an effective method of aspheric fabrication. According to the calculated results of elastic mechanics, this method exerts an external force on the mirror to form a deformation which opposite to the desired deformation from spherical surface to off-axis aspheric surface. Under the state of deformation, the mirror is polished into sphere surface. After removing the external force, the required off-axis aspheric surface can be obtained. Because aspheric fabrication is converted to spherical fabrication, tools with large diameter can be used and efficiency is greatly improved.
The key to achieve high precision of stressed polishing is to test the deformation of mirror with high precision. However, the main methods of surface measurement nowadays are interferometer and CMM. If interferometer is used, its dynamic range can only support the detection below micron deformation. If CMM is used, probe may scratch the mirror surface, and the detection tempo is very slow. Furthermore, interferometer and CMM are both expensive and complex equipments.
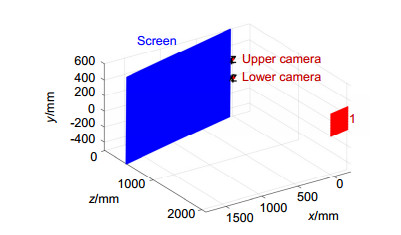
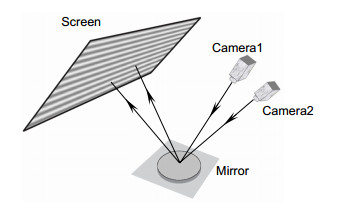
So, aimed at stressed polishing above micron deformation, stereoscopic phase measuring deflectometry was used to test its surface topography and deformation. It is low cost and convenient technique and only screen, camera, and computer were needed when implemented. More importantly, characteristics such as high dynamic range, full-field three-dimensional measurement and excellent performance in medium and high frequency were brought in, which are very suitable for the test of stressed mirror.
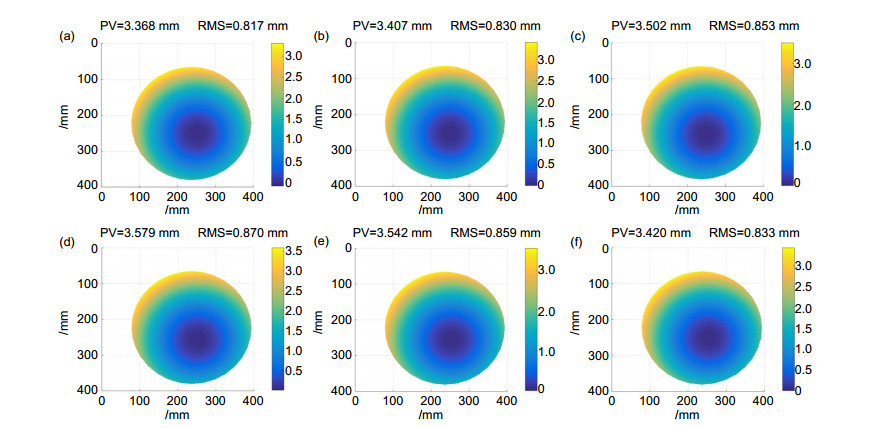
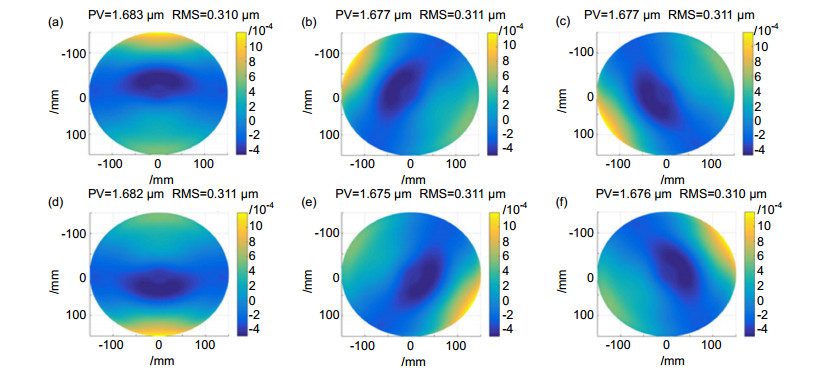
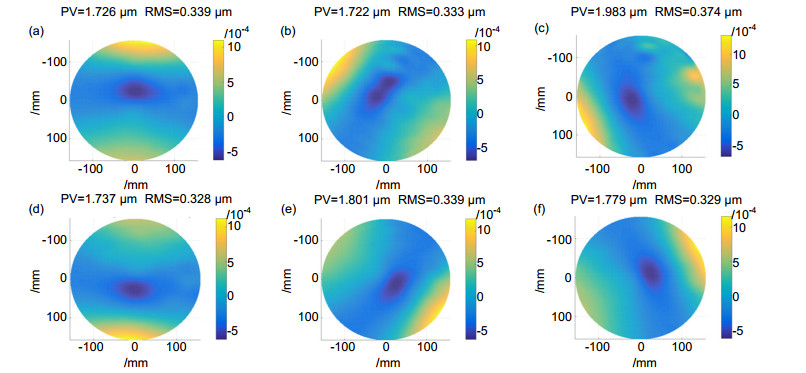
When measuring, firstly calculating the unwrapped phase distribution through CCD cameras, then calculating the height of a specific point on the measured surface using normal consistency constraint, and finally the full-field height distribution was obtained by Southwell gradient integral algorithm. To improve the measuring accuracy, composition of systematic errors were simulated, proved that it mainly includes low-order non-rotational symmetry items. According to simulating results, errors were calibrated and removed by N-step averaging method to get a absolute surface topography.
In this paper, the absolute surface topography and the deformation of a stressed mirror with a diameter of 320 mm, spherical radius of 5200 mm were measured. The measuring results were consistent with the corresponding result of CMM and finite element simulation, indicating that this proposed method is on the level of micron in terms of accuracy and more suitable for the test of stressed mirror compared with interferometer and CMM.
-
-
图 6 系统位置参数标定结果示意图
Figure 6. Schematic diagram of system pose parameter in calibration results
图 8 6个旋转角度下的薄镜表面矢高测量结果。
Figure 8. Heights measuring results of stressed mirrors at 6 rotation angles.
图 12 各个促动电机单独施力的理论影响力函数。
Figure 12. Theoretical influence function of each actuating motor.
图 13 各个促动电机单独施力的变形量测量结果。
Figure 13. Deformation measurement results of each actuating motor.
图 14 电机理论变形与实测变形对比。
Figure 14. Comparison of theoretical deformation and measuring deformation of each actuating motor.
图 15 4种像差的理论目标校正函数。
Figure 15. Theoretical target correction functions of 4 aberrations.
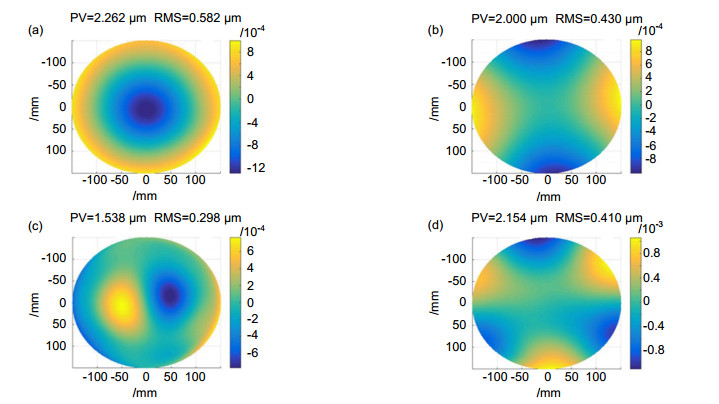
表 1 系统误差的Zernike系数
Table 1. Zernike polynomial coefficient for systematic error
n m Coefficient 0 0 0.1126 1 -1 -1.0312 1 1 1.6773 2 -2 -1.1339 2 0 -0.1915 2 2 0.2706 3 -3 1.6649E-04 3 -1 -1.3508E-04 3 1 9.5479E-04 3 3 0.0026 4 -4 0.2042 4 -2 1.3475E-04 4 0 1.4586E-04 4 2 1.4092E-04 4 4 -4.8459E-04 
下载: 导出CSV
表 2 像差理论值与实际测量值对比
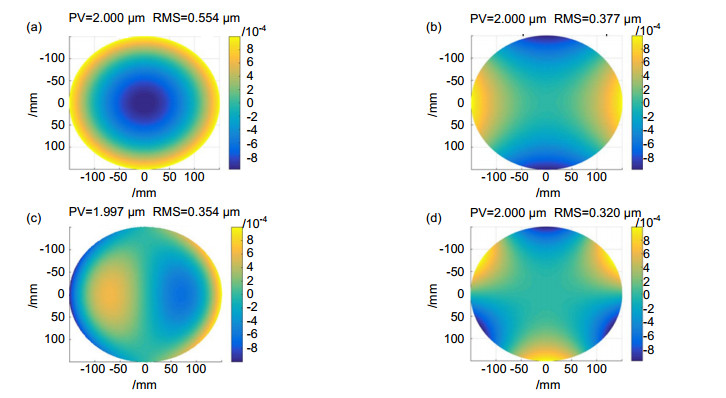
Table 2. Comparison between theoretical aberration and measured aberration
Aberrations Spherical Astigmatism Coma Trefoil PV/μm Correction function 2.000 2.000 1.997 2.000 Measuring results 2.262 2.000 1.538 2.154 RMS/μm Correction function 0.554 0.377 0.354 0.320 Measuring results 0.582 0.430 0.298 0.410
下载: 导出CSV
-
参考文献
[1] Li X N, Jiang Z B, Gong X F, et al. Stressed mirror annular polishing for scale-down TMT primary segments[J]. Proceedings of SPIE, 2016, 9912: 99120A. http://spie.org/Publications/Proceedings/Paper/10.1117/12.2231612?origin_id=x4318
[2] Lubliner J, Nelson J E. Stressed mirror polishing. 1: A technique for producing nonaxisymmetric mirrors[J]. Applied Optics, 1980, 19(14): 2332-2340. doi: 10.1364/AO.19.002332
[3] Nelson J E, Gabor G, Hunt L K, et al. Stressed mirror polishing. 2: fabrication of an off-axis section of a paraboloid[J]. Applied Optics, 1980, 19(14): 2341-2352. doi: 10.1364/AO.19.002341
[4] 李新南, 章海鹰, 崔向群, 等.大口径离轴非球面镜预应力环抛方法研究[J].天文学报, 2012, 53(2): 161-170. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=twxb201202008
Li X N, Zhang H Y, Cui X Q, et al. Study on stressed mirror polishing with continoues polishing machine for large aperture off-axis aspheric mirror[J]. Acta Astronomica Sinica, 2012, 53(2): 161-170. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=twxb201202008
[5] Valente M, Lewis B, Melena N, et al. Advanced surface metrology for meter-class optics[J]. Proceedings of SPIE, 2013, 8838: 88380F. http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2035141
[6] Huang L, Idir M, Zuo C, et al. Review of phase measuring deflectometry[J]. Optics and Lasers in Engineering, 2018, 107: 247-257. doi: 10.1016/j.optlaseng.2018.03.026
[7] 赵文川, 周敏, 刘海涛, 等.离轴非球面的条纹反射检测技术[J].光电工程, 2018, 45(7): 170663. doi: 10.12086/oee.2018.170663
Zhao W C, Zhou M, Liu H T, et al. The off-axis aspheric mirror testing based on the fringe reflection technique[J]. Opto-Electronic Engineering, 2018, 45(7): 170663. doi: 10.12086/oee.2018.170663
[8] 刘方明, 林嘉睿, 孙岩标, 等.一种立体相位偏折测量系统标定方法[J].激光与光电子学进展, 2020, 57(5): 051202. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz202005014
Liu F M, Lin J R, Sun Y B, et al. Calibration method for stereo phase measuring deflectometry system[J]. Laser & Optoelectronics Progress, 2020, 57(5): 051202. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz202005014
[9] Knauer M C, Kaminski J, Häusler G. Phase measuring deflectometry: a new approach to measure specular free-form surfaces[J]. Proceedings of SPIE, 2004, 5457: 366-376. doi: 10.1117/12.545704
[10] 毛心洁.基于双目立体视觉的镜面物体三维轮廓测试技术[D].南京: 南京理工大学, 2017: 48-49.
[11] Southwell W H. Wave-front estimation from wave-front slope measurements[J]. Journal of the Optical Society of America, 1980, 70(8): 998-1006. doi: 10.1364/JOSA.70.000998
[12] 朱勇建, 朱立新, 钟建平, 等.条纹反射法测量三维面形中的积分算法[J].光子学报, 2018, 47(11): 110-119. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gzxb201811015
Zhu Y J, Zhu L X, Zhong J P, et al. Integration algorithm in three-dimensional plane Shape measuring by fringe reflection[J]. Acta Photonica Sinica, 2018, 47(11): 110-119. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gzxb201811015
[13] 易京亚.基于条纹投影和条纹反射的手机壳内外表面质量检测方法[D].成都: 电子科技大学, 2016: 41-43.
Yi J Y. Study on mobile phone shell inside and outside surface quality inspection based on fringe projection and fringe reflection technologies[D]. Chengdu: University of Electronic Science and Technology of China, 2016: 41-43.
[14] Zhao W C, Graves L R, Huang R, et al. Iterative surface construction for blind deflectometry[J]. Proceedings of SPIE, 2016, 9684: 96843X.
[15] 赵文川, 苏显渝, 刘元坤, 等.基于相位偏折术的非球面镜检测方法[J].中国激光, 2010, 37(5): 1338-1341. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201005036
Zhao W C, Su X Y, Liu Y K, et al. Testing an aspheric mirror based on phase measuring deflectometry[J]. Chinese Journal of Lasers, 2010, 37(5): 1338-1341. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201005036
[16] Faber C, Olesch E, Krobot R, et al. Deflectometry challenges interferometry: the competition gets tougher![J]. Proceedings of SPIE, 2012, 8493: 84930R. doi: 10.1117/12.957465
[17] Korsch D, Hunter W R. Reflective optics[M]. Academic Press, 1991.
[18] Su P, Khreishi M, Huang R, et al. Precision aspheric optics testing with SCOTS: a deflectometry approach[]. Proceedings of SPIE, 2013, 8788: 87881E.
[19] Song W H, Wu F, Hou X. Method to test rotationally asymmetric surface deviation with high accuracy[J]. Applied Optics, 2012, 51(22): 5567-5572. doi: 10.1364/AO.51.005567
[20] Song W, Wu F, Hou X, et al. Absolute calibration of a spherical reference surface for a Fizeau interferometer with the shift-rotation method of iterative algorithm[J]. Optical Engineering, 2013, 52(3): 033601. doi: 10.1117/1.OE.52.3.033601
[21] 杨鹏, 伍凡, 侯溪.旋转非对称项面形误差绝对检测的仿真分析[J].光电工程, 2011, 38(1): 93-97, 102. doi: 10.3969/j.issn.1003-501X.2011.01.018
Yang P, Wu F, Hou X. Simulation analysis of absolute measurement for rotationally asymmetric surface error[J]. Opto-Electronic Engineering, 2011, 38(1): 93-97, 102. doi: 10.3969/j.issn.1003-501X.2011.01.018
[22] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. doi: 10.1109/34.888718
[23] Gai Q Y. Optimization of stereo matching in 3D reconstruction based on binocular vision[J]. Journal of Physics: Conference Series, 2018, 960: 012029. doi: 10.1088/1742-6596/960/1/012029
[24] Liu Y K, Su X Y. Camera calibration with planar crossed fringe patterns[J]. Optik, 2012, 123(2): 171-175. doi: 10.1016/j.ijleo.2011.02.026
[25] Zhou T, Chen K, Wei H Y, et al. Improved system calibration for specular surface measurement by using reflections from a plane mirror[J]. Applied Optics, 2016, 55(25): 7018-7028. doi: 10.1364/AO.55.007018
[26] Saldner H O, Huntley J M. Temporal phase unwrapping: application to surface profiling of discontinuous objects[J]. Applied Optics, 1997, 36(13): 2770-2775. doi: 10.1364/AO.36.002770
[27] 赵文静, 陈文静, 苏显渝.几种时间相位展开方法的比较[J].四川大学学报(自然科学版), 2016, 53(1): 110-117. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=scdxxb201601019
Zhao W J, Chen W J, Su X Y. The comparison of several time phase unwrapping methods[J]. Journal of Sichuan University (Natural Science Edition), 2016, 53(1): 110-117. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=scdxxb201601019
-
访问统计
点击扫一扫
图(16)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
