E-mail Alert
RSS
Oblique incidence dynamic phase-shifting interferometer based on inclination angle deflection
-
摘要
为了快速获取不平整度达数微米量级的光学表面面形分布，提出一种基于变倾角移相的斜入射动态干涉仪方案。基于迈克耳逊干涉仪主光路系统，采用2×2点光源阵列，通过精确控制各点光源在干涉腔的入射倾角，引入等间隔移相，结合透镜阵列实现空间分光，在单个CCD上同时采集四幅移相干涉图，实现动态测量。在68°斜入射角下测量了口径35 mm硅片的平整度，均方根(RMS)值为1.631 μm，峰谷(PV)值为9.082 μm。实验结果表明，将变倾角同步移相技术引入斜入射干涉系统，可以克服环境震动的干扰，在保证高精度的前提下拓宽了可见光干涉仪的测量范围。
Abstract
An oblique incidence dynamic phase-shifting interferometer based on inclination angle deflection is proposed to quickly obtain the surface distribution of optical surface with flatness of micron dimension. A 2×2 point source array is introduced into a Michelson interference system, and the incidence angle of each point source on the interferometer cavity is adjusted precisely to induce equal phase shift. Spatial separation is realized in combination with a lens array. The four phase-shifting interferograms are captured simultaneously on a single CCD, thereby realizing dynamic measurement. The flatness of a 35 mm aperture silicon wafer is measured at oblique incidence angle of 68°, the root mean square (RMS) is 1.631 μm and peak-to-valley (PV) is 9.082 μm. The experimental results indicate that the proposed interferometer overcomes the disturbance of vibration environment and extends the measurement range of interferometer with high precision by introducing the simultaneous phase-shifting interferometry based on inclination angle deflection into the oblique incidence interference system.
-
Key words:
- interferometry /
- oblique incidence /
- dynamic interferometer /
- surface flatness
-
Overview
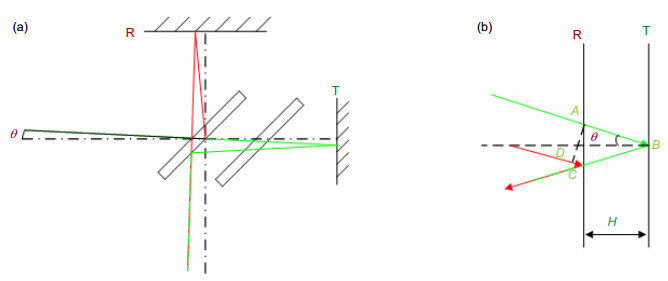
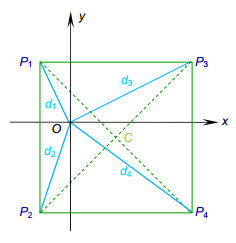
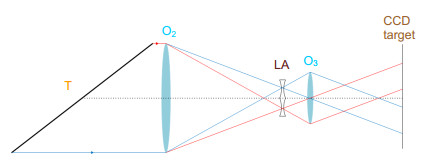
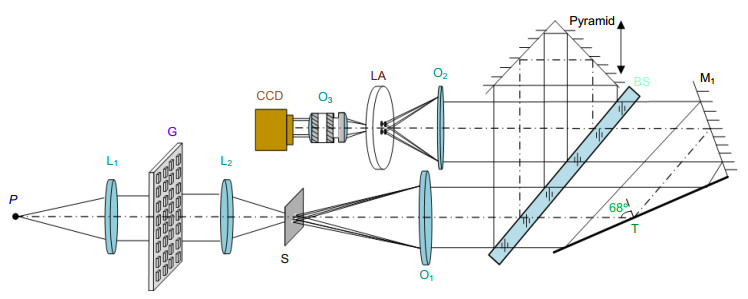
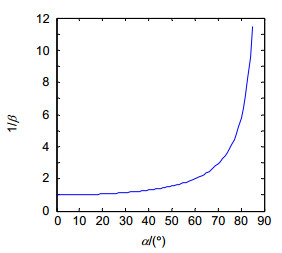
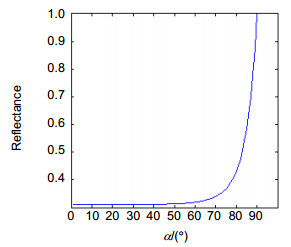
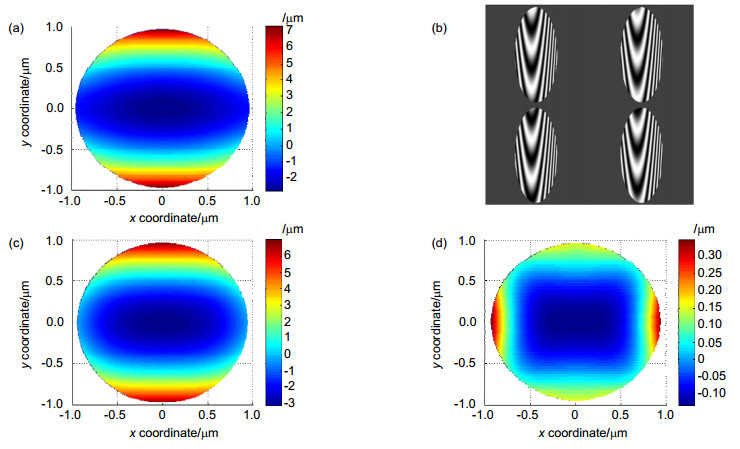
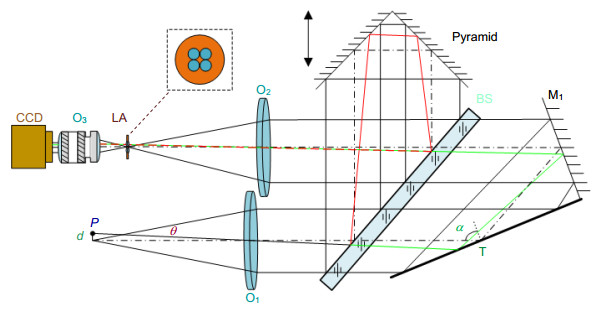
Overview: An oblique incidence dynamic phase-shifting interferometer based on inclination angle deflection is proposed to quickly obtain the surface distribution of optical surface with flatness of micron dimension. The measurement is based on the Michelson interference system. The He-Ne laser which operates at 632.8 nm is used as the light source. In combination with a phase mask grating, the four (±1, ±1) diffraction orders is selected to generate a 2×2 point source array which is introduced into the interference system as light source configuration. Adjust the distance of each point source off the optical axis precisely, the incidence angle of each point source on the interferometer cavity is changed to induce phase shift. In this work, we introduce equal phase shift interval of π/2 in the interferograms. We choose double telecentric imaging system to ensure the entire test part can be clearly imaged. By inducing a lens array into the imaging system, the four interferograms can be separated spatially on a single CCD. Then the four phase-shifting interferograms are captured simultaneously on the CCD target, and the initial phase will be retrieved exactly by employing the four-bucket algorithm, thereby realizing dynamic measurement. To analyze the measurement error which is introduced by the offset amounts of each point source, we establish a simulation model to study the effect of the collimated wavefront quality on the measurement. It is necessary to ensure that the aberrations which collimated wavefront contains smaller than λ/4, and the F-number of the collimating objective lens should be greater than 8.5. We also design the imaging system to ensure image quality through Zemax software. We build up the experiment device and choose a silicon wafer with aperture of 35 mm as the test part. The flatness of silicon wafer is about 10 μm dimension, and the measurement of the thin wafer is susceptible to vibration. Furthermore, to study the influence of the oblique incidence angle on the sensitivity factor and the range of measurement, a mathematical model based on the oblique incidence measurement is established to select the best incidence angle. Considering the sensitivity factor, the aperture of the test part, the surface reflectance and the spatial resolution, the silicon wafer is measured at oblique incidence angle of 68°, the root mean square (RMS) is 1.631 μm and peak-to-valley (PV) is 9.082 μm. The experimental results indicate that the proposed interferometer overcomes the disturbance of vibration environment and extends the measurement range of interferometer with high precision by introducing the simultaneous phase-shifting interferometry based on inclination angle deflection into the oblique incidence interference system.
-
-
图 2 变倾角移相原理。(a)等效迈克尔逊干涉仪光路；(b)等效等厚干涉光路
Figure 2. Principle of phase shifting based on the variation of inclination. (a) The alternative representation of optical path in the Michelson interferometer; (b) The alternative representation of optical path in an equal-thickness interferometer
图 5 变倾角斜入射干涉仪光路图
Figure 5. Optical layout of oblique incidence interferometer based on inclination angle deflection
图 6 变倾角斜入射干涉仪实验装置
Figure 6. Experimental device of oblique incidence interferometer based on inclination angle deflection
图 7 实验结果。(a) CCD采集的干涉图; (b)硅片面形恢复结果
Figure 7. Experimental results. (a) The interferograms recorded by CCD; (b) The retrieved surface distribution of silicon substrate
图 8 拓展范围与斜入射角关系
Figure 8. Expanded measurement range with different oblique incidence angles
图 10 仿真结果。(a)原始相位; (b)同步移相干涉图; (c)四步移相恢复相位; (d)残差
Figure 10. Simulation result. (a) The simultaneous phase shift interferogram; (b) Original phase; (c) Phase derived by four-step phase-shifting method; (d) Residual surface
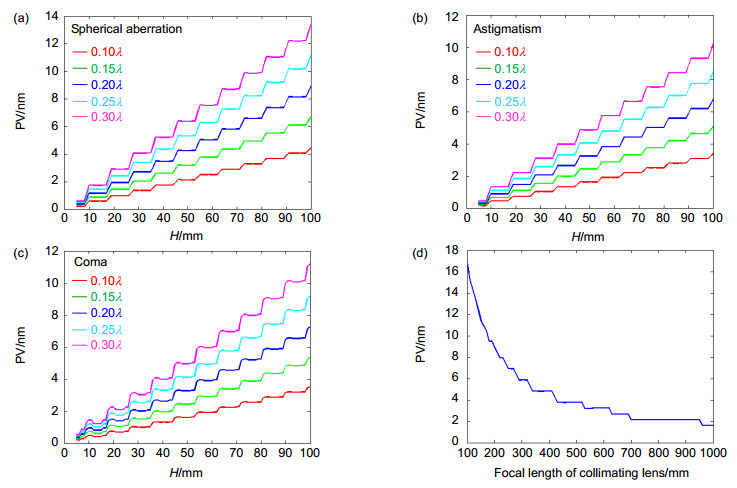
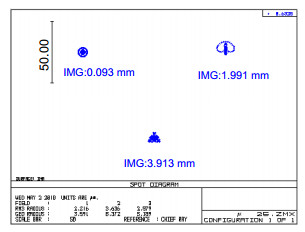
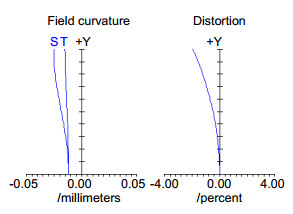
图 11 变倾角移相引入的系统误差。(a)准直波前包含球差；(b)准直波前包含像散；(c)准直波前包含彗差；(d)与准直物镜焦距的关系
Figure 11. Calculation error introduced by the light deflection. (a) Collimated wavefront with spherical aberration; (b) Collimated wavefront with astigmatism; (c) Collimated wavefront with coma; (d) Relationship with focal length of collimating lens
-
参考文献
[1] Malacara D. Optical Shop Testing[M]. 3rd ed. New York: John Wiley & Sons, 2007: 33-59.
[2] Vannoni M, Martìn I F. Surface measurements in "grazing incidence" interferometry for long x-ray mirrors: theoretical limits and practical implementations[J]. Proceedings of SPIE, 2016, 9962: 996207. doi: 10.1117/12.2238623
[3] Mizutani Y, Iwata T, Otani Y. Time-resolved vibrational surface profile measurement of ultrasonic motor using stroboscopic oblique incidence interferometer[J]. Proceedings of SPIE, 2010, 7855: 78550N. doi: 10.1117/12.871749
[4] Wen H, Kemble C K, Bennett E E. Theory of oblique and grazing incidence Talbot-Lau interferometers and demonstration in a compact source x-ray reflective interferometer[J]. Optics Express, 2011, 19(25): 25093-25112. doi: 10.1364/OE.19.025093
[5] Szwaykowski P, Bushroe F N, Castonguay R J. Interferometric system with reduced vibration sensitivity and related method: 8004687.B2[P]. 2011-12-09.
[6] Millerd J E, Brock N J, Hayes J B, et al. Pixelated phase-mask dynamic interferometer[J]. Proceedings of SPIE, 2004, 5531: 304-310. doi: 10.1117/12.560807
[7] Kimbrough B T. Pixelated mask spatial carrier phase shifting interferometry algorithms and associated errors[J]. Applied Optics, 2006, 45(19): 4554-4562. doi: 10.1364/AO.45.004554
[8] Yu Y J, Peng J, Wang Z Q. Spatial phase-shifting interferential system on polarization interference and grating beam-splitting: phase-shifting error testing[J]. Journal of Physics: Conference Series, 2006, 48(1): 992-997. doi: 10.1088/1742-6596/48/1/185
[9] Zhu W H, Chen L, Zheng D H, et al. Dynamic Fizeau interferometer based on the lateral displacements of the point sources[J]. Optics and Lasers in Engineering, 2017, 91: 216-220. doi: 10.1016/j.optlaseng.2016.12.007
[10] Robledo-Sanchez C, Juarez-Salazar R, Meneses-Fabian C, et al. Phase-shifting interferometry based on the lateral displacement of the light source[J]. Optics Express, 2013, 21(14): 17228-17233. doi: 10.1364/OE.21.017228
[11] Langenbeck P. Interferometry for Precision Measurement[M]. Bellingham, Washington: SPIE, 2014: 39-53.
[12] Born M, Wolf E. Principles of Optics[M]. 7th ed. Cambridge: Cambridge University Press, 1999: 261-270.
[13] Geary J M. Introduction to Lens Design[M]. Viriginia: Willmann Bell, Inc, 2002: 389-396.
-
访问统计
下载:
点击扫一扫
图(14)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
