E-mail Alert
RSS
-
摘要
多帧图像超分辨理论是通过融合多帧低分辨率图像的信息来重构高空间分辨率图像。准确估计低分辨率图像的模糊核是进行有效信息融合的先决条件。传统超分辨方法通常假设模糊核已知且采用固定的高斯滤波模糊核，并且模型参数需要费时的手动调整。本文在变分贝叶斯框架下获得相应的超分辨算法，该算法对高分辨率图像、模糊核和模型参数同时进行最优估计。对比实验表明，模糊核自适应估计的盲超分辨方法总体性能优于现有的变分贝叶斯框架下的图像超分辨方法，特别是在高信噪比场景，推荐方法优势更加明显。
-
关键词:
- 盲超分辨 /
- 分辨率增强 /
- 变分贝叶斯 /
- 模糊核 /
- Kullback-Leibler散度
Abstract
Multi-frame image super-resolution method fuses the information of multi-frame low-resolution images to reconstruct high-resolution images. For multi-frame image super-resolution, the accurate estimation of blur kernel of low-resolution image is prerequisite for efficiency information fusion. Traditional super-resolution method usually assumes a known blur kernel and uses the Gaussian filter blur kernel for the enhancement. It also needs to tune the parameters by time-consuming hand-tuning. The proposed method acquires the super-resolution method based on the variational Bayesian method. The high-resolution image, the blur kernel and the model parameters are estimated simultaneously and automatically in the optimal stochastic sense. Experiments and simulations demonstrate that the proposed blind super-resolution method based on blur kernel self-adaptive estimation outperforms the state-of-art super-resolution method in variational Bayesian framework, especially, for the high signal to noise ratio scenarios.
-
Overview
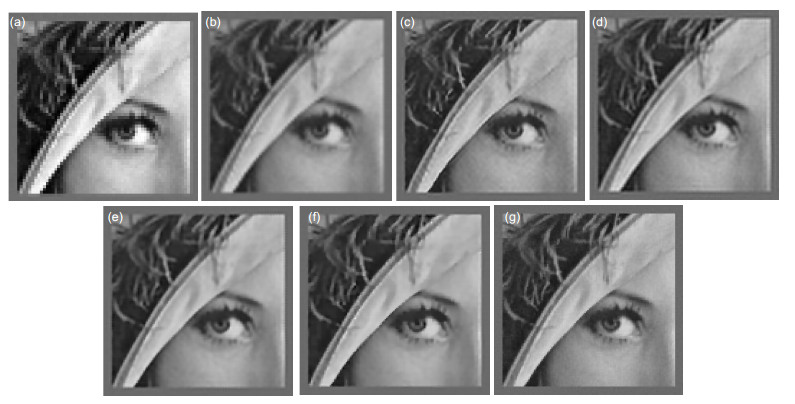
Overview: Images with high spatial resolution are usually desirable in real applications. The most direct approaches to increase the spatial resolution are: 1) increasing the bandwidth of the optics; 2) increasing the sampling frequency of the image sensor. However, these hardware-based approaches usually increase the volume or cost of the imaging system. Different from the hardware-based approaches, we use digital signal processing algorithm to increase the spatial resolution by a set of low-resolution (LR) images of the same scene. This approach is termed as multi-frame image super-resolution (SR). Variational Bayesian framework has been used to derive the SR algorithms for its model flexibility and parameter adaptivity. For multi-frame image SR, the accurate estimation of blur kernel of LR image is prerequisite for high-efficiency SR reconstruction. However, in variational Bayesian SR framework, all the methods assume a known and fixed blur kernel for LR images. We propose a blind SR method containing blur kernel self-adaptive estimation. First, the desired high-resolution (HR) image and the blur kernel are modeled in the imaging degradation model. Next, the total variation model is used to model the HR image and the blur kernel, and the Gamma distribution is used to model the corresponding parameters. Finally, the variational Bayesian inference based on Kullback-Leibler divergence and majorization-minimization approach is utilized to derive the SR algorithm. For the proposed method, the HR image, the blur kernel and the model parameters are estimated simultaneously and automatically. Experiments demonstrate that the proposed method outperforms the state-of-art methods. For the experiments on simulated data, the performance of the resolution enhancement method is quantitatively measured by the peak signal-to-noise ratio (PSNR) and structural similarity measure (SSIM). For typical ground truth HR image and blur kernel setup, the proposed method has the highest PSNR and SSIM and improves the PSNR by at least 1 dB~5 dB. For the visual effect, the proposed method has better blur removing performance. For the real data experiments using resolution chart LR images, the proposed method has better performance in preserving image details, suppressing noise and removing artifacts. The comparison experiments demonstrate the advantage of the proposed method. Especially, for the high signal-to-noise ratio (SNR) scenarios, the accuracy of blur kernel estimation dominates the performance and the proposed method can improve the performance dramatically. By the visual effect, the proposed method has better trade-off in preserving image details and removing noise and artifacts.
-
-
图 1 仿真实验数据真实高分辨率图像。(a) Lena；(b) EIA
Figure 1. The ground truth high-resolution image for simulated experiment data. (a) Lena; (b) EIA
图 2 EIA图像35 dB高斯噪声，模糊核设置1，增强结果。(a)第一幅低分辨率图像；(b) BBC；(c) SRCNN；(d) SAR；(e) TV；(f) NS；(g)本文方法
Figure 2. The enhancement result on EIA for 35 dB and blur kernel case 1. (a) First LR image; (b) BBC; (c) SRCNN; (d) SAR; (e) TV; (f) NS; (g) Proposed
图 3 Lena图像35 dB高斯噪声，模糊核设置2，增强结果。(a)第一幅低分辨率图像；(b) BBC；(c) SRCNN；(d) SAR；(e) TV；(f) NS；(g)本文方法
Figure 3. The enhancement result on Lena for 35 dB and blur kernel case 2. (a) First LR image; (b) BBC; (c) SRCNN; (d) SAR; (e) TV; (f) NS; (g) Proposed
图 4 分辨率板图像增强结果。(a)第一幅低分辨率图像；(b) BBC；(c) SRCNN；(d) SAR；(e) TV；(f) NS；(g)本文方法
Figure 4. The enhancement result on resolution chart image. (a) First LR image; (b) BBC; (c) SRCNN; (d) SAR; (e) TV; (f) NS; (g) Proposed
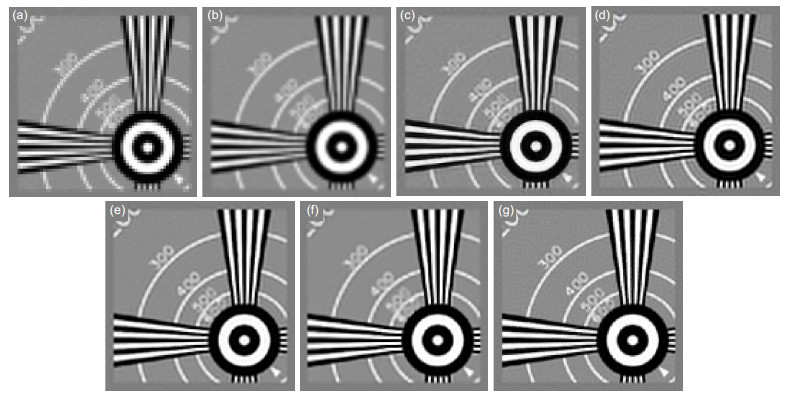
表 1 模糊核SAR和总变差先验模型时推荐方法PSNR(dB)值比较
Table 1. Comparison of PSNR(dB) derived by SAR and TV prior blur kernel
模糊核模型 Case1 Case2 15 dB 35 dB 55 dB 15 dB 35 dB 55 dB SAR先验 30.76 34.86 36.96 30.92 35.50 40.12 总变差先验 30.77 35.82 40.20 30.93 37.99 45.74 
下载: 导出CSV
表 2 模糊核SAR和总变差先验模型时推荐方法SSIM值比较
Table 2. Comparison of SSIM derived by SAR and TV prior blur kernel
模糊核模型 Case1 Case2 15 dB 35 dB 55 dB 15 dB 35 dB 55 dB SAR先验 0.9893 0.9959 0.9971 0.9899 0.9965 0.9971 总变差先验 0.9895 0.9967 0.9988 0.9899 0.9980 0.9997
下载: 导出CSV
表 3 模糊核设置1时，各图像分辨率增强方法PSNR(dB)值比较
Table 3. Comparison of PSNR(dB) derived by several image resolution enhancement methods for blur kernel case 1
Image SNR/dB BBC SRCNN SAR TV NS Proposed Lena 15 25.50 24.08 29.85 30.76 30.76 30.77 35 26.84 27.03 33.60 34.45 33.96 35.82 55 28.86 27.07 34.04 34.94 34.29 40.20 EIA 15 17.12 17.23 23.18 24.04 23.77 24.16 35 17.54 18.29 25.29 26.96 25.40 30.50 55 17.55 18.31 25.36 27.01 25.47 34.73
下载: 导出CSV
表 4 模糊核设置1时，各图像分辨率增强方法SSIM值比较
Table 4. Comparison of SSIM derived by several image resolution enhancement methods for blur kernel case 1
Image SNR/dB BBC SRCNN SAR TV NS Proposed Lena 15 0.9641 0.9515 0.9870 0.9895 0.9895 0.9895 35 0.9734 0.9748 0.9946 0.9951 0.9947 0.9967 55 0.9735 0.9750 0.9951 0.9960 0.9954 0.9988 EIA 15 0.8456 0.8680 0.9685 0.9746 0.9736 0.9752 35 0.8598 0.8955 0.9815 0.9873 0.9824 0.9943 55 0.8601 0.8959 0.9818 0.9874 0.9826 0.9978
下载: 导出CSV
表 5 模糊核设置2时，各图像分辨率增强方法PSNR(dB)值比较
Table 5. Comparison of PSNR(dB) derived by several image resolution enhancement methods for blur kernel case 2
Image SNR/dB BBC SRCNN SAR TV NS Proposed Lena 15 25.78 23.63 29.95 30.91 30.80 30.93 35 27.22 26.25 33.12 33.99 33.58 37.99 55 27.24 26.29 33.54 34.17 34.11 45.74 EIA 15 17.43 16.23 22.98 24.02 22.64 24.04 35 17.88 16.97 25.00 25.81 25.57 32.72 55 17.89 16.98 25.06 25.92 25.76 38.04
下载: 导出CSV
表 6 模糊核设置2时，各图像分辨率增强方法SSIM值比较
Table 6. Comparison of SSIM derived by several image resolution enhancement methods for blur kernel case 2
Image SNR/dB BBC SRCNN SAR TV NS Proposed Lena 15 0.9668 0.9476 0.9874 0.9899 0.9897 0.9899 35 0.9759 0.9707 0.9940 0.9950 0.9946 0.9980 55 0.9760 0.9710 0.9945 0.9952 0.9952 0.9997 EIA 15 0.8656 0.8513 0.9675 0.9733 0.9663 0.9734 35 0.8790 0.8738 0.9799 0.9836 0.9828 0.9966 55 0.8793 0.8741 0.9802 0.9840 0.9836 0.9990
下载: 导出CSV
-
参考文献
[1] 郭迎辉, 蒲明博, 马晓亮, 等.电磁超构材料色散调控研究进展[J].光电工程, 2017, 44(1): 3-22. doi: 10.3969/j.issn.1003-501X.2017.01.001
Guo Y H, Pu M B, Ma X L, et al. Advances of dispersion-engineered metamaterials[J]. Opto-Electronic Engineering, 2017, 44(1): 3-22. doi: 10.3969/j.issn.1003-501X.2017.01.001
[2] Dong C, Loy C C, He K M, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. doi: 10.1109/TPAMI.2015.2439281
[3] Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, 2017: 105-114.
[4] 汪荣贵, 汪庆辉, 杨娟, 等.融合特征分类和独立字典训练的超分辨率重建[J].光电工程, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542
Wang R G, Wang Q H, Yang J, et al. Image super-resolution reconstruction by fusing feature classification and independent dictionary training[J]. Opto-Electronic Engineering, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542
[5] Nasrollahi K, Moeslund T B. Super-resolution: a comprehensive survey[J]. Machine Vision and Applications, 2014, 25(6): 1423-1468. doi: 10.1007/s00138-014-0623-4
[6] Yue L W, Shen H F, Li J, et al. Image super-resolution: the techniques, applications, and future[J]. Signal Processing, 2016, 128: 389-408. doi: 10.1016/j.sigpro.2016.05.002
[7] Tsai R Y, Huang T S. Multi-frame image restoration and registration[M]//Huang T S. Advances in Computer Vision and Image Processing. Greenwich: JAI Press, 1984: 317-339.
[8] Shen H F, Peng L, Yue L W, et al. Adaptive norm selection for regularized image restoration and super-resolution[J]. IEEE Transactions on Cybernetics, 2016, 46(6): 1388-1399. doi: 10.1109/TCYB.2015.2446755
[9] Zeng X Y, Yang L H. A robust multiframe super-resolution algorithm based on half-quadratic estimation with modified BTV regularization[J]. Digital Signal Processing, 2013, 23(1): 98-109. doi: 10.1016/j.dsp.2012.06.013
[10] Huang S Y, Sun J, Yang Y, et al. Multi-frame super-resolution reconstruction based on gradient vector flow hybrid field[J]. IEEE Access, 2017, 5: 21669-21683. doi: 10.1109/ACCESS.2017.2757239
[11] Molina R, Vega M, Abad J, et al. Parameter estimation in Bayesian high-resolution image reconstruction with multisensors[J]. IEEE Transactions on Image Processing, 2003, 12(12): 1655-1667. doi: 10.1109/TIP.2003.818117
[12] Babacan S D, Molina R, Katsaggelos A K. Variational Bayesian super resolution[J]. IEEE Transactions on Image Processing, 2011, 20(4): 984-999. doi: 10.1109/TIP.2010.2080278
[13] Villena S, Vega M, Molina R, et al. A non-stationary image prior combination in super-resolution[J]. Digital Signal Processing, 2014, 32: 1-10. doi: 10.1016/j.dsp.2014.05.017
[14] Liu C, Sun D Q. On Bayesian adaptive video super resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(2): 346-360. doi: 10.1109/TPAMI.2013.127
[15] Ng M K, Shen H F, Lam E Y, et al. A total variation regularization based super-resolution reconstruction algorithm for digital video[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2007: 074585. doi: 10.1155/2007/74585
[16] Beal M J. Variational algorithms for approximate Bayesian inference[D]. London, UK: University College London, 2003.
[17] Bioucas-Dias J M, Figueiredo M A T, Oliveira J P. Total variation-based image deconvolution: a majorization-minimization approach[C]//Proceedings of 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, 2006: 861-864.
[18] Dong C, Loy C C, He K M, et al. Image super-resolution using deep convolutional networks[EB/OL]. http://mmlab.ie.cuhk.edu.hk/projects/SRCNN.html.
[19] Lucas B, Kanade T. An iterative image registration technique with an application to stereo vision[C]//Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, 1981: 674-679.
[20] Wang Z, Bovik A C. Mean squared error: love it or leave it? A new look at signal fidelity measures[J]. IEEE Signal Processing Magazine, 2009, 26(1): 98-117. doi: 10.1109/MSP.2008.930649
[21] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. doi: 10.1109/TIP.2003.819861
-
访问统计
点击扫一扫
图(4)
表(6)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
