E-mail Alert
RSS
Electrostatically driven membrane deformable mirror edge effects and their influence on the evaluation of correction capability
-
摘要
静电驱动薄膜变形镜通过静电驱动实现波前像差校正，其校正能力评估主要依赖于驱动载荷分析的准确性。由于电极边缘产生电荷集聚导致区域载荷非线性变化产生非均匀变形，引起静电驱动薄膜变形镜校正面型评估不准或错误评估。基于此，开展静电驱动薄膜变形镜电极边缘效应及其对校正能力评估影响研究，建立电极边缘效应理论模型，并基于该模型对电极边缘形变响应和校正能力评估准确性的影响进行定量分析。分析结果表明，边缘效应前后校正能力评估误差从25.49%降低至6.83%甚至更低，且适用于不同电极间距参数，验证所提理论模型正确性。
Abstract
Electrostatically driven membrane deformable mirrors correct wavefront aberrations through electrostatic forces, whose correction capability dependent on driving load accuracy. Due to the charge aggregation at the electrode edges, non-uniform deformation occurs due to the nonlinear change of the regional load, which causes inaccurate or incorrect assessment of the calibrated wavefront aberration of electrostatically driven membrane deformable mirrors. Based on this, this work carries out a study on electrostatically driven membrane deformable mirror electrode edge effect and its influence on correction capability assessment, establishes a theoretical model of electrode edge effect, and quantitatively analyzes the influence of electrode edge deformation response and correction capability assessment accuracy based on the model, and the results show that before and after the consideration of the edge effect, the error of correction capability assessment is improved from 25.49% to 6.83% or even lower, and applies to different electrode spacing parameters, which verifies the correctness of the theoretical model proposed in this paper.
-
Overview
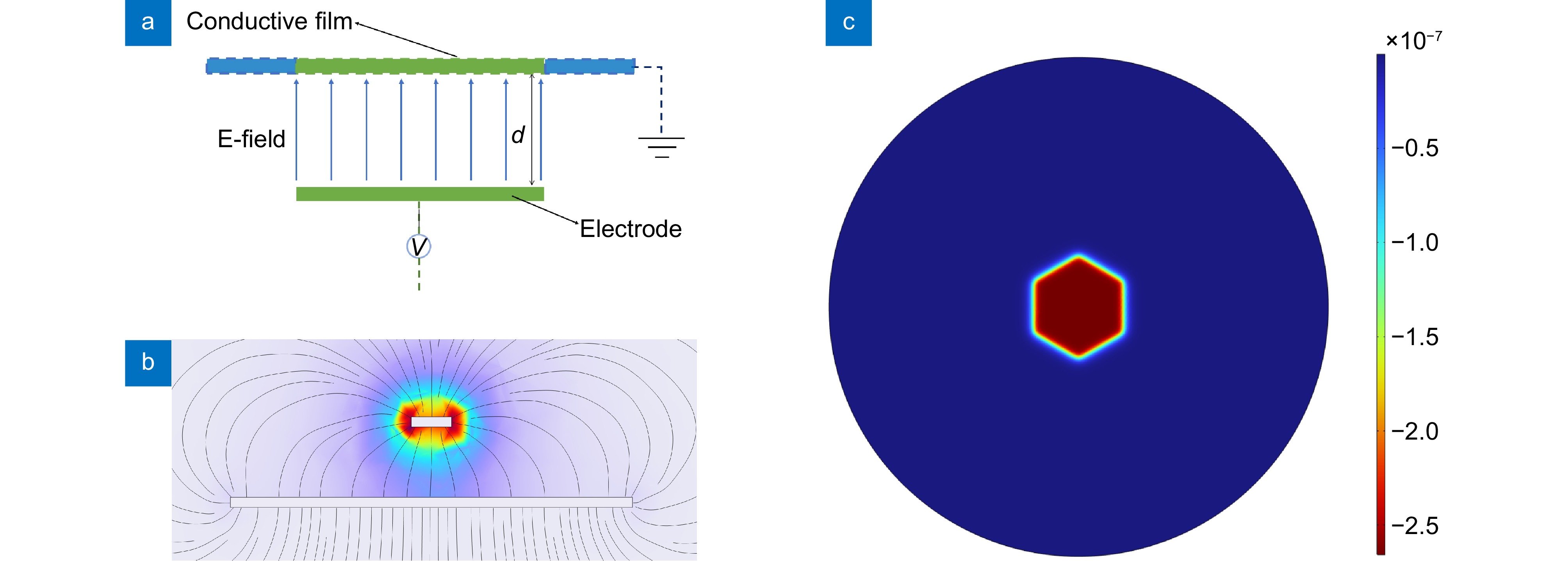
Overview: Electrostatically driven membrane deformable mirrors (EMDMs), as key components in adaptive optical systems, overcoming the limitations of traditional mechanical deformable mirrors in terms of size, response speed, and stability. EMDMs offer high surface precision, low power consumption, fast response speed, and long-term stability, which makes them essential for applications such as microscopy imaging and vision correction. The correction capabilities of EMDMs directly determine the overall performance of adaptive optical systems, with an accurate electrostatic load distribution model being critical for predicting the membrane deformation and evaluating the mirror's correction performance. However, current models often neglect the edge effects of the electrodes, which reduces the accuracy of deformation calculations and impacts the system's optimization and performance evaluation.
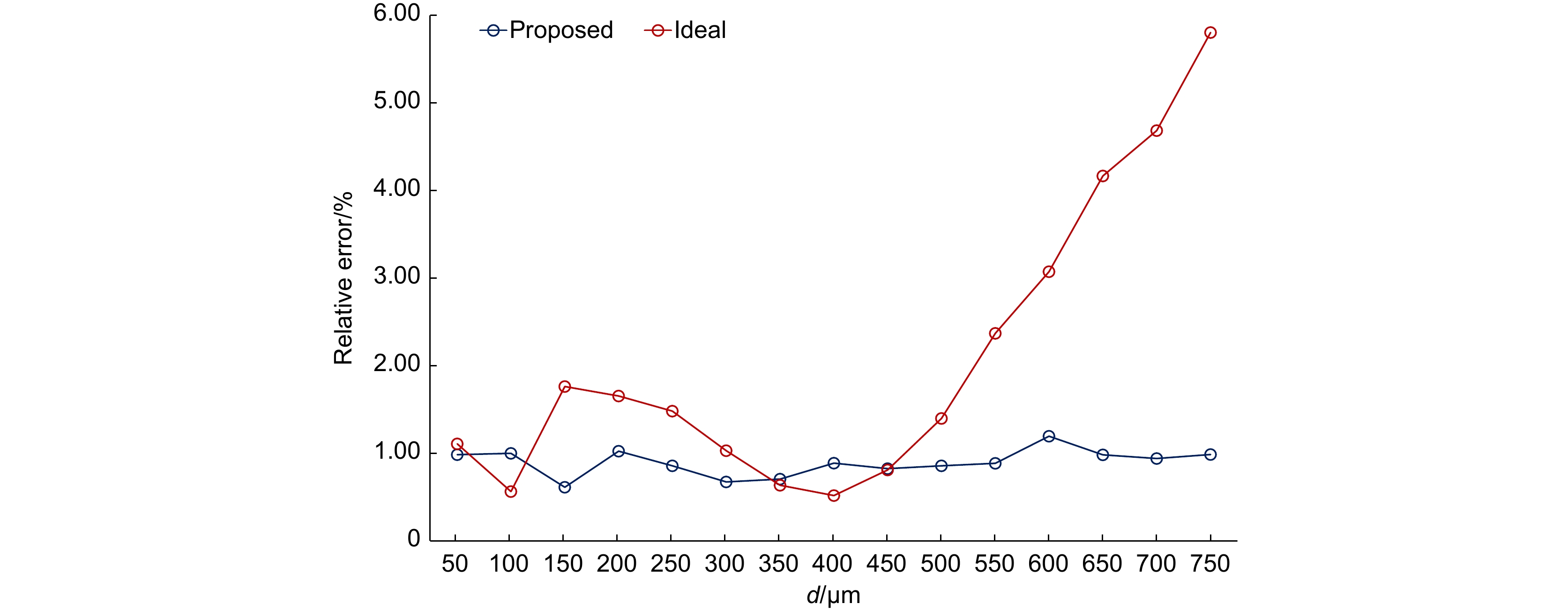
Traditionally, EMDM designs are based on ideal parallel capacitor models, assuming uniform electrostatic loads across the electrode's and conductive membrane's projection area. While this simplifies calculations and provides reasonable accuracy, it fails to account for the edge effects, in which the electric field strength near the edges of the electrodes is significantly stronger. This edge effect exacerbates membrane deformation, and affects the control accuracy and wavefront correction capability. To address this issue, this study improves the existing models by considering the edge effects, employing the method of image electrodes and the moment method to compute the charge distribution and electrostatic potential. This approach provides a more realistic description of the non-uniformity of the electric field at the edges of the electrodes. The proposed model overcomes the limitations of previous models by offering a more accurate charge distribution, which improves the deformation prediction accuracy. Compared with COMSOL simulation results shows that the relative error in membrane deformation calculations does not exceed 2%, and the wavefront correction evaluation error is reduced from 25.49% to 6.83%. These results demonstrate the effectiveness and accuracy of the model, and offers a theoretical foundation and application basis for the optimization of EMDM parameters and high-precision wavefront correction.
-
-
图 2 平行平板电容的边缘效应。(a)理想的平行电容驱动器模型；(b) EMDM电场分布；(c) EMDM导电薄膜的电荷分布
Figure 2. Edge effect of parallel flat capacitor. (a) Ideal parallel capacitance driver model; (b) EMDM electric field distribution; (c) Charge distribution of EMDM conductive membranes
图 4 EMDM中心电极作用下的镜面面型。(a)数值仿真的镜面面型；(b)所提模型的镜面面型；(c)理想模型的镜面面型
Figure 4. Mirror surface pattern under the action of EMDM center electrode. (a) Mirror surface profile for numerical simulation; (b) Mirror surface profile for the proposed model; (c) Mirror surface profile for the ideal model
图 5 在不同电极间距d下，所提模型与理想模型的面型拟合误差
Figure 5. Surface shape fitting error between proposed model and ideal model under different electrode spacing d
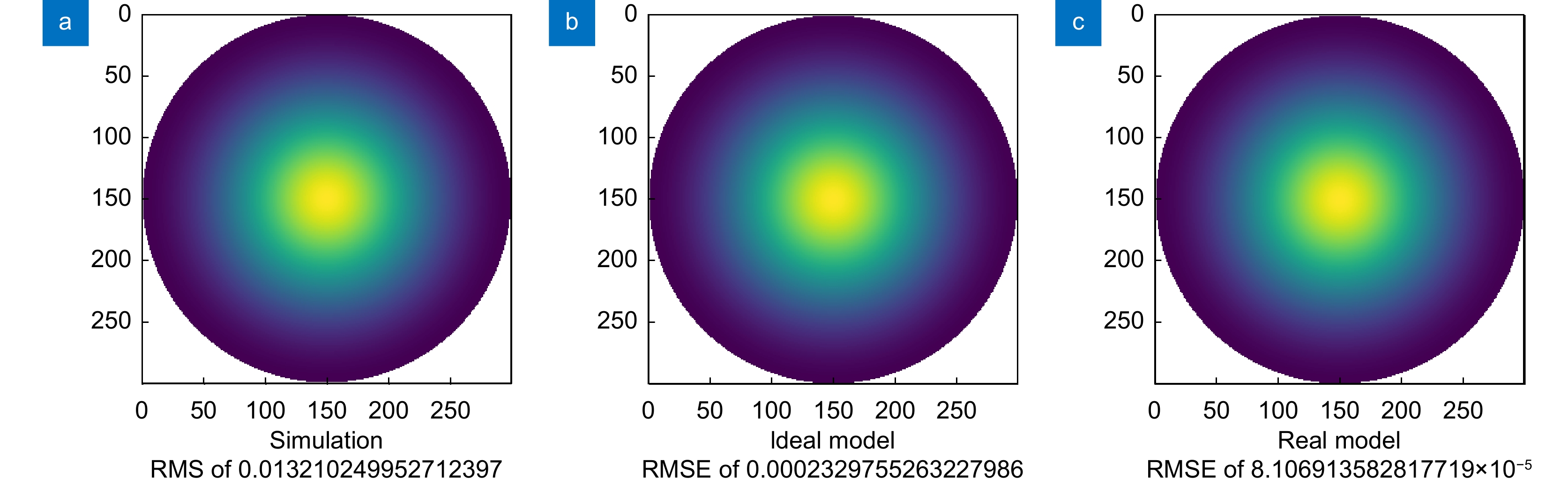
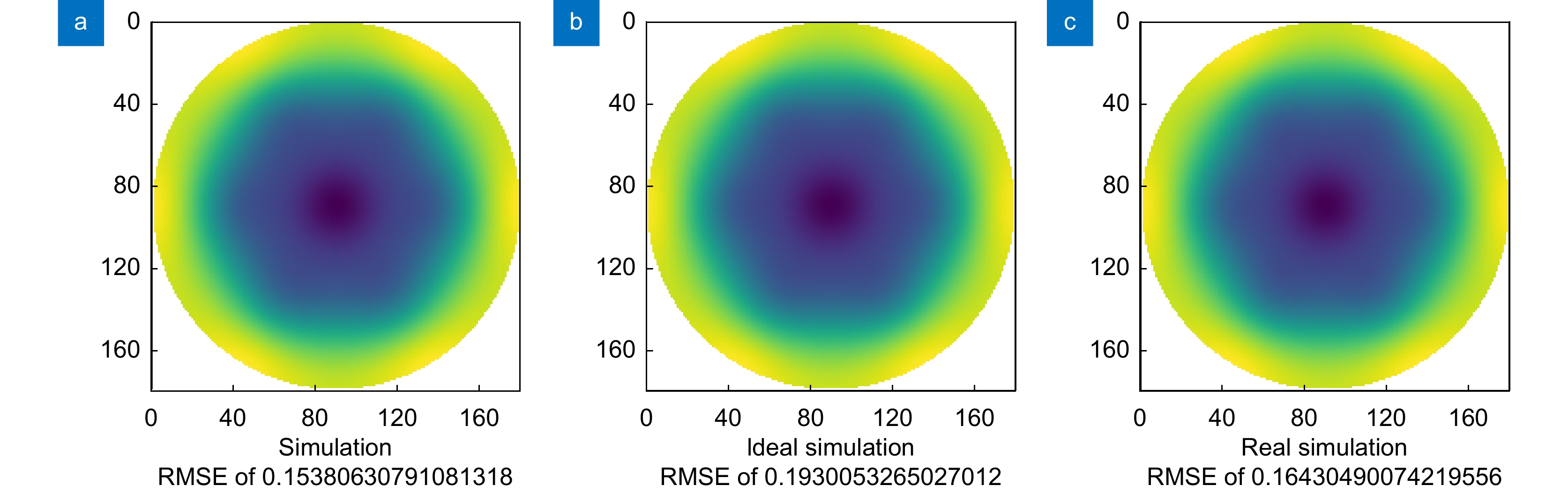
图 6 不同模型对离焦像差的实际校正效果。(a)校正离焦像差的仿真结果；(b)理想模型校正离焦像差的实际效果；(c)所提模型校正离焦像差的实际效果
Figure 6. Actual results of correcting the out-of-focus aberration by different models. (a) Simulation results of correcting the out-of-focus aberration; (b) Practical results of the ideal model for correcting the out-of-focus aberration; (c) Practical results of proposed model for correcting the out-of-focus aberration
图 7 波前校正能力评估分析对比流程图
Figure 7. Process flow diagram for comparing wavefront correction capability analysis
图 8 所提模型与理想模型对前15项Zernike像差生成评估准确性对比分析曲线
Figure 8. Comparative analysis curves of the accuracy of the proposed model in this thesis and the ideal model for the first 15 Zernike aberration generation assessment
表 1 EMDM结构尺寸
Table 1. EMDM structure dimensions
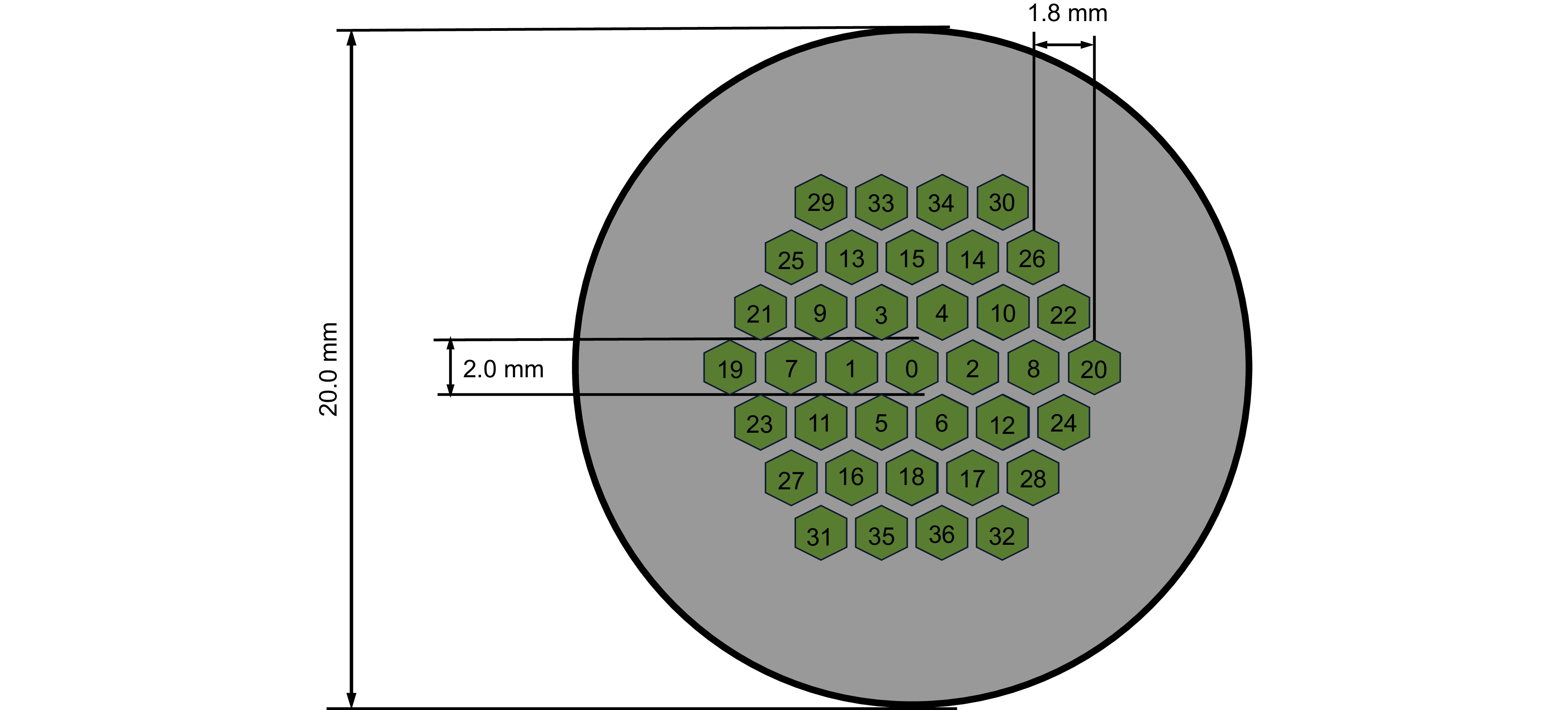
组件 参数 值 薄膜 半径($ {R}_{{\mathrm{m}}} $)/mm 10 厚度($ \delta $)/mm 0.1 泊松比($ \mu $) 0.49 杨氏模量(E)/KPa 750 电介质 相对介电常数(εr) 3 电极 外接圆半径(R)/mm 1 电压(V)/V 1 
下载: 导出CSV
-
参考文献
[1] 姜文汉. 自适应光学发展综述[J]. 光电工程, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
Jiang W H. Overview of adaptive optics development[J]. Opto-Electron Eng, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
[2] Booth M J, Neil M A A, Juškaitis R, et al. Adaptive aberration correction in a confocal microscope[J]. Proc Natl Acad Sci USA, 2002, 99(9): 5788−5792. doi: 10.1073/pnas.082544799
[3] Guo Y M, Chen K L, Zhou J H, et al. High-resolution visible imaging with piezoelectric deformable secondary mirror: experimental results at the 1.8-m adaptive telescope[J]. Opto-Electron Adv, 2023, 6(12): 230039. doi: 10.29026/oea.2023.230039
[4] 罗帅, 王家秋, 张彬. 压电陶瓷驱动器疲劳特性对变形镜校正能力的影响[J]. 中国激光, 2018, 45(9): 0905002. doi: 10.3788/CJL201845.0905002
Luo S, Wang J Q, Zhang B. Influence of fatigue characteristics of piezoelectric ceramics actuators on correction ability of deformable mirror[J]. Chin J Lasers, 2018, 45(9): 0905002. doi: 10.3788/CJL201845.0905002
[5] Hermann B, Fernández E J, Unterhuber A, et al. Adaptive-optics ultrahigh-resolution optical coherence tomography[J]. Opt Lett, 2004, 29(18): 2142−2144. doi: 10.1364/OL.29.002142
[6] Zhao H X, Li K, Yang F, et al. Customized anterior segment photoacoustic imaging for ophthalmic burn evaluation in vivo[J]. Opto-Electron Adv, 2021, 4(6): 200017. doi: 10.29026/oea.2021.200017
[7] Ren J, Lin H, Zheng X R, et al. Giant and light modifiable third-order optical nonlinearity in a free-standing h-BN film[J]. Opto-Electron Sci, 2022, 1(6): 210013. doi: 10.29026/oes.2022.210013
[8] 金柯, 刘永强, 韩俊, 等. 基于光学薄膜的高效超构表面研究[J]. 光学学报, 2024, 44(10): 1026032. doi: 10.3788/AOS231534
Jin K, Liu Y Q, Han J, et al. Study of high-efficiency metasurfaces based on optical thin films[J]. Acta Opt Sin, 2024, 44(10): 1026032. doi: 10.3788/AOS231534
[9] Kim D, Choi H, Brendel T, et al. Advances in optical engineering for future telescopes[J]. Opto-Electron Adv, 2021, 4(6): 210040. doi: 10.29026/oea.2021.210040
[10] 熊光昀, 唐奥, 兰斌, 等. 基于连续镜面变形镜本征模方法的复杂涡旋光场调控[J]. 光电工程, 2022, 49(11): 220066. doi: 10.12086/oee.2022.220066
Xiong G Y, Tang A, Lan B, et al. Vortex field manipulation based on deformation mirror with continuous surface[J]. Opto-Electron Eng, 2022, 49(11): 220066. doi: 10.12086/oee.2022.220066
[11] 赵思旻, 顾乃庭, 黄林海, 等. 太阳望远镜低时空频率波前像差校正技术[J]. 红外与激光工程, 2023, 52(7): 20220887. doi: 10.3788/IRLA20220887
Zhao S M, Gu N T, Huang L H, et al. Low spatio-temporal frequency wavefront aberration correction technology of solar telescope[J]. Infrared Laser Eng, 2023, 52(7): 20220887. doi: 10.3788/IRLA20220887
[12] Zhu L J, Sun P C, Bartsch D U, et al. Adaptive control of a micromachined continuous-membrane deformable mirror for aberration compensation[J]. Appl Opt, 1999, 38(1): 168−176. doi: 10.1364/AO.38.000168
[13] 曾志革, 凌宁. 分立式变形反射镜薄镜面的应力分析方法研究[J]. 光学 精密工程, 1997, 5(5): 21−29.
Zeng Z G, Ling N. Research of analysis method for stress of discrete deformable thin mirror[J]. Opt Precis Eng, 1997, 5(5): 21−29.
[14] Yan J L, Zhao Y, Yu F, et al. Theory and simulation of MEMS deformable mirror[J]. Proc SPIE, 2006, 6032: 60320J. doi: 10.1117/12.667868
[15] 陈力子, 关小伟, 张政. 微变形反射镜技术应用及发展[J]. 激光与光电子学进展, 2010, 47(2): 022201. doi: 10.3788/lop47.022201
Chen L Z, Guan X W, Zhang Z. Development and application of MEMS deformable mirror[J]. Laser Optoelectron Prog, 2010, 47(2): 022201. doi: 10.3788/lop47.022201
[16] 马剑强, 刘莹, 陈俊杰, 等. 200单元硅基单压电变形镜的设计与测试[J]. 光学 精密工程, 2014, 22(8): 2047−2053. doi: 10.3788/OPE.20142208.2047
Ma J Q, Liu Y, Chen J J, et al. Design and performance testing of 200-element silicon unimorph deformable mirror[J]. Opt Precis Eng, 2014, 22(8): 2047−2053. doi: 10.3788/OPE.20142208.2047
[17] 熊藜, 胡晋, 杨曌, 等. 微电容器的研究进展: 从制备工艺到发展趋势[J]. 光学 精密工程, 2021, 29(12): 2818−2831. doi: 10.37188/OPE.20212912.2818
Xiong L, Hu J, Yang Z, et al. Research progress of microcapacitors: from preparation technology to development trend[J]. Opt Precis Eng, 2021, 29(12): 2818−2831. doi: 10.37188/OPE.20212912.2818
[18] 张鹰, 金光. 薄膜反射镜静电成形机理研究[J]. 光学 精密工程, 2009, 17(2): 267−273.
Zhang Y, Jin G. Research on electrostatic deformation of membrane mirror[J]. Opt Precis Eng, 2009, 17(2): 267−273.
[19] 闫泽昊, 周子夜, 李杨, 等. 空间引力波望远镜超前瞄准机构致动器电荷驱动位移行为研究[J]. 光电工程, 2023, 50(11): 230223. doi: 10.12086/oee.2023.230223
Yan Z H, Zhou Z Y, Li Y, et al. Study on the charge driven displacement behavior of the actuator of the point ahead angle mechanism of a space gravitational wave telescope[J]. Opto-Electron Eng, 2023, 50(11): 230223. doi: 10.12086/oee.2023.230223
[20] Chien W Z, Wang Z Z, Xu Y G, et al. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its central portion[J]. Appl Math Mech, 1981, 2(6): 599−612. doi: 10.1007/BF01897638
[21] 李顺才, 董正筑. 非连续载荷作用下圆板弯曲的自然边界元法[J]. 广东工业大学学报, 2003, 20(4): 96−100. doi: 10.3969/j.issn.1007-7162.2003.04.021
Li S C, Dong Z Z. The natural boundary element method for the bending of the elastic thin circular plate under the discontinuous load[J]. J Guangdong Univ Technol, 2003, 20(4): 96−100. doi: 10.3969/j.issn.1007-7162.2003.04.021
[22] Eriksson E. Low-order aberration correction with a membrane deformable mirror for adaptive optics[D]. Gothenburg: Chalmers University of Technology, 2004.
[23] Fernández E J, Artal P. Membrane deformable mirror for adaptive optics: performance limits in visual optics[J]. Opt Express, 2003, 11(9): 1056−1069. doi: 10.1364/OE.11.001056
[24] 安源, 金光, 齐迎春, 等. 薄膜反射镜的单电极控制静电成形[J]. 光学 精密工程, 2009, 17(8): 1964−1970. doi: 10.3321/j.issn:1004-924X.2009.08.028
An Y, Jin G, Qi Y C, et al. The test design of shape controlled with single electrode Electrostatic about the membrane mirror[J]. Opt Precis Eng, 2009, 17(8): 1964−1970. doi: 10.3321/j.issn:1004-924X.2009.08.028
[25] 雷建华. 极板间距对平行板电容边缘效应的影响研究[J]. 电脑与电信, 2013, (7): 57−58,64. doi: 10.3969/j.issn.1008-6609.2013.07.033
Lei J H. Influence of plate spacing on capacitive edge effect[J]. Comput Telecommun, 2013, (7): 57−58,64. doi: 10.3969/j.issn.1008-6609.2013.07.033
[26] Yariv E. Edge corrections for parallel-plate capacitors[J]. Eur J Appl Math, 2021, 32(2): 226−241. doi: 10.1017/s0956792520000108
[27] 刘耀波, 苑伟政, 乔大勇, 等. 一种新型静电驱动二维微型扫描镜的设计及模态[J]. 光学学报, 2013, 33(6): 0623001. doi: 10.3788/AOS201333.0623001
Liu Y B, Yuan W Z, Qiao D Y, et al. Design and modes of a novel two-dimensional microscanner with electrostatic actuation[J]. Acta Opt Sin, 2013, 33(6): 0623001. doi: 10.3788/AOS201333.0623001
[28] 王少刚, 关鑫璞, 王党卫, 等. 求解电场积分方程的高阶矩量法[J]. 电子与信息学报, 2007, 29(9): 2265−2268. doi: 10.3724/SP.J.1146.2006.00628
Wang S G, Guan X P, Wang D W, et al. Solution of the electric field integral equation using higher-order method of moments[J]. J Electron Inf Technol, 2007, 29(9): 2265−2268. doi: 10.3724/SP.J.1146.2006.00628
[29] 刘燕婻, 潘小敏, 盛新庆. 一种矩量法精度分析验证方法研究[J]. 北京理工大学学报, 2016, 36(7): 723−726. doi: 10.15918/j.tbit1001-0645.2016.07.012
Liu Y N, Pan X M, Sheng X Q. A new method for accuracy analysis in method of moments[J]. Trans Beijing Inst Technol, 2016, 36(7): 723−726. doi: 10.15918/j.tbit1001-0645.2016.07.012
[30] Jebri Z, Taleb Ali M. Calculations and strategies to mitigate edge phenomena in planar capacitors[J]. 2023. https://doi.org/10.21203/rs.3.rs-3754607/v1.
-
访问统计
点击扫一扫
图(9)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
