-
摘要:
随着电磁隐身方法的发展,能够使物体的散射截面接近零的电磁隐身结构已成为研究热点,并在未来的军事设备隐身、电磁防护、隐形传感器等领域具有重要的应用价值。本文介绍了不同类型隐身结构的原理、工作条件和性能指标,解释了雷达隐身与完美隐身、全空间与半空间隐身之间的区别,回顾了光线绕射和散射抵消这两种主要的隐身机制,梳理了设计隐身结构常用的理论方法、材料类型和优化算法,对国内外隐身相关的关键理论研究和实验进展进行了总结。最后,对隐身结构存在的主要问题进行了总结,并对其未来的发展方向进行了展望。
Abstract:With the advancement of electromagnetic cloaking techniques, structures that can reduce an object's radar cross-section to nearly zero have become a focal point of research and are expected to have substantial application value in areas such as military equipment cloaking, electromagnetic shielding, and invisible sensors. This paper outlines the principles, operating conditions, and performance metrics of various types of cloaking structures, clarifies the distinctions between radar cloaking and perfect cloaking, as well as between full-space and carpet cloaking. It reviews the two primary cloaking mechanisms of light bending and scattering cancellation, and provides a summary of the theoretical approaches, material types, and optimization algorithms commonly employed in the design of cloaking structures. Additionally, it compiles a review of the key theoretical studies and experimental advancements in cloaking both domestically and internationally. Finally, a summary of the main issues existing in cloaking structures is provided, and a prospective view on their future development direction is presented.
-
Key words:
- cloaking /
- metamaterial /
- scattering cancellation /
- transformation optics
-
Overview: Electromagnetic cloaking technology has emerged as a pivotal area of research, transcending its original objective of minimizing the electromagnetic scattering cross-section of objects. It has significant implications for military equipment cloaking, electromagnetic protection, and the development of invisible sensors. This comprehensive review delves into the diverse principles underlying cloaking structures, their operating conditions, and key performance metrics. It clarifies distinctions between radar cloaking and perfect cloaking, as well as the concepts of full-space versus carpet cloaking. Fundamental cloaking mechanisms, such as light bending and scattering cancellation, are examined, providing insights into the strategies that manipulate electromagnetic waves to achieve invisibility. The paper also consolidates the theoretical approaches, material classifications, and optimization strategies commonly employed in the design of cloaking structures. It offers a synthesis of the critical theoretical studies and experimental advancements in the field of cloaking, both domestically and internationally. The exploration of cloaking structures has broadened to encompass a spectrum of physical domains beyond electromagnetic and optical waves, including acoustic waves, thermal flows, static magnetic fields, chemical potentials, and mechanical and elastic waves. The advent of structures capable of addressing multiple physical fields concurrently heralds a new era in cloaking technology, where multi-physical field cloaking structures are poised to become a cornerstone of future progress. Especially promising are the prospects of multi-physical field zero-space media and topological optimization strategies, which may unlock new potential for cloaking across different physical phenomena. The integration of smart optics and advanced materials is set to give future cloaking technology the agility to adapt its operational modalities in response to varying environmental conditions. This adaptive, intelligent cloaking is anticipated to be a breakthrough, with artificial intelligence algorithms potentially playing a central role in the design of multi-modal intelligent cloaking systems. While the ambition to achieve cloaking that is universally effective, broadband, bi-polarized, omni-directional for three-dimensional, electrically large objects remains a challenging horizon, the convergence of novel materials and artificial intelligence is expected to catalyze further breakthroughs in cloaking technology. These interdisciplinary innovations are projected to enhance the efficacy and sophistication of cloaking, thereby heightening their applicability and value across a spectrum of practical scenarios. The future of electromagnetic cloaking is bright, with ongoing research and technological evolution set to expand its capabilities and solidify its relevance in modern science and technology.
-

-
图 1 半空间隐身结构。 (a)全空间隐身示意图;(b)半空间隐身示意图[40];(c)地毯式隐身结构是在由硅层和二氧化硅层组成的SOI 晶圆中设计的,其中C1为梯度指数斗篷,C2为均匀指数背景[41];(d)由非共振超材料单元设计的地毯式隐身结构(左图)以及单元格几何形状与有效指数之间的关系(右图)[42];(e)由硅纳米柱分布在 SOI 晶圆中设计的地毯式隐身结构(上图)以及在 SOI 晶圆上蚀刻的不同密度硅柱的扫描电子显微镜图像(下图)[40];(f) 三维微波地毯式隐身结构示意图 [43];(g) 三维地毯斗篷结构蓝图,三维光锥红色显示的是与NA = 0.5显微镜镜头相对应的三维光锥[44];(h) 由两个方解石棱柱粘合而成的三角形地毯式隐身结构 [45];(i)在低折射率纳米多孔氧化硅衬底上的氮化硅波导中实现的隐形装置的横截面示意图[46];(j)非磁性智能超材料隐形结构的实验样品,插图是有效介电常数曲线与雅各布值的关系[47];(k)频率为 1 GHz 的平面电磁波穿过由 Zn-Ni-Fe 复合材料(蓝色)和空气(白色)设计的地毯式隐身结构,周围背景为聚四氟乙烯[48];(l)三维非欧几里得元表面地毯隐身结构的照片,插图显示了封闭金属环的细节[49];(m) 全极化梯形共形皮肤斗篷样品的照片,插图显示了沿中心 x 轴的相位轮廓[50];(n)由固化树脂单元格设计的地毯式隐身结构样品的照片(左图)和固化树脂单元格样品的照片(右图)[51]
Figure 1. The structures of carpet cloaking. (a) Schematic of full-space cloaking; (b) Schematic of carpet cloaking [40]; (c) The carpet cloaking is designed in a SOI wafer consisting of silicon and silica layers, where C1 is the gradient index cloaking and C2 is a uniform index background [41]; (d) The carpet cloaking designed from non-resonant metamaterial cells (left subfigure) and the relationship between unit cell geometry and effective index (right subfigure) [42]; (e) Scanning electron microscope images of the carpet cloaking designed from silicon nanopillars distributed in SOI wafers (top subfigure) and different densities of silicon pillars etched on SOI wafers (bottom subfigure) [40]; (f) Schematic diagram of the three-dimensional microwave carpet cloaking [43]; (g) Blueprint of the 3D carpet cloaking structure, with the 3D cone of light shown in red corresponding to the NA = 0.5 microscope lens [44]; (h) The triangular carpet cloaking is made of two calcite prisms glued together [45]; (i) Cross-sectional schematic of the cloaking implemented in a silicon nitride waveguide on a low-index nanoporous silicon oxide substrate [46]; (j) Experimental sample of a non-magnetic smart metamaterial invisibility cloaking, and the inset shows the effective dielectric constant curve versus Jacobian value [47]; (k) A planar electromagnetic wave at 1 GHz frequency passes through the carpet cloaking designed from Zn-Ni-Fe composites (blue) and air (white), surrounded by a background of polytetrafluoroethylene [48]; (l) Photographs of the 3D non-Euclidean metasurface carpet cloaking, with insets showing details of the closed metallic rings [49]; (m) Photograph of the full-polarization trapezoid conformal-skin cloaking sample, with the inset illustrating the phase profile along the central x-axis [50]; (n) Photographs of a sample of the carpet cloaking designed from cured resin cells (left subfigure) and a sample of cured resin cells (right subfigure) [51]
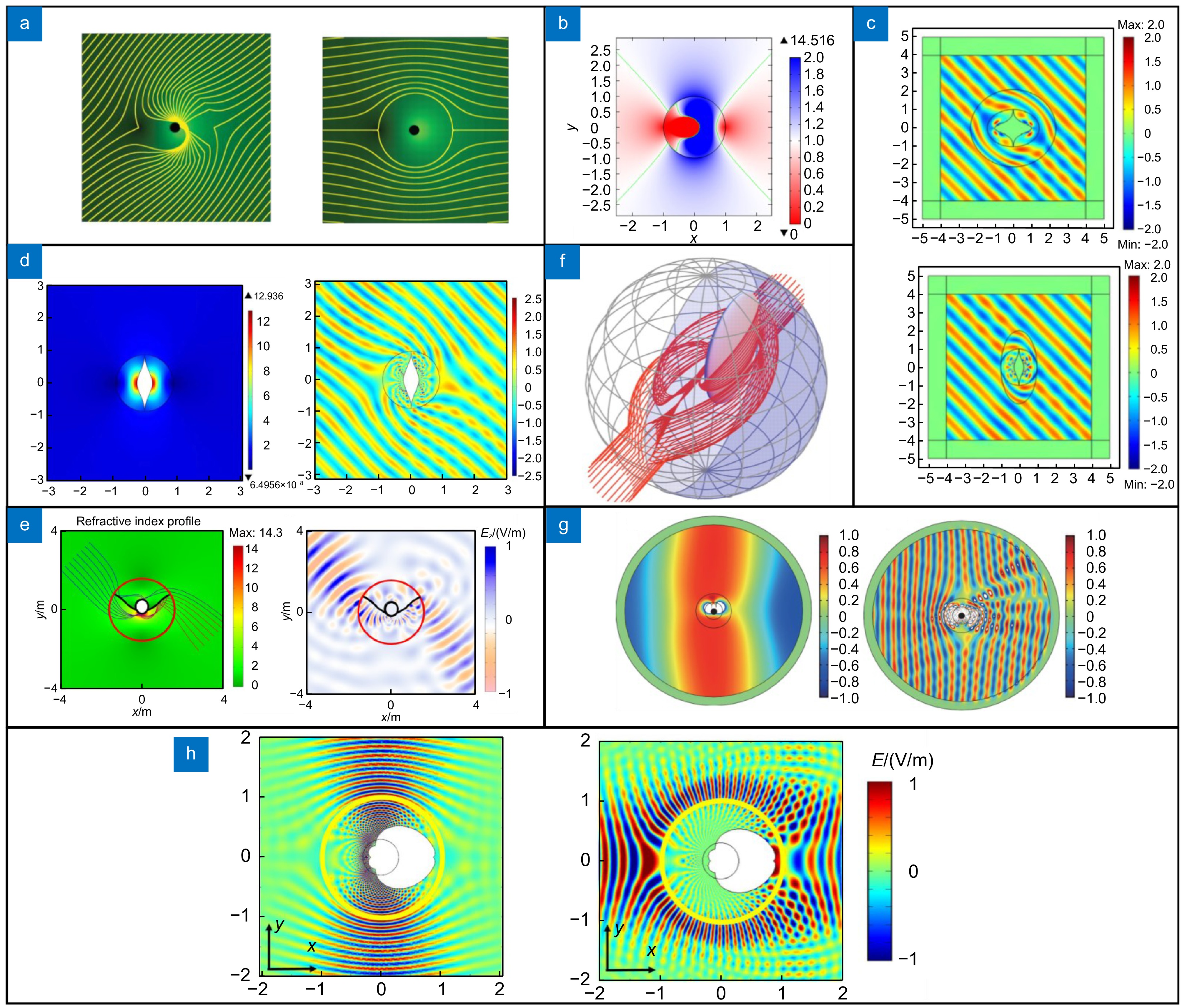
图 2 基于TO的原理图及基于TO的隐身衣示意图。 (a) TO中的参考空间(左图)与真实空间(右图)的关系[1];(b)球壳状隐身衣的球体剖面图[1];(c)由开环谐振器设计的微波隐身衣[74]. (d)用于λ=623.8 nm的圆柱形隐身衣,右图展示了圆柱形斗篷的一小部分,即纳米线全部垂直于圆柱体的内外界面[75];(e)由介质 A 层(蓝)和 B 层(灰)交替排列的同心层隐身衣[76];(f)基于开环谐振器的红外隐身衣扇区示意图[77];(g)由铜制的开环谐振器嵌入在介电介质中实现的隐身衣[78];(h)由开环谐振器和金属条实现的隐身衣[79];(i)测试隐形性能的实验装置图:隐身衣里坐着一只猫,一台投影仪通过隐形装置将影片投射到隐形装置后面的屏幕上,可以看到隐身装置的部分没有影子[80];(j)用于红外隐身的实验装置图[81];(k)多天线环境示意图和耦合减弱方法(左上图),天线 1 在自由空间辐射(右上图),天线 1 在圆柱形天线(天线 2)的存在下辐射(左下图),天线 2 被设计的隐身衣覆盖(右下图)[82];(l)在三维空间的三个正交方向上有效简化立方体隐身衣示意图[83];(m)由多个黄铜条和两个铝板组成的实验样品图[84];(n)全向超材料隐身衣以及其超材料单元设计[85];(o)通过金属板和电介质设计的全空间全向隐形结构的折射率分布图[86];(p)使用亚波长介电通道实现折射率从1到10的渐变以及金属板包围的均匀介电恢复核心的隐身衣示意图[87]; (q)实现全向隐身的超材料隐身衣示意图[88];(r) 由金属片和两个电介质组成的多波段隐身衣实验样品图[89];(s)左边两个图为制作的四层空间压缩 TO 超材料样品照片,右图为基于设计的全参数空间压缩 TO 超材料和法布里-佩罗层的理想隐身衣示意图[90]
Figure 2. Schematic diagram of TO and TO-based cloaking. (a) Relationship between reference space (left subfigure) and real space (right subfigure) in TO [1]; (b) Sphere cross-section of the spherical-shell cloaking [1]; (c) Microwave cloaking structure designed by split-ring resonators [74]; (d) For the cylindrical cloaking structure with λ = 623.8 nm, the right subfigure shows a small fraction of the cylindrical cloaking, i.e., the nanowires are all perpendicular to the cylinder’s inner and outer interfaces [75]; (e) Concentric layer cloaking structure with alternating layers of medium A (blue) and B (grey) [76]; (f) Schematic of infrared cloaking structure sector based on split-ring resonators [77]; (g) Photograph of the cloaking structure realized by copper split-ring resonators embedded in a dielectric medium [78]; (h) Photograph of the cloaking structure realized by split-ring resonators and metal strips [79]; (i) Diagram of the experimental setup for testing cloaking performance: a cat sits in the cloaking structure, and a projector projects a film through the cloaking device onto a screen behind the cloaking device, and parts of the cloaking device can be seen without shadows [80]; (j) Diagram of the experimental setup used for infrared cloaking [81]; (k) Schematic of multiple antenna environment and the proposed method to coupling reduction (top left subfigure), with antenna 1 radiating in free space (top right subfigure), and antenna 1 radiating in the presence of a cylindrical antenna (antenna 2) (bottom left subfigure), with antenna 2 being covered by a designed cloaking structure (bottom right subfigure) [82]; (l) Schematic diagram of an effective simplified cubic cloaking structure in three orthogonal directions in three-dimensional space [83]; (m) Diagram of the experimental sample with several copper bars and two aluminum plates [84]; (n) Omnidirectional metamaterial cloaking structure and its metamaterial cell design [85]; (o) Refractive index distribution of the full-space omnidirectional cloaking structure designed with metal plates and dielectrics [86]; (p) Schematic of the cloaking structure with sub-wavelength dielectric channels to achieve a refractive index gradient from 1 to 10, and a uniform dielectric core surrounded by metal plates [87]; (q) Schematic diagram of the metamaterial cloaking structure for omnidirectional cloaking [88]; (r) Diagram of the experimental sample of a multi-band cloaking structure with metal sheets and two types of dielectrics [89]; (s) The two left subfigures show photographs of fabricated four-layer space-compressed TO metamaterial samples, and the right subfigure shows a schematic view of the ideal cloaking based on the designed full-parameter spatial-compression TO metamaterial and the Fabry-Pérot layer [90]
图 3 基于OCM设计的隐身衣示意图。(a)光线在隐身装置中的传播,黄线为光线,绿色背景的亮度表示折射率轮廓,不可见区域显示为黑色[91];(b)可用于电声双场的隐身衣的折射率剖面图[92];(c)两个不同入射TE偏振波对两个不同映射的隐身衣的模拟结果[93]; (d)基于对数共形变换的优化折射率分布图(左图)和电场分布模式(右图)[94];(e) 左图为基于非欧几里得变换隐身衣的折射率剖面图及光线轨迹,右图为一束入射角为π/4 rad的高斯光束对隐身衣产生的电场分布[95];(f) 在三维空间中,一些光线会在双曲空间中进行两次循环,在物理空间中表现为光线缠绕在不可见的内部[96];(g)带有伊顿透镜的隐形效果:伊顿透镜被放置在下层薄片中,用于引导入射光线返回,使外部区域呈现出黑洞所代表的隐形效果。左图和右图分别是伊顿透镜在l=2阶和40阶谐波特征模对应的电场分布[97]; (h)双向隐形性能模拟,白色区域的边界代表反射镜[98]
Figure 3. Schematic of the OCM-based cloaking. (a) Propagation of light in the cloaking device, yellow line is the light, the brightness of the green background indicates the refractive index contour, and the invisible region is shown in black [91]; (b) Refractive index profile of the cloaking structure that can be used in electro-acoustic double fields [92]; (c) Simulation results of two different incident TE polarized waves on two different mapping cloaking structures [93]; (d) Optimized refractive index profile (left subfigure) and electric field distribution pattern (right subfigure) based on logarithmic conformal transformation [94]; (e) The left subfigure shows the refractive index profile and the ray trajectory of the cloaking structure based on the non-Euclidean transformation, and the right subfigure shows the electric field distribution generated by a Gaussian beam with an incidence angle of π/4 rad on the cloaking structure [95]; (f) In three dimensions, some rays turn out to perform two loops in hyperspace that appear in physical space as light wrapped around the invisible interior [96]; (g) Invisibility effect with Eaton lens: An Eaton lens is placed in the lower sheet to guide back the incident light, giving the outer region the invisibility effect represented by a black hole. The left and right subfigures show the electric field distributions corresponding to the l = 2 and 40 orders harmonic eigenmodes of the Eaton lens, respectively[97]; (h) Bidirectional cloaking performance simulation, the boundary of the white area represents the reflector [98]
图 4 基于几何光学的隐身衣示意图。(a)左图和右图分别为两个L形水箱和两个L形反射镜的隐身衣示意图[101];(b)利用四个光学透镜演示准轴向隐形原理[102];(c)隐身衣由安装在玻璃板上的偏振镜和反射镜组成[103];(d)二维数字积分隐形装置[104]
Figure 4. Schematic of the cloaking based on geometrical optics. (a) Schematic diagrams of the cloaking with two L-shaped water tanks and two L-shaped mirrors on the left and right, respectively [101]; (b) Demonstration of the principle of quasi-axial invisibility using four optical lenses [102]; (c) The cloaking consists of polarizers and mirrors that are attached on glass plates [103]; (d) 2D digital integral cloaking setup [104]
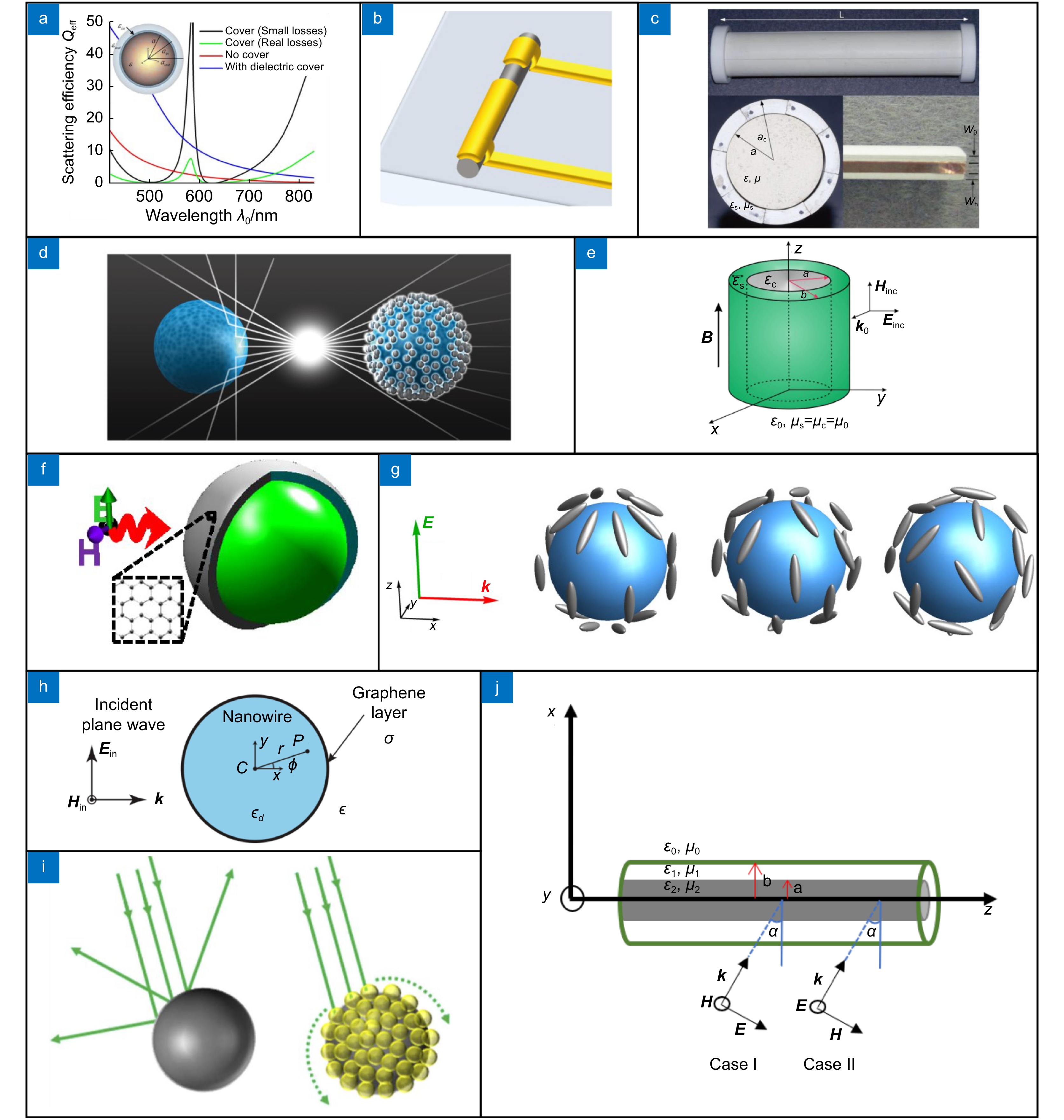
图 5 基于plasmonic外壳的隐身衣示意图。(a) 插图中描述的双层外壳隐身衣的几何形状,图中四条曲线分别表示四种情况的总散射效率[109];(b) 用两个金电极(黄色)连接硅纳米线(灰色)的示意图[32];(c)带端盖的测试圆筒上的组装隐身衣的照片 (上图);去掉端盖后的组装截面图(左下图);用于形成超材料隐身衣的金属铜带的壳段边缘(右下图)[110];(d) 左图表示电介质物体通过散射光线向外部观察者表示存在,右图表示由金属纳米粒子制成的外壳会散射与内核相同数量但相位不相等的光,这就抑制了散射场,故该物体无法被探测到[111];(e)一个无限长的非磁性圆柱体的示意图:介电常数为εc,半径为a,表面镀有磁导率为μ0、半径为 b>a 的磁光活性圆柱形外壳[112];(f)石墨烯外壳包裹的具有复介电常数介电球的示意图[113];(g)电介质球上分布着不同分布和方向的银椭球体[114];(h)表面电导率为σ的原子级薄石墨烯层包覆相对介电常数为εd的纳米级散射圆柱体的示意图,其中环境介质的介电常数为ε [115];(i)三维纳米裸球(左图)和涂有AuNPs的球体(右图)的光散射差异示意图[116];(j)斜入射下的锆氮化物(ZrN)核壳纳米线示意图[117]
Figure 5. Schematic of the cloaking structures based on plasmonic shells. (a) The geometry of the double-shell cloaking structure depicted in the inset, and the four curves in the figure represent the total scattering efficiency for each of the four cases [109]; (b) Schematic of a silicon nanowire (grey) hooked up by two gold electrodes (yellow) [32]; (c) Photographs of the assembled cloaking structure on the test cylinder with end caps (top subfigure); cross-section of the assembly with the end caps removed (bottom left subfigure); a shell segment edge with copper tape used to form the metallic strip for the metamaterial cloaking (bottom right subfigure) [110]; (d) The left subfigure represents a dielectric object reveals its presence to an external observer by scattering the light. The diagram on the right indicates that a shell made from metallic nanoparticles scatters the same amount of light as the core but π out-of-phase. This suppresses the scattered field. It therefore makes the object undetectable [111]; (e) Schematic representation of an infinitely long non-magnetic cylinder with dielectric constant εc and radius a, coated with a magneto-optical active cylindrical shell with magnetic permeability μ0 and radius b>a [112]; (f) Schematic representation of a dielectric sphere with complex dielectric constant wrapped in a graphene shell [113]; (g) The dielectric sphere is covered with silver ellipsoids of different distributions and orientations [114]; (h) Illustration of the atomically thin graphene layer of surface conductivity σ coating a nano-sized scattering cylinder of relative permittivity εd, where the environment medium has a permittivity ε [115]; (i) Schematic illustration of the difference in light scattering between 3D bare nanospheres (left subfigure) and spheres coated with AuNPs (right subfigure) [116]; (j) Schematic representation of zirconium nitride (ZrN) core-shell nanowires under oblique incidence [117]
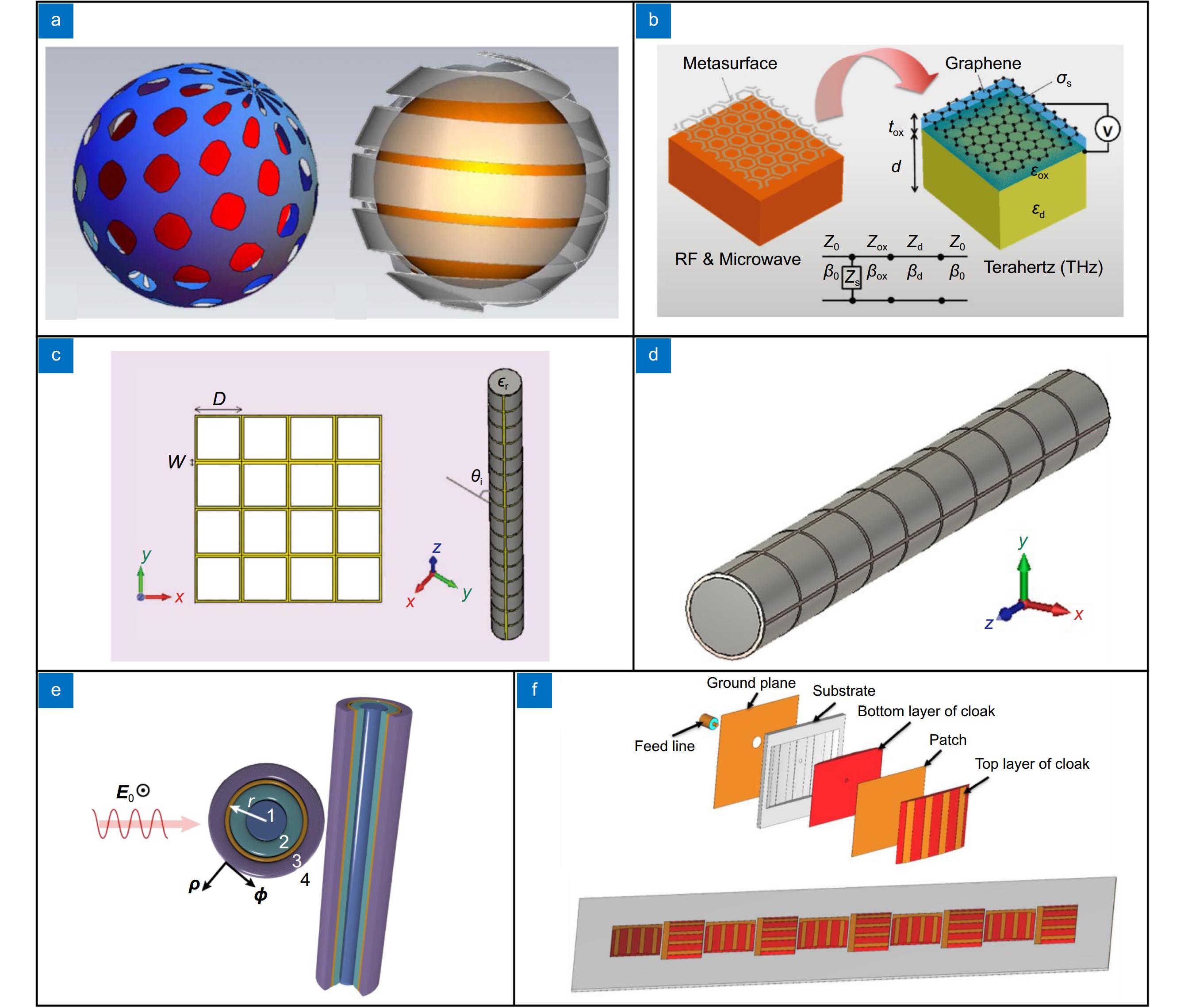
图 6 基于人造结构材料的隐身衣示意图。(a)可实现mantle cloaking的金属几何图案示例[119];(b)石墨烯超表面的示意图[128];(c) 网格FSS几何结构[122];(d) 双波段圆柱形mantle cloaking示意图[129];(e)多层无限长圆柱结构示意图[36];(f)上图为地幔隐形贴片天线的不同层的示意图,下图为两个同频交错隐形阵列的三维视图[127]
Figure 6. Schematic diagram of cloaking based artifical structural materials. (a) Examples of patterned metallic geometries that may realize a mantle cloaking[119]; (b) Diagram of the graphene metasurface [122]; (c) The mesh-grid FSS geometry [122]; (d) Schematic diagram of a dual-band cylindrical mantle cloaking[129]; (e) Schematic of a general multilayer infinitely long cylindrical structure [36]; (f) The top subfigure shows the schematic diagram of the different layers of the mantle cloaking patch antenna, and the bottom subfigure shows the three-dimensional view of two co-frequency interleaved cloaking arrays [127]
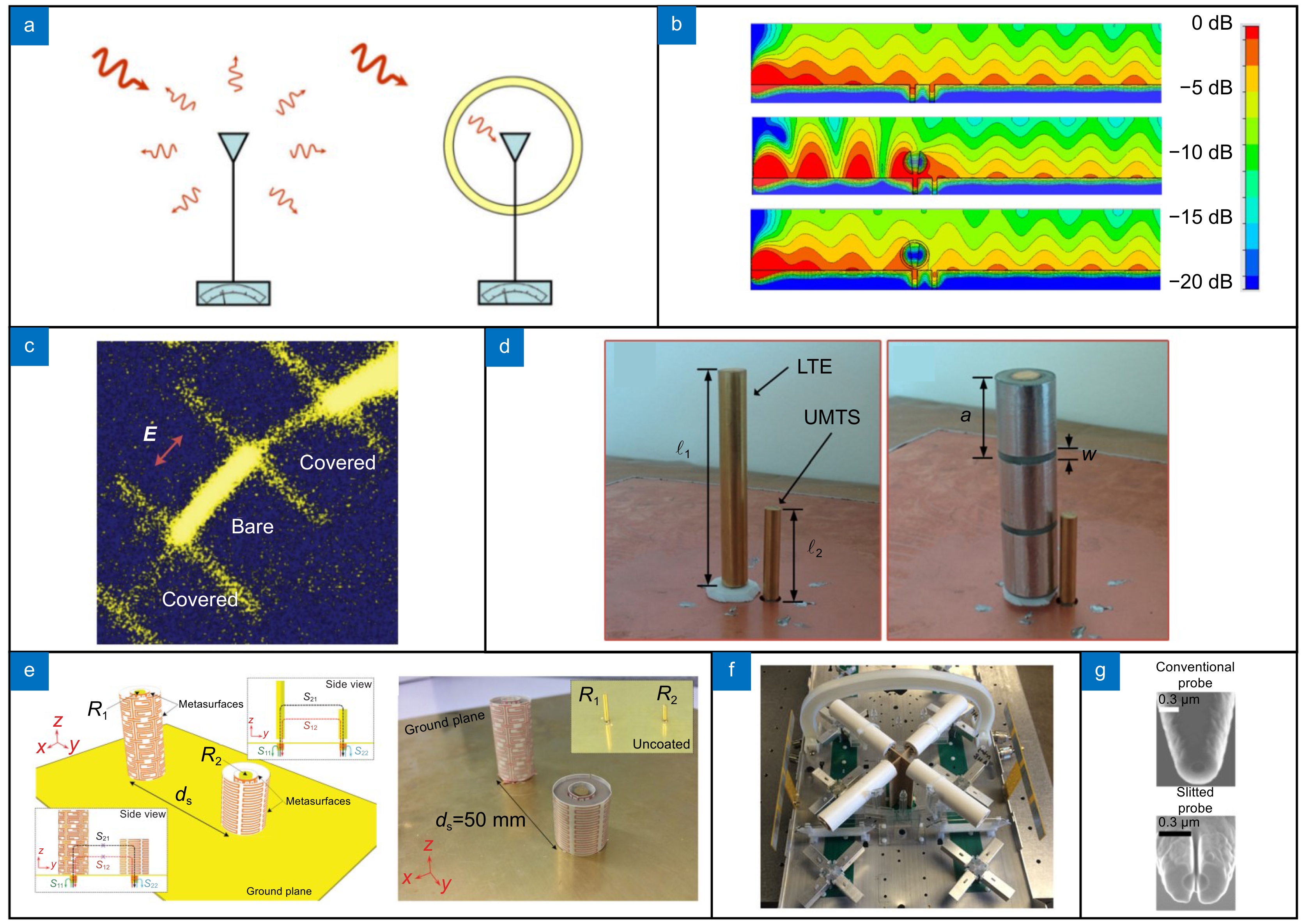
图 7 传感器隐身衣示意图。(a)传感器隐身的基本原理[29];(b) Plasmonic外壳用于实现近场扫描光学扫描显微镜探针的隐身效果模拟[31];(c)硅纳米线周围包裹金涂层和单独硅纳米裸线在共焦显微镜下的照片[32];(d)左图表示没有使用隐身衣的两个天线,右图表示在一个天线周围使用了散射抵消式隐身衣[34];(e)利用超表面将两个天线同时隐身的示意图(左图)和实物照(右图)[35];(f)利用超表面将偶极天线宽带隐身的实物图[36];(g)利用散射抵消隐身的机制实现对扫描显微镜探针的隐身:传统探头(上图)和引入开槽微结构的探头(下图)[37]
Figure 7. Schematic diagram of invisible sensors. (a) Basic principle of invisible sensors [29]; (b) Plasmonic shell used to achieve the cloaking effect simulation of the near-field scanning optical scanning microscope probe [31]; (c) Photographs of silicon nanowires surrounded by wrapped gold coating (covered) and silicon nanowires alone (bare) under confocal microscope [32]; (d) The left subfigure shows two antennas without the cloaking structure, and the right subfigure shows a scatter-cancelling cloaking structure around one antenna [34]; (e) Schematic (left subfigure) and physical photograph (right subfigure) of the simultaneous cloaking of two antennas using a metasurface [35]; (f) Photogragh of broadband cloaking of a dipole antenna using a metasurface [36]; (g) Cloak of a scanning microscope probe using a scatter-cancelling cloaking mechanism: a conventional probe (top subfigure) and a probe with the introduction of slotted microstructures (bottom subfigure) [37]
图 8 具有实验验证的基于优化算法的隐身衣示意图。(a)六层圆柱形隐身衣的样品图以及裸 PEC 内核和带有斗篷(黄色环形区域)的 PEC 周围的计算散射电能分布[170];(b) 由特氟龙制成“眼睑 ”状斗篷(白色),中心隐形区域由一个铝盘代替[138];(c)由丙烯腈-丁二烯-苯乙烯制成的隐身衣样品照片[176];(d)由介电聚乳酸介质方柱构成的隐身衣示意图[171]; (e)采用传统的印刷电路板技术制成的隐身衣样品照片[195];(f)透射元面隐形衣由两个平面元面组成,标为层1和层2,用于隐藏内部物体,例如一只猫[196]
Figure 8. Schematic diagram of cloaking structures based on optimization algorithm with experimental verification. (a) Sample view of the six-layer cylindrical cloaking structure and the calculated scattered electrical energy distribution around the bare PEC core and the PEC with the cloaking (yellow ringed area) [170]; (b) "Eyelid"-shaped cloaking made of Teflon (white) with the central cloaking region replaced by an aluminum disk [138]; (c) Photograph of a sample cloaking structure made of acrylonitrile-butadiene-styrene [176]; (d) Schematic of a cloaking structure made of dielectric PLA dielectric square columns [171]; (e) Photograph of a sample invisibility cloaking structure made using conventional printed circuit board technology [195]; (f) Transmissive metasurface cloaking consisting of two planar metasurfaces labelled Layer 1 and Layer 2 used to hide an internal object, e.g. a cat [196]
表 1 全空间隐身结构和半空间隐身结构的主要区别
Table 1. Main differences between full-space and carpet cloaking structures
全空间隐身结构 半空间隐身结构 观察方向 任意方向 地面的一侧 工作带宽 完美参数下只能窄带;牺牲性能可以宽带 完美参数可以宽带 效果 物体散射截面为零,对外不可见 将一个存在凸起的地面对外界看上去是一个平坦的地面 材料 复杂:各向异性、非均匀、磁性材料、奇异点 对特殊偏振使用拟共形变换可是材料很大程度简化,
仅需渐变折射率介质即可实现设计方法 变换光学、光学共形变换、优化算法 变换光学、拟光学共形变换、优化算法 工作环境 自由空间 地面附近 已经获得实
验的频段微波、光波、红外、静磁场和静电场 微波、光波、红外 表 2 具有实验验证的半空间隐身的研究历程
Table 2. Research history of carpet cloaking with experimental validation
年份 偏振 频率(波长)
/波段工作角度 材料 是否实验
验证2009[41] 图1(c) TM 1400~1800 nm 二维面内波30°和60°入射有效 由250 nm的Si层和3 μm的
SiO2层组成的SOI 晶圆是 2009[42] 图1(d) TE 13~16 GHz 二维面内波40°入射有效 由非共振超材料单元实现
折射率从1.08到1.67的渐变2009[40] 图1(e) TE 1550 nm 二维面内波45°入射有效 50 nm的硅纳米柱分布在 SOI 晶圆中
实现折射率从1.45到2.42的渐变2010[43] 图1(f) TE 9~12 GHz 二维面内波45°入射有效 通过在多层电介质板(由聚四氟乙烯和玻璃纤维组成)上钻不均匀孔实现折射率从1到1.63 2010[44] 图1(g) 非偏振光 1.5~2.6 μm 二维面内波0°~60°入射有效 具有特定聚合物填充分数的木堆
结构光子晶体实现折射率从1到1.522011[45] 图1(h) TM 532 nm和650 nm 二维面内波39.5°、64.5°和88°入射有效 天然双折射晶体方解石 2011[46] 图1(i) TE 400~700 nm 二维面内波45°入射有效 硅氮化物波导打孔实现折射率小于1.25 2012[47] 图1(j) TE 10~12 GHz 二维面内波0°~90°入射有效 硅胶橡胶圈单元实现折射率从1到2.88 2015[48] 图1(k) TM 1 GHz 二维面内波 Zn-Ni-Fe复合材料和空气层构成的层状结构 2020[49] 图1(l) 双偏振光 4~12 GHz 二维面内波0°、30°、90°和135°有效 闭合谐振环嵌入到光固化树脂基底中 2021[50] 图1(m) 双偏振光 15.5 GHz 二维面内波0°~45°入射有效 各向异性金属-绝缘体-金属
反射型超原子排列构成2023[51] 图1(n) 双偏振光 10 GHz 二维面内波任意入射角有效 由固化树脂单元格实现介电常数为2.9 表 3 基于TO的光线绕射式隐身衣
Table 3. Structures of TO-based light-bypassing cloaking
年份 偏振 频率(波长)/波段 方向性 结构 材料 是否实验验证 2006[74] 图1(c) TE 8.5 GHz 全向二维面内波 圆柱形结构 开环谐振器 是 2007[75] 图1(d) TM 632.8 nm 全向二维面内波 电介质中嵌入尺寸
渐变的纳米线否 2007[76] 图1(e) TM 取决于其中介电常
数趋向于0的超材料
单元的工作频段全向二维面内波 介电常数大于1和趋向于
0的两种亚波长圆环状介
质交错排列否 2008[77] 图1(f) TM 100 THz 全向二维面内波 开环谐振器 否 2009[78] 图1(g) TM 11 GHz 全向二维面内波 铜制的开环谐振器嵌入在
介电介质中是 2012[79] 图1(h) TE 10.2 GHz 单向二维面内波 开环谐振器和金属条 是 2013[80] 图1(i) 双偏振光 380~780 nm 四/六个方向
二维面内波三维四/六角形结构 光学玻璃和空气组合设计 是 2015[81] 图1(j) 双偏振光 1.8~18 μm 三维空间中对单个
方向入射的探测波四个等腰三角形和四个直角
三角形围成的多边形结构折射率为4的锗块 是 2017[82] 图1(k) TM 1~4 GHz 四个方向二维面内波 三维方形结构 渐变折射率介质 否 2018[83] 图1(l) 双偏振光 532 nm, 650 nm 三维空间中对三个
独立方向有效立方体结构 玻璃四棱锥和七面体的玻璃 是 2019[84] 图1(m) TM 2.83 cm 单向二维面内波 多层菱形结构 由多个黄铜条和两个铝板
组成的波导结构是 2019[85] 图1(n) TM 9.8 GHz 全向二维面内波 长方体结构 非谐振超材料 是 2022[86] 图1(o) TM 1 cm 全向二维面内波 二维正方形结构 使用亚波长金属通道填充均匀
各向同性介质实现折射率从1
到2的渐变否 2023[87] 图1(p) TM 5 m 全向二维面内波 二维球形结构 使用亚波长介电通道实现折射
率从1到10的渐变以及金属板
包围的均匀介电恢复核心否 2023[88] 图1(q) TE 5 GHz 全向二维面内波 长方柱 金属阵列超材料 是 2024[89] 图1(r) TM 5 GHz, 10 GHz 全向二维面内波 三维三角形外接三个
半圆的结构填充电介质的亚波长
金属槽阵列是 2024[90] 图1(s) TM 8 GHz 单向二维面内波 多层菱形结构 两个相互垂直的分形环谐
振器实现的超材料单元格是 表 4 基于OCM的光线绕射式隐身衣
Table 4. Structures of OCM-based light-bypassing cloaking
年份 偏振 频率/波段 方向性 结构 材料 是否实验
验证2006[91] 图3(a) TE 取决于实现所需
渐变折射率材料
的超材料单元工
作的频段单向二维面内波 圆柱状结构 折射率为正的渐变折射率材料 否 2012[92] 图3(b) TE 单向二维面内波 三维球形结构 折射率从0到2的渐变折射率材料 2013[93] 图3(c) TE 单向二维面内波 三维球形结构 渐变介电常数和磁导率,
存在磁各向异性2016[94] 图3(d) TE 单向二维面内波 二维结构 折射率从9.779到 12.936的
渐变折射率材料2024[95] 图3(e) TE 单向二维面内波 三维球形结构 折射率从零到十几的
渐变折射率材料2009[96] 图3(f) TE 单向二维面内波 三维球形 折射率为正的渐变折射率材料 2012[97] 图3(g) 波长非常小的几何光学
近似下的双偏振全向二维面内波 圆柱状结构 在下层黎曼片放置伊顿透镜,
透镜是由正负折射率材料复合而成2018[98] 图3(h) TE 双向二维面内波 二维结构 渐变折射率材料填充 表 5 基于几何光学的光线绕射式隐身衣
Table 5. Structures of light-bypassing cloaking based on geometrical optics
表 6 不同方法的光线绕射式隐身衣特点与局限性
Table 6. Structural characteristics and limitations of light bypassing cloaking with different methods
理论方法 特点 局限性 TO ● 可用于设计三维隐身衣;
● 探测波幅度和相位均未改变的完美隐身。● 材料复杂:可能需要磁性材料、各向异性非均匀介质、存在奇异点等;
● 需要坐标变换、张量计算等数学推导;
● 实验验证困难,需要简化参数、牺牲偏振;
● 通常窄带工作。保形变换 ● 无需磁性材料;
● 无需各向异性介质;
● 探测波幅度和相位均未改变的完美隐身。● 针对于TE偏振或者几何光学近似下有效;
● 需要非均匀介质;
● 仅限于二维隐身衣;
● 实验验证困难,需要简化参数;
● 通常窄带工作。几何光学 ● 可见光波段的宽带隐身;
● 容易实验验证;
● 全偏振有效。● 观察角度受限制,无法实现全方向隐身;
● 只保证光线绕过隐藏区域后恢复原先轨迹,
但不保证电磁波相位在入射和出射隐身结构前后不变。表 7 基于plasmonic 外壳实现的散射抵消式隐身
Table 7. Scatter-cancelling cloaking implemented based on plasmonic shells
年份 偏振 频率/波段 结构 材料和被隐藏物体 是否实验
验证2008[109] 图5(a) 双偏振 500 nm和625 nm 球壳镀膜 Drude色散模型的工作频率处介电常
数为0.2的两层plasmonic外壳,
将相对介电常数为3的介质球隐身否 2012[32] 图5(b) TM 600 nm 有限高的圆柱镀膜 通过金膜将存在吸收的硅纳米线隐身 是 2012[110] 图5(c) TM 3~3.3 GHz 有限高的圆柱镀膜 通过高介电常数材料中嵌入铜片,
将相对介电常数为3的介质柱隐身是 2013[111] 图5(d) 双偏振 338 nm 球壳镀膜 通过银纳米粒子非晶态排列,
将半径为55 nm、介电常数为2.18的
熔融二氧化硅球隐身否 2013[112] 图5(e) TM 2.93 THz 无限高的圆柱镀膜 通过磁光材料,将介质柱隐身 否 2013[113] 图5(f) 双偏振 58 THz附近 球壳镀膜 通过石墨烯,将半径为100 nm的、
相对介电常数为3的介质球隐身否 2016[114] 图5(g) 单偏振,与椭球分
布的取向有关430~700 THz范围内随着
椭球的长宽比和分布方式
而改变球形结构 用24个银椭球分散地包裹在介质
球周围,实现对半径为61 nm相对
介电常数为2.1的介质球隐身否 2017[115] 图5(h) TM 10~50 μm范围内根据石墨
烯管的化学势调节无限高的圆柱镀膜 通过石墨烯管,将半径为0.5 μm的、
相对介电常数为3.9二氧化硅纳米线否 2020[116] 图5(i) 双偏振 400~600 nm 球壳镀膜 通过金纳米粒涂层,将直径为
55 nm、折射率为1.4的硅球隐身否 2020[117] 图5(j) 双偏振 400~800 nm范围内与使用
外壳的金属材料选取和
厚度有关无限高的圆柱结构 锆氮化物(ZrN)作为涂层,将直径为
28 nm的硅纳米线隐身否 表 8 基于人造结构材料的散射抵消式隐身
Table 8. Scatter-cancelling cloaking based on artifical structural materials
年份 偏振 频率/波段 结构 材料和被隐藏物体 是否实验
验证2009[119]
图6(a)双偏振 在微波段可以根据需要设计 球壳周围包裹具有
结构的金属表面电抗分别为175 Ω和92 Ω的频率选择表面,将半
径为工作波长十分之一的介质球(εr=10)和金属球隐身否 2011[128]
图6(b)TE 通过改变石墨烯化学势可在
2~7 THz范围内调节无限高的圆柱镀膜 单层石墨烯包裹在介电常数为3.9的介质柱,
实现对介质柱的隐身是 2018[122]
图6(c)TM 3.4~3.7 GHz 圆柱体结构 矩形铜网格组成的频率选择表面,将介电常数为2.7、
高度为1 m的聚氯乙烯柱子中间0.51 m部分隐身是 2023[129]
图6(d)TM 2.05 GHz和3.75 GHz 圆柱体结构 两套不同周期的金属矩形频率选择表面,
将金属柱隐身是 2022[36]
图6(e)TM 1.7~2.7 GHz 圆柱体结构 刻有特殊分布微带线的印刷电路板,
将金属柱子组成的偶极天线隐身是 2023[127]
图6(f)TM 3.7 GHz 椭圆柱 金属贴片阵列天线结构,将椭圆柱隐身;
实验仅测量了金属贴片组成平板结构的
反射系数,并未用于真实椭圆柱结构。是 表 9 基于不同材料的散射抵消式隐身衣特点与局限性
Table 9. Structural characteristics and limitations of scatter-cancelling cloaking based on different materials
材料 特点 局限性 plasmonic外壳 ● 可以具有一定的工作带宽;
● 无需磁性材料;
● 无需各向异性介质;● 通常被隐藏物体是金属或者介质,且形状规则;
● 通常对电小尺寸物体隐身,当被隐藏物体尺寸增大时,
需要多层plasmonic外壳来抵消高阶散射级次。人造结构材料 ● 可以具有一定的工作带宽;
● 无需磁性材料;
● 可以仅用一层表面结构实现。● 通常被隐藏物体是金属或者介质,且形状规则;
● 实验验证主要在射频和微波段,光波段利用石墨烯层的
设计缺乏实验验证;
● 通常对电小尺寸物体隐身,当被隐藏物体尺寸增大时,
需要多层人造结构材料来抵消高阶散射级次。互补介质 ● 隐身衣和被隐藏物体在空间位置上分离;
● 被隐藏物体材料、尺寸、形状均不受限制;
● 完美的散射抵消,不仅仅限于某个散射级次的抵消。● 只能窄带工作;
● 实验验证困难。表 10 传感器隐身的研究进展
Table 10. Research progress on invisible sensors
年份 频率/波段 主要工作 是否实验验证 2009[29]
图7(a)微波段,工作频率可
根据需要设计在3个正交的偶极天线周围包裹了介电常数为0.1的plasmonic球壳,
保持其接受到的电压最大,但是散射截面显著降低。否 2010[31]
图7(b)500 THz 在球形探针外部包裹了plasmonic球壳,用于对银和空气表面的表面等
离子体极化子波检测时,可在不影响表面电场分布的同时,收集表面的电磁能量。否 2012[32]
图7(c)600 nm 在硅纳米线周围包裹金层后,TM偏振光照射结构下,可基本维持硅纳米线的
光电流产生率,同时在共焦显微镜下对整个结构隐身。是 2016[34]
图7(d)1900~2200 MHz 用金属带状超表面包住圆柱状低频天线后,放置在另外一个高频天线的近场区域,
获得了低频天线不影响高频天线近远场辐射分布的隐身效果。是 2017[35]
图7(e)2.4 GHz和5.2 GHz 用超表面分别包裹在两个单极子天线周围,实现了两个天线之间的相互隐身。 是 2022[36]
图7(f)1.7~2.7 GHz 特殊分布微带线的超表面结构包括在尺寸较大的十字形偶极天线周围,
使其对旁边尺寸更小的十字形偶极天线阵列宽带隐身。是 2022[37]
图7(g)1576 nm 近场光学扫描显微镜探针表面引入开槽的表面结构,
将扫描探针对外界电磁场分布的扰动减少超过70%。是 表 11 具有实验验证的基于优化算法设计的隐身衣
Table 11. Cloaking structures with experimentally verified design based on optimization algorithm
年份 偏振 频率/波段 结构 材料 基于的优化算法 工作维度 是否实验
验证2012[170] 图8(a) TE 1.89~2.08 GHz 6层柱状结构 非谐振的闭环超材料 基因算法 二维面内波 是 2013[138] 图8(b) TE 14.7~15.6 GHz 不连续的“眼睑”状结构 介电常数为2的特氟龙 拓扑优化 2013[176] 图8(c) TE 9.7~10.1 GHz 带有空隙的圆柱结构 介电常数为2.45的ABS 拓扑优化 2018[171] 图8(d) TM 10 GHz 椭圆柱结构 介电常数为2.4的介电聚乳酸介质方柱 基因算法 2020[195] 图8(e) TM 6.7~9.2 GHz 地毯式结构 F4B材料作为基板,使用传统的
印刷电路板技术制造的超表面深度学习 2021[196] 图8(f) TM 7.5~9 GHz 两个平行的超表面 由多个子波长超表面元构成的
两个平行平面的超表面神经网络 -
[1] Pendry J B, Schurig D, Smith D R. Controlling electromagnetic fields[J]. Science, 2006, 312(5781): 1780−1782. doi: 10.1126/science.1125907
[2] Chen H Y, Chan C T, Sheng P. Transformation optics and metamaterials[J]. Nat Mater, 2010, 9(5): 387−396. doi: 10.1038/nmat2743
[3] Xu L, Chen H Y. Transformation metamaterials[J]. Adv Mater, 2021, 33(52): 2005489. doi: 10.1002/adma.202005489
[4] Luo J, Xu P, Chen H Y, et al. Realizing almost perfect bending waveguides with anisotropic epsilon-near-zero metamaterials[J]. Appl Phys Lett, 2012, 100(22): 221903. doi: 10.1063/1.4723844
[5] Pu M B, Ma X L, Li X, et al. Merging plasmonics and metamaterials by two-dimensional subwavelength structures[J]. J Mater Chem C, 2017, 5(18): 4361−4378. doi: 10.1039/C7TC00440K
[6] 朱潜, 田翰闱, 蒋卫祥. 电磁超表面对辐射波的调控与应用[J]. 光电工程, 2023, 50(9): 230115. doi: 10.12086/oee.2023.230115
Zhu Q, Tian H W, Jiang W X. Manipulations and applications of radiating waves using electromagnetic metasurfaces[J]. Opto-Electron Eng, 2023, 50(9): 230115. doi: 10.12086/oee.2023.230115
[7] Liang s://doi.org/10.12086/oee.2024.240068.
[8] 范辉颖, 罗杰. 无反射电磁超构表面研究进展[J]. 光电工程, 2023, 50(9): 230147. doi: 10.12086/oee.2023.230147
Fan H Y, Luo J. Research progress of reflectionless electromagnetic metasurfaces[J]. Opto-Electron Eng, 2023, 50(9): 230147. doi: 10.12086/oee.2023.230147
[9] Ma X L, Pan W B, Huang C, et al. An active metamaterial for polarization manipulating[J]. Adv Opt Mater, 2014, 2(10): 945−949. doi: 10.1002/adom.201400212
[10] Nan T, Zhao H, Guo J Y, et al. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces[J]. Opto-Electron Sci, 2024, 3(5): 230052. doi: 10.29026/oes.2024.230052
[11] Fu R, Chen K X, Li Z L, et al. Metasurface-based nanoprinting: principle, design and advances[J]. Opto-Electron Sci, 2022, 1(10): 220011. doi: 10.29026/oes.2022.220011
[12] Wei P J, Xiao S Y, Xu Y D, et al. Metasurface-loaded waveguide for transformation optics applications[J]. J Opt, 2016, 18(4): 044015. doi: 10.1088/2040-8978/18/4/044015
[13] Chen H Y, Miao R X, Li M. Transformation optics that mimics the system outside a Schwarzschild black hole[J]. Opt Express, 2010, 18(14): 15183−15188 doi: 10.1364/OE.18.015183
[14] Zhang Z B, Zhao P F, Liao J K, et al. Vortex decomposition and reconfiguration via transformation optics[J]. Phys Rev Appl, 2024, 21(5): 054006. doi: 10.1103/PhysRevApplied.21.054006
[15] Jie S S, Xue S W, Yang Z W, et al. Shear polaritons from transformation optics[J]. Opt Lett, 2023, 48(10): 2688−2691. doi: 10.1364/OL.486774
[16] Xu Y D, Fu Y Y, Chen H Y. Steering light by a sub-wavelength metallic grating from transformation optics[J]. Sci Rep, 2015, 5(1): 12219. doi: 10.1038/srep12219
[17] Liu Y C, Sun F, He S L. Novel thermal lens for remote heating/cooling designed with transformation optics[J]. Opt Express, 2016, 24(6): 5683−5692. doi: 10.1364/OE.24.005683
[18] Xu R L, Chen Z N. A hemispherical wide-angle beamsteering near-surface focal-plane metamaterial luneburg lens antenna using transformation-optics[J]. IEEE Trans Antennas Propag, 2022, 70(6): 4224−4233. doi: 10.1109/TAP.2021.3138554
[19] Sun F, Guo S W, Liu Y C, et al. A magnifying glass for virtual imaging of subwavelength resolution by transformation optics[J]. Adv Mater, 2018, 30(30): 1801641. doi: 10.1002/adma.201801641
[20] Yang C F, Huang M, Yang J J, et al. Design of open devices based on multi-folded transformation optics[J]. J Phys Commun, 2020, 4(4): 045007. doi: 10.1088/2399-6528/ab8266
[21] Peng L, Liu D Q, Cheng H F, et al. A multilayer film based selective thermal emitter for infrared stealth technology[J]. Adv Opt Mater, 2018, 6(23): 1801006. doi: 10.1002/adom.201801006
[22] Wu Y, Tan S J, Zhao Y, et al. Broadband multispectral compatible absorbers for radar, infrared and visible stealth application[J]. Prog Mater Sci, 2023, 135: 101088. doi: 10.1016/j.pmatsci.2023.101088
[23] Kim S H, Lee S Y, Zhang Y L, et al. Carbon-based radar absorbing materials toward stealth technologies[J]. Adv Sci, 2023, 10(32): 2303104. doi: 10.1002/advs.202303104
[24] Chen H H, Ma W L, Huang Z Y, et al. Graphene-based materials toward microwave and terahertz absorbing stealth technologies[J]. Adv Opt Mater, 2019, 7(8): 1801318. doi: 10.1002/adom.201801318
[25] Gartner Z J, Hu J L. Guiding tissue-scale self-organization[J]. Nat Mater, 2021, 20(1): 2−3. doi: 10.1038/s41563-020-00885-1
[26] Zhao Y, Ji G B. Multi-spectrum bands compatibility: new trends in stealth materials research[J]. Sci China Mater, 2022, 65(11): 2936−2941. doi: 10.1007/s40843-022-2074-5
[27] Kim J, Han K, Hahn J W. Selective dual-band metamaterial perfect absorber for infrared stealth technology[J]. Sci Rep, 2017, 7(1): 6740. doi: 10.1038/s41598-017-06749-0
[28] Balaji Ananth P, Abhiram N, Hari Krishna K, et al. Synthesis of radar absorption material for stealth application[J]. Mater Today: Proc, 2021, 47: 4872−4878. doi: 10.1016/j.matpr.2021.06.196
[29] Alù A, Engheta N. Cloaking a sensor[J]. Phys Rev Lett, 2009, 102(23): 233901. doi: 10.1103/PhysRevLett.102.233901
[30] Greenleaf A, Kurylev Y, Lassas M, et al. Cloaking a sensor via transformation optics[J]. Phys Rev E, 2011, 83(1): 016603. doi: 10.1103/PhysRevE.83.016603
[31] Alù A, Engheta N. Cloaked near-field scanning optical microscope tip for noninvasive near-field imaging[J]. Phys Rev Lett, 2010, 105(26): 263906. doi: 10.1103/PhysRevLett.105.263906
[32] Fan P Y, Chettiar U K, Cao L Y, et al. An invisible metal-semiconductor photodetector[J]. Nat Photonics, 2012, 6(6): 380−385. doi: 10.1038/nphoton.2012.108
[33] Vellucci S, Monti A, Barbuto M, et al. Satellite applications of electromagnetic cloaking[J]. IEEE Trans Antennas Propag, 2017, 65(9): 4931−4934. doi: 10.1109/TAP.2017.2722865
[34] Monti A, Soric J, Barbuto M, et al. Mantle cloaking for co-site radio-frequency antennas[J]. Appl Phys Lett, 2016, 108(11): 113502. doi: 10.1063/1.4944042
[35] Jiang Z H, Sieber P E, Kang L, et al. Restoring intrinsic properties of electromagnetic radiators using ultralightweight integrated metasurface cloaks[J]. Adv Funct Mater, 2015, 25(29): 4708−4716. doi: 10.1002/adfm.201501261
[36] Soric J, Ra’di Y, Farfan D, et al. Radio-transparent dipole antenna based on a metasurface cloak[J]. Nat Commun, 2022, 13(1): 1114. doi: 10.1038/s41467-022-28714-w
[37] Arango F B, Alpeggiani F, Conteduca D, et al. Cloaked near-field probe for non-invasive near-field optical microscopy[J]. Optica, 2022, 9(7): 684−691. doi: 10.1364/OPTICA.449216
[38] Li J, Pendry J B. Hiding under the carpet: a new strategy for cloaking[J]. Phys Rev Lett, 2008, 101(20): 203901. doi: 10.1103/PhysRevLett.101.203901
[39] Zhang P, Jin Y, He S L. Cloaking an object on a dielectric half-space[J]. Opt Express, 2008, 16(5): 3161−3166. doi: 10.1364/OE.16.003161
[40] Gabrielli L H, Cardenas J, Poitras C B, et al. Silicon nanostructure cloak operating at optical frequencies[J]. Nat Photonics, 2009, 3(8): 461−463. doi: 10.1038/nphoton.2009.117
[41] Valentine J, Li J, Zentgraf T, et al. An optical cloak made of dielectrics[J]. Nat Mater, 2009, 8(7): 568−571. doi: 10.1038/nmat2461
[42] Liu R, Ji C, Mock J J, et al. Broadband ground-plane cloak[J]. Science, 2009, 323(5912): 366−369. doi: 10.1126/science.1166949
[43] Ma H F, Cui T J. Three-dimensional broadband ground-plane cloak made of metamaterials[J]. Nat Commun, 2010, 1(1): 21. doi: 10.1038/ncomms1023
[44] Ergin T, Stenger N, Brenner P, et al. Three-dimensional invisibility cloak at optical wavelengths[J]. Science, 2010, 328(5976): 337−339. doi: 10.1126/science.1186351
[45] Chen X Z, Luo Y, Zhang J J, et al. Macroscopic invisibility cloaking of visible light[J]. Nat Commun, 2010, 2(1): 176. doi: 10.1038/ncomms1176
[46] Gharghi M, Gladden C, Zentgraf T, et al. A carpet cloak for visible light[J]. Nano Lett, 2011, 11(7): 2825−2828. doi: 10.1021/nl201189z
[47] Shin D, Urzhumov Y, Jung Y, et al. Broadband electromagnetic cloaking with smart metamaterials[J]. Nat Commun, 2012, 3(1): 1213. doi: 10.1038/ncomms2219
[48] Shi X H, Gao F, Lin X, et al. Electromagnetic detection of a perfect carpet cloak[J]. Sci Rep, 2015, 5(1): 10401. doi: 10.1038/srep10401
[49] Jiang Z J, Liang Q X, Li Z H, et al. A 3D carpet cloak with non-euclidean metasurfaces[J]. Adv Opt Mater, 2020, 8(19): 2000827. doi: 10.1002/adom.202000827
[50] Xu H X, Hu G W, Wang Y Z, et al. Polarization-insensitive 3D conformal-skin metasurface cloak[J]. Light Sci Appl, 2021, 10(1): 75. doi: 10.1038/s41377-021-00507-8
[51] Maegawa Y, Nakata Y, Sanada A. All-dielectric carpet cloaks with three-dimensional anisotropy control[J]. Nanophotonics, 2023, 12(13): 2623−2636. doi: 10.1515/nanoph-2022-0786
[52] Lv C, Ding P, Tian X M, et al. Broadband and wide-angle terahertz carpet cloaks based on pattered graphene metasurfaces[J]. J Phys D Appl Phys, 2020, 53(15): 155107. doi: 10.1088/1361-6463/ab6d1d
[53] Tian X M, Xu J W, Xu K, et al. Phase-change reconfigurable metasurface for broadband, wide-angle, continuously tunable and switchable cloaking[J]. Opt Express, 2021, 29(4): 5959−5971. doi: 10.1364/OE.418200
[54] Fallah A, Kalhor A, Yousefi L. Developing a carpet cloak operating for a wide range of incident angles using a deep neural network and PSO algorithm[J]. Sci Rep, 2023, 13(1): 670. doi: 10.1038/s41598-023-27458-x
[55] Esfahani A M, Yousefi L. Low profile multi-layered invisibility carpet cloak using quantum dot core-shell nanoparticles[J]. Sci Rep, 2023, 13(1): 3450. doi: 10.1038/s41598-023-30389-2
[56] Fakheri M H, Abdolali A. Ultrathin carpet cloak enabled by infinitely anisotropic medium[J]. Sci Rep, 2023, 13(1): 17695. doi: 10.1038/s41598-023-44984-w
[57] Sun F, Zheng B, Chen H S, et al. Transformation optics: from classic theory and applications to its new branches[J]. Laser Photonics Rev, 2017, 11(6): 1700034. doi: 10.1002/lpor.201700034
[58] Zhang B L. Electrodynamics of transformation-based invisibility cloaking[J]. Light Sci Appl, 2012, 1(10): e32. doi: 10.1038/lsa.2012.32
[59] Greenleaf A, Kurylev Y, Lassas M, et al. Cloaking devices, electromagnetic wormholes, and transformation optics[J]. SIAM Rev, 2009, 51(1): 3−33. doi: 10.1137/080716827
[60] van Dantzig D. The fundamental equations of electromagnetism, independent of metrical geometry[J]. Math Proc Camb Phil Soc, 1934, 30(4): 421−427. doi: 10.1017/S0305004100012664
[61] Dolin L S. On the possibility of comparison of three-dimensional electromagnetic systems with non-uniform anisotropic filling. Izv. VUZov, Radiofizika[J], 1961, 4(5): 964–967.
[62] Lax M, Nelson D F. Maxwell equations in material form[J]. Phys Rev B, 1976, 13(4): 1777−1784. doi: 10.1103/PhysRevB.13.1777
[63] Ward A J, Pendry J B. Refraction and geometry in Maxwell's equations[J]. J Mod Opt, 1996, 43(4): 773−793. doi: 10.1080/09500349608232782
[64] Teixeira F L, Chew W C. Lattice electromagnetic theory from a topological viewpoint[J]. J Math Phys, 1999, 40(1): 169−187. doi: 10.1063/1.532767
[65] Teixeira F L, Chew W C. Differential forms, metrics, and the reflectionless absorption of electromagnetic waves[J]. J Electromagn Waves Appl, 1999, 13(5): 665−686. doi: 10.1163/156939399X01104
[66] Leonhardt U, Philbin T. Geometry and Light: The Science of Invisibility[M]. North Chelmsford: Courier Corporation, 2010.
[67] Chen H Y. Transformation optics in orthogonal coordinates[J]. J Opt A Pure Appl Opt, 2009, 11(7): 075102. doi: 10.1088/1464-4258/11/7/075102
[68] Miñano J C, Benítez P, González J C. Perfect imaging with geodesic waveguides[J]. New J Phys, 2010, 12(12): 123023. doi: 10.1088/1367-2630/12/12/123023
[69] Garcia-Vidal F J, Martin-Moreno L, Ebbesen T W, et al. Light passing through subwavelength apertures[J]. Rev Mod Phys, 2010, 82(1): 729−787. doi: 10.1103/RevModPhys.82.729
[70] Sadeghi M M, Li S C, Xu L, et al. Transformation optics with Fabry-Pérot resonances[J]. Sci Rep, 2015, 5(1): 8680. doi: 10.1038/srep08680
[71] Xu L, Wu Q N, Zhou Y Y, et al. Transformation devices with optical nihility media and reduced realizations[J]. Front Phys, 2019, 14(4): 42501. doi: 10.1007/s11467-019-0891-6
[72] Zhao P F, Xu L, Cai G X, et al. A feasible approach to field concentrators of arbitrary shapes[J]. Front Phys, 2018, 13(4): 134205. doi: 10.1007/s11467-018-0771-5
[73] Chen A C, Fu Y Y, Xu Y D, et al. Total transmission through a sub-wavelength slit based on Fabry–Pérot resonance and zero-index metamaterials[J]. J Opt, 2015, 17(10): 105602. doi: 10.1088/2040-8978/17/10/105602
[74] Schurig D, Mock J J, Justice B J, et al. Metamaterial electromagnetic cloak at microwave frequencies[J]. Science, 2006, 314(5801): 977−980. doi: 10.1126/science.1133628
[75] Cai W S, Chettiar U K, Kildishev A V, et al. Optical cloaking with metamaterials[J]. Nat Photonics, 2007, 1(4): 224−227. doi: 10.1038/nphoton.2007.28
[76] Huang Y, Feng Y J, Jiang T. Electromagnetic cloaking by layered structure of homogeneous isotropic materials[J]. Opt Express, 2007, 15(18): 11133−11141. doi: 10.1364/OE.15.011133
[77] Kanté B, De Lustrac A, Lourtioz J M, et al. Infrared cloaking based on the electric response of split ring resonators[J]. Opt Express, 2008, 16(12): 9191−9198. doi: 10.1364/OE.16.009191
[78] Kanté B, Germain D, de Lustrac A. Experimental demonstration of a nonmagnetic metamaterial cloak at microwave frequencies[J]. Phys Rev B, 2009, 80(20): 201104. doi: 10.1103/PhysRevB.80.201104
[79] Landy N, Smith D R. A full-parameter unidirectional metamaterial cloak for microwaves[J]. Nat Mater, 2013, 12(1): 25−28. doi: 10.1038/NMAT3476
[80] Chen H S, Zheng B, Shen L, et al. Ray-optics cloaking devices for large objects in incoherent natural light[J]. Nat Commun, 2013, 4(1): 2652. doi: 10.1038/ncomms3652
[81] Shen L, Zheng B, Liu Z Z, et al. Large‐scale far‐infrared invisibility cloak hiding object from thermal detection[J]. Adv Opt Mater, 2015, 3(12): 1738−1742. doi: 10.1002/adom.201500267
[82] Keivaan A, Fakheri M H, Abdolali A, et al. Design of coating materials for cloaking and directivity enhancement of cylindrical antennas using transformation optics[J]. IEEE Antennas Wirel Propag Lett, 2017, 16: 3122−3125. doi: 10.1109/LAWP.2017.2764064
[83] Zheng B, Zhu R R, Jing L Q, et al. 3D Visible‐light invisibility cloak[J]. Adv Sci, 2018, 5(6): 1800056. doi: 10.1002/advs.201800056
[84] Sun F, Zhang Y J, Evans J, et al. A camouflage device without metamaterials[J]. Prog Electromagn Res, 2019, 165: 107−117. doi: 10.2528/PIER19080803
[85] Zheng B, Yang Y H, Shao Z P, et al. Experimental realization of an extreme-parameter omnidirectional cloak[J]. Research, 2019, 2019: 8282641. doi: 10.34133/2019/8282641
[86] Wang B, Sun F, Chen H C, et al. Full-space omnidirectional cloak by subwavelength metal channels filled with homogeneous dielectrics[J]. Opt Express, 2022, 30(12): 21386−21395. doi: 10.1364/OE.460395
[87] Liu Y C, Sun F, Yang Y B, et al. A metamaterial-free omnidirectional invisibility cloak based on thrice transformations inside optic-null medium[J]. Opt Laser Technol, 2023, 157: 108779. doi: 10.1016/j.optlastec.2022.108779
[88] Zheng B, Lu H, Qian C, et al. Revealing the transformation invariance of full-parameter omnidirectional invisibility cloaks[J]. Electromagn Sci, 2023, 1(2): 0020092. doi: 10.23919/emsci.2023.0009
[89] Hu X J, Luo Y, Wang J, et al. Multiband omnidirectional invisibility cloak[J]. Adv Sci, 2024, 11(28): 2401295. doi: 10.1002/advs.202401295
[90] Gao Y, Luo Y, Zhang J J, et al. Full-parameter omnidirectional transformation optical devices[J]. Natl Sci Rev, 2024, 11(3): nwad171. doi: 10.1093/nsr/nwad171
[91] Leonhardt U. Optical conformal mapping[J]. Science, 2006, 312(5781): 1777−1780. doi: 10.1126/science.1126493
[92] Urzhumov Y, Landy N, Smith D R. Isotropic-medium three-dimensional cloaks for acoustic and electromagnetic waves[J]. J Appl Phys, 2012, 111(5): 053105. doi: 10.1063/1.3691242
[93] Xu L, Chen H Y. Transformation optics with artificial Riemann sheets[J]. New J Phys, 2013, 15(11): 113013. doi: 10.1088/1367-2630/15/11/113013
[94] Zhu C H, Liu L J, Song Z Y, et al. Optimized invisibility cloaks from the Logarithm conformal mapping[J]. Sci Rep, 2016, 6(1): 38443. doi: 10.1038/srep38443
[95] Lv W J, Zhou J J, Liu Y J, et al. Non-Euclidean conformal devices with continuously varying refractive-index profiles based on bispheres[J]. Phys Rev A, 2024, 109(6): 063506. doi: 10.1103/PhysRevA.109.063506
[96] Leonhardt U, Tyc T. Broadband invisibility by non-Euclidean cloaking[J]. Science, 2009, 323(5910): 110−112. doi: 10.1126/science.1166332
[97] Xu T, Liu Y C, Zhang Y, et al. Perfect invisibility cloaking by isotropic media[J]. Phys Rev A, 2012, 86(4): 043827. doi: 10.1103/PhysRevA.86.043827
[98] Liu Y C, Sun F, He S L. Controlling lightwave in Riemann space by merging geometrical optics with transformation optics[J]. Sci Rep, 2018, 8(1): 514. doi: 10.1038/s41598-017-19015-0
[99] Xu L, Chen H Y. Conformal transformation optics[J]. Nat Photonics, 2015, 9(1): 15−23. doi: 10.1038/nphoton.2014.307
[100] Ma Y G, Liu Y C, Lan L, et al. First experimental demonstration of an isotropic electromagnetic cloak with strict conformal mapping[J]. Sci Rep, 2013, 3(1): 2182. doi: 10.1038/srep02182
[101] Howell J C, Howell J B, Choi J S. Amplitude-only, passive, broadband, optical spatial cloaking of very large objects[J]. Appl Opt, 2014, 53(9): 1958−1963. doi: 10.1364/AO.53.001958
[102] Choi J S, Howell J C. Paraxial ray optics cloaking[J]. Opt Express, 2014, 22(24): 29465−29478. doi: 10.1364/OE.22.029465
[103] Banerjee D, Ji C G, Iizuka H. Invisibility cloak with image projection capability[J]. Sci Rep, 2016, 6(1): 38965. doi: 10.1038/srep38965
[104] Choi J S, Howell J C. Digital integral cloaking[J]. Optica, 2016, 3(5): 536−540. doi: 10.1364/OPTICA.3.000536
[105] Bělín J, Tyc T, Grunwald M, et al. Ideal-lens cloaks and new cloaking strategies[J]. Opt Express, 2019, 27(26): 37327−37336. doi: 10.1364/OE.27.037327
[106] Courtial J, Bělín J, Soboňa M, et al. Shifty invisibility cloaks[J]. Opt Express, 2024, 32(1): 11−25. doi: 10.1364/OE.500512
[107] Alù A, Engheta N. Plasmonic materials in transparency and cloaking problems: mechanism, robustness, and physical insights[J]. Opt Express, 2007, 15(6): 3318−3332. doi: 10.1364/OE.15.003318
[108] Alù A, Engheta N. Achieving transparency with plasmonic and metamaterial coatings[J]. Phys Rev E, 2005, 72(1): 016623. doi: 10.1103/PhysRevE.72.016623
[109] Alù A, Engheta N. Multifrequency optical invisibility cloak with layered plasmonic shells[J]. Phys Rev Lett, 2008, 100(11): 113901. doi: 10.1103/PhysRevLett.100.113901
[110] Rainwater D, Kerkhoff A, Melin K, et al. Experimental verification of three-dimensional plasmonic cloaking in free-space[J]. New J Phys, 2012, 14(1): 013054. doi: 10.1088/1367-2630/14/1/013054
[111] Mühlig S, Cunningham A, Dintinger J, et al. A self-assembled three-dimensional cloak in the visible[J]. Sci Rep, 2013, 3(1): 2328. doi: 10.1038/srep02328
[112] Kort-Kamp W J M, Rosa F S S, Pinheiro F A, et al. Tuning plasmonic cloaks with an external magnetic field[J]. Phys Rev Lett, 2013, 111(21): 215504. doi: 10.1103/PhysRevLett.111.215504
[113] Farhat M, Rockstuhl C, Bağcı H. A 3D tunable and multi-frequency graphene plasmonic cloak[J]. Opt Express, 2013, 21(10): 12592−12603. doi: 10.1364/OE.21.012592
[114] Fruhnert M, Monti A, Fernandez-Corbaton I, et al. Tunable scattering cancellation cloak with plasmonic ellipsoids in the visible[J]. Phys Rev B, 2016, 93(24): 245127. doi: 10.1103/PhysRevB.93.245127
[115] Naserpour M, Zapata-Rodríguez C J, Vuković S M, et al. Tunable invisibility cloaking by using isolated graphene-coated nanowires and dimers[J]. Sci Rep, 2017, 7(1): 12186. doi: 10.1038/s41598-017-12413-4
[116] Khan M I, Ghosh S, Baxter R, et al. Modeling broadband cloaking using 3D nano-assembled plasmonic meta-structures[J]. Opt Express, 2020, 28(15): 22732−22747. doi: 10.1364/OE.395840
[117] Hansen K, Dutta A, Cardona M, et al. Zirconium nitride for plasmonic cloaking of visible nanowire photodetectors[J]. Plasmonics, 2020, 15(5): 1231−1241. doi: 10.1007/s11468-020-01145-3
[118] Chu H C, Li Q, Liu B B, et al. A hybrid invisibility cloak based on integration of transparent metasurfaces and zero-index materials[J]. Light Sci Appl, 2018, 7(1): 50. doi: 10.1038/s41377-018-0052-7
[119] Alù A. Mantle cloak: invisibility induced by a surface[J]. Phys Rev B, 2009, 80(24): 245115. doi: 10.1103/PhysRevB.80.245115
[120] Chen P Y, Alù A. Mantle cloaking using thin patterned metasurfaces[J]. Phys Rev B, 2011, 84(20): 205110. doi: 10.1103/PhysRevB.84.205110
[121] Qin F F, Liu Z Z, Zhang Q, et al. Mantle cloaks based on the frequency selective metasurfaces designed by Bayesian optimization[J]. Sci Rep, 2018, 8(1): 14033. doi: 10.1038/s41598-018-32167-x
[122] Yuste P, Rius J M, Romeu J, et al. A microwave invisibility cloak: the design, simulation, and measurement of a simple and effective frequency-selective surface-based mantle cloak[J]. IEEE Antennas Propag Mag, 2018, 60(4): 49−59. doi: 10.1109/MAP.2018.2839903
[123] Lee H, Kwon D H. Microwave metasurface cloaking for freestanding objects[J]. Phys Rev Appl, 2022, 17(5): 054012. doi: 10.1103/PhysRevApplied.17.054012
[124] Monti A, Barbuto M, Toscano A, et al. Nonlinear mantle cloaking devices for power-dependent antenna arrays[J]. IEEE Antennas Wirel Propag Lett, 2017, 16: 1727−1730. doi: 10.1109/LAWP.2017.2670025
[125] Vellucci S, Monti A, Barbuto M, et al. Waveform-selective mantle cloaks for intelligent antennas[J]. IEEE Trans Antennas Propag, 2020, 68(3): 1717−1725. doi: 10.1109/TAP.2019.2948736
[126] Vellucci S, Monti A, Barbuto M, et al. On the use of nonlinear metasurfaces for circumventing fundamental limits of mantle cloaking for antennas[J]. IEEE Trans Antennas Propag, 2021, 69(8): 5048−5053. doi: 10.1109/TAP.2021.3061010
[127] Masoumi R, Kazemi R, Fathy A E. Design and implementation of elliptical mantle cloaks for polarization decoupling of two tightly spaced interleaved co-frequency patch array antennas[J]. Sci Rep, 2023, 13(1): 2885. doi: 10.1038/s41598-023-29889-y
[128] Chen P Y, Alù A. Atomically thin surface cloak using graphene monolayers[J]. ACS Nano, 2011, 5(7): 5855−5863. doi: 10.1021/nn201622e
[129] Bodur H, Çimen S. Scattering suppression with dual-band single-layer mantle cloak for cylindrical metasurface[J]. AEU-Int J Electron Commun, 2023, 168: 154741. doi: 10.1016/j.aeue.2023.154741
[130] Chen P Y, Soric J, Padooru Y R, et al. Nanostructured graphene metasurface for tunable terahertz cloaking[J]. New J Phys, 2013, 15(12): 123029. doi: 10.1088/1367-2630/15/12/123029
[131] Hamzavi-Zarghani Z, Yahaghi A, Matekovits L, et al. Tunable mantle cloaking utilizing graphene metasurface for terahertz sensing applications[J]. Opt Express, 2019, 27(24): 34824−34837. doi: 10.1364/OE.27.034824
[132] Hamzavi-Zarghani Z, Yahaghi A, Matekovits L. Electrically tunable mantle cloaking utilizing graphene metasurface for oblique incidence[J]. AEU-Int J Electron Commun, 2020, 116: 153080. doi: 10.1016/j.aeue.2020.153080
[133] Pawar S, Bernety H M, Yakovlev A B. Graphene-metal metasurface for cloaking of cylindrical objects at low-terahertz frequencies[J]. IEEE Access, 2022, 10: 130200−130211. doi: 10.1109/ACCESS.2022.3228833
[134] Lai Y, Chen H Y, Zhang Z Q, et al. Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell[J]. Phys Rev Lett, 2009, 102(9): 093901. doi: 10.1103/PhysRevLett.102.093901
[135] Zheng B, Madni H A, Hao R, et al. Concealing arbitrary objects remotely with multi-folded transformation optics[J]. Light Sci Appl, 2016, 5(12): e16177. doi: 10.1038/lsa.2016.177
[136] Sun F, He S L. A third way to cloak an object: cover-up with a background object (Invited Paper)[J]. Prog Electromagn Res, 2014, 149: 173−182. doi: 10.2528/PIER14100303
[137] Sun F, Liu Y C, Yang Y B, et al. Full space destructive interference by acoustic-null medium[J]. Appl Phys Express, 2019, 12(7): 074003. doi: 10.7567/1882-0786/ab27df
[138] Lan L, Sun F, Liu Y C, et al. Experimentally demonstrated a unidirectional electromagnetic cloak designed by topology optimization[J]. Appl Phys Lett, 2013, 103(12): 121113. doi: 10.1063/1.4821951
[139] Fujii G, Akimoto Y. Electromagnetic-acoustic biphysical cloak designed through topology optimization[J]. Opt Express, 2022, 30(4): 6090−6106. doi: 10.1364/OE.450787
[140] Vasquez F G, Milton G W, Onofrei D. Active exterior cloaking for the 2D Laplace and Helmholtz equations[J]. Phys Rev Lett, 2009, 103(7): 073901. doi: 10.1103/PhysRevLett.103.073901
[141] Philbin T. Cloaking at a distance[J]. Physics, 2009, 2: 17. doi: 10.1103/Physics.2.17
[142] Lai Y, Ng J, Chen H Y, et al. Illusion optics: the optical transformation of an object into another object[J]. Phys Rev Lett, 2009, 102(25): 253902. doi: 10.1103/PhysRevLett.102.253902
[143] Pendry J. All smoke and metamaterials[J]. Nature, 2009, 460(7255): 579−580. doi: 10.1038/460579a
[144] Luo X D, Yang T, Gu Y W, et al. Conceal an entrance by means of superscatterer[J]. Appl Phys Lett, 2009, 94(22): 223513. doi: 10.1063/1.3149694
[145] Sun F, He S L. Invisible gateway for both light waves and rays[J]. Opt Express, 2018, 26(1): 165−172. doi: 10.1364/OE.26.000165
[146] Xu Y C, Liu Y C, Fei H M, et al. Asymmetric universal invisible gateway[J]. Opt Express, 2020, 28(23): 35363−35375. doi: 10.1364/OE.408826
[147] Yang T, Chen H Y, Luo X D, et al. Superscatterer: enhancement of scattering with complementary media[J]. Opt Express, 2008, 16(22): 18545−18550. doi: 10.1364/OE.16.018545
[148] Zang X F, Shi C, Li Z, et al. Illusion induced overlapped optics[J]. Opt Express, 2014, 22(1): 582−592. doi: 10.1364/OE.22.000582
[149] Sun F, He S L. Overlapping illusions by transformation optics without any negative refraction material[J]. Sci Rep, 2016, 6(1): 19130. doi: 10.1038/srep19130
[150] Sun F, Liu Y, He S. True dynamic imaging and image composition by the optical translational projector[J]. J Opt, 2016, 18(4): 044012. doi: 10.1088/2040-8978/18/4/044012
[151] Sun F, Li S C, He S L. Translational illusion of acoustic sources by transformation acoustics[J]. J Acoust Soc Am, 2017, 142(3): 1213−1218. doi: 10.1121/1.5000483
[152] Li C, Meng X K, Liu X, et al. Experimental realization of a circuit-based broadband illusion-optics analogue[J]. Phys Rev Lett, 2010, 105(23): 233906. doi: 10.1103/PhysRevLett.105.233906
[153] Jiang W X, Luo C Y, Ge S, et al. An optically controllable transformation-dc illusion device[J]. Adv Mater, 2015, 27(31): 4628−4633. doi: 10.1002/adma.201500729
[154] Jiang W X, Ma H F, Cheng Q, et al. Illusion media: generating virtual objects using realizable metamaterials[J]. Appl Phys Lett, 2010, 96(12): 121910. doi: 10.1063/1.3371716
[155] Sun F, He S L. Transformation magneto-statics and illusions for magnets[J]. Sci Rep, 2014, 4(1): 6593. doi: 10.1038/srep06593
[156] Yang C F, Yang J J, Huang M, et al. An external cloak with arbitrary cross section based on complementary medium and coordinate transformation[J]. Opt Express, 2011, 19(2): 1147−1157. doi: 10.1364/OE.19.001147
[157] Huo F F, Li L, Li T, et al. External invisibility cloak for multiobjects with arbitrary geometries[J]. IEEE Antennas Wirel Propag Lett, 2014, 13: 273−276. doi: 10.1109/LAWP.2014.2304640
[158] Vura P, Rajput A, Srivastava K V. Composite-shaped external cloaks with homogeneous material properties[J]. IEEE Antennas Wirel Propag Lett, 2016, 15: 282−285. doi: 10.1109/LAWP.2015.2441557
[159] Shi Y, Tang W, Li L, et al. Three-dimensional complementary invisibility cloak with arbitrary shapes[J]. IEEE Antennas Wirel Propag Lett, 2015, 14: 1550−1553. doi: 10.1109/LAWP.2015.2412171
[160] Rajput A, Srivastava K V. Approximated complementary cloak with diagonally homogeneous material parameters using shifted parabolic coordinate system[J]. IEEE Trans Antennas Propag, 2017, 65(3): 1458−1463. doi: 10.1109/TAP.2016.2639015
[161] Holland J H. Genetic algorithms[J]. Sci Am, 1992, 267(1): 66−73. doi: 10.1038/scientificamerican0792-66
[162] Holland J H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence[M]. Cambridge: MIT Press, 1992. https://doi.org/10.7551/mitpress/1090.003.0002.
[163] Michalewicz Z, Schoenauer M. Evolutionary algorithms for constrained parameter optimization problems[J]. Evol Comput, 1996, 4(1): 1−32. doi: 10.1162/evco.1996.4.1.1
[164] Katoch S, Chauhan S S, Kumar V. A review on genetic algorithm: past, present, and future[J]. Multimed Tools Appl, 2021, 80(5): 8091−8126. doi: 10.1007/s11042-020-10139-6
[165] Xi S, Chen H S, Zhang B L, et al. Route to low-scattering cylindrical cloaks with finite permittivity and permeability[J]. Phys Rev B, 2009, 79(15): 155122. doi: 10.1103/PhysRevB.79.155122
[166] Martins T C, Dmitriev V. Design of dielectric cloaks by scattering cancellation technique using genetic algorithms[C]//2009 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), 2009: 766–769. https://doi.org/10.1109/IMOC.2009.5427478.
[167] Yu Z Z, Feng Y J, Xu X F, et al. Optimized cylindrical invisibility cloak with minimum layers of non-magnetic isotropic materials[J]. J Phys D Appl Phys, 2011, 44(18): 185102. doi: 10.1088/0022-3727/44/18/185102
[168] Wang X H, Semouchkina E. A route for efficient non-resonance cloaking by using multilayer dielectric coating[J]. Appl Phys Lett, 2013, 102(11): 113506. doi: 10.1063/1.4796171
[169] Mirzaei A, Miroshnichenko A E, Shadrivov I V, et al. All-dielectric multilayer cylindrical structures for invisibility cloaking[J]. Sci Rep, 2015, 5(1): 9574. doi: 10.1038/srep09574
[170] Xu S, Cheng X X, Xi S, et al. Experimental demonstration of a free-space cylindrical cloak without superluminal propagation[J]. Phys Rev Lett, 2012, 109(22): 223903. doi: 10.1103/PhysRevLett.109.223903
[171] Bor E, Babayigit C, Kurt H, et al. Directional invisibility by genetic optimization[J]. Opt Lett, 2018, 43(23): 5781−5784. doi: 10.1364/OL.43.005781
[172] Bendsøe M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J]. Comput Methods Appl Mech Eng, 1988, 71(2): 197−224. doi: 10.1016/0045-7825(88)90086-2
[173] Andkjær J, Sigmund O. Topology optimized low-contrast all-dielectric optical cloak[J]. Appl Phys Lett, 2011, 98(2): 021112. doi: 10.1063/1.3540687
[174] Andkjær J, Asger Mortensen N, Sigmund O. Towards all-dielectric, polarization-independent optical cloaks[J]. Appl Phys Lett, 2012, 100(10): 101106. doi: 10.1063/1.3691835
[175] Fujii G, Watanabe H, Yamada T, et al. Level set based topology optimization for optical cloaks[J]. Appl Phys Lett, 2013, 102(25): 251106. doi: 10.1063/1.4812471
[176] Urzhumov Y, Landy N, Driscoll T, et al. Thin low-loss dielectric coatings for free-space cloaking[J]. Opt Lett, 2013, 38(10): 1606−1608. doi: 10.1364/OL.38.001606
[177] Sha W, Xiao M, Wang Y H, et al. Topology optimization methods for thermal metamaterials: a review[J]. Int J Heat Mass Transfer, 2024, 227: 125588. doi: 10.1016/j.ijheatmasstransfer.2024.125588
[178] Lu Y F, Tong L Y. Concurrent multiscale topology optimization of metamaterials for mechanical cloak[J]. Comput Methods Appl Mech Eng, 2023, 409: 115966. doi: 10.1016/j.cma.2023.115966
[179] Fujii G, Akimoto Y. dc electric cloak concentrator via topology optimization[J]. Phys Rev E, 2020, 102(3): 033308. doi: 10.1103/PhysRevE.102.033308
[180] Noguchi Y, Yamada T, Izui K, et al. Topology optimization for hyperbolic acoustic metamaterials using a high-frequency homogenization method[J]. Comput Methods Appl Mech Eng, 2018, 335: 419−471. doi: 10.1016/j.cma.2018.02.031
[181] Fujii G. Biphysical undetectable concentrators manipulating both heat flux and direct current via topology optimization[J]. Phys Rev E, 2022, 106(6): 065304. doi: 10.1103/PhysRevE.106.065304
[182] Fujii G, Akimoto Y. Optimizing the structural topology of bifunctional invisible cloak manipulating heat flux and direct current[J]. Appl Phys Lett, 2019, 115(17): 174101. doi: 10.1063/1.5123908
[183] Zhu Z, Wang Z C, Liu T F, et al. Arbitrary-shape transformation multiphysics cloak by topology optimization[J]. Int J Heat Mass Transfer, 2024, 222: 125205. doi: 10.1016/j.ijheatmasstransfer.2024.125205
[184] Sato Y, Izui K, Yamada T, et al. Robust topology optimization of optical cloaks under uncertainties in wave number and angle of incident wave[J]. Int J Numerical Methods Eng, 2020, 121(17): 3926−3954. doi: 10.1002/nme.6393
[185] Guo Y M, Zhong L B, Min L, et al. Adaptive optics based on machine learning: a review[J]. Opto-Electron Adv, 2022, 5(7): 200082. doi: 10.29026/oea.2022.200082
[186] Krasikov S, Tranter A, Bogdanov A, et al. Intelligent metaphotonics empowered by machine learning[J]. Opto-Electron Adv, 2022, 5(3): 210147. doi: 10.29026/oea.2022.210147
[187] Lin H, Hou J J, Jin J, et al. Machine-learning-assisted inverse design of scattering enhanced metasurface[J]. Opt Express, 2022, 30(2): 3076−3088. doi: 10.1364/OE.448051
[188] Wang J Y, Xi R, Cai T, et al. Deep neural network with data cropping algorithm for absorptive frequency‐selective transmission metasurface[J]. Adv Opt Mater, 2022, 10(13): 2200178. doi: 10.1002/adom.202200178
[189] Yao K, Unni R, Zheng Y B. Intelligent nanophotonics: merging photonics and artificial intelligence at the nanoscale[J]. Nanophotonics, 2019, 8(3): 339−366. doi: 10.1515/nanoph-2018-0183
[190] Zhang X R, Cui T J. Artificial intelligence-assisted chiral nanophotonic designs[J]. Opto-Electron Adv, 2023, 6(10): 230057. doi: 10.29026/oea.2023.230057
[191] Xie C, Li H N, Cui C Y, et al. Deep learning assisted inverse design of metamaterial microwave absorber[J]. Appl Phys Lett, 2023, 123(18): 181701. doi: 10.1063/5.0171437
[192] Patel S K, Parmar J, Katkar V. Ultra-broadband, wide-angle plus-shape slotted metamaterial solar absorber design with absorption forecasting using machine learning[J]. Sci Rep, 2022, 12(1): 10166. doi: 10.1038/s41598-022-14509-y
[193] Li L L, Zhao H T, Liu C, et al. Intelligent metasurfaces: control, communication and computing[J]. eLight, 2022, 2(1): 7. doi: 10.1186/s43593-022-00013-3
[194] Shin S, Shin D, Kang N. Topology optimization via machine learning and deep learning: a review[J]. J Comput Des Eng, 2023, 10(4): 1736−1766.
[195] Qian C, Zheng B, Shen Y C, et al. Deep-learning-enabled self-adaptive microwave cloak without human intervention[J]. Nat Photonics, 2020, 14(6): 383−390. doi: 10.1038/s41566-020-0604-2
[196] Zhen Z, Qian C, Jia Y T, et al. Realizing transmitted metasurface cloak by a tandem neural network[J]. Photonics Res, 2021, 9(5): B229−B235. doi: 10.1364/PRJ.418445
[197] Blanchard-Dionne A P, Martin O J F. Successive training of a generative adversarial network for the design of an optical cloak[J]. OSA Continuum, 2020, 4(1): 87−95. doi: 10.1364/OSAC.413394
[198] Wu N X, Jia Y T, Qian C, et al. Pushing the limits of metasurface cloak using global inverse design[J]. Adv Opt Mater, 2023, 11(7): 2202130. doi: 10.1002/adom.202202130
[199] 左建坤, 潘美妍, 段辉高, 等. 新型红外隐身结构材料研究综述[J]. 光电工程, 2023, 50(5): 220218. doi: 10.12086/oee.2023.220218
Zuo J K, Pan M Y, Duan H G, et al. Review on new infrared stealth structural materials[J]. Opto-Electron Eng, 2023, 50(5): 220218. doi: 10.12086/oee.2023.220218
[200] Sanchis L, García-Chocano V M, Llopis-Pontiveros R, et al. Three-dimensional axisymmetric cloak based on the cancellation of acoustic scattering from a sphere[J]. Phys Rev Lett, 2013, 110(12): 124301. doi: 10.1103/PhysRevLett.110.124301
[201] Cummer S A, Popa B I, Schurig D, et al. Scattering theory derivation of a 3D acoustic cloaking shell[J]. Phys Rev Lett, 2008, 100(2): 024301. doi: 10.1103/PhysRevLett.100.024301
[202] Sun K Y, Zhang F L, Chen S, et al. Broadband acoustic illusion coating based on thin conformal metasurface[J]. iScience, 2024, 27(8): 110504. doi: 10.1016/j.isci.2024.110504
[203] Ma Y G, Lan L, Jiang W, et al. A transient thermal cloak experimentally realized through a rescaled diffusion equation with anisotropic thermal diffusivity[J]. NPG Asia Mater, 2013, 5(11): e73. doi: 10.1038/am.2013.60
[204] Wang J, Dai G L, Huang J P. Thermal metamaterial: fundamental, application, and outlook[J]. iScience, 2020, 23(10): 101637. doi: 10.1016/j.isci.2020.101637
[205] Xu H Y, Shi X H, Gao F, et al. Ultrathin three-dimensional thermal cloak[J]. Phys Rev Lett, 2014, 112(5): 054301. doi: 10.1103/PhysRevLett.112.054301
[206] Narayana S, Sato Y. Heat flux manipulation with engineered thermal materials[J]. Phys Rev Lett, 2012, 108(21): 214303. doi: 10.1103/PhysRevLett.108.214303
[207] Schittny R, Kadic M, Guenneau S, et al. Experiments on transformation thermodynamics: molding the flow of heat[J]. Phys Rev Lett, 2013, 110(19): 195901. doi: 10.1103/PhysRevLett.110.195901
[208] Xu L J, Huang J P. Transformation Thermotics and Extended Theories: Inside and Outside Metamaterials[M]. Singapore: Springer, 2023. https://doi.org/10.1007/978-981-19-5908-0.
[209] Han T C, Bai X, Gao D L, et al. Experimental demonstration of a bilayer thermal cloak[J]. Phys Rev Lett, 2014, 112(5): 054302. doi: 10.1103/PhysRevLett.112.054302
[210] Gömöry F, Solovyov M, Šouc J, et al. Experimental realization of a magnetic cloak[J]. Science, 2012, 335(6075): 1466−1468. doi: 10.1126/science.1218316
[211] Sun F, He S L. DC magnetic concentrator and omnidirectional cascaded cloak by using only one or two homogeneous anisotropic materials of positive permeability[J]. Prog Electromagn Res, 2013, 142: 683−699. doi: 10.2528/PIER13092509
[212] Narayana S, Sato Y. DC magnetic cloak[J]. Adv Mater, 2012, 24(1): 71−74. doi: 10.1002/adma.201104012
[213] Avanzini F, Falasco G, Esposito M. Chemical cloaking[J]. Phys Rev E, 2020, 101(6): 060102. doi: 10.1103/PhysRevE.101.060102
[214] Xu X C, Wang C, Shou W, et al. Physical realization of elastic cloaking with a polar material[J]. Phys Rev Lett, 2020, 124(11): 114301. doi: 10.1103/PhysRevLett.124.114301
[215] Stenger N, Wilhelm M, Wegener M. Experiments on elastic cloaking in thin plates[J]. Phys Rev Lett, 2012, 108(1): 014301. doi: 10.1103/PhysRevLett.108.014301
[216] Sun F, Liu Y C, He S L. Surface transformation multi-physics for controlling electromagnetic and acoustic waves simultaneously[J]. Opt Express, 2020, 28(1): 94−106. doi: 10.1364/OE.379817
[217] Ma Y G, Liu Y C, Raza M, et al. Experimental demonstration of a multiphysics cloak: manipulating heat flux and electric current simultaneously[J]. Phys Rev Lett, 2014, 113(20): 205501. doi: 10.1103/PhysRevLett.113.205501
[218] Li J Y, Gao Y, Huang J P. A bifunctional cloak using transformation media[J]. J Appl Phys, 2010, 108(7): 074501. doi: 10.1063/1.3490226
[219] Raza M, Liu Y C, Ma Y G. A multi-cloak bifunctional device[J]. J Appl Phys, 2015, 117(2): 024502. doi: 10.1063/1.4905618
[220] Ahsan M, Sun F. A thermal-electric cloak via nonlinear transformation[J]. IEEE Photonics J, 2023, 15(6): 4601406. doi: 10.1109/JPHOT.2023.3327236
[221] Liu Y C, Ma X M, Chao K, et al. Simultaneously realizing thermal and electromagnetic cloaking by multi-physical null medium[J]. Opto-Electron Sci, 2024, 3(2): 230027. doi: 10.29026/oes.2024.230027
[222] Liu Y C, Chen H C, Zhao G, et al. On-chip omnidirectional electromagnetic-thermal cloak[J]. iScience, 2024, 27(7): 110105. doi: 10.1016/j.isci.2024.110105
[223] Yang Y H, Wang H P, Yu F X, et al. A metasurface carpet cloak for electromagnetic, acoustic and water waves[J]. Sci Rep, 2016, 6(1): 20219. doi: 10.1038/srep20219
[224] Xu J, Jiang X, Fang N, et al. Molding acoustic, electromagnetic and water waves with a single cloak[J]. Sci Rep, 2015, 5(1): 10678. doi: 10.1038/srep10678
[225] Chen H C, Liu Y C, Sun F, et al. A thermal–EM concentrator for enhancing EM signals and focusing heat fluxes simultaneously[J]. Laser Photonics Rev, 2024. doi: 10.1002/lpor.202400488
[226] Chen Z H, Sun F, Liu Y C, et al. Electromagnetic-acoustic splitter with a tunable splitting ratio based on copper plates[J]. Opt Lett, 2023, 48(13): 3407−3410. doi: 10.1364/OL.492941
[227] Yang J F, Qu S B, Ma H, et al. Ultra-broadband co-polarization anomalous reflection metasurface[J]. Appl Phys A, 2017, 123(8): 537. doi: 10.1007/s00339-017-1162-4
[228] Ji C, Huang C, Zhang X, et al. Broadband low-scattering metasurface using a combination of phase cancellation and absorption mechanisms[J]. Opt Express, 2019, 27(16): 23368−23377. doi: 10.1364/OE.27.023368
[229] Xie X, Pu M B, Li X, et al. Dual-band and ultra-broadband photonic spin-orbit interaction for electromagnetic shaping based on single-layer silicon metasurfaces[J]. Photonics Res, 2019, 7(5): 586−593. doi: 10.1364/PRJ.7.000586
[230] Akram M R, Ding G W, Chen K, et al. Ultrathin single layer metasurfaces with ultra‐wideband operation for both transmission and reflection[J]. Adv Mater, 2020, 32(12): 1907308. doi: 10.1002/adma.201907308
[231] Lu X J, Li X Y, Guo Y H, et al. Broadband high-efficiency polymerized liquid crystal metasurfaces with spin-multiplexed functionalities in the visible[J]. Photonics Res, 2022, 10(6): 1380−1393. doi: 10.1364/PRJ.452272
[232] Zhang H C, Zhang Z J, Ma X L, et al. Polarization multiplexing metasurface for dual-band achromatic focusing[J]. Opt Express, 2022, 30(7): 12069−12079. doi: 10.1364/OE.454805
[233] Yang J N, Huang C, Wu X Y, et al. Dual‐wavelength carpet cloak using ultrathin metasurface[J]. Adv Opt Mater, 2018, 6(14): 1800073. doi: 10.1002/adom.201800073
[234] Huang Y J, Pu M B, Zhang F, et al. Broadband functional metasurfaces: achieving nonlinear phase generation toward achromatic surface cloaking and lensing[J]. Adv Opt Mater, 2019, 7(7): 1801480. doi: 10.1002/adom.201801480
[235] Hsu L, Ndao A, Kanté B. Broadband and linear polarization metasurface carpet cloak in the visible[J]. Opt Lett, 2019, 44(12): 2978−2981. doi: 10.1364/OL.44.002978
[236] Ding P, Li M Y, Tian X M, et al. Graphene metasurface for broadband, wide-angle and polarization-insensitive carpet cloak[J]. Opt Mater, 2021, 121: 111578. doi: 10.1016/j.optmat.2021.111578
[237] Li Y L, Xu J F, Liu F H, et al. Broadband achromatic transmission stealth cloak based on all dielectric metasurfaces[J]. Phys Scr, 2024, 99(7): 075536. doi: 10.1088/1402-4896/ad5803
[238] Liang Q X, Yin H Y, Feng J K, et al. An additively manufactured wide angle and broadband electromagnetic camouflage metasurface[J]. Adv Eng Mater, 2023, 25(10): 2201728. doi: 10.1002/adem.202201728
[239] Cui T J, Qi M Q, Wan X, et al. Coding metamaterials, digital metamaterials and programmable metamaterials[J]. Light Sci Appl, 2014, 3(10): e218. doi: 10.1038/lsa.2014.99
[240] Zhang Z Y, Shi H Y, Wang L Y, et al. Recent advances in reconfigurable metasurfaces: principle and applications[J]. Nanomaterials, 2023, 13(3): 534. doi: 10.3390/nano13030534
[241] Tian J T, Cao W H. Reconfigurable flexible metasurfaces: from fundamentals towards biomedical applications[J]. PhotoniX, 2024, 5(1): 2. doi: 10.1186/s43074-023-00116-1
[242] Huang C, Sun B, Pan W B, et al. Dynamical beam manipulation based on 2-bit digitally-controlled coding metasurface[J]. Sci Rep, 2017, 7(1): 42302. doi: 10.1038/srep42302
[243] Huang C, Zhang C L, Yang J N, et al. Reconfigurable metasurface for multifunctional control of electromagnetic waves[J]. Adv Opt Mater, 2017, 5(22): 1700485. doi: 10.1002/adom.201700485
[244] Zhang X G, Tang W X, Jiang W X, et al. Light‐controllable digital coding metasurfaces[J]. Adv Sci, 2018, 5(11): 1801028. doi: 10.1002/advs.201801028
[245] Yang W H, Qu G Y, Lai F X, et al. Dynamic bifunctional metasurfaces for holography and color display[J]. Adv Mater, 2021, 33(36): 2101258. doi: 10.1002/adma.202101258
[246] She Y, Ji C, Huang C, et al. Intelligent reconfigurable metasurface for self-adaptively electromagnetic functionality switching[J]. Photonics Res, 2022, 10(3): 769−776. doi: 10.1364/PRJ.450297
[247] Huang C, Zhao B, Song J K, et al. Active transmission/absorption frequency selective surface with dynamical modulation of amplitude[J]. IEEE Trans Antennas Propag, 2021, 69(6): 3593−3598. doi: 10.1109/TAP.2020.3037813
[248] Huang C, Pan W B, Ma X L, et al. Multi-spectral metasurface for different functional control of reflection waves[J]. Sci Rep, 2016, 6(1): 23291. doi: 10.1038/srep23291
[249] Yan L B, Zhu W M, Wu P C, et al. Adaptable metasurface for dynamic anomalous reflection[J]. Appl Phys Lett, 2017, 110(20): 201904. doi: 10.1063/1.4983782
[250] Cui T, Bai B F, Sun H B. Tunable metasurfaces based on active materials[J]. Adv Funct Mater, 2019, 29(10): 1806692. doi: 10.1002/adfm.201806692
[251] Estakhri N M, Alù A. Ultra-thin unidirectional carpet cloak and wavefront reconstruction with graded metasurfaces[J]. IEEE Antennas Wirel Propag Lett, 2014, 13: 1775−1778. doi: 10.1109/LAWP.2014.2371894
[252] Yang Y H, Jing L Q, Zheng B, et al. Full‐polarization 3D metasurface cloak with preserved amplitude and phase[J]. Adv Mater, 2016, 28(32): 6866−6871. doi: 10.1002/adma.201600625
[253] Huang C, Yang J N, Wu X Y, et al. Reconfigurable metasurface cloak for dynamical electromagnetic illusions[J]. ACS Photonics, 2018, 5(5): 1718−1725. doi: 10.1021/acsphotonics.7b01114
[254] Xu S, Dong F Y, Guo W R, et al. Cross-wavelength invisibility integrated with various invisibility tactics[J]. Sci Adv, 2020, 6(39): eabb3755. doi: 10.1126/sciadv.abb3755
[255] Liao J M, Ji C, Yuan L M, et al. Polarization-insensitive metasurface cloak for dynamic illusions with an electromagnetic transparent window[J]. ACS Appl Mater Interfaces, 2023, 15(13): 16953−16962. doi: 10.1021/acsami.2c21565
[256] Ma Q, Bai G D, Jing H B, et al. Smart metasurface with self-adaptively reprogrammable functions[J]. Light Sci Appl, 2019, 8(1): 98. doi: 10.1038/s41377-019-0205-3
[257] Ma Q, Hong Q R, Gao X X, et al. Smart sensing metasurface with self-defined functions in dual polarizations[J]. Nanophotonics, 2020, 9(10): 3271−3278. doi: 10.1515/nanoph-2020-0052
[258] Lin C H, Chen Y S, Lin J T, et al. Automatic inverse design of high-performance beam-steering metasurfaces via genetic-type tree optimization[J]. Nano Lett, 2021, 21(12): 4981−4989. doi: 10.1021/acs.nanolett.1c00720
[259] Zhang X G, Sun Y L, Yu Q, et al. Smart Doppler cloak operating in broad band and full polarizations[J]. Adv Mater, 2021, 33(17): 2007966. doi: 10.1002/adma.202007966
[260] Jia Y T, Qian C, Fan Z X, et al. In situ customized illusion enabled by global metasurface reconstruction[J]. Adv Funct Mater, 2022, 32(19): 2109331. doi: 10.1002/adfm.202109331
[261] Huang M, Zheng B, Li R C, et al. Evolutionary games‐assisted synchronization metasurface for simultaneous multisource invisibility cloaking[J]. Adv Funct Mater, 2024, 34(36): 2401909. doi: 10.1002/adfm.202401909
[262] Qian C, Jia Y T, Wang Z D, et al. Autonomous aeroamphibious invisibility cloak with stochastic-evolution learning[J]. Adv Photonics, 2024, 6(1): 016001. doi: 10.1117/1.AP.6.1.016001
[263] Ma T G, Wang H Z, Guo L. OptoGPT: a foundation model for inverse design in optical multilayer thin film structures[J]. Opto-Electron Adv, 2024, 7(7): 240062. doi: 10.29026/oea.2024.240062
-


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: