-
摘要
非互易热辐射是一种突破传统基尔霍夫定律对称互易性的辐射传热新方式,它打破了物体光谱定向发射率与光谱定向吸收率必须相等的限制,实现了辐射器光谱、角度发射率和吸收率在时间和空间上的独立控制。本文综述了非互易热辐射在理论计算、实验验证和应用方面的研究进展,从基尔霍夫定律与洛伦兹互易性之间的内在联系出发,阐述了非互易热辐射产生的必要条件,以磁光材料InAs和外尔半金属两种典型材料为例探讨了如何构建非对称结构和利用外部场调控,产生多波段、多角度的非互易热辐射,并应用于太阳能电池、热光伏系统等领域,成功突破了热辐射的黑体极限并在理论上达到朗斯堡极限,提升了能源的转换效率。未来非互易热辐射有望为能源有效利用和节能减排提供有力的支持,推动前沿材料研究和技术创新,为可持续发展注入新的动力和活力。
Abstract
Nonreciprocal thermal radiation is a novel approach to radiative heat transfer that breaks through the symmetric reciprocity of traditional Kirchhoff's law. It overcomes the restriction that the spectrally oriented emissivity and spectrally oriented absorptivity of an object must be equal, allowing independent control of the spectral and angular emissivity and absorptivity of a radiator in both time and space. This paper reviews the progress of research on nonreciprocal thermal radiation in theoretical calculations, experimental verifications, and applications. Starting from the intrinsic connection between Kirchhoff's law and Lorentz reciprocity, it elaborates on the necessary conditions for the generation of nonreciprocal thermal radiation. Using two typical materials, magneto-optical materialsof InAs and Weyl semimetal, as examples, the paper explores how to construct asymmetric structures and utilize external field modulation to generate multi-wavelength and multi-angle nonreciprocal thermal radiation. These advancements have been applied in many fields, such as solar cells and thermophotovoltaic systems, successfully surpassing the blackbody limit of thermal radiation and theoretically reaching the Landsberg limit, thereby improving energy conversion efficiency. In the future, nonreciprocal thermal radiation is expected to provide strong support for efficient energy utilization and emission reduction, promote cutting-edge materials research and technological innovation, and inject new impetus and vitality into sustainable development.
-
Overview
Overview: Thermal radiation is a natural phenomenon in which an object emits electromagnetic waves as a result of its temperature, and any object with a non-zero temperature has the ability to emit and absorb such radiation. Kirchhoff's law, an important cornerstone of thermal radiation theory, details the intrinsic correlation between the energy emitted and absorbed by an object. However, in certain application scenarios, the limitation inherent in Kirchhoff's law, such as the upper limit of energy conversion efficiency and the limitation of spectral selectivity, becomes a bottleneck for technological advancement. In order to deeply understand and overcome these limitations, this paper first provides an in-depth analysis of the fundamentals of Kirchhoff's law and explores its close connection with Lorentz reciprocity. By analyzing the relationship between Kirchhoff's law and Lorentz reciprocity, we reveal the physical mechanism of the phenomenon of non-reciprocal thermal radiation, that is, an object can exhibit different absorption and emission properties for thermal radiation of specific wavelengths or directions under specific conditions. In order to overcome the limitations of Kirchhoff's law, this paper reviews the progress of research on realizing non-reciprocal thermal radiation using advanced material structures, such as magneto-optical materials InAs and Weyl semimetals. These material structures have successfully realized the phenomenon of non-reciprocal radiation in narrowband, broadband, multi-band, and multi-angle, which not only exhibit excellent performance but also have the ability to actively tune the non-reciprocal radiation, providing a wide scope for experimental fabrication and practical applications. In addition, this paper further explores the application potential of non-reciprocal thermal radiation in the field of energy conversion and radiation control. In solar cells and thermophotovoltaic systems, the application of nonreciprocal thermal radiation not only breaks through the traditional Landsberg limit and significantly improves the energy conversion efficiency, but also provides greater flexibility and freedom for system design and optimization. These innovative applications not only highlight the great potential of non-reciprocal thermal radiation technology, but also open up a completely new direction for future research in the field of energy conversion and radiation control.
-

-
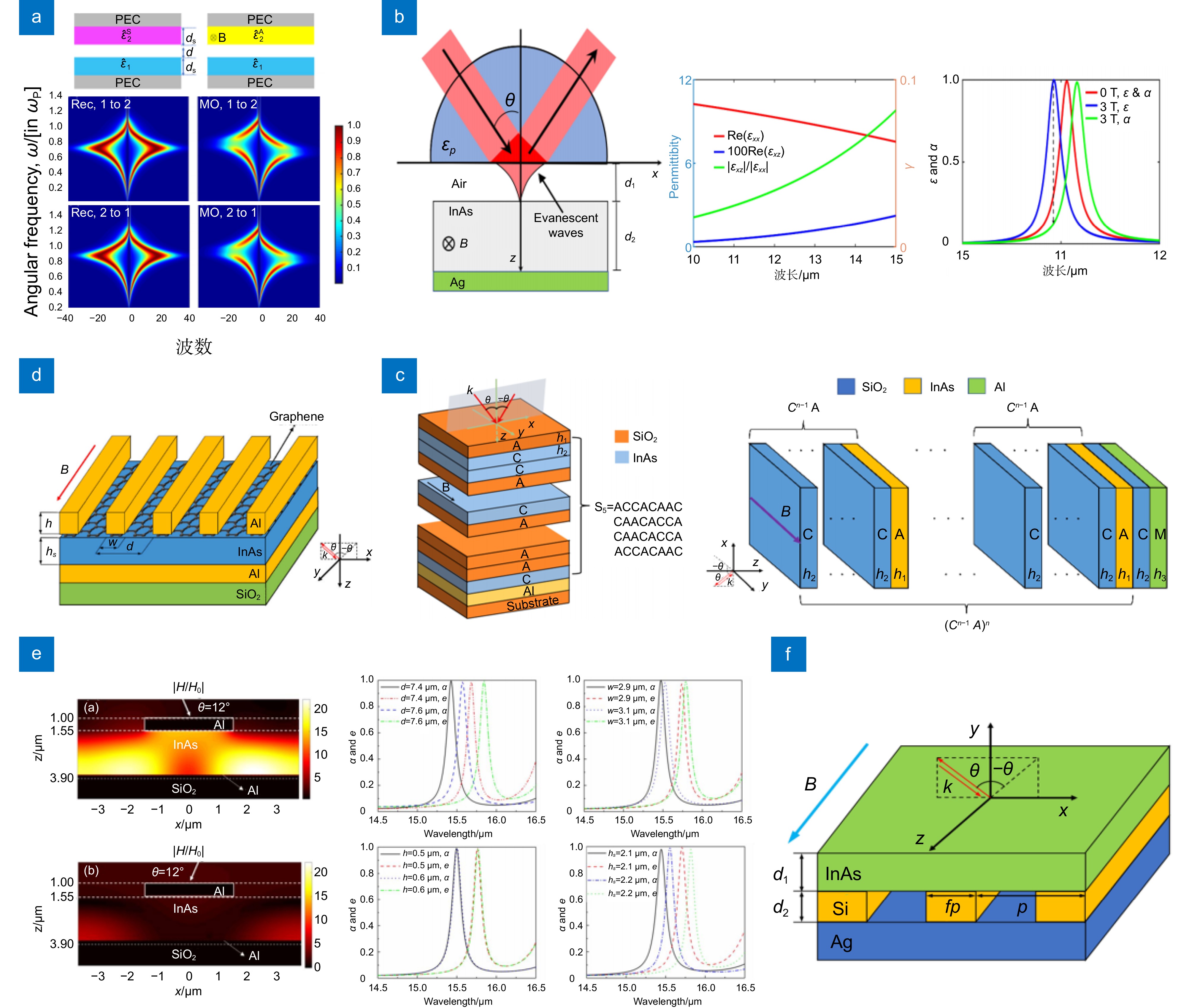
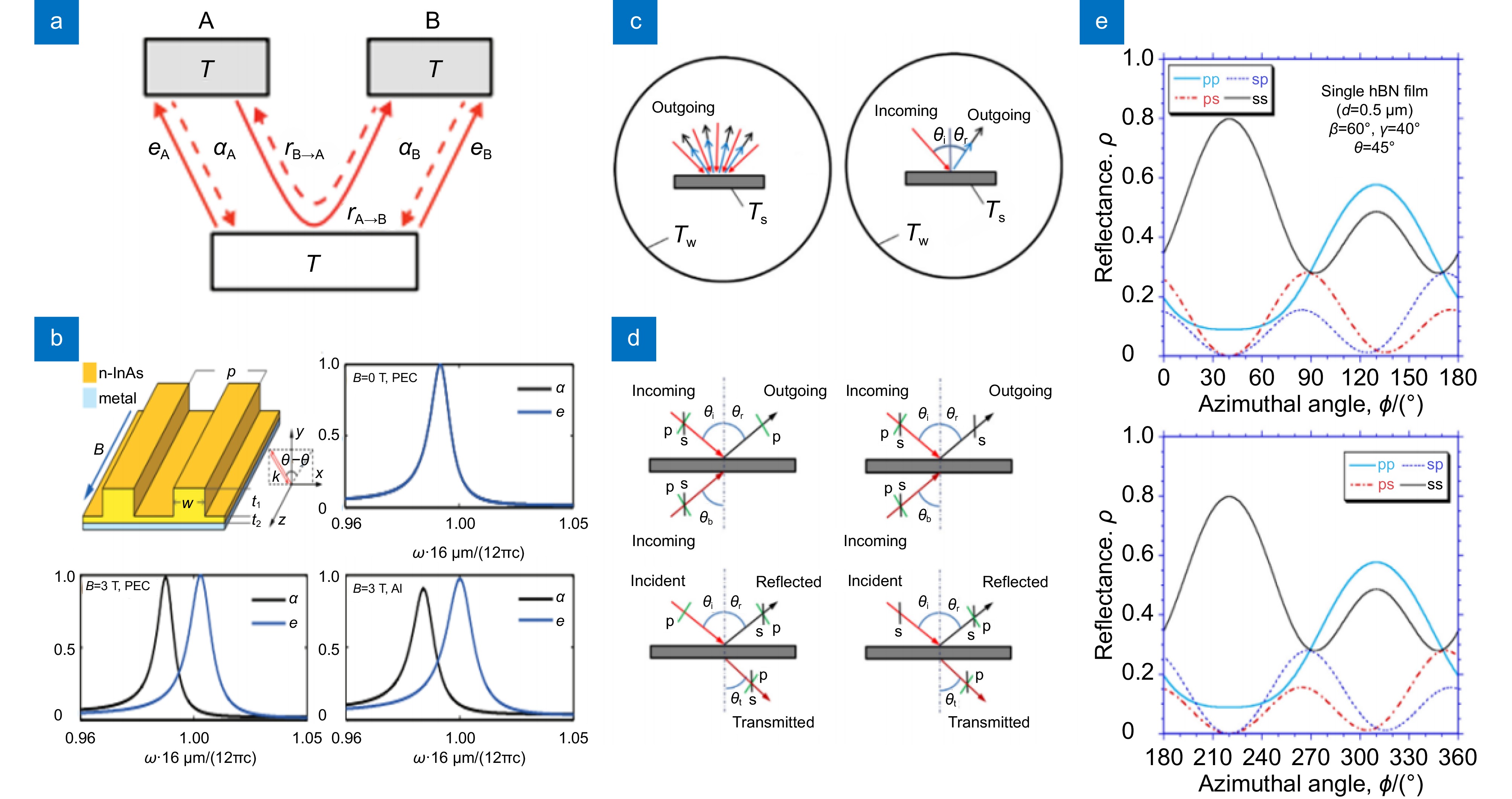
图 1 (a) 满足互易定理的能量流图[34];(b) 光子晶体结构由均匀金属层上的n-InAs光栅组成,参数(μm): p = 7.24, w = 3.2, t1 = 1.981, t2 = 0.485。射镜顶部结构在θ = 61.28°,B = 0 T或B = 3 T处的吸收率和发射率光谱,以及铝反射镜顶部结构在θ = 61.28°和B = 3 T处的吸收率和发射率光谱光子晶体结构由均匀金属层上的n-InAs光栅组成,参数(μm): p = 7.24, w = 3.2, t1 = 1.981, t2 = 0.485。射镜顶部结构在θ = 61.28°,B = 0 T或B = 3 T处的吸收率和发射率光谱,以及铝反射镜顶部结构在θ = 61.28°和B = 3 T处的吸收率和发射率光谱[34];(c) 各向同性半球形特性和定向特性的黑体外壳示意图[35];(d) 各向异性外壳内的半透明薄膜示意图,入射波既有p分量,也有s分量时,输出波为p极化或s极化;入射波是p偏振或s偏振,而反射波和透射波包含p和s两种偏振成分[35];(e) 单hBN膜反射率随方位角$\phi $的变化规律[35]
Figure 1. (a) Energy flow graphs satisfying the reciprocity theorem[34];(b) The photonic crystal structure consists of an n-InAs grating on a homogeneous metal layer with parameters (μm): p = 7.24, w = 3.2, t1 = 1.981, t2 = 0.485. Absorption and emissivity spectra of the top structure of the mirror at θ = 61.28°, B = 0 T or B = 3 T, and absorption and emissivity spectra of the top structure of the aluminum mirror at θ = 61.28°and B = 3 T[34];(c) Schematic representation of a blackbody shell with isotropic hemispherical and directional characteristics[35];(d) Schematic diagram of a translucent film in an anisotropic shell where the incident wave has both p and s components and the output wave is p-polarized or s-polarized; Incident waves are either p or s polarized, while reflected and transmitted waves contain both p and s polarized components[35];(e) Variation of reflectance of single hBN film with azimuth angle[35]
图 2 (a)各向同性等离子体介质和具有不对称介电常数张量的各向异性材料在两平面体间的热流密度[46];(b)外磁场沿着y轴的磁光材料InAs表面衰减全反射的几何结构示意图、B=3 T时InAs的介电常数分量及吸收率和发射率[47];(c)基于Tamm激发的Thue-morse非周期结构和Fibonacci光子晶体结构示意图[48-49];(d)加入石墨烯层的光栅结构示意图[50];(e)去除石墨烯层后,光栅结构在强非互易波长处的磁场分布和各几何参数对发射率和吸收率的影响[51];(f)光栅层在中间的强非互易辐射的结构示意图[52]
Figure 2. (a) Heat flux between two planes of isotropic plasma media and anisotropic materials with asymmetric permittivity tensor[46]; (b) Schematic diagram of the geometric structure of the total reflection attenuated by the external magnetic field along the y-axis of the magneto-optical material InAs surface. Right pannels indicate the dielectric constant component of the InAs and the absorption and emissivity when B=3 T[47]; (c) Schematic diagram of the Thue-morse aperiodic structure and Fibonacci photonic crystal structure based on Tamm excitation[48-49]; (d) Schematic diagram of grating structures with a graphene layer[50]; (e) Magnetic field distribution and the effects of geometric parameters on emissivity and absorptivity of the grating structure at strongly non-reciprocal wavelengths after the graphene layer is removed[51]; (f) Schematic diagram of the structure of the strong non-reciprocal radiation in the middle of the grating layer[52]
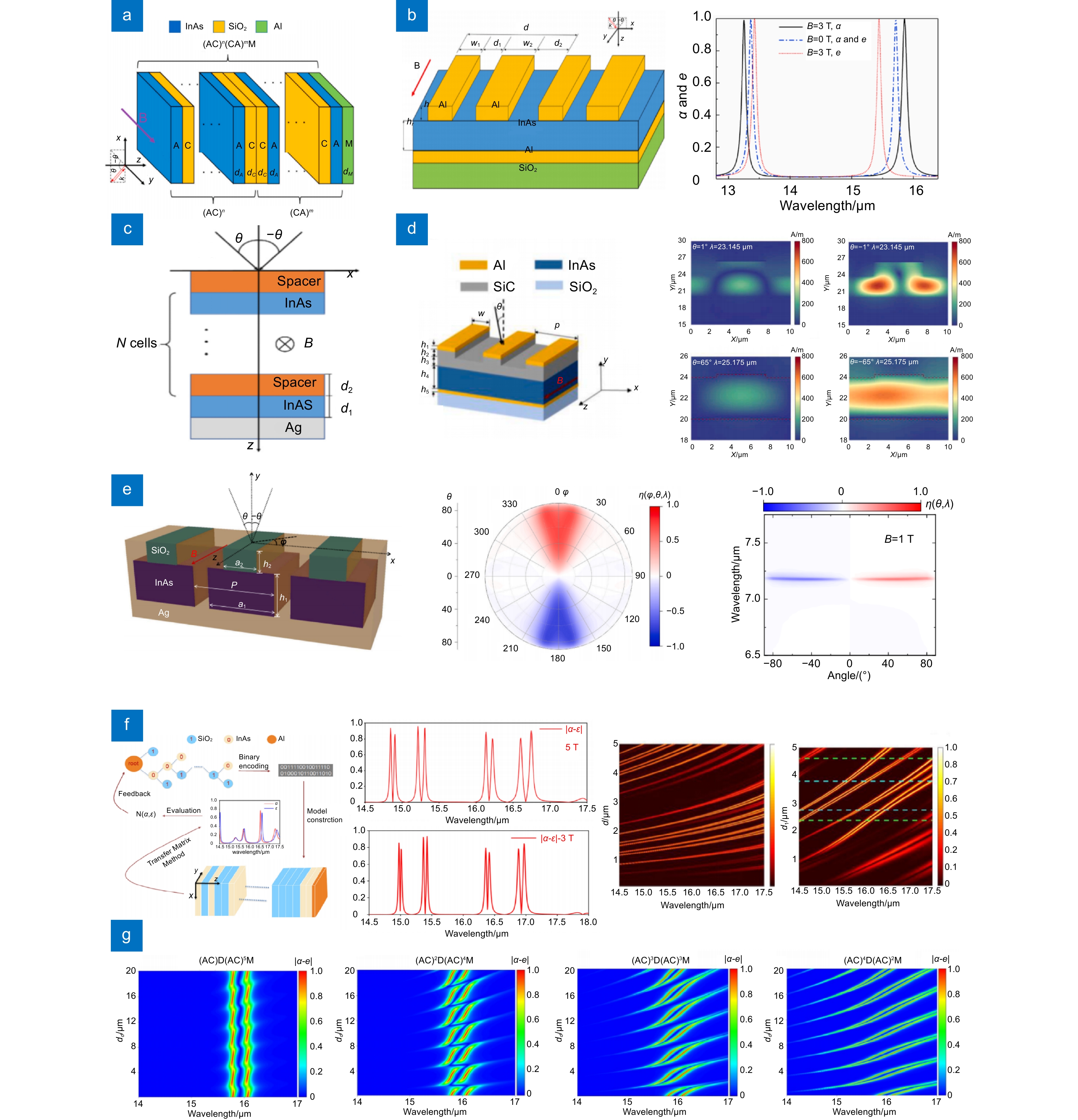
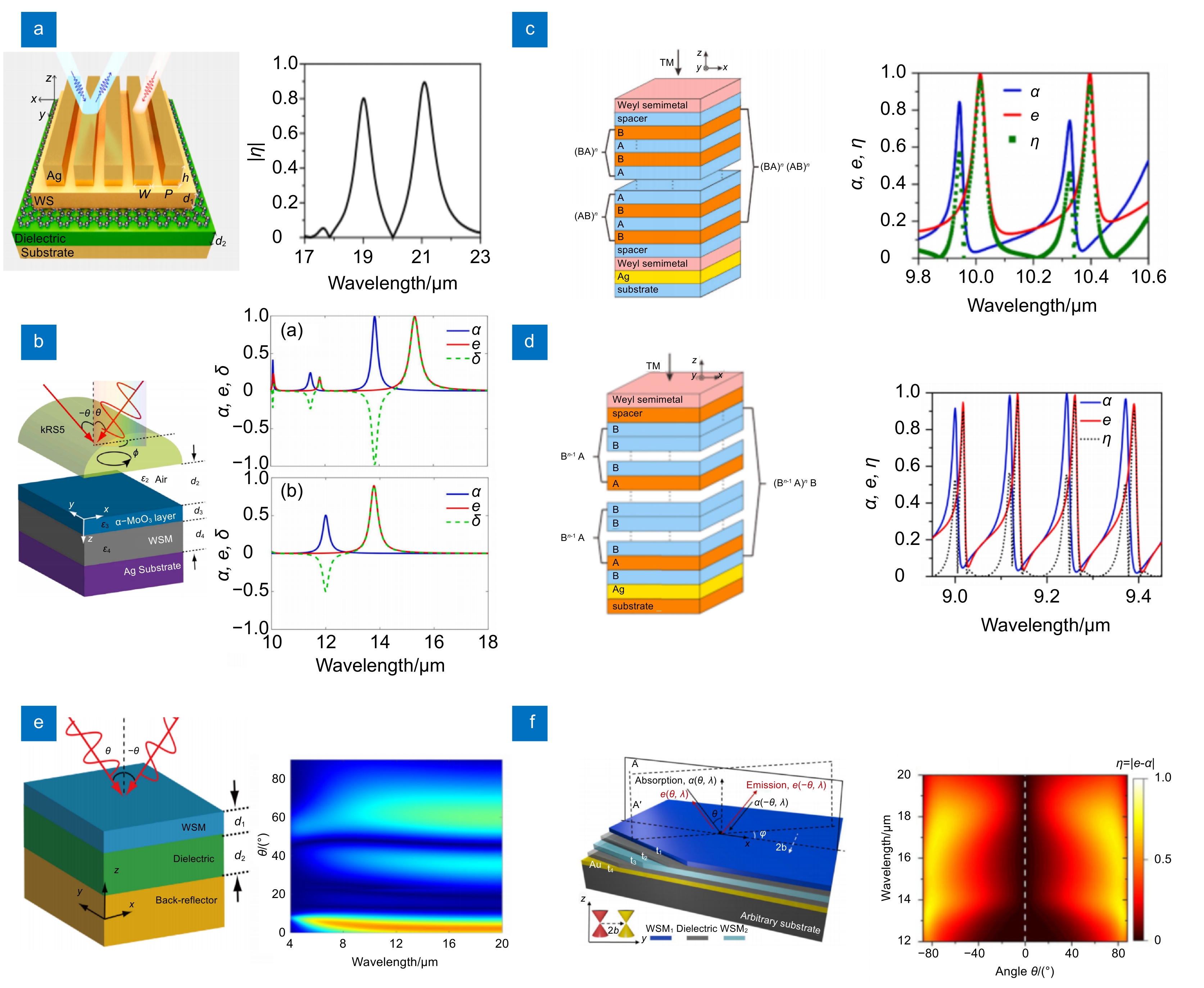
图 3 (a)双频非互易热发射器原理图[53];(b)强双频非互反辐射结构的原理图和几何参数,外磁场沿y轴;B= 0 T和B= 3 T时θ = 25°处的吸收(α)和发射(e)光谱[54];(c) 利用MPCs实现强非互反辐射结构示意图;(d) B=0.3 T实现非互易热辐射的光栅结构示意图;θ =±1°和θ =±65°的磁场分布[58];(e)广角窄带非互易结构体示意图,6.52 μm和7.18 μm 处结构在0°~89°的广角范围内的非互易性[59];(f) 基于机器学习的多波段非互反热辐射原理图;B= 5 T和B=3 T时吸收率与发射率之差;吸收和发射差值分别随波长、InAs层和SiO2层厚度的变化情况[60]; (g) 缺陷位置对多波段非互易热辐射的影响[61]
Figure 3. (a) Schematic diagram of a dual-frequency non-reciprocal heat emitter[53]; (b) Schematic diagram and geometric parameters of the strong dual-frequency non-reciprocal radiation structure, with the external magnetic field along the y-axis; Absorption (α) and emission (e) spectra at θ = 25° for B= 0 T and B= 3 T[54]; (c) Schematic diagram of strong non-reciprocal radiation using MPCs; (d) Schematic diagram of grating structures with B=0.3 T to achieve non-reciprocal thermal radiation; Magnetic field distribution of θ =±1° and θ =±65°[58]; (e) Schematic representation of wide-angle narrow-band non-reciprocal structural bodies, non-reciprocity of the structures at 6.52 and 7.18 μm over a wide angle range from 0° to 89°[59]; (f) Left: schematic diagram of multi-band non-reciprocal thermal radiation based on machine learning. Middle: difference between absorptivity and emissivity when B= 5 T and B=3 T. Right: difference of absorption and emission with wavelength, InAs layer and SiO2 layer thickness, respectively[60]; (g) Nonreciprocities under different defect locations[61]
图 4 (a) 硅基纳米孔阵列双极化非互易辐射的三维视图和xz面视图以及在 TE极化波和TM极化波下结构的吸收、发射和非互易性随波长的变化[62];(b) 近红外双偏振窄带非互易辐射器原理图;TE极化波和TM极化波在0.8°入射角下的吸收光谱和发射光谱以及TE极化电场|Ey|在共振波长1684.90 nm处和TM极化磁场|Hy|共振波长在1669.74 nm的场分布[63]
Figure 4. (a) Three-dimensional view and xz plane view of dual-polarized nonreciprocal radiation of silicon-based nanopore arrays, showing the changes of absorption, emission and nonreciprocity of structures with wavelength under TE and TM polarized waves[62]; (b) Schematic diagram of a near-infrared dual-polarization narrow-band nonreciprocal radiator, showing the absorption and emission spectra of TE polarized wave and TM polarized wave at 0.8° incidence angle, and the field distribution of TE polarized electric field |Ey| at the resonance wavelength of 1684.90 nm and TM polarized magnetic field |Hy| at the resonance wavelength of 1669.74 nm[63]
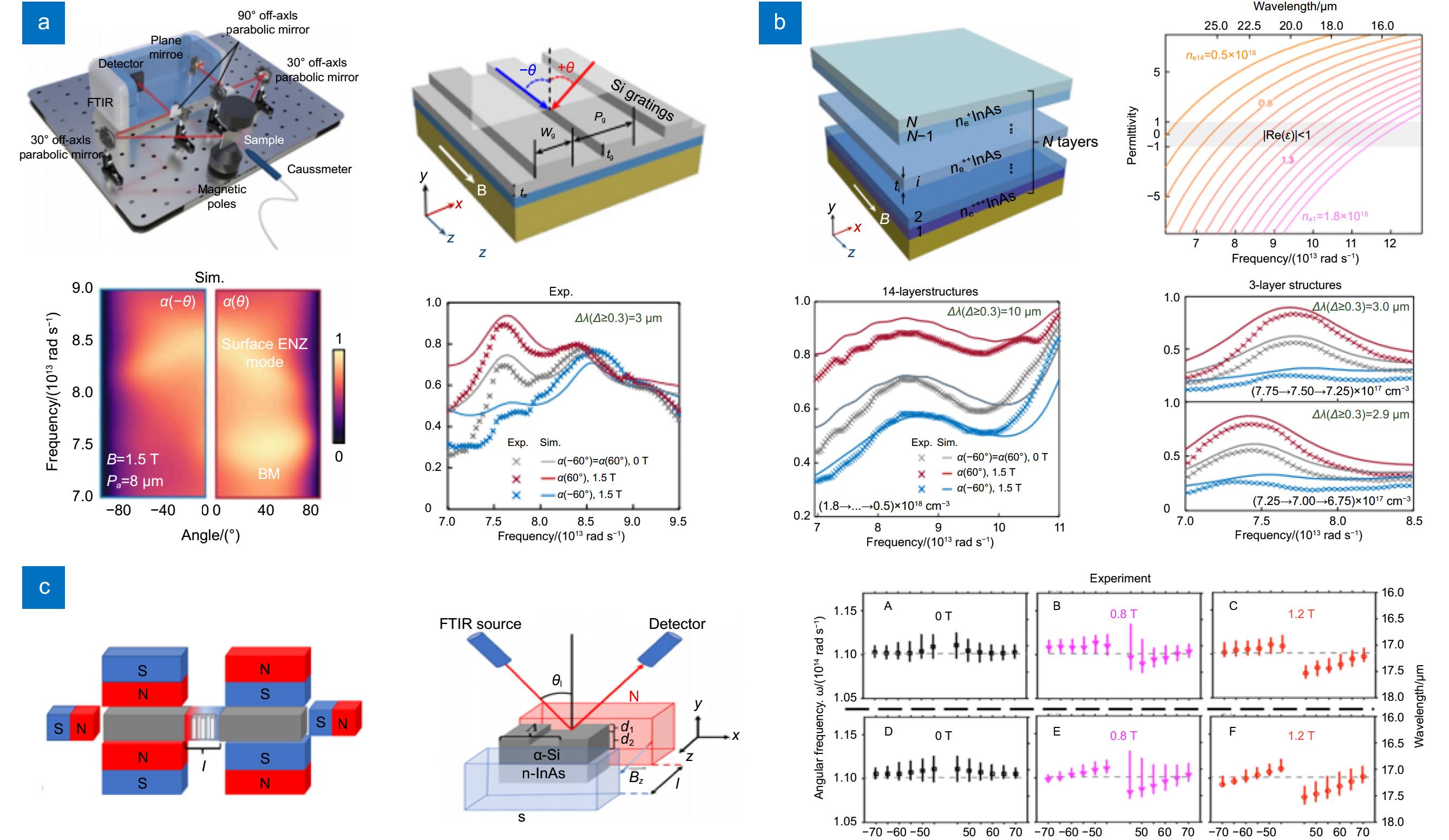
图 5 (a) 定制红外MO Kerr效应表征装置,单层结构上的介质光栅示意图及θ= ±60°和B= 1.5 T下模拟和实验的非互易光谱[64];(b) 具有梯度ne的磁化ENZ多层的示意图、不同掺杂浓度的InAs薄膜的介电常数实部图和θ= 60°时14层样品和三层样品测量和模拟的不对称吸收光谱[64]; (c)测量方案示意图以及TM极化波的吸收率最大值随磁场和入射角的函数[65]
Figure 5. (a) Customized infrared MO Kerr effect characterization device, dielectric grating diagram on a single layer structure, and nonreciprocal spectra of simulation and experiment at θ= ± 60° and B= 1.5 T[64]; (b) Schematic diagram of magnetized ENZ multilayers with gradient ne, real part diagram of permittivity of InAs films with different doping concentrations, and measured and simulated asymmetric absorption spectra for 14 and three-layer samples at θ= 60°[64]; (c) Customized schematic diagram of the measurement scheme and the maximum absorptivity of the TM polarized wave as a function of the magnetic field and the incidence angle[65]
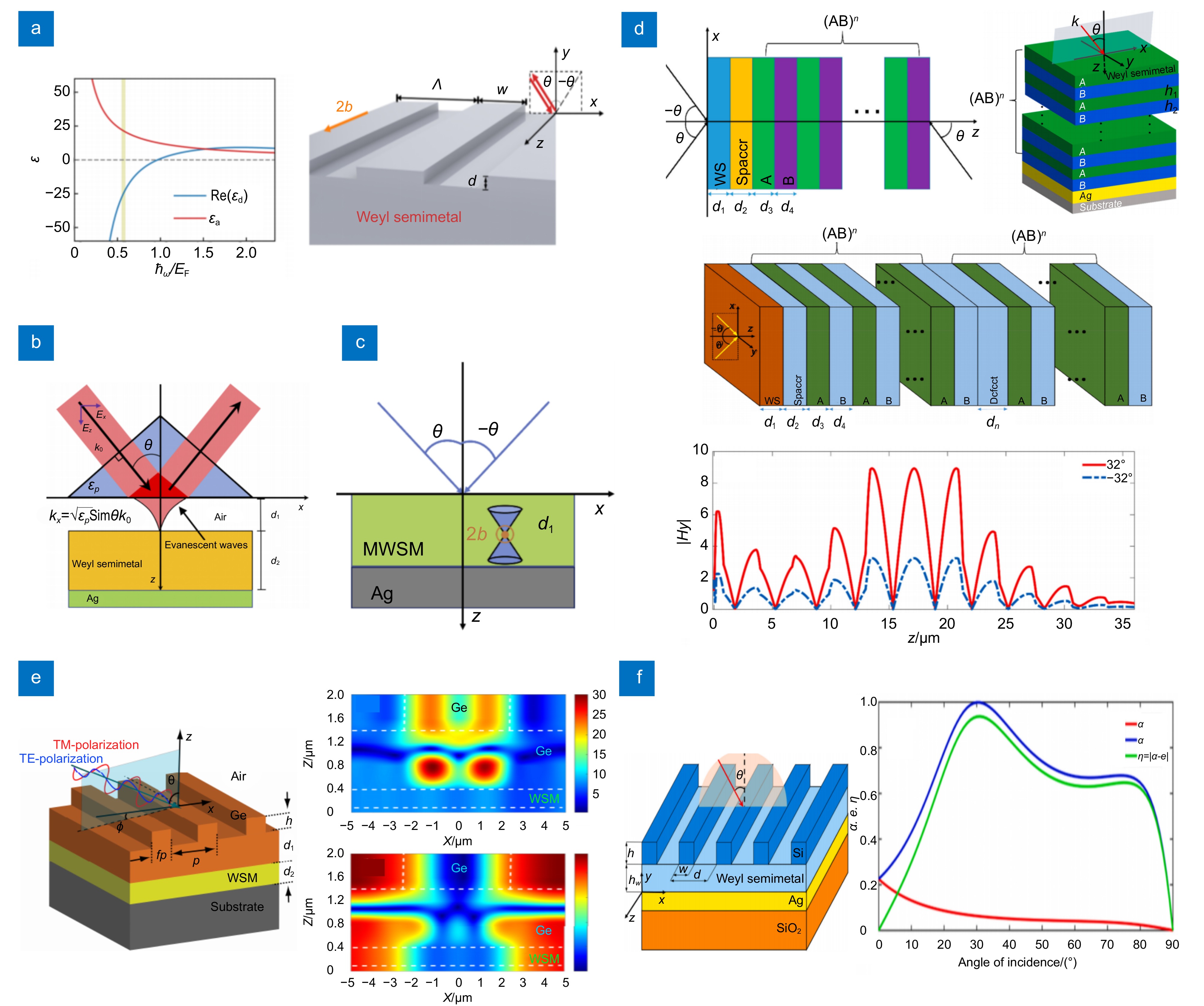
图 6 (a) 外尔半金属的介电常数张量分量(ɛd和ɛa分别为对角分量和非对角分量)和非互易热发射的外尔半金属光子晶体示意图[69];(b) 外尔半金属表面衰减全反射的几何形状。入射平面为x-z平面[70];(c) 非互易热辐射器示意图。厚度为d1的MWSM薄膜位于金属基板的顶部[71];(d) 外尔半金属与介质光子晶体多层结构示意图,及第三种多层结构的内部磁场强度分布图[72-74];(e)由ZCG、WSM层和Ag衬底组成的非互易热发射器的原理图和θ =±1°时,波长为10.39 µm处Hy的振幅分布[75];(f)极广角非互易热辐射效应的方案设计图[76]
Figure 6. (a) Schematic diagram of Weyl semi-metallic photonic crystals with dielectric constant tensor components (${\varepsilon _{\rm{d}}}$and ${\varepsilon _{\rm{a}}}$diagonal and non-diagonal components, respectively) and non-reciprocal thermal emission[69]; (b) Geometry of the attenuated total reflection of the Weyl semi-metal surface. The plane of incidence is the x-z plane[70]; (c) Schematic diagram of a non-reciprocal heat radiator. The MWSM film of thickness d1 is located on top of the metal substrate[71]; (d) Schematic diagram of the multilayer structure of Weyl semi-metallic and dielectric photonic crystals, and diagram of the internal magnetic field intensity distribution of the third multilayer structure[72-74]; (e) Schematic diagram of a non-reciprocal heat emitter consisting of a ZCG, WSM layer, and Ag substrate; the amplitude distribution of Hy at a wavelength of 10.39 µm at θ =±1°[75]; (f) Schematic design of extremely wide-angle non-reciprocal thermal radiation effects[76]
图 7 (a) 杂化石墨烯- 外尔结构及效果示意图[77];(b) KRS5/Air/α-MoO3/WSM/Ag结构;有无α-MoO3时的非互易值[78]; (c) 实现多波段非互易的多层光子晶体结构示意图[79];(d) 优化光子晶体序列为斐波那契多层实现四通道非互易辐射[80];(e)由WSM薄膜、介电间隔器和后反射器组成的非互易热发射器的原理图和波长为8~20 µm处非互易值[81];(f)宽带极广角非互易热辐射效应的方案设计图[82]
Figure 7. (a) Structure and effect diagram of hybridized graphene-Weyl[77]; (b) KRS5/Air/ α-MoO3 /WSM/Ag structure; non-reciprocal value with or without α-MoO3[78]; (c) Schematic diagram of multi-layer photonic crystal structures that achieve multi-band nonreciprocity[79]; (d) Optimizing photonic crystal sequences for Fibonacci multilayers to achieve four-channel nonreciprocal radiation[80]; (e) Schematic diagram of a non-reciprocal heat emitter consisting of a WSM film, a dielectric spacer and a rear reflector and non-reciprocal values at wavelengths 8-20 µm[81]; (f) Schematic design of wideband extremely wide-angle non-reciprocal thermal radiation effects[82]
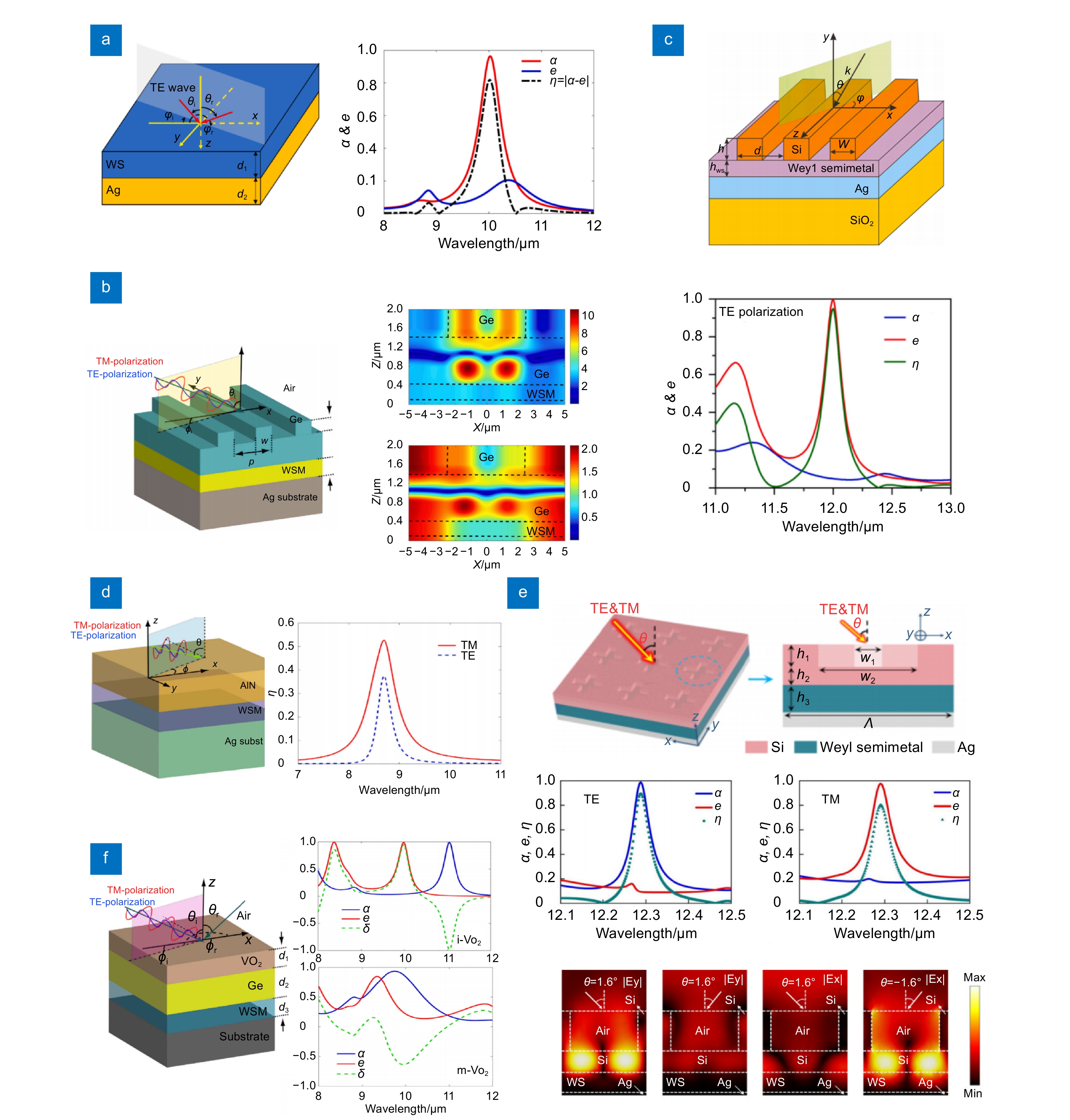
图 8 (a)由WS膜和Ag层组成实现TE波下非互易的热发射器原理图及其吸收率、发射率和非互易值[83];(b) ZCG、WSM层和Ag衬底组成结构示意图及10.32 µm处电场分布图[84]; (c) 由硅光栅和由SiO2衬底支撑的银夹层和WS薄膜组成的结构示意图及其吸收率、发射率和非互易值[85]; (d)双极化非互易热发射器原理图[86];(e) 外尔半金属双偏振辐射体的原理图;TE和TM偏振吸收率、发射率和角度为1.6°的非互易性和对应的电场分布图[87];(f)由VO2、Ge、WSM层和Mo衬底组成的结构示意图;VO2表现非金属性和金属性时的吸收率、发射率和非互易值[88]
Figure 8. (a) Schematic diagram of the thermal emitter composed of a WS film and a Ag layer to achieve non-reciprocity under TE wave, showing the absorption rate, emissivity, and non-reciprocity values[83]; (b) ZCG, WSM layer, and Ag substrate composition structure diagram and electric field distribution diagram at 10.32 µm[84]; (c) Schematic diagram of the structure composed of silicon gratings, a silver interlayer supported by a SiO2 substrate and a WS film, showing the absorptivity, emissivity, and non-reciprocal values[85]; (d) Schematic diagram of a dual-polarization non-reciprocal heat emitter[86]; (e) Schematic diagram of Weyl semimetallic dual-polarized radiator, showing the TE and TM polarization absorptivity, emissivity, and angle non-reciprocity of 1.6° and corresponding electric field distribution diagram[87]; (f) Structural diagram consisting of VO2, Ge, WSM layers, and a Mo substrate, showing the absorption rate, emissivity, and non-reciprocal value of VO2 for nonmetallic and metallic properties[88]
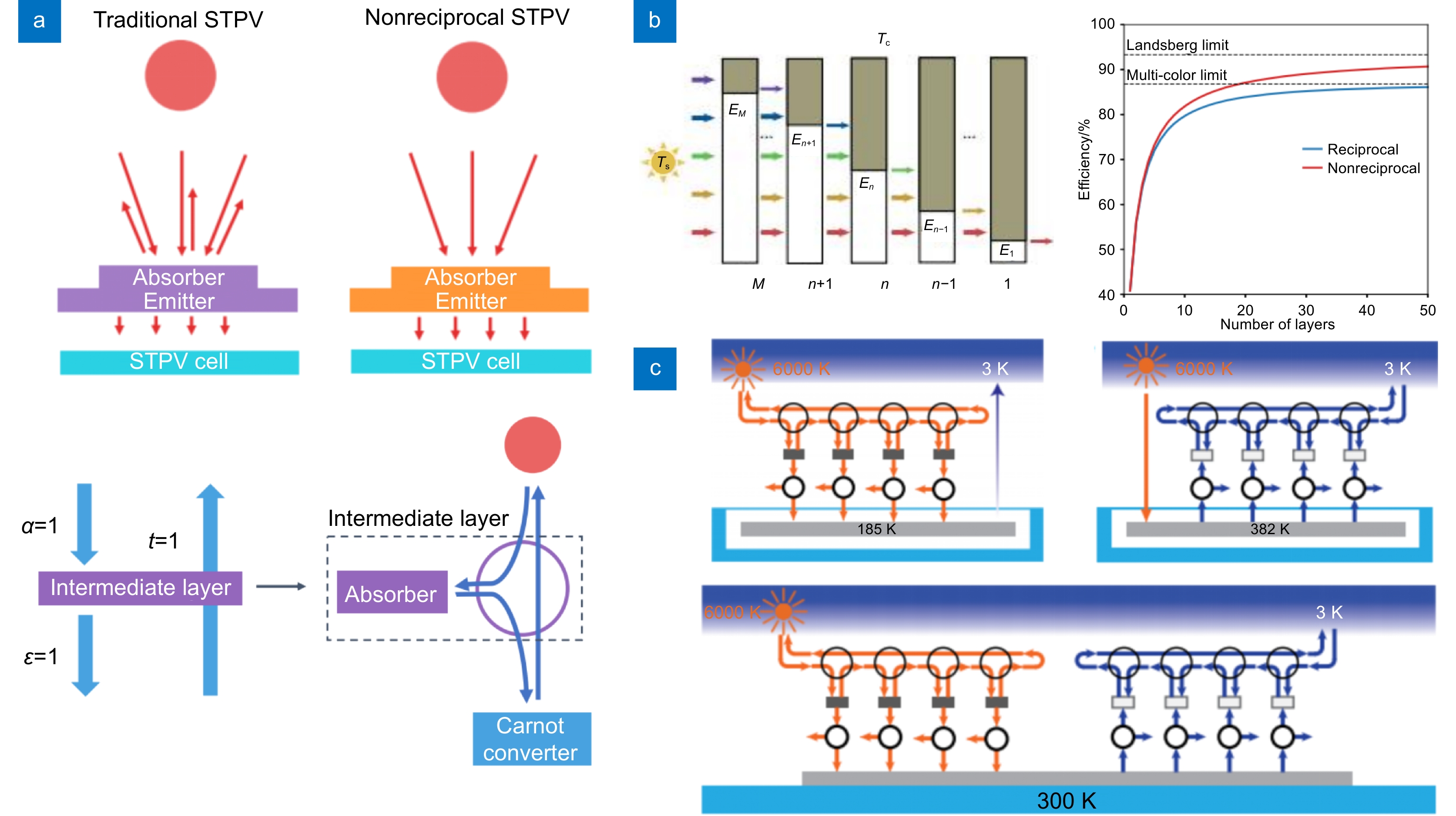
图 9 (a)传统STPV和非互易STPV系统[92];(b) 非互易多结太阳能电池及效率极限[97]; (c) 结合辐射冷却和太阳能加热的Landsberg极限系统示意图[98]
Figure 9. (a) Traditional STPV and non-reciprocal STPV systems[92]; (b) Nonreciprocal multijunction solar cells and efficiency limits[97]; (c) Schematic diagram of the Landsberg limit system combining radiant cooling and solar heating[98]
-
参考文献
[1] Luo C Y, Narayanaswamy A, Chen G, et al. Thermal radiation from photonic crystals: a direct calculation[J]. Phys Rev Lett, 2004, 93(21): 213905. doi: 10.1103/PhysRevLett.93.213905
[2] Francoeur M, Mengüç M P, Vaillon R. Solution of near-field thermal radiation in one-dimensional layered media using dyadic Green's functions and the scattering matrix method[J]. J Quant Spectrosc Radiat Transfer, 2009, 110(18): 2002−2018. doi: 10.1016/j.jqsrt.2009.05.010
[3] Baranov D G, Xiao Y Z, Nechepurenko I A, et al. Nanophotonic engineering of far-field thermal emitters[J]. Nat Mater, 2019, 18(9): 920−930. doi: 10.1038/s41563-019-0363-y
[4] Fan S H, Li W. Photonics and thermodynamics concepts in radiative cooling[J]. Nat Photonics, 2022, 16(3): 182−190. doi: 10.1038/s41566-021-00921-9
[5] Landsberg P T, Tonge G. Thermodynamic energy conversion efficiencies[J]. J Appl Phys, 1980, 51(7): R1−R20. doi: 10.1063/1.328187
[6] Snyder W C, Wan Z M, Li X W. Thermodynamic constraints on reflectance reciprocity and Kirchhoff’s law[J]. Appl Opt, 1998, 37(16): 3464−3470. doi: 10.1364/AO.37.003464
[7] Snyder W C. Structured surface bidirectional reflectance distribution function reciprocity: theory and counterexamples[J]. Appl Opt, 2002, 41(21): 4307−4313. doi: 10.1364/AO.41.004307
[8] Baltes H P. I on the validity of Kirchhoff's law of heat radiation for a body in a nonequilibrium environment[J]. Prog Opt, 1976, 13: 1−25. doi: 10.1016/S0079-6638(08)70017-9
[9] Greffet J J, Nieto-Vesperinas M. Field theory for generalized bidirectional reflectivity: derivation of Helmholtz’s reciprocity principle and Kirchhoff’s law[J]. J Opt Soc Am A, 1998, 15(10): 2735−2744. doi: 10.1364/JOSAA.15.002735
[10] Green M A. Third Generation Photovoltaics: Advanced Solar Energy Conversion[M]. Berlin: Springer, 2003. https://doi.org/10.1007/b137807.
[11] Huang G, Wang K, Markides C N. Efficiency limits of concentrating spectral-splitting hybrid photovoltaic-thermal (PV-T) solar collectors and systems[J]. Light Sci Appl, 2021, 10(1): 28. doi: 10.1038/s41377-021-00465-1
[12] Shockley W, Queisser H J. Detailed balance limit of efficiency of p-n junction solar cells[J]. J Appl Phys, 1961, 32(3): 510−519. doi: 10.1063/1.1736034
[13] Yu Z F, Raman A, Fan S H. Fundamental limit of nanophotonic light trapping in solar cells[J]. Proc Natl Acad Sci USA, 2010, 107(41): 17491−17496. doi: 10.1073/pnas.1008296107
[14] Harder N P, Würfel P. Theoretical limits of thermophotovoltaic solar energy conversion[J]. Semicond Sci Technol, 2003, 18(5): S151−S157. doi: 10.1088/0268-1242/18/5/303
[15] Taretto K, Rau U. Modeling extremely thin absorber solar cells for optimized design[J]. Prog Photovolt, 2004, 12(8): 573−591. doi: 10.1002/pip.549
[16] Ries H. Complete and reversible absorption of radiation[J]. Appl Phys B, 1983, 32(3): 153−156. doi: 10.1007/BF00688821
[17] Hsu P C, Liu C, Song A Y, et al. A dual-mode textile for human body radiative heating and cooling[J]. Sci Adv, 2017, 3(11): e1700895. doi: 10.1126/sciadv.1700895
[18] Shi N N, Tsai C C, Camino F, et al. Keeping cool: enhanced optical reflection and radiative heat dissipation in Saharan silver ants[J]. Science, 2018, 349(6245): 298−301. doi: 10.1126/science.aab3564
[19] Raman A P, Anoma M A, Zhu L X, et al. Passive radiative cooling below ambient air temperature under direct sunlight[J]. Nature, 2014, 515(7528): 540−544. doi: 10.1038/nature13883
[20] Zhu L X, Raman A P, Fan S H. Radiative cooling of solar absorbers using a visibly transparent photonic crystal thermal blackbody[J]. Proc Natl Acad Sci USA, 2015, 112(40): 12282−12287. doi: 10.1073/pnas.1509453112
[21] Ilic O, Bermel P, Chen G, et al. Tailoring high-temperature radiation and the resurrection of the incandescent source[J]. Nat Nanotechnol, 216, 11(4): 320−324. doi: 10.1038/nnano.2015.309
[22] Kirchhoff G. I. On the relation between the radiating and absorbing powers of different bodies for light and heat[J]. Phil Mag, 1860, 20(130): 1−21. doi: 10.1080/14786446008642901
[23] Howell J R, Mengüç M P, Siegel R. Thermal Radiation Heat Transfer[M]. Boca Raton: CRC Press, 2016.
[24] Modest M F. Radiative Heat Transfer[M]. New York: Academic Press, 2013.
[25] Bergman T L, Lavine A S, Incropera F P, et al. Fundamentals of Heat and Mass Transfer[M]. New York: Wiley, 2011.
[26] Balfour Stewart E. I. -An account of some experiments on radiant heat, involving an extension of Prevost’s theory of exchanges[J]. Earth Environ Sci Trans Royal Soc Edinburgh, 1861, 22(1): 1−20 doi: 10.1017/S0080456800031288
[27] Boltzmann L. The second law of thermodynamics[M]//Boltzmann L. Theoretical Physics and Philosophical Problems: Selected Writings. Dordrecht: Springer-Verlag, 1974. https://doi.org/10.1007/978-94-010-2091-6_2.
[28] Planck M. The Theory of Heat Radiation[M]. Masius M, trans. New York: Dover Publications, 1959, 1991.
[29] Rytov S M, Kravtsov Y A, Tatarskii I T. Principles of Statistical Radiophysics 3: Elements of Random Fields[M]. Berlin: Springer-Verlag, 1989.
[30] Zhang Z M. Nano/Microscale Heat Transfer[M]. New York: McGraw-Hill, 2007.
[31] Krüger M, Bimonte G, Emig T, et al. Trace formulas for nonequilibrium Casimir interactions, heat radiation, and heat transfer for arbitrary objects[J]. Phys Rev B, 2012, 86(11): 115423. doi: 10.1103/PhysRevB.86.115423
[32] Geist J. Effect of wall roughness on the spectral density of radiation within symmetric closed cavities in good conductors[J]. J Opt Soc Am, 1972, 62(4): 602−604. doi: 10.1364/JOSA.62.000602
[33] Robitaille P M. Kirchhoff’s law of thermal emission: 150 years[J]. Prog Phys, 2009, 5(4): 3−13.
[34] Zhu L X, Fan S H. Near complete violation of detailed balance in thermal radiation[J]. Phys Rev B, 2014, 90(22): 220301. doi: 10.1103/PhysRevB.90.220301
[35] Zhang Z M, Wu X H, Fu C J. Validity of Kirchhoff’s law for semitransparent films made of anisotropic materials[J]. J Quant Spectrosc Radiat Transfer, 2020, 245: 106904. doi: 10.1016/j.jqsrt.2020.106904
[36] Wu X H, Fu C J, Zhang Z M. Effect of orientation on the directional and hemispherical emissivity of hyperbolic metamaterials[J]. Int J Heat Mass Transfer, 2019, 135: 1207−1217. doi: 10.1016/j.ijheatmasstransfer.2019.02.066
[37] Wu X H, Fu C J, Zhang Z M. Chiral response of a twisted bilayer of hexagonal boron nitride[J]. Opt Commun, 2019, 452: 124−129. doi: 10.1016/j.optcom.2019.07.015
[38] Zhao B, Sakurai A, Zhang Z M. Polarization dependence of the reflectance and transmittance of anisotropic metamaterials[J]. J Thermophys Heat Transfer, 2016, 30(1): 240−246. doi: 10.2514/1.T4587
[39] Malone C G, Choi B I, Flik M I, et al. Spectral emissivity of optically anisotropic solid media[J]. J Heat Transfer, 1993, 115(4): 1021−1028. doi: 10.1115/1.2911356
[40] Potton R J. Reciprocity in optics[J]. Rep Prog Phys, 2004, 67(5): 717−754. doi: 10.1088/0034-4885/67/5/R03
[41] Shu W X, Fu N, Lü X F, et al. Integral equation method for electromagnetic wave propagation in stratified anisotropic dielectric-magnetic materials[J]. Commun Theor Phys, 2010, 54(5): 879−885. doi: 10.1088/0253-6102/54/5/21
[42] Menzel C, Helgert C, Rockstuhl C, et al. Asymmetric transmission of linearly polarized light at optical metamaterials[J]. Phys Rev Lett, 2010, 104(25): 253902. doi: 10.1103/PhysRevLett.104.253902
[43] Li L F. Symmetries of cross-polarization diffraction coefficients of gratings[J]. J Opt Soc Am A, 2000, 17(5): 881−887. doi: 10.1364/JOSAA.17.000881
[44] Armelles G, Cebollada A, García-Martín A, et al. Magnetoplasmonics: combining magnetic and plasmonic functionalities[J]. Adv Opt Mater, 2013, 1(1): 10−35. doi: 10.1002/adom.201200011
[45] Yang S H, Liu M Q, Zhao C Y, et al. Nonreciprocal thermal photonics[J]. Nat Photonics, 2024, 18(5): 412−424. doi: 10.1038/S41566-024-01409-Y
[46] Fan L L, Guo Y, Papadakis G T, et al. Nonreciprocal radiative heat transfer between two planar bodies[J]. Phys Rev B, 2020, 101(8): 085407. doi: 10.1103/PhysRevB.101.085407
[47] Wu X H. The promising structure to verify the Kirchhoff’s Law for nonreciprocal materials[J]. ES Energy Environ, 2021, 12: 46−51. doi: 10.30919/esee8c1047
[48] Wu J, Wang Z M, Wu B Y, et al. The giant enhancement of nonreciprocal radiation in Thue-morse aperiodic structures[J]. Opt Laser Technol, 2022, 152: 108138. doi: 10.1016/j.optlastec.2022.108138
[49] Wu J, Wu F, Zhao T C, et al. Nonreciprocal thermal radiation based on Fibonacci quasi-periodic structures[J]. Eng Sci, 2022, 18: 141−147. doi: 10.30919/es8d575
[50] Wu J, Wu F, Zhao T C, et al. Tunable nonreciprocal thermal emitter based on metal grating and graphene[J]. Int J Therm Sci, 2022, 172: 107316. doi: 10.1016/j.ijthermalsci.2021.107316
[51] Wu J, Sun Y S, Wu B Y, et al. Strong nonreciprocal mid-infrared radiation at small angles based on the excitation of guided modes[J]. Eng Sci, 2022, 19: 198−204. doi: 10.30919/es8d650
[52] Wu X H, Chen Z X, Wu F. Strong nonreciprocal radiation in a InAs film by critical coupling with a dielectric grating[J]. ES Energy Environ, 2021, 13: 8−12. doi: 10.30919/esee8c442
[53] Wu J, Wu F, Zhao T C, et al. Dual-band nonreciprocal thermal radiation by coupling optical Tamm states in magnetophotonic multilayers[J]. Int J Therm Sci, 2022, 175: 107457. doi: 10.1016/j.ijthermalsci.2022.107457
[54] Wu J, Wu F, Wu X H. Strong dual-band nonreciprocal radiation based on a four-part periodic metal grating[J]. Opt Mater, 2021, 120: 111476. doi: 10.1016/j.optmat.2021.111476
[55] Shi K Z, Xing Y X, Sun Y W, et al. Thermal vertical emitter of ultra-high directionality achieved through nonreciprocal magneto-optical lattice resonances[J]. Adv Opt Mater, 2022, 10(24): 2201732. doi: 10.1002/adom.202201732
[56] Chen Z H, Yu S L, Yuan C, et al. Ultra-efficient machine learning design of nonreciprocal thermal absorber for arbitrary directional and spectral radiation[J]. J Appl Phys, 2023, 134(20): 203101. doi: 10.1063/5.0177207
[57] Wu X H, Liu R Y, Yu H Y, et al. Strong nonreciprocal radiation in magnetophotonic crystals[J]. J Quant Spectrosc Radiat Transfer, 2021, 272: 107794. doi: 10.1016/j.jqsrt.2021.107794
[58] Chen Z H, Yu S L, Yuan C, et al. Near-normal nonreciprocal thermal radiation with a 0.3T magnetic field based on double-layer grating structure[J]. Int J Heat Mass Transfer, 2024, 222: 125202. doi: 10.1016/j.ijheatmasstransfer.2024.125202
[59] Wang J S, Shi K Z, Xing X B. Nonreciprocal wide-angle and narrowband thermal emitter[J]. Mater Today Phys, 2024, 46: 101515. doi: 10.1016/j.mtphys.2024.101515
[60] Chen Z H, Yu S L, Hu B, et al. Multi-band and wide-angle nonreciprocal thermal radiation[J]. Int J Heat Mass Transfer, 2023, 209: 124149. doi: 10.1016/j.ijheatmasstransfer.2023.124149
[61] Chen Z H, Yu S L, Yuan C, et al. Defect-mode and Fabry-Perot resonance induced multi-band nonreciprocal thermal radiation[J]. Sci China Technol Sci, 2024. doi: 10.1007/s11431-023-2555-y
[62] Fang J M, Wang M Z, Liu T Y, et al. Dual-polarization strong nonreciprocal thermal radiation with silicon-based nanopore arrays[J]. International Journal of Thermal Sciences, 2024, 195: 108602. doi: 10.1016/j.ijthermalsci.2023.108602
[63] Fang J M, Zou J Q, Liu T Y, et al. Dual-polarization near-infrared narrow-band unidirectional nonreciprocal thermal radiator[J]. Int J Heat Mass Transfer, 2024, 223: 125229. doi: 10.1016/j.ijheatmasstransfer.2024.125229
[64] Liu M Q, Xia S, Wan W J, et al. Broadband mid-infrared non-reciprocal absorption using magnetized gradient epsilon-near-zero thin films[J]. Nat Mater, 2023, 22(10): 1196−1202. doi: 10.1038/s41563-023-01635-9
[65] Shayegan K J, Zhao B, Kim Y, et al. Nonreciprocal infrared absorption via resonant magneto-optical coupling to InAs[J]. Sci Adv, 2022, 8(18): eabm4308. doi: 10.1126/sciadv.abm4308
[66] Armitage N P, Mele E J, Vishwanath A. Weyl and dirac semimetals in three-dimensional solids[J]. Rev Mod Phys, 2018, 90(1): 015001. doi: 10.1103/RevModPhys.90.015001
[67] Hosur P, Qi X L. Recent developments in transport phenomena in Weyl semimetals[J]. C R Phys, 2013, 14(9-10): 857−870. doi: 10.1016/j.crhy.2013.10.010
[68] Hofmann J, Sarma S D. Surface Plasmon polaritons in topological Weyl semimetals[J]. Phys Rev B, 2016, 93(24): 241402(R). doi: 10.1103/PhysRevB.93.241402
[69] Zhao B, Guo C, Garcia C A C, et al. Axion-field-enabled nonreciprocal thermal radiation in Weyl semimetals[J]. Nano Lett, 2020, 20(3): 1923−1927. doi: 10.1021/acs.nanolett.9b05179
[70] Wu X H, Yu H Y, Wu F, et al. Enhanced nonreciprocal radiation in Weyl semimetals by attenuated total reflection[J]. AIP Adv, 2021, 11(7): 075106. doi: 10.1063/5.0055418
[71] Wu J, Wang Z M, Zhai H, et al. Near-complete violation of Kirchhoff’s law of thermal radiation in ultrathin magnetic Weyl semimetal films[J]. Opt Mater Express, 2021, 11(12): 4058−4066. doi: 10.1364/OME.444308
[72] Wu J, Sun Y S, Wu F, et al. Enhancing nonreciprocal thermal radiation in Weyl semimetals based on optical Tamm states by integrating with photonic crystals[J]. Waves Random Complex Media, 2022. doi: 10.1080/17455030.2022.2139426
[73] Wu J, Wu B Y, Wang Z M, et al. Strong nonreciprocal thermal radiation in Weyl semimetal-dielectric multilayer structure[J]. Int J Therm Sci, 2022, 181: 107788. doi: 10.1016/j.ijthermalsci.2022.107788
[74] Wu J Z, Li H J, Fu C J, et al. High quality factor nonreciprocal thermal radiation in a weyl semimetal film via the strong coupling between Tamm Plasmon and defect mode[J]. Int J Therm Sci, 2023, 184: 107902. doi: 10.1016/j.ijthermalsci.2022.107902
[75] Cui F P, Wang Z H, Ye J F, et al. Nonreciprocal thermal radiation with zero-contrast gratings for extreme small incident angle[J]. IEEE Photonics Technol Lett, 2024, 36(2): 131−134. doi: 10.1109/LPT.2023.3336599
[76] Wu J, Sun Y S, Wu B Y, et al. Extremely wide-angle nonreciprocal thermal emitters based on Weyl semimetals with dielectric grating structure[J]. Case Stud Therm Eng, 2022, 40: 102566. doi: 10.1016/j.csite.2022.102566
[77] Qing Y M, Wu J. Tunable wide-angle dual-channel nonreciprocal radiation in a hybrid graphene–Weyl semimetal structure[J]. Results Phys, 2024, 60: 107657. doi: 10.1016/J.RINP.2024.107657
[78] Gu Z H, Zang Q, Zheng G G. Near-unity nonreciprocal thermal radiation in biaxial van der Waals material-Weyl semimetal heterostructures[J]. Int Commun Heat Mass Transfer, 2024, 153: 107346. doi: 10.1016/j.icheatmasstransfer.2024.107346
[79] Wu J, Qing Y M. Multichannel nonreciprocal thermal radiation with Weyl semimetal and photonic crystal heterostructure[J]. Case Stud Therm Eng, 2023, 48: 103161. doi: 10.1016/j.csite.2023.103161
[80] Wu J, Qing Y M. Strong multi-band nonreciprocal radiation with Fibonacci multilayer involving Weyl semimetal[J]. Results Phys, 2023, 51: 106642. doi: 10.1016/j.rinp.2023.106642
[81] Cui F P, Sun M R, Qian L M, et al. Broadband nonreciprocal thermal radiation with Weyl semimetal-based Pattern-Free heterostructure[J]. IEEE Photonics Technol Lett, 2023, 35(13): 717−720. doi: 10.1109/LPT.2023.3274161
[82] Shi K Z, Sun Y W, Hu R, et al. Ultra-broadband and wide-angle nonreciprocal thermal emitter based on Weyl semimetal metamaterials[J]. Nanophotonics, 2024, 13(5): 737−747. doi: 10.1515/nanoph-2023-0520
[83] Wu J Z, Wu B Y, Shi K Z, et al. Strong nonreciprocal thermal radiation of transverse electric wave in Weyl semimetal[J]. Int J Therm Sci, 2023, 187: 108172. doi: 10.1016/j.ijthermalsci.2023.108172
[84] Sun M R, Qian L M, Xian F L, et al. Large nonreciprocity of thermal radiation for transverse electric wave with extremely small incident angle[J]. Opt Laser Technol, 2024, 170: 110308. doi: 10.1016/j.optlastec.2023.110308
[85] Wu J, Qing Y M. The enhanced nonreciprocal radiation in a grating structure containing a Weyl semimetal film under conical incidence[J]. Int Commun Heat Mass Transfer, 2024, 151: 107254. doi: 10.1016/j.icheatmasstransfer.2024.107254
[86] Li H J, Zheng G G. Polarization-independent nonreciprocal radiation in polar dielectric-Weyl semimetal planar heterostructure[J]. Opt Commun, 2024, 550: 130002. doi: 10.1016/j.optcom.2023.130002
[87] Fang J M, Zou J Q, Liu T Y, et al. Dual-polarization small-angle strong nonreciprocal thermal radiator with Weyl semimetal[J]. Appl Phys Lett, 2024, 124(17): 171702. doi: 10.1063/5.0180575
[88] Shen Y T, Qian L M, Sun M R, et al. Thermally tunable nonreciprocal radiation in lithography-free vanadium dioxide-dielectric-Weyl semimetal stack[J]. Opt Commun, 2024, 562: 130569. doi: 10.1016/j.optcom.2024.130569
[89] Chan W, Huang R, Wang C, et al. Modeling low-bandgap thermophotovoltaic diodes for high-efficiency portable power generators[J]. Sol Energy Mater Sol Cells, 2010, 94(3): 509−514. doi: 10.1016/j.solmat.2009.11.015
[90] Chan W R, Bermel P, Pilawa-Podgurski R C N, et al. Toward high-energy-density, high-efficiency, and moderate-temperature chip-scale thermophotovoltaics[J]. Proc Natl Acad Sci USA, 2013, 110(14): 5309−5314. doi: 10.1073/pnas.1301004110
[91] Datas A, Martí A. Thermophotovoltaic energy in space applications: review and future potential[J]. Sol Energy Mater Sol Cells, 2017, 161: 285−296. doi: 10.1016/j.solmat.2016.12.007
[92] Ghalekohneh S J, Zhao B. Nonreciprocal solar thermophotovoltaics[J]. Phys Rev Appl, 2022, 18(3): 034083. doi: 10.1103/PhysRevApplied.18.034083
[93] Rinnerbauer V, Lenert A, Bierman D M, et al. Metallic photonic crystal absorber-emitter for efficient spectral control in high-temperature solar thermophotovoltaics[J]. Adv Energy Mater, 2014, 4(12): 1400334. doi: 10.1002/aenm.201400334
[94] Wang Y, Zhou L, Zheng Q H, et al. Spectrally selective solar absorber with sharp and temperature dependent cut-off based on semiconductor nanowire arrays[J]. Appl Phys Lett, 2017, 110(20): 201108. doi: 10.1063/1.4983711
[95] Wang Y, Liu H Z, Zhu J. Solar thermophotovoltaics: progress, challenges, and opportunities[J]. APL Mater, 2019, 7(8): 080906. doi: 10.1063/1.5114829
[96] Amy C, Seyf H R, Steiner M A, et al. Thermal energy grid storage using multi-junction photovoltaics[J]. Energy Environ Sci, 2019, 12(1): 334−343. doi: 10.1039/C8EE02341G
[97] Park Y, Zhao B, Fan S H. Reaching the ultimate efficiency of solar energy harvesting with a nonreciprocal multijunction solar cell[J]. Nano Lett, 2022, 22(1): 448−452. doi: 10.1021/acs.nanolett.1c04288
[98] Li W, Buddhiraju S, Fan S H. Thermodynamic limits for simultaneous energy harvesting from the hot sun and cold outer space[J]. Light Sci Appl, 2020, 9: 68. doi: 10.1038/s41377-020-0296-x
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: