-
摘要
聚焦评价是叠焦扩展显微景深的关键,为了准确快速地获取叠焦图像序列像素点聚焦位置,生成高质量全聚焦图像,提出了一种基于颜色向量空间的聚焦评价算法。该算法直接在RGB向量空间中计算彩色图像梯度,充分利用了颜色通道间的相关性,避免了传统聚焦评价算法将彩色图转化为灰度图时造成的信息损失,且相较于彩色分量梯度的简单叠加具有更高的准确度;将中心像素与邻域像素在RGB空间的曼哈顿距离均值作为聚焦评价权值,可增强聚焦部分的敏感度,降低离焦部分的评价值,使聚焦评价曲线特性趋向理想化。选取空域、频域和统计学中7种聚焦评价算法与所提算法进行性能对比实验,结果表明:所提算法在仿真图像和真实显微图像中,具有更好的灵敏度、聚焦分辨力和抗噪声能力,曲线特性提升显著,应用于显微镜景深扩展可进一步提升叠焦大景深成像的质量。
Abstract
Focusing evaluation is the key to extending the depth of field in microscopy with stacked focus. To accurately and quickly obtain the pixel focusing position of the stacked focus image sequences and generate high-quality all-in-focus images, a focusing evaluation algorithm based on color vector space is proposed. This algorithm directly calculates color image gradients in the RGB vector space, fully utilizing the correlation between color channels, avoiding the information loss caused by traditional focus evaluation algorithms when converting color images into grayscale images, and has higher accuracy compared to simple stacking of color component gradients; Using the average Manhattan distance between the center pixel and neighboring pixels in RGB space as the focus evaluation weight can enhance the sensitivity of the focusing part, reduce the evaluation value of the defocused part, and make the focus evaluation curve characteristics tend to be idealized. Seven focusing evaluation algorithms in spatial domain, frequency domain, and statistics were selected for performance comparison experiments with the proposed algorithm. The results indicate that the proposed algorithm has better sensitivity, focusing resolution, and noise resistance in simulated and real microscopic images. The curve characteristics were significantly improved, and its application in microscope depth extension can further improve the quality of stacked focal large-depth imaging.
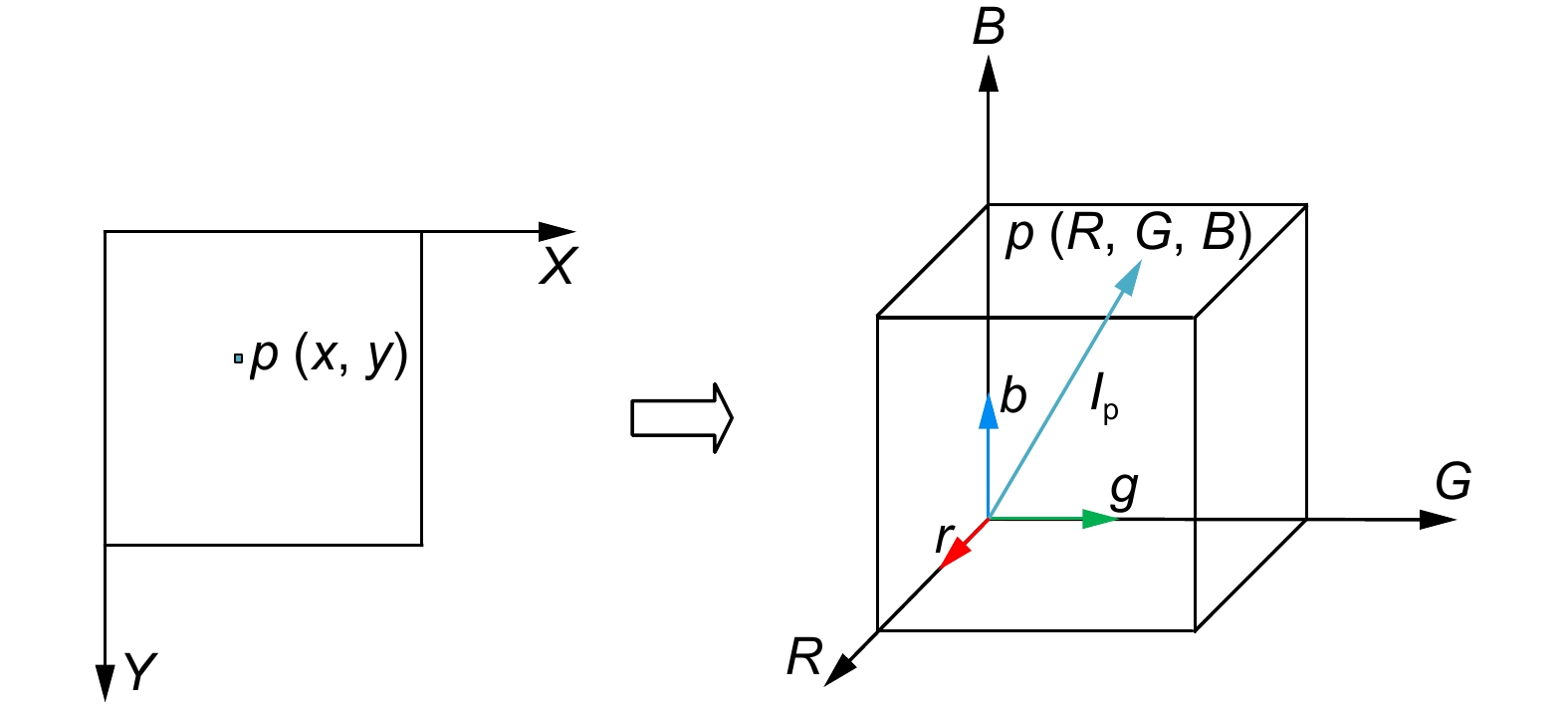
-
Key words:
- focusing evaluation /
- focus stacking image fusion /
- color space /
- depth of field /
- color image gradient /
- microscope
-
Overview
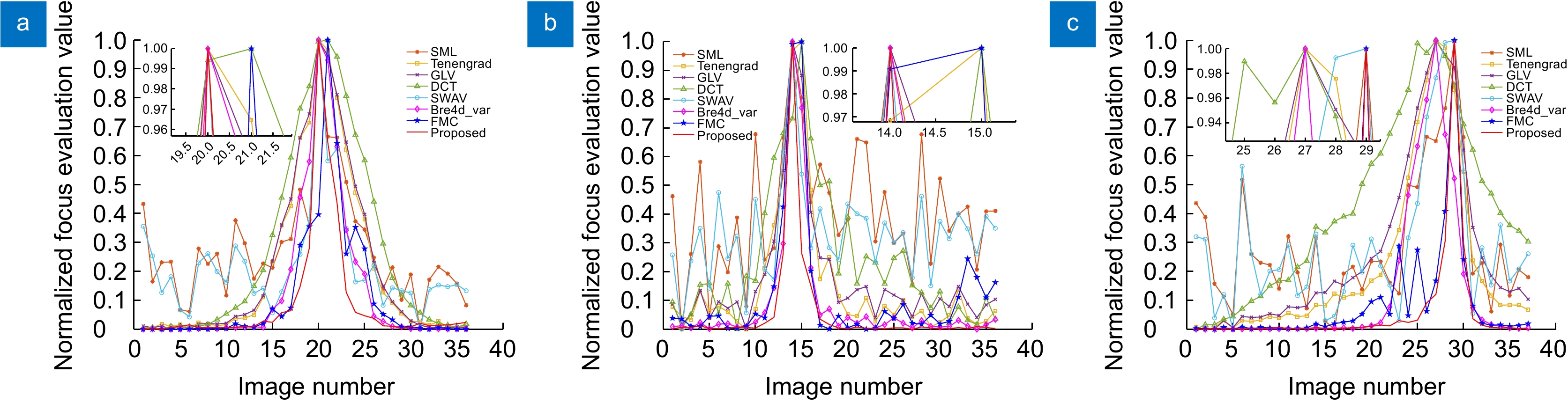
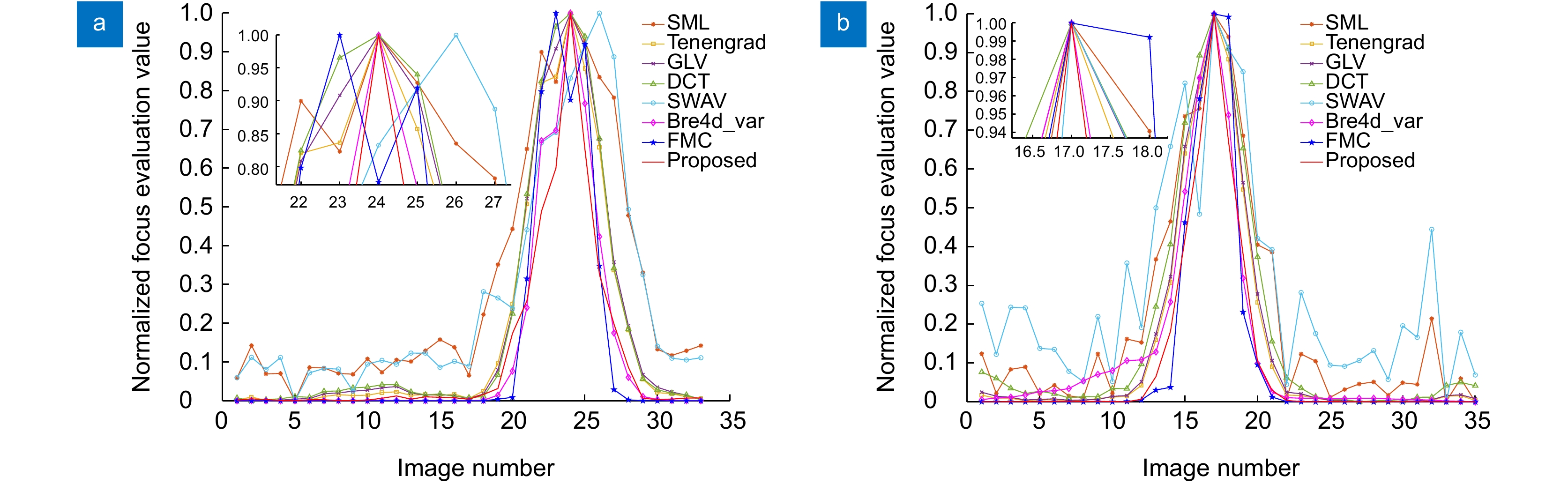
Overview: Focusing evaluation is the key to stacked focus extended depth of field imaging, and traditional spatial domain focusing evaluation algorithms mostly use the degree of drastic changes in image grayscale values as the basis for clarity evaluation. However, converting color images to grayscale images can result in multiple pixels with different color values being mapped onto the same grayscale pixels. This imprecise pixel mapping relationship can cause serious loss of image information, greatly affecting the accuracy of the focus evaluation algorithm, thereby reducing the overall accuracy of the stacked depth of field. Moreover, color images formed by this calculation method of stacked focus may yield results that are inconsistent with human visual characteristics. Based on the above issues, this article proposes a focus evaluation algorithm based on color vector space to more accurately and quickly obtain the pixel focus position of color image sequences and generate high-quality panoramic deep images. This algorithm extends the concept of gradients to vector functions, directly calculating color image gradients in the RGB color vector space, preserving image color information, and fully utilizing the correlation of various color channels. Compared to calculating gradients based on image grayscale and individual color components, it has higher accuracy and sensitivity. The average Manhattan distance between the central pixel and neighboring pixels in RGB space is used as the focus evaluation weight to enhance the sensitivity of the focusing part and reduce the evaluation value of the defocus part, effectively improving the resolution and anti-interference ability of the focusing evaluation function. This article selects seven focusing evaluation algorithms in the spatial domain, frequency domain, and statistics to conduct simulation comparison experiments and real environment comparison experiments with the proposed algorithm from two aspects: focusing evaluation function curve characteristics and stacked focus extended depth of field imaging performance. The experimental results show that compared with several selected focusing evaluation operators, the color vector space focusing evaluation algorithm achieved the best peak sensitivity, steepness, and gentle fluctuation indicators on three sets of simulated images and two sets of real microscopic images, and generated higher-quality panoramic depth images. Especially for the focus evaluation problem of images with a wide variety of colors and rich information, the proposed focus evaluation algorithm can accurately calculate the pixel focus value and has a significant overlapping fusion effect, which can meet the requirements of expanding the depth of field in microscopy and has practical application value.
-

-
图 8 全聚焦参考图和叠焦融合图对比。 (a)参考图;(b) Proposed融合图;(c) SML融合图;(d) Tenengrad融合图;(e) GLV融合图;(f) DCT融合图;(g) SWAV融合图;(h) Bre4d_var融合图;(i) FMC融合图
Figure 8. Comparison between all-in-focus reference image and stacked focal fusion image. (a) Reference image; (b) Proposed fusion image; (c) SML fusion image; (d) Tenengrad fusion image; (e) GLV fusion image; (f) DCT fusion image; (g) SWAV fusion image; (h) Bre4d_var fusion image; (i) FMC fusion image
表 1 仿真图像聚焦评价算法性能对比
Table 1. Performance comparison of focusing evaluation algorithms in simulated images
Algorithm Se Sp Sv Table Boxes Sideboard Table Boxes Sideboard Table Boxes Sideboard SML[15] 0.0314 0.4468 0.5089 0.1516 0.1523 0.1603 0.0407 0.0566 0.0434 Tenengrad[16] 0.0185 0.4089 — 0.1357 0.2730 — 0.0363 0.0279 — GLV[19] 0.0180 0.5020 — 0.1334 0.2747 — 0.0408 0.0275 — DCT[18] — 0.1468 — — 0.1099 — — 0.0557 — SWAV[17] 0.0434 0.6111 0.6479 0.1942 0.2135 0.1886 0.0446 0.0499 0.0469 Bre4d_var[25] 0.0430 0.9420 — 0.1995 0.3248 — 0.0275 0.0211 — FMC[21] — 1.6460 1.5413 — 0.3264 0.2090 — 0.0375 0.0652 Proposed 0.0565 1.7056 1.6963 0.3437 0.3562 0.3372 0.0138 0.0186 0.0144 表 2 有噪声仿真图像聚焦评价算法性能对比
Table 2. Performance comparison of focused evaluation algorithms for noisy simulated images
Algorithm Se Sp Sv Table Boxes Sideboard Table Boxes Sideboard Table Boxes Sideboard SML[15] 1.1429 0.3731 0.4045 0.0666 0.2073 0.1052 0.1109 0.1812 0.1343 Tenengrad[16] 0.2184 — — 0.1356 — — 0.0607 — — GLV[19] 0.2007 0.4734 — 0.1335 0.2033 — 0.0664 0.0441 — DCT[18] — — — — — — — — — SWAV[17] 1.1798 0.7384 0.4153 0.1649 0.2201 0.1892 0.0768 0.1150 0.1290 Bre4d_var[25] 0.3997 1.3292 — 0.2002 0.2381 — 0.0408 0.0275 — FMC[21] — — 2.2969 — — 0.5292 — — 0.0933 Proposed 1.5584 2.7864 2.3209 0.3450 0.5284 0.5303 0.0263 0.0266 0.0173 表 3 有参考的图像融合质量客观评价指标
Table 3. Objective evaluation indicators for image fusion quality with reference
Algorithm SSIM MSE/$ {10}^{-3} $ PSNR/dB Table Boxes Sideboard Table Boxes Sideboard Table Boxes Sideboard SML[15] 0.9807 0.9612 0.9125 1.193 1.454 6.003 34.447 32.321 26.989 Tenengrad[16] 0.9789 0.9493 0.9267 1.765 1.861 3.528 34.051 32.247 27.795 GLV[19] 0.9718 0.9533 0.9203 1.607 1.744 2.751 34.204 33.009 27.863 DCT[18] 0.9645 0.9237 0.9132 1.774 2.156 2.988 33.221 32.119 28.017 SWAV[17] 0.9709 0.9563 0.9518 1.151 1.575 5.272 34.691 33.151 27.552 Bre4d_var[25] 0.9791 0.9655 0.9549 0.986 1.460 2.765 34.835 33.127 30.355 FMC[21] 0.9798 0.9654 0.9591 0.929 1.470 2.525 35.091 33.098 30.749 Proposed 0.9824 0.9702 0.9634 0.856 1.404 2.254 35.447 33.297 30.827 表 4 显微图像中聚焦评价算法性能对比
Table 4. Performance comparison of focusing evaluation algorithms in microscopic images
Algorithm Se Sp Sv Wafer Wire Wafer Wire Wafer Wire SML[15] 0.069211 0.053887 0.131535 0.145214 0.038350 0.057453 Tenengrad[16] 0.164669 0.131634 0.195886 0.226235 0.020496 0.033131 GLV[19] 0.093996 0.099731 0.197076 0.214817 0.019743 0.036844 DCT[18] 0.063470 0.094970 0.198803 0.199834 0.017233 0.034720 SWAV[17] — 0.085089 — 0.124962 — 0.103253 Bre4d_var[25] 0.303990 0.352239 0.221513 0.196865 0.037180 0.038064 FMC[21] — 0.279225 — 0.220262 — 0.019089 Proposed 0.540521 0.490454 0.232581 0.285745 0.006771 0.013223 表 5 无参考的图像融合质量客观评价指标
Table 5. Objective evaluation indicators for image fusion quality without reference
Algorithm V $\overline G $ E Wafer Wire Wafer Wire Wafer Wire SML[15] 53.0300 56.6424 5.2157 7.3129 22.3707 24.0012 Tenengrad[16] 51.4233 55.8814 5.5069 7.2025 22.3595 23.3725 GLV[19] 51.5650 55.8463 5.0237 7.0928 22.5127 22.5874 DCT[18] 53.9928 55.0012 5.3671 7.0364 22.2967 23.1296 SWAV[17] 52.7727 56.3165 4.8681 6.9621 21.1231 23.5237 Bre4d_var[25] 53.5243 56.6069 5.6032 7.2851 22.3441 23.9367 FMC[21] 52.6920 55.9306 5.5443 7.3126 22.3583 23.9773 Proposed 54.2706 58.3882 5.7012 7.3877 23.3557 25.1254 -
参考文献
[1] 张子建, 徐欣, 王吉祥, 等. 光片荧光显微镜研究进展[J]. 光电工程, 2023, 50(5): 220045. doi: 10.12086/oee.2023.220045
Zhang Z J, Xu X, Wang J X, et al. Review of the development of light sheet fluorescence microscopy[J]. Opto-Electron Eng, 2023, 50(5): 220045. doi: 10.12086/oee.2023.220045
[2] 李晟, 王博文, 管海涛, 等. 远场合成孔径计算光学成像技术: 文献综述与最新进展[J]. 光电工程, 2023, 50(10): 230090. doi: 10.12086/oee.2023.230090
Li S, Wang B W, Guan H T, et al. Far-field computational optical imaging techniques based on synthetic aperture: a review[J]. Opto-Electron Eng, 2023, 50(10): 230090. doi: 10.12086/oee.2023.230090
[3] 张平, 吴嘉敏, 林靖宇, 等. 显微镜景深拓展技术研究[J]. 应用光学, 2014, 35(6): 1075−1082. doi: 10.5768/JAO201435.0605005
Zhang P, Wu J M, Lin J Y, et al. Extended depth of field in microscopy[J]. J Appl Opt, 2014, 35(6): 1075−1082. doi: 10.5768/JAO201435.0605005
[4] 王伟, 张露鹤, 傅天文. 基于波前编码的扩展景深短波红外成像系统[J]. 激光与光电子学进展, 2023, 60(10): 1011005. doi: 10.3788/LOP223156
Wang W, Zhang L H, Fu T W. Wavefront coding-based short-wave infrared imaging system for extended depth of field[J]. Laser Optoelectron Prog, 2023, 60(10): 1011005. doi: 10.3788/LOP223156
[5] 胡杰, 唐紫依, 蓝翔, 等. 基于相变材料Ge2Sb2Se4Te1的可切换边缘检测与聚焦成像超表面[J]. 光电工程, 2023, 50(8): 220284. doi: 10.12086/oee.2023.220284
Hu J, Tang Z Y, Lan X, et al. Switchable edge detection and imaging based on a phase-change metasurface with Ge2Sb2Se4Te1[J]. Opto-Electron Eng, 2023, 50(8): 220284. doi: 10.12086/oee.2023.220284
[6] Seyler T, Fratz M, Beckmann T, et al. Extending the depth of field beyond geometrical imaging limitations using phase noise as a focus measure in multiwavelength digital holography[J]. Appl Sci, 2018, 8(7): 1042. doi: 10.3390/app8071042
[7] 于春水, 卢荣胜. 叠焦大景深成像中的聚焦评价算子性能评估方法[J]. 激光与光电子学进展, 2022, 59(14): 1415027. doi: 10.3788/LOP202259.1415027
Yu C S, Lu R S. Performance evaluation method for focusing evaluation operator in superposed large depth imaging[J]. Laser Optoelectron Prog, 2022, 59(14): 1415027. doi: 10.3788/LOP202259.1415027
[8] Ali U, Mahmood M T. Energy minimization for image focus volume in shape from focus[J]. Pattern Recognit, 2022, 126: 108559. doi: 10.1016/J.PATCOG.2022.108559
[9] 梁鑫, 卿粼波, 要小涛, 等. 一种基于中频滤波的动态步长聚焦算法[J]. 智能计算机与应用, 2022, 12(1): 35−40. doi: 10.3969/j.issn.2095-2163.2022.01.007
Liang X, Qing L B, Yao X T, et al. A dynamic step-size focusing algorithm based on intermediate frequency filtering[J]. Intell Comput Appl, 2022, 12(1): 35−40. doi: 10.3969/j.issn.2095-2163.2022.01.007
[10] 熊锐, 顾乃庭, 徐洪艳. 一种适应多方向灰度梯度变化的自动对焦评价函数[J]. 激光与光电子学进展, 2022, 59(4): 0418001. doi: 10.3788/LOP202259.0418001
Xiong R, Gu N T, Xu H Y. An auto-focusing evaluation function adapted to multi-directional gray gradient change[J]. Laser Optoelectron Prog, 2022, 59(4): 0418001. doi: 10.3788/LOP202259.0418001
[11] 吕美妮, 玉振明. 基于DCT零系数和局部标准差的自动聚焦算法[J]. 激光技术, 2018, 42(1): 66−71. doi: 10.7510/jgjs.issn.1001-3806.2018.01.013
Lv M N, Yu Z M. Automatic focusing algorithm based on DCT coefficient of zero and local standard deviation[J]. Laser Technol, 2018, 42(1): 66−71. doi: 10.7510/jgjs.issn.1001-3806.2018.01.013
[12] Mahmood M T. Cross-scale focus measure aggregation in depth recovery of microscopic objects[J]. Microsc Res Tech, 2019, 82(6): 872−877. doi: 10.1002/jemt.23230
[13] Shim S O. Multidirectional focus measure for accurate three-dimensional shape recovery of microscopic objects[J]. Microsc Res Tech, 2022, 85(3): 940−947. doi: 10.1002/jemt.23963
[14] Pertuz S, Puig D, Garcia M A. Analysis of focus measure operators for shape-from-focus[J]. Pattern Recognit, 2013, 46(5): 1415−1432. doi: 10.1016/j.patcog.2012.11.011
[15] Jang H S, Yun G, Mutahira H, et al. A new focus measure operator for enhancing image focus in 3D shape recovery[J]. Microsc Res Tech, 2021, 84(10): 2483−2493. doi: 10.1002/jemt.23781
[16] 曹震, 巢渊, 徐魏, 等. 基于改进梯度加权的零件图像高精度聚焦方法[J]. 电子测量与仪器学报, 2023, 37(11): 132−142. doi: 10.13382/j.jemi.B2306767
Cao Z, Chao Y, Xu W, et al. High-precision focusing method for parts image based on improved gradient weighting[J]. J Electron Meas Instrum, 2023, 37(11): 132−142. doi: 10.13382/j.jemi.B2306767
[17] 王秀峰, 孙小伟, 王加科, 等. 余弦变换与拉普拉斯算子结合的聚焦评价方法[J]. 激光与光电子学进展, 2021, 58(24): 2410005. doi: 10.3788/LOP202158.2410005
Wang X F, Sun X W, Wang J K, et al. Focus measure operator combining cosine transform and Laplacian operator[J]. Laser Optoelectron Prog, 2021, 58(24): 2410005. doi: 10.3788/LOP202158.2410005
[18] Zhang Z, Liu Y, Xiong Z H, et al. Focus and blurriness measure using reorganized DCT coefficients for an autofocus application[J]. IEEE Trans Circuits Syst Video Technol, 2018, 28(1): 15−30. doi: 10.1109/TCSVT.2016.2602308
[19] 刘斌, 谯倩, 赵静, 等. 基于高频方差熵清晰度评价函数的聚焦三维测量方法[J]. 红外与激光工程, 2021, 50(5): 20200326. doi: 10.3788/IRLA20200326
Liu B, Qiao Q, Zhao J, et al. 3D profile measurement based on depth from focus method using high-frequency component variance weighted entropy image sharpness evaluation function[J]. Infrared Laser Eng, 2021, 50(5): 20200326. doi: 10.3788/IRLA20200326
[20] 翟永平, 周东翔, 刘云辉, 等. 聚焦函数性能评价指标设计及最优函数选取[J]. 光学学报, 2011, 31(4): 0418002. doi: 10.3788/AOS201131.0418002
Zhai Y P, Zhou D X, Liu Y H, et al. Design of evaluation index for auto-focusing function and optimal function selection[J]. Acta Opt Sin, 2011, 31(4): 0418002. doi: 10.3788/AOS201131.0418002
[21] Mutahira H, Ahmad B, Muhammad M S, et al. Focus measurement in color space for shape from focus systems[J]. IEEE Access, 2021, 9: 103291−103310. doi: 10.1109/ACCESS.2021.3098753
[22] Chatoux H, Richard N, Lecellier F, et al. Gradient in spectral and color images: from the Di Zenzo initial construction to a generic proposition[J]. J Opt Soc Am A, 2019, 36(11): C154−C165. doi: 10.1364/JOSAA.36.00C154
[23] Di Zenzo S. A note on the gradient of a multi-image[J]. Comput Vision Graphics Image Process, 1986, 33(1): 116−125. doi: 10.1016/0734-189X(86)90223-9
[24] Koschan A, Abidi M. Detection and classification of edges in color images[J]. IEEE Signal Process Mag, 2005, 22(1): 64−73. doi: 10.1109/MSP.2005.1407716
[25] 董正琼, 杨清锋, 黄贤文, 等. 基于梯度方差聚焦评价的三维显微测量方法[J]. 激光与光电子学进展, 2024. https://doi.org/10.3788/LOP232028.
Dong Z Q, Yang Q F, Huang X W, et al. Three-dimensional microscopic measurement method based on gradient variance focus evaluation[J]. Laser Optoelectron Prog, 2024. https://doi.org/10.3788/LOP232028.
[26] Honauer K, Johannsen O, Kondermann D, et al. A dataset and evaluation methodology for depth estimation on 4D light fields[C]//13th Asian Conference on Computer Vision, 2017: 19–34. https://doi.org/10.1007/978-3-319-54187-7_2.
[27] 张雅玲, 吉琳娜, 杨风暴, 等. 基于余弦相似性的双模态红外图像融合性能表征[J]. 光电工程, 2019, 46(10): 190059. doi: 10.12086/oee.2019.190059
Zhang Y L, Ji L N, Yang F B, et al. Characterization of dual-mode infrared images fusion based on cosine similarity[J]. Opto-Electron Eng, 2019, 46(10): 190059. doi: 10.12086/oee.2019.190059
[28] Li Y, Li X Y, Wang J Q, et al. Multi-focus image fusion for microscopic depth-of-field extension of waterjet-assisted laser processing[J]. Int J Adv Manuf Technol, 2024, 131(3-4): 1717−1734. doi: 10.1007/s00170-024-13118-5
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: