E-mail Alert
RSS
-
摘要
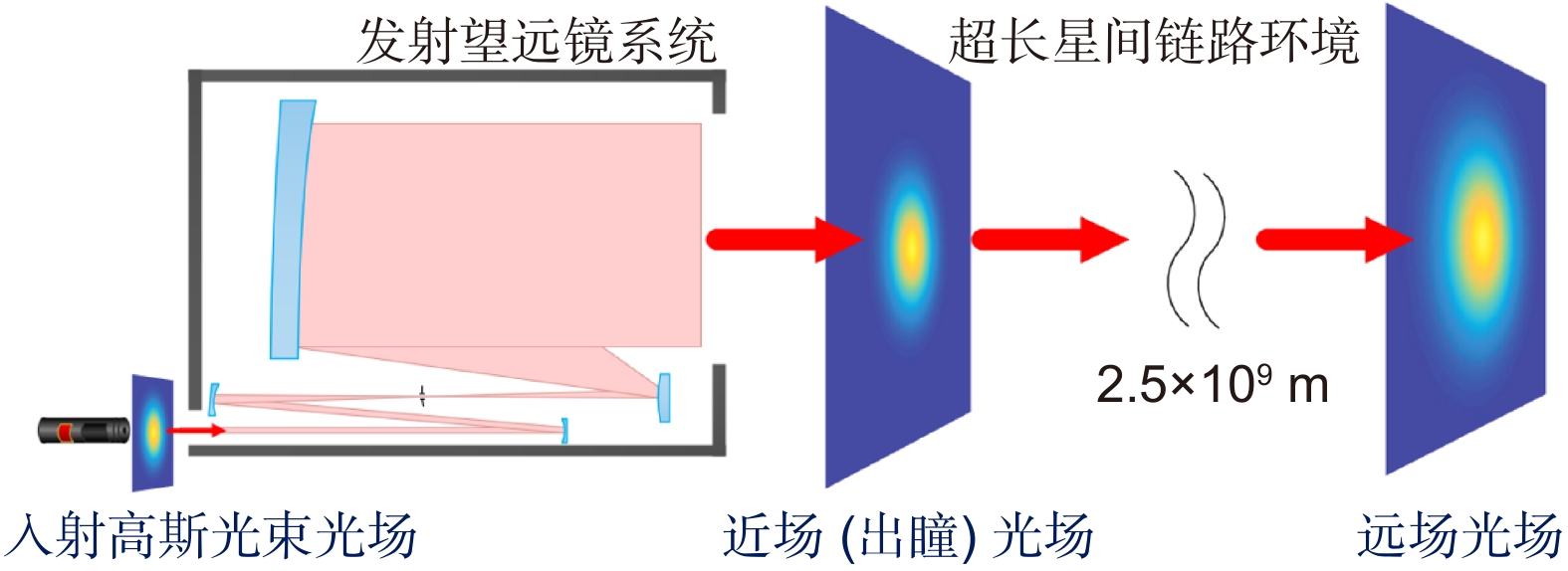
文章主要围绕空间引力波探测中超长空间链路传输部分进行介绍，概述了目前国内外星间传输仿真时采用的计算方法，以及指向抖动引起的相位噪声分析方法。相较于地基引力波探测，空间引力波探测可以有效降低噪声，增加干涉臂长度，从而实现更高精度、更低频率的探测。在长达数百万公里的传输距离，以及皮米量级数值模拟的精度要求下，需要考虑指向角变化引起的相位噪声。研究表明，在2.5×109 m的传输距离下，离焦和像散是影响指向抖动噪声的主要像差。通常情况下，相位驻点位置与原点位置存在一定偏离，需要对望远镜角度进行调整，才能使相位噪声最小化。在相位驻点位置进行引力波探测，可以有效降低相位噪声，并降低望远镜出瞳波前的质量要求。而大的离焦像差与小的彗差可以使相位驻点接近光轴，提高接收到的激光功率。
Abstract
This paper mainly introduces the development of space gravitational wave transmission and laser propagation in space gravitational wave detection. We profile the calculation methods used in the simulation of laser propagation and jitter noise in space-based laser interferometry. Compared with ground detection, space gravitational wave detection can effectively reduce noise and increase the length of the interference arm to realize high-precision gravitational wave detection. Under the distance of millions of kilometers and the precision requirements of the picometer level, it is necessary to consider the phase noise caused by pointing jitter with the telescope. Research has shown that defocus and astigmatism are the main aberrations affecting jitter noise at a distance of 2.5×109 m. There is a deviation between the phase stationary point and the origin position. To minimize the phase noise, the telescope angle needs to be adjusted. The gravitational wave detection at the phase stationary point can effectively reduce the phase noise and the requirements of the telescope exit pupil wavefront RMS. The large defocus and small coma can make the phase stationary point close to the optical axis and increase the received laser power.
-
Key words:
- gravitational wave detection /
- space propagation /
- jitter noise /
- phase stationary point
-
Overview
Overview: Compared with ground gravitational wave detection, space gravitational wave detection can avoid the low-frequency noise caused by ground vibration and the interference of climate change on the transmission. The space environment can also greatly increase the arm length of laser interference to achieve high-precision gravitational wave detection. However, the ultra-long inter-satellite link transmission distance also puts forward extremely high requirements for pointing accuracy and dynamic measurement capabilities. At a transmission distance of millions of kilometers, the detection accuracy needs to reach the picometer level.
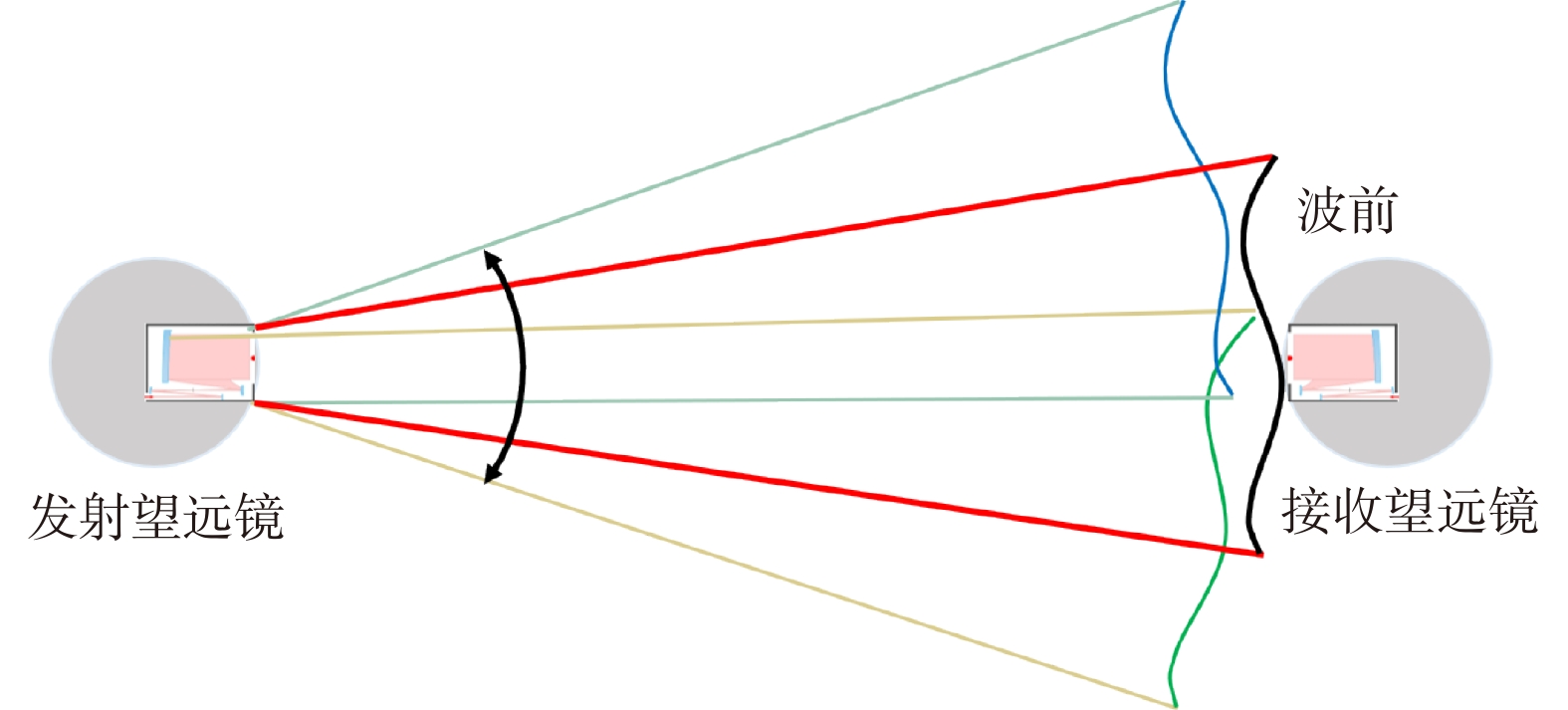
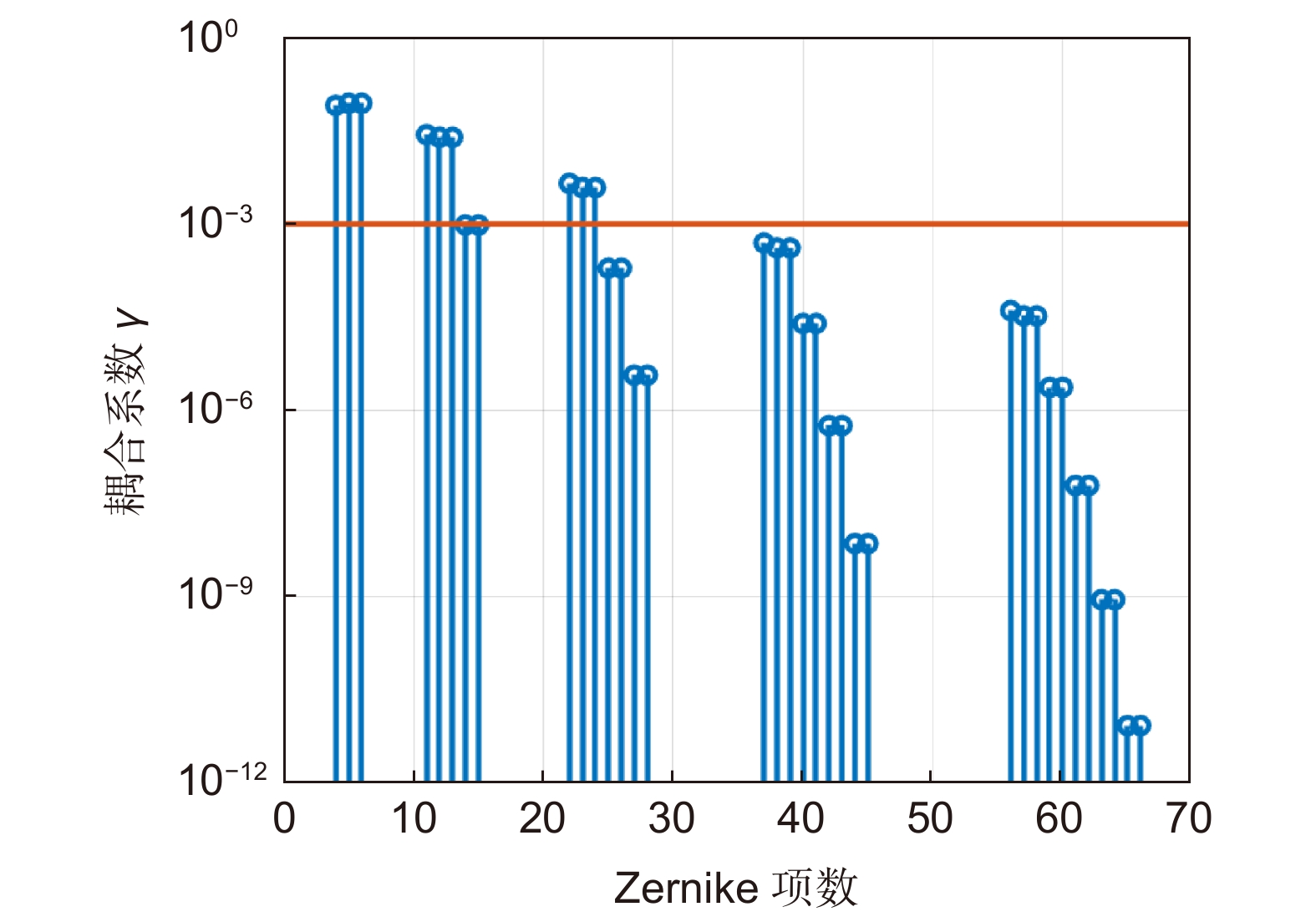
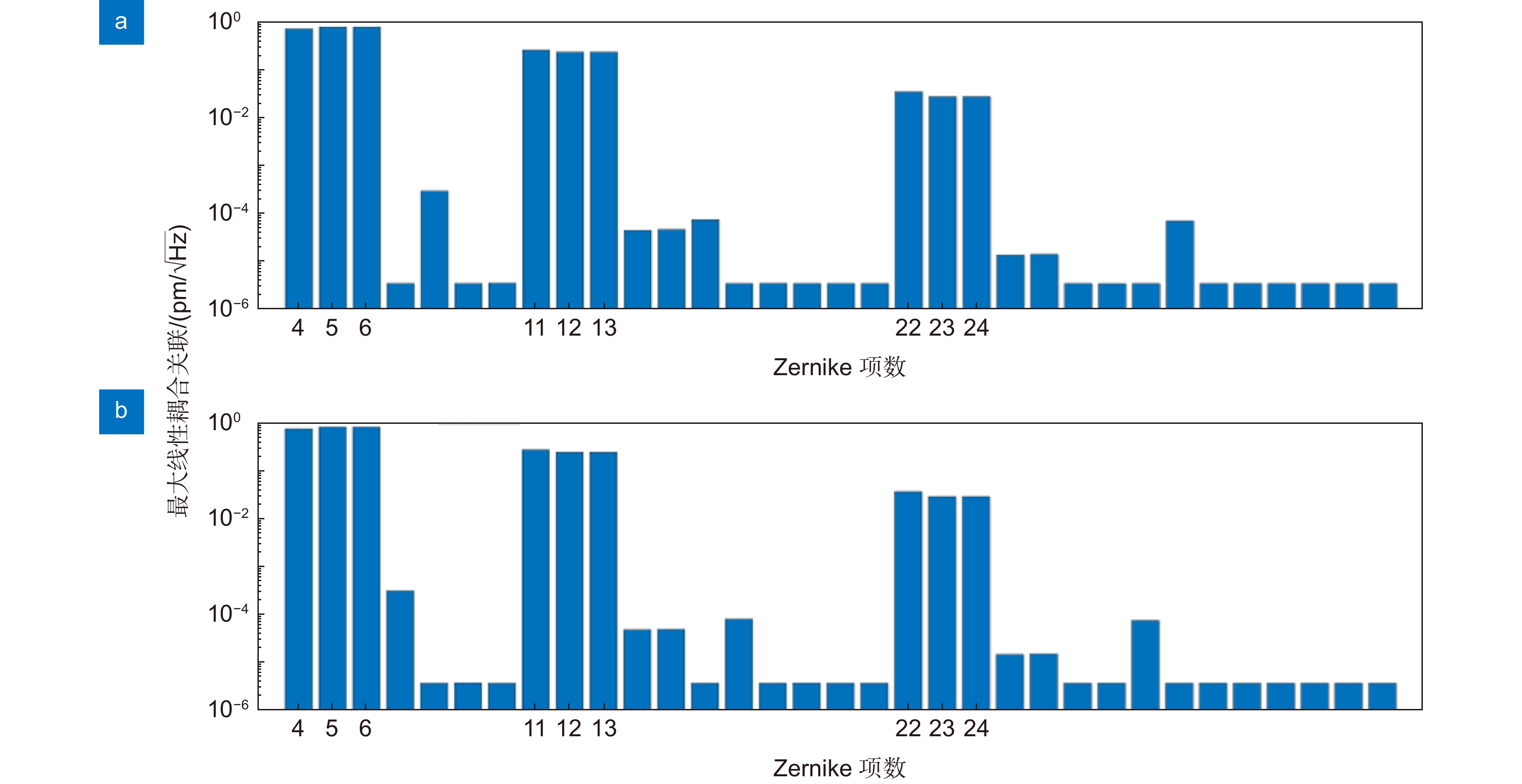
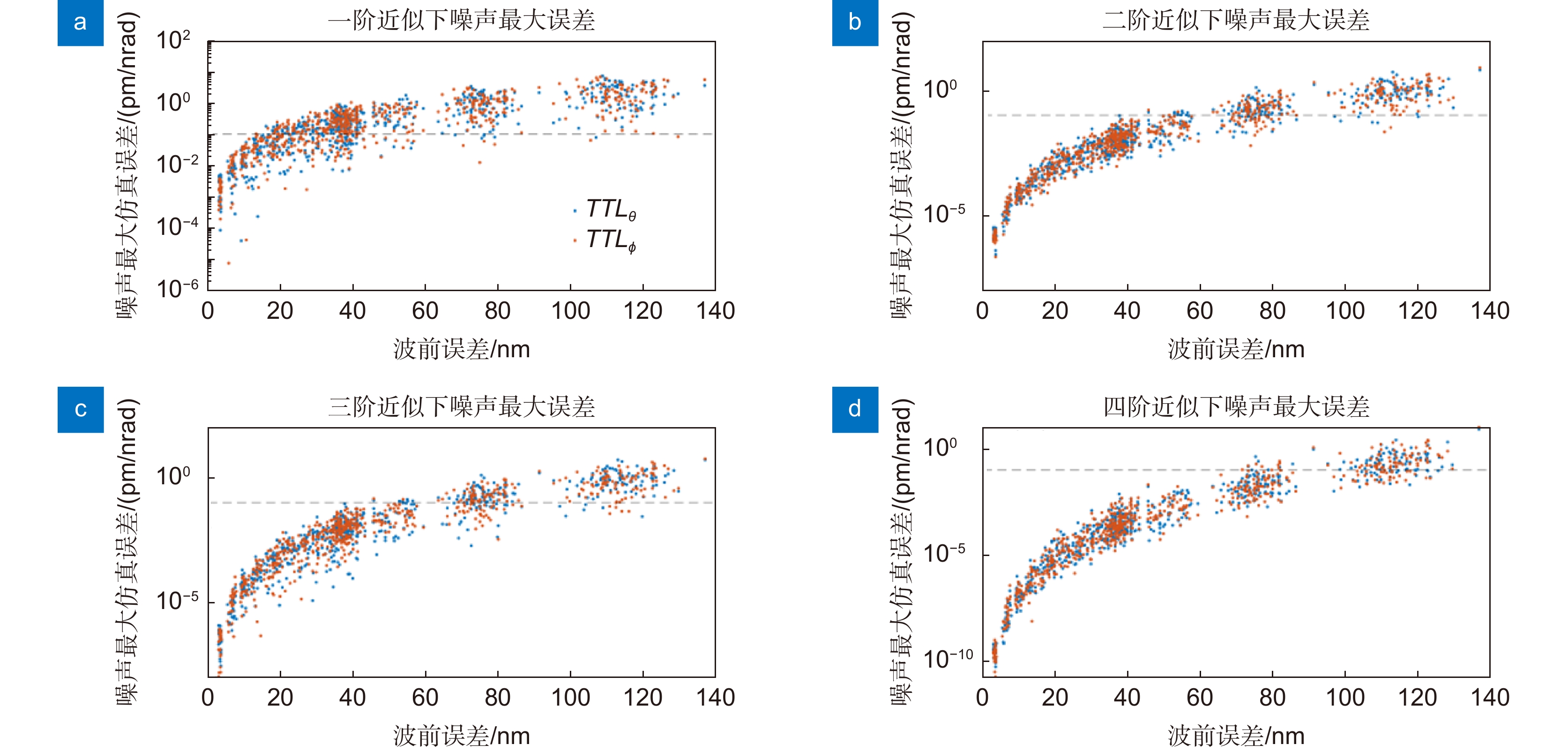
To minimize the influence of noises on the detection, we must simulate the system with high precision. The simulation of inter-satellite transmission can be realized by Hermite Gaussian beam fitting, Fourier transform or numerical integration. The plasma has little effect on inter-satellite transmission under most circumstances. It will thus not affect the detection. Pointing jitter noise is the focus of research in inter-satellite transmission. In the actual system, there are aberrations in the exit pupil wavefront of the telescope, so the far-field wavefront is no longer close to the ideal spherical wave. An angle offset of 10 nrad will cause a position offset of tens of meters in the far field. In the analysis, the far-field origin is usually taken as the object, and the phase part of the telescope exit pupil complex amplitude is expanded to simplify the model in a Taylor series. The coupling coefficients between the far field and the exit pupil Zernike aberration of the telescope can be calculated by the integral calculation or the least square fitting. To satisfy the simulation accuracy of the picometer level, the Taylor expansion and the coupling coefficients should retain at least the second-order term.
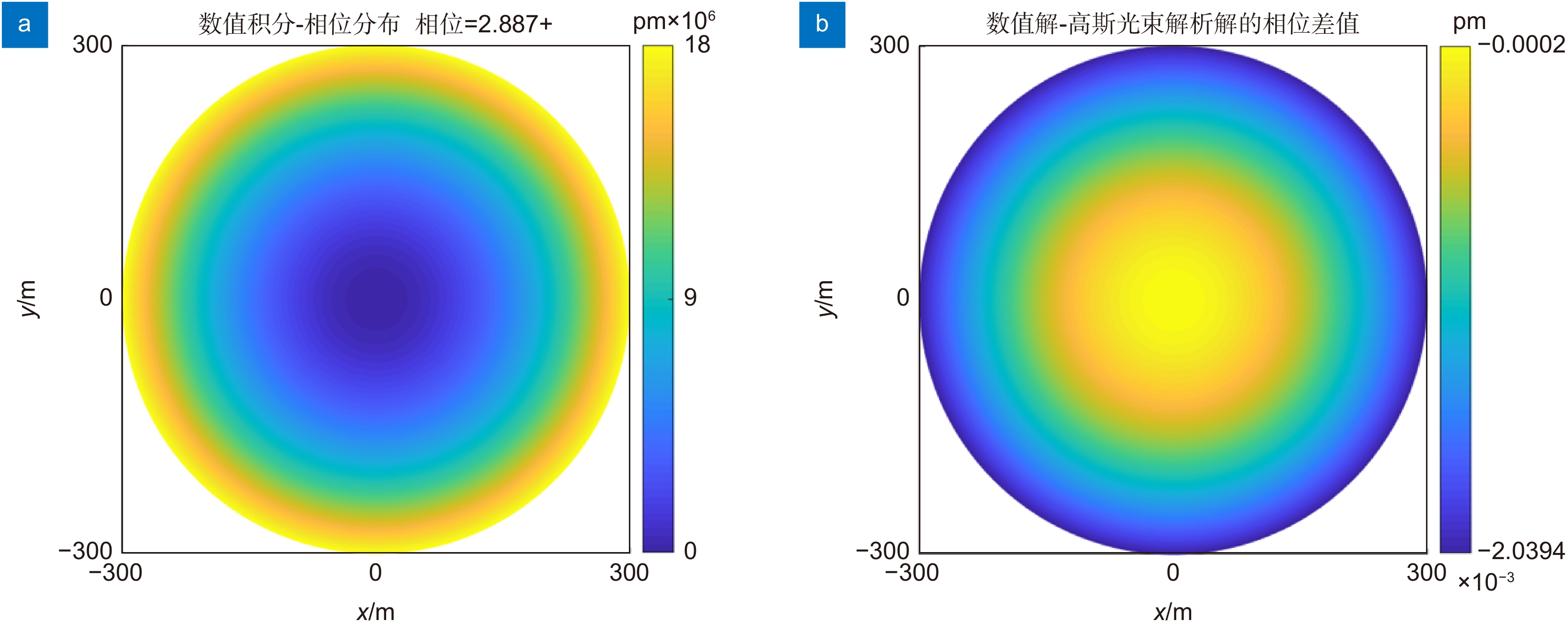
Taking the LISA system as a reference, the phase noise of the inter-satellite transmission needs to be less than 1 pm. Research has shown that the defocus and the astigmatism are the main aberrations affecting jitter noise at a distance of 2.5×109 m. There is a deviation between the phase stationary point and the origin position. To minimize the phase noise, the telescope angle needs to be adjusted. The gravitational wave detection at the phase stationary point can effectively reduce the phase noise and the requirements of the telescope exit pupil wavefront RMS. The large defocus and small coma can make the phase stationary point close to the optical axis and increase the received laser power.
-
-
图 4 数值积分与高斯光束解析解相位对比
Figure 4. The comparison between numerical integration method and analytical expression of Gaussian beam
图 6 700 nrad静态角下，耦合系数γ与泽尼克项数的关联
Figure 6. The correlation between the coupling coefficient γ and Zernike indices at 700 nrad static angle.
-
参考文献
[1] Einstein A. Approximative integration of the field equations of gravitation[J]. Sitzungsber Preuss Akad Wiss, 1916, 1916: 688−696.
[2] Taylor J H, Weisberg J M. A new test of general relativity - gravitational radiation and the binary pulsar PSR 1913+16[J]. Astrophys J, 1982, 253: 908−920. doi: 10.1086/159690
[3] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Phys Rev Lett, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102
[4] 黄玉梅, 王运永, 汤克云, 等. 引力波理论和实验的新进展[J]. 天文学进展, 2007, 25(1): 58−73. doi: 10.3969/j.issn.1000-8349.2007.01.006
Huang Y M, Wang Y Y, Tang K Y, et al. The new development of gravitational waves theory and detection[J]. Prog Astron, 2007, 25(1): 58−73. doi: 10.3969/j.issn.1000-8349.2007.01.006
[5] 李建聪, 林宏安, 罗佳雄, 等. 空间引力波探测望远镜光学系统设计[J]. 中国光学(中英文), 2022, 15(4): 761−769. doi: 10.37188/CO.2022-0018
Li J C, Lin H A, Luo J X, et al. Optical design of space gravitational wave detection telescope[J]. Chin Opt, 2022, 15(4): 761−769. doi: 10.37188/CO.2022-0018
[6] 罗子人, 白姗, 边星, 等. 空间激光干涉引力波探测[J]. 力学进展, 2013, 43(4): 415−447. doi: 10.6052/1000-0992-13-044
Luo Z R, Bai S, Bian X, et al. Gravitational wave detection by space laser interferometry[J]. Adv Mech, 2013, 43(4): 415−447. doi: 10.6052/1000-0992-13-044
[7] 位希雅,宋奇林,杨金生,等. 基于夏克-哈特曼传感器的星载望远镜波前测量技术研究[J]. 光电工程, 2023, 50(11): 230215. doi: 10.12086/oee.2023.230215
Wei X Y, Song Q L, Yang J S, et al. Research on wavefront measurement technology of space-based telescope using Shack-Hartmann wavefront sensor[J]. Opto-Electron Eng, 2023, 50(11): 230215. doi: 10.12086/oee.2023.230215
[8] Danzmann K, The LISA Study Team. LISA: laser interferometer space antenna for gravitational wave measurements[J]. Class Quantum Grav, 1996, 13(11A): A247. doi: 10.1088/0264-9381/13/11A/033
[9] Danzmann K, The LISA Study Team. LISA - An ESA cornerstone mission for a gravitational wave observatory[J]. Class Quantum Grav, 1997, 14(6): 1399. doi: 10.1088/0264-9381/14/6/002
[10] 王智, 沙巍, 陈哲, 等. 空间引力波探测望远镜初步设计与分析[J]. 中国光学, 2018, 11(1): 131−151. doi: 10.3788/co.20181101.0131
Wang Z, Sha W, Chen Z, et al. Preliminary design and analysis of telescope for space gravitational wave detection[J]. Chin Opt, 2018, 11(1): 131−151. doi: 10.3788/co.20181101.0131
[11] 倪维斗, 门金瑞, 梅晓红, 等. ASTROD空间引力波探测优化方案: ASTROD-GW[C]//中国宇航学会深空探测技术专业委员会第六届学术年会暨863计划“深空探测与空间实验技术”重大项目学术研讨会, 三亚, 2009.
[12] Bender P L. Additional astrophysical objectives for LISA follow-on missions[J]. Class Quantum Grav, 2004, 21(5): S1203. doi: 10.1088/0264-9381/21/5/120
[13] Corbin V, Cornish N J. Detecting the cosmic gravitational wave background with the Big Bang Observer[J]. Class Quantum Grav, 2006, 23(7): 2435. doi: 10.1088/0264-9381/23/7/014
[14] Luo J, Chen L S, Duan H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Class Quantum Grav, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010
[15] Hu W R, Wu Y L. The Taiji Program in Space for gravitational wave physics and the nature of gravity[J]. Natl Sci Rev, 2017, 4(5): 685−686. doi: 10.1093/nsr/nwx116
[16] 王芸, 林栩凌, 郭忠凯, 等. 空间应用激光干涉测距技术发展综述[J]. 航天返回与遥感, 2021, 42(2): 68−78. doi: 10.3969/j.issn.1009-8518.2021.02.008
Wang Y, Lin X L, Guo Z K, et al. Review of high precision distance metrology in space applications[J]. Spacecr Recovery Remote Sens, 2021, 42(2): 68−78. doi: 10.3969/j.issn.1009-8518.2021.02.008
[17] 胡新春. 基于天琴的大质量双黑洞引力波数据处理研究[D]. 武汉: 华中科技大学, 2021.
Hu X C. Gravitational wave data analysis of massive black hole binaries for TianQin[D]. Wuhan: Huazhong University of Science and Technology, 2021.
[18] 罗俊, 艾凌皓, 艾艳丽. 天琴计划简介[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
Luo J, Ai L H, Ai Y L. A brief introduction to the TianQin project[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
[19] 高瑞弘, 刘河山, 罗子人, 等. 太极计划激光指向调控方案介绍[J]. 中国光学, 2019, 12(3): 425−431. doi: 10.3788/CO.20191203.0425
Gao R H, Liu H S, Luo Z R, et al. Introduction of laser pointing scheme in the Taiji program[J]. Chin Opt, 2019, 12(3): 425−431. doi: 10.3788/CO.20191203.0425
[20] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测"太极计划"及"太极1号"在轨测试[J]. 深空探测学报, 2020, 7(1): 3−10. doi: 10.15982/j.issn.2095-7777.2020.20191230001
Luo Z R, Zhang M, Jin G, et al. Introduction of Chinese space-borne gravitational wave detection program “Taiji” and “Taiji-1” satellite mission[J]. J Deep Space Explor, 2020, 7(1): 3−10. doi: 10.15982/j.issn.2095-7777.2020.20191230001
[21] 赵梦阳, 高瑞弘, 张强涛, 等. 太极计划激光链路构建地面模拟控制系统研究[J]. 中国激光, 2023, 50(19): 1906003.
Zhao M Y, Gao R H, Zhang Q T, et al. Research on simulated laser link construction control system of Taiji program[J]. Chin J Lasers, 2023, 50(19): 1906003.
[22] Kenny F, Devaney N. Beam propagation simulations for LISA in the presence of telescope aberrations[J]. Class Quantum Grav, 2021, 38(3): 035010. doi: 10.1088/1361-6382/abccdd
[23] Weaver A, Fulda P, Mueller G. Analytic HG-mode propagation through circular apertures with Zernike phase offset[J]. OSA Continuum, 2020, 3(7): 1891−1916. doi: 10.1364/OSAC.394476
[24] Lu L F, Liu Y, Duan H Z, et al. Numerical simulations of the wavefront distortion of inter-spacecraft laser beams caused by solar wind and magnetospheric plasmas[J]. Plasma Sci Technol, 2020, 22(11): 115301. doi: 10.1088/2058-6272/abab69
[25] Noll R J. Zernike polynomials and atmospheric turbulence[J]. J Opt Soc Am, 1976, 66(3): 207−211. doi: 10.1364/JOSA.66.000207
[26] Bender P L. Wavefront distortion and beam pointing for LISA[J]. Class Quantum Grav, 2005, 22(10): S339−S346. doi: 10.1088/0264-9381/22/10/027
[27] Sasso C P, Mana G, Mottini S. Coupling of wavefront errors and jitter in the LISA interferometer: far-field propagation[J]. Class Quantum Grav, 2018, 35(18): 185013. doi: 10.1088/1361-6382/aad7f5
[28] Sasso C P, Mana G, Mottini S. Telescope jitters and phase noise in the LISA interferometer[J]. Opt Express, 2019, 27(12): 16855−16870. doi: 10.1364/OE.27.016855
[29] Vinet J Y, Christensen N, Dinu-Jaeger N, et al. Numerical solutions for phase noise due to pointing jitter with the LISA telescope[J]. J Phys Commun, 2020, 4(4): 045005. doi: 10.1088/2399-6528/ab852e
[30] Ming M, Jiang Y Z, Zhang J Y, et al. Analysis on the coupling effect of wavefront distortion and pointing misalignment in space laser interferometry[J]. Class Quantum Grav, 2021, 38(19): 195010. doi: 10.1088/1361-6382/ac1be2
[31] 赵亚. 面向空间激光干涉引力波探测的星间干涉链路中抖动光程耦合噪声研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2021.
Zhao Y. The research on the tilt to length coupling noise in inter-satellite interference link for the space-based gravitational wave detection[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2021.
[32] Weaver A J, Mueller G, Fulda P J. Wavefront error based tilt-to-length noise analysis for the LISA transmitted beam[J]. Class Quantum Grav, 2022, 39(19): 195016. doi: 10.1088/1361-6382/ac8a88
[33] Tao Y Z, Jin H B, Wu Y L. Estimation of far-field wavefront error of tilt-to-length distortion coupling in space-based gravitational wave detection[J]. Chin Phys B, 2023, 32(2): 024212. doi: 10.1088/1674-1056/aca9c5
[34] Xiao Q, Duan H Z, Ming M, et al. The analysis of the far-field phase and the tilt-to-length error contribution in space-based laser interferometry[J]. Class Quantum Grav, 2023, 40(6): 065009. doi: 10.1088/1361-6382/acbadc
-
访问统计
下载:
点击扫一扫
图(9)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
